Conformance Checking of Real-Time Models

Abstract

We compare conformance checking based on symbolic execution to conformance checking via bounded model checking. The application context is fault-based test case generation, focusing on real-time faults. The existing bounded model checking approach is performed on timed automata. It supports time-relevant mutation operators and a preprocessing functionality for removing silent transitions and non-determinism. The new symbolic execution approach is performed on timed action systems, which are a novel variant of Back’s action systems augmented by clock variables and real-time semantics. It supports the same set of mutation operators, silent transitions, non-determinism and data variables. We show how to encode timed automata as timed action systems and perform experiments on three variants of a car alarm system, to investigate the influence of silent transitions, non-determinism and data variables. Both approaches rely on the SMT solver Z3.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Time-critical systems can often be far more complex than their untimed counterparts. Due to this raised complexity, they require an especially thorough verification and validation. For example, in the automotive domain, companies rely heavily on testing to ensure the quality of their systems. Manual test generation is a tedious and error-prone process, without guarantee of capturing all relevant parts of the system. Model-based test-case generation deals with these problems by automatically generating test cases on the basis of a test model. The tests are usually generated based on coverage criteria, like e.g., state or transition coverage of the test model. Model-based mutation testing is a fault-based approach: we define a set of fault models, so called mutation operators, that are systematically applied to the test model, creating a set of faulty models, called mutants. The main part of the test-case generation consists of performing a conformance check between the original test model and its mutants. In case of non-conformance, we build a test case covering the shortest path from the initial state to the conformance violation. Thus, we gain a test suite covering all non-equivalent mutants, able to detect every faulty implementation that implements any of the specified fault models. In this paper we present two methods for this conformance check, based on two types of timed models: the first approach is done via bounded model checking and performed on timed automata. This approach was already published [5]. The second new one is based on symbolic execution and works on timed action systems. We define a novel variant of timed action systems closely related to timed automata, giving them a trace based semantics. We compare both approaches in terms of runtime, applied to different models of a car alarm system. Given that the mutation operators might yield hundreds of mutants, the performance of the conformance check is crucial.

The present paper, written for the Festschrift in honour of Frank S. de Boer, touches upon three of his active research topics: symbolic execution [1, 30], real-time behaviour [8, 12, 18], and testing [23, 24, 30]. Our study indicates that symbolic execution is a promising candidate for automatically analysing real-time behaviour. As it has been pointed out [7], this is especially relevant to expressive modelling languages, like e.g. Real-Time ABS [8, 12].

Running Example. We will illustrate the different approaches on a car alarm system, that was provided by Ford as a use case for the past EU FP7 project MOGENTES (http://www.mogentes.eu), and was since used as an internal benchmark for various publications [3, 5]. The car alarm system is illustrated as a timed automata in Fig. 1: it provides the user with the options to open, close, lock and unlock the doors. If the doors stay locked and closed for 20 s, the system is armed. Forcing the doors open, without unlocking them first, will cause the activation of the sound and flash alarm. The alarms will deactivate either if the doors are unlocked, or after 30 and 300 s, respectively.

Fig. 1.

Car alarm system: correct specification (left) and a mutant (right).

The remainder of the paper is structured as follows: first, in Sect. 2 we will give some preliminaries, covering timed automata, model-based mutation testing and bounded model checking. Then, in Sect. 3 we will introduce timed action systems, giving them symbolic trace semantics and explaining how to apply a symbolic conformance check based on the Symbolic Timed Input Output Conformance (stioco) relation. In Sect. 4 we will present our experimental results, comparing symbolic execution to the bounded model checking approach. Finally, in Sect. 5 we discuss related work and conclude the paper in Sect. 6.

2 Preliminaries

2.1 Timed Automata

Timed Automata (TA) [9] are a widely used formalism for specifying time critical systems. They are used in several areas, as for instance schedulability analysis [18]. Basic TA are finite state machines, augmented by clocks to measure the passage of time. Time is considered to only pass in states, and may be restricted by invariants, enforcing that the states are left before the invariants are broken. Transitions are considered to take zero time. They can be restricted by clock constraints in their guard, and each transition may be linked to a set of clocks that are reset upon passage of the transition. The automaton in Fig. 1 (left) contains 5 clocks. The transition from $q_1$ to $q_2$ resets the clock c. In $q_2$ the passage of time is restricted by the invariant $c\le 20$ and the transition from $q_2$ to $q_3$ is restricted by the time guard $c==20$.

The experiments conducted for this work were applied on three classes of Timed Automata with Inputs and Outputs, meaning that the set of observable actions is spilt into two disjoint sets of inputs (denoted by a question mark) and outputs (denoted by an exclamation mark):

• 1. Deterministic Timed Automata. We consider a TA to be deterministic, if it does not contain silent transitions and for all transitions with same source state and same action label, their guards cannot be satisfied simultaneously.

• 2. Non-Deterministic Timed Automata with Silent Transitions. Silent transitions are considered internal actions, that are not observable to the user. Both, non-determinism and silent transitions cannot be removed in general [11]. Recently, we presented a bounded approach for silent transition removal and determinization [22]: it unfolds the automaton up to a certain depth and determinizes it, creating a deterministic tree-shaped TA.

• 3. Timed Automata with Data Variables. Another extension to timed automata is the support for data variables. These are integer variables, that can be used both in guards and assignments of transitions. They can also be used as parameters for transitions, where the parameters for input transitions are chosen by the user, and all other parameters are chosen by the system.

2.2 Model-Based Mutation Testing

As already stated by Dijkstra [14], one of the main downsides of testing is the fact that it can never prove the complete absence of bugs in a system under test (SUT). Model-based mutation testing addresses this problem, by generating tests able to prove the absence of certain kinds of bugs in deterministic SUTs.

The workflow of model-based mutation testing is illustrated in Fig. 2. It starts from the requirements to produce a test model (top left corner), that is processed by the mutation tool (according to a set of mutation operators), to create a set of mutated models (top right corner). For a mutant example see Fig. 1. Next, each of the model mutants is checked for conformance to the test model. If no conformance violation is detected, the mutant is considered equivalent, indicating that the concrete mutation did not propagate to any visible failure. However, if non-conformance is detected, the mutation introduced a fault with observable consequences. In that case, we produce an abstract test case, covering the shortest path to the observed conformance violation. The test suite consisting of all produced abstract test cases is then passed on to the test case executer. There, the test cases are concretized and executed on the SUT. If a deterministic SUT shows the same faulty behaviour as any of the mutants, the corresponding test case is guaranteed to detect the fault and returns the verdict fail. If the SUT conforms to the test model, a pass verdict is issued.

The conformance relation may vary: in untimed systems, the Input Output Conformance (ioco) by Tretmans [25] is widely used. The intuition behind ioco is that for all traces of the specification, the outputs of the implementation (in our case, the mutants) must be a subset of the outputs of the specification. Several extensions of ioco to real-time exist. For our bounded-model checking of TAs, we use the Timed Input Output Conformance (tioco) introduced by Krichen & Tripakis [19]. Here, time is seen as output. For the theory and first experimental results on model-based mutation testing with TA we refer to [5].

For the symbolic execution approach on timed action systems, we rely on a symbolic conformance relation. The first Symbolic Input Output Conformance (sioco) relation was introduced by Frantzen et al. [16]. Von Styp et al. [26] expanded the relation by adding support for time, defining the sioco relation for Symbolic Timed Automata (STA). We use a very similar conformance relation to stioco, based on timed action systems. Additionally we also support silent transitions, which are not handled by Von Styp. et al. The symbolic conformance check for untimed action systems was recently published [6].

Together with the Austrian Institute of Technology, we developed a model-based mutation testing tool-chain working on UML-models, Action Systems and TA (www.momut.org). Timed action systems are not yet officially supported.

Fig. 2.

Model-based mutation testing [4]

2.3 Bounded Model Checking

In our first work on model-based mutation testing for TA [5], we proposed a conformance check via bounded model checking. We used tioco as a conformance relation and showed how to encode the conformance-check as a language inclusion problem. Via bounded model checking, we searched for a state where the mutant can perform an output (since we check tioco conformance, this includes the passage of time) that is not allowed by the specification.

We bounded the language inclusion by a bound k, and encoded it as an SMT-formula. This formula is split into two parts: the first part is the reachability check, which contains the correct step relation for k steps, of both the specification and the mutants. It calculates all states that are reachable within k steps. The second part performs the conformance check for all states that are found by the reachability. The conformance formula is a conjunction of a valid step in the mutant (taking only the outputs into account) and the negation of all valid steps of the specification. Thus, the formula is satisfiable, if the mutant is at some point able to generate an output that is not allowed by the specification. If that happens, the SMT solver returns a concrete model that serves as a counter example for the conformance.

This counter example can then be transformed into a real test case by adding verdicts and symbolic time constraints. We use the SMT solver Z3 and its feature for incremental solving.

2.4 Conventions

Generally, we assume the usage of two-sorted logic, where one sort d is defined for discrete data and the other sort t for time-related formulas and terms. We further require that the constant $0_t$ of sort t and the binary addition $+_t$ for pairs of sort t must be defined. In addition, the relations $\le , <, =, > \ge$ must be defined for all pairs of sorts d and t, i.e. any comparison between time and data must be possible. Note that in practise, we allow for more sorts in our models, such as user-defined enumeration sorts, but we use a type checker to ensure that only meaningful comparisons are performed.

We will denote the set of terms containing variables from a set X by $Te(X)$ and first-order formulas containing free variables from the same set by $Fr(X)$. The function $free (\varphi )$ maps a formula $\varphi$ to the set of all free variables in $\varphi$.

The set $CC(X, Y)$ denotes the set of clock constraints, with clock variables in X and constraint operands in $Y \cup Te(\emptyset )$. A clock constraint is of the form $x \otimes y$, with $x \in X$, $y \in Y \cup Te(\emptyset )$ and $\otimes \in \{\le , <, =, > \ge \}$, i.e. it is comparison between a clock variable and a variable or a constant term.

The set of all total functions from A to B shall be denoted by $B^A$. The substitution of variables shall be denoted by $g[\sigma ]$, where $\sigma$ is a function from variables to terms and g is some formula or term. Hence, the signature of $[\sigma ]$ is given by $[\sigma ] : Te(X) \cup Fr(X) \rightarrow Te(X) \cup Fr(X)$, where X is a set of variables. The term $f_X$ denotes the domain restriction of a function f to the set X.

Sequences containing $e_1,e_2,\ldots , e_n$ will be denoted by $\langle e_1 \cdot e_2 \cdots e_n \rangle$ and the concatenation of two sequences $\sigma _1$ and $\sigma _2$ will be denoted by .

3 Timed Action Systems

Action Systems (ASs) were introduced by Back and Kurkio-Suonio [10] for modelling distributed systems. In more recent work, ASs have been used as a modelling formalism for mutation-based test-case generation for reactive systems [2, 4]. An event-centred view of ASs has been taken in this context, for deriving test cases and for checking of ioco conformance between ASs. More concretely, for model-based mutation testing each action is assigned a label and an action type, which identifies the action as being an output, input or internal action.

For the definition of Timed Action Systems (TASs), we also follow this approach. However, the modelling formalism discussed in the following is more restricted with respect to discrete actions than other variants of the AS formalism. Nevertheless, we also extend traditional ASs by explicitly accounting for time, which is inspired by TA.

In our approach, an AS defines a set of actions and corresponding guarded commands, a set of state variables and an initialisation for these variables. An action defines a set of parameters and has an action type. For each action, the corresponding guarded command defines the conditions in which the action may be executed and the effect of the action execution. The guarded commands may access state variables and the parameters of the corresponding action. There may be several actions with the same label and if multiple action share the same label, they must also have the same parameters and action type.

During the execution of an AS, at each step an enabled action is chosen non-deterministically and executed. Through this the state is continuously updated until the execution terminates, when none of the actions is enabled. An action is enabled if the guard of its corresponding guarded command is satisfiable.

In order to allow for the modelling of time, we extend ASs by adding clock variables as in TA. In between the execution of two discrete actions, the system may wait for certain amounts of time, which increases the values of the clock variables. This act of waiting will also be referred to as delay in the following. To be able to define the conditions for the actual waiting time, we add time invariants to ASs. The time invariant of an AS must hold in all states and consists of several clauses. A clause defines a time constraint which must hold if the state variables satisfy the condition defined by the clause. Finally, guarded commands may define conditions using clocks and may reset clocks.

In the following, we define the syntax and a trace-based semantics for TASs. Both are inspired by the work of Frantzen et al. [16] and von Styp et al. [26], who use STA. Since STA are similar to TA, our version of stioco can be seen as an extension of the original definition [26], as we also allow internal actions.

3.1 Syntax

Figure 3 illustrates the structure of the concrete syntax of TASs and models a part of the CAS. It specifies 5 real-valued clocks, that the initial state of the system shall be , that the system must not wait longer than 20 time units in state and defines the actions. The actions are labelled with and . These two events are fully defined through two and three actions respectively. In the following, we present the abstract syntax of TASs.

Fig. 3.

A snippet of the TAS model of the CAS.

Definition 1

(Abstract Syntax of Timed Action Systems). A timed action system is a tuple $\mathcal {T\!AS} = \langle \mathcal {V},\mathcal {I},\mathcal {C},\varLambda _I,\varLambda _U,\iota ,Inv,A\rangle$, where $\mathcal {V}$ is the set of state variables, $\mathcal {I}$ is the set of parameter variables and $\mathcal {C}$ is the set of clock variables , with $\mathcal {V}$, $\mathcal {I}$, $\mathcal {C}$ being mutually disjoint. $\varLambda = \varLambda _I \cup \varLambda _U$ is the set of action labels, with $\varLambda _I$ being the set of input action labels and $\varLambda _U$ being the set of output action labels. The constant $\tau \notin \varLambda$ denotes an internal action and we set $\varLambda _{\tau } = \varLambda \cup \{\tau \}$. The initialisation of the action system is $\iota \in Te(\emptyset )^\mathcal {V}$. Inv is the time invariant of $\mathcal {T\!AS}$, which is of the form $\bigwedge _i dc_i \rightarrow cc_i$, with $dc_i \in Fr(\mathcal {V})$ and $cc_i \in CC(\mathcal {C}, \mathcal {V})$ for all i. The set $A\ \subseteq \varLambda _{\tau } \times Fr(\mathcal {V} \cup \mathcal {I}) \times CC(\mathcal {C},\mathcal {V}) \times Te(\mathcal {V} \cup \mathcal {I})^\mathcal {V} \times \mathcal {P}(\mathcal {C})$ is the set of all actions. For $a = (\lambda ,g,g_c,up,r) \in A$, $\lambda$ is called label, g is called guard, $g_c$ is the clock guard, up is the update mapping, defined by assignments in the guarded command and r is a set of clocks, which are reset by executing a.

Before we define semantics for TASs, we introduce two requirements and two auxiliary functions. These are similar to the requirements defined for Symbolic Transition Systems (STSs) by Frantzen et al. [16]. The functions arity and para associate each action with its number of parameters and a tuple containing its parameters respectively.

• 1. For all actions $\lambda$, para maps $\lambda$ to a tuple of distinct parameter variables and for $(\lambda ,g,g_c, up,r) \in A$ it holds that $free (g) \subseteq \mathcal {V} \cup para(\lambda )$ and $up \in Te(\mathcal {V} \cup para(\lambda ))^\mathcal {V}$.

• 2. As for $\tau$-edges of STSs, we disallow the definition of parameter variables for internal actions of TASs, i.e. for all $\tau$-actions, it must hold that $arity(\tau ) = 0$.

Example 1

(Abstract Syntactical Representation of the CAS). The CAS defined in Fig. 3 is a TAS $\langle \mathcal {V},\mathcal {I},\mathcal {C},\varLambda _I,\varLambda _U,\iota ,Inv,A\rangle$, where $\mathcal {V} = \{location\}$, $\mathcal {I} = \{\}$, $\mathcal {C}= \{c,d,e,f,g\}$, $\varLambda _I = \{open,\ldots \}$, $\varLambda _U = \{armedOn,\ldots \}$, $\iota = \{location \mapsto OpenAndUnlocked\}$, $Inv = (location = ClosedAndLocked) \rightarrow c \le 20 \wedge \ldots$ and $A\ = \{o,a,\ldots \}$. With actions $o = (open,location = Armed,\top ,\{location \mapsto BeforeAlarm\},\{e\})$ and $a = (armedOn,location = ClosedAndLocked,c = 20,\{location \mapsto Armed\},\{\})$. Parts omitted in Fig. 3 are represented by dots.

3.2 Semantics and Stioco

In this subsection, we give a symbolic trace semantics for TASs and discuss stioco checking. A symbolic trace represents one (sequential) run of the symbolic execution of a TAS. This symbolic trace semantics forms the basis for our implementation of the symbolic executor and the stioco conformance checker.

The trace-based semantics must fulfil four requirements: a trace must (1) start with a delay, (2) consist of alternating sequences of discrete actions and delays, and (3) end in a delay. The first two requirements are placed on the semantics in correspondence to the definition of traces by von Styp et al. [26]. Conversely, the third requirement serves to simplify conformance checking while it does not limit generality as zero delays are possible. Additionally, (4) a trace should handle internal actions appropriately: consider the concrete timed trace $ct = \langle 1\cdot !a\cdot 2\cdot \tau \cdot 3\cdot ?b\cdot 0 \rangle$. For checking tioco conformance one is only interested in observable traces of the specification [19]. Thus, we would project ct to the set of observable input and output actions, erasing the $\tau$-action and summing up the two consecutive delays: $ct'= \langle 1\cdot !a\cdot 5\cdot ?b\cdot 0 \rangle$.

In the symbolic setting, we use symbolic traces where constant time delays are replaced by symbolic delay variables. As common in symbolic execution, these symbolic delays are defined via constraints. We distinguish between two kinds of delay variables: observable delays $t_i$, which are part of the observable trace and unobservable delays $d_{i,j}$ that appear only in constraints. Observable delays are always defined in terms of unobservable delays. For example, the symbolic trace $st = \langle d_1\cdot !a\cdot d_{2,1}\cdot \tau \cdot d_{2,2}\cdot ?b\cdot d_3 \rangle$ including an unobservable $\tau$-action would be projected to an observable trace $st' = \langle t_1\cdot !a\cdot t_{2}\cdot ?b\cdot t_3 \rangle$ with the constraints $t_1 = d_1$, $t_2 = d_{2,1} + d_{2,2}$ and $t_3 = d_3$. Note that while observing the delay $t_2$, it is not possible to distinguish between the internal delays $d_{2,1}$ and $d_{2,2}$.

So far, we only considered delays. For the trace-based semantics we need to update the state of variables and clocks along a trace and collect the constraints: discrete and time guards of actions, time invariants and constraints which express that consecutive unobservable delays sum up to observable delays. In addition, it is necessary to keep track of the set of unobservable delays along a trace, because we will hide these via existential quantification for the conformance check.

In order to define the formal semantics, we introduce concepts similar to those used for the original definition of stioco [26]. For elegant clock update definitions, we introduce the singleton sets $\mathcal {D} = \{d\}$ and $\mathcal {T} = \{t\}$ containing an unobservable and an observable delay, respectively. Since we need to distinguish between different occurrences of variables in a trace we introduce the disjoint indexed sets for observable delays $\mathcal {T}_i$, unobservable delays $\mathcal {D}_{i,j}$ and parameters $\mathcal {I}_i$ with $i,j \in \mathbb {N}$. The index i corresponds to the position in the trace and j corresponds to the number of delays since the last observable action.

Furthermore we assume that there exists a bijective variable-renaming $r_i : \mathcal {I}\cup \mathcal {T}\rightarrow \mathcal {I}_i \cup \mathcal {T}_i$, which adds an index i to non-indexed variables and there exists a bijective variable-renaming $dr_{i,j} : \mathcal {D}\rightarrow \mathcal {D}_{i,j}$, which adds indexes i and j to unobservable delay variables. We set $\widehat{\mathcal {T}} = \bigcup _i \mathcal {T}_i$, $\widehat{\mathcal {I}} = \bigcup _i \mathcal {I}_i$ and $\widehat{\mathcal {D}} = \bigcup _i \bigcup _j \mathcal {D}_{i,j}$.

We model symbolic clock updates with a function $\varrho \in Te(\mathcal {C}\cup \mathcal {D})^\mathcal {C}$, with $\varrho (c) = c + d \text { for all } c \in \mathcal {C}$ and $d \in \mathcal {D}$. With this machinery we can now elegantly define clock updates in step i, j as a composed substitution function $[dr_{i,j}] \circ \varrho$, first replacing the clocks with the term $c + d$ and then indexing d appropriately.

For clock resets of all clocks in a set r, we define a term-mapping FO(r), such that $FO(r)(c) = 0_t$ for $c \in r$ and $FO(r)(c) = c$ otherwise, i.e. it sets clocks in r to zero. Finally, we define the set of all variables as $\widehat{Var} = \mathcal {V}\cup \widehat{\mathcal {I}} \cup \widehat{\mathcal {D}} \cup \widehat{\mathcal {T}} \cup \mathcal {C}$.

Symbolic Trace Semantics. The symbolic trace semantics of a TAS representing its symbolic execution is then given by the generalised transition relation $\Rightarrow \ \subseteq ((\widehat{\mathcal {T}} \cdot \varLambda )^* \cdot \widehat{\mathcal {T}}) \times Fr(\widehat{Var}) \times Te(\mathcal {V}\cup \widehat{\mathcal {I}})^\mathcal {V}\times Te(\mathcal {C}\cup \widehat{\mathcal {D}})^\mathcal {C}\times \mathcal {P}(\widehat{\mathcal {D}})$, which is defined below. It is a set of 5-tuples $(\sigma , pc,q,q_c,D)$, where $\sigma$ is an alternating sequence of delays and actions; pc is the path condition, i.e. the conditions which need to be satisfied for $\sigma$ to be executable; q is the discrete symbolic state of the variables $\mathcal {V}$, i.e. a mapping from state variables to terms over state variables and parameters $\widehat{\mathcal {I}}$; $q_c$ is the symbolic state of the clocks $\mathcal {C}$, i.e. a mapping from clocks to sums of unobservable delays, and D contains the set of unobservable delays $d_{i,j}$ collected along the observable symbolic trace $\sigma$.

Definition 2

(Generalized Transition Relation). Given a timed action system $\mathcal {T\!AS} = \langle \mathcal {V},\mathcal {I},\mathcal {C},\varLambda _I,\varLambda _U,\iota ,Inv,A\rangle$, its generalised transition relation $\Rightarrow$ is defined to be the smallest set, which satisfies the following three rules:

• 
• 

  where

  • $q' = ([q] \circ ([r_{i+1}] \circ up))_\mathcal {V}$,

  • $q_c' = ([q_c] \circ ([FO(r)] \circ ([dr_{i+1,1}] \circ \varrho )))_\mathcal {C}$,

  • $dc = (g[r_{i+1}])[q] \wedge (g_c[q])[q_c] \wedge (Inv[q'])[[q_c] \circ FO(r)]$ and

  • $tc = (Inv[q'])[q_c']$

• 

  where

  • $q' = [q] \circ up$,

  • $q_c' = ([q_c] \circ ([FO(r)] \circ ([dr_{i,k+1}] \circ \varrho )))_\mathcal {C}$,

  • $dc = g[q] \wedge (g_c[q])[q_c] \wedge (Inv[q'])[[q_c] \circ FO(r)]$ and

  • $tc = (Inv[q'])[q_c']$

Rule $\mathbf {T\epsilon }$ is the base case expressing the initial delay $t_1$ before the first action, if any. It states that the time invariant must hold before and after this delay. The identity function id expresses the unchanging of the discrete state. The clocks $\mathcal {C}$ are updated accordingly.

Rule $\mathbf {T\lambda }$ expresses that the symbolic execution of an observable action extends the observable trace by a sequence $\langle \lambda \cdot t_{i+1}\rangle$, where $\lambda$ is the corresponding action label and $t_{i+1}$ is an observable delay. A new unobservable delay in step $i\!+\!1,1$ is added to the set of unobservable delays and set to be equal to the observable delay in the path condition. Additionally, the discrete (dc) and time constraints (tc) are added to the path condition as well. Furthermore, the discrete state q is updated to $q'$ according to the update function up of the action. This discrete state update takes also care of the proper variable renaming (or variable indexing) via function $r_{i+1}$. The clocks are partially reset according to the reset set r and then delayed.

Rule $\mathbf {T\tau }$ expresses that the symbolic execution of an internal action (with a $\tau$ label) does not change the observable trace , but adds a new delay $d_{i,k+1}$ to the set of unobservable delays D. The new delay in step $i,k\!+\!1$ is added to the path condition, together with the discrete (dc) and time constraints (tc). Furthermore, the discrete state q is updated to $q'$ according to the update function up of the action. The clocks are partially reset according to r and then delayed according to $d_{i,k+1}$.

The discrete constraint dc mentioned in both rules $\mathbf {T\lambda }$ and $\mathbf {T\tau }$ contains not only discrete conditions but constrains the execution of discrete actions. For a discrete action to be executable, the guard g and the clock guard $g_c$ must be satisfied in the pre state and the time invariant must be satisfied after updating the discrete state and resetting the clocks. The time constraint tc analogously constrains the length of the delay, by specifying that the time invariant must hold after executing the discrete action, resetting and updating clocks.

Example 2

(Generalized Transition Relation of the CAS). In this example, we list two elements of the generalised transition relation of the CAS. It contains by definition through rule $\mathbf {T\epsilon }$ the element $(\langle t_1 \rangle , I \wedge I' \wedge t_1 = d_{1,1},\{location \mapsto location\},\bigcup _{x \in \mathcal {C}} \{x \mapsto x + d_{1,1}\},\{d_{1,1}\})$, where $I = (location = ClosedAndLocked) \rightarrow c \le 20 \wedge \ldots$ and $I' = (location = ClosedAndLocked) \rightarrow c + d_{1,1} \le 20 \wedge \ldots$. A trace consisting of only the open-action, which executes the open-action as defined in Fig. 3 corresponds to the tuple $(\langle t_1 \cdot ?open \cdot t_2 \rangle , pc, q,q_c,\{d_{1,1},d_{2,1}\})$, where $q = \{location \mapsto BeforeAlarm\}$, $qc = \{e \mapsto d_{2,1}\} \cup \bigcup _{x \in \mathcal {C}\setminus \{e\}} \{x \mapsto x + d_{1,1} + d_{2,1}\}$ $pc = I \wedge I' \wedge t_1 = d_{1,1} \wedge t_2 = d_{2,1} \wedge dc \wedge tc$, with $dc = (location = Armed) \wedge (BeforeAlarm = ClosedAndLocked) \rightarrow c + d_{1,1} \le 20 \wedge \ldots$ and $tc = (BeforeAlarm = ClosedAndLocked) \rightarrow c + d_{1,1} + d_{2,1} \le 20 \wedge \ldots$

Conformance Checking. Since the stiocos conformance relation for TASs is very similar to the definition of stioco of von Styp et al. [26], we will not give the full definition, but rather list the three most important differences:

• We use the semantics discussed above. As unobservable delays along a trace are relevant for conformance, symbolic states and symbolic observations consider these as well. Hence, states and observations are tuples, where one tuple element contains the unobservable delays which have been collected before reaching a symbolic state or before observing some symbolic observation.

• The symbolic observation of delays needs to be adapted as well, i.e. a symbolic counterpart of the elapse(s)-function [19] must be defined, which maps a state s to the set of delays, which can be executed without executing an observable action. Hence, a symbolic elapse(s)-function could be defined as a trace, which consists of only one delay, executed in state s. More concretely, it could be defined as $(t_1, pc,q,q_c,D) \in \Rightarrow$, but with shifted indexes and a substitution of the actual state into pc, q and $q_c$.

• The original stioco definition uses a function $\varPhi$, which gives a condition for observing some observation after a given trace $\sigma$. To account for internal actions, this function needs to existentially quantify over the sets of unobservable delays collected along $\sigma$.

The conformance check is implemented in the same fashion as the sioco conformance check for untimed action systems [6], which is itself inspired by the ioco conformance checker used in [2, 3]. More concretely, it performs a bounded depth-first search for unsafe states, which are states in which non-conformance may be observed. For this purpose, both mutant and specification are symbolically executed in parallel, such that they synchronise on observable actions, but execute internal actions independently from each other. In order to ensure input-enabledness of the mutant, which is a requirement for stioco, we perform an angelic completion for the mutant. Hence, we implicitly add self-loops to states for all non-specified inputs. At each step, a conformance check is performed and if non-conformance is detected, the trace leading to the current state and the satisfiable non-conformance condition are returned.

However, a naive implementation of this procedure would suffer from problems such as path explosion [13] and thus be far too slow to be useful. Consequently, several optimisations have been implemented, which can roughly be grouped into three categories:

• Pruning of search tree. If during the search for unsafe states, we reach a symbolic state which has already been visited, we prune the search tree. For this purpose, we implemented symbolic checks for equivalence of states, which are based on the state inclusion condition defined by Gaston et al. [17]. These checks deem two symbolic states to be equivalent, if they correspond to the same sets of concrete states.

• Precomputation. We precompute symbolic execution graphs, which encode all executable traces for the specification. This information can be reused during the conformance check and results in a performance gain, as we check conformance for hundreds of different mutants with the same specification.

• Syntactic mutation analysis. As long as the mutation has not been executed, the number of satisfiability checks can be reduced drastically, e.g. by using the precomputed execution graph for the mutant as well.

3.3 Encoding Timed Automata Using Timed Action Systems

In order to encode a Timed Automaton (TA) as a TAS, we essentially create a TAS having the same set of state variables plus one additional state variable representing the current location and having the same set of transitions. The procedure for translating TA into TASs can be structured as follows:

• 1. Create a TAS with the same set of state variables, clocks and action labels.

• 2. Create a set of constants Loc, where each constant represents a location in the TA. Define a function rep, which maps locations to their respective constants.

• 3. Add an additional state variable called location, which takes values in Loc, and rename an existing variable with the same name, if such a variable exists. Initialise location with $rep(l_0)$, where $l_0$ is the initial location of the TA.

• 4. For each transition of the TA with source location l and target location $l'$:

  • 4.1 Create an action with same guards, clock resets, state updates and label.

  • 4.2 Add $location = rep(l)$ to the guard and add $location \mapsto rep(l')$ to the state update.

• 5. Initialise the time invariant to $\top$, then for each invariant i of a location l: Conjunct the clause $rep(l) = location\rightarrow i$ to the time invariant of the TAS.

Any TAS that was built according to this structure, can also be encoded as a TA, by reverting the steps above.

4 Experimental Results

To give a first comparison of the two approaches we use the car alarm system that was introduced in Sect. 1. We defined different variants, containing model elements such as silent transitions and data variables, that can be challenging for the conformance checks. In all the experiments we use the following settings: we translated from timed automata to timed action systems as closely as possible: The different models contain the same number of states and transitions and the same sets of clocks and variables. We used eight different mutation operators (similar to those in [5], excluding the changing of action labels, that would have been problematic to implement for the TAs), that were implemented equally for both types of models. However, due to the different modelling styles, the amount of mutants did vary slightly in some cases. All experiments were run on a MacBook Pro with a 2.8 GHz Intel Core i7 and 8 GB RAM.

Table 1. Computation time for the different conformance checks on the deterministic version of the car alarm system.

4.1 Deterministic Car Alarm System

We first investigate the model in Fig. 1. It is deterministic and has 5 clocks, 16 locations and 25 transitions. The results of applying both approaches are displayed in Table 1. The bounded model checking performed slightly faster and at a very constant rate, without many statistical outliers. The symbolic execution, with the median far below the mean value, was very fast for most of the mutants, however there were some that took significantly longer than the rest, and increased the average processing time. The overall runtime of the bounded model checking was 30.0 min for 1, 320 mutants, compared to 27.5 min for 968 mutants in the symbolic execution.

Fig. 4.

Partial models of the car alarm system with silent transitions.

4.2 Non-deterministic Car Alarm System

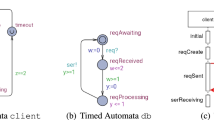
The next model contains a silent transition that non-deterministically delays the 20 s timer responsible for arming the system by up to two seconds. This changes the time constraints for the arming of the system and adds non-determinism for the unlock and open transitions leaving the locations. We used this model previously [22]. Besides the non-determinism, it differs from the original car alarm system, by underspecifying whether the sound alarm or the flash alarm is activated first. The bounded model checking approach can neither deal with non-determinism, as it might lead to spurious counterexamples, nor with silent transitions. As already described in Sect. 2, this can be tackled, by a bounded determination of the automaton in a preprocessing step. However, this preprocessing leads to a severe state space explosion. If applied to the non-deterministic car alarm system, with a maximum depth of 12, the deterministic automaton contains 13, 545 locations, and can not be processed by the test case generation tool anymore. We thus split the original model into two tioco-conform partial models, where the first one captures the different variants of locking, unlocking, closing and opening the doors, up to the first arming transition. The second one only contains one direct path to the armed state, but covers the rest of the system. Both partial models are illustrated in Fig. 4. This keeps most of the branching in the first smaller system, and the main functionality in the second and larger system. The results of applying the approaches to these models are illustrated in Table 2. The overall runtime for the first partial model was 32.8 min for 220 mutants for applying the bounded model checking and 48.1 s for 168 mutants for the symbolic execution. For the second partial model, the bounded model checking took 34.1 min for 1, 263 mutants and the symbolic execution only needed 68.1 s for 832 mutants.

Table 2. Computation time for the different conformance checks on the partial models of the non-deterministic version of the car alarm system.

The ability of the symbolic approach, to process the models without unfolding them first, clearly gives it an advantage here. Not only is it a lot faster on the partial models, it was also able to process the complete model. Additionally, it has on average even been faster than in the deterministic case. There are two main reasons for this behaviour. Firstly, three mutants have not been checked for conformance automatically, because they ran into a timeout (ten minutes), and were excluded from the experiments. However, manual inspection revealed that these mutants conform to the specification. Secondly, the introduction of a silent transition led to a much larger portion of nonequivalent mutants. Aichernig et al. showed that ioco checking of equivalent mutants takes significantly longer than ioco checking of non-equivalent mutants [3], thus a lower number of equivalent mutants can explain the reduction in average runtime from $1.7\,\mathrm{s}$ to $0.79\,\mathrm{s}$.

4.3 Car Alarm System with PIN Code

This final model treats the ability of processing data variables. The unlock and lock transitions of the car alarm system are augmented by a PIN code. If the code is entered correctly, the system acknowledges it with a new ack-output, and continues as before. If it was entered incorrectly, the system will start the alarms, after a nack- output. This model only uses one clock, whereas five clocks were used in the original car alarm system.

The PIN code did not have any negative influence on both approaches, as illustrated in Table 3. For the symbolic execution, the mean conformance check time was even reduced. This was most likely caused by the fact that only one clock was used in this model. Furthermore, there were several more mutants, most of which were non-equivalent.

Altogether, the bounded model checking was applied to 1, 702 mutants and needed 41.4 min on depth 8 and 116.8 min on depth 12. The symbolic execution was again faster, needing 143.0 (depth 8) and 460.8 (depth 12) s for 1, 918 mutants. For the reported numbers, we restricted the PIN code to three digits. However, we also applied the experiments with higher values (four and five digits), without any negative consequences.

Table 3. Computation time for the different conformance checks on the deterministic version of the car alarm system, augmented by a PIN code.

4.4 Lessons Learned

During the experiments, we found several model elements that influence the presented approaches in different ways:

• 1. The number of clocks has a big influence on the runtime of the symbolic execution approach. Adding clock variables slows the check down, whereas merging two independent clocks reduces the runtime noticeably. In contrast, for the bounded model checking, the number of clocks does not have a significant influence on the runtime.

• 2. Non-determinism is an obstacle for conformance checking. For the bounded model checking, where determination has to be done beforehand, this leads to a state-space explosion and the complete model even became infeasible. The symbolic execution, however, only experienced a reduction in performance for some problematic mutants such as the two mutants which had to be excluded from the experiments. Nevertheless, it was still able to process the remaining mutants in reasonable time, though it should be noted that the maximum runtime increased from about 40 s in the deterministic case to about six minutes. This can be attributed to the fact that multiple symbolic states can be reached by executing observable traces if non-determinism is involved, which in turn increases the complexity for satisfiability checking of the non-conformance condition.

• 3. Statistical outliers with respect to runtime are more frequent and more extreme in symbolic execution, than on bounded model checking. In bounded model checking, the processing time of different equivalent mutants is usually the same. For symbolic execution, some mutants are harder to check than others. Usually, these are equivalent mutants, which contain mutations that are executed early during the search for conformance violations, while mutations that are executed at higher depths generally cause a much lower performance penalty. This is due to the fact, that in the latter situation, optimisations based on syntactic mutation analysis have a larger impact.

5 Related Work

Several time extensions for action systems have already been proposed: Fidge and Wellings [15] proposed timed action systems, assuming time-consuming actions and discrete time. Westerlund and Plosila [29] proposed action systems based on continuous time, where each action system contains a clock to measure the time since start of the system. Again, time is considered to be consumed by actions, and may not pass between them. Wabenhorst [27] proposes a formalism combining time-consuming actions and an additional wait action executed if none of the other actions are enabled. In contrast to these proposals, we consider actions that take zero time, followed by delays. This keeps our definition of timed action systems very close to timed automata.

Kurki-Suonio [20] proposed a time extension to action systems, using, equal to our approach, zero time actions, but using only one global variable to track time. Each action has a parameter specifying its time of execution. They can only be executed if the global time is smaller or equal to their time of execution. If an action is chosen, it raises the global time to its time of execution. Contrary to this approach, we use invariants instead of deadlines for limiting time progress and we support multiple clocks, allowing for more complex time constraints.

We also encoded the language inclusion problem within UPPAAL [21], by adding a trap-property to the product of the specification and a mutant. First experiments showed that UPPAAL is very fast in detecting non-conformance in the deterministic case. In the non-deterministic case, the encoding we used suffered from the same problem as the bounded-model checking: it lead to spurious counter examples. Adding a PIN code with a range of $0-500$ to the deterministic model already slowed the conformance check down and expanding it to 5000 made the whole approach infeasible.

Wang et al. [28] presented a zone-based language inclusion check for timed automata. It seems to be faster then ours, however it does not support silent transitions, and only terminates for determinizable classes of timed automata.

6 Conclusion

We have introduced timed action systems in a fashion as close to timed automata as possible. We showed how to translate timed automata into timed action systems and defined a symbolic trace semantics for them. Using this semantics, we applied a symbolic conformance check based on the stioco conformance relation. We then compared bounded model checking and symbolic execution in the context of test-case generation, applied to different models of a car alarm system. The results showed that symbolic execution was able to handle non-determinism very well, and that data variables did have no negative influence on both approaches.