On the Verification for Realizing Multi-scroll Chaotic Attractors with High Maximum Lyapunov Exponent and Entropy

Abstract

Nowadays, many works have been presented regarding the modeling, simulation and circuit realization of different kinds of continuous-time multi-scroll chaotic attractors. However, very few works describe the experimental realization of attractors having high maximum Lyapunov exponent (MLE) and high entropy, which are desirable characteristics to guarantee better chaotic unpredictability. For instance, two chaotic oscillators having the same MLE values can behave in a very different way, e.g. showing different entropy values. That way, we describe the experimental realization of an optimized multi-scroll chaotic oscillator with both high MLE and entropy. First, the MLE is optimized by applying an evolutionary algorithm, which provides a set of feasible solutions. Second, the associated entropy is evaluated for each feasible solution. In this chapter, experimental results are shown for the electronic implementation of a chaotic oscillator generating 2-, 5- and 10-scrolls. Finally, the experimental results show that by increasing the number of scrolls both the MLE and its associated entropy increase in a similar proportion, thus guaranteeing better unpredictability.

1 Introduction

In Electronics, a great variety of chaotic oscillators has been implemented with different kinds of electronic devices [7, 15, 19], using integrated circuits technology [20], and more recently by using field programmable gate arrays [17]. In addition, recent works show a relationship between the number of scrolls and the value of the maximum Lyapunov exponent (MLE) [2, 18], and also a relationship between the number of scrolls and the associated entropy [23]. Both characteristics associated to MLE and entropy are quite desirable to improve for the development of enhanced applications in nonlinear systems, like for example: the implementation of random number generators [1, 4, 10, 23] that are quite useful in robotics [16, 21].

In this chapter we show the experimental realization of multi-scroll chaotic attractors that are optimized to provide a high value of the MLE, and for each attractor it is also guaranteed to have a good distribution of the trajectories that is visualized in the phase-space portraits. As concluded in [23], the next sections show that the MLE increases by increasing the number of scrolls, indicating a better unpredictability of the dynamical system due to the increment of its associated entropy. In addition, we also show the experimental realization of multi-scroll chaotic attractors having a uniform distribution of its trajectories in the phase-space portrait, because when the phases are not well distributed among all the scrolls, some scrolls cannot be formed, thus leading to a pretty difficult problem for the electronic implementation.

The optimization algorithm proposed in [2], is applied herein. It is based on the evolutionary algorithm known as non-dominated sorting genetic algorithm (NSGA-II) [3], and it optimizes two characteristics, namely: (a) Maximizing the positive Lyapunov exponent, and (b) minimizing the dispersions of the phase transitions among all scrolls in an attractor. The results of the optimization algorithm show that both characteristics are in conflict, so that a feasible set of solutions is provided to select the best one according to the problem at hand.

From the set of feasible solutions provided by applying [2], we select some multi-scroll chaotic attractors having high MLE, and then we realize experiments by implementing the chaotic oscillators with commercially available operational amplifiers. The purpose of the experiments are oriented to verify the relationship on the number of scrolls, their MLE value and the associated entropy.

The case of study is the multi-scroll chaotic oscillator based on saturated nonlinear function series, already described in [7]. It is a third order continuous-time dynamical system, and then it has three Lyapunov exponents, one being positive, which is known as MLE and its value indicates the degree of chaotic behavior. It is optimized by applying the evolutionary algorithm given in [2], and its associated entropy is evaluated from both numerical simulations and experimental data for generating 2-, 5- and 10-scrolls. The goal of performing the experiments is to verify that the higher the number of scrolls the higher the MLE and its associated entropy [9]. Further, optimized chaotic oscillators should improve applications like random number generators [1, 4, 10, 16, 21, 23], synchronization [6], and secure communication systems [5], for instance.

2 Multi-scroll Chaotic Oscillators

The study of chaotic dynamical systems traces its origin to the findings of E.N. Lorenz in the early 1960s. His interest in weather forecasting led him to the discovery of a nonlinear dynamical system that displayed high sensitivity to the initial conditions, an essential property of chaotic systems. Ever since then, decades of research have expanded the understanding of this ubiquitous phenomena and produced several applications in different areas of engineering.

Dynamical systems describe motion in nature that can be modeled by equations of the following forms:

$$\begin{aligned} \dot{x}(t)= f(a,x(t)) \quad t>0 \end{aligned}$$

(1)

and

$$\begin{aligned} x(n+1)=f(a,x(n)) \quad n\in {\mathbb {N}} \end{aligned}$$

(2)

In these equations, the state variables of the dynamical system are represented by x(t) and x(n). The possible values of the state variables imply that (1) is a differential equation while (2) is a difference equation or map. In both cases, $x$ represents a q-dimensional state vector, i.e. $x\in {R^q}$. The control parameter $a$ (also called bifurcation parameter) has $m$ components such that $a\in {R^m}$. The control parameter affects the evolution of the state variables, and the relationship between the parameters and the state variables is defined by a function $f$. The range of $f$ is in the same space of the state vector $x$. Chaos, defined colloquially as irregular an unpredictable behavior, can stem from dynamical systems as long as $f$ has the suitable properties. Likewise, $a$ must be set to the appropriate values in order to precipitate a transition to chaos. The chaotic behavior product of dynamical systems is known as deterministic chaos.

In electronics, chaotic oscillators have been implemented to generate double or multi-scroll chaotic attractors. In the last case, multi-scrolls have been generated by using different kinds of electronic devices [7, 15, 19], as well as by designing integrated circuits [20] or by using configurable digital architectures [17]. However, analog realizations suffer the limitations of the electronic devices [11], or suffer the variations problems from integrated circuit fabrication technologies as shown in [20], where a variation in process, voltage or temperature (PVT) may degrade or even eliminate the normal behavior of a chaotic oscillator, rendering it useless. That way, still more research is done regarding the design of chaotic oscillators using analog devices. In this chapter, the chaotic oscillator is realized by using commercially available operational amplifiers.

The case of study is the multi-scroll chaotic oscillator based on saturated nonlinear function series [7], which can be described by the system of differential equations given by (3), where a, b, c, and $d_1$ are positive constants that can have values in the interval [0, 1]. In (3), the dynamical system is controlled by a saturated nonlinear function series f that is approximated by piecewise-linear functions.

$$\begin{aligned} \begin{aligned} \dot{x}&= y\\ \dot{y}&= z\\ \dot{z}&= -ax -by -cz + d_1 f(x; m)\\ \end{aligned} \end{aligned}$$

(3)

In the following, we describe in detail how the saturated function f in (3) is obtained. Let $f_0$ be the saturated function:

$$\begin{aligned} f_0 (x; m) = {\left\{ \begin{array}{ll} 1,&{}\quad \text {if }x > m\\ \frac{x}{m},&{}\quad \text {if }|x| \le m\\ -1,&{}\quad \text {if }x < -m, \end{array}\right. } \end{aligned}$$

(4)

where 1 / m is the slope of the middle segment and $m>0$; the upper radial $\{ f_0(x; m) = 1 \; | x > m \}$, and the lower radial $\{ f_0(x; m) = -1 \; | x < -m \}$ are called saturated plateaus, and the segment $\{ f_0(x; m) = x/m \; | \; |x| \le m \}$ between the two saturated plateaus is called saturated slope.

Lets us consider now the saturated functions $f_h$ and $f_{-h}$ defined as:

$$\begin{aligned} f_h ( x; m, h ) = {\left\{ \begin{array}{ll} 2,&{}\quad \text {if }x > h + m\\ \frac{x-k}{m}+1,&{}\quad \text {if }|x-h| \le m\\ 0,&{}\quad \text {if }x < h-m, \end{array}\right. } \end{aligned}$$

(5)

and

$$\begin{aligned} f_{-h} ( x; m, -h ) = {\left\{ \begin{array}{ll} 0,&{}\quad \text {if }x > h + m\\ \frac{x-k}{m}-1,&{}\quad \text {if }|x-h| \le m\\ -2,&{}\quad \text {if }x < h-m, \end{array}\right. } \end{aligned}$$

(6)

where h is called the saturated delay time and $h>m$. Therefore, a saturated function series for a chaotic oscillator with s scrolls is defined as the function:

$$\begin{aligned} f(x; m) = \sum _{i=0}^{s-2} f_{2i-s+2}( x; m, 2i-s+2 ) \end{aligned}$$

(7)

where $s>2$.

For example, using $f=f_0$ in (3), a 2-scrolls chaotic oscillator can be generated. Therefore, the saturated function series to generate 3-scrolls is $f(x; m) = f_{-1}( x; m, -1) + f_{1}( x; m, 1)$. To generate a 4-scrolls attractor it will be $f(x; m) = f_{-2}( x; m, -2) + f_0( x; m) + f_{2}( x; m, 2)$, and so on.

In [2], the optimization of the MLE requires as input data, the number of scrolls to be generated. Then, a bi-objective optimization problem is encoded: (i) to maximize MLE, and (ii) to minimize the variability in the oscillator’s phase-space transitions or the trajectories. From (3), the optimization problem is devoted to find the values of the four coefficient variables a, b, c and $d_1$ that solve both objectives (i) and (ii). Those four coefficients can take values within the range [0.0, 1.0], and one decides how many decimal numbers to use.

3 Computing Lyapunov Exponents and Entropy

Lyapunov exponents are asymptotic measures that characterize the average rate of growth (or shrinking) of small perturbations to the solutions of a dynamical system. Lyapunov exponents provide quantitative measures of response sensitivity of a dynamical system to small changes in initial conditions. The number of Lyapunov exponents is equal to the number of states variables in the dynamical system, and at least three state variables are required to generate chaotic behavior. In this chapter, the case of study is a multi scroll chaotic oscillator having three state variables, described by (3). The experimental results presented in the next sections will verify what is already known that by increasing the number of scrolls both the MLE and its associated entropy increase in a similar proportion [23].

3.1 Lyapunov Exponents

Lets us consider an n-dimensional dynamical system:

$$\begin{aligned} \dot{x}=f(x), \ \ \ \ t>0, \ \ \ \ x(0)=x_0 \in \mathbb {R}^n \end{aligned}$$

(8)

where x and f are n-dimensional vector fields. To determine the n-Lyapunov exponents of the system one have to find the long term evolution of small perturbations to a trajectory, which are determined by the variational equation of (8),

$$\begin{aligned} \dot{y}=\frac{\partial f}{\partial x} \big (x(t)\big )y=J\big (x(t)\big )y \end{aligned}$$

(9)

where J is the $n \times n$ Jacobian matrix of f. A solution to (9) with a given initial perturbation y(0) can be written as

$$\begin{aligned} y(t)=Y(t)y(0) \end{aligned}$$

(10)

with Y(t) as the fundamental solution satisfying

$$\begin{aligned} \dot{Y}=J\big (x(t)\big )Y, \ \ \ \ Y(0)=I_n \end{aligned}$$

(11)

Here $I_n$ denotes the $n \times n$ identity matrix. If we consider the evolution of an infinitesimal n-parallelepiped $[p_1(t ),\dots , p_n(t)]$ with the axis $p_i(t)=Y(t)p_i(0)$ for $i=1,\dots ,n,$ where $p_i(0)$ denotes an orthogonal basis of $\mathbb {R}^n$. The ith Lyapunov exponent, which measures the long-time sensitivity of the flow x(t) with respect to the initial data x(0) at the direction $p_i(t)$, is defined by the expansion rate of the length of the ith axis $p_i(t)$ and is given by

$$\begin{aligned} \lambda _{i}=\lim _{t \rightarrow \infty }\frac{1}{t}\ln {\big \Vert p_i(t)\big \Vert } \end{aligned}$$

(12)

In summary, the Lyapunov exponents can be computed as follows [2, 13, 18, 22]:

• 1. Initial conditions of the system and the variational system are set to $\mathbf {X_{0}}$ and $\mathbf {{I}_{n \times n}}$, respectively.

• 2. The systems are integrated by several steps until an orthonormalization period TO is reached. The integration of the variational system $\mathbf {Y}=[y_1, y_2 ,y_3]$ depends on the specific Jacobian that the original system $\mathbf {X}$ is using in the current step.

• 3. The variational system is orthonormalized by using the standard Gram-Schmidt method [12], and the logarithm of the norm of each Lyapunov vector contained in $\mathbf {Y}$ is obtained and accumulated in time.

• 4. The next integration is carried out by using the new orthonormalized vectors as initial conditions. This process is repeated until the full integration period T is reached.

• 5. The Lyapunov exponents are obtained by

  $$\begin{aligned} \mathbf {\lambda _{i} \approx \frac{1}{T}\sum _{j\,=\,\text {TO}}^{T} \ln {\big \Vert y_i\big \Vert }} \end{aligned}$$

The time-step selection was set as in [18], by using the minimum absolute value of all the eigenvalues of the system $\lambda _{\min }$, and $\psi$ was chosen well above the sample theorem as 50.

$$\begin{aligned} t_\text {step}=\frac{1}{\lambda _{\min }\psi } \end{aligned}$$

The orthogonalization period TO was chosen about $50\ t_{\text {step}}$. This procedure is used herein as in [2] to optimize the MLE.

3.2 Evaluation of Entropy

For chaotic oscillators, the entropy is an alternative choice to Lyapunov exponents because it reveals aspects of the underlying dynamical system (i.e., it quantifies the stretching and the folding aspects at the same time). In this manner, in this chapter the entropy is evaluated because its rate of growth is an interesting parameter to quantify disorder in chaotic oscillators. In the same direction, as chaotic attractors can be recognized by visual inspection in their phase-space portraits, we perform a numerical quantification of chaos by optimizing the MLE of the chaotic oscillator described by (3). The entropy has also some relationships of interest as for the sum of Lyapunov exponents [13, 14], which measure the instability of nearby trajectories.

The entropy is computed herein by applying the algorithm presented by Moddemeijer, which is online available at http://www.cs.rug.nl/~rudy/matlab/. That way, in Sect. 5, we list 10 values of the MLE and their associated entropy that is evaluated from both numerical simulation and experimental data for generating 2-, 5- and 10-scrolls attractors.

4 Circuit Realization with Commercially Available Operational Amplifiers

The multi-scroll chaotic oscillator based on saturated nonlinear function series f is described by (3). For the circuit realization, one should approximate function f by piecewise-linear (PWL) segments as follows:

$$\begin{aligned} f(x;k,h,p,q)=\left\{ \begin{array}{l} (2q+1)k, \\ k(x-ih)+2ik, \\ (2i+1)k, \\ -(2p+1)k. \end{array} \right. \end{aligned}$$

(13)

with

$$\begin{aligned} \begin{array}{l} x>qh+1 \\ |x-ih|\le 1,\quad -p\le i\le q \\ ih+1<x<(i+1)h-1,\quad -p\le i \le q-1 \\ x<-ph-1. \end{array} \nonumber \end{aligned}$$

For instance, Fig. 1 shows two kinds of saturated functions. The one with 5 linear segments is used to generate odd number of scrolls, and the one with 7 segments is used to generate even number of scrolls. The difference is that the one on the right has an slope crossing the origin of the plane. Thus, by increasing the number of segments from the three near the origin in Fig. 1b, one generates as many even number of scrolls as the number of saturated levels, which are the linear segments with slope $=$ 0. In a similar way, starting from five segments, as the PWL description in Fig. 1a, one can generate as many odd number of scrolls as the number of saturated levels.

Fig. 1

PWL descriptions of a saturated nonlinear function series to generate a 3-scrolls, and b 4-scrolls

In simulating multi-scroll chaotic oscillators, one should scale the values to be realized with electronic devices. For example, by simulating 6-scrolls one needs a PWL description like the one in Fig. 1b but with 11 segments (6 saturated levels plus 5 slopes). Therefore, by setting $a,b,c,d_1=0.7$, $k=10$, $h=20$, $p=q=2$, the simulation result is shown in Fig. 2. As one sees, the ranges for the vertical and horizontal axes are around $\pm$12 and $\pm$60, respectively. It is pretty clear that the horizontal range cannot be realized using commercially available operational amplifiers because they can be biased only up to $\pm$18 V.

Fig. 2

Generating a 6-scrolls attractor without scaling

Fig. 3

Generating 6-scrolls with ranges that can be processed by commercially available operational amplifiers

Fig. 4

Block diagram description of (3)

To cope with this problem one can scale the PWL description by modifying (13) by $\alpha$. Now, the saturated nonlinear function series is redefined by (14), where $\alpha$ allows that $k<1$, because the chaos condition now applies on $s=\frac{k}{\alpha }$, the new slope. In this manner, k and $\alpha$ can be selected to allow $k<1$, so that the ranges in (13) can be scaled. As a result, now the generation of a 6-scrolls attractor with $a=b=c=d_1=0.7$, $k=1$, $\alpha =0.1$, $s=10$, $h=2$, and $p=q=2$, is shown in Fig. 3. As one sees, the ranges of the attractor are within the ranges that can be processed by commercially available operational amplifiers. Besides, it is possible to compute small ranges for realizing attractors with integrated circuit technology [20], it just depends on setting the values of k and $\alpha$.

$$\begin{aligned} \,{f(x_1;k,h,p,q)} = \left\{ \begin{array}{ll} (2q+1)k &{}\quad x_1>qh+\alpha \\ \frac{k}{\alpha }(x_1-ih)+2ik &{}\quad \mid x_1-ih\mid \le \alpha \\ &{}\quad -p\le i \le q\\ (2i+1)k &{}\quad {ih+\alpha <x_1<(i+1)h-\alpha } \\ &{}\quad -p\le i \le q-1\\ -(2p+1)k &{}\quad x_1<-ph-\alpha \\ \end{array} \right. \end{aligned}$$

(14)

By applying flow diagrams from linear systems, the dynamical system in (3) can be described by the block diagram shown in Fig. 4. An analogy to electronics, the diagram consists of 3 integrators, 1 adder, one current-to-voltage (I/V) converter, one block for the saturated nonlinear function series ($f(x_1)$) and amplifiers. In this manner, each block can be realized with commercially available operational amplifiers. One of the realizations is shown in Fig. 5, where the block for ($f(x_1)$) is labeled SNLF.

Fig. 5

Circuit realization of (3) by using commercial operational amplifiers

For realizing the nonlinear saturated function series, one can take advantage of the saturation properties of the operational amplifiers. In this manner, two saturated levels can be implemented in voltage mode by using the finite-gain model of the operational amplifier, as shown in Fig. 6. It is clear that by simulation, several limitations can be included, for example: gain, bandwidth, slew rate and saturation [11]. Therefore, if a shift-voltage $(\pm E)$ is added, one gets the shifted-voltage saturated functions described by (15) for positive and negative shifts, respectively, these effects are shown in Fig. 7.

$$\begin{aligned} V_o= & {} \frac{A_v}{2}\left( |V_i+\frac{V_{sat}}{A_v}-E|-|V_i-\frac{V_{sat}}{A_v}-E|\right) \\ \nonumber V_o= & {} \frac{A_v}{2}\left( |V_i+\frac{V_{sat}}{A_v}+E|-|V_i-\frac{V_{sat}}{A_v}+E|\right) \end{aligned}$$

(15)

The saturated nonlinear function series can now be implemented as shown in Fig. 8, where the number of operational amplifiers equals the number of scrolls to be generated, minus one. The reason is that one operational amplifier can generate 2-scrolls, then one needs three amplifiers to generate 3-scrolls, and so on. In the same manner, to generate a saturated nonlinear function with different voltage-shifts, then E takes different values in (15). On the other hand, the values of the plateaus k, in voltage and current, the breakpoints $\alpha$, the slope s and the saturated delays h are evaluated by (16) [15, 19].

$$\begin{aligned} k=R_{ix}I_{sat}, \quad I_{sat}=\frac{V_{sat}}{R_c}, \quad \alpha =\frac{R_{iz}|V_{sat}|}{R_{fz}}, \quad h=\frac{E_i}{(1+\frac{R_{iz}}{R_{fz}})} \end{aligned}$$

(16)

Fig. 6

Finite gain model of the operational amplifier

Fig. 7

Shift of the voltage when E takes a Negative and b Positive values

Fig. 8

Realization of the saturated nonlinear function series using operational amplifiers

Table 1 Optimized MLE and its associated entropy for generating 2-scrolls

5 Experimental Verification Results

To have control on varying the coefficients a, b, c and $d_1$ in (3), the multi-scroll chaotic oscillator was implemented as shown in Fig. 5, where the block sketching the saturated nonlinear function (SNLF) is shown in Fig. 8. The values of the circuit elements are: $C=1$ nF, $R=1\,\mathrm{M}\Omega$, $R_{ia}=R_{ib}=R_{ic}=R_{id}=10\,\mathrm{k}\Omega$, $R_i=R_f$, with $V_{sat} = \pm 16$ to $\pm 18\,\mathrm{V}$. Besides, to set the corresponding values of the coefficients a, b, c and $d_1$, associated to the optimized values for MLE listed in Tables 1, 2 and 3, linear precision potentiometers were used to tune the four decimals. In Fig. 5, the resistances associated to the four coefficients are labeled as: $R_{fa}$, $R_{fb}$, $R_{fc}$, $R_{fd}$.

Table 2 Optimized MLE and its associated entropy for generating 5-scrolls

Table 3 Optimized MLE and its associated entropy for generating 10-scrolls

The measurements were performed using a $200\,\text {MHz}$ oscilloscope with a sampling frequency of $1\,\text {G}/\text {s}$. This equipment introduces errors in saving the samples, so that it is reflected in the differences when computing the entropy from simulated and experimental results, as shown in Tables 2 and 3.

The experimental results for the realization of the saturated nonlinear function series with 3 and 19 segments, to generate 2- and 10-scrolls, respectively, are shown in Fig. 9. Other saturated nonlinear function series can be generated as already shown in [8, 11].

Fig. 9

Experimental results for the saturated nonlinear function series with a 3, and b 19 segments

Figure 10 shows the simulation results for six cases from Table 1. As one sees, case 11 has the lowest MLE, where all coefficients are set to traditional values of 0.7, as used in [8]. Furthermore, when applying [2], the other 10 cases provide higher MLEs, because the coefficients a, b, c and $d_1$ were varied (optimized). The simulated entropy also shown in Table 1, shows slight variations when the MLE increases, but it can be appreciated that in general it increases as MLE does it.

Fig. 10

Simulation results generating 2-scrolls for six cases in Table 1

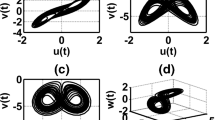
Figure 11 shows experimental results for generating two-scrolls for six cases in Table 1. As one sees, the more complex behavior appears for the highest MLE. This is better appreciated when incrementing the number of scrolls, as shown in the following cases for generating 5- and 10-scrolls.

Fig. 11

Experimental results generating 2-scrolls for six cases in Table 1

Figure 12 shows six cases from Table 2. In these cases it is better appreciated that the higher the value of the MLE, the better the complex behavior of the 5-scrolls attractor, i.e. the scrolls are less defined in the phase-space portraits, as already shown in [2]. This is indeed confirmed in Fig. 13 for generating a 5-scrolls attractor, for which we list the entropy computed from experimental data. It can be appreciated that the entropy increases as MLE does it.

Fig. 12

Simulation results generating 5-scrolls for six cases in Table 2

Fig. 13

Experimental results generating 5-scrolls for six cases in Table 2

Figure 14 shows six simulation results for generating 10-scrolls from Table 3. As one sees, case 11 is generated when the four coefficients have the same value of 0.7, for which the 10-scrolls are pretty good appreciated. However, the scrolls become more complex as the MLE increases, so that case 2 in Fig. 14 shows a more complex attractor.

The simulated entropy in Table 3 shows a little bit difference for the 11 cases, where cases 2 and 6 have the higher simulated entropy value.

Figure 15 shows six experimental cases from Table 3. The 10-scrolls attractors for those cases were generated using the saturated nonlinear function series shown in Fig. 9b, with 19 segments. As supposed, case 1 has the more complex chaotic behavior because it has the highest MLE. The other 5 cases shown in Fig. 15 are also complex because MLE is higher than when using traditional coefficient values of 0.7 [8]. In that case, the scrolls are more defined in the phase space diagram, as for the simulated case 11 in Fig. 14. As it was done for the 5-scrolls attractor, we list the entropy computed from experimental data in Table 3. Again, it can be appreciated that the entropy varies as MLE does it.

Figure 16 shows the state variable x for case 11, where one can count quite clearly the 10 levels that are associated to the 10 saturated levels of the saturated nonlinear function series shown in Fig. 9b. A similar behavior is for the state variable x for the other cases, but the phase space portraits are more complex as MLE being increased, as shown in Figs. 14 and 15.

Fig. 14

Simulation results generating 10-scrolls for six cases in Table 3

Fig. 15

Experimental results generating 10-scrolls for six cases in Table 3

Fig. 16

Counting 10 levels when generating a 10-scrolls attractor

From the simulated and experimental data, it can be concluded that the more scrolls are generated the higher the values for the entropy and MLE.

It is worth mentioning that because we used a $200\,\text {MHz}$ oscilloscope with a sampling frequency of $1\,\text {G}/\text {s}$, the saved experimental data is contaminated with undesired frequencies, as shown in Fig. 17. It means that one should filter the experimental signal to avoid aliasing and then recover the chaotic signal. Figure 18 shows the comparison of the signals in the phase space portraits, when they are plotted directly from the experimental data, and after the signal is filtered.

Fig. 17

Signal from experimental data and after it is filtered in MATLAB$^{TM}$

Fig. 18

Phase space portraits for the 10-scrolls attractor from: a experimental data and, b after it is filtered

The signals were filtered in MATLAB using y$\,=\,$sgolayfilt(x, k, f) (a Savitzky–Golay Finite Impulse Response smoothing filter). If x is a matrix, sgolayfilt operates on each column. The polynomial order k must be less than the frame size f, which must be odd. In our experiments, we used $k=9$ and $f=31$, to approximate the experimental data to the observed signals in the oscilloscope.

Finally, from the filtered data and from Tables 2 and 3, we selected the cases with the highest values for the MLE and their associated entropy computed from experimental data, so that they are shown in Figs. 19 and 20 for generating 5- and 10-scrolls, respectively.

Fig. 19

Phase space portraits from experimental data showing 5-scrolls with the highest a MLE and, b entropy

Fig. 20

Phase space portraits from experimental data showing 10-scrolls with the highest a MLE and, b entropy

6 Conclusion

This article showed the experimental verification on optimizing the MLE in a multi-scroll chaotic oscillator based on saturated function series, and its associated entropy. The optimization of MLE was performed by applying an evolutionary algorithm for generating 2-, 5- and 10-scrolls.

The laboratory experiments confirmed that the chaotic behavior becomes more complex as MLE is maximized. Furthermore, to better confirm the chaotic complexity associated to the value of MLE, we listed the associated entropy from simulated and experimental data for generating 2-, 5- and 10-scrolls attractors.

It was also discussed that to eliminate the undesired frequencies introduced by the poor sampling of the oscilloscope, the experimental data (signal) should be filtered.

As a final conclusion, the experiments showed that multi-scroll chaotic oscillators have a more complex chaotic behavior when the number of scrolls increases. For instance, Tables 1, 2 and 3 clearly show that by increasing the number of scrolls, when the chaotic oscillator is optimized, both MLE and the entropy increases.