Keywords

1 Introduction

Shooting method is the basic numerical method used to solve ordinary differential equations, when instead of initial conditions for the state trajectory, as in Cauchy problem (aka initial value problem—IVP), we have terminal conditions. Such a problem is called boundary value problem (BVP) [13]. This approach can be easily adapted to solve these optimal control problems, which need a higher precision of the solution, than obtained from the standard numerical approach, based on time discretization. In the latter, state and control trajectories are represented by vectors and from the differential state equations difference equations are obtained, which are treated as a set of equality constraints in a static nonlinear programming problem.

There are two possible approaches to transform an optimal control problem to BVP: direct and indirect.

In the direct approach the control interval is divided into a certain number of subintervals, on which Cauchy problem is solved by an ordinary differential equation (ODE) solver. The initial conditions are generated iteratively by an optimizer, the constraints on state and mixed are checked in the discretization points of the time interval.

In the indirect approach BVP concerns not only state equations, but also the equations describing adjoint variables. It means, that for an optimal control problem, before using a solver we have to make a kind of preprocessing on the paper, based on the appropriate theory. In particular, we have to determine the number of switching points, where the state trajectory enters and leaves the constraint boundary. Moreover, in this approach we have to provide the function connecting the optimal control at a given time instant with current value of state and adjoint variables (i.e., the control law). Only general formulas should be given, their parameters: Lagrange multipliers, initial values of adjoint variables and the concrete values of switching points (i.e., times) will be the subject of optimization. Actually, in the fundamental book of Pontryagin et al. [11] one may found a suitable version of the maximum principle to formulate BVP for problems with the constraints function of order one (in Chap. 6). The generalization to problems of higher orders was first given by Bryson et al. [1, 2].

In the author’s opinion, the BVPs corresponding to necessary conditions of optimality for quite a big class of optimal control problems with state and mixed control-state constraints can be derived in a simpler way, using local optimality theory. We adapt here the approach proposed by Wierzbicki [15], based on looking for stationary points of Lagrange functionals in abstract spaces. A similar reasoning, using generalized Kuhn-Tucker conditions in a Banach space, was presented by Jacobson et al. [5], but the derivation presented here is more straightforward.

In this paper we consider a Mayer-type problem with one state constraint of the order one with one boundary arc. The approach can be easily adapted to solve other problems with state and mixed constraints. After the derivation of the necessary conditions of optimality, a numerical approach where it can be used—the indirect shooting method—and an alternative to it—the direct shooting method—are shortly described and compared on a test problem taken from the literature.

2 Necessary Optimality Conditions for a General Optimal Control Problem with State and Mixed State-Control Constraints

For simplicity of formulas our presentation concerns problems with scalar control and constraint functions. The passage to the multidimensional case is obvious.

We want to determine a piecewise continuous control function \(u(t) \in \mathbb {R}\), \(t_0 \le t \le t_f\), which minimizes the Mayer functional

$$\begin{aligned} J(u)= g(x(t_f)) \end{aligned}$$
(1)

subject to the constraints

$$\begin{aligned} \dot{x}(t)=f(x(t), u(t),t), \;\; t_0 \le t \le t_f \end{aligned}$$
(2)
$$\begin{aligned} x(t_0)=x_0 \end{aligned}$$
(3)
$$\begin{aligned} r(x(t_f),t_f) = 0 \in \mathbb {R}^m \end{aligned}$$
(4)
$$\begin{aligned} S(x(t),t) \le 0, \;\; t_0 \le t \le t_f \end{aligned}$$
(5)
$$\begin{aligned} C(x(t),u(t),t) \le 0, \;\; t_0 \le t \le t_f \end{aligned}$$
(6)

Here, \(x(t) \in \mathbb {R}^n\) denotes a vector of the state variables, the constraint (4) describes boundary conditions, (5), (6) are nonstationary inequality constraints on current values of, respectively, state and state and control simultaneously. For simplicity, it is assumed, that the functions S, C are sufficiently continuously differentiable. The function f(x(t), u(t), t) is allowed to be merely piecewise continuously differentiable with respect to time variable, for \(t \in [t_0, t_f]\). The final time \(t_f\) is fixed. Problems with free final time or problems with integral terms in the performance index (Bolza or Lagrange) can be easily transformed into a problem of the type (1) by means of additional state variables. The constraints on control of the type:

$$\begin{aligned} u(t) \in U \subset \mathbb {R} \end{aligned}$$
(7)

can be expressed as a specific case of the mixed functional constraints (6).

The Lagrangian for the problem (1)–(6) will contain the standard components:

  • from the objective function

    $$\begin{aligned} g(x(t_f)) \end{aligned}$$
    (8)

  • from the initial conditions

    $$\begin{aligned} \langle \rho , x(t_0)-x_0 \rangle \end{aligned}$$
    (9)

  • from the state equation

    $$\begin{aligned} \int _{t_0}^{t_f} \langle \eta (t), \dot{x}(t)-f(x(t),u(t),t)\rangle \, dt, \end{aligned}$$
    (10)

where \(\rho \in \mathbb {R}^n\), \(\eta \) is the adjoint function with values in \(\mathbb {R}^n\) and \(\langle .,. \rangle \) denotes the scalar product, and some additional terms coming from the terminal, state and mixed constraints. These will be:

  • the product

    $$\begin{aligned} \nu ^T r(x(t_f),t_f) , \;\; \nu \in \mathbb {R}^m \end{aligned}$$
    (11)

    from the terminal constraint (4)

  • the integral

    $$\begin{aligned} \int _{t_0}^{t_f} \mu _C(t) \,C(x(t),u(t),t) \,dt \end{aligned}$$
    (12)

    where

    $$\begin{aligned} \mu _C(t) = \left\{ \begin{array}{ll} = 0,&{} C(x(t),u(t),t) < 0 \\ \ge 0, &{}C(x(t),u(t),t) = 0, \end{array} \right. \end{aligned}$$
    (13)

    from mixed control-state constraint (6).

The situation with the state constraint (5) is more complicated. When this constraint is active, that is \(S(x(t),t) = 0\), e.g. on some interval \([t_1,t_2] \subseteq [t_0, t_f]\), its time derivative along the path must vanish. That is, we must haveFootnote 1 [1, 2]

$$\begin{aligned} \frac{dS}{dt} = \frac{\partial S}{\partial t} + \left( \frac{\partial S}{\partial x}\right) ^T \dot{x} = \frac{\partial S}{\partial t} + \left( \frac{\partial S}{\partial x}\right) ^T f(x,u,t) = 0 \end{aligned}$$
(14)

The expression (14) may or may not have explicit dependence on u. If it does, the expression (14) for \(\frac{dS}{dt}\) plays on the boundary arc the same role as the function C defining mixed state-control variable constraint of the type (6). If it does not, we may take the next time derivative. We may repeat this procedure until, finally, some explicit dependence on u does occur [1, 2].

If this occurs on the qth time derivative, we will tell, that we have a qth-order state variable inequality constraint. In this case, the qth total time derivative of S(x(t), t) will be the component representing state inequality constraint (5) in the Lagrangian. More precisely, let \(S^{(k)}\) denotes the kth total time derivative of the state constraint function S, i.e.,

$$\begin{aligned} S^{(0)}(x(t),u(t),t):=S(x(t), t), \end{aligned}$$
(15)
$$ S^{(k+1)}(x(t),u(t),t) = \frac{d^{k+1}S}{dt^{k+1}}(x(t),u(t),t) $$
$$\begin{aligned} = \frac{\partial S^{(k)}}{\partial t}(x(t),u(t),t) + \left[ \frac{\partial S^{(k)}}{\partial x}(x(t),u(t),t) \right] ^T f(x(t),u(t),t), \;\; k \ge 0 \end{aligned}$$
(16)

The order q is the lowest order of derivative such, that \(S^{(q)}\) contains the control explicitly:

$$\begin{aligned} \frac{\partial S^{(k)}(x,u,t)}{\partial u} \equiv 0,\;\; k=0 ,\ldots , q-1,\; \frac{\partial S^{(q)}}{\partial u} \ne 0 \end{aligned}$$
(17)

Hence, we may write in the following:

$$\begin{aligned} S^{(k+1)}(x(t),u(t),t) \equiv S^{(k+1)}(x(t),t),\;\; k=0 ,\ldots , q-1 \end{aligned}$$
(18)

and the actual constraint will be:

$$\begin{aligned} S^{(q)}(x(t),u(t),t)=0, \;\; \text{ for } t \in [t_1,t_2] \end{aligned}$$
(19)

The corresponding component of the Lagrangian will have the form

$$\begin{aligned} \int _{t_0}^{t_f} \mu _S(t) \,S^{(q)}(x(t),u(t),t) \,dt \end{aligned}$$
(20)

where

$$\begin{aligned} \mu _S(t)= 0, \;\; \text{ for } t \notin [t_1,t_2] \end{aligned}$$
(21)

Since control of S(x(t), t) is obtained only by changing its qth time derivative, to keep the system on the constraint boundary, the path entering onto the constraint boundary has to meet the following “tangency” constraints at time \(t_1\) (or, equivalently at \(t_2\)) [1, 2]:

$$\begin{aligned} N(x(t_1),t_1) = \left[ \begin{array}{c} S(x(t_1),t_1)\\ S^{(1)}(x(t_1),t_1)\\ \vdots \\ S^{(q-1)}(x(t_1), t_1) \end{array} \right] =0 \end{aligned}$$
(22)

The corresponding component of the Lagrangian will be the scalar product:

$$\begin{aligned} \gamma ^T N(x(t_1),t_1) \end{aligned}$$
(23)

As an example we will consider the optimal control problem (1)–(5) (i.e. without mixed state-control constraint (6)) with the state constraint active on the interval \([t_1,t_2]\):

$$\begin{aligned} J(u)= g(x(t_f)) \end{aligned}$$
(24)

subject to the constraints

$$\begin{aligned} \dot{x}(t)=f(x(t), u(t),t), \;\; t_0 \le t \le t_f \end{aligned}$$
(25)
$$\begin{aligned} x(t_0)=x_0 \end{aligned}$$
(26)
$$\begin{aligned} r(x(t_f),t_f) = 0 \in \mathbb {R} \end{aligned}$$
(27)
$$\begin{aligned} S(x(t),t) \le 0, \;\; t_0 \le t \le t_f \end{aligned}$$
(28)

We assume, that the state-constraint (28) is of order one, that is \(q=1\), \(\gamma \in \mathbb {R}\).

The Lagrangian for this problem will be as follows:

$$ L(x,u,\eta , \rho , \mu _S,\gamma , \nu ) = g(x(t_f)) + \langle \rho , x(t_0)-x_0 \rangle + \int _{t_0}^{t_f} \langle \eta (t), \dot{x}(t)-f(x(t),u(t),t)\rangle \, dt + $$
$$\begin{aligned} \qquad \qquad \qquad \quad + \int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t)\, dt + \gamma S(x(t_1),t_1) + \nu r(x(t_f),t_f) \end{aligned}$$
(29)

Because of the possible discontinuity of the adjoint function \(\eta (t)\) at time \(t_1\), we will partition the integral stemming from the state equation, that is \( \int _{t_0}^{t_f} \langle \eta (t), \dot{x}(t)-f(x(t),u(t),t)\rangle \, dt\) into two components concerning two subintervals: \([t_0,t_1)\) and \((t_1,t_f]\). It is not necessary to partition the second integral stemming from the state constraint, that is \(\int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t)\, dt\), although its Lagrange multiplier function \(\mu _S(t)\) can be discontinuous at \(t_1\) too, because this discontinuity has no possibility to transform itself further into independent, different components of the Lagrangian, including those being functions of the state vector at time \(t_1\), that is \(x(t_1)\). The reason is, that to the first integral the integration by parts can be applied, while to the second it cannot.

After the mentioned partition, the Lagrangian (29) will take the form:

$$ L(x,u,\eta , \rho , \mu _S,\gamma ,\nu ) = g(x(t_f)) + \langle \rho , x(t_0)-x_0 \rangle + \int _{t_0}^{t_1^-} \langle \eta (t), \dot{x}(t)-f(x(t),u(t),t)\rangle \, dt + $$
$$ + \int _{t_1^+}^{t_f} \langle \eta (t), \dot{x}(t)-f(x(t),u(t),t)\rangle \, dt + \int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t)\, dt + $$
$$ + \gamma (S(x(t_1),t_1) + \nu r(x(t_f),t_f) = g(x(t_f)) + \langle \rho , x(t_0)-x_0 \rangle + $$
$$ + \int _{t_0}^{t_1^-} \langle \eta (t), \dot{x}(t) \rangle \,dt -\int _{t_0}^{t_1^-} \langle \eta (t), f(x(t),u(t),t)\rangle \, dt + $$
$$ +\int _{t_1^+}^{t_f} \langle \eta (t), \dot{x}(t) \rangle \, dt -\int _{t_1^+}^{t_f} \langle \eta (t), f(x(t),u(t),t) \rangle \, dt + $$
$$\begin{aligned} + \int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t)\, dt + \gamma S(x(t_1),t_1) + \nu r(x(t_f),t_f) \end{aligned}$$
(30)

Applying integration by parts to components with state velocity \(\dot{x}(t)\) we will get:

$$ L(x,u,\eta , \rho , \mu _S,\gamma ,\nu ) = g(x(t_f)) + \langle \rho , x(t_0)-x_0 \rangle + \langle \eta (t_1^-), x(t_1^-) \rangle - \langle \eta (t_0),x(t_0)\rangle + $$
$$ - \int _{t_0}^{t_1^-} \langle \dot{\eta }(t),x(t)\rangle \, dt - \int _{t_0}^{t_1^-} \langle \eta (t), f(x(t),u(t),t)\rangle \, dt + \langle \eta (t_f),x(t_f)\rangle -\langle \eta (t_1^+),x(t_1^+)\rangle + $$
$$ - \int _{t_1^+}^{t_f} \langle \dot{\eta }(t), x(t)\rangle \, dt -\int _{t_1^+}^{t_f} \langle \eta (t),f(x(t),u(t),t)\rangle \, dt + \int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t) \,dt + $$
$$\begin{aligned} +\gamma (S(x(t_1),t_1)) + \nu r(x(t_f),t_f) \end{aligned}$$
(31)

Grouping together similar terms, taking into account the continuity of the state variables, we will get:

$$ L(x,u,\eta , \rho , \mu _S,\gamma ,\nu ) = \langle \rho , x(t_0)-x_0 \rangle - \langle \eta (t_0),x(t_0)\rangle + $$
$$ +\,\langle \eta (t_1^-), x(t_1)\rangle +\gamma (S(x(t_1),t_1))- \langle \eta (t_1^+),x(t_1)\rangle + $$
$$ - \int _{t_0}^{t_1^-} \left[ \langle \dot{\eta }(t),x(t) \rangle +\langle \eta (t), f(x(t),u(t),t)\rangle \right] \, dt+ $$
$$ - \int _{t_1^+}^{t_f} \left[ \langle \dot{\eta }(t), x(t)\rangle + \langle \eta (t),f(x(t),u(t),t)\rangle \right] \,dt + \int _{t_0}^{t_f} \mu _S(t) S^{(1)}(x(t),u(t),t)\, dt + $$
$$ +\,g(x(t_f)) + \langle \eta (t_f),x(t_f)\rangle + \nu r(x(t_f),t_f)=\left[ \langle \rho , x(t_0)-x_0 \rangle - \langle \eta (t_0),x(t_0)\rangle \right] + $$
$$ +\left[ \langle \eta (t_1^-), x(t_1)\rangle +\gamma (S(x(t_1),t_1))- \langle \eta (t_1^+),x(t_1)\rangle \right] + $$
$$ - \int _{t_0}^{t_f} \left[ \langle \dot{\eta }(t), x(t)\rangle + \langle \eta (t),f(x(t),u(t),t)\rangle - \mu _S(t) S^{(1)}(x(t),u(t),t)\right] \, dt + $$
$$\begin{aligned} + \left[ g(x(t_f)) + \langle \eta (t_f),x(t_f)\rangle + \nu r(x(t_f),t_f)\right] \end{aligned}$$
(32)

It will be convenient now to define the Hamiltonian function for a part of the integrand expression:

$$\begin{aligned} H(x,u,\eta ,\mu _S,t) = \langle \eta , f(x,u,t)\rangle - \mu _S S^{(1)}(x,u,t) \end{aligned}$$
(33)

According to the theory presented in [15], the optimal solution is a stationary point of the Lagrangian. Owing to that, we will get the following conditions of optimality:  

State equation::
$$\begin{aligned} \dot{x}(t)=f(x(t), u(t),t), \;\; t \in [t_0, t_f],\; x(t_0)=x_0 \end{aligned}$$
(34)
Adjoint differential equation::
$$\begin{aligned} \dot{\eta }= - H_x(x, u,\eta ,\mu _S,t), \;\; t \in [t_0, t_f],\; \eta (t_0)=\eta _0 \end{aligned}$$
(35)
Initial point multipliers vector::
$$\begin{aligned} \rho = \eta (t_0) \end{aligned}$$
(36)
Natural boundary conditions::
$$\begin{aligned} \eta (t_f) =-\frac{\partial (g +\nu r)}{\partial x(t_f)} \end{aligned}$$
(37)
Switching (tangency) condition::
$$\begin{aligned} S(x(t_1),t_1)=0 \end{aligned}$$
(38)
Boundary arc condition::
$$\begin{aligned} S^{(1)}(x,u,t) = 0, \;\; t \in [t_1, t_2] \end{aligned}$$
(39)
Complementarity (sign) conditions::
$$\begin{aligned} \mu _S(t) =\left\{ \begin{array}{lcl} =0,&{} S(x(t),t) < 0 \\ \ge 0,&{} S(x(t),t) =0 \end{array} \right. \end{aligned}$$
(40)
Junction conditions::
$$\begin{aligned} \eta (t^+_1) = \eta (t_1^-) + \gamma S_x(x(t_1),t_1) \end{aligned}$$
(41)
Optimality condition::

Assuming, that \( \forall t \in [t_0,t_f]\) the Hamiltonian \(H(x,u,\eta ,\mu _S,t)\) is strictly convex with respect to u

$$\begin{aligned} \frac{\partial H}{\partial u} (x,u,\eta ,\mu _S,t)=0,\;\; \forall t \in [t_0,t_f] \end{aligned}$$
(42)

Otherwise (e.g., when the Hamiltonian is linear with respect to u), the modifications proposed by Maurer and Gillessen [7, 8] can be applied.

 

The (unknown) parameters in this problem are: \(\eta _{0}, t_1, t_2, \nu , \gamma \).

3 Indirect Multiple Shooting Technique

This short presentation is adapted from the Oberle article [9].

In the previous section we saw, that the necessary conditions for the general optimal control problems lead to BVP with switching conditions for the state x(t) and adjoint \(\eta (t)\) trajectory. The basic idea of the numerical treatment of such problems by multiple shooting technique is to consider the switching conditions as boundary conditions to be satisfied at some interior multiple shooting nodes [9]. Thus, the problem is transformed into a classical multipoint BVP [9, 13]:

Determine a piecewise smooth vector function \(y(t)=[x(t),\eta (t)]\), which satisfies

$$\begin{aligned} \dot{y}(t)=f(y,u,t), \;\; t_0 \le t \le t_f, \end{aligned}$$
(43)
$$\begin{aligned} u =u_k(t,y), \;\; \tau _k \le t \le \tau _{k+1},\;\; k=0,\ldots , p, \end{aligned}$$
(44)
$$\begin{aligned} y(t_0)= \left[ \begin{array}{c} x_0 \\ \eta _0 \end{array} \right] \end{aligned}$$
(45)
$$\begin{aligned} y(\tau ^+_k)=h_k(y(\tau ^-_k),\gamma _k), \;\; k=1,\ldots , p, \end{aligned}$$
(46)
$$\begin{aligned} r_i(y(t_f), \nu )=0, \;\;i=1,\ldots ,n_1, \end{aligned}$$
(47)
$$\begin{aligned} \tilde{r}_k(\tau _{k},y(\tau ^-_{k}))=0, \;\;k= 1,\ldots ,p. \end{aligned}$$
(48)

In this formulation, \(\eta _0, \gamma , \nu , \tau _k,k = 1,\ldots ,p\) are unknown parameters of the problem, where the latter satisfy

$$\begin{aligned} t_0=: \tau _0 < \tau _1 < \tau _2< \cdots < \tau _p< \tau _{p+1} := t_f \end{aligned}$$
(49)

The trajectory may possess jumps of size given by Eq. (46). If a coordinate of y(t) is continuous, then its \(h_k\) is identity. The boundary conditions and the switching conditions are described by Eqs. (47) and (48), respectively.

In every time stage k the numerical integration over the interval \([\tau _k, \tau _{k+1}]\) is done by any conventional IVP solver with stepsize control. The resulting system of nonlinear equations (47)–(48) can be solved numerically by a quasinewton method, e.g. from the Broyden family.

The approach presented in this section, where the solution is sought basing on the necessary optimality conditions, is called the indirect method.

4 Direct Multiple Shooting Technique

As it was shown in Sect. 2, the necessary conditions of optimality for general optimal control problems lead to BVP for the set of ODEs describing the evolution of the state x(t) and adjoint variables \(\eta (t)\) trajectories. Unfortunately, while the state variables are continuous, the adjoint variables may have jumps in points, where there are changes in the activity of constraints. Due to these jumps in \(\eta (t)\) trajectory, the only possible method to solve this problem is the multiple shooting algorithm presented in Sect. 3. The problem is, that rather a good initial approximation of the optimal trajectory is needed and rather a large amount of work has to be done by the user to derive the necessary conditions of optimality, in particular the adjoint differential equations [14]. Moreover, the user has to know a priori the switching structure of the constraints (the number and the sequence of the switching points), that is, he/she must have a deep insight into the physical and mathematical nature of the optimization problem [10, 14]. When the structure of the optimal control is more complicated and the solution consists of several arcs, it may lead to a very coarse approximation of the optimal control trajectory. Another drawback of the indirect approach is its sensitivity to parameters of the model, e.g., even small change of them, or an additional constraint, may lead to complete change of the switching structure [12].

In direct approaches, at the beginning the optimal control problem is transformed into a nonlinear programming problem [3, 6, 14]. In direct shooting method this is done through a parameterization of the controls u(t) on the subintervals of the control interval. That is, we take:

$$\begin{aligned} t_0 < t_1 <t_2 <\cdots t_{p} < t_{p+1} = t_f \end{aligned}$$
(50)
$$\begin{aligned} u(t) = u_j(t,\alpha _j), \;\; t \in I_j=[t_j,t_{j+1}],\; \text{ for } j=0,1,\ldots ,p \end{aligned}$$
(51)

where \(\alpha \in \mathbb {R}^{n_\alpha }\) is a vector of parameters. For example, u(t) may be: piecewise constant, piecewise linear or higher order polynomials, linear combination of some basis functions, e.g. B-splines. The basic idea is to simultaneously integrate numerically the state equations (2) on the subintervals \(I_j\) for guess initial points

$$\begin{aligned} z_j= x(t_j) \end{aligned}$$
(52)

Then the values obtained at the ends of subintervals—we will denote them by \(x(t_{j+1};z_j,\alpha _j)\)—are compared with the guesses \(z_{j+1}\).

The differential equations, initial and end points conditions and path constraints define the constraints of the nonlinear programming problem, that is the problem (1)–(6) is replaced with:

$$\begin{aligned} \min _{\alpha ,z} g(z_{p+1}) \end{aligned}$$
(53)
$$\begin{aligned} z_{j+1}-x(t_{j+1};z_j,\alpha _j)=0,\;\; j=0,\ldots ,p \end{aligned}$$
(54)
$$\begin{aligned} r(z_{p+1})=0 \end{aligned}$$
(55)
$$\begin{aligned} S(z_j,t_j) \le 0,\;\; j=0,\ldots ,p+1 \end{aligned}$$
(56)
$$\begin{aligned} C(z_j,\alpha _j,t_j) \le 0,\;\; j=0,\ldots ,p+1 \end{aligned}$$
(57)

where \(x(t_{j+1};z_j,\alpha _j)\) for \( j=0,\ldots ,p\) is the solution of ODE:

$$\begin{aligned} \dot{x}(t)=f(x(t), u_j(t,\alpha _j),t), \;\; t_j \le t \le t_{j+1} \end{aligned}$$
(58)
$$\begin{aligned} x(t_j)=z_j \end{aligned}$$
(59)

at \(t=t_{j+1}\).

This nonlinear programming problem can be solved by any constrained, continuous optimization solver.

5 A Case Study

Let us consider the following optimal control problem taken from Jacobson and Lele paper [4]:

$$\begin{aligned} \min _{u \in \mathbb {R}} \int _0^1 (x_1^2 +x_2^2+0.005u^2) dt \end{aligned}$$
(60)

where

$$\begin{aligned} \dot{x}_1&= x_2, \;\; x_1(0)=0 \end{aligned}$$
(61)
$$\begin{aligned} \dot{x}_2&=-x_2+u, \;\; x_2(0)=-1 \end{aligned}$$
(62)
$$\begin{aligned} x_2(t) \le 8(t-0.5)^2-0.5 \end{aligned}$$
(63)

To transform this problem into a Mayer problem form (1)–(6) we have to introduce an additional state variable \(x_3\) governed by the state equation:

$$\begin{aligned} \dot{x}_3= x_1^2+x_2^2+0.005u^2, \;\; x_3(0)=0 \end{aligned}$$
(64)

and replace the objective function (60) with

$$\begin{aligned} g(x(t_f))=x_3(1) \end{aligned}$$
(65)

which will be also minimized.

Now we may rewrite the optimization problem over the time interval \([t_0,t_f]=[0,1]\), introducing the vector notation from the Sect. 2, as the Mayer problem:

$$\begin{aligned} \min _{u \in \mathbb {R}} g(x(t_f)) = x_3(1) \end{aligned}$$
(66)
$$\begin{aligned} \dot{x} = f(x,u)= \left[ \begin{array}{c} x_2\\ -x_2+u\\ x_1^2+x_2^2+0.005u^2 \end{array} \right] \end{aligned}$$
(67)
$$\begin{aligned} x(t_0)=\left[ \begin{array}{c} 0\\ -1\\ 0 \end{array} \right] \end{aligned}$$
(68)
$$\begin{aligned} S(x,t) = x_2- 8(t-0.5)^2 + 0.5 \le 0 \end{aligned}$$
(69)

First, the problem (66)–(69) was solved by direct shooting method, described in Sect. 4, for \(p=20\) time subintervals of equal length with the help of two Matlab functions: ode45 (ODE solver; medium order method), fmincon (constrained nonlinear multivariable optimization solver).

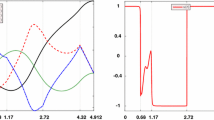
After 254.3 s we obtained the performance index value equal 0.2796. The resulting trajectories of the state variables \(x_1\) and \(x_2\) are presented in Fig. 1. Analyzing the resulting \(x_2\) state variable trajectory we may see, that it contains one boundary arc. To find its precise course the indirect shooting method described in Sect. 3, based on the theory presented in Sect. 2, was used.

Fig. 1
figure 1

Optimal state trajectories, obtained from the direct shooting method

Full size image

To derive optimality conditions for our problem we will start from the determination of the order q of the state constraint (69).

We have from Eqs. (15), (16):

$$ S^1(x,u,t)=\frac{\partial S}{\partial t} + \frac{\partial S^T}{\partial x} \cdot f(x,u) =-16(t-0.5)+[0\;\; 1\;\; 0] \left[ \begin{array}{c} x_2\\ -x_2+u\\ x_1^2+x_2^2+0.005u^2 \end{array} \right] = $$
$$\begin{aligned} =-16(t-0.5)-x_2+u \end{aligned}$$
(70)

It means, that \(q=1\). Hence, according to Eq. (33) the Hamiltonian function will be as follows:

$$ H(x,u,\eta ,\mu _S,t)=\langle \eta ,f(x,u)\rangle -\mu _S S^{(1)}(x,u,t) = \eta _1 x_2+\eta _2(-x_2+u)+ $$
$$\begin{aligned} +\eta _3(x_1^2+x_2^2+0.005 u^2)-\mu _S\left[ -16(t-0.5)-x_2+u\right] \end{aligned}$$
(71)

Applying the optimality condition (42) we will get:

$$\begin{aligned} \frac{\partial H}{\partial u} = \eta _2+0.01\eta _3\cdot u - \mu _S = 0 \end{aligned}$$
(72)

Taking into account the complementary condition (40), it means, that:

$$\begin{aligned} \hat{\mu }_S(t)= \left\{ \begin{array}{ll} \eta _2 + 0.01 \eta _3 \cdot u, &{} t \in [t_1,t_2]\\ 0, &{} t \notin [t_1,t_2] \\ \end{array}\right. \end{aligned}$$
(73)

From Eq. (35) the adjoint equation will be:

$$\begin{aligned} \dot{\eta }_1&=-\frac{\partial H}{\partial x_1} = -2\eta _3 x_1 \end{aligned}$$
(74)
$$\begin{aligned} \dot{\eta _2}&=-\frac{\partial H}{\partial x_2} = -\eta _1+\eta _2-2\eta _3 x_2 - \mu _S \end{aligned}$$
(75)
$$\begin{aligned} \dot{\eta _3}&=-\frac{\partial H}{\partial x_3}=0 \end{aligned}$$
(76)
Fig. 2
figure 2

Optimal trajectories of the state variables \(x_1\) and \(x_2\), obtained from the indirect shooting method

Full size image

Let us notice, that the Eq. (76) indicates, that

$$\begin{aligned} \eta _3(t) = const. \end{aligned}$$
(77)

We may find its value from the natural boundary conditions (37). Using it, we will get:

$$\begin{aligned} \eta (1)=-\frac{\partial g}{\partial x(1)} = \left[ \begin{array}{c} 0\\ 0\\ -1 \end{array}\right] \end{aligned}$$
(78)

Hence,

$$\begin{aligned} \eta _3(t) \equiv -1,\;\; t \in [0,1] \end{aligned}$$
(79)

From (70) and (72), applying (39) and (79), the optimal control will be expressed as:

$$\begin{aligned} \hat{u}(t)= \left\{ \begin{array}{ll} 16(t-0.5)+x_2(t), &{}\;\;\; t \in [t_1,t_2]\\ 100 \eta _2(t), &{}\;\;\; t \notin [t_1,t_2] \\ \end{array}\right. \end{aligned}$$
(80)

Finally, the junction conditions (41) will give us the equation:

$$\begin{aligned} \eta (t_1^+)=\eta (t_1^-)+\gamma \left[ \begin{array}{c} 0\\ 1\\ 0 \end{array}\right] = \left[ \begin{array}{c} \eta _1(t_1^-)\\ \eta _2(t_1^-)+\gamma \\ \eta _3(t_1^-) \end{array}\right] \end{aligned}$$
(81)
Fig. 3
figure 3

Optimal trajectory of the state variable \(x_3\), obtained from the indirect shooting method

Full size image
Fig. 4
figure 4

Optimal trajectories of the adjoint variables \(\eta _1\), \(\eta _2\) and the Lagrange multiplier for state constraint \(\mu _S\), obtained from the indirect shooting method

Full size image

Now we may put all these things together and express them in the format required by the indirect shooting method, described in Sect. 3, that is a system of nonlinear equations, with unknowns: \(\eta _{10}, \eta _{20}, t_1, t_2, \gamma \), to be satisfied at final and switching points, resulting from solution of ODEs with time functions: \(x_1(t),x_2(t),x_3(t),\eta _1(t),\eta _2(t)\), defined on three intervals: \([0,t_1], [t_1,t_2],[t_2,1]\), where starting points are defined by initial and junction conditions. Such a problem was solved under Matlab with the help of two Matlab functions: ode45 (mentioned above) and fsolve (a solver of systems of nonlinear equations of several variables). The calculations took 4.1 s, the obtained optimal value of the performance index was 0.1698. The results are presented in Figs. 2, 3, 4 and 5. One may see, that indeed, the solution is much more precise than that of the direct method, despite that the number of unknowns in the indirect method was much smaller than the dimension of the decision vector in the direct method (5 vs. 83) and the time of calculations was much shorter (4.1 s vs. 254.3 s on PC with Intel Core i7-2600K CPU@3.40 GHz processor).

Fig. 5
figure 5

Optimal control trajectory obtained from the indirect shooting method

Full size image

6 Conclusions

The advantage of the direct shooting approach is, that the user does not have to be concerned with adjoint variables or switching structures. The main disadvantage of it is the lower accuracy of the obtained solution, than that of the indirect method, where the infinite-dimensional problem is solved. In particular, in the indirect method, in contrast to direct methods, no approximations of the controls have been undertaken [3, 6, 14]. However, as the number of states is large compared to the number of controls, direct methods may be more efficient.

Nowadays, indirect methods are most often applied, when high accuracy of the solution is crucial [12], e.g., in the aerospace, chemical and nuclear reactors, robot manipulators, medical apparatus domain. Typically, initial guesses of the optimal state and control trajectories are generated by applying direct methods.

In the paper this methodology was applied to a case study concerning a Lagrange problem with a single state constraint and fully confirmed its usefulness.