Keywords

1 Introduction

A stock index is a mathematical weighted sum of some values that are listed in the same market. Since its creation in 1884, the stock indices have been used as an economic and financial activity measurement of a particular trade sector or a country.

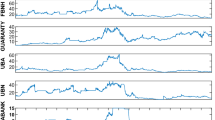
In this paper we wish to inquire about the statistical and fractal structure of the daily closing prices of five international stock indices (Eurostoxx 50, Ibovespa, Nikkei 225, Sensex, and Standard & Poor’s 500, of Europe, Brazil, Japan, India, and USA, respectively) through the years 2000–2014, using two different types of procedures. The stock data are freely available in the web Yahoo Finance [10]. We chose these selectives because they are a good representation of the trends of the market, since they collect and reflect the behaviors and performances of new and old economies. We wish to check if they have a similar statistical and self-affine structure (Figs. 1 and 2).

Since the founding work of L. Bachelier in this thesis “La théorie de la spéculation,” the random walk model has been present in almost all the mathematical approaches to the economic series.

Fig. 1
figure 1

Chart of Eurostoxx in the period 2000–2014

Full size image

Our goal is to check the hypothesis stating that these time data are Brownian motions. To this end we compute the following parameters: Hurst scalar, fractal dimension, and exponent of colored noise.

The Hurst exponent characterizes fractional Brownian variables, giving a measure of the self-similarity of the records. This number was proposed by H.E. Hurst in a hydrological study [1] and it has been applied over years in very different fields. Its recent popularity in the financial sector is due to later works like, for instance, those of Peters et al. [7–9]. Through the exponent we obtain the fractal dimension, describing the fractal patterns involved in the complexity of the chart.

Fig. 2
figure 2

Chart of Sensex in the period 2000–2014

Full size image

We compute the annual dimensions, providing an indication of the chaoticity of data, that is to say, whether every record is a pure random variable (fractal dimension equal to 2) or on the contrary it owns strong underlying trends (dimension near 1). We have performed statistical tests as well, in order to elucidate if the computed parameters are significantly different between the indices studied.

In all the cases we analyze the closing prices. The returns can be treated as time series considering, for instance, GARCH models [6].

2 Exponent of Colored Noise

In general it is said that the economical series are well represented by colored noises, and we wished to test this hypothesis. A variable of this type satisfies an exponential power law:

$$\displaystyle{S(\,f) \simeq kf^{-\exp },}$$

where f is the frequency and S( f) is the spectral power. In our case we compute discrete powers corresponding to discrete frequencies (mf 0), where \(f_{0} = 2\pi /T\) is the fundamental frequency and m = 1, 2, … (T is the length of the recording). A logarithmical regression of the variables provides the exponent as slope of the fitting.

For it we construct first a truncated trigonometric series in order to fit the data [5]. Since the Fourier methods are suitable for variable of stationary type, we subtracted previously the values on the regression line of the record. We analyzed the index year by year and obtained an analytical formula for every period, as sum of the linear part and the spectral series. We compute in this way a discrete power spectrum which describes numerically the great cycles of the index. We performed a graphical test in order to choose the number of terms for the truncate sum. We find that 52 summands are enough for the representation of the yearly data, that corresponds to the inclusion of the cycles of weekly length. The formula is almost interpolatory. The harmonics of the series allow us to obtain the spectral powers. These quantities enable a numerical comparison between different indicators, for instance. In this case we used the method to inquire into the mathematical structure of the quoted indices. The numerical procedure is described in the reference [5] (Fig. 2).

In Table 1 the exponents computed for the years listed are presented. The mean values obtained on the period are: 1. 95, 1. 94, 1. 99, 1. 93, and 1. 97 for Eurostoxx 50, Ibovespa, Nikkei 225, Standard & Poor’s 500, and Sensex, respectively, with standard deviations 0. 16, 0. 22, 0. 20, 0. 13. , and 0. 17. The results suggest fairly a structure close to a red noise, whose exponent is 2. The correlations obtained in their computation are about 0. 8.

Table 1 Exponent of colored noise
Full size table

3 Fractional Brownian Motion

For stock indices, the Hurst exponent H is interpreted as a measure of the trend of the index. A value such that 0 < H < 0. 5 suggests anti-persistence, and the values 0. 5 < H < 1 give evidence of a persistent series. Thus, the economical interpretation is that a value lower than 0. 5 points to high volatility, that is to say, changes more frequent and intense, meanwhile H > 0. 5 shows a more defined tendency. By means of the Hurst parameter, one can deduce whether the record admits a model of fractional Brownian motion [3].

It is said that the Brownian motion is a good model for experimental series and, in particular, for economic historical data. The fractional (or fractal) Brownian motions (fBm) were studied by Mandelbrot (see for instance [2, 3]). They are random functions containing both independence and asymptotic dependence and admit the possibility of a long-term autocorrelation. Another characteristic feature of fBm’s is the self-similarity [3]. In words of Mandelbrot and Van Ness [3]: “fBm falls outside the usual dichotomy between causal trends and random perturbation.” The fractional Brownian motion is generally associated with a spectral density proportional to \(1/f^{2H+1},\) where f is the frequency. For \(H = 1/2\) one has an \(1/f^{2}-\) noise (Brownian or red).

A fractional Brownian motion with Hurst exponent H, B H (t, ω), is characterized by the following properties:

  1. 1.

    B H (t, ω) has almost all sample paths continuous (when t varies in a compact interval I).

  2. 2.

    Almost all trajectories are Hölder continuous for any exponent β < H, that is to say, for each such path, there exists a constant c such that

    $$\displaystyle{\vert B_{H}(t,\omega ) - B_{H}(s,\omega )\vert \leq c\,\vert t - s\vert ^{\,\beta }.}$$
  3. 3.

    With probability one, the graph of B H (t, ω) has both Hausdorff and box dimension equal to 2 − H. 

  4. 4.

    If \(H = \frac{1} {2}\), B H (t, ω) is an ordinary Brownian function (or Wiener process). In this case the increments in disjoint intervals are independent.

  5. 5.

    The increments of B H (t, ω) are stationary and self-similar, in fact

    $$\displaystyle{\{B_{H}(t_{0} + T,\omega ) - B_{H}(t_{0},\omega )\}\thickapprox\{h^{-H}(B_{ H}(t_{0} + hT,\omega ) - B_{H}(t_{0},\omega ))\},}$$

    where \(\thickapprox\) means that they have the same probability distribution.

  6. 6.

    The increments \(\{B_{H}(t_{0} + T,\omega ) - B_{H}(t_{0},\omega )\}\) are Gaussian with mean zero and variance proportional to T 2H [3, Corollary 3.4].

  7. 7.

    For \(H > \frac{1} {2}\), the process exhibits long-range dependence.

The goal of our numerical experiment is to inquire about the structure of the daily stock data as fractional Brownian motions. Are they really variables of this type?

We take advantage of the defining property 6 in order to compute the exponent H, instead of using the R/S algorithm. We consider annual records and delays of 1,2 …, days [4]. The procedure itself constitutes a test to check the model. The method performs much better than the technique described in the previous section. Consequently we think that the current framework improves the latter largely.

Table 2 Hurst parameter
Full size table

Table 2 displays the Hurst exponents computed for the period considered. The mean values obtained are: 0. 45, 0. 46, 0. 48, 0. 44, and 0. 50, for Eurostoxx 50, Ibovespa, Nikkei 225, Standard & Poor’s 500, and Sensex, respectively. The results emphasize an evident model of fractional Brownian motion, whose exponents range from 0 to 1. The correlations obtained in the computation of the parameter are close to 1, pointing to a more accurate description of the series considered in the Mandelbrot theory. A classical Brownian motion corresponds to an exponent of 0. 5.

We summarize now the results obtained for the Hurst parameter:

Regarding Eurostoxx index, the maximum value (0. 506) is recorded in 2009 and the minimum (0. 390) in 2008. Thus, the range variation is 0. 116 which represents a 22. 92 % with respect to the maximum value.

In the Brazilian data, the highest Hurst exponent is reached in 2003, with value 0. 518. The minimum occurs in the year 2008, with a value of 0. 413. The parameter varies in the period 0. 105 points, representing a 22. 27 % of the peak value.

In the Japanese index the absolute extremes occur in 2012 and 2001 with values 0. 585 and 0. 409, respectively. The second minimum (0. 412) is recorded in 2008. The range of variation is 0. 176 (30. 08 %).

For the S&P index, the maximum is reached in 2014 with value 0. 510, and in 2008 there is a minimum of 0. 352. The range of variation in the scalar in the S&P index is 0. 158 (30. 98 %).

Regarding Sensex, the maximum is set to 0. 575 in 2003, which represents the global highest exponent recorded. A minimum of the Hurst exponent is found in 2009 with value 0. 455. The range of absolute variation is 0. 12, a 20. 87 % with respect to the peak value of the period.

In 2008, beginning of the financial crisis, a general drop occurs in the Hurst exponent of the indices, reaching the absolute minimum of the period in the Western countries. The fall on Eastern countries is lower, pointing to less influence of the financial crisis on these selectives.

Table 3 Mean and standard deviation of the Hurst parameter of the indices in the periods pre-crisis and crisis
Full size table

Table 3 displays the average Hurst parameters of the indices in the periods 2000–2007 (pre-crisis) and 2008–2014 (crisis). These exponents increase very slightly in the second term, except in the Indian case, but the number of samples is insufficient (and the difference too small) to perform statistical tests in order to check the increment. The variability is higher in the second period too, with the exception of Sensex.

Table 4 Variance fractal dimension
Full size table

Table 4 shows the annual fractal dimensions computed for the years considered. The average values obtained are: 1. 55, 1. 54, 1. 52, 1. 56, and 1. 50, for Eurostoxx 50, Ibovespa, Nikkei 225, Standard & Poor’s 500, and Sensex respectively, with standard deviations 0. 03, 0. 03, 0. 04, 0. 04, and 0. 03.The typical fractal dimension of a Brownian motion is 1. 5. The highest fractal dimension (1. 648) is recorded in the American index during the year 2008 (outbreak of the crisis). The second maximum is European (1.610).

3.1 Statistical Tests

We have performed a nonparametric Mann–Whitney test to the parameters obtained for the five selectives. The objective was to find (if any) significant differences in the values with respect to the index considered. The samples were here the annual Hurst values of each selective. The parametric tests require some hypotheses on the variables like, for instance, normality, equality of variances, etc. In our case we cannot assume the normality of the distribution because it is unknown. Commonly this condition may be acceptable for large samples, but the size is small here, and for this reason we chose a nonparametric test, being Mann–Whitney a valid alternative. We provide the results of the test applied to the outcomes of the Hurst parameter of the five indices and 15 years. The p-values are shown in Table 5.

We can observe that, with a significance level of 0.05, there are differences in Sensex with respect to Standard & Poor’s 500, Eurostoxx, and Ibovespa. The same occurs in the Japanese selective, which performs differently from Eurostoxx and S&P. The larger means correspond to the Eastern countries in both periods (see Table 3).

Table 5 p-Values obtained in the statistical test
Full size table
Fig. 3
figure 3

Fractal dimensions of Eurostoxx (squares) and Sensex (dots) over the period considered

Full size image

4 Conclusions

The fractal tests in the stock records analyzed in the period 2000–2014 provide a variety of outcomes which we summarize below.

  • The numerical results present a great uniformity. Nevertheless, the p-values provided by the statistical test support, at 95 % confidence level, the numerical differences in the Indian index with respect to S& P, Europe, and Brazil, and those of Japan with respect to Eurostoxx and S&P.

  • The fractal dimensions of India and Japan are slightly lower than the rest of the indices, pointing to a bit less complex pattern of the records (see Fig. 3).

  • The year 2008 (beginning of the crisis) records a global minimum of the Hurst exponent in the Western countries. The drop of this oscillator is less evident in the Eastern economies, pointing to a more reduced (or delayed) influence of the financial crisis. The location of the maxima is not so uniform and moves over the period.

  • The mean average of the Hurst exponents is 0. 47. The standard deviations are around 0. 03.

  • The results obtained from the exponent α are around 1. 95, very close to the characteristic value of a red noise or Brownian motion (α = 2), with a typical deviation of 0. 02.

  • The correlograms of the different indices, whose tendency to zero is slow, preluded a type of random variable very different of a white noise. The computations performed confirmed this fact. The stock records may admit a representation by means of colored noises, in particular of red noise, refined by a model of fractional Brownian motion quite strict. The numerical results suggest that the Hurst exponent is a good predictor of changes in the market.

  • The Hurst scalar is suitable for the numerical description of this type of economical signals. The exponent gives a measure of the self-similarity (fractality) of the data.

In general, we observe a mild anti-persistent behavior in the markets (H < 0. 5) that is slightly weaker in the Eastern economies (mainly in India during the first years of the period). Nevertheless, it is likely that the globalization process will lead to a greater uniformity.

Concerning the methodology, we think that the first test performed is merely exploratory. The necessary truncation of the series defined to compute the powers collects only the macroscopic behavior of the variables and omits the fine self-affine oscillations. The fractal test is however robust. There is absolutely no doubt that the tools provided by the Fractal Theory allow us to perform a more precise stochastic study of the long-term trends of the stocks, and give a higher consistency than the classical hypotheses.