A Trajectory Prediction Method for Location-Based Services

Abstract

Most existing location prediction techniques for moving objects on road network are mainly short-term prediction methods. In order to accurately predict the long-term trajectory, this paper first proposes a hierarchical road network model, to reduce the intersection vertexes of road network, which not only avoids unnecessary data storage and reduces complexity, but also improves the efficiency of the trajectory prediction algorithm. Based on this model, this paper proposes a detection backtracking algorithm, which deliberately selects the highest probability road fragment to improve the accuracy and efficiency of the prediction. Experiments show that this method is more efficient than other existing prediction methods.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

At present, most of the holistic trajectory prediction algorithms focus on free spaces solution [1, 2], only few of them are based on moving objects in a real road network. And for those ones, they mostly just focus on the short-term predictions [3, 4]. However, existing long-term prediction algorithms also fail to consider contextual information, which leads to a lot less accurate results especially at certain turning points.

To go beyond short-term prediction, this paper formulates a road network hierarchical model by analyzing a large number of historical trajectory data of moving objects. The model aims to reduce network complexity and capture the turning patterns at intersections. Based on the model, this paper presents a detection-backtracking algorithm to improve the accuracy and efficiency. It applies to both the short-term and long-term predictions even if the destination remains unknown, which also deals with dead ends and overlapping trajectories.

The rest of this paper is organized as follows. Section 2 discusses the related work. Section 3 formally introduces our prediction model. Section 4 introduces the prediction algorithm. Section 5 presents the experimental results of performance evaluation. Our conclusions are contained in Sect. 6.

2 Preliminaries

The existing methods of location prediction for moving objects are roughly categorized to linear predictions [1, 2] and non-linear predictions [3, 5, 6]. Usually, linear predictions are based on constant speeds and linear functions of time, while their variants may assume the constant speed at first but calculate the trajectories by factors such as edges or paths. And for those who combine edges with vectors [7], they surely perform well in predicting trajectories of moving objects with constant speeds in free spaces, but they might all readily break as they can’t fit objects who are subject to real road networks which turn out to be much more perplexing.

Non-linear predictions use more complex mathematical equations than linear predictions do. Chen et al. [8] introduces SP method, which depends on Generalized Cellular Automata (GCA), using simulation and linear regression to predict the borders of future trajectories. Tao et al. [3] introduces a prediction model based on recursively-moving functions for those moving with uncertainty. Gaussian process regression model is also applied in trajectory predictions [5, 6]. Those methods can only apply to non-linear movements instead of sudden turnings.

Karimi and Liu [9] introduce a Predictive Location Model (PLM), which applies a probability matrix to each intersection for calculating the probability of objects’ turning each upcoming edge by analyzing their historical trajectories, and then uses a depth-wise algorithm to get new trajectories. However, Depth-wise search doesn’t consider the probability of each turning, and the search range is based on the Euclidean Distance, namely, the object’s current speed is multiplied by the time. That is might not accurate because the objects in real networks are always changing.

Kim et al. [10] comes up with a method that is similar to ours, but under their consideration, the destination is already known, while we assume it is not. Jeung et al. [11] introduces a PLM-based model as well as two prediction algorithms-Maximum Likelihood Algorithm (MLA) and Greedy Algorithm (GA). MLA is able to predict long trajectories, but once the duration is long enough to some level, it will need a lot more sub-trajectories to support its predictions, which drastically degrades the efficiency of the program. GA, in comparison, has a better performance on long-term predictions, but still, hasn’t covered contextual information and leaves the problem of overlapping trajectories. Besides, it will be terminated as soon as a dead end comes up. A. Houenou et al. [4] combines CYRA with MRM, to predict vehicles’ trajectories. The method tends to avoid collisions, but only in a very short period of time (namely, a few seconds), certainly not appealing to our interests of long-term predictions.

3 Prediction Model

In this section, we first define a hierarchical sketch on road network. Next we give some basic concepts and definitions for trajectory prediction based on the model. Then we describe our establishment of turning patterns at intersections.

3.1 Road Network Diagram and Sketch

Definition 1

Road Network Diagram

Road network diagram can be described as an undirected graph $G=<V, E>$, where V is the vertex set (the size is |V|) and E is the edge set (the size is |E|). Each vertex v ($v\in V$) represents an intersection, also a coordinate point $p={x, y}$ in a two-dimensional space. Each edge $e=(v_i, v_j)$ ($v_i, v_j\in V, e\in E$) represents the edge between two intersections. Figure 1 illustrates the idea.

Fig. 1.

Road network diagram

Fig. 2.

Road network sketch

Definition 2

Vertex Degree and Connection Vertex

Given road network diagram $G=<V, E>$, $v_i \in V$, $deg(v_i)$ is equal to the number of edges connected to $v_i$. Vertex $v_i$ is a connection vertex if $deg(v_i)\ge 2$.

Definition 3

Side Chain

Given a sequence of edges $S=<e_i, e_{i+1},\cdots ,e_{i+k}>$, S is a side chain if each vertex between two adjacent edges is a connection vertex.

Definition 4

Road Network Sketch

$G'=<V', E'>$ is the road network sketch, where $V'$ is the vertex set after the removal of all the connection vertexes from V and $E'$ is the edge set of side chains as well as those non-adjacent edges.

As shown in Fig. 1, the size of vertex set V (| V |) is 13 and that of edge set E (| E |) is 17. In Fig. 2, $| V'|$ is only 8 and $| E' |$ is 12. Note that by transferring G into $G'$, we will be able to reduce the amount of vertexes and edges to simplify the whole model. The following discussions will all based on road network sketch. If not specified, We replace $G'=<V', E'>$ with $G=<V, E>$ for convenience.

3.2 Road Network Hierarchy

Given a large-scale network, trajectories of each moving object only cover relatively small part, leaving many roads and intersections unvisited. To further reduce the road network complexity and narrow down the search range, we adopt hierarchical strategy by observing the visit of an edge or an intersection.

Figure 2 contains 8 vertexes and 12 edges. Given $E_v$ as the edge set of the visited trajectories, we divide the network into two layers-$G_1=<V_1, E_1>$ and $G_2=<V_2, E_2>$. Details about major steps of the process are as follows:

• Step1. Randomly select an $e_i=<v_i, v_j>(e_i \in G)$, where $deg(v_i)=1$. If $e_i$ is already in $E_v$, store (ei, vi, vj) into $G_1$. Otherwise, store them into $G_2$.

• Step2. Get the adjacent edge set of $v_j$ as $E_n$. If $E_n$ is not empty, iterate each edge $e_n=<v_j, v_k> \in E_n$. If $e_n \in E_v$, store $(e_n, v_j, v_k)$ into $G_1$. Otherwise, store them into $G_2$. So far, if $e_i$ is not in the same layer as $e_n$, connect corresponding vertex $v_j$ in both $G_1$ and $G_2$ and establish a virtual edge $ve_n$.

• Step3. Repeat Step 2 until iterate all the vertexes in G, and formulate the hierarchical road network model.

Figure 3(a) shows part of a road network, where thick lines denote the historical trajectories. We first pick up $e_1=<v_1,v_2>$ as the starting edge. Since $e_1$ has been visited, we store $(e_1, v_1, v_2)$ into $G_1$. Then we get $E_n={e_2,e_7}$ as the adjacent edge set of $v_2$. As $e_2$ has been visited but $e_7$ has not, we store $(e_2, v_2, v_3)$ and $(e_7, v_2, v_6)$ into $G_1$ and $G_2$ respectively. Note that $e_1$ and $e_7$ are not in the same layer, so we establish a virtual edge $ve_1$ to connect the corresponding vertex $v_2$ in both $G_1$ and $G_2$. Similarly, $e_3$ and $e_6$ go to $G_1$, while $e_4, e_5, e_8$ and $e_9$ go to $G_2$. So we establish $ve_2$ and $ve_3$. Figure 3(b) shows the network model after hierarchy.

Fig. 3.

Example of hierarchical road network processing

3.3 Concepts and Definitions for Trajectory Predictions

Suppose $e=(v_i, v_j)(e \in G)$, then the position of a moving object on this edge can be expressed as $L=(e, d, p, t)$, with direction heading to vertex $v_j$, where e represents the current edge of the object, d is the distance between the object and $v_i$, p is the object’s coordinate, t is the current time. The prediction duration T represents a time period as the object is moving from the current time $t_c$ to a future time $t_f$. Given L and T, we can narrow down the trajectory prediction problem to analyzing the trajectory in $[t_c, t_{c+T}]$.

Definition 5

Trajectory

If we map each p to its corresponding position $L_i (i=1, 2, 3\cdots n)$, then a trajectory can be considered as an ascending time sequence with series of positions, which can be expressed as $Traj=<L_i, L_2\cdots L_n>$.

Definition 6

Position Distance

Suppose $L_i$ and $L_j$ are two different positions of the same edge (both can be endpoints), then the distance between $L_i$ and $L_j$ is $Dist(L_i, L_j)$.

In order to evaluate the trajectory prediction query, consider two erroneous measurements: mean absolute error [12] and trajectory matching degree. As the position is described in two dimensional coordinate, we adopts $L^2$ norm.

Definition 7

Mean Absolute Error (MAE)

Suppose $\{L_{act1}, L_{act2},\cdots , L_{actN}\}$ is the trajectory of a moving object in time period $[t_c, t_{c+T}]$, while $\{L_{pre1}, L_{pre2},\cdots , L_{preN}\}$ is the predicted trajectory, we can calculate MAE as follows:

$$\begin{aligned} MAE=\frac{\sum _{i=1}^{N}|L_{prei}-L_{acti}|}{N}=\frac{\sum _{i=1}^{N}\biggl [(x_{prei}-x_{acti})^2+(y_{prei}-y_{acti})^2\biggl ]^{1/2}}{N} \end{aligned}$$

(1)

Definition 8

Trajectory Matching Degree (TMD)

Assume $E_{act}$ is the actual trajectory edges set in between $L_c$ and $L_{act}$, and $E_{pre}$ is the predicted trajectory edges set in between $L_c$ and $L_{pre}$, the precision and recall of the prediction can be described as $precision=\frac{|E_{act}\cap E_{pre}|}{|E_{pre}|}$ and $recall=\frac{|E_{act}\cap E_{pre}|}{|E_{act}|}$. Thus we adopts F1-score [13] as TMD:

$$\begin{aligned} F1=\frac{2\cdot precision\cdot recall}{precision+recall} \end{aligned}$$

(2)

3.4 Turning Pattern at Intersections

The turning pattern problem of moving objects is the decisive factor to the prediction accuracy. In fact, many turning scenarios come with certainties, e.g., a car will make a specific turn when entering the highway and a man’s daily drive usually follows a fixed route (home-company-home). We will take advantage of these information to find turning patterns for trajectory prediction.

Figure 4 shows part of a user’s historical trajectories at an intersection. Each line represents a certain trajectory with an arrow pointing the direction and a label showing the class it belongs to. As during different time periods, the trajectories are different. Hence N number of time periods can divide trajectories into N classes, labeled as 0, 1, 2, ... N. To simplify, we only use 1 and 0 as our class labels, which represents workday and weekend respectively.

Fig. 4.

Example of mobile object’s historical trajectory at intersection

Fig. 5.

Offset angle of road segment

Suppose the object has a state at every edge, when its current trajectory covers a new edge, we name it state transition. To illustrate state transition, we define O as the historical trajectory set, $Traj_o$ as the visited trajectory, $e_{cur}$ as the current edge, $e_i$ as the upcoming edge, c as the class label and $E_v$ as the edge set connected to the vertex v.

So $Traj_o\rightarrow e_i$ is a state transition. If $Traj\rightarrow e_i$ is already covered in O and with a class c, we define $SP_o(Traj_o\rightarrow e_i)[c]$ as its support degree. So we give the state transition probability (STP) of $Traj_o$ with a class c that is turning to $e_i$ from v:

$$\begin{aligned} STP(v,Traj_o\rightarrow e_i)[c]=\frac{SP_o^\alpha (Traj_o\rightarrow e_i,c)\times \phi ^\beta (e_i)}{\sum {e_j\notin Traj_o}^{}SP_o^\alpha (Traj_o\rightarrow e_j,c)\times \phi ^\beta (e_j)} \end{aligned}$$

(3)

We also define the STP of $e_{cur}$:

$$\begin{aligned} STP(v,e_{cur}\rightarrow e_i)[c]=\frac{SP_o^\alpha (e_{cur}\rightarrow e_i,c)\times \phi ^\beta (e_i)}{\sum {e_j\notin Traj_o}^{}SP_o^\alpha (e_{cur}\rightarrow e_j,c)\times \phi ^\beta (e_j)} \end{aligned}$$

(4)

$\phi (e_i)$ in Eqs. 3 and 4 represents offset factor on $e_i$, which is usually considered to be the reciprocal of offset angle $\theta _i$ (see Eq. 6). For a moving object, the smaller $\theta _i$ it has, the bigger $\phi (e_i)$ it gets, so is STP. $\alpha$ and $\beta$ are the support degree and offset factor weight, respectively.

According to Eqs. 3 and 4, we can predict the next edge $e_{next}$ that the object is about to turn:

$$\begin{aligned} e_{next}=\left\{ \begin{array}{ll} arg_{e_i}max(STP(v_{cur},Traj_o\rightarrow e_i)[c]) &{} \text {if }\,Traj_o\rightarrow e_i exist\\ arg_{e_i}max(STP(v_{cur},e_{cur}\rightarrow e_i)[c]) &{} else \end{array} \right. \end{aligned}$$

(5)

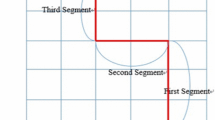
In the lack of historical trajectories, driving directions become the decisive factor to predict $e_{next}$. As shown in Fig. 5, $\theta$ is the offset angle between direction vector n and edge vector e, $L_c$ is the initial position of a moving object, $L_s$ is the intersection the object currently in, $E_a$ is the set of unvisited edges connected to the vertex, we choose the edge as our $e_{next}$ with the smallest $\theta$ by using cosine formula:

$$\begin{aligned} e_{next}=arg_{e_i\in E_a}min(\theta _{e_i})=\left\{ \begin{array}{ll} \theta _i \in (0^{\circ },180^{\circ })\\ n=(x_c-x_s,y_c-y_s)\\ e_i=(x_i-x_c,y_i-y_c)\\ arg_{e_i\in E_a}max(cos\theta _{e_i})=arg_{e_i\in E_a}max(\frac{n\cdot e_i}{|n|\cdot |e_i|}) \end{array} \right. \end{aligned}$$

(6)

4 Prediction Algorithm

4.1 Algorithm Design

This paper presents a detection backtracking algorithm (DBT). Algorithm 1 searches the edge with maximum STP and Algorithm 2 is the detailed pseudo code of DBT.

In reality, a single factor sometimes can lead to a very complex prediction model, so most existing algorithms exclude the factors we mentioned in Sect. 1 (e.g. contextual information, loop and etc.). We list four cases below:

• Arrest point. Moving objects are not moving all the time. For example, in situations like buying coffee when heading off to work or going shopping on the way home, it usually takes several minutes or hours to stay at a certain spot, which referred as arrest point. Given the current trajectory’s class, by analyzing historical trajectories and calculating the gathering numbers of spots, we are able to tell which case the arrest point belongs to.

• Loop. In most cases, it is not possible to form a loop, because moving objects usually head toward their designated places, which is closely related to human behaviors. However, there are some exceptions. For example, a driver has to go home for some important documents even though he or she is half way to work. But these are small probability events, so we leave them out.

• Partially overlapping trajectories will lead to turning errors. In Fig. 6, if we use probability matrix [9] and mobile transferring probabilistic method [11], $e_2\rightarrow e_4\rightarrow e_6$ will increase the probability of turning $e_6$ at intersection $v_2$ to 2 / 3, the predicted trajectory will be $e_1\rightarrow e_4\rightarrow e_6$, which is obviously wrong. As the trajectories partially overlapped in some edges might lead to wrong trajectory, we gave $e_{next}$ in Eq. 5 at first to avoid the problem.

• No historical trajectory exists. Refer to Eq. 6, it will help to pick the right edge to turn to by calculating deviation angle $\theta$ of a moving object.

Fig. 6.

Overlapping road segment of trajectory

4.2 Time Complexity Analysis

Suppose the number of traversed vertexes during one prediction is $|V'|$, then $O(|V'|)$ is the time complexity for one traversal. But we also have to calculate the highest STP at each vertex and query the historical time spent on the current edge. In this paper, we use binary search algorithm, the time complexity is $O(2\cdot log|V|)$. Together, the total time complexity of our algorithm is $O(2\cdot |V'|\cdot log|V|)$. In fact, we only count O(log|V|) because $|V'|$ can be taken as a constant since our algorithm usually only traverse a few vertexes. As k increases, it needs more time to do pruning, also has to compute more MBRs, leading to the increasing time consumption of the algorithm.

5 Experimental Evaluation

We compare our algorithm with OLM [9] and Greedy [11] on calculating MAE and F1-score. The data set used covers trajectories of 182 individuals in 5 years of Beijing traffic, with total 18,670 trajectories and 24,876,978 positions. And our road network data consist of 433,391 edges and 171,504 intersections.

Since all the trajectories are GPS records, the presence of sampling error is inevitable. Besides, the trajectories in experiment need to be generated from real road network. Therefore, we preprocess the data set by analyzing the trajectory similarity [14] and using trajectory interpolation and map-matching [15]. In the paper, we use simple linear interpolation [16] and ST-Matching algorithm [17], more specifically in [14, 16, 17].

We randomly select 1, 000 processed trajectories as the test set. $\alpha$ and $\beta$ are set to 4 and 1, respectively. For each trajectory, we choose an initial position, then predict under different prediction duration (increments by 5 min).

Figure 7 compares different methods by MAE under different predicted duration with total 2000 trajectories, where MAE values of DBT are about 2km and 14km lower than those of Greedy and PLM on average. In Fig. 7, DBT algorithm is more accurate in predicting destinations than the other two methods.

We also consider the F1-score in Fig. 8. By comparison, even though the F1-score of DBT is falling with the rising predicted time, it still maintains a relatively high and stable performance better than Greedy algorithm, while PLM turns out to be the worst.

Fig. 7.

MAE under fixed data size and different prediction durations

Fig. 8.

F1-score under fixed data size and different prediction durations

By observing Figs. 7 and 8, we can conclude that DBT performs better in shorter period of time, namely, 10 min. This is because when running into an intersection, DBT only calculates the STP of $Traj_o$, not the STP of $e_{cur}$, avoiding the presence of turning errors caused by overlapping trajectories. Note that PLM performs very bad in both cases, because the calculating errors of finding the exit point tend to be pretty large in PLM. Also seen from Figs. 9 and 10, as data scale grows, MAE becomes lower, but Fl-score gets higher, which means more information can be obtained to improve our predictions.

Fig. 9.

MAE under fixed prediction duration and different data sizes

Fig. 10.

F1-score under fixed prediction duration and different data sizes

Fig. 11.

CPU processing time under different prediction durations

Fig. 12.

CPU processing time under different circumstances

Next, we compare our algorithm performance by analyzing the average computation time. We use Python to implement the algorithms. All experiments are run on a PC with 2.60 GHz CPU and 4 GB of main memory. As shown in Fig. 11, DBT maintains its high performance due to the road network hierarchy. Greedy also has a good performance, but not as well as DBT, since it doesn’t consider contextual information at all. Meanwhile, as PLM always has to traverse all the trajectories from current position to find the exit point, when the length of prediction increases, PLM’s efficiency will significantly decrease.

We compare the CPU processing time under different circumstances in Fig. 12. The results are pretty clear that both the hierarchy of road network and the removal of vertexes with degree 2 have discernible effects on efficiency improvement, especially the hierarchy.

6 Conclusion

This paper presents a hierarchical road network model to reduce complexity and improve the efficiency of prediction algorithm. We propose BDT to deal with contextual information and trajectories’ overlapping problems that most existing algorithms haven’t covered yet. Our experiments show that BDT is more accurate with high performance in both short-term and long-term predictions. Our future work will take more context information [18] into account to further improve the accuracy.