Probabilistic Labeling of Cerebral Vasculature on MR Angiography

Abstract

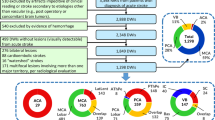
Automatic labeling of cerebrovascular territories would greatly advance our ability to systematically study large datasets and also provide rapid decision support during the assessment of stroke patients, for example. Previous attempts have been challenged by the wide inter-subject variation in vascular topography. We investigate the use of a probabilistic model that learns the configurational characteristics of vascular territories to better annotate the cerebrovasculature. In the George Mason Brain Vasculature database, we identified patients with MRA reconstructions segmented into seven major regions (left and right MCA, PCA, and ACA and Circle of Willis). We then augmented these labels by manually segmenting the MCA territory into an additional eight regions. Among 54 patients that met the inclusion criteria, 39 reconstructions were used as training input to the MCA, ACA, and PCA model among the 61 digital reconstructions of human brain arterial structures available. The model was then validated on an independent cohort of 15 patients. The MCA segmentation algorithm was trained and tested using leave-one-out crossvalidation. The algorithm was found to be $94 \pm 5.2\,\%$ accurate in annotating the seven major regions and $88 \pm 9.3\,\%$ accurate in annotating the MCA subterritories.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Advancements in medical imaging and computational methods have led to a new wave of algorithmic-based techniques to analyze patient data. In the past, cerebral scans have been studied in a more case-by-case basis, leaving the interpretations subject to debate and reducing analysis efficiency. The inherent lack of quantification limits the recognition of correlations and patterns, obscuring meaningful clinical findings within the noise. Digitizing data and automating interpretation paves the way for deeper and more objective analysis, and in the case of cerebral angiography, moves towards more unbiased assessments that can directly improve clinical decision-making.

Previous attempts at automated 3D vessel segmentation [14] and labeling [1, 3, 15] have been challenged by the difficulties related to the quality of the images and the wide inter-subject variability that normally occurs. Image processing and computer vision methods can play a major role in solving these issues if the algorithms are well trained to handle highly variable data. A study [2] conducted at the University of Toronto has investigated the use of Bayesian-based inference to label cerebral vasculature of mice. An arterial set is initialized with random labels and then a relaxation algorithm iteratively re-labels segments in manner that minimizes the data’s energy function, a negated summation of each label’s posterior probability. Despite being $\ge 75\,\%$ accurate in recognizing each of the sample’s 54 territories, the method took an average of $100 \pm 18$ h to segment each image. Recently, promising advances [13] have also been achieved for the automatic segmentation and labeling of the arterial tree from whole-body MRA data. Labeling of the vascular tree was performed by using a combination of graph-based and atlas-based approaches.

The characteristics chosen as inputs in the training data have proven to be a critical element in determining the robustness of an algorithm. Shape recognition, through use of principal component analysis, for example, provides a reasonably effective and computationally efficient way to quantify cerebral territories in segmenting the majority of vasculature sets [5]. The dependence on consistent arterial structure made by this technique is not resilient to the wide variation in morphological structure present in cerebral anatomy. Instead, selecting spatial features as inputs seem to lead to better results when performing vascular segmentation because of the visual nature of territorial labeling [2]. Labeling studies based on other modalities such as CT [6] have successfully used various features such as diameter, curvature, direction, and running vectors of a branch to infer the labels on abdominal arteries.

In this paper, we propose and test a method to automatically label the major vascular territories of cerebral reconstructions through use of kernel density estimation (KDE) and Bayesian inference. Through this form of probabilistic estimation, we are able to create accurate approximations of multi-dimensional density functions describing the cartesian coordinates of the right and left MCA, PCA, and ACA regions. From these probabilistic distributions, each vascular segment is evaluated as a function of the likelihoods of each sub-segment. A maximum a posteriori algorithm decides the appropriate label based on the optimal characterization of the evaluation.

2 Methods

2.1 Dataset Acquisition and Properties

The 3D arterial models were collected from the George Mason Brain Vasculature database [17] which is freely available at http://cng.gmu.edu/brava/ and contains 61 digital reconstructions created from magnetic resonance angiography (MRA) scans of healthy adult subjects (mean age, 31 years; age range, 19 to 64; 36 women). The dataset was created using Neuron_Morpho, a plug-in of ImageJ [5]. Through Neuron_Morpho, users are able to trace neurons contained in image stacks and export them in swc format, representing the cerebral vasculature as a series of interconnected cylindrical segments (segments have a specified x, y, and z coordinate, type, radius, and parent segment). Following the use of this software, the reconstructions were additionally verified for accuracy through juxtaposition with 3D renderings of the MRA scans. In the Brain Vasculature database, each reconstruction is available both unlabeled and labeled, with the labeled models identifying seven major regions (Fig. 1): Circle of Willis and the left and right middle cerebral artery (MCA), posterior cerebral artery (PCA), and anterior cerebral artery (ACA). Vaa3D [9], an open source tool for 3D bio-image visualization and editing, was used to render and view these models.

While the arterial data from BraVa is pre-segmented into the seven aforementioned regions, we are interested in further annotating the MCA territory, a site of interest in stroke patients. To create the necessary training data, we used Vaa3D’s built-in neuron utilities to expand the MCA territory into eight additional regions [7] (Fig. 2): (1) Posterior Temporal, (2) Temporo-Occipital, (3) Angular, (4) Posterior Parietal, (5) Rolandic, (6) Precental, (7) Prefrontal, and (8) Orbitofrontal. A neurologist from UCLA manually labeled the MCA regions of training images. Vasculatures in the database were co-registered using landmark points placed manually so that the relative location of the vessel segments could be used. Data registration is necessary to properly characterize the vasculatures anatomical locations with the respective territories.

Fig. 1.

Figures (a) and (b) show the unlabeled reconstructions of a cerebral vasculature. Figures (d) and (e) show their respective labels using color mapping. The annotations were chosen as Pink = LMCA, Blue = RMCA, Cyan = LACA, Red = RACA, Green = LPCA, Yellow = RPCA, White = Circle of Willis and ICA. The corresponding graphical representations of the unlabeled and labeled vessel segments are shown in (c) and (f). The vascular model shown in this figure was composed of 3514 vessel segments (Color figure online).

2.2 Bayesian Labeling Framework

We assume that the labeling framework is presented with a set of unlabeled vessel segments $S_{i=1 \ldots n}$ that can be represented as a tree-structured graph. Each segment $S_i$ is characterized by a state $x_i$ in the model that represents the label probabilities of vascular territories. Because of the natural variations occurring in the vasculature across subjects, the number of states N for a specific model varies $[x_1, \ldots , x_N]$. A state $x_{i}$ is a M-dimensional discrete vector that associates a probability to each of the M possible labels of the segment.

To each state $x_i$ is associated an observation $y_i$, directly obtained from the normalized location of the segment and its radius. It differs from the state $x_i$ in the sense that it comes vessel detectors that can be affected by noise and transient artifacts present in the image, whereas the value $x_i$ is obtained through inference, thus believed to be more robust.

The labeling model is assumed to follow the general properties of a tree-structured Markov model where each state $x_i$ is connected to at most one parent state $x^{p}_i$ and can have several children states $x^{c}_{i, 1 \ldots N_c}$ where $N_c \ge 0$. This means that the probability of a segment $x_i$ given all the states available $x_{1 \ldots N}$ depends only its parent and children states,

$$\begin{aligned} p(x_{i}|x_{\{1 \ldots N\}}) = p(x_i) \; p(x_{i}|x^p_{i}) \; p(x_{i}|x^c_{i, 1 \ldots N_c} ) \end{aligned}$$

(1)

where $p(x_i)$ is the prior distribution and $p(x_i|x_j)$ represents the conditional dependency between two connected vessel segments. By introducing observations $y_{i}$ in the model, the posterior marginal of the state is defined as follows,

$$\begin{aligned} p(x_{i}|y_{\{1 \ldots N\}}) \propto p(y_{i}|x_{i}) \; p(x_i) \; \int p(x_{i}|x^p_{i}) \; p(x^p_{i}|y_{\{1 \ldots N\}, 1}) dx^p_{i} \; \ldots \nonumber \\ \prod ^{N_c}_j \int p(x_{i}|x^c_{i,j}) \; p(x^c_{i,j}|y_{\{1 \ldots N\}}) \; dx^c_{i,j} \end{aligned}$$

(2)

where $p(y_{i}|x_{i})$ is the likelihood. We propose to use a graphical model to represent this recursive problem, and Belief Propagation to perform the labeling process.

Graphical Model. The graphical model used in our labeling framework defines relations between pairs of nodes only. It is usually referred to as Pairwise Markov Random Field (PMRF) in the literature. As illustrated in Fig. 3, states $x_i \in x$ and observations $y_i \in y$ are represented in the graphical model by white, and shaded nodes, respectively. Edges represent dependencies between states by two types of functions: observation potentials $\phi (x_i, y_i)$ that are the equivalent of the likelihood part $p(y_i|x_i)$, and compatibility potentials $\psi _{ij}(x_i, x_j)$ that embed the conditional parts $p(x_i|x_j)$, $p(x_j|x_i)$ of the Bayesian formulation and can be used by conditioning them in either directions during inference. In addition, the prior distribution over the labels is denoted $\psi _i(x_i)$.

Fig. 2.

Illustration of the additional annotations made by a neurologist on the middle cerebral artery (MCA) territory indicating the eight sub-territories of interest.

Fig. 3.

In this graphical representation, $y_1,y_2,y_3$ indicate each node’s observational features and $x_1,x_2,x_3$ represent their respective states. Messages received by state $x_i$ are denoted by directed arrows.

Observation Model. An observation $y_i$ represents the label information about the $i^{ {th}}$ vessel segment that is directly extracted from the image. An observation $y_i \in R^{M}$ assigns a likelihood to each possible label with respect to the position of the segment a, b, c and its radius r using a previously learned kernel density estimation (KDE) $\hat{f}(S_{i};\varTheta _l)$ (Eq. 3) that is constructed by collecting a total of N labeled vessel segments $\{a_k, b_k, c_k, r_k\}_{1 \ldots N}$ across the training set,

$$\begin{aligned} \hat{f}(S_{i};\varTheta _l) = \frac{1}{N} \sum _{k=1}^{N} \mathcal {G}(S_{i};\{a_k, b_k, c_k, r_k\},\varSigma _{i}) \end{aligned}$$

(3)

where $\mathcal {G}(S_i;\{a_k, b_k, c_k, r_k\},\varSigma _{i})$ is a Gaussian kernel centered at $\{a_k, b_k, c_k, r_k\}$ with standard deviation $\varSigma _{i,l}$ which is common to all the components k of a given label l. $\varTheta _l = \{ \{a_i^k, b_j^k, c_j^k, r_j^k\}_{1 \ldots N_c}, \varSigma _{i}\}$ denotes the parameter set of the KDE associated with a given label l.

Observations $y_{i}$ are linked probabilistically to their state $x_{i}$ through a Gaussian observation potential $\phi (x_{i}, y_{i})$,

$$\begin{aligned} \phi (x_{i}, y_{i}) = \mathrm{exp}(- \;|y_{i} - x_{i}|^2/\sigma _o^2) \end{aligned}$$

(4)

where $\sigma _o$ is a smoothing parameter.

Compatibility Potentials. Compatibility potentials $\psi (x_i, x_j)$ define the relationship between two connected states. They are defined as a Gaussian difference between their arguments,

$$\begin{aligned} \psi (x_{i}, x_{j}) = \mathrm{exp}(- |x_i - x_j|^2/\sigma _t^2) \end{aligned}$$

(5)

where the standard deviation $\sigma _t$ of the model can be estimated using maximum likelihood (ML) on training data.

2.3 Labeling Using Belief Propagation

Labeling vessel segments in the 3D vasculature amounts to estimating $p(x_{i} | y_{\{1 \ldots N\}})$, the posterior belief associated with the state $x_{i}$ given all observations $y_{\{1 \ldots N\}}$ accumulated. Thus, labeling is achieved through inference in our graphical model. One way to do this efficiently is to use Belief Propagation (BP) [8], a method implemented successfully in numerous computer vision applications such as for image segmentation [16] and object recognition [10–12].

It is a message passing algorithm for graphical models where messages are repeatedly exchanged between nodes to perform inference. Following the notation of BP, a message $m_{ij}$ sent from node i to j is written,

$$\begin{aligned} m_{i,j}(x_j) \leftarrow \int \mathcal {\psi }_{i,j} (x_i,x_j) \; \mathcal {\psi }_{i}(x_i) \; \mathcal {\phi }_i(x_i,y_i) \prod _{k \in \mathcal {N}_i \backslash j} m_{k,i}(x_i) \, \text {d}x_i \end{aligned}$$

(6)

where $\mathcal {N}_{i \backslash j}$ is the set of neighbors of state i where j is excluded, $\mathcal {\psi }_{i,j}(x_i,x_j)$ is the pairwise potential between nodes i, j, and $\mathcal {\phi }_{i}(x_i,y_i)$ is the observation potential.

After any iteration of message exchanges, each state can compute an approximation $\hat{p}(x_i | y_{\{1 \ldots N\}})$, called belief, to the marginal distribution $p(x_i |y_{\{1 \ldots N\}})$ by combining the incoming messages with the local observation:

$$\begin{aligned} \hat{p}(x_i | y_{\{1 \ldots N\}}) \leftarrow \mathcal {\psi }_{i}(x_i) \; \mathcal {\phi }_{i} (x_i,y_i) \prod _{k \in \mathcal {N}_i} m_{k,i}(x_i) \end{aligned}$$

(7)

For tree-structured graphs like ours, the beliefs (Eq. 7) will converge to the exact solution $p(x_i | y_{\{1 \ldots N\}})$ [4].

3 Experiments

The goal of the experiments presented in this section is to demonstrate the effectiveness of the developed probabilistic labeling algorithm. To evaluate the model, two sets of experiments were ran; the first one using the 7 major vascular territories provided as part of BraVa, and the second one based on the 8 additional MCA sub-territories established in this study (as described in Sect. 2.1). In both experiments, we evaluate the accuracy by finding the percentage of segment labels in the testing data consistent with the manual annotation.

Table 1. Results of the probabilistic labeling model on 15 test subjects.

Fig. 4.

Results of the MCA segmentation algorithm on two vascular models. Black = Posterior Temporal, Red = Temporo-Occipital, Blue = Angular, Cyan = Posterior Parietal, Yellow = Rolandic, Green = Precental, Brown = Prefrontal, Beige = Orbifrontal (Color figure online).

Fig. 5.

The left and middle columns show the unlabeled models and their respective probabilistic segmentation results for five subjects obtained from BraVa [17]. The right column indicates the automated labeling errors in red (Color figure online).

To quantify the performance of the ACA, MCA, and PCA labeling, we used 39 annotated reconstructions from BraVa as training to build and optimize the graphical model, utilizing the cartesian data and radii as inputs. The algorithm was then tested on the data of 15 remaining subjects. The split between the training and testing set was done randomly. For the MCA subdivision, we tested the algorithm using leave-one-out crossvalidation. In this method, we train the model using all subjects except one, and test on the remaining subject, repeating the process for each set.

Table 1 summarizes the accuracy of the ACA, MCA, and PCA segmentation over the 15 tested data sets was $94 \pm 5.2\,\%$ (as illustrated in Fig. 5). For the MCA subdivision, we observed an accuracy of $88 \pm 9.3\,\%$ for the 7 tested sets (Fig. 4). These results demonstrate that our model is effective in predicting vascular regions in arterial reconstructions. The larger MCA subdivision deviation is a result of one experiment producing an accuracy of 67 %, indicating that our model is not totally impervious to the wide variation in vascular topography. The major artery segmentation algorithm proved to be more consistent in its results; the accuracy for any test never fell below 79 %.

4 Discussion

The results obtained during our experiments have demonstrated that the use of a graphical model that combines kernel density estimation (KDE) in conjunction with belief propagation inference is capable to learn and label vascular territories automatically with high accuracy. We believe this performance can be attributed to both the robustness of nonparametric estimation of the likelihood model and the optimal sharing of information by the message passing algorithm. Training and labeling times allow for processing of a large cohort of subject data; reconstructions can be labeled in a matter of seconds, and complete training and optimization in a few minutes.

In order to fully evaluate how well the model performs in real clinical conditions, a larger, more diverse pool of subjects needs to be tested. Because all training and test sets were retrieved from a single database, we are exposed to sampling bias, perhaps overly estimating the accuracy of the results of the framework on a new dataset where the input features would be extracted with a vessel segmentation technique different from Neuron_Morpho.

More importantly, the ability of our framework to study brain vasculatures automatically is hindered by pre-processing tasks that require manual input, preventing large data sets from being analyzed. Being able to automatically label vascular territories solves a piece of that puzzle, however, more efforts should be invested in the automatic vessel segmentation process.

In terms of clinical relevance of the developed tool for stroke patients, the automatic labeling allows us to quantify arterial regions missing due to occlusion and assess brain health. The MCA territory is a common site of occlusion in ischemic stroke and, through automated labeling, we can identify areas of the MCA that are frequently targeted and recognize features symptomatic of stroke. The proposed algorithm provides a framework for the learning and labeling of other vascular territories as well; whole-body and abdominal vessel segmentation are also very relevant clinical applications that could benefit from the probabilistic framework presented in this paper.

5 Conclusion

The results indicate that the developed framework, which is based on Bayesian formulation of the labeling problem, is effective in labeling vascular features in 3D reconstructions using belief propagation algorithm. We anticipate that this approach will prove useful for learning arterial characteristics in any setting, particularly neurovascular, and circumventing the need for manual annotation. In order to fully automate the labeling process, an effective registration method should be considered. This requirement will be addressed in future work.