Measure Quantifier in Monadic Second Order Logic

Abstract

We study the extension of Monadic Second Order logic with the “for almost all” quantifier $\forall ^{=1}$ whose meaning is, informally, that $\forall ^{=1}X.\phi (X)$ holds if $\phi (X)$ holds almost surely for a randomly chosen X. We prove that the theory of $\mathrm {MSO}+\forall ^{=1}$ is undecidable both when interpreted on $(\omega ,<)$ and the full binary tree. We then identify a fragment of $\mathrm {MSO}+\forall ^{=1}$, denoted by $\mathrm {MSO}+\forall ^{=1}_\pi$, and reduce some interesting problems in computer science and mathematical logic to the decision problem of $\mathrm {MSO}+ \forall ^{=1}_\pi$. The question of whether $\mathrm {MSO}+\forall ^{=1}_\pi$ is decidable is left open.

H. Michalewski—Author supported by Poland’s National Science Centre grant no. 2012/07/D/ST6/02443

M. Mio—Author supported by grant “Projet Émergent PMSO” of the École Normale Supérieure de Lyon and Poland’s National Science Centre grant no. 2014-13/B/ST6/03595.

1 Introduction

Monadic Second Order logic (MSO) is the extension of first order logic with quantification over subsets of the domain. For example, when interpreted over the relational structure $(\omega ,<)$ of natural numbers with the standard order, the formula $\exists A. \forall n. \exists m. ( n <m \wedge m \in A)$ expresses the existence of set A of natural numbers which is infinite (see Sect. 2 for definitions).

One of the first results about MSO was proved by Robinson [14] in 1958. He showed, answering a question of Tarski, that the theory $\mathrm {MSO}(\omega ,+,<)$ is undecidable. In 1962 Büchi [5] proved that the weaker theory $\mathrm {MSO}(\omega ,<)$ is decidable and in 1969 Rabin [13] extended this positive result to the MSO theory of the full binary tree (see Sect. 3 for definitions). Büchi and Rabin’s theorems are widely regarded among the deepest decidability results in theoretical computer science. Their importance stems from the fact that many problems in the field of formal verification of programs can be reduced to these logics.

A long standing open problem in the field of verification of probabilistic programs is the decidability of the SAT(isfability) problem of probabilistic temporal logics such as pCTL* and its extensions (see, e.g., [2, 4]). In the attempt of making some progress, it seems worthwhile to formulate some aspects of the SAT problem as questions expressed in the logical framework of MSO. Given the vast literature on $\mathrm {MSO}$, this might facilitate the application of known results and would make the SAT problem of pCTL* simpler to access by a broader group of logicians.

As a first step in this direction, following the seminal work of Harvey Friedman, who introduced and investigated similar concepts in the context of First Order logic in unpublished manuscripts in 1978–79¹, we have recently considered in [12] the extension of MSO on the full binary tree with Friedman’s “for almost all” quantifier ($\forall ^{*}$) interpreted using the concept of Baire Category as:

$$\begin{aligned} \forall ^{*}X.\phi (X)\, \mathrm { holds } \Leftrightarrow \mathrm{{the\, set }}\{ { A} \mid \phi (A)\,\mathrm{{ holds}}\}\, \mathrm{{is\,topologically\,large}} \end{aligned}$$

where “topologically large” means comeager in the Cantor space topology of subsets of the full binary tree. We proved in [12] that the sets definable using the quantifier $\forall ^{*}$ can actually be defined without it: $\mathrm {MSO}=\mathrm {MSO}+\forall ^{*}$. This is a result of some independent interest but, most importantly, it fits into the research program outlined above since we successfully used it to prove [12] the decidability of the finite-SAT problem (a variant of the SAT problem mentioned above) for the qualitative fragment of pCTL* and similar logics.

In this paper we consider a natural variant of the above extension. We introduce the logic $\mathrm {MSO}+\forall ^{=1}$, interpreted both on $(\omega ,<)$ and on the binary tree, obtained by extending MSO with Friedman’s “for almost all” quantifier ($\forall ^{=1}$) interpreted using the concept of Lebesgue measure as:

$$ \forall ^{=1}X.\phi (X)\, \mathrm { holds } \Leftrightarrow \mathrm {the\, set }\{ { A} \mid \phi ({ A})\,\mathrm { holds}\}\, \mathrm { is\, of\, Lebesgue\, measure\, 1}. $$

Thus, informally, $\forall ^{=1}X.\phi (X)$ holds if $\phi (A)$ is true for a random A. We prove, using results from [1] and [7], that unlike the case of $\mathrm {MSO}+\forall ^{*}$:

Theorem 1

The theory of $\mathrm {MSO}+\forall ^{=1}$ on $(\omega ,<)$ is undecidable.

The proof of this result is presented in Sect. 5. As a consequence also the theory of $\mathrm {MSO}+\forall ^{=1}$ on the full binary tree is undecidable (Corollary 1).

Motivated by this negative result, we investigate the theory of a weaker fragment of $\mathrm {MSO}+\forall ^{=1}$ on trees which we denote by $\mathrm {MSO}+\forall ^{=1}_\pi$. Informally, $\forall ^{=1}_\pi X.\phi (X)$ holds if $\phi (P)$ is true for a random path P in the full binary tree. We observe (Proposition 3) that $\mathrm {MSO}+\forall ^{=1}_\pi$ is strictly more expressive than $\mathrm {MSO}$. However we have not been able to answer the following question²:

Problem 1

Is the theory of $\mathrm {MSO}+\forall ^{=1}_\pi$ on the binary tree decidable?

This problem, which we leave open, seems to deserve some attention. Indeed in Sect. 7 we show that the decidability of $\mathrm {MSO}+\forall ^{=1}_\pi$ would have some interesting applications. Most importantly, from the point of view of our research program, if the theory of $\mathrm {MSO}+\forall ^{=1}_\pi$ is decidable then the SAT problem for the qualitative fragment of pCTL* is decidable (Theorem 5). Regarding applications in mathematical logic, we prove (Theorem 8) that the first order theory of the lattice of $F_\sigma$ subsets of the Cantor space with the predicates $C(X) \Leftrightarrow$ “X is a closed set” and $N(X) \Leftrightarrow$ “X is a Lebesgue null set” is interpretable in $\mathrm {MSO}+\forall ^{=1}_\pi$. As another example, we show (Theorem 9) that the first order theory of the Lebesgue measure algebra with Scott’s closure operator is interpretable in $\mathrm {MSO}+\forall ^{=1}_\pi$. Hence if $\mathrm {MSO}+\forall ^{=1}_\pi$ is decidable, these two theories are also decidable. Lastly, we also establish (Theorem 6) that the qualitative languages of trees, recently investigated in [6], are definable by $\mathrm {MSO}+\forall ^{=1}_\pi$ formulas.

2 Measure and Probabilistic Automata

The set of natural numbers and their standard total order are denoted by the symbols $\omega$ and $<$, respectively. Given sets X and Y we denote with $X^Y$ the space of functions $X \rightarrow Y$. We can view elements of $X^Y$ as Y-indexed sequences $\{x_i\}_{i\in Y}$ of elements of X. We refer to $\varSigma ^\omega$ as the collection of $\omega$ -words over $\varSigma$. The collection of finite sequences of elements in $\varSigma$ is denoted by $\varSigma ^*$. As usual we denote with $\epsilon$ the empty sequence and with $ww^\prime$ the concatenation of $w,w^\prime \in \varSigma ^*$.

The set $\{0,1\}^\omega$ of $\omega$-words over $\{0,1\}$, endowed with the product topology (where $\{0,1\}$ is given the discrete topology) is called the Cantor space. Given a finite set $\varSigma$, the spaces $\varSigma ^{\omega }$ and $\{0,1\}^{\varSigma ^*}$ are homeomorphic to the Cantor space. The Cantor space is zero-dimensional, i.e., it has a basis of clopen (both open and closed) sets. A subset of $\{0,1\}^\omega$ is a $F_\sigma$ set if it is expressible as a countable union of closed sets. For a detailed exposition of these topological notions see introductory chapters of [9]. We summarize below the basic concepts related to Borel measures. For more details see, e.g., Chap. 17 of [9]. The smallest $\sigma$-algebra of subsets of $\{0,1\}^\omega$ containing all open sets is denoted by $\mathcal {B}$ and its elements are called Borel sets. Given a $A \in \mathcal {B}$ we denote its complement by $\lnot B$. A Borel probability measure on $\{0,1\}^\omega$ is a function $\mu :\mathcal {B} \rightarrow [0, 1]$ such that: $\mu (\emptyset ) = 0$, $\mu (\{0,1\}^\omega ) =1$ and, if $\{B_n\}_{n\in \omega }$ is a sequence of disjoint Borel sets, $\mu (\bigcup _{n}B_n) = \sum _{n}\mu (B_n)$. Every Borel measure $\mu$ on the Cantor space is regular: for every Borel set B there exists a $F_\sigma$ set $A \subseteq B$ such that $\mu (A) =\mu (B)$. We will be mostly interested in one specific Borel measure on the Cantor space which we refer to as the Lebesgue measure. This is the unique Borel measure satisfying the equality $\mu (B_{n=0})=\mu (B_{n=1}) =\frac{1}{2}$, where $B_{n=0}= \{ (b_i)_{i\in \omega } \mid b_n = 0\}$ and $B_{n=1}= \{ (b_i)_{i\in \omega } \mid b_n = 1\}$, respectively. Intuitively, the Lebesgue measure on $\{0,1\}^{\omega }$ generates an infinite sequence $(b_0,b_1,\dots )$ by deciding to fix $b_n= 0$ or $b_n= 1$ by tossing a fair coin, for every $n\in \omega$.

2.1 Probabilistic Büchi Automata

In this section we define the class of probabilistic Büchi automata introduced in [1] and state the undecidability of their emptiness problem under the probable semantics [1, Theorem 7.2]. This is the key technical result used in our proof of undecidability of MSO $+ \forall ^{=1}$ in Sect. 5.

Definition 1

(Probabilistic Büchi Automaton). A probabilistic Büchi automaton is a tuple $\AA = \langle \varSigma , Q, q_I, F, \varDelta \rangle$ where: $\varSigma$ is a finite nonempty input alphabet, Q is a finite nonempty set of states, $q_I\in Q$ is the initial state, $F\subseteq Q$ is the set of accepting states and $\varDelta : Q\rightarrow (\varSigma \rightarrow \mathcal {D}(Q))$ is the transition function, where $\mathcal {D}(Q)$ denotes the collection of probability distributions on Q.

To illustrate the above definition consider the probabilistic Büchi automaton (from [1, Lemma 4.3]) $\AA = \langle \{a,b\}, Q, q_1 F, \varDelta \rangle$ where $Q= \{q_1,q_2,\bot \}$, $F= \{q_1\}$ and $\varDelta$ is defined as in Fig. 1.

Fig. 1.

A probabilistic Büchi automaton with three states. Boxes denote accepting states and circles denote not accepting states.

We now describe the intended interpretation of probabilistic Büchi automata. As for ordinary Büchi Automata (see [17] for a detailed introduction to this classical concept) a probabilistic Büchi automaton “reads” $\omega$-words over the finite alphabet $\varSigma$. However, unlike ordinary Büchi automata, a probabilistic Büchi automaton “accepts” an input $\omega$-word w with some probability $\mathbb {P}^{\mathcal A}_w$. We now describe this notion.

A probabilistic Büchi automaton starts reading a $\omega$-word $w= (a_0,a_1,\dots )\in \varSigma ^\omega$ from the state $q_0= q_I$. After reading the first letter $a_0$, the automaton moves to state $q\in Q$ with probability $\varDelta (q_0, a_0, q)$. If the state q is reached, after the second letter $a_1$ is read, the automaton reaches the state $q^\prime$ with probability $\varDelta (q, a_1, q^\prime )$. More generally, if at stage n the automaton is in state q, after reading the letter $a_n$ of w, the automaton reaches the state $q^\prime$ with probability $\varDelta (q,a_n,q^\prime$). Hence, a $\omega$-word w induces a random walk on the set of states Q of the automaton $\mathcal {A}$. One can naturally formalize this random walk as a Borel probability measure $\mu ^{{\mathcal A}}_w$ on the space $Q^\omega$ (see [1, §3.1] for detailed definitions).

Considering the example in Fig. 1 and the $\omega$-word $a^\omega = (a,a,a\dots )$, the probability measure $\mu ^{{\mathcal A}}_{w}$ assigns probability $\frac{1}{4}$ to the set of sequences $q_1q_1q_1Q^{\omega }$ starting with three consecutive $q_1$’s.

A sequence $(q_0q_1\dots q_n\dots )\in Q^\omega$ of states of $\mathcal {A}$ is accepting if for infinitely many $i \in \omega$, the state $q_i$ belongs to the set F of accepting states. We denote with $Acc \subseteq Q^\omega$ the set of accepting sequences of states. Clearly Acc is a Borel set. We say that $\mathcal {A}$ accepts the $\omega$-word $w \in \varSigma ^\omega$ with probability $\mathbb {P}^{{\mathcal A}}_w = \mu ^{{\mathcal A}}_{w}(Acc)$. We are now ready to state a fundamental result about probabilistic Büchi automata.

Theorem 2

(Theorem 7.2 in [1]). It is undecidable if for a given probabilistic Büchi automaton ${\mathcal A}$ there exists $w \in \varSigma ^{\omega }$ such that $\mathbb {P}^{{\mathcal A}}_w > 0$.

An inspection of the proof of Theorem 2 from [1] reveals that the problem remains undecidable if we restrict to the class of probabilistic Büchi automaton $\mathcal {A}$ such that, for some $k \in \omega$, all probabilities appearing in (the matrices of) $\varDelta$ of $\mathcal {A}$ belong³ to the set $\{0,\frac{1}{2^k},\ldots ,\frac{i}{2^k},\ldots ,1\}$. We can further restrict attention to the class of simple probabilistic Büchi automata defined below.

Definition 2

A probabilistic Büchi automaton ${\mathcal A}$ is simple if, for some $k \in \omega$ all probabilities appearing in (the matrices of) $\varDelta$ are either 0 or $\frac{1}{2^k}$.

Proposition 1

It is undecidable if for a given simple probabilistic Büchi automaton ${\mathcal A}$ there exists $w \in \varSigma ^{\omega }$ such that $\mathbb {P}^{{\mathcal A}}_w > 0$.

Proof

We can transform an automaton $\mathcal {A}$ with probabilities in $\{0,\frac{1}{2^k}\ldots \frac{i}{2^k},\ldots , 1\}$ to an equivalent one having only probabilities in $\{0,\frac{1}{2^k}\}$ by “splitting probabilities” introducing new copies of the states.    $\square$

3 Syntax and Semantics of Monadic Second Order Logic

In this section we define the syntax and the semantics of the MSO logic interpreted over the linear order of natural numbers (“MSO on $\omega$-words”) and over the full binary tree (“MSO on trees”). This material is standard and a more detailed exposition can be found in [17].

MSO on $\omega$ -words. We first define the syntax and the semantics of MSO on $(\omega ,<)$. We follow the standard presentation of MSO on $(\omega ,<)$ where only second order variables are considered. We refer to Sect. 2.3 of [17] for more details.

Definition 3

(Syntax). The set of formulas of the logic MSO is generated by the following grammar: $\phi :\,\!:=$ Sing$(X) \mid X < Y \mid X\subseteq Y\mid \lnot \phi \mid \phi _1 \vee \phi _2 \mid \forall X.\phi$, where X, Y range over a countable set of variables. We write $\phi (X_1,\dots , X_n)$ to indicate that $\overrightarrow{X} = (X_1,\ldots ,X_n)$ is the list of free variables in $\phi$.

This presentation is convenient since MSO formulas can be regarded as first-order formulas over the signature $\mathcal {S}$ consisting of the unary symbol Sing and the two binary symbols $<$ and $\subseteq$. MSO formulas are interpreted over the collection of subsets of $\omega$ (i.e., the collection $\{0,1\}^\omega$ of $\omega$-words over $\{0,1\}$) with the following interpretations of the symbols in $\mathcal {S}$:

• $Sing^{I} (X) \Leftrightarrow X=\{n\}$, for some $n \in \omega$, i.e., $X \subseteq \omega$ is a singleton.

• $<^{I}(X,Y) \Leftrightarrow$ $X=\{n\}$, $Y = \{m\}$ and $n < m$.

• $\subseteq ^{I}(X,Y) \Leftrightarrow X \subseteq Y$, i.e., X is a subset of Y.

Definition 4

(Semantics). Let $\mathbb {W}$ be the structure for the signature $\mathcal {S}$ defined as $\mathbb {W} = (\{0,1\}^{\omega }, Sing^{I}, <^{I}, \subseteq ^{I})$. The truth of MSO formulas $\phi$ is given by the relation $\mathbb {W}\models \phi$, where $\models$ is the standard first-order satisfaction relation. Given parameters $A_1,\dots , A_n \in \{0,1\}^\omega$, we write $\overrightarrow{A} \in \phi (\overrightarrow{X})$ to indicate that $\mathbb {W} \models \phi (\overrightarrow{A})$, i.e., that $\mathbb {W}$ satisfies the formula $\phi$ with parameters $\overrightarrow{A}$.

Thus a formula $\phi (X_1,\dots , X_n)$ defines a subset of $(\{ 0,1\}^{\omega })^n$ or, equivalently, a subset of $(\{0,1\}^n)^{\omega }$ that is a set of $\omega$-words over $\varSigma = \{0,1\}^{n}$. The subsets of $\varSigma ^{\omega }$ definable by a MSO formula $\phi$ are called regular.

Remark 1

The presentation of MSO($\omega , <$) as the first order theory of $\mathbb {W}$ is technically convenient. Yet it is often useful to express concisely formulas such as $\forall x. (x\in Y\rightarrow \phi (x,Z))$ where the lowercase letter x ranges over natural numbers and the relation symbol $\in$ is interpreted as membership, as expected. Formulas of this kind can always be rephrased in the language of the signature $\{ Sing, <, \subseteq \}$. For example the formula above can be expressed as: $\forall X. \big ( Sing(X) \rightarrow ( X\subseteq Y \rightarrow \phi (X,Z))$. We refer to [17] for a detailed exposition.

MSO on Trees. We now introduce, following a similar approach, the syntax and the semantics of MSO on trees.

Definition 5

(Full Binary Tree). The collection $\{L,R\}^*$ of finite words over the alphabet $\{L,R\}$ can be seen as the set of vertices of the infinite binary tree. We refer to $\{L,R\}^*$ as the full binary tree. We use the letters v and w to range over elements of the full binary tree.

Definition 6

(Syntax). The set of formulas of the logic $\mathrm {MSO}$ on the full binary tree is generated by the following grammar:

$$\phi :\,\!:=\, \mathrm{Sing}\,(X) \mid \texttt {Succ}_L(X, Y) \mid \texttt {Succ}_R(X, Y) \mid X\subseteq Y\mid \lnot \phi \mid \phi _1 \vee \phi _2 \mid \forall X.\phi $$

where X, Y range over a countable set of variables.

Hence MSO formulas are conventional first-order formulas over the signature $\mathcal {S}$ consisting of one unary symbol Sing and three binary symbols $\texttt {Succ}_L,\texttt {Succ}_R, \subseteq$. We interpret MSO formulas over the collection $\{0,1\}^*\rightarrow \{0,1\}$ of subsets of the full binary. To improve the notation, given a set $\varSigma$ we write ${\mathcal T}_{\varSigma }$ to denote the set $\{0,1\}^* \rightarrow \varSigma$. Thus MSO formulas are interpreted over the universe ${\mathcal T}_{\{0,1\}}$ with the following interpretations of the symbols in $\mathcal {S}$:

• $Sing^{I} (X) \Leftrightarrow X=\{v\}$, for some $v \in \{L,R\}^*$, i.e., if $X \in {\mathcal T}_{\{0,1\}}$ is a singleton.

• $\texttt {Succ}_L^{I}(X,Y) \Leftrightarrow ``X=\{v\}, Y = \{w\} \,\mathrm{and}\, w = vL$.

• $\texttt {Succ}_R^{I}(X,Y) \Leftrightarrow ``X=\{v\}, Y = \{w\} \,\mathrm{and}\, w = vR$.

• $\subseteq ^{I}(X,Y) \Leftrightarrow X \subseteq Y$, i.e., if X is a subset of Y.

Definition 7

(Semantics). Let $\mathbb {T}$ be the structure for the signature $\mathcal {S}$ defined as $\langle {\mathcal T}_{\{0,1\}}, Sing^{I}, \texttt {Succ}_L^I, \texttt {Succ}_R^I, \subseteq ^{I}\rangle$. The truth of a MSO formula $\phi$ is given by the relation $\mathbb {T} \models \phi$. Given parameters $\overrightarrow{A} \in {\mathcal T}_{\{0,1\}}$, we write $\overrightarrow{A} \in \phi (\overrightarrow{X})$ to indicate that $\mathbb {T} \models \phi (A_1,\dots , A_n)$, i.e., that $\mathbb {T}$ satisfies the formula $\phi$ with parameters $\overrightarrow{A}$.

Thus a formula $\phi (X_1,\dots , X_n)$ defines a subset of $({\mathcal T}_{\{0,1\}})^n$ or, equivalently, a subset of ${\mathcal T}_{\varSigma }$ with $\varSigma = \{0,1\}^n$.

4 MSO with Measure Quantifier: MSO $+\forall ^{=1}$

In this section we introduce the logic $\mathrm{MSO}+\forall ^{=1}$, interpreted both on $\omega$-words and on trees, obtained by extending ordinary MSO with Friedman’s “for almost all” quantifier interpreted using the concept of Lebesgue measure.

4.1 MSO $+\forall ^{=1}$ on $\omega$-words

Definition 8

The syntax of $\mathrm {MSO}+\forall ^{=1}$ on $\omega$-words is obtained by extending that of MSO (Definition 3) with the quantifier $\forall ^{=1}X.\phi$ as follows:

$$ \phi :\,\!:= \mathrm {Sing}(X) \mid X<Y \mid X\subseteq Y\mid \lnot \phi \mid \phi _1 \vee \phi _2 \mid \forall X.\phi \mid \forall ^{=1}X.\phi $$

The following definition specifies the semantics $\mathrm {MSO}+\forall ^{=1}$ on $\omega$-words.

Definition 9

Each formula $\phi (X_1,\dots , X_n)$ of $\mathrm {MSO}+\forall ^{=1}$ is interpreted as a subset of $(\{0,1\}^{\omega })^n$ by extending Definition 4 with the following clause:

where $A_i$, B range over $\{0,1\}^{\omega }$ and $\mu _{\{0,1\}^{\omega }}$ is the Lebesgue measure on $\{0,1\}^{\omega }$. For a given formula $\phi$ we define $\exists ^{>0}X.\phi$ as a shorthand for $\lnot \forall ^{=1}X.\lnot \phi$.

Fig. 2.

The large sections selected by the quantifier $\forall ^{=1}$ are marked in grey.

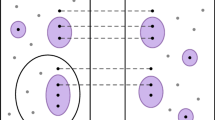
The set denoted by $\forall ^{=1}X. \phi (X,\overrightarrow{Y})$ can be illustrated as in Fig. 2, as the collection of tuples $\overrightarrow{A}$ having a large section $\phi (X,\overrightarrow{A})$, that is a section having Lebesgue measure 1. Informally, $(A_1,\dots , A_n)$ satisfies $\forall ^{=1}X. \phi (X,\overrightarrow{Y})$ if “for almost all” $B \in \{0,1\}^\omega$, the tuple $(B,A_1,\dots , A_n)$ satisfies $\phi$. Similarly, $\overrightarrow{A} \in \exists ^{>0}X.\phi (X,\overrightarrow{Y})$ iff the section $\phi (X,\overrightarrow{A})$ has positive measure.

Remark 2

Every relation on $\{0,1\}^{\omega }$ definable by a $\mathrm {MSO}+\forall ^{=1}$ formula clearly belongs to a finite level of the projective hierarchy. However, since the family of $\mathrm {MSO}+\forall ^{=1}$ definable relations is closed under Boolean operations and projections, it is not clear if every $\mathrm {MSO}+\forall ^{=1}$ definable relation is Lebesgue measurable. We formulate this as Problem 2 is Sect. 8. In the rest of the paper we assume sufficiently strong set-theoretical assumptions (e.g., Projective Determinacy, see [9, Sect. 38.C]) to guarantee that Definition 9 is well specified, i.e., that all considered sets are measurable.

On Fubini’s Theorem. The Fubini theorem is a classical result in analysis which states that the measure of a set $A \subseteq X\times Y$ can be expressed by iterated integration over the X and Y axis. In terms of $\mathrm {MSO}+\forall ^{=1}$, the Fubini theorem corresponds (see [9, Sect. 17.A]) to the fact that

$$\forall ^{=1}X.\forall ^{=1}Y. \phi (X,Y,\overrightarrow{Z}) = \forall ^{=1}X.\forall ^{=1}Y. \phi (X,Y,\overrightarrow{Z})$$

and, importantly for the proof of Theorem 3, that:

where $\mu _{{(\{0,1\}^2)}^{\omega }}$ is the Lebesgue measure on the product space ${(\{0,1\}^2)}^{\omega }= \{0,1\}^\omega \times \{0,1\}^\omega$ defined as the product measure $\mu _{\{0,1\}^{\omega }} \otimes \mu _{\{0,1\}^{\omega }}$.

4.2 $\mathrm {MSO}+\forall ^{=1}$ on Trees

The definition of $\mathrm {MSO}+\forall ^{=1}$ on trees is similar to that of $\mathrm {MSO}+\forall ^{=1}$ on words and extends the syntax of MSO on trees (Definition 6) with the new quantifier $\forall ^{=1}X.\phi$. The semantics of $\mathrm {MSO}+\forall ^{=1}$ on trees is obtained by extending Definition 7 by the following interpretation of $\forall ^{=1}$:

where $\mu _{{\mathcal T}_{\{0,1\}}}$ is the Lebesgue measure on $\mu _{{\mathcal T}_{\{0,1\}}}$.

The Lebesgue measure $\mu _{{\mathcal T}_{\{0,1\}}}$ can be seen as the random process of generation of a tree $A \in {\mathcal T}_{\{0,1\}}$ by fixing the label (either 0 or 1) of each vertex $v \in \{L,R\}^*$ of the binary tree by tossing a fair coin. Hence, intuitively, the formula $\forall ^{=1}X.\phi (X)$ holds true if $\phi (A)$ holds for a random tree $A \in {\mathcal T}_{\{0,1\}}$.

5 Undecidability of MSO + $\forall ^{=1}$

In this section we prove that the theory of MSO$+ \forall ^{=1}$ on $\omega$-words is undecidable. This is done by reducing the (undecidable by Proposition 1) emptiness problem of simple probabilistic Büchi automaton ${\mathcal A}$ to the decision problem of $\mathrm {MSO} + \forall ^{=1}$. The reduction closely resembles the standard translation between ordinary Büchi automata and MSO on $\omega$-words (see, e.g., [17, Sect. 3.1]).

In what follows, let us fix an arbitrary k-simple probabilistic Büchi automaton $\AA = \langle \{a,b\},q_I, Q, F, \varDelta \rangle$ with $Q = \{q_1,q_2,\dots , q_n\}$. We write $q_i < q_j$ if $i < j$. Without loss of generality, let us assume that $|\varSigma | = 2^m$, for some number $m \in \omega$, so that we can identify $\varSigma$ with $\{0,1\}^m$. Hence a $\omega$-word $w \in \varSigma ^\omega$ can be uniquely identified with a tuple $\overrightarrow{X}= (X_1,\dots , X_m)$ with $X_i\in \{0,1\}^{\omega }$.

Since ${\mathcal A}$ is k-simple (see Definition 2), for each state $q \in Q$ and letter $a \in \varSigma$, there are exactly $2^k$ possible transitions in $\varDelta$, each one having probability $\frac{1}{2^k}$. Therefore, for each state q and letter a, we can identify the available transitions by numbers in $\{0,\ldots ,2^k-1\}=\{0,1\}^k$ as follows: the number i denotes the transition to the i-th (with respect to the total order $<$ on Q) reachable (with probability $\frac{1}{2^k}$) state. We can identify an infinite sequence of transitions with an infinite sequence $\overrightarrow{Y} = (\{0,1\}^k)^\omega$, i.e., by a tuple $(Y_1,\dots , Y_k)$ with $Y_j\in \{0,1\}^{\omega }$. The existence of a $\omega$-word $w \in \varSigma ^{\omega }$ such that $\mathbb {P}^{{\mathcal A}}_w >0$ is expressed in $\mathrm {MSO}+\forall ^{=1}$ by

$$\phi _{\mathcal {A}} = \exists \overrightarrow{X}. \exists ^{>0} \overrightarrow{Y}. \psi _{{\mathcal A}}(\overrightarrow{X}, \overrightarrow{Y})$$

where $\exists \overrightarrow{X}$ and $\exists ^{>0}\overrightarrow{Y}$ stand for $\exists X_1.\exists X_2.\dots \exists X_m$ and $\exists ^{>0} Y_1.\exists ^{>0} Y_2.\dots \exists ^{>0} Y_k$, respectively. The formula $\psi _{{\mathcal A}}$, which we define below, expresses that when interpreting $\overrightarrow{X}$ as a $\omega$-word $w \in \varSigma ^\omega$ and $\overrightarrow{Y}$ as an infinite sequence of transitions, the infinite sequence $(q_n)$ of states visited in ${\mathcal A}$, which is uniquely determined by $\overrightarrow{X}$ and $\overrightarrow{Y}$, contains infinitely many accepting states, that is, $(q_n) \in Acc$.

Due to the Fubini Theorem (see Sect. 4) and the fact that an $\omega$-word $A \in (\{0,1\}^{k})^\omega$ randomly generated with the Lebesgue measure on $\{0,1\}^{k}$ assumes at a given position $n \in \omega$ a value in $\{0,1\}^{k}$ with uniform probability $\frac{1}{2^k}$, the formula $\phi _{\mathcal A}$ indeed expresses that there exists $w \in \varSigma ^\omega$ such that $\mathbb {P}^{{\mathcal A}}_{w} >0$. The formula $\psi _{{\mathcal A}}(\overrightarrow{X},\overrightarrow{Y})$ is defined using standard ideas (see, e.g., [17, Sect. 3.1]):

The formula expresses that: (a) there exists an assignment of states to positions $i \in \omega$ such that each position is assigned a unique state; that (b) if position i is labeled by state q, $(X^i_1,\dots , X^i_m)$ represents the letter $a \in \varSigma$ and $(X^i_1,\dots , X^i_k)$ represent the transition $0\le t < 2^k$, then $i+1$ belongs to the state (denoted in the formula by (q, a, t)) which is the t-th reachable state from q on letter a; (c) the sequence contains infinitely many accepting states. Hence we get a more detailed version of Theorem 1 stated in the Introduction:

Theorem 3

For each simple probabilistic Büchi automaton ${\mathcal A}$, the $\mathrm {MSO}+\forall ^{=1}$ sentence $\phi _{\mathcal {A}}$ is true if and only there exists $w \in \varSigma ^\omega$ such that $\mathbb {P}^{{\mathcal A}}_{w}>0$. Hence the theory of $\mathrm {MSO}+\forall ^{=1}$ is undecidable.

Undecidability of MSO + $\forall ^{=1}$ on Trees. The theory of $\mathrm {MSO}+\forall ^{=1}$ on $(\omega ,<)$ can be interpreted within the theory of $\mathrm {MSO}+\forall ^{=1}$ on the full binary tree by the standard interpretation of $(\omega ,<)$ as the set of vertices of the leftmost branch in the full binary tree and it is not difficult to see that this interpretation preserves the meaning of the $\forall ^{=1}$ measure quantifier. We only state the following result. A detailed proof will be published elsewhere.

Corollary 1

The theory of $\mathrm {MSO}+\forall ^{=1}$ on the full binary tree is undecidable.

6 The Logic MSO+$\forall ^{=1}_\pi$ on Trees

In this section we identify a variant of $\mathrm {MSO}+\forall ^{=1}$ on trees which we denote by $\mathrm {MSO}+\forall ^{=1}_{\pi }$. This logic is obtained by extending ordinary MSO with the quantifier $\forall ^{=1}_{\pi }$. Intuitively, the quantifier $\forall ^{=1}_{\pi }$ is defined by restricting the range of the measure quantifier $\forall ^{=1}$ to the collection of paths in the full binary tree (see definition 10 below) so that the formula $\forall ^{=1}_{\pi } X. \phi (X)$ holds if a randomly chosen path X satisfies the property $\phi$ with probability 1. More precisely,

Definition 10

A subset $X \subseteq \{L,R\}^{*}$ (equivalently, $X \in {\mathcal T}_{\{0,1\}}$) is called a path if it satisfies the following conditions: (1) X is closed downward: for all $x,y \in \{L,R\}^{*}$, if $x \in X$ and y is a prefix of x then $y \in X$; (2) X is not empty: $\epsilon \in X$; and (3) X branches uniquely: for every $x \in \{L,R\}^{*}$, if $x \in X$ then either $xR \in X$ or $xL \in X$ but not both. Let $\mathcal {P} \subseteq {\mathcal T}_{\{0,1\}}$ be the collection of all paths.

In other words, $X \in \mathcal {P}$ if the set of vertices in X describe an infinite branch in the full binary tree. Clearly $\mathcal {P}$ is homeomorphic as a subspace of ${\mathcal T}_{\{0,1\}}$ to the set $\{L,R\}^{\omega }$ of $\omega$-words over the alphabet $\{L,R\}$ and it is simple to verify that:

Proposition 2

The equality $\mu _{{\mathcal T}_{\{0,1\}}}(\mathcal {P}) = 0$ holds.

However the space $\mathcal {P}$ carries the natural Lebesgue measure $\mu _{\{L,R\}^{\omega }}$ which we use below to define the semantics of $\mathrm {MSO}+\forall ^{=1}_{\pi }$.

Definition 11

(Syntax of $\mathrm {MSO}+\forall ^{=1}_\pi$ ). The syntax of $\mathrm {MSO}+\forall ^{=1}_\pi$ formulas $\phi$ is generated by the following grammar:

$$ \phi :\,\!:= \mathrm {Sing}(X) \mid \texttt {Succ}_L(X,Y) \mid \texttt {Succ}_R(X,Y) \mid X\subseteq Y\mid \lnot \phi \mid \phi _1 \vee \phi _2 \mid \forall X.\phi \mid \forall ^{=1}_{\pi }X.\phi $$

Definition 12

(Semantics of $\mathrm {MSO}+\forall ^{=1}_\pi$ ). The semantics of $\mathrm {MSO}+\forall ^{=1}_\pi$ is defined by extending the semantics of $\mathrm {MSO}$ on trees (Definition 7) as follows:

Hence, informally, $(A_1,\dots , A_n)\in \forall ^{=1}_\pi X.\phi (X,Y_1,\dots , Y_n)$ if, for a randomly chosen $B \in \mathcal {P}$, the formula $\phi (B,A_1,\dots , A_n)$ holds almost surely.

It is not immediately clear from the previous definition if the quantifier $\forall ^{=1}_\pi$ can be expressed in $\mathrm {MSO}+\forall ^{=1}$ on trees. Indeed note that, since $\mu _{{\mathcal T}_{\{0,1\}}}(\mathcal {P}) = 0$, the naive definition $\forall ^{=1}_\pi X. \phi ( X) = \forall ^{=1} X. \big ($ “X is a path” $\wedge \phi (X) \big )$, where the predicate “X is a path” is easily expressible in MSO, but does not work. Indeed the $\mathrm {MSO}+\forall ^{=1}$ expression on the right always defines the empty set because the collection of $X \in {\mathcal T}_{\{0,1\}}$ satisfying the conjunction is a subset of $\mathcal {P}$ and therefore has $\mu _{{\mathcal T}_{\{0,1\}}}$ measure 0.

Nevertheless the quantifier $\forall ^{=1}_\pi$ can be expressed in $\mathrm {MSO}+\forall ^{=1}$ on trees with a more elaborate encoding presented below. The main ingredient of the encoding is a MSO definable continuous function f which maps a tree $X \in {\mathcal T}_{\{0,1\}}$ to a path $f(X) \in \mathcal {P}$ preserving measure in the sense stated in Lemma 1.2 below.

Definition 13

Define the binary relation f(X, Y) on ${\mathcal T}_{\{0,1\}}$ by the following MSO formula: “Y is a path” and $\forall y \in Y. \exists z. ( \texttt {Succ}_L(y,z)$ and ($z \in Y \Leftrightarrow y \in X$)).

Lemma 1

For every $X \in {\mathcal T}_{\{0,1\}}$ there exists exactly one $Y \in \mathcal {P} \subseteq {\mathcal T}_{\{0,1\}}$ such that f(X, Y). Hence the relation f is a function $f : {\mathcal T}_{\{0,1\}} \rightarrow \mathcal {P}$. Furthermore f satisfies the following properties:

• 1. f is a continuous, open and surjective function,

• 2. Assume $B \subseteq \mathcal {P}$ is $\mu _{\{L,R\}^{\omega }}$ measurable. Then $\mu _{\{L,R\}^{\omega }}(B) =\mu _{{\mathcal T}_{\{0,1\}}}(f^{-1}(B))$.

A proof of Lemma 1 will be published elsewhere.

We can now present the correct $\mathrm {MSO}+\forall ^{=1}$ encoding of the quantifier $\forall ^{=1}_\pi$.

Theorem 4

For every $\mathrm {MSO}+\forall ^{=1}_\pi$ formula $\psi (\overrightarrow{Z})$ there exists a $\mathrm {MSO}+\forall ^{=1}$ formula $\psi ^\prime (\overrightarrow{Z})$ such that $\psi$ and $\psi ^\prime$ denote the same set.

Proof

The proof goes by induction on the complexity of $\psi$ with the interesting case being $\phi (\overrightarrow{Z}) = \forall ^{=1}_\pi Y. \psi (Y,\overrightarrow{Z})$. By induction hypothesis, there exists a $\mathrm {MSO}+\forall ^{=1}$ formula $\psi ^\prime$ defining the same set as $\psi$. Then the $\mathrm {MSO}+\forall ^{=1}$ formula $\phi ^\prime$ corresponding to $\phi$ is: $\phi ^\prime (\overrightarrow{Z}) = \forall ^{=1} X. \big ( \exists Y. \big ( f(X, Y) \wedge \psi ^\prime (Y,\overrightarrow{Z}) \big )\big )$. We now show that $\phi$ and $\phi ^\prime$ indeed define the same set. The following are equivalent:

• 1. $\overrightarrow{C} \in \forall ^{=1}_\pi Y. \psi (Y,\overrightarrow{Z})$,

• 2. (by Definition of $\forall ^{=1}_\pi X$) The set $A = \big \{ Y \in \mathcal {P} \mid \psi (Y,\overrightarrow{C}) \big \}$ is such that $\mu _{\{L,R\}^{\omega }}(A) = 1$,

• 3. (by Lemma 1.(2)) The set $B \subseteq {\mathcal T}_{\{0,1\}}$, defined as $B = f^{-1}(A)$, i.e., as $B = \big \{X\in {\mathcal T}_{\{0,1\}} \mid \exists Y.\big ( f(X,Y) \wedge \psi (Y,\overrightarrow{C})\big )\big \}$. is such that $\mu _{{\mathcal T}_{\{0,1\}}}(B) = 1$.

• 4. (by definition of $\forall ^{=1}$ and using $\psi = \psi ^\prime$) $\overrightarrow{C}\in \forall ^{=1} X. \big ( \exists Y. \big ( f(X,Y) \wedge \phi ^\prime$ $(Y, \overrightarrow{Z}) \big )\big )$.

   $\square$

7 On the Expressive Power of MSO+$\forall ^{=1}_\pi$

In Sect. 5 we proved that the theory of $\mathrm {MSO}+\forall ^{=1}$ on $\omega$-words and trees is undecidable. Motivated by this negative result, in Sect. 6 we introduced the logic $\mathrm {MSO}+\forall ^{=1}_\pi$ on trees and in Theorem 4 we proved that it can be regarded as a syntactical fragment of $\mathrm {MSO}+\forall ^{=1}$ on trees.

We have not been able to establish if the logic $\mathrm {MSO}+\forall ^{=1}_\pi$ on trees is decidable or not (Problem 1 in the Introduction). On the one hand we observe (Proposition 3 below), by applying a result of [6], that $\mathrm {MSO}+\forall ^{=1}_\pi$ can define non-regular sets. On the other hand, it does not seem possible to apply the methods utilized in this paper to prove its undecidability.

In the rest of this section we investigate the expressive power of $\mathrm {MSO}+\forall ^{=1}_\pi$. We show that the the decidability of $\mathrm {MSO}+\forall ^{=1}_\pi$ implies the decidability of the SAT problem for the qualitative fragment of the probabilistic logic pCTL*. We establish a connection between $\mathrm {MSO}+\forall ^{=1}_\pi$ and automata theory by showing that the class of qualitative languages of trees of [6] can be expressed by $\mathrm {MSO}+\forall ^{=1}_\pi$ formulas (Theorem 6). We prove that the first order theory of the lattice of $F_\sigma$ subsets of the Cantor space with the predicates $C(X) \Leftrightarrow$ “X is a closed set” and $N(X) \Leftrightarrow$ “X is a Lebesgue null set” is interpretable in $\mathrm {MSO}+\forall ^{=1}_\pi$ (Theorem 9). Lastly, we show that the first order theory of the Lebesgue measure algebra equipped with Scott’s closure operator is interpretable in $\mathrm {MSO}+\forall ^{=1}_\pi$.

7.1 SAT Problem of Probabilistic Temporal Logics

In this subsection we sketch the essential arguments that allow to reduce the SAT problem of the qualitative fragment of pCTL* and similar logics to the decision problem of $\mathrm {MSO}+\forall ^{=1}_\pi$. We assume the reader is familiar with the logic pCTL*. We refer to the textbook [2] for a detailed introduction.

The logic pCTL* and its variants are designed to express properties of Markov chains. The following is a long standing open problem (see, e.g., [4]).

SAT Problem. Given a pCTL* state-formula $\phi$ , is there a Markov chain M and a vertex $v \in M$ such that v satisfies $\phi$ ?

Without loss of generality (see, e.g., Sect. 5 of [12] for details), we can restrict the statement of the SAT problem to range over Markov chains M whose underlying directed graph has the structure of the full binary tree, where each edge (connecting a vertex to one of its two children) has probability $\frac{1}{2}$. This is a convenient restriction that allows to interpret pCTL* formulas $\phi (P_1,\dots , P_n)$ with n propositional variables as denoting sets $\llbracket \phi \rrbracket \subseteq {\mathcal T}_{\varSigma }$ for $\varSigma = \{0,1\}^n$.

It is well known that there exists pCTL* formulas such that $\llbracket \phi \rrbracket \ne \emptyset$ but $\llbracket \phi \rrbracket$ does not contain any regular tree. This means the logic pCTL* can define non-regular sets of trees. We show now that every pCTL* definable set $\llbracket \phi \rrbracket$ is $\mathrm {MSO}+\forall ^{=1}_\pi$ definable. The argument is similar⁴ to the one used in [16] to prove that sets of trees defined in the logic CTL* can be defined in $\mathrm {MSO}$. Each pCTL* state formula $\phi (P_1,\dots , P_n)$ is translated to a $\mathrm {MSO}+\forall ^{=1}_\pi$ formula $F_\phi (X_1,\dots , X_n, y)$ and each pCTL* path formula $\psi (P_1,\dots , P_n)$ is translated to a $\mathrm {MSO}+\forall ^{=1}_\pi$ formula $F_\psi (X_1,\dots , X_n, Y)$ such that:

• a vertex v of the full binary tree satisfies the pCTL* state-formula $\phi (P_1,\dots , P_n)$ if and only if $F_\phi (P_1,\dots , P_n,v)$ is a valid $\mathrm {MSO}+\forall ^{=1}_\pi$ formula with parameters,

• a path $A \in \mathcal {P}$ in the the full binary tree satisfies the pCTL* path-formula $\psi (P_1,\dots , P_n)$ if and only if $F_\psi (P_1,\dots , P_n,A)$ is a valid $\mathrm {MSO}+\forall ^{=1}_\pi$ formula with parameters.

The only case different from [16] is for a pCTL state-formula of the form $\phi =\mathbb {P}_{>0}\psi (P_1,\dots , P_n)$ which holds at a vertex v if the collection of paths starting from v and satisfying $\psi$ has positive measure; $\phi$ is is translated to $\mathrm {MSO}+\forall ^{=1}_\pi$ as follows:

$$\begin{aligned} F_\phi (X_1,\dots ,&X_n,y) = \exists ^{>0}_\pi Y. \big (\mathrm{{ Y\, is\, a\, path\, containing}}\, x, and \\&F_\psi (X_1\dots , X_n,Z) \, \mathrm{{holds\, where}}\, Z\, \mathrm{{is\, the\, set\, of\, descendants\, of}}\, x\, \mathrm{in}\, Y \big ) \end{aligned}$$

We state the correctness of this translation as the following

Theorem 5

The decidability of the SAT problem for the qualitative fragment of pCTL* is reducible to the decidability of $\mathrm {MSO}+\forall ^{=1}_\pi$.

7.2 On the Qualitative Languages of Carayol, Haddad and Serre

In a recent paper [6] Carayol, Haddad and Serre have considered a probablistic interpretation of standard nondeterministic tree automata. Below we briefly discuss this interpretation referring to [6] for more details. The standard interpretation of a nondeterministic tree automaton $\mathcal {A}$ over the alphabet $\varSigma$ is the set $\mathcal {L}(A) \subseteq {\mathcal T}_{\varSigma }$ of trees $X \in {\mathcal T}_{\varSigma }$ such that there exists a run $\rho$ of X on $\mathcal {A}$ such that for all paths $\pi$ in $\rho$, the path $\pi$ is accepting. The probabilistic interpretation in [6] associates to each nondeterministic tree automaton the language $\mathcal {L}^{=1}(\mathcal {A}) \subseteq {\mathcal T}_{\varSigma }$ of trees $X \in {\mathcal T}_{\varSigma }$ such that there exists a run $\rho$ of X on $\mathcal {A}$ such that for almost all paths $\pi$ in $\rho$, the path $\pi$ is accepting, where “almost all” means having Lebesgue measure 1. Using the language of MSO $+ \forall ^{=1}_\pi$ the language $\mathcal {L}^{=1}(\mathcal {A})$ can be naturally expressed by the following formula $\psi _{\mathcal {A}}(\overrightarrow{X})$:

Theorem 6

Let $L \subseteq {\mathcal T}_{\varSigma }$ be a set of trees definable by a nondeterministic tree automaton with probabilistic interpretation. Then L is definable in $\mathrm {MSO}+\forall ^{=1}_\pi$.

Let $L \subseteq {\mathcal T}_{\{0,1\}}$ consists of $A \in {\mathcal T}_{\{0,1\}}$ such that the set of branches having infinitely many vertices labeled by 1 has measure 1. In [6, Example 7] it is proved that L is not regular and definable by a nondeterministic tree automata with probabilistic interpretation. Therefore:

Proposition 3

$\mathrm {MSO}+\forall ^{=1}_\pi$ is a proper extensions of $\mathrm {MSO}$ on trees.

7.3 An Extension of Rabin’s Theory of the Lattice of $F_\sigma$ Sets

Rabin in [13] proved the decidability of MSO on the full binary tree and as corollaries obtained several decidability results. One of them ([13, Theorem 2.8]) states that the first order theory of the lattice of $F_\sigma$ subsets of the Cantor space $\{0,1\}^\omega$, with the predicate $C(X) \Leftrightarrow$ “X is a closed set”, is decidable. Formally this result can be stated as follows.

Theorem 7

(Rabin). The FO theory of the structure $\langle F_\sigma , \cup , \cap , C\rangle$ is decidable.

Rabin proved this theorem by means of a reduction to the MSO theory of the full binary tree. He observed that the Cantor space $\{0,1\}^{\omega }$ is a homeomorphic copy of the set of paths $\mathcal {P}$ in the full binary tree (see Definition 10). He then noted that an arbitrary set of vertices $X \in {\mathcal T}_{\{0,1\}}$ can be viewed as a set $\langle X\rangle \subseteq \mathcal {P}$ of paths by the MSO expressible definition $\langle X\rangle = \{Y\in \mathcal {P} \mid Y \cap X\, \mathrm{is finite}\}$. He showed that a set of paths $A \subseteq \mathcal {P}$ is $F_\sigma$ if and only if there exists some $X \in {\mathcal T}_{\{0,1\}}$ such that $A = \langle X\rangle$ and that it is possible to express in MSO that $\langle X\rangle$ is closed. For details we refer to [13, §2].

We now consider an extension of the structure $\langle F_\sigma , \cup , \cap , C\rangle$ by a new predicate $N(X) \Leftrightarrow$ “X is a Lebesgue null set”.

Theorem 8

The first order theory of the structure $\langle F_\sigma , \cup , \cap , C, N\rangle$ is interpretable in $\mathrm {MSO}+\forall _\pi$.

Proof

It is straightforward to extend Rabin’s interpretation by an appropriate $\mathrm {MSO}+\forall _\pi$ interpretation of the predicate N. Let $\phi (X)$ be the formula with one free-variable defined as: $\forall ^{=1}_\pi Y. (Y \in \langle X\rangle )$ where, in accordance with Rabin’s interpretation, the predicate $Y \in \langle X\rangle$ is defined as “$Y\cap X$ is a finite set”, which is easily expressible in MSO. Then one has $\langle X\rangle \in N$ if and only if $\phi (X)$ holds, and this completes the proof.    $\square$

Hence if the theory of $\mathrm {MSO}+\forall ^{=1}_\pi$ is decidable then the first order theory of $\langle F_\sigma , \cup , \cap , C, N\rangle$ is also decidable.

7.4 On the Measurable Algebra with Scott’s Closure Operation

In the classic paper “The algebra of Topology” [11] McKinsey and Tarski defined closure algebras as pairs $\langle B, \Diamond \rangle$ where B is a Boolean algebra and $\Diamond : B\rightarrow B$ is unary operation satisfying the axioms: $\Diamond \Diamond x = \Diamond x$, $x\le \Diamond x$, $\Diamond (x\vee y) = \Diamond x \vee \Diamond y$ and $\Diamond \top = \top$.

Let $\mathcal {B}$ denote the collection of Borel subsets of the Cantor space $\{0,1\}^{\omega }$. Define the equivalence relation $\sim$ on $\mathcal {B}$ as $X \sim Y$ if $\mu _{\{0,1\}^{\omega }}(X \triangle Y) = 0$, where $X \triangle Y = (X\setminus Y) \cup (Y\setminus X)$. The quotient $\mathcal {B}/_{\sim }$ is a complete Boolean algebra with operations defined as $[X]_\sim \vee [Y]_\sim = [X\cup Y]_\sim$ and $\lnot [X]_\sim = [\{0,1\}^{\omega }\setminus X]_\sim$. It is called the (Lebesgue) measure algebra (see, e.g., [9, 17.A]) and denoted by $\mathcal {M}$.

Recently Dana Scott has observed⁵ that the (Lebesgue) measure algebra $\mathcal {M}$ naturally carries the structure of a closure algebra.

Definition 14

An element $[X]_\sim \in \mathcal {M}$ is called closed if it contains a closed set, i.e., if there exists a closed set Y such that $Y \in [X]_\sim$. Let $\Diamond _{\mathcal {M}} : \mathcal {M} \rightarrow \mathcal {M}$ be defined as follows: $\Diamond ( [X]_\sim ) = \bigwedge \{[Y]_\sim \mid [X]_{\sim }\le [Y]_{\sim }$ and $[Y]_{\sim }$  is closed$\}$. Note that the infimum exists because $\mathcal {M}$ is complete.

Proposition 4

(Scott). The pair $\mathcal {S} = \langle \mathcal {M}, \Diamond _{\mathcal {M}}\rangle$ is a closure algebra.

Interestingly, it was proved in [10, Theorem 6.3] that $\mathcal {S}$ is universal among the class of all closure algebras: an equation holds in $\mathcal {S}$ if and only if it holds in all closure algebras. We make the following observation.

Theorem 9

The first order theory of $\mathcal {S}$ is interpretable in $\mathrm {MSO}+\forall _\pi$.

Proof

By Theorem 8 it is sufficient to observe that the theory of $\mathcal {S}$ can be interpreted within the theory of $\langle F_\sigma , \cup , \cap , C, N\rangle$. This is possible as, by regularity of Borel measures, any element $[X]_{\sim }$ contains an $F_\sigma$ sets. A detailed proof will be published elsewhere.    $\square$

Hence if $\mathrm {MSO}+\forall ^{=1}_\pi$ is decidable then the first order theory of $\mathcal {S}$ is also decidable.

8 Open Problems

In the Introduction we formulated Problem 1 regarding the decidability of the theory of $\mathrm {MSO}+\forall ^{=1}_\pi$. In light of Theorems 8 and 9, the decidability of the theories of $\langle F_\sigma , \cup , \cap , C, N\rangle$ and $\langle \mathcal {M}, \Diamond _{\mathcal {M}}\rangle$ is a closely related problem. In particular, if one of these two theories is undecidable, then also $\mathrm {MSO}+\forall ^{=1}_\pi$ is undecidable.

In Sect. 4 in Remark 2 we noticed that the definition of the semantics of $\mathrm {MSO}+\forall ^{=1}$ involves potentially non-measurable sets. One encounters the same problem in the definition of $\mathrm {MSO}+\forall ^{=1}_\pi$. Hence:

Problem 2

Are relations defined by $\mathrm {MSO}+\forall ^{=1}_\pi$ formulas Lebesgue measurable?

In previous work [8] we proved that the all regular sets of trees are $\mathcal {R}$-sets and, as a consequence, Lebesgue measurable. Therefore a variant of Problem 2 above asks whether all $\mathrm {MSO}+\forall ^{=1}_\pi$ definable sets are $\mathcal {R}$-sets. In the other direction, $\mathcal {R}$-sets belong to the ${\varvec{\varDelta }}^{1}_{2}$ class of the projective hierarchy. So we can ask:

Problem 3

Is the class of sets definable by $\mathrm {MSO}+\forall ^{=1}_\pi$ formulas contained in a certain fixed level of the projective hierarchy?

A negative answer would likely lead to undecidability of $\mathrm {MSO}+\forall ^{=1}_\pi$ (see [3]).