Abstract
General conditions for the existence of stable, minimum energy configurations in the full N-body problem are derived and investigated. Then the minimum energy and stable configurations for the spherical, equal mass full body problem are investigated for \(N = 2, 3, 4\). This problem is defined as the dynamics of finite density spheres which interact gravitationally and through surface forces. This is a variation of the gravitational N-body problem in which the bodies are not allowed to come arbitrarily close to each other (due to their finite density), enabling the existence of resting configurations in addition to orbital motion. Previous work on this problem has outlined an efficient and simple way in which the stability of configurations in this problem can be defined. This methodology is reviewed and derived in a new approach and then applied to multiple body problems. In addition to this, new results on the Hill stability of these configurations are examined and derived. The study of these configurations is important for understanding the mechanics and morphological properties of small rubble pile asteroids. These results can also be generalized to other configurations of bodies that interact via field potentials and surface contact forces.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Celestial Mechanics systems have two fundamental conservation principles: conservation of momentum and conservation of (mechanical) energy. While conservation of momentum is always conserved for a closed system, mechanical energy is often not conserved and can be dissipated through non-conservative internal interactions. Thus, for any closed mechanical system it makes sense to seek out what their local and global minimum energy configurations are at a fixed level of angular momentum. We can use the existence of these local and global minima to define what we consider stable states for a system, which provides a strict and robust limit for any mechanical system and is distinguished from particle motion systems in astrodynamics which often are only oscillatory stable and in fact do not minimize the total energy. The ubiquity and pervasiveness of energy dissipation in the solar system and its role in the long-term evolution of bodies of all sizes motivates these questions concerning the minimum energy states for celestial mechanics systems at a given value of angular momentum.
If this question is applied to the traditional N-body gravitational problem, however, it can be shown that there are no minimum energy configurations for \(N\ge 3\) [9]. This is due to the point-mass nature of the traditional N-body problem, as when there are more than 3 bodies it is always possible to drive the total energy of the system to \(-\infty \) while maintaining a constant angular momentum. This issue is considered in an earlier paper [9], where it is shown that replacing point mass bodies with finite density, rigid bodies enables the system N-body gravitational problem to have unique minimum energy configurations. This occurs as now bodies can rest on each other, meaning that their relative gravitational potential energies are bounded from below. That paper explores this phenomenon for celestial mechanics systems and finds all possible relative equilibria for the 2 and 3-body problem assuming the bodies have equal size and density and are spherical. Among other results, it is found that the so-called “full” 3-body problem has seven distinct relative equilibria, five additional beyond the familiar orbiting Lagrange and Euler configurations. Out of these, only 3 can be stable and only one of these three can be the minimum energy configuration for a given angular momentum. In [11] the problem is developed for the equal mass, spherical 4-body problem and a number of candidate relative equilibria are also found. An interesting result in both studies is that the relative stability of these minimum energy configurations change as the angular momentum of the system is modified.
In the current chapter a new derivation of some of the fundamental results in these papers is given, with the criteria for stable configurations generalized and extended to constraints on when the system can also be bound energetically. This chapter also provides more detailed evaluation of the energetic stability conditions for the 3-body orbiting conditions and relates the energy values of the existing relative equilibria to the Hill stability energy levels. This overall methodology is also applied to the 4-body problem, restricted so that the bodies are spheres of equal size and density. The computational issues related to the 4-body problem are significant, as even for the point-mass case the total number of relative equilibria are not known and are at best bounded [3]. Due to this we do not analyze purely orbital relative equilibria in the 4-body problem, motivated by a theorem from Moeckel [5] that these can never be minimum energy configurations for the point-mass N body problem. Instead, we focus on resting configurations, or configurations that are separated into a mixture of two groups of bodies that orbit each other (motivated by the Hypothesis in [9]).
The original method used for this analysis relies on a novel application of the Cauchy Inequality to find a modified version of the Sundman Inequality. From this approach the minimum energy function can be derived, which is in spirit the same function as Smale’s Amended potential [13, 14]. The minimum energy function is defined for a given level of angular momentum and only involves internal degrees of freedom in the system. Thus, whenever this function is stationary or positive definite with respect to all degrees of freedom, then the system is in a relative equilibrium. Further, if the function is positive definite about this relative equilibria then the given configuration is energetically stable, meaning that it is impossible for it to deviation from its current configuration without the addition of exogenous energy. It can be shown that at a given angular momentum there may be multiple stable relative equilibria, in this case there is always a minimum energy configuration which corresponds to the lowest energy level that the system can exist in.
In addition to reviewing and summarizing current results on the equal mass, spherical N-body problem for \(N = 2, 3, 4\), this paper develops a new derivation of the amended potential that is based on Lagrangian mechanics, providing a dynamical foundation for the previous derivation which only used integrals of motion for the system. Specifically, we show that when the N-body problem is transformed into a rotating frame, with the rotation rate chosen based on the angular momentum of the system and its instantaneous moment of inertia, that the resultant Lagrangian can be reduced by Routh reduction to a system that only depends on the internal degrees of freedom of the system. This derivation is also extended to gravitationally interacting rigid bodies as well, sometimes termed the “Full-Body Problem.”
The outline of the paper is as follows. First, a number of fundamental results and definitions are reviewed, leading to the statement of the Lagrange equations of motion for the Full N-body problem. The angular momentum magnitude is then removed through an application of Routhian reduction. Then the necessary and sufficient conditions for relative equilibria and their stability in the Full N-body problem is derived and proven. Following this derivation we consider the simplified case of equal mass, finite density spheres. We specifically review previously published results for \(N = 2, 3, 4\) with additional insight into the energetics of these cases and conditions under which they will be Hill stable. This chapter is designed to provide a rigorous introduction to this general problem, and is intended as serving as a starting point for future analyses of the Full N-body problem.
2 Fundamental Quantities and Specification of the Full N-Body Problem
Consider the dynamics of a set of N rigid bodies that interact with each other through gravitation and surface contact forces. We specify these bodies in general as mass distributions, denoted as \({\mathscr {B}}_i, i = 1, 2, \ldots , N\). Each body has its own center of mass location, velocity and body orientation and rotation. Thus in total there are 6N degrees of freedom for the system, although we assume that we trivially remove the three degrees of freedom associated with linear momentum by fixing the system barycenter at the origin. Following the motivation in [9], we also assume that each body has a finite density and mass, and thus has finite dimensions. We do not account for the flexure or movement of the mass distributions relative to themselves, only relative to each other. We note that these body, so defined, will place mutual gravitational forces and torques across each other, independent of contact.
2.1 Implicit Energy Dissipation Interaction Models
We qualify our rigid body assumption, in that while we do not allow the mass distributions to distort, we assume that they will cause infinitesimal distortions of mass distribution and hence tidal torques across each other. This will allow otherwise decoupled spherical bodies to place infinitesimal torques on each other, and will essentially enable the transfer of angular momentum between non-touching components and cause energy to be dissipated. When surfaces are in contact, we again assume that there will be some coefficient of friction between the components along with infinitesimal distortions of the bodies, again leading to transfer of angular momentum with energy dissipation. These physical effects serve dual purpose, in that they will tend to synchronize collections of bodies, either resting on each other or orbiting each other, and will also dissipate excess energy in the system. This is needed in order for a resting or orbiting collection of particles to dissipate relative motion between each other. Inclusion of this notional model ensures that configurations will, when reduced to their minimum energy state, all rotate at a common rate.
2.2 Density Distributions and Fundamental Quantities
To more easily discuss the following derivations for the finite density N body problem we state our problem in an integral form. Consider an arbitrary collection of N mass distributions, denoted as \({\mathscr {B}}_i, i = 1,2, \ldots , N\), following the derivation in [7]. Each body \({\mathscr {B}}_i\) is defined by a differential mass distribution \(dm_i\) that is assumed to be a finite density distribution, denoted as
where \(m_i\) is the total mass of body \({\mathscr {B}}_i\), \(\rho _i\) is the density of body \({\mathscr {B}}_i\) (possibly constant) and dV is the differential volume element. If \({\mathscr {B}}_i\) is described by a point mass density distribution, the body itself is just defined as a single point \({\mathbf{r}}_i\). Instead, if the body is defined as a finite density distribution, \({\mathscr {B}}_i\) is defined as a compact set in \(\mathbb {R}^3\) over which \(\rho _i({\mathbf{r}}) \ne 0\). In either case the \({\mathscr {B}}_i\) are defined as compact sets.
We assume that each differential mass element \(dm_i({\mathbf{r}})\) has a specified position and an associated velocity. For components within a given body \({\mathscr {B}}_i\) a rigid body assumption is made so that the entire body can be defined by the position and velocity of its center of mass, its attitude, and its angular velocity. Finally, we assume that these positions and velocities are defined relative to the system barycenter, which is chosen as the origin, or
Given these definitions an integral form of the kinetic energy, total system inertia dyad, gravitational potential energy, and angular momentum vector can be stated as [7]
where \({\mathbf{r}}_{ij} = {\mathbf{r}}_j - {\mathbf{r}}_i\), a bolded quantity with an overline, \(\overline{{\mathbf{I}}}\), denotes a dyad and \(\widetilde{{\mathbf{r}}}\) is the cross-product dyad associated with a vector \({\mathbf{r}}\). Note that the definition of \(\mathscr {U}\) in Eq. 7 eliminates the self-potentials of these bodies from consideration. As the finite density mass distributions are assumed to be rigid bodies this elimination is reasonable. This notation can be further generalized by defining the single and joint general mass differentials
and the total mass distribution \({\mathscr {B}} = \left\{ {\mathscr {B}}_i, i = 1, 2, \ldots , N\right\} \). Then the above definitions can be reduced to integrals over \({\mathscr {B}}\):
2.3 Relative Reduction
As stated for the discrete forms of these results, a key simplification results since the barycenter and barycentric velocity are both zero. Applying Lagrange’s Identity we can express all of the above as relative integrals. Applying the standard result provides:
We note a distinct shift in this statement, as we go from assuming that all vectors are expressed relative to an inertial frame to a more general idea that all vectors are expressed in a frame that is only defined relative to each other. This necessitates the introduction of a transformation dyad that takes this internal frame and rotates it into an inertial frame, which we denote as \(\overline{{\mathbf{A}}}\). Thus the expressions for the angular momentum vector and the inertia dyadic must now be transformed into the inertial frame, as is indicated above. The scalar quantities do not need this, of course.
Thus all of these quantities are reduced to integrals of relative vectors over the mass distribution, and mimic the potential energy function. This change is significant, as it explicitly shows some of the fundamental symmetries of the problem.
2.4 Degrees of Freedom
Despite the integral form of the kinetic and potential energies, we recall that there are only finite degrees of freedom for the system. Specifically, for N bodies there are 3N translational degrees of freedom and 3N rotational degrees of freedom for a total of 6N DOF. In our formulation we have already removed 3 DOF by setting the center of the system at the barycenter, reducing the total to \(3(2N-1)\). The degrees of freedom are split between three general classes, the relative positions of the bodies, the orientations of the bodies relative to each other, and the overall inertial orientation of the system.
It is instructive to review these degrees of freedom. For \(N=1\) there are no relative position or attitude degrees of freedom, and thus there is only the inertial orientation degrees of freedom for the system, yielding a total of 3 DOF in agreement with the general rule. For \(N=2\) we start with one central body with no degrees of freedom. The position of a second body relative to this has 3 DOF and its relative attitude has 3 DOF. Finally, we add the inertial orientation to get a total of 9 DOF. Each additional body then adds 6 DOF again, reproducing our general rule.
We distinguish between the internal, relative degrees of freedom and the inertial orientation degrees of freedom. For the current system we represent the internal degrees of freedom as \(q_i\): \(i = 1, 2, \ldots , 6(N-1)\). These are specifically the relative positions of the centers of mass and the orientations of the rigid bodies relative to each other. For convenience we can imagine these to be Cartesian position vectors and Euler angles. We note that their time derivatives are expressed with respect to an inertial frame. The additional 3 DOF that orient the system relative to inertial space is represented as the rotation dyad \(\overline{{\mathbf{A}}}\) which takes the relative frame into inertial space.
Note again that in our general statements, the final 3 DOF that orient the system relative to inertial space do not change any of our fundamental integral quantities except that of \({\mathbf{H}}\) and \(\overline{{\mathbf{I}}}\). This is because each of these orientations acts on the entire system but do not change the relative orientations or speeds. This invariance is tied to the existence of the angular momentum integral. Despite this, since the speeds are all defined relative to an inertial frame there remains a fundamental connection between the inertial and relative frames.
2.5 Transformation into a Rotating System
Of specific interest to us is the overall rotation of the system due to the non-zero but constant angular momentum. A specific goal is to remove this integral of motion, commonly termed the elimination of the nodes. In our analysis we can remove one degree of freedom quite simply, and by doing so define the fundamental quantity that we use to discuss relative equilibria and their stability.
We define a very specific rotating frame from which we will measure motion. This is done by defining a system angular velocity which is a function of the angular momentum integral. Specifically, define an angular velocity vector
where \(I_H = \hat{{\mathbf{H}}}\cdot \overline{{\mathbf{I}}}\cdot \hat{{\mathbf{H}}}\) is the moment of interia of the system about the angular momentum direction (which is fixed in space). We note that \(I_H\) is a function of both the internal system and its orientation relative to \(\hat{{\mathbf{H}}}\), but not to rotations around this unit vector which we denote by the angle \(\theta \). Since the angular momentum is fixed in space the angular velocity \({\mathbf{\omega }} = \dot{\theta } \hat{{\mathbf{H}}}\) is a true velocity and not a quasi-velocity and thus do not need to worry about this aspect of Lagrangian systems. We can then rewrite our system relative to this rotating frame, noting that the rotation rate \(\dot{\theta }\) is not necessarily constant as the moment of inertia \(I_H\) is not a constant in general.
Now reformulate the system kinetic energy in this rotating frame, with rotation vector defined by \({\mathbf{\omega }}\). The main change is that the time derivatives will now be expressed relative to a rotating frame. Given an inertial velocity \(\varDelta \dot{{\mathbf{r}}}\), it can be expressed relative to a rotating frame as
where \({\mathbf{v}}\) represents the speed relative to the rotating frame and \({\mathbf{r}}\) is the location of the mass elements in question. The dot product of this with itself, which is the kinetic energy integrand, then becomes
where we have used the properties of the cross product dyad and rearranged the terms.
Now consider the double integration over each of these three terms. The first term is the kinetic energy relative to the rotating frame
The final term takes on a simple form as well, once one recalls the definition of the inertia dyad \(\overline{{\mathbf{I}}}\)
From the definition of \({\mathbf{\omega }} = {\mathbf{H}} / I_H = \dot{\theta } \hat{{\mathbf{H}}}\), we find that
Finally consider the middle term. It can be shown that
This serves as a constraint between the coordinates and velocities, and even if the value must be zero its partials with respect to individual terms may not be. Thus we can show this to be true, but must also retain this term in the Lagrange equations and only apply this after the equations are formulated. The proof is easy, and consists of rewriting \(\varDelta {\mathbf{v}} = \varDelta \dot{{\mathbf{r}}} - \widetilde{{\mathbf{\omega }}}\cdot \varDelta {\mathbf{r}}\). Then the first term equals
The second term equals
By definition the first term equals \(H^2 / I_H\). The second term equals \(- H^2 / I_H\), and thus the sum is zero.
The result is that the kinetic energy becomes
2.5.1 Lagrangian Function and Dynamics
The Lagrangian of the original system is just \(L = T - \mathscr {U}\). In this new coordinate system it is
We note that the kinetic energy and gravitational potential are both independent of the angle \(\theta \), and thus \(\partial L / \partial \theta = 0\) leading to the momentum integral.
where we note that the value of H is just \(I_H \dot{\theta }\) due to Eq. 30 but that we retain the functional form still as it is a constraint that must be applied after the equations of motion are derived. Then we find
We can apply Routhian reduction to this system (see [1, 12] for a rigorous application of this approach), yielding
We note that the term \(\frac{1}{2 I_H} \left( \hat{{\mathbf{H}}}\cdot {\mathbf{H}}_r \right) ^2\) will not arise in the Lagrange equations as its first partial will always equal zero and its total time derivative must equal zero by Eq. 30, thus we leave it out of the following discussion. The term \(\frac{H}{I_H} \hat{{\mathbf{H}}}\cdot {\mathbf{H}}_r \) is important, however, and leads to the Coriolis and frame tie acceleration terms in the Lagrange equations.
This reduced Lagrangian has an integral of motion, equal to
where the terms from \(\frac{H}{I_H} \hat{{\mathbf{H}}}\cdot {\mathbf{H}}_r\) will cancel out due to the skew-symmetric form between coordinates and rates. We note that this is just equal to the original energy of the system, given that \(T = T_r + \frac{H^2}{2 I_H}\), and thus is nominally conserved. We denote the new, amended potential as
There are several conclusions we can draw from this analysis. First, from the energy equation we see that
and thus we have
with equality occurring when the relative kinetic energy is \(T_r = 0\). We note that it is not clear whether this minimum in the kinetic energy is possible, as for the earlier system we evidently could not have \(T = 0\) for non-zero angular momentum. Thus, we need to do more work to claim that \(E = \mathscr {E}\) can exist.
2.5.2 Limits on the Energy
First we derive the amended potential through the use of Cauchy’s Inequality. This approach (first presented in [9]) provides a separate rigorous bound on the system energy.
Recall that \({\mathbf{H}} = H \hat{{\mathbf{H}}} = \int _{\mathscr {B}} {\mathbf{r}}\times \dot{{\mathbf{r}}} \ dm\). Dotting both sides by the (constant) unit vector aligned with the angular momentum vector yields the equality
Now apply the triangle inequality to the integral to find:
Squaring the original term, equal to \(H^2\), and applying the Cauchy-Schwarz inequality yields the main result.
But \(\int _{\mathscr {B}} \dot{{r}}^2 \ dm = 2T\) and \(\int _{\mathscr {B}} (\hat{{\mathbf{H}}}\times {\mathbf{r}})\cdot (\hat{{\mathbf{H}}}\times {\mathbf{r}}) \ dm = \hat{{\mathbf{H}}}\cdot \int _{\mathscr {B}} -\widetilde{{\mathbf{r}}}\cdot \widetilde{{\mathbf{r}}} \ dm \cdot \hat{{\mathbf{H}}} =\hat{{\mathbf{H}}}\cdot \overline{{\mathbf{I}}}\cdot \hat{{\mathbf{H}}} = I_H\). Thus, \(H^2 \le 2 T I_H\).
If we then use \(T = E - \mathscr {U}\) the Sundman inequality becomes \(\frac{H^2}{2 I_H} + \mathscr {U} = \mathscr {E} \le E\), which is exactly the same conclusion as we had from our Lagrangian analysis. This modified Sundman Inequality provides an important, and sharp, lower bound on the system energy for a given angular momentum. We note that the traditional Sundman inequality, using the polar moment of inertia, yields an angular momentum terms \(H^2 / (2 I_P) \le H^2 / (2 I_H)\) and thus the limit on the energy is not as sharp and the amended potential from that approach may not be equal to the energy.
Finally, to establish that the case \(E = \mathscr {E}\) can exist, we construct a configuration and system state where this occurs. Consider the system energy when the entire system is at least momentarily stationary and spinning at a single, constant rate. If this occurs, then the inertial speeds are all \(\dot{{\mathbf{r}}} = {\mathbf{\omega }}\times {\mathbf{r}}\) and all the rigid body rotation speeds are \({\mathbf{\omega }}\). At this momentary condition we can show that
Applying the same situation to the angular momentum yields
with the magnitude then being \(H^2 = {\mathbf{\omega }}\cdot \overline{{\mathbf{I}}}\cdot \overline{{\mathbf{I}}}\cdot {\mathbf{\omega }}\).
Now, forming the total energy we find
This cannot be directly related to the angular momentum as of yet. To do that, assume that the \({\mathbf{\omega }}\) is chosen along a principal moment of inertia at this instantaneous configuration. Then we can state that \(H^2 = \omega ^2 I_\omega ^2\), where \(I_\omega \) is a principal moment of inertia. Also, then \(T = \frac{1}{2} \omega ^2 I_{\omega } = \frac{1}{2} H^2 / I_\omega \). Then the energy equals
which is identically equal to \(\mathscr {E}\). Thus, by construction, we prove that the lower limit can be achieved, or \(E = \mathscr {E}\), and thus the relative kinetic energy can be identically zero at an instant of time, \(T_r = 0\).
We note that the condition \(E=\mathscr {E}\) is not sufficient for the system to be in a relative equilibrium, as the forces acting within the system may not be balanced and thus may cause the system to evolve in time.
2.6 Additional Integrals of Motion
In this new rotating frame the angular momentum magnitude is explicitly removed, yielding a quadrature for the total system rotation once the internal motion is known
Still, the additional two integrals of motion for conservation of angular momentum transverse to the angular momentum direction are not explicitly present. These can be transformed into the relative frame as follows. Consider the projection of the internal angular momentum into the inertial frame \(\overline{{\mathbf{A}}} \cdot {\mathbf{H}}_r\). We know that \({\mathbf{H}}_r\) is already perpendicular to \(\hat{{\mathbf{H}}}\) and that for our defined frame the rotation is always about this direction. Thus we can infer that \(\overline{{\mathbf{A}}} \cdot {\mathbf{H}}_r = {\mathbf{0}}\).
3 Equilibrium and Stability Conditions
With these results we can determine conditions for relative equilibrium and conditions for stability. In fact, given the classical form of the Energy, split into a quadratic and a potential part, the derivation of stability conditions is simple. The only catch involves the presence of uni-lateral constraints which exist when the rigid bodies are in contact. We consider the cases separately. First we present some definitions.
Definition 1
(Relative Equilibrium) A given configuration is said to be in “Relative Equilibrium” if its internal kinetic energy is null (\(T_r = 0\)), meaning that \({\mathscr {E}} = E\) at an instant, and that it remains in this state over at least a finite interval of time.
Definition 2
(Energetic Stability) A given relative equilibrium is said to be “Energetically Stable” if any equi-energy deviation from that relative equilibrium requires a negative internal kinetic energy, \(T_r < 0\), meaning that this motion is not allowed.
Note that energetic stability is different than Lyapunov or spectral stability, which are the usual notions of stability in astrodynamics (these distinctions are discussed in detail for the Full Body Problem in [8]). Energetic stability is stronger in general, as it is robust to any energy dissipation and in fact—if it applies—means that a given relative equilibrium configuration cannot shed any additional energy and thus is static without the injection of exogenous energy, a condition we refer to as being in a minimum energy state.
3.1 No Contact Case
When there are no contacts between the bodies, there are necessarily no active unilateral constraints and all of the degrees of freedom are unconstrained. We also note that the kinetic energy is quadratic in the generalized coordinate rates and has the form of a natural system ([2], p. 72). Then the condition for a relative equilibrium are that all of the \(\dot{{\mathbf{q}}} = 0\) (yielding \(T_r = 0\)) and \(\partial \mathscr {E} / \partial {\mathbf{q}} = {\mathbf{0}}\). Energetic stability of the configuration occurs when the Hessian of the amended potential is positive definite, or \(\partial ^2 \mathscr {E} / \partial {\mathbf{q}}^2 > 0\), meaning that it has only positive eigenvalues. Neutral stability can occur when \(\partial ^2 \mathscr {E} / \partial {\mathbf{q}}^2 \ge 0\), meaning that at least one eigenvalue is equal to zero. In this case it is possible for the system to drift at a constant rate relative to the equilibrium, ultimately destroying the configuration. If the configuration is not positive definite or semi-definite, then there exists at least one negative eigenvalue and the system can escape from the equilibrium configuration while conserving energy. Another way to consider this case is that the system can still dissipate energy, and thus can evolve to a lower energy state. We note that this is a stronger form of stability than is sometimes used in celestial mechanics and astrodynamics, where spectral stability of linearized motion can sometimes be stable (as in the Lagrange configurations of the 3-body problem that satisfy the Routh criterion).
It is a remarkable fact of celestial mechanics that in the point mass n-body case for \(n\ge 3\), the Hessian of any relative equilibrium configuration has at least one negative eigenvalue and is unstable [5]. Thus for the point mass n-body problem all central configurations are always energetically unstable except for the 2-body problem. For the \(n=2\) body problem there is only a single relative equilibrium and it is positive definite and thus stable. If we consider the 3-body problem, we note that while the Lagrange configurations may be spectrally stable when they satisfy the Routh criterion, they are not at a minimum of the amended potential and thus if energy dissipation occurs they can progressively escape from these configurations. We note that for the finite density cases there are always stable configurations at any angular momentum [9].
In keeping with a variational approach, in the no-contact case (i.e., when there are no constraints on the coordinates), the equilibrium condition is
where \(\delta {\mathscr {E}} = \sum _{i=1}^n \left( \partial {\mathscr {E}}/{\partial q_i}\right) \delta q_i\) which corresponds to \(\partial {\mathscr {E}}/{\partial q_i} = 0\) for all i. The stability condition is
which corresponds to the Hessian \(\left[ \partial ^2\mathscr {E} / \partial q_i \partial q_j \right] \) being positive definite.
3.2 Contact Case
The equilibrium and stability conditions must be modified if there are constraints which are activated. We assume, without loss of generality, that generalized coordinates are chosen to correspond to each contact constraint, such that in the vicinity of their being active the unilateral constraint can be restated as
for \(j = 1, 2, \dots , m\) constraints. We note that these constrained generalized coordinates may either be relative positions or Euler angles between bodies. Assume we have the system at a configuration \({\mathbf{q}}\) with m active constraints as just enumerated and \(T_r = 0\). Further, assume that the \(n-m\) unconstrained states satisfy \({\mathscr {E}}_{q_i} = 0\) for \(i = m+1, \ldots , n\). For this system to be at rest the principle of virtual work and energy states that the variation of the m constrained states are such that the amended potential only increases, or
which, for our assumed constraints on the states, is the same as \({\mathscr {E}}_{q_j} \ge 0\) for \(j=1,2,\ldots , m\). The derivation of this just notes that, as defined, if the amended potential can only increase in value then motion is not allowed, as this corresponds to a decrease in kinetic energy from its zero value, which of course is non-physical.
For stability, we require the \(n-m\) unconstrained variables to satisfy the same positive definite condition as derived earlier. For the constrained states we only need to tighten the condition to \(\delta {\mathscr {E}} > 0\) or \({\mathscr {E}}_{q_j} > 0\) for \(j = 1,2, \ldots , m\). This last assertion demands some more specific proof and motivates the following general theorem on necessary and sufficient conditions for a relative equilibrium.
Theorem 1
Consider a system with an amended potential \({\mathscr {E}}\) as defined above with n degrees of freedom, m of which are activated in such a way that only the variations \(\delta q_j \ge 0\), \(j = 1, 2, \ldots , m\) are allowed. The degrees of freedom \(q_i\) for \(m < i \le n\) are unconstrained.
The Necessary and Sufficient conditions for the system to be in a relative equilibrium are that:
-
1.
\(T_r = 0 \)
-
2.
\({\mathscr {E}}_{q_i} = 0 \ \forall \ m < i \le n \)The Necessary and Sufficient conditions for
-
3.
\({\mathscr {E}}_{q_j} \ge 0 \ \forall \ 1 \le j \le m\)
The Necessary and Sufficient conditions for a system in a relative equilibrium to be energetically stable are that:
-
1.
\( \left[ \frac{\partial ^2 {\mathscr {E}}}{\partial q_i \partial q_k} \right] > 0 \ \forall \ m < i,k \le n\)
-
2.
\( {\mathscr {E}}_{q_j} > 0 \ \forall \ 1 \le j \le m\)
Proof
First, note that by construction the relative kinetic energy \(T_r\) is of the form \(T_r = \frac{1}{2} \sum _{i,j} a_{ij}({\mathbf{q}}) \dot{q}_i \dot{q}_j\) where \([a_{ij}] > 0\) (is positive definite as a matrix) and \(\partial L / \partial \dot{q}_i = \partial T_r / \partial \dot{q}_i = \sum _j a_{ij} \dot{q}_j\) (c.f. [2]). Thus it can be easily shown that all \(\dot{q}_i = 0\) if and only if \(T_r = 0\). Also note that \(d/dt( H/I_H \hat{{\mathbf{H}}}\cdot {\mathbf{H}}_r\) will be linear in the \(\dot{q}_i\) and thus will also go to zero if \(T_r = 0\). Furthermore, even though the \(a_{ij}\) can be a function of the \({\mathbf{q}}\), if \(T_r = 0\) then \(\left. \partial L / \partial {\mathbf{q}} \right| _{T_r = 0} = - \partial {\mathscr {E}} / \partial {\mathbf{q}}\).
Next consider the relative equilibrium conditions for the unconstrained degrees of freedom. It is easily shown that if \({\mathscr {E}}_{q_i} = 0 \) and \(T_r = 0\) then \(d/dt (\partial L / \partial \dot{q}_i) = 0\), meaning that all \(\ddot{q}_i = 0\). Conversely, if all \(\dot{q}_i = 0\) then for all \(\ddot{q}_i = 0\) to hold we must have \(\partial L / \partial q_i = 0\). However, for zero speeds we have \(L = {\mathscr {E}}\), completing the proof for the conditions of the unconstrained relative equilibria.
Next we develop the stability conditions for the unconstrained coordinates. Note that conservation of energy implies that under all finite variations we must have \(\varDelta T_r + \varDelta {\mathscr {E}} = 0\), where \(\varDelta {\mathscr {E}} = {\mathscr {E}}({\mathbf{q}}+\delta {\mathbf{q}}) - {\mathscr {E}}({\mathbf{q}})\). If the system is at a relative equilibrium at the test point \({\mathbf{q}}^*\) (and only these unconstrained coordinates are varied) we find \(T_r = \varDelta T_r = - \frac{1}{2} \delta {\mathbf{q}} \cdot \left. \frac{\partial ^2{\mathscr {E}}}{\partial {\mathbf{q}}^2}\right| ^* \cdot {\mathbf{q}} + \ldots \), as the first order partials are all zero. If the amended potential \({\mathscr {E}}\) is positive definite at the relative equilibria, then the quantity on the right is \(< 0\) and we have \( T_r < 0\), which is impossible, meaning that finite variations cannot occur. Conversely if \(\delta ^2{\mathscr {E}} = 0\) for some specific variations, then the configuration can be deviated from the relative equilibrium, and it is considered to be indeterminate as higher orders must be considered to determine stability. If \(\delta ^2{\mathscr {E}} < 0\) for some variation, then \(T_r > 0\) for this variation and the system is no longer at a relative equilibrium, implying instability.
For the constrained coordinates, first assume that all of the unconstrained coordinates are in a stable relative equilibrium. As all of the m constraints are active, for zero speeds we have \(E = {\mathscr {E}}\). Consider a variation consistent with the constraints, yielding \(\delta E = \delta T_r + \delta {\mathscr {E}} = 0\), where \(\delta {\mathscr {E}} = \sum _{j=1}^m {\mathscr {E}}_{q_j} \delta q_j\). If \(\delta {\mathscr {E}} > 0\) for all possible variations, then by necessity \(\delta T_r < 0\), which is impossible. Thus in this case no motion can occur and, in fact, the system is stable against all variations in both the constrained and unconstrained variations.
If, instead, \(\delta {\mathscr {E}} = 0\) for all variations of at least a subset of the constrained coordinates, then \(\delta T_r = 0\) and by extension \(\dot{{\mathbf{q}}} = 0\) for this subset. Then, since \(\delta {\mathscr {E}} = 0\) for all allowable variations of this subset, this implies that \({\mathscr {E}}_{q_j} = 0\) and by Lagrange’s equations all \(\ddot{q}_j = 0\), leaving the system in equilibrium. The stability of this configuration is considered to be indeterminate, however, as the higher order partials must be considered, incorporating constraints at a higher order as well.
Finally, consider the case when \(\delta {\mathscr {E}} < 0\) for some specific variation \(\delta {\mathbf{q}}'\), chosen such that the unconstrained variations are all zero and the constrained variations are allowable. Given the assumed restrictions on \(\delta q_j \ge 0\), this means that some values of \({\mathscr {E}}_{q_j} < 0\). Then we can form the test variation \(\delta T_r = - \delta {\mathscr {E}} > 0\), which is allowed. Furthermore, writing the Lagrange equations yields \(d/dt (\partial T_r / \partial {\mathbf{q}}) = - \partial {\mathscr {E}}/\partial {\mathbf{q}}\). Taking the dot product of this with the allowable variation \(\delta {\mathbf{q}}'\) yields
This can be integrated over time from \(t = 0\) to \(t = \varDelta t\) to find
Thus, after a finite time in such a configuration we see that the velocities in the relative kinetic energy are non-zero, meaning that the system is no longer in a relative equilibrium. \(\square \)
4 Fundamental Quantities in the Full N-Body Problem
Now that the dynamical analyses are complete, we can progress to the main problem. This requires us to develop explicit expressions for the amended potential, and eventually will result in applying our restrictions on the bodies being equal mass and size spheres.
4.1 Rigid Body Expressions
We first restate the fundamental quantities of the total kinetic energy, gravitational potential energy, moments of inertia and angular momentum of this system in explicit coordinates. Since finite density distributions are assumed for each body we must also incorporate rotational kinetic energy, rigid body moments of inertia, angular velocities and explicit mutual potentials that are a function of body attitude [7].
In the following the ith rigid body’s center of mass is located by the position \({\mathbf{r}}_i\) and has a velocity \(\dot{{\mathbf{r}}}_i\) in the inertial frame and velocity \({\mathbf{v}}_i\) in the rotating frame. In addition to its mass \(m_i\), the ith body has an inertia dyadic \(\overline{{\mathbf{I}}}_i\), an angular velocity vector \({\mathbf{\omega }}_i\) and an attitude dyadic that maps its body-fixed vectors into inertial space, \(\overline{{\mathbf{A}}}_i\). For expressing the kinetic energy of the rigid bodies relative to the rotating frame it is important to define their angular velocity relative to the rotating frame. If their inertial angular velocity is \({\mathbf{\omega }}_i\), then the relative angular velocity will be \(\varOmega _i = {\mathbf{\omega }}_i - {\mathbf{\omega }}\). Using this definition the basic quantities are then defined as [9]:
In the above we have implicitly assumed that all vector quantities are expressed in an inertial frame, thus the only place where the relative orientations \(\overline{{\mathbf{A}}}_i\) occur are in the potential energy, \(\mathscr {U}_{ij}\), which must specify the orientation between two different rigid bodies i and j as \(\overline{{\mathbf{A}}}_{ij} = \overline{{\mathbf{A}}}_j^T\cdot \overline{{\mathbf{A}}}_i\), which transfers a vector from the body i frame into the body j frame.
The kinetic energy, moments of inertia and angular momentum can also be stated in relative form between the center of masses (assuming barycentric coordinates and applying Lagrange’s Identity). In introducing these specifications we also note that we can decouple the relative orientations of the bodies from their inertial orientations. Thus we add the rotation dyad \(\overline{{\mathbf{A}}}\) which represents the rotation of a single internal body-relative frame into inertial space. This quantity is only needed for those expressions which are stated in an inertial frame. We assume all relative vectors to be specified in the internal frame, including inertia dyads of each individual rigid body.
where \(\hat{{\mathbf{H}}}_r\) denotes the unit vector \(\hat{{\mathbf{H}}}\) specified in the body-relative frame.
4.2 Finite Density Sphere Restriction
This paper focuses on the sphere-restriction of the Full-Body problem, where all of the bodies have finite, constant densities and spherical shapes defined by a diameter \(d_i\). This allows for considerable simplification of the mutual potentials, although the rotational kinetic energy, moments of inertia and angular momentum of the systems are still tracked. In this case the moment of inertia of a constant density sphere is \(m_i d_i^2 / 10\) about any axis and the minimum distance between two bodies will be \(d_{ij} = (d_i + d_j)/2\). The resultant quantities for these systems are
Although we state several different quantities that are of interest, for our analysis of relative equilibrium and its stability we only need to know the two scalar quantities \(I_H\) and \({\mathscr {U}}\). This discussion is restricted to bodies having equal sizes and densities. Thus, all particles have a common spherical diameter d and mass m. Given this restriction the moment of inertia and potential energy take on simpler forms.
where m is the common mass of each body and d the common diameter. For these spherical bodies the first term of \(I_H\) denotes the moment of inertia of the point masses, with the assumption that they are all lying in the plane perpendicular to \({\mathbf{H}}\). The second terms of \(I_H\) denotes the rotational moments of inertia of the spheres. We also note that the gravitational potential is unchanged from the N-body potential for these spherical bodies. Then \(r_{ij} \ge d\) for all of the relative distances.
4.3 Normalization
Now introduce some convenient normalizations, scaling the moment of inertia by \(m d^2\) and scaling the potential energy by \({\mathscr {G}}m^2 / d\). For the moment we use the overline symbol to denote normalization, however we will discard this notation below. Then the minimum energy function is
where
and the constraint from the finite density assumption becomes \(\overline{r}_{ij} \ge 1\).
In the following the \(\overline{\left( -\right) }\) notation is dropped for \(r_{ij}\) and H, as it will be assumed that all quantities are normalized.
5 \(N=2\)
We first revisit a specialized version of the derivation for \(N=2\) from [9], only considering equal mass grains. The minimum energy function is explicitly written as
where we keep the term \(I_s\) explicitly symbolic to aid in later interpretation. There is only a single degree of freedom in this system, r, which is subject to the constraint \(r \ge 1\).
5.1 Equilibria and Stability
For the Full 2-body problem, there are two types of equilibria that occur—contact (or resting) equilibria and non-contact (or orbiting) equilibria. The addition of finite density changes the structure of equilibria in the 2-body problem drastically, and was thoroughly explored previously in [9]. In the following we first discuss the orbiting equilibria, noting that the inclusion of finite density creates up to two orbiting equilibria at the same level of angular momentum—one of which is energetically unstable. Then we discuss the resting equilibria, and note that conditions for them to exist are related to the unstable orbiting equilibria.
5.1.1 Non-contact Equilibria
First consider the non-contact equilibrium case. This is a single degree of freedom function so relative equilibria are found by taking a variation with respect to r
Setting the variation equal to zero yields an equation for r:
From the Descartes rule of signs we note that there are either 0 or 2 roots to this equation. We note that both conditions appear [9], thus to find the specific condition for when the roots bifurcate into existence we also consider the condition for a double root of the polynomial, when the derivative of this expression with respect to r is also zero. Taking the derivative of the first expression and solving for \(H^2\) yields
Substituting this into the original expression yields an immediate factorization of the condition
The only physical root is the second one, which yields the angular momentum and location where the roots come into existence
There are a few important items to note here. First, as \(r^* > 1\) the two roots will bifurcate into existence at a finite separation and thus are both physical. Second, for \(H^2 < H^{*2}\) there are no roots for \(r > 1\), although this does not mean that there are no minimum energy configurations, just that they are not orbiting configurations.
To develop a more global view of the equilibria, solve for \({H}^2\) as a function of r, yielding
This has a minimum point, corresponding to the double root where the equilibria came into existence. For higher values of H the system will then have two roots, one to the right of \(r^*\) (the outer solution) and the other to the left (the inner solution). At the bifurcation point the system technically only has one solution.
The stability of each of these solutions is determined by inspecting the second variation of \({\mathscr {E}}\) with respect to r, evaluated at the relative equilibrium. Taking the variation and making the substitution for \(H^2\) from Eq. 101 yields
Checking for when \(\delta ^2{\mathscr {E}} > 0\) yields the condition \(r^2 > 12{I}_s\). Thus, the outer solution will always be stable while the inner solution will always be unstable, with the relative equilibria occurring at a minimum and maximum of the minimum energy function, respectively. Figure 1 shows characteristic energy curves and the locus of equilibria for different levels of angular momentum for the spherical full 2-body problem. This should be contrasted with the energy function for the point mass 2-body problem which only has one relative equilibrium.
Locus of orbital equilibria across a range of angular momentum values. Plotted is the minimum energy function versus the system configuration, r, the distance between the two particles. This plot assumes equal masses and sizes of the two particles. For clarity, equilibrium solutions are shown below the physical limit \(r \ge 1\)
For the inner, unstable solution the solution will only exist when \(r \ge 1\), which corresponds to angular momentum values from \(0.9737\ldots = H^{*2} \le H^2 \le {2\left( \frac{1}{2} + 2{I}_s\right) ^2} = 0.98\). This is a somewhat narrow, but finite, interval.
5.1.2 Contact Equilibria
There is only one constraint that can be activated for the \(N=2\) case, \(r \ge 1\). The condition is \(\delta \mathscr {E} \ge 0\), so evaluating this variation at \(r=1\) given that \(\delta r \ge 0\) yields
which is precisely the same angular momentum at which the inner orbital solution terminates. Thus the contact relative equilibria exists across \(0 \le H^2 \le 0.98\), at which point it disappears by colliding with the unstable inner solution. For \(H^2 > 0.98\) only the stable, outer solution exists. At the bifurcation point the energy of the system equals \(\mathscr {E} = -0.3\). We denote this point as the “fission” point.
The relative equilibrium results are presented in an energy—angular momentum plot (Fig. 2) that plots the energy of the different equilibria as a function of the angular momentum. We note that the resting condition is just linear as a function of \(H^2\) as \({\mathscr {E}} = H^2 / 1.4 - 1\). The Orbital energy curves are more complex and are plotted by generating the angular momentum and energy as a function of distance. The limiting energy as \(r \rightarrow \infty \) is \(\mathscr {E} \rightarrow - 1 / (2r)\), and thus steadily approaches zero.
5.2 Hill Stability Conditions
A key constraint can be placed on when the system is Hill stable, meaning that the two bodies cannot escape from each other. While a sufficient condition for escape is difficult to construct in general, the necessary conditions are simple to specify. To do so, assume that the two bodies escape with \(r \rightarrow \infty \). The minimum energy function then takes on a value \(\lim _{r \rightarrow \infty } \mathscr {E} = 0\), and the energy inequality remains \(0 \le E\), which is the necessary condition for mutual escape.
If the energy has a value \(E < 0\), then the corresponding limit on the distance between the bodies can be developed by solving the implicit equation \(\mathscr {E}(r) = E\). Rewriting this we see that it can be expressed as a cubic equation
From the Descartes rule of signs we note that this will either have 1 or 3 positive roots. This can be linked to the system having the proper combination of energy and angular momentum. From observation of Fig. 1 it is clear that a line drawn at constant, negative energy will intersect the constant angular momentum lines either once or three times. The outermost intersection delineates the largest separation possible while the lower ones denote additional regions the body can be trapped in. We note that if the intersection occurs at \(r < 1\) then the system is in a contact case.
6 \(N=3\)
For the case where \(N=3\) the minimum energy function is explicitly written as
where we again keep the term \(I_s = 0.1\) explicitly symbolic to aid in later interpretation. In this problem the function has 3 degrees of freedom, which can be enumerated as \(r_{12}\), \(r_{23}\) and \(r_{31}\) with the constraint that \(r_{31} \le r_{12} + r_{23}\). If this constraint is active, then it is sometimes more convenient to use the angle \(\theta _{31}\), defined via the rule of cosines as \(r_{31}^2 = r_{12}^2 + r_{23}^2 - 2 r_{12} r_{23} \cos \theta _{31}\).
6.1 Equilibria and Stability
For this case there are 7 unique configurations that can result in a relative equilibrium, which are classified into 9 types of relative equilibrium in [9]. These are shown in Fig. 3 and described below. In [9] the existence and stability of these were proven. Here we provide a summary derivation of this result.
6.1.1 Static Resting Configurations
There are two static resting relative equilibrium configurations, the Euler Resting and Lagrange Resting configurations. The Lagrange Resting configuration is energetically stable whenever it exists while the Euler Resting configuration transitions from unstable to stable as a function of angular momentum while it exists.
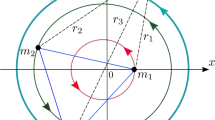
First consider the static resting configurations, defined as when all of the bodies are in contact and maintain a fixed shape over a range of angular momentum values. When in contact there is only one degree of relative freedom for the system, defined as the angle between the two outer particles as measured relative to the center of the middle particle and shown in Fig. 4. As defined the angle must always lie in the limit \(60^\circ \le \theta \le 300^\circ \).
Given the geometric relationships in Fig. 4, the minimum energy function can be written as
where the S subscript stands for “Static.” The first variation is then
The second variations will be considered on a case-by-case basis. Since this system has a constraint on the angle \(\theta \), both the free variations of \(\theta \) and the constrained variations when at the limit must be considered.
Euler Rest Configuration
If \(\theta = \pi \) the minimum energy function will be stationary. Define this as the Euler Rest Configuration, which consists of all three particles lying in a single line. The stability of this configuration is evaluated by taking the second variation of the energy function and evaluating it at \(\theta = \pi \), yielding
Recall that the stability condition is that the second variation of the energy be positive definite, yielding an explicit condition for stability as \(H^2 > 1.98375\), with lower values of \(H^2\) being definitely unstable. The Euler Rest Configuration energy can be specified as a function of angular momentum:
Lagrange Rest Configuration
Now consider the constrained stationary point with \(\theta = 60^\circ \) (\(300^\circ \)). Define this as the Lagrange Rest Configuration. Here it suffices to evaluate the first variation at the boundary condition, yielding
At the \(60^\circ \) constraint \(\delta \theta \ge 0\) and the Lagrange Rest Configuration will exist and be stable for \(H^2 < 5.07\), but beyond this limit an increase in \(\theta \) will lead to a decrease in energy and the relative equilibrium will no longer exist. Note that if the \(\theta = 300^\circ \) limit is taken, the sign of the first variation switches but the constraint surface is now \(\delta \theta \le 0\), and the same results hold.
The Lagrange Rest Configuration energy can be specified as a function of angular momentum:
Comparing the energy of these two rest configurations shows that the Lagrange configuration has lower energy for \(H^2 < 2.99\) while the Euler configuration has a lower energy above this level of angular momentum.
6.1.2 Variable Contact Configurations
In addition to the static resting configurations it is also possible to have full contact configurations which change as the angular momentum varies. These are not fully static, as they depend on having a specific level of angular momentum, generating centripetal accelerations that balance the gravitational and contact forces. For these configurations, as the level of angular momentum varies the configuration itself shifts, adjusting to the new environment. For the \(N=3\) case there is only one such “variable contact” configuration when restricted to the plane. This particular configuration is always unstable, yet plays an important role in mediating the stability of the other configurations.
This equilibrium configuration yields the final way for a stationary value of the minimum energy function to exist, with the terms within the parenthesis of Eq. 108 equaling zero. Instead of solving the resulting quartic equation in \(\sin (\theta /2)\) it is simpler to evaluate the angular momentum as a function of the system configuration to find
The range of angular momenta that correspond to this configuration can be traced out by following the degree of freedom \(\theta \) over its range of definition. Thus this equilibrium will exist for angular momentum values ranging from \(H^2 = 1.98375\) at \(\theta = 180^\circ \) to \(H^2 = 5.07\) at \(\theta = 60^\circ \). Note that the angles progress from \(\theta = 180^\circ \rightarrow 60^\circ \) as the angular momentum increases, and that the limiting values occur when the Euler Rest Configuration stabilizes and the Lagrange Rest Configuration destabilizes. Note that a symmetric family moves from \(\theta = 180^\circ \) to \(\theta =300^\circ \) at the same levels of angular momentum.
Taking the second variation and evaluating the sign of \(\delta ^2{\mathscr {E}}_{C}\) along the V configuration for arbitrary variations shows that it is always negative definite over the allowable values of \(\theta \) and thus that the V Rest Configuration is always unstable.
The energy of this configuration is found by setting \(r_{12} = r_{23} = 1\) and \(r_{31} = 2\sin (\theta /2)\). Then we find
Substituting in the angular momentum then yields
6.1.3 Mixed Configurations
Now consider mixed configurations where both resting and orbital states can co-exist. For \(N=3\) there is only one fundamental topology of this class allowed, two particles rest on each other and the third orbits. Further, from simple symmetry arguments two candidate states for relative equilibrium can be identified, a Transverse Configuration where the line joining the two resting particles is orthogonal to the third particle (\(\theta = \pm 90^\circ \)), and an Aligned Configuration where a single line joins all of the mass centers (\(\theta = 0^\circ , 180^\circ \)). To enable a stability analysis a full configuration description of these systems is introduced which requires two coordinates: the distance from the center of the resting pair to the center of the third particle to be R, and the angle between the line R and the line joining the resting pair as \(\theta \) (see Fig. 4).
The distances between the different components can be worked out as
Thus the minimum energy function takes on the form
where the M stands for “Mixed.” Taking the variation with respect to \(\theta \) yields
As expected, the variation is stationary for the Aligned Configuration, \(\theta = 0^\circ , 180^\circ \), and for the Transverse Configuration, \(\theta = \pm 90^\circ \). The variation in the distance yields
and is discussed in the following.
Transverse Configurations
First consider the Transverse Configurations with \(\theta = \pm 90^\circ \). Evaluating the variation of \({\mathscr {E}}_M\) with respect to R, setting this to zero, and substituting \(\theta = 90^\circ \) allows us to solve for the angular momentum explicitly as a function of the separation distance
This function has a minimum value of angular momentum of \(H_{MT}^2 \sim 4.002\ldots \) which occurs at \(R = \sqrt{2.6}\). This is an allowable value of separation and thus this bifurcation will indeed occur. For higher values of angular momentum there are two relative equilibria, one with separation less than \(\sqrt{2.6}\) and the other with separation larger than this. The inner solution touches the other two particles, forming a Lagrange-like configuration, when \(R = \sqrt{3}/2\). Substituting this into the above equation for \(H_{MT}^2\) shows that this occurs at a value of 5.07, which is precisely the value at which the Lagrange Rest Configuration becomes unstable. Recall that this was also the value of angular momentum at which point the V Rest Configuration terminated by reaching \(60^\circ \). Thus at this value, which is also equal to the Lagrange Orbit Configuration angular momentum at this distance, the inner Transverse Configuration family of solutions terminates. Conversely, the outer Transverse Configuration persists for all angular momentum values above the bifurcation level.
Now consider the energetic stability of this class of relative equilibria. First note that the cross partials, \(\delta ^2_{\theta R}{\mathscr {E}}_M\) are identically equal to zero for the Transverse Configuration. This can be easily seen by taking partials of Eq. 121 with respect to \(\theta \) and inserting the nominal value \(\theta = \pm 90^\circ \). Next, taking the second partial of Eq. 121 with respect to \(\theta \) and evaluating it at the nominal configuration yields
and \(\delta ^2_{\theta \theta }{\mathscr {E}}_{MT} < 0\). It is not necessary to check further as this tells us that none of the Transverse Configurations are energetically stable. The explicit energy of the Transverse Configurations is
Aligned Configurations
Now consider the Aligned Configurations with \(\theta = 0^\circ ,180^\circ \). Again solve for the angular momentum as a function of separation
Finding the minimum point of this equation as a function of R yields a cubic equation in \(R^2\) without a simple factorization. Root finding shows that it bifurcates into existence at a distance of \(R = 2.33696\ldots \) with a value of \(H_{MA}^2 = 5.32417\ldots \). Again, there is an inner and an outer solution. The inner solution continues down to a distance of \(R = 3/2\), where the two groups touch and form an Euler configuration. The value of the angular momentum at this point equals 6.6125 and equals the value at which the Euler Rest Configuration terminates and the Euler Orbit Configuration is born. The outer solution continues its growth with increasing angular momentum.
Now consider the energetic stability of these solutions. Similar to the Transverse Configurations, the mixed partials of the minimum energy function are identically zero at these relative equilibria. The second partials of Eq. 121 with respect to \(\theta \) yields
which is always positive. The second partial of Eq. 121 with respect to R is
The resulting polynomial is of high order and is not analyzed. Alternately, inspecting the graph of this function shows that it crosses from negative to positive at the bifurcation point, as expected. Thus the outer Aligned Configurations are energetically stable while the inner Aligned Configurations are unstable, and remain so until they terminate at the Euler configuration. To make a final check, evaluate the asymptotic sign of the second energy variation. For \(R \gg 1\), \(H^2_{MA} \sim 4/3R\). Substituting this into the above and allowing \(R\gg 1\) again yields \(\delta ^2_{RR}{\mathscr {E}}_{AM} \sim 1/R^3 \delta R^2\), and thus the outer relative equilibria remain stable from their bifurcation onwards.
The explicit energy of the Aligned Configurations are
A direct comparison between \({\mathscr {E}}_{MA}\) and \({\mathscr {E}}_{MT}\) at the same levels of angular momentum shows that the Aligned Configurations always have a lower energy than the Transverse Configurations. This is wholly consistent with the energetic stability results found throughout.
6.1.4 Purely Orbital Configurations
There are 2 purely orbital relative equilibrium configurations, the Lagrange and Euler configurations. These are always energetically unstable.
Finally consider the purely orbital configurations for this case. As this is the sphere restricted problem, the orbital relative equilibria will be the same as exist for the point mass problem.
Euler Solution
For the Euler solution take the configuration where \(r_{12} = r_{23} = R\) and \(r_{31} = 2R\), \(R \ge 1\), reducing the configuration to one degree of freedom. The minimum energy function then simplifies to
Taking the variation of the minimum energy function with respect to this configuration then yields
Set this equal to zero and solving for the corresponding angular momentum to find
It can be shown that there are two orbital Euler configurations for \(H_{OE}^2 > 8\sqrt{5}/3\) and none for lower values. The non-existence of solutions at a given total angular momentum occurs due to the coupling of the rotational angular momentum of the different bodies. In this case, however, the lower solutions all exist at \(R <1\) and thus are not real for this system. In fact, given the constraint \(R\ge 1\) there will be a single family of orbital Euler solutions at \(H_{OE}^2 \ge 6.6125\) with corresponding radii ranging from \(R = 1\rightarrow \infty \) as \(H_{OE}^2 = 6.6125\rightarrow \infty \). The correspond energy of these Euler solutions as a function of R is
Our simple derivation of the orbital Euler solutions only considers one-dimensional variations in the distance. However for a complete stability analysis it is necessary to consider variations of each component in turn. We provide a brief derivation here. First, at this configuration the constraint \(r_{31} \le r_{12} + r_{23}\) is active, meaning that it is better to use the degrees of freedom \(r_{12}\), \(r_{23}\) and \(\theta _{31}\), assuming that body 2 is in the center. We know that the relative equilibrium occurs at \(\theta _{31} = \pi \) and \(r_{12} = r_{23} = R\) and \(H^2\) as above, so we only need to consider the Hessian matrix of \(\mathscr {E}\) evaluated at these conditions. The relevant partials are
As the \(\theta \) terms are decoupled and as \(\mathscr {E}_{\theta _{31} \theta _{31}} > 0\) we only need to consider the 2-by-2 matrix for the radius variations. For the structure of this matrix, symmetric with equal diagonal components, the eigenvalues can be shown to equal the diagonal plus or minus the off-diagonal terms. Thus the eigenvalues of the Hessian matrix are
The first eigenvalue can be shown to be positive when \(R^2 > 1.65\) and negative for values less than this, while the second is obviously negative for all distances R. Thus the Euler orbiting solutions are always unstable.
Lagrange Solution
To find the conditions for the Lagrange solution take the configuration to be \(r_{12} = r_{23} = r_{31} = R \ge 1\), again reducing the minimum energy function to a single degree of freedom.
The variation now yields the condition
which can be solved for the angular momentum of the orbital Lagrange solutions as a function of orbit size
Again, two solutions exist for \(H_{OL}^2 > 16/\sqrt{10}\), however the inner solution has radius \(R< 1\) and is not allowed by this model. Thus, again for the constraint \(R\ge 1\) there is a single family of Lagrange solution orbits that range from \(R = 1\rightarrow \infty \) as \(H_{OL}^2 = 5.07\rightarrow \infty \). The corresponding energy of these Lagrange solutions as a function of R is
Our simple derivation of the orbital Lagrange solutions only considers one-dimensional variations in the distance, again. As before for a complete stability analysis it is be necessary to consider variations of each component in turn. First, at this configuration we have \(r_{31} = r_{12} = r_{23}\) and the inequality constraint is not active, meaning that we can use the radii as the degrees of freedom, which simplifies the evaluation of the Hessian. We know that the relative equilibrium occurs at \(r_{12} = r_{23} = r_{31} = R\) and \(H^2\) as above, so we only need to consider the Hessian matrix of \(\mathscr {E}\) evaluated at these conditions. Indeed, due to the symmetry we have \(\mathscr {E}_{r_{12} r_{12}} = \mathscr {E}_{r_{23} r_{23}} = \mathscr {E}_{r_{31} r_{31}}\) and \(\mathscr {E}_{r_{12} r_{23}} = \mathscr {E}_{r_{23} r_{31}} = \mathscr {E}_{r_{31} r_{12}}\). The relevant partials are
In this case the Hessian again is symmetric and has equal diagonal values, and has equal off-diagonal values. This matrix also has a simple eigenstructure and will have three eigenvalues, a repeated eigenvalue with value \(\mathscr {E}_{r_{12} r_{12}} - \mathscr {E}_{r_{12} r_{23}} \) and a single eigenvalue with value \(\mathscr {E}_{r_{12} r_{12}} + 2 \mathscr {E}_{r_{12} r_{23}} \).
The first, double eigenvalue is negative making the Hessian negative definite and thus unstable. The second eigenvalue will be positive for \(R^2 > 0.9\), making it positive for all possible configurations.
As a final point, note that the energy of the Euler solutions is actually less than the energy of the Lagrange solutions when \(R^2 < 63/60\), i.e., when R is near unity. For larger values of R the Lagrange solution is always lower energy.
The complete bifurcation chart of relative equilibria, minimum energy states, and global minimum energy states of the sphere restricted \(N=3\) full body problem as a function of angular momentum is graphically illustrated in Fig. 5.
6.2 Hill Stability Conditions
Now we consider conditions for the system to be bounded, or Hill stable, and unbounded. As with the 2 body case, we can easily derive the conditions for the complete dispersal of the system. If all components escape from each other we have \(r_{12}, r_{23}, r_{31} \rightarrow \infty \) and the amended potential then goes to zero again, defining the necessary condition \(E \ge 0\). Indeed, if \(E < 0\) then there will necessarily be some components that are bound to each other, either resting or orbiting.
In [10] a sharper condition is derived for when a single body can escape from the system. This is summarized here. Assume that body 3 escapes, meaning that \(r_{23}, r_{31} \rightarrow \infty \). Then the mutual potential becomes \(\mathscr {E} = - \frac{1}{r_{12}} \le E\). Here, however, we know that \(r_{12} \ge 1\), which provides additional constraints, specifically that \(-\frac{1}{r_{12}} \ge -1\). From this inequality we see that if \(E \le -1\) that the system is bound and Hill-stable, meaning that none of the bodies can escape. Note from Fig. 5 that all of the resting and mixed configurations exist at energies less than \(-1\), meaning that these are Hill stable.
It is instructive to consider the energy of the aligned configuration for large separation distances. Equation 128 when \(R \gg 1\) is approximated as
using the fact that \(H^2 \sim 4/3 R + \cdots \). Thus we see that the aligned configurations are always Hill stable. Consider also the unstable transverse configurations. Again for \(R \gg 1\) Eq. 124 can be expanded as
and has the same asymptotic form. Thus these unstable configurations are also Hill stable asymptotically. Indeed, only the Orbital Lagrange and Euler solutions are Hill Unstable for large enough angular momentum.
7 \(N=4\)
For the case where \(N=4\) the minimum energy function is explicitly written as
where we again keep the term \(I_s = 0.1\) explicitly symbolic to aid in later interpretation. There are now a total of 6 degrees of freedom for this system, three more than the previous case. There are several different topologies in which these degrees of freedom can exists, depending on whether there is contact between the bodies or if they are unconstrained.
7.1 Equilibria and Stability
For the case of \(N=4\) the number of possible configurations grows significantly as compared to the 7 unique configurations identified above for the \(N=3\) body problem. First of all, for orbital configurations the full set of relative equilibria for all mass values is not known and only bounded [3]. However, none of these are expected to be energetically stable and thus can be left out of this analysis [5]. Based on this same premise, and as articulated in the Hypothesis in [9], it can also be surmised that the only energetically stable orbital configurations will have the system collected in two orbiting clusters, further restricting the space to be considered a priori. Beyond this, one can also rely on principles of symmetry to identify the potential relative equilibrium candidates. An album of possible relative equilibrium configurations for the equal mass and size case is shown in Fig. 6. These candidate configurations were identified by noting symmetries in the configurations but do not preclude the possibility of missed symmetric configurations or asymmetric configurations, which are sure to become more significant as the number of particles increases.
No assertion that all possible relative equilibria have been identified is being made, however the ones listed in Fig. 6 are hypothesized to control the minimum energy configurations. To carry out a detailed analysis would require the development of appropriate configuration variables for the different classes of motion and the formal evaluation of stationary conditions and second variations. This is tractable in general, as the different possible planar configurations of the contact structures can all be described by two degrees of freedom. Some specific examples are given later.
Instead of taking a first principles approach, as was done for the \(N=3\) case in [9] and reviewed above, a number of alternate and simpler approaches to determining the global minimum configurations as a function of angular momentum are developed in the paper [11], and are again summarized here.
7.2 Static Rest Configurations
Assuming that all of the relevant static rest relative equilibria have been identified, or at least those which may be a global minimum, the global minimum can be found by directly comparing the minimum energy functions of the various configurations as a function of angular momentum. By default the minimum energy state must be stable, independent of a detailed stability analysis. This approach cannot detect when a configuration is energetically stable but not the global minimum. For these static rest structures, the minimum energy function is affine in \(H^2\) since the polar moment of inertia and the potential take on constant values. Thus a graph of \((H^2, \min { \sum _{i=1}^M H^2/(2I_i) + \mathscr {U}_i})\) will simply delineate the global minimum structures.
Alternately, one can directly determine the moments of inertia and the gravitational potentials of all of the different candidate configurations. Given two configurations, it is then simple to determine the angular momentum at which their minimum energies are equal, and thus where the transitions between these two configurations would occur independent of all other global results. Table 1 presents the computed polar moment of inertia and gravitational potential for each of the static configurations.
Finally, note that configuration “0” is a 3-dimensional configuration, and thus when its moment of inertia \(I_H\) is computed a direction for evaluating the moment of inertia about its rotation axis must be defined, however the tetrahedron has a uniform moment of inertia which is equal about any arbitrary axis through its center of mass. All the other configurations lie in a plane with the rotation axis perpendicular to this plane (note that this always yields the maximum moment of inertia and thus minimizes the energy, all else being fixed).
Assume two candidate configurations, i and j, then their minimum energy functions are equal for the same value of angular momentum if
The angular momentum at which this occurs can be solved for as
and represents the angular momentum at which the minimum of the two switch. Inputing the values from Table 1 into this formula generates a transition table for the different static configurations. Table 2 shows the different transitions that occur between the static configurations. Figure 7 graphically shows the energy vs. angular momentum squared plot with the minimum energy configuration taking turns in number from 0 to 3.
With this approach it is not possible to identify the precise transition points or the excess energy when the different states switch, unlike the more detailed analysis that can be given for the \(N=3\) case [9]. Evaluation of these transitions requires that the variable resting configurations be identified, as they mediate the loss and gain of stability for the various resting configurations.
7.3 Mixed Equilibrium Configurations
To identify the global minimum energy configurations it is also necessary to consider the mixed equilibrium configurations. Each different candidate configuration can be analyzed using a single degree of freedom. As an example, Fig. 8 shows configuration D with its single degree of freedom identified.
For any of the mixed configurations the polar moment of inertia and the gravitational potential as a function of the distance between the components can be defined as d and represented as I(d) and \(\mathscr {U}(d)\). Then the minimum energy function is \({\mathscr {E}}(d) = H^2 / (2 I(d)) + \mathscr {U}(d)\). By definition, relative equilibrium will exist when \(\partial {\mathscr {E}}/\partial d = {\mathscr {E}}_d = 0\). This is expressed as a function of I and \(\mathscr {U}\) as
Equating this to zero solves for the angular momentum for a relative equilibrium as a function of the distance between the components, d. The functions I(d) and \(\mathscr {U}(d)\) and their partials are listed below for configurations A through D, which are the most relevant to the discussion. In addition to these values the value of \(H^2\) is also given when the components are touching, which defines the angular momentum when a given static rest configuration (defined when \(d=1\)) fissions into the given mixed equilibrium configuration, and the energy of the system when this occurs.
Configuration A:
Configuration B:
Configuration C:
Configuration D:
Note that configuration C has a lower limit of \(d = \sqrt{3}/2\). In the following plots the substitution \(d' = d - 1 + \sqrt{3}/2\) is made for this configuration, allowing all of the energy functions and angular momenta to be compared across the same range of \(d \in [1,\infty )\). When touching, each of these configurations is equivalent to one of the static resting configurations. Specifically, A and B are equivalent to 3, C is equivalent to 1, and D is equivalent to 2. The bifurcation values of \(H^2\) and their associated energies and distances can be directly read off of the graphs. Also, their relative energy ordering is apparent (Fig. 9).
Energy versus angular momentum for the orbital relative equilibria A through D. The endpoints show where these families terminate by touching the static resting configurations. There are portions of these curves where there exist two of the orbital equilibria for a given angular momentum, although for large enough angular momentum there is only one member per family
7.4 Transitions Between Resting and Mixed Configurations
To start to sketch out the more detailed picture of transitions as a function of angular momentum several specific transition states are investigated. Specifically the angular momentum values when static configurations 0, 1, 2 and 3 either become stable, lose stability, or both are found.
7.4.1 Fission Transitions
First, given the results on the mixed relative equilibria the angular momentum values at which the different static configurations no longer exist, i.e., when they fission, can be identified. Static configuration 1 terminates when the inner orbital configuration C collides with it. Similarly static configuration 2 terminates when the inner orbital configuration D collides with it. For static configuration 3, there are two possible configurations it could fission into, A or B. It is interesting to note that configuration A consistently has a lower energy than configuration B, however the static configuration 3 fissions into configuration B at a lower value of angular momentum. Thus, in terms of a sequence of local minimum energy configurations linked geometrically, A is isolated from the static configuration 3. This is discussed in more detail later. In Table 3 the fission conditions and the angular momentum and energy values at which these occur are listed.
7.4.2 Stability Transitions
Of additional interest are the stability transitions for the various static configurations, specifically, the range of \(H^2\) where they are stable. Of specific interest are the values of angular momentum at which static configuration 0 becomes unstable and at which 1, 2, and 3 become stable. These are dealt with in turn in the following. Figure 10 shows the different degrees of freedom that are considered in the following analysis.
Stability of Static Configurations 0 and 1
The stability transitions of configurations 0 and 1 can be treated with the same model, with a single degree of freedom. Starting from the 1 configuration, if the outer two particles are brought up out of the plane the angle between them defines an allowable degree of freedom. In configuration 1 this angle equals 180\(^\circ \), while at the tetrahedron limit it defines an angle \(\sin (\theta /2)=1/\sqrt{3}\), or \(\theta = 70.5288\ldots ^\circ \). Take the angular momentum vector \(\hat{{\mathbf{H}}}\) to be perpendicular to the plane of configuration 1 and assume that the two outermost particles symmetrically rise out of the plane, then a general description of the distance between these two particles is expressed as \(\sqrt{3} \sin (\theta /2)\). At the lower limit of \(\theta \) the distance between the particles is unity, forming the tetrahedron, while at 180\(^\circ \) the total distance is \(\sqrt{3}\). Then the moment of inertial about the normal to the planar direction and the gravitational potential as a function of \(\theta \) is
The first variation of the minimum energy function with respect to this degree of freedom yields
First consider the stability of configuration 0, defined by setting \(\sin (\theta /2) = 1/\sqrt{3}\). The condition for this static configuration to exist is that \(\delta {\mathscr {E}} \ge 0\) for \(\delta \theta \ge 0\). Then the explicit condition for stability is that the term within the brackets be positive, and for this to hold true the angular momentum \(H^2\) must be limited. Setting the values at the configuration 0 values (where \(I_H = 1.4\)) the stability condition becomes
At values of angular momentum larger than this the 0 configuration does not exist.
Next setting \(\theta = 180^\circ \) yields the stationarity condition that corresponds to configuration 1. To evaluate the stability of this, take the second partial of \({\mathscr {E}}\) and set \(\theta = 180^\circ \) to find
where \(I_H = 2.4\) now. Solving for when \(\delta ^2{\mathscr {E}} \ge 0\) (note the minus sign in front) places the constraint on the angular momentum to be
at a corresponding energy of \({\mathscr {E}} = -5.1155\ldots \). Note that configuration 1 becomes stable before configuration 0 goes unstable.
Stability of Static Configuration 2
For this configuration suppose that the degree of freedom of interest is the angle defined in the plane from the nominal single contact particle to its location as it rolls on the contact particle. For a positive angle the distance from this particle to the two particles at the far end are
Then the moment of inertia and the gravitational potential are found as
Evaluating \(\delta {\mathscr {E}}\), this equals zero for \(\theta = 0\), as expected. Evaluating the second variation and evaluating when it is positive yields the condition for stability of configuration 2:
and has a corresponding energy of \({\mathscr {E}} = -3.91904\ldots \).
Stability of Static Configuration 3
For configuration 3 the two general degrees of freedom allow the end particles to roll relative to the central pair. Define the outer-right body as 1, the outer left body as 2 and measure the angles \(\theta _1\) and \(\theta _2\) as defined in Fig. 10. The distances of the outer bodies to the furthest of the inner pair is
and the distance of these two bodies from each other is
The moment of inertia and the potential energy are then
Evaluating \(\delta {\mathscr {E}}\), this equals zero for \(\theta _1 = \theta _2 = 0\), again as expected. At this configuration the moment of inertia takes on a value of 5.4.
Evaluating the second variation and evaluating when it is positive yields the following entries that must be put into a matrix:
The two diagonal entries are equal as are the two off-diagonal entries. To be positive definite the following conditions must hold:
The controlling condition is the second one, and holds true for \(H^2 > 9.45\) and has a corresponding energy of \({\mathscr {E}} = -3.458333\ldots \).
Stability of Static Configuration 5
Finally, it is also of interest to study the stability of static configuration 5. This is similar to configuration 2, except the masses are equally spaced about the central body. This modifies the distances to
Repeating the analysis we now find the controlling condition for this configuration to be stable relative to variations in \(\theta \) to be
However, if we analyze the variation \(\delta _d {\mathscr {E}}\) with respect to the distance of the rightmost particle from the rest of the configuration we find that the condition for stability in this direction is
Thus this configuration is never stable, as it would undergo fission prior to the angles becoming stabilized. It is important to note that this particular configuration was also found to never be a minimum energy configuration, which is now to be expected given this result.
7.5 Compilation of Possible Relative Equilibria
Figure 11 shows a global view of the identified stable static relative equilibria and stable and unstable orbital equilibria. Figure 12 shows a detail of this figure on the right indicating some of the transition points. At an angular momentum of zero Configuration 0 is the only stable relative equilibrium. As angular momentum is increased Configuration 1 becomes stable at \(H^2 = 2.217\ldots \) and soon thereafter becomes the global minimum configuration. Configuration 0 remains stable until \(H^2 = 3.92\) when it ceases to exist. At this point Configuration 1 is the only stable relative equilibrium and remains stable until fission into the unstable Orbital Configuration C occurs at \(H^2 = 13.737\). During this evolution both Configurations 2 and 3 become stable. Further, Configuration 2, while the global minimum for an interval, fissions into Orbital Configuration D at \(H^2 = 13.684\), before the fission of Configuration C occurs.
Energy versus angular momentum showing the relationship between the static resting configurations and the orbital configurations. The static configurations are only shown for when they exist and are stable. As angular momentum is increased or decreased there are transition points where multiple possible stable states exist
At \(H^2 = 23.49\) Configuration 3 will fission into the inner, unstable Orbital Configuration B. At this angular momentum level there are four possible stable orbital configurations for the system. The energies of these relative equilibria are, in order, B, A, C, D. For configurations B, C or D the resulting systems will remain stable for arbitrarily large values of angular momentum, which yield low spin rates for the separate components. For Configuration A at high enough angular momentum the Euler rest configuration of the primary will become essentially decoupled from the distant grain and, once the total spin rate becomes slow enough will become unstable. We do not provide a precise calculation of this, but an order of magnitude analysis indicates that this will occur at a value of \(H^2 > 30\). It is evident that stepping from \(N=3\) to \(N=4\) particles creates a much richer set of possible outcomes and removes the determinism that was present for the sphere-restricted \(N\le 3\) Full Body problem.
7.6 Hill Stability Conditions
Hill stability results can again be developed for this case. As was seen in the 3-body case, different criterion can be developed depending on how many of the bodies become dispersed. Starting with complete dispersal again, we see that a necessary condition for all \(r_{ij}\rightarrow \infty \) is that \(E\ge 0\). Thus, if the total energy is negative some of the bodies must remain bound to each other orbitally.
Now consider that two of the bodies, say 3 and 4, escape to infinity. Then we have \(r_{23}, r_{31}, r_{41}, r_{42}, r_{43} \rightarrow \infty \) and the amended potential becomes \(\mathscr {E} \rightarrow - \frac{1}{r_{12}}\). This leads to a necessary condition for this instability to occur as \(E \ge -1\), and if \(E < -1\) this cannot occur. We note that all of the non-orbital relative equilibrium configurations satisfy this inequality.
A slightly more restrictive case occurs when bodies 3 and 4 escape from bodies 1 and 2, but do not escape from each other. Then the distance \(r_{43}\) remains bounded and the amended potential becomes \(\mathscr {E} \rightarrow - \left[ \frac{1}{r_{12}} + \frac{1}{r_{34}} \right] \ge -2\). Thus if \(E < -2\) this form of escape cannot occur. Again we note that all non-orbital relative equilibria satisfy this inequality too.
The final case to consider is when only one body escapes, assume it is body 4. Then \(r_{4i} \rightarrow \infty \) and the amended potential approaches \(\mathscr {E} \rightarrow - \left[ \frac{1}{r_{12}} + \frac{1}{r_{23}} + \frac{1}{r_{31}} \right] \ge -3\). Thus if \(E < -3\) the system is Hill stable against any of the bodies escaping. Here the lower limit can be achieved if the three bodies are mutually touching in a resting Lagrange configuration, which is the minimum potential energy configuration of this system. It is relevant to note that in this case there are relative equilibria that exceed this level of energy and thus that they can lose one of their members through escape. All of the resting configurations shown in Fig. 12 that are brought to fission can thus lose one of their component bodies, but only one. This is the first instance where this can occur. We note that fission of configurations 1 and 2 will directly lose a single body, which then can escape from the system. We note that in doing so it must take angular momentum and energy from the spinning contact configuration, and thus will leave it in a slowly spinning configuration (as has been seen in the asteroid pair population [6]). In this aspect we note that configuration 2 fissions just barely above the energy level of \(-3\), meaning that the primary would need to essentially stop spinning should escape occur. Another interesting aspect relates to the in-line configuration 3. This configuration fissions into two equal pieces, and is prevented from directly fissioning one body from its end. Thus, even though the body fissions, it is initially in a configuration which cannot escape (as the energy is less than \(-2\)). Thus, in order to lose the single body, one of the two components must itself split, which has been termed “secondary fission” and has been hypothesized as a geophysical process for rubble pile asteroids [4].
8 Summary
This chapter revisits the derivation of the Full N-body problem, introducing a new approach to deriving the amended potential and showing its direct utility for computing relative equilibria and evaluating their stability. The paper then reviews the equal mass and density spherical N-body problem and presents the detailed relative equilibria for \(N = 2, 3, 4\). In addition it derives and discusses the Hill stability for each of these cases, providing sharp conditions for stability for when different numbers of bodies are ejected from the system. Taken together, this chapter provides a restatement of this problem that can be generalized for future studies and collects in one place the significant solutions which already exist to the question of relative equilibria, stability and minimum energy configurations in the Full N-body problem.
References
Cendra H, Marsden JE (2005) Geometric mechanics and the dynamics of asteroid pairs. Dyn. Syst. Int. J. 20:3–21
Greenwood, D.T.: Classical Dynamics. Dover (1997)
Hampton M, Moeckel R (2006) Finiteness of relative equilibria of the four-body problem. Inventiones Math 163(2):289–312
Jacobson SA, Scheeres DJ (2011) Dynamics of rotationally fissioned asteroids: source of observed small asteroid systems. Icarus 214:161–178
Moeckel R (1990) On central configurations. Math Z 205(1):499–517
Pravec P, Vokrouhlickỳ D, Polishook D, Scheeres DJ, Harris AW, Galád A, Vaduvescu O, Pozo F, Barr A, Longa P et al (2010) Formation of asteroid pairs by rotational fission. Nature 466(7310):1085–1088
Scheeres DJ (2002) Stability in the full two-body problem. Celest Mech Dyn Astron 83(1):155–169
Scheeres DJ (2006) Relative equilibria for general gravity fields in the sphere-restricted full 2-body problem. Celest Mech Dyn Astron 94:317–349
Scheeres DJ (2012) Minimum energy configurations in the n-body problem and the celestial mechanics of granular systems. Celest Mech Dyn Astron 113(3):291–320
Scheeres DJ (2014) Hill stability in the full 3-body problem. Proc Int Astron Union 9(S310):134–137
Scheeres DJ (2015) Stable and minimum energy configurations in the spherical, equal mass full 4-body problem. In: International conference on computational and experimental engineering and sciences, special symposium on computational methods in celestial mechanics
Simo JC, Lewis D, Marsden JE (1991) Stability of relative equilibria. Part I: the reduced energy-momentum method. Arch Ration Mech Anal 115(1):15–59
Smale S (1970) Topology and mechanics. I. Inventiones Math 10(4): 305–331
Smale S (1970) Topology and mechanics. II. Inventiones Math 11(1): 45–64
Acknowledgments
The author acknowledges support from NASA grant NNX14AL16G from the Near Earth Objects Observation programs and from NASA’s SSERVI program (Institute for the Science of Exploration Targets) through institute grant number NNA14AB03A.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Scheeres, D.J. (2016). Relative Equilibria in the Full N-Body Problem with Applications to the Equal Mass Problem. In: Bonnard, B., Chyba, M. (eds) Recent Advances in Celestial and Space Mechanics. Mathematics for Industry, vol 23. Springer, Cham. https://doi.org/10.1007/978-3-319-27464-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-27464-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-27462-1
Online ISBN: 978-3-319-27464-5
eBook Packages: EngineeringEngineering (R0)