Autoregressive Conditional Duration Model with an Extended Weibull Error Distribution

Abstract

Trade duration and daily range data often exhibit asymmetric shape with long right tail. In analysing the dynamics of these positively valued time series under autoregressive conditional duration (ACD) models, the choice of the conditional distribution for innovations has posed challenges. A suitably chosen distribution, which is capable of capturing unique characteristics inherent in these data, particularly the heavy tailedness, is proved to be very useful. This paper introduces a new extension to the class of Weibull distributions, which is shown to perform better than the existing Weibull distribution in ACD and CARR modelling. By incorporating an additional shape parameter, the Weibull distribution is extended to the extended Weibull (EW) distribution to enhance its flexibility in the tails. An MCMC based sampling scheme under a Bayesian framework is employed for statistical inference and its performance is demonstrated in a simulation experiment. Empirical application is based on trade duration and daily range data from the Australian Securities Exchange (ASX). The performance of EW distribution, in terms of model fit, is assessed in comparison to two other frequently used error distributions, the exponential and Weibull distributions.

1 Introduction

With the recent advancements in computational technology , data capturing and storage capabilities, the use of high frequency data (HFD) has gathered considerable momentum in recent years. Consequently, there has been a surge in the interest of research in many business related areas such as economics and finance. This was propelled by the enhanced availability and easy access to HFD linked with financial market transactions. As an important economic variable, the irregularly spaced trade durations convey useful information about market dynamics. The literature on market micro structure bears evidence to the economic significance of this variable [1]. Most often this is modelled by autoregressive conditional duration (ACD) models introduced by [2].

Empirical evidence suggests that duration data generally has a unimodal distribution with high density around zero as the majority of transactions have durations close to zero. The data display an asymmetric shape with a long right tail [3, 4]. Such conditional distribution for the data has proven to be challenging to model parametrically, in spite of there being significant methodological developments in analysing the dynamics of ACD models. Frequently, the conditional distribution has been modelled by the exponential and Weibull distributions while the log-normal, generalised gamma and Burr have also been considered. However, most of these distributions have shown limitations in the specification of conditional duration distribution [5–7]. They are unable to capture some of the characteristics of duration distributions precisely, especially the long right tail. This may have a negative impact on forecasting and hence trading strategy formulation. Consequently, the choice of standard parametric error distributions in the application to a dynamic duration model is still of much interest in the literature.

The increased prevalence of rich data sources, particularly in financial markets across the globe motivates the development of flexible financial time series models to capture the subtle movements and intricacies of HFD distributions. In this context, we propose a variation of the Weibull distribution with an extra parameter to add flexibility in the tail behaviour. This will be referred to as the extended Weibull (EW) distribution. The proposed distribution will prove useful to develop financial risk management strategies and evaluating properties such as the Value-at-risk (VaR) and Time-at-risk (TaR) for optimum capital allocation.

The modelling structure for an ACD model is not confined to modelling duration data alone, but has been extended to other positive valued time series. One example is the daily range of an asset price, which is defined as the difference between the highest and lowest log asset price within a trading day. The daily range could be used as an efficient measure of the local volatility of an asset price [8]. The conditional autoregressive range (CARR) model [9] analyses the daily range data and showed improved performance in out-of-sample volatility forecasts over other frequently used volatility models. The CARR model shares the same model structure as the ACD model and both models belong to the family of multiplicative error models [10]. In this paper, we assess the performance of the ACD and CARR models with the EW distribution by simulation and demonstrate their applicability through two real data sets from the Australian Securities Exchange (ASX), one of trade durations for a stock and the other of daily range data for a market index.

In summary, the main objective of this paper is to introduce the EW distribution to model the conditional distribution of positively valued time series in an ACD or CARR framework. Secondly, we derive the salient features and moments that characterise this distribution. Thirdly we assess the effectiveness of the estimation procedure based on Bayesian methodology through an extensive simulation study. The fourth objective is to produce empirical applications involving two different data sets to ascertain the applicability and comparative performance of EW distribution.

The remainder of this paper is organised as follows. Section 2 introduces the EW distribution with illustrations on the shapes of its probability density function (pdf) and some properties. Section 3 discusses the model formulation under the ACD model framework. Then the estimation of parameters based on the Bayesian approach is described in Sect. 4. A simulation experiment is performed in Sect. 5 while Sect. 6 reports the outcomes of the empirical application for two stock market data on trade durations and daily range. Further, this section compares the proposed model with two models using exponential and Weibull distributions, respectively. Section 7 summarises the results and concludes the paper.

2 Extended Weibull Distribution

Compared to the Weibull distribution, the EW distribution has an extra shape parameter, which allows for more flexibility in skewness and kurtosis. Suppose that X is a random variable following the EW distribution, denoted by $EW(\lambda , k, \gamma )$, with scale parameter $\lambda >0$, shape parameter $k>0$ and the additional shape parameter $\gamma >0$. Then X has the following pdf

$$\begin{aligned} \displaystyle f(x)= \left( 1+\frac{1}{\gamma ^k}\right) \frac{k}{\displaystyle \lambda ^k}x^{k-1}e^{-\left( \frac{x}{\lambda }\right) ^k}\left[ 1-e^{-\left( \frac{\gamma x}{\lambda }\right) ^k}\right] , x>0. \end{aligned}$$

(1)

From (1), it is clear that EW distribution provides more flexibility than the Weibull distribution. When $\gamma \rightarrow \infty$, it becomes the Weibull ($\lambda$, k) distribution. Figure 1 illustrates the varying shapes of the EW pdf for selected parameter values. Further, it is evident that for the shape parameter $k<1$, the distribution is more skewed and the asymmetry is accentuated by the additional $\gamma$ parameter as well. However, the impact of $\gamma$ is low when both $k <1$ and $\lambda <1$.

Fig. 1

Pdf of the EW distribution for selected sets of parameters

2.1 Properties of EW Distribution

The general expression for the rth moment of X is given by

$$\begin{aligned} E(X^r)= & {} \int _{0}^{\infty }\left( 1+\frac{1}{\gamma ^k}\right) \frac{k}{\lambda ^k}x^{\displaystyle r+k-1}\displaystyle e^{-\left( \frac{x}{\lambda }\right) ^k}\left[ 1-e^{ -\left( \frac{ \gamma x}{\lambda }\right) ^k}\right] dx \\= & {} \left( 1+\frac{1}{\gamma ^k}\right) \lambda ^r\quad \varGamma \left( 1+\frac{r}{k}\right) \left[ 1-\frac{1}{(1+{\gamma ^{k})}^{1+ \frac{r}{k}}}\right] . \end{aligned}$$

The mean ($\mu$), variance ($\sigma ^2$), skewness ($\rho$) and kurtosis ($\zeta$), which describes the characteristics of the EW distribution can be obtained accordingly from $E(X^r)$. See Appendix for derivations. The cumulative distribution function (cdf) F(x), survivor function S(x) and hazard function h(x) of the EW distribution are given by

$$\begin{aligned} F(x)= & {} 1 + \frac{1}{\gamma ^k}e^{\displaystyle -\left( \frac{x}{\lambda }\right) ^k}\left[ e^{\displaystyle -\left( \frac{\gamma x}{\lambda }\right) ^k}- 1 -\gamma ^k \right] , \end{aligned}$$

(2)

$$\begin{aligned} S(x)= & {} \left[ \gamma ^k+1-e^{\displaystyle -\left( \frac{\gamma x}{\lambda }\right) ^k}\right] \frac{1}{\gamma ^k} e^{\displaystyle -\left( \frac{x}{\lambda }\right) ^k}, \end{aligned}$$

(3)

$$\begin{aligned} h(x)= & {} \frac{\left( \gamma ^k+1\right) k x^{k-1}\left( 1-e^{-\left( \frac{\displaystyle \gamma x}{\displaystyle \lambda }\right) ^k}\right) }{\left[ \gamma ^k+1-e^{\displaystyle -\left( \frac{\gamma x}{\lambda }\right) ^k}\right] \lambda ^k}, \end{aligned}$$

(4)

Fig. 2

Hazard function of the EW distribution for selected parameter values

respectively. For the derivations, see Appendix.

The intensity of transaction arrivals has important implications in analysing durations. Figure 2 displays the various shapes of hazard function with different sets of parameter values as in Fig. 1 for comparison. For $k>$1, the hazard function is monotonically increasing at different rates. However, for $0<k<1$, it is unimodal, implying non-monotonocity. Further, this characteristic is more prominent for larger values of $\gamma$. In the special case of $k=1$, the hazard function converges to a constant rate given by $1/\lambda$, as x increases. Grammig and Maurer [3] assert that a distribution with non-monotonic hazard function can better capture the behaviour of durations.

Fig. 3

a Variation of skewness and b variation of kurtosis over $\gamma$ for selected values of k for the EW distribution

The relative impact of $\gamma$ on the skewness and kurtosis of the distribution, across various values of k, is presented in Fig. 3. For smaller k (i.e. $k<2$), both the skewness and kurtosis tend to increase with $\gamma$. However, for larger k, there exists a non-monotonic relationship between these characteristics and $\gamma$. For a given value of $\gamma$, skewness is inversely related to k, although there is no such a distinct relationship in the case of kurtosis, particularly when $k>2$.

Fig. 4

Comparison of the EW distribution with a the Weibull and b the exponential with similar shape and scale parameters

In comparison to the Weibull distribution, the EW distribution tends to capture more of the right tail indicating more flexibility, irrespective of the value of $\gamma$. Figure 4a compares the two distributions for similar values of k and $\lambda$ with varying $\gamma$. The same phenomenon is observed in the case of the exponential distribution where the EW density is plotted for $k=1$ in Fig. 4b.

3 ACD Model with EW Distribution

In modelling positively valued time series under an ACD model framework, the exponential distribution is too restrictive and the Weibull distribution is superior to the exponential distribution as it has a shape parameter that increases its modelling flexibility considerably. Then our proposed EW distribution is motivated by an additional shape parameter $\gamma$, which entails better capturing of the heavier tail than the Weibull distribution. Hence, this distribution can provide a better fit.

Under the ACD model, the unit mean restriction for the innovations has to be imposed. One option is to consider a standardised distribution, incorporating the mean as a standardised parameter. The alternative is to directly restrict the mean to be unity so that one parameter (usually the scale parameter) can be expressed as a function of others, under the unit mean condition. In either case there will be one less (free) parameter, reducing the number of parameters for the EW distribution to two instead of three.

ACD model is generally applied to irregularly spaced financial market transaction data. The most primary economic time series analysed under this framework is the time interval between two consecutive trades of a given stock, popularly known as trade durations. In such a scenario, let $\{t_0, t_1,\ldots ,t_i,\ldots \}$ be a sequence of time points the stock under consideration is traded in the stock exchange, such that $t_0 \le t_1\le \cdots \le t_i\le \cdots$. Here $t_0$ denotes the starting time point and $t_T$ is the last time point of the observed sequence, where T is the length of the series. Modelling a financial point process in a duration framework, as waiting times characterises the point process as a discrete time series. In a generic sense, $x_i = t_i - t_{i-1}$ denotes the ith duration between two transactions that occur at times $t_i$ and $t_{i-1}$. Therefore, ignoring simultaneous transactions, which is the preferred practice as evidenced in literature, the sequence $\{{x_1}, {x_2},\ldots , {x_T}\}$ will generate a time series of positive measurements. ACD models are concerned with modelling such positive valued time series. On the other hand, positively valued time series also arise in the study of price volatility using price range such as the intraday high low prices. CARR models analyse range data applying an identical model structure and hence the following description is equally valid for CARR models.

Let $x_i, i=1,\ldots ,T$ be a time series of trade durations under the ACD modelling framework,

$$\begin{aligned} x_i= \psi _i\epsilon _i \end{aligned}$$

(5)

in a multiplicative error structure, where the deterministic component, $\psi _i = E(X_i)$ is the conditional expectation of the ith duration, given the past information, that is,

$$\psi _i=E(x_i|x_{i-1},\ldots , x_1).$$

The main assumption here is that the standardized durations

$$\epsilon _i = \frac{x_i}{\psi _i}$$

are independent and identically distributed (i.i.d), having a positive support and a unit mean, and $\psi _i$ is formulated under the ACD(${ p,q}$) model as

$$\psi _i=\alpha _0 + \sum _{j=1}^{p} \alpha _jx_{i-j} + \sum _{l=1}^{q} \beta _l\psi _{i-l},$$

where p and q are non-negative integers. The following restrictions

$$\begin{aligned} \alpha _0>0, \alpha _j\ge 0, \beta _l \ge 0, \sum _{j=1}^{p} \alpha _j +\sum _{l=1}^{q} \beta _l < 1 \end{aligned}$$

(6)

ensure positivity and stationarity of durations, respectively.

For most practical purposes, a basic version of ACD model suffices and hence an ACD (1, 1) model is considered in this paper. The conditional expectation $\psi _i$ is estimated via the following recursive formula

$$\begin{aligned} \psi _i = \alpha _0 +\alpha _1x_{i-1} + \beta \psi _{i-1} \end{aligned}$$

(7)

The long term mean is $\displaystyle \frac{\alpha _0}{1-\alpha _1-\beta }$. The random disturbance $\epsilon _i$ is assumed to follow the $EW(\lambda ,k,\gamma )$ distribution; imposing the unit mean restriction using (11) yields

$$\begin{aligned} \lambda =\frac{k \gamma ^k \left( 1+\gamma ^k\right) ^{1/k}}{\varGamma (1/k)\left[ \left( 1+\gamma ^k\right) ^{1+1/k} -1\right] } \end{aligned}$$

(8)

Then the distributional form of duration $X_i$ is as follows:

$$ X_i \sim EW (\lambda \psi _i, k,\gamma ) $$

Substituting for $\lambda$ in (8), the parameters to be estimated are ${\varvec{\theta }}{}=(\alpha _0,\alpha _1, \beta , k,\gamma )$.

Under this framework, the conditional likelihood has the following expression

$$\begin{aligned} L({{\varvec{x}}{}}|{{\varvec{\theta }}{}})=\prod _{i=1}^{T}\frac{1}{\psi _i}\frac{k}{\lambda ^k} \left( 1+\frac{1}{\gamma ^k}\right) \left( \frac{x_i}{\psi _i}\right) ^{k-1}e^{-\left( \frac{x_i}{\lambda \psi _i}\right) ^k}\left[ 1-e^{-\left( \gamma \frac{x_i}{\lambda \psi _i}\right) ^k}\right] \end{aligned}$$

(9)

The ACD model incorporating EW errors is denoted as an EW-ACD model. The exponential and Weibull distributions are also considered for comparison and their ACD models are denoted as EACD and WACD models respectively.

4 Bayesian Estimation Methodology

The statistical inference is carried out using the Bayesian simulation approach, which allows simultaneous finite sample inference. The main advantage of using Bayesian techniques is the ability to incorporate prior knowledge into the estimation process. Further, positivity and stationarity constraints given in (6) can be directly incorporated into the prior distribution. For fast convergence of the Markov chain, the parameter generation is executed in blocks [11].

Without prior knowledge, most non-informative priors we adopted are flat over the feasible region, with the likelihood function dominating the inference. Mostly a uniform prior is adopted for ${\varvec{\alpha }}{}= (\alpha _0, \alpha _1, \beta )$, over the constraint region in (6), ensuring the enforcement of these restrictions. We also choose the uniform prior for the shape parameter of k, while ensuring $k>0$. On the other hand an inverse prior is assumed for $\gamma$, with positivity constraint, $f(\gamma )\propto \frac{1}{\gamma }$. Under the assumption of independence of the individual blocks of parameters, the prior distribution can be specified as follows

$$f({{\varvec{\theta }}{}})= f_{\alpha }({\varvec{\alpha }}{})f_k(k)f_{\gamma }(\gamma )$$

The joint posterior pdf of ${{\varvec{\theta }}{}}$ is proportional to the product of the prior density $f({{\varvec{\theta }}{}})$ and the likelihood function of (9). If ${\varvec{\theta }}{}_J, J=1,2,3$ represents a parameter block, ${\varvec{\alpha }}{}$, k or $\gamma$ at a given simulation step, then ${\varvec{\theta }}{}_{-J}$ represents the vector of paramters excluding ${\varvec{\theta }}{}_J$. For each updating step, the posterior distributions for the chosen element ${\varvec{\theta }}{}_{J}$ conditional on the data and other parameters, in the MCMC setup is

$$\begin{aligned} f({\varvec{\theta }}{}_J|{{\varvec{x}}{}, {\varvec{\theta }}{}_{-J}}) \propto L({{\varvec{x}}{}}|{{\varvec{\theta }}{}})f({\varvec{\theta }}{}_J) \end{aligned}$$

(10)

where $L({{\varvec{x}}{}}|{{\varvec{\theta }}{}})$ is given in (9). The posterior distributions for each choice of ${\varvec{\theta }}{}_J$ do not have a standard distributional form due to lack of conjugacy between the likelihood function and the prior distributions. Therefore, the Metropolis-Hastings (MH) algorithm is used to generate samples for each block of parameters from (10). This method was introduced by [12] involving a symmetric transition density, which was later generalised by [13].

We adopted a two stage MH method to draw parameters in an adaptive MCMC sampling scheme, similar to [14]. In the first stage, random walk (RW) Metropolis algorithm is employed, to sample parameters from the posterior distribution. The algorithm uses a multivariate normal (MVN) proposal density q(.|.) with its mean at the current value ${\varvec{\theta }}{}_J^{(k-1)}$ at iteration k and the covariance matrix being a multiple of that of a certain matrix, that is, $a {\varvec{\varSigma }}{}_{\theta _J}$, where ${\varvec{\varSigma }}{}_{\theta _J}$ is set to be an identity matrix for convenience. The RW metropolis proposal density has proven to be quite useful in Bayesian inference, where the acceptance rate of the draws could be tuned by adjusting the scalar a attached to the covariance matrix to ensure optimal acceptance probability, around 0.44 for one dimension and could be as low as 0.23 as the dimensionality increases [15]. The sample mean $\bar{{\varvec{\theta }}{}_J}$ and sample covariance ${\varvec{S}}{}_{\theta _J}$ are formed using M iterates of ${{\varvec{\theta }}{}_J}$ after burn-in, from the first stage. In the second stage, an independent kernel MH algorithm is applied for parameter sampling, using the Gaussian proposal distribution with mean $\bar{{\varvec{\theta }}{}_J}$ and covariance ${\varvec{S}}{}_{\theta _J}$.

In the simulation and empirical analyses, the burn-in sample is 15,000 iterates from the MCMC to ensure proper convergence and 10,000 iterates are sampled thereafter for estimation purposes, during the first stage. The burn-in value is chosen based on the trace plots of the iterates. In the second stage, we use an independent MVN density q(. ), with the mean and the covariance being estimated using the 10,000 values generated from the first stage, after the burn-in. In this stage, a sample of 10,000 iterates is generated from the thus formulated independent proposal after a burn-in of 5000 and the sample average form the parameter estimates.

5 Simulation Study

In order to assess the performance of the estimation methodology, a simulation study is performed prior to its empirical applications.

5.1 Random Variates Generation

Simulation of the innovation $\epsilon _i$ of the ACD model from $f(\epsilon )$ is not straight forward as the cdf is not invertible. Therefore, the rejection sampling method is used to draw $\epsilon _i$ from the EW distribution. Weibull $(\lambda ,k)$ is used as the envelope distribution $g(\epsilon )$, as the EW pdf encompasses the Weibull pdf.

The algorithm for generating a sample from $f(\epsilon )$ as developed by [16] is given as follows:

• 1. Sample $\epsilon$ from $g(\epsilon )$.

• 2. Generate a uniform (0,1) random number u.

• 3. Compute $q=f(\epsilon )/Mg(\epsilon )$. where M is a quantity such that $M\ge$ $\sup _{\epsilon } {f(\epsilon )/g(\epsilon )}$.

• 4. If $u<q$, accept $\epsilon$ as a realisation of $f(\epsilon )$.

• 5. Otherwise reject the value and repeat from step 1 onwards.

The supremum of $f(\cdot )/g(\cdot )$ happens to be $(1+1/\gamma ^k)$; Therefore M could be fixed at this value as it is $>1$. Accordingly $q=1-e^{-\left( \frac{\gamma \epsilon }{\lambda }\right) ^k }$.

5.2 Simulation

This simulation study validates the effectiveness of the proposed estimation methodology and is conducted under four sets of values for $(k,\gamma )$, where the series length is $T=$ 10,000 and the number of replications is $R=$ 200. As the empirical evidence suggested relatively large values for $\gamma$, the simulated examples were generated by fixing relatively high values for $\gamma$, except for one case. The parameters of the mean equation are kept fixed as its estimation is fairly straight forward but the estimation of shape parameters $(k,\gamma )$ are more problematic.

Table 1 Simulation study of 200 replications from ACD (1, 1) with EW innovations and T $=$ 10,000 for four sets of $(k,\gamma )$

The simulation results presented in Table 1 display the true values, average of posterior mean estimates, standard errors and 95 $\%$ credible intervals of the 200 replications, for the model parameters. Coverage percentages indicate the number of times the credible interval contains the true parameter value, as a percentage of R. True values of all parameters are contained within the average 95 $\%$ credible intervals of the posterior samples and the estimates are very close to their true values. The precision of estimates is fairly good except for $\gamma$, particularly when it is less than one. Coverage percentages are quite satisfactory, except for $\beta$ of the second panel. Overall, the estimation of model parameters appears to perform well under the proposed methodology.

6 Empirical Analysis

This section demonstrates the application of the ACD (1, 1) model with the EW distribution fitted to two real life financial time series of trade duration and daily range respectively.

Fig. 5

a Time series plot and b histogram of adjusted trade durations of TLS stock during the period 1 to 7 October, 2014

6.1 Trade Duration Data

Adjusted duration data of Telstra (TLS) stock traded in the Australian Securities Exchange (ASX) during the one week period from 1 to 7 October, 2014 is considered in the analysis. The relevant tick by tick trade data can be obtained from the Securities Industry Research Centre of Asia-Pacific (SIRCA) in Australia. The original durations were based on trades occurred during normal trading hours, ignoring overnight intervals and zero durations. Thereafter, data was adjusted for its daily seasonality. The observed trade durations are generally subjected to intraday seasonality or ‘diurnal’ effect. Engle and Russell [2] and several other authors have recognised this to be a deterministic component. This factor should be accounted for, prior to carrying out any empirical analysis on the stochastic properties of duration processes. The estimation of the deterministic diurnal factor, was done via a cubic spline with knots at each half hour interval [17]. Thus adjusted duration, $x_i$, which is referred to as duration hereafter, is modelled under this framework.

The total length of the series is 19473. The time series plot of Fig. 5a reveals the clustering effect generally observed in trade durations. On the other hand, Fig. 5b shows the excessive amount of values close to zero and the long right tail which are common characteristics of such data.

The summary statistics reported in Table 2 indicate overdispersion, generally prevalent in trade durations. Moreover, the series is positively skewed with a heavy tail according to the values of skewness and kurtosis. Sample autocorrelation function (ACF) of the adjusted durations is given in Fig. 6. The ACF clearly shows longterm serial dependence in the data, although the values appear to be small in magnitude.

Table 2 Summary statistics of TLS trade durations during the period 1 to 7 October, 2014

Fig. 6

Sample ACF for adjusted durations of TLS stock during the period 1 to 7 October, 2014

Three competing models EACD (1, 1), WACD (1, 1) and EW-ACD (1, 1) are fitted to TLS trade durations. The parameter estimates are given in Table 3 together with the standard errors in parentheses. All the parameter estimates are significant at the 5 $\%$ level. The EW-ACD model seems to be the best performing model, in terms of model fit based on both BIC and DIC. For WACD as well as EW-ACD models, the estimated shape parameter, k is less than one. This indicates a monotonously decreasing hazard function for adjusted TLS trade durations. It is reasonable for the high liquid asset. Although the extra shape parameter $\gamma$ of EW distribution is considerably large, showing heavy skewness and approaching Weibull distribution it still possesses a heavier tail than Weibull distribution and hence a better model fit. That is the main reason for its superior performance.

Table 3 Parameter estimates from ACD (1, 1) with errors from exponential, Weibull and EW distributions fitted to TLS duration data

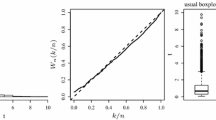
The fitted conditional expected mean of trade durations $\hat{\psi }_i$ from the EW-ACD model is plotted against durations of TLS in Fig. 7a. The model seems to adequately capture the mean durations. On the other hand, the P-P plot of the residuals from the same model confirms adequate fit of the distribution as depicted in Fig. 7b. In regions of high probability mass for near zero durations, the difference between theoretical and empirical cdfs is more apparent and negative than those in the low density regions for higher level durations, where the difference is less and positive. The pattern of the plot is consistent with heavier tail than observed and represent a uni-modal distribution. For further details on P-P plots, refer [18].

Fig. 7

a Fitted conditional mean of adjusted trade durations and b P-P plot of residuals from the EW-ACD model fitted to TLS duration data during the period 1 to 7 October, 2014

6.2 Daily Range Data

As mentioned earlier, the ACD model can be fitted to a time series with non-negative observations, such as the daily range and trade duration. Hence, the second real life example is on stock volatility modelling based on the daily range. We consider a time series of daily range of the log of All Ordinaries index (AOI) of ASX for the period from 1 May 2009 to 26 April 2013, consisting of 1008 observations. The data can be downloaded from Yahoo Finance. The daily percentage log-range $R_i$ is given by

$$R_i= 100 \times [\ln (\max _{z}P_{i_z}) - \ln (\min _{z}P_{i_z})],$$

where $P_{i_z}$ is the AOI measured at discrete time z in day i and max (min) is the maximum (minimum) of $P_{i_z}$ over all time z in day i.

Time series plot, histogram and sample ACF are given in Figs. 8a, b and 9, respectively. Volatility clustering, heavy tailedness and long term serial dependence appear to be common features of the AOI daily range series. On the other hand, the histogram shows that it has a uni-modal distribution having the mode shifted away from zero and has a relatively lower skewness and kurtosis, in comparison to the duration data, as indicated by the descriptive statistics in Table 4. Hence, the two series considered differ in their distributional shapes.

Fig. 8

a Time series plot and b histogram of daily range of AOI during the period 1 May 2009 to 26 April 2013

Fig. 9

Sample ACF of daily range of AOI for the period from 1 May 2009 to 26 April 2013

Again, three models EACD (1, 1), WACD (1, 1) and EW-ACD (1, 1) are fitted to the range data. The parameter estimates are reported in Table 5 together with the standard errors in parentheses. All the estimates are significant, at the usual 5 $\%$ level, except $\alpha _0$ of the EACD model. The best performing model is again the EW-ACD model, while the worst performer is the EACD model, in terms of both BIC and DIC. The estimated shape parameters, k for both WACD and EW-ACD models are greater than one, contrary to those of duration data. This indicates a monotonously increasing hazard function for the range data series of AOI. This is consistent with the phenomenon of volatility clustering where large volatility tends to be followed by large volatility and vice versa. Furthermore, the extra shape parameter $\gamma$ of the EW distribution has a small value, which is less than 2, catering to the relatively low skewness prevalent in range data.

The fitted conditional expected mean of daily range from the EW-ACD model is plotted against the observed daily range of AOI in Fig. 10a. The model seems to adequately capture the average volatility. On the other hand, the pdf plot fitted to residuals from the same model displayed in Fig. 10b indicates a good fit of the EW distribution and hence a suitable distribution for the residuals. The mean, standard deviation, skewness and kurtosis of the standardised residuals are 1.000, 0.4364, 0.7248 and 3.6147 respectively, indicating positive skewness and higher kurtosis than normal. Obviously, the skewness and kurtosis are lower than the original data after modelling the mean structure. The hazard and the cdf are plotted in Fig. 11a and b respectively, to get an idea about their behaviour.

Table 4 Summary statistics of AOI daily range during the period 1 May, 2009 to 26 April, 2013

Table 5 Parameter estimates of the ACD (1, 1) model with errors from the exponential, Weibull and EW distributions fitted to AOI range data

Fig. 10

a Fitted conditional mean of AOI daily range and b fitted pdf of residuals from the EW-ACD model fitted to AOI daily range during the period 1 May, 2009 to 26 April, 2013

Fig. 11

a Empirical hazard and b cumulative distribution function for the EW-ACD residuals of AOI daily range

7 Conclusion

A new distribution named as Extended Weibull (EW) is developed to allow a more flexible error distribution in ACD models. An additional shape parameter included in the variant form of the existing Weibull distribution provides this added flexibility. This parameter tends to capture heavier tails better than the Weibull distribution, which is a commonly used error distribution, due to its simplicity. In the presence of high skewness and kurtosis, this parameter tends to be large, in general, especially for small values of k.

The main attributes of the EW distribution are investigated, including the derivation of first four moments, cdf, survivor and hazard functions. The flexibility of the distribution is envisaged not only in terms of different shapes of the density function but also the hazard function. Interestingly, unlike the exponential or the Weibull distributions, the hazard function could be non-monotonic when $0.5<k<1$, which is more prominent when $\gamma >0.5$. This is a useful feature, particularly in modelling duration data.

The empirical performance of the EW distribution is investigated based on two real life data sets from the ASX, which share some common features but yet different in nature. One is the trade durations of TLS, characterising the mean duration and the other is daily range data of AOI, characterising average volatility. Its performance was compared with two other widely considered distributions, the exponential and Weibull distributions. In terms of both data sets, the EW distribution outperformed the other two distributions, irrespective of the magnitude of $\gamma$. Although theoretically the EW distribution converges to the Weibull distribution, when $\gamma$ tends to infinity, it showed an improvement in model fit. This highlights the EW distribution’s usefulness as a potential contender for the error distribution of ACD models.

Appendices

Appendix

Calculation of Moments and Main Characteristics for EW Distribution

Let X be a random variable following the EW distribution with parameters $\lambda$, k and $\gamma$. The distribution of X will be denoted as EW($\lambda$,k,$\gamma$) with the following pdf

$$\begin{aligned} \displaystyle f(x)= \left( 1+\frac{1}{\gamma ^k}\right) \frac{k}{\lambda ^k}x^{k-1}e^{-\left( \frac{x}{\lambda }\right) ^k}\left[ 1-e^{-\left( \frac{\gamma x}{\lambda }\right) ^k}\right] . \end{aligned}$$

1. Derivation of mean, E(X)

$$\begin{aligned} E(X) = \mu= & {} \int _{0}^{\infty }x f(x) dx \nonumber \\= & {} \frac{k}{\lambda ^k}\left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \int _{0}^{\infty }x^{k}e^{-\left( \frac{x}{\lambda }\right) ^k} dx -\int _{0}^{\infty }x^{k}e^{-\left( \frac{1+\gamma ^ k}{\lambda ^k}\right) \left( X\right) ^k}dx\right] \nonumber \\= & {} \lambda \left( 1+\frac{1}{\gamma ^{k}}\right) \varGamma \left( {1+\frac{1}{k}}\right) \left[ 1-\frac{1}{(1+{\gamma ^{k})}^{1+\frac{1}{k}}}\right] \nonumber \\= & {} \frac{\lambda }{k \gamma ^{k}}\varGamma \left( {\frac{1}{k}}\right) \left[ \frac{\left( 1+\gamma ^k\right) ^{1+\frac{1}{k}} - 1}{(1+\gamma ^k)^{\frac{1}{k}}}\right] \end{aligned}$$

(11)

2. Derivation of variance, Var(X)

$$\begin{aligned} Var(X)= & {} \sigma ^2 = E(X^2)-[E(X)]^2 \nonumber \\ E(X^2)= & {} \frac{k}{\lambda ^k}\left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \int _{0}^{\infty }x^{k+1}e^{-\left( \frac{x}{\lambda }\right) ^\alpha } dx -\int _{0}^{\infty }x^{k+1}e^{-\left( \frac{1+\gamma ^ k}{\lambda ^k}\right) \left( x\right) ^k}dx\right] \nonumber \\= & {} \lambda ^{2}\left( 1+\frac{1}{\gamma ^{k}}\right) \varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+\gamma ^{k})}^{1+\frac{2}{k}}}\right] \nonumber \\ \sigma ^2= & {} \lambda ^{2}\left( 1+\frac{1}{\gamma ^{k}}\right) \left\{ \varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+\gamma ^{k})}^{1+\frac{2}{k}}}\right] \right. \nonumber \\&-\left. \left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \varGamma \left( 1+\frac{1}{k}\right) \right] ^{2}\left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{1}{k}}}\right] ^{2}\right\} \end{aligned}$$

(12)

3. Derivation of skewness, Skew(X)

$$\begin{aligned} Skew(X)= & {} \rho = \frac{E\left[ X-E(X)\right] ^3}{\sigma ^3} =\frac{S_1}{S_2} \end{aligned}$$

(13)

$$\begin{aligned} \text {where}\quad E\left[ X-E(X)\right] ^3&= \frac{k}{\lambda ^k}\left( 1+\frac{1}{\gamma ^{k}}\right) \left( \int _{0}^{\infty }\left( x-\mu \right) ^3 x^{k-1}e^{-\left( \frac{x}{\lambda }\right) ^k} dx \right. \nonumber \\&\quad - \left. \int _{0}^{\infty }\left( x-\mu \right) ^3 x^{k-1}e^{-\left( \frac{1+\gamma ^ k}{\lambda ^k}\right) x^k}dx\right] , \nonumber \\ S_1&= \varGamma \left( 1+\frac{3}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+ \frac{3}{k}}}\right] \nonumber \\&\quad - \frac{3\mu }{\lambda }\varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{2}{k}}}\right] \nonumber \\&\quad + \frac{3\mu ^2}{\lambda ^2}\varGamma \left( 1+\frac{1}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{1}{k}}}\right] -\frac{\mu ^3}{\lambda ^3}\left( 1-\frac{1}{1+{\gamma ^{k}}}\right) , \nonumber \\ S_2&=\left[ 1+\frac{1}{\gamma ^{k}}\right] ^{1/2}\left\{ \varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{2}{k}}}\right] \right. \nonumber \\&\quad -\left. \left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \varGamma \left( 1+\frac{1}{k}\right) \right] ^2 \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{1}{k}}}\right] ^2\right\} ^{\frac{3}{2}}\nonumber \end{aligned}$$

4. Derivation of kurtosis, Kurt(X)

$$\begin{aligned} Kurt(X)= & {} \zeta = \frac{E\left[ X-E(X)\right] ^4}{\sigma ^4}=\frac{K_1}{K_2} \end{aligned}$$

(14)

$$\begin{aligned} \text {where}\quad E\left[ X-E(X)\right] ^4= & {} \frac{k}{\lambda ^k}\left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \int _{0}^{\infty }\left( x-\mu \right) ^4 x^{k-1}e^{-\left( \frac{x}{\lambda }\right) ^k} dx \right. \nonumber \\&- \left. \int _{0}^{\infty }\left[ x-\mu \right) ^4 x^{k-1}e^{-\left( \frac{1+\gamma ^ k}{\lambda ^k}\right) x^k}dx\right] , \nonumber \\ \end{aligned}$$

$$\begin{aligned} K_1= & {} \varGamma \left( 1+\frac{4}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{4}{k}}}\right] -\frac{4\mu }{\lambda }\varGamma \left( 1+\frac{3}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{3}{k}}}\right] \nonumber \\&+\frac{6\mu ^2}{\lambda ^2}\varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{2}{k}}}\right] -\frac{4\mu ^3}{\lambda ^3}\varGamma \left( 1+\frac{1}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{1}{k}}}\right] \nonumber \\&+\frac{\mu ^4}{\lambda ^4}\left( 1-\frac{1}{1+{\gamma ^{k}}}\right) ,\nonumber \\ K_2= & {} \left( 1+\frac{1}{\gamma ^{k}}\right) \left\{ \varGamma \left( 1+\frac{2}{k}\right) \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{2}{k}}}\right] \right. \nonumber \\&-\left. \left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \varGamma \left( 1+\frac{1}{k}\right) \right] ^2 \left[ 1-\frac{1}{{(1+{\gamma ^{k}})}^{1+\frac{1}{\alpha }}}\right] ^2\right\} ^{2} \nonumber \end{aligned}$$

5. Derivation of the cumulative distribution function, cdf, F(x)

$$\begin{aligned} F(x)= & {} \int _{0}^{x} f(y)dy \nonumber \\ \displaystyle= & {} \frac{k}{\lambda ^k}\left( 1+\frac{1}{\gamma ^{k}}\right) \left[ \int _{0}^{x}y^{k-1}e^{-\left( \frac{y}{\lambda }\right) ^k} dy -\int _{0}^{x}y^{k-1}e^{-\left( \frac{1+\gamma ^ k}{\lambda ^k}\right) y^k}dy\right] \nonumber \\= & {} 1 + \frac{1}{\gamma ^k}e^{-\left( \frac{x}{\lambda }\right) ^k}\left[ e^{-\left( \frac{\gamma x}{\lambda }\right) ^k}- 1 -\gamma ^k \right] \end{aligned}$$

(15)