Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A comprehensive analysis of a helicopter requires fast and reliable methods to model the structural and aerodynamical rotor behavior [9]. Computing the unsteady airloads of a helicopter rotor using computational fluid dynamics (CFD) simulations is still a challenging and computationally expensive task, particularly if dynamic stall occurs. Therefore, blade element methods still play an important role during the design and certification process of a helicopter. Unsteady aerodynamics and dynamic stall are taken into account using semi-empirical models, which exist in a huge variety [12].

Most of these models combine a physics based formulation with an empirical correction, and thereby describe the lift, drag and moment coefficient of a blade element under unsteady or even dynamic stall conditions, with low expense. The quality of the modeled aerodynamic coefficients for a particular blade element, strongly depends on the selected empirical parameters. Usually, wind tunnel experiments of an airfoil pitching around its quarter chord are used to determine the empirical parameters for a specific airfoil and case.

Fig. 1
figure 1

Schematics of the superposition of flight velocity \(\text {V}_f\) with the rotational velocity, combined with the resulting incident velocity V and angle of attack \(\alpha \) variation of a blade section over a rotor revolution

Full size image

Helicopter rotors encounter dynamic stall during fast forward flight or at flight maneuvers with a high load factor. During these flight states, blade sections are subjected to a periodically varying incident velocity, resulting from the superposition of the helicopter’s flight speed and the rotational velocity of the rotor, as schematically shown in Fig. 1. At the advancing blade side \(\psi _1\) the periodic incident velocity of the blade section achieves its maximum value, while the angle of attack is minimal. Whereas, at the retreating blade side \(\psi _2\) the blade section experiences the highest angle of attack and the lowest flow velocity.

Experimental investigations have been performed to study the dynamic stall behavior under varying flow velocity [4, 5, 8, 13]. However, complexity of the experimental setup limits these studies to either low mean flow velocity or low velocity amplitudes, compared to the flow characteristics of a blade section on a helicopter rotor. For this study, a representative test case is defined. As a consequence, all considerations are based on numerical results obtained by solving the unsteady Reynolds-averaged Navier-Stokes (URANS) equations.

2 Test Case

A typical blade section of a helicopter rotor represented by a two-dimensional blade element, is used for the present study. The blade element consists of the ONERA OA209 rotorcraft airfoil with a chord length of \(c = 0.3\text { m}\). The average Mach number of this element is \(M_0 = 0.5\) and varies during the blade revolution by an amplitude of \(\varDelta M = 0.2\), while the angle of attack \(\alpha \) changes with a phase shift of \(180^\circ \) about its average value \(\alpha _0 = 13^\circ \) with the amplitude \(\varDelta \alpha = 7^\circ \). The local incident angle \(\alpha \) and the local Mach number M at the azimuth positions \(\psi \) are given by:

$$\begin{aligned}&\alpha (\psi ) = \alpha _0\,-\,\varDelta \alpha \,\cdot \,\sin (\psi )\end{aligned}$$
(1)
$$\begin{aligned}&M(\psi ) = M_0\,+\,\varDelta M\,\cdot \,\sin (\psi ) \end{aligned}$$
(2)

The rotational frequency of the rotor is 7 Hz and the local Reynolds number of the blade section varies during one revolution from about \(2.1 \times 10^6\) at the retreating blade to \(4.8 \times 10^6\) on the advancing side.

3 Numerical Methods

The numerical simulation results of this study are based on computations using the DLR-TAU code [15]. The DLR-TAU code solves the URANS equations on unstructured grids by applying the finite-volume method. To achieve second order accuracy, numerical fluxes are discretized by central differences and a second order dual time-stepping scheme is applied for time integration. The Spalart-Allmaras model with Edwards modification was used for the fully turbulent computations [3].

As discussed in [16], the periodically varying flow velocity can be approximated following two approaches, which lead to different flow conditions at the airfoil. First, the varying velocity can be generated by a forward and backward motion of the blade element, resulting in an uniform freestream velocity along the entire airfoil. In the second method the airfoil encounters a time-varying inflow velocity, which is realized by a series of horizontal gusts acting on it. This second case corresponds to the velocity change resulting from the superposition of the helicopter’s flight speed and the rotational velocity of the blade, while the first case represents the velocity change created by a lead-lag motion of the rotor blade. Both cases are considered in the present study. All computations are carried out on a two-dimensional hybrid grid. Figure 2 schematically shows the computational domain used for the two approaches.

Fig. 2
figure 2

Schematics of the computational domain used for the forward-backward motion (a) and the traveling gust series (b)

Full size image

The hybrid grid, which is used for the steady computations and for the forward-backward motion of the airfoil, is composed of hexahedral cells in the boundary layer region with the height of the first layer adjusted to satisfy \(y^+ \le 1\). The remaining part of the flow field between the boundary region and the circular farfield, with radius \(r = 1000\)c, is set up using prismatic cells. Richter et al. [14] investigated the necessary grid resolution in the boundary layer region and in the outer field, for the OA209 profile in deep dynamic stall at \(M = 0.3\). Besides the overprediction of the vortex size and strength, which may be a result of the two-dimensional consideration [10], these computations show very good correlation with the experimental data. Therefore, the grid resultion for the present simulations was determined based on the findings of this study. At each time step the whole computational domain is rotated to the actual angle of attack and horizontally moved to generate the varying inflow velocity.

In order to resolve the series of horizontal gusts traveling through the computational domain, a grid system was used composed of a background grid and a circular near body grid containing the airfoil [7]. The structure of the circular grid is similar to the previously described hybrid grid up to a radius \(r = 10\)c. The resolution of the background grid is chosen to resolve every gust along its wave length with 100 cells. A mainly cartesian grid structure is used with the outer edges of the rectangular domain having a length of 2000c. Both grids are connected using the Chimera technique. Therefore, a circular hole is introduced into the background grid at the position of the circular near body grid. The interpolation region of both grids are assembled by prismatic cells with equal size.

The number of computed pitching cycles was choosen to reach periodicity in the aerodynamic coefficients. For the two cases with varying flow velocity periodicity was reached after the fourth pitch cycle, while three cycles were sufficient in the case of steady flow velocity. Each period of the cycles was resolved by 1500 physical time steps. In the traveling gust case an initialization with 100 physical time steps was performed to stationary resolve the gust series shortly upstream of the airfoil. The number of inner iterations per physical time step has not been fixed to achieve a reduction of the density residual, by 6 orders of magnitude compared to the initial value, in every time step.

4 Semi-Empirical Modeling

The commonly used Gangwani [6] and Leishman-Beddoes [11] dynamic stall models are applied to the numerical results in order to study the modeling capabilites of the aerodynamic coefficients. Both models differentiate several phases, which an airfoil encounters during dynamic stall, namely attached flow, trailing edge separation, leading edge separation with vortex shedding and reattachement of the flow. The formulation of the unsteady attached flow in both models is based on the indicial response functions formulated by Beddoes [1].

Dependent on the resulting effective angle of attack the Gangwani (GA) model adapts its formulation to account for the different flow phases. The aerodynamic coefficients are obtained by the evaluation of the underlying steady airfoil polar at a shifted angle. These looked up values are corrected by a series of empirical terms, which need to be adapted in order to represent the specific case.

The Leishman-Beddoes (LB) model has distinct formulations for every flow phase. The steady airfoil polar is only needed to derive the empirical coefficients used to formulate the trailing edge separation. All formulations are based on deficiency functions to account for the time dependency of the flow.

As a consequence of the formulation, the empirical parameters of the LB model have a clear physical meaning, whereas a large number of empirical coefficients within the GA model can not be interpreted directly. The empirical model coefficients of both models are adapted to ideally represent the regarded test case in the least-squares sense. The utilized steady polars for the OA209 airfoil have been computed using the Euler boundary-layer code MSES [2].

5 Results

The numerical predicted effect of the varying incident velocity on the aerodynamic forces during dynamic stall is presented in this section. These aerodynamic forces are represented by the dimensionless lift, drag and moment coefficient, which are normalized using the airfoil’s actual incident velocity. In the traveling gust case, the actual incident velocity is determined at the position of the airfoil’s leading edge.

In Sect. 5.1 the predicted aerodynamic coefficients during the pitching cycle are presented, along with the modeled coefficients for the GA and LB dynamic stall model, at constant flow velocity. The effect of the periodic flow velocity on the resulting aerodynamic forces is discussed in Sect. 5.2.

5.1 Steady Flow Velocity

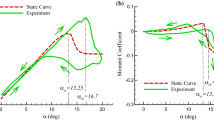
The predicted aerodynamic coefficients for the pitching OA209 airfoil are strongly influenced by the Mach number of the steady flow velocity. Figure 3 shows the progress of the lift, drag and moment coefficient during the pitch cycle at \(M = 0.3\) and \(M = 0.5\). As a result of the constant chord length and the constant rotational frequency of the considered airfoil a change of the inflow velocity also affects the reduced frequency and the Reynolds number. Therefore, the differences between the two cases arise not solely from compressibility effects.

Fig. 3
figure 3

Numerical predicted lift, drag and moment coefficient for the test case at constant inflow Mach number \(M = 0.3\) (a) and \(M = 0.5\) (b) with results from the GA and LB dynamic stall model

Full size image

During the upstroke of the pitching cycle at \(M = 0.3\) the formation of a leading-edge vortex is observed at an angle of attack of about \(17.5^\circ \). The stall point is reached at \(\alpha = 18.4^\circ \), followed by a steep drop of the lift coefficient. The resulting lift coefficient of both dynamic stall models is in good agreement with the predicted lift drop. The peak of the drag coefficient during the presence of the vortex is better approximated by the GA model, while the LB model shows an advantage in the representation of the moment coefficient peak. The drag peak is not modeled by the LB model. Both models show deviations during the attached flow and reattachment phase for all coefficients. For this case the overall conformity with the numerical results is slightly better for the GA model compared to the LB model.

Increasing the freestream Mach number to \(M = 0.5\) leads to a supersonic region on the suction side of the airfoil close to the leading edge, which terminates with a shock. The size of the supersonic region and the strength of the shock increase until the formation of the stall vortex begins downstream of the shock. The first stall event occurs at a considerably smaller angle (\(\alpha = 12.7^\circ \)) compared to the case at \(M = 0.3\). After the first vortex detaches from the trailing edge, a short flow reattachement occurs followed by the formation of a second leading edge vortex. The lift overshoot, as well as the magnitude of the drag and momentum peak, is predicted higher for the second stall event at \(\alpha = 16.0^\circ \). In general both dynamic stall models are able to consider a second stall during the pitch cycle. However, the GA model forms four stall events with decreasing magnitude. In contrast, the occurence of the stall events described by the LB model shows good agreement.The lift overshoot of the LB model during the second stall event is too high, while the coefficients from the GA model are too low compared to the numerical predicted coefficients. Both models fail in considering the momentum peaks during the upstroke of the airfoil. In case of a strong second stall event the LB model’s formulation is advantageous over the GA model.

5.2 Periodic Flow Velocity

The predicted aerodynamic coefficients of the pitching OA209 airfoil undergoing periodic flow velocity are presented in Fig. 4. The results for the airfoil performing a forward-backward motion, in order to derive the unsteady flow velocity, differ tremendously from those obtained for the airfoil encountering a series of horizontal gusts. Whereas, both cases are treated equivalently by the semi-empirical stall models. The applied parameter set is the only possibility to take the differences into account.

Fig. 4
figure 4

Numerical predicted lift, drag and moment coefficient for the test case at periodic incident velocity resulting from a lead-lag motion (a) and horizontal gusts (b) with results from the GA and LB dynamic stall model

Full size image

Three stall events occur during the pitch cycle of the airfoil performing the lead-lag motion. In the initial phase of the upstroke the supersonic region is decreasing, while the shock is traveling towards the leading edge of the airfoil. Passing \(\alpha = 11.8^{\circ }\) the formation of the first stall vortex begins. The first stall event occurs at higher angle of attack (\(\alpha = 14.7^{\circ }\)) compared to the case with steady freestream Mach number \(M = 0.5\). After the first vortex detaches from the trailing edge (\(\alpha = 16.^{\circ }\)) a second vortex is formed. This second vortex produces comparable peaks in the aerodynamic coefficients (\(\alpha = 18.0^{\circ }\)), while the third stall event (\(\alpha = 19.6^{\circ }\)) results in lower peaks.

In the case of the horizontal gusts acting on the airfoil the leading edge vortex is formed at an angle of \(18.2^{\circ }\). The stall point is reached at \(19.2^{\circ }\), followed by the immediate formation of a second leading edge vortex at \(19.8^{\circ }\) (upstroke) and a short reattachement of the flow. The secondary stall event occurs at about \(19.3^{\circ }\) during the downstroke of the airfoil.

The parameter sets obtained at steady flow velocity were applied individual and in combination to the cases with periodic flow velocity. The obtained progress of the aerodynamic coefficients does not show any similarities to either the lead-lag motion case or the gust case. Therefore, specific parameter sets were obtained for the two cases. The GA model underestimates the occuring lift overshoot for all three stall events of the moving airfoil. While the aerodynamic coefficients of the LB model show good agreement for the second stall event, the first stall is delayed and the magnitude of the peak is too low compared to the numerical prediction.

Considering the horizontal gust case, both models show good accordance regarding the lift, drag and moment coefficient peaks.

6 Conclusion

URANS computations were performed to obtain the aerodynamic coefficients for a test case at varying flow velocity. According to the numerical prediciton for the considered test case, the periodic flow velocity was found to have a strong influence on the dynamic stall behavior. Validation needs to be performed for the numerical computations, especially for the horizontal gust series acting on the airfoil.

The application of the empirical model parameters obtained from steady free-stream velocity was not leading to reasonable results in the regarded case, whereas the derivation of parameters for the specific case was leading to better results. Both dynamic stall models show strengths and weaknesses, however, further development of the model capabilites is necessary to enable a wider applicability of the empirical model coefficients.