Comparison Between Two-Dimensional and Three-Dimensional Dynamic Stall

Abstract

Numerical computations using the DLR-TAU code investigate the differences and similarities between dynamic stall on the two-dimensional OA209 airfoil and the three-dimensional OA209 finite wing. The mean angle of attack in the two-dimensional computations is reduced to match the effective angle of attack at the spanwise position where in the finite wing computations the dynamic stall vortex starts to evolve. Small variations of the mean angle of attack in the two-dimensional numerical simulations show a change from trailing edge separation only to deep dynamic stall. The analysis of the three-dimensional flow field reveals that after the evolution of the dynamic stall vortex the flow field is split into two parts: 1. High spanwise velocities towards the wing’s root in the region between the plane of the first occurrence of stall and the wing’s root. 2. High spanwise velocities towards the wing’s tip in the region between the plane of the first occurrence of stall and wing tip.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In forward flight conditions and during maneuvers the helicopter airfoil can dynamically stall leading to strong pitching moment peaks and thus to a limitation of the helicopter flight envelope. Traditionally, research into dynamic stall relies strongly on two-dimensional experiments [1, 2] where the wing spans the whole width of the wind tunnel and on two-dimensional numerical simulations [3, 4]. But as dynamic stall is a strongly three-dimensional phenomenon, it is necessary to understand how three-dimensional dynamic stall differs from two-dimensional dynamic stall, so that the value of existing two-dimensional dynamic stall data can be maximized.

Investigations of three-dimensional dynamic stall with one free end were experimentally investigated by Lorber [5] and numerically by Spentzos [6]. Both showed the three-dimensional stall results in a generation of a dynamic stall vortex near the wing root, which then spreads rapidly in the spanwise direction. In the wing tip region the dynamic stall vortex is suppressed due to the interaction with the blade tip vortex and the flow in this region is strongly curved.

A finite wing model (Fig. 1) using an untwisted OA209 cross section with thickened root at y/s = 0 and rounded tip at y/s = 1 was previously numerically investigated [7] using the DLR-TAU code and ONERA’s elsA code under dynamic stall conditions ($Ma = 0.16$, $Re = 1\,\times \,10^{6}$, $\alpha = 17^{\circ }\,\pm \,5^{\circ }$, $k = \pi fc/U_{\infty } = 0.1$). The geometry was selected to match the ONERA finite wing experiment which was performed in the ONERA F2 wind tunnel [8].

In this work, two-dimensional and three-dimensional computations on the OA209 finite wing using DLR-TAU are compared to investigate the differences and similarities between two-dimensional and three-dimensional dynamic stall effects.

Fig. 1

CAD model of the finite wing showing the positions of PIV, LDV and pressure measurements with contours of the non-dimensional streamwise velocity $U_x$ = $U_{x_{local}}/U_{\infty }$

2 Numerical Method

RANS and URANS computations were performed with the two-dimensional OA209 airfoil and with the three-dimensional OA209 finite wing based on the experiment of Le Pape et al. [8]. The OA209 finite wing model (Fig. 1) was numerically investigated using the DLR-TAU code [9] under the following dynamic stall conditions: Ma = 0.16, Re = 1$\times$10$^{6}$, $\alpha$ = 17$^{\circ }\pm$5$^{\circ }$ and k = $\pi fc/U_{\infty }$ = 0.1. The two-dimensional computations were investigated under the same flow conditions, but with a different mean angle of attack to match the effective angle of attack at the position where dynamic stall first occurred in 3D. The wing and the airfoil were pitched around the quarter chord line by changing the farfield boundary conditions.

The numerical simulations were solved on an unstructured mixed element grid using a finite volume approach. A Roe scheme and a central method with artificial scalar dissipation were used to solve the viscous fluxes and the inviscid fluxes, respectively. To prevent accuracy from degrading and convergence from degeneration due to the small onflow Mach number, low Mach number preconditioning was applied. The computations did not consider transition and the two-equation Menter SST turbulence model [10] was used to close the RANS and URANS equations. The three-dimensional URANS computations were run for 5 pitching cycles with 1500 iterations per period and 3000 iterations for the fifth period computed and the two-dimensional URANS computations were run for 3 pitching cycles using 3000 iterations per period leading to a physical time step of $\varDelta t$ = 0.000057 s. 300 inner iterations were used for both cases to produce a time-converged solution with a drop of the Newton residuals by at least 1 order of magnitude during the whole dynamic stall cycle.

For the three-dimensional mesh a hemispherical computational domain with 500 chord radius, symmetry conditions at the side of the wing’s root and far field conditions at all other boundaries was used. An unstructured mixed element grid with 30 prisms in the normal direction to resolve the boundary layer and tetrahedral cells in the outer flow field was created with the method used by Richter et al. [4]. The height of the first prismatic layer and the stretching factor were adjusted to reach $y^{+}\le$1 and the boundary layer thickness, respectively. The prerefined trapezoidal area with a streamwise length of 6c, a maximum height of 5c and cell sizes of l/c = 3.33 %, of Richter et. al. [4] was stretched in the spanwise direction. It extends from the wing’s root over the whole wing up to a half chord length over the wing’s tip to resolve the wake and the vortices from dynamic stall and the blade tip.

To obtain comparable results the two-dimensional grid had the same resolution as the three-dimensional grid at y/s = 0.36 (Fig. 2), a circular far field with 500 chord radius and symmetry conditions in the spanwise direction.

Fig. 2

Grid resolution in the outer field of the three-dimensional grid at y/s = 0.36 (left) and the two-dimensional grid (right)

3 Results

The three-dimensional DLR-TAU dynamic stall computations using the Menter SST turbulence model were visualized using isosurfaces of the $\lambda _{2}$ criterion and color plots of C$_{P}$ at a snapshot of $\alpha$ = 20.6$^\circ \downarrow$ on the downstroke, showing the strongly three-dimensional flow around the finite wing in Fig. 3. The evolution of an $\varOmega$-shaped dynamic stall vortex at y/s$\approx$0.40 can be seen and that separation close to the wing tip and the wing root is suppressed due to the reduction of the effective angle of attack. Furthermore, the blunt shape of the root leads to a continuous shedding of vortices. Figure 4 shows the sectional lift coefficient at y/s = 0.36 and y/s = 0.50. During the upstroke the behavior is identical, but stall at y/s = 0.50 is triggered by the arrival of the $\varOmega$-shaped dynamic stall vortex first formed further inboard, resulting in additional lift as the base point of the vortex passes the section, whereas y/s = 0.36 stalls as a two-dimensional airfoil.

Fig. 3

Three-dimensional dynamic stall behavior around the OA209 wing. Visualized by means of isosurfaces of the $\lambda _{2}$ criterion at $\alpha$ = 20.6$^\circ \downarrow$

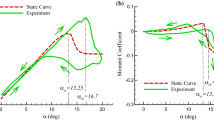
Figure 5 compares the sectional lift coefficient of static two-dimensional computations with the lift coefficient of static three-dimensional simulations at y/s = 0.36, approximately where the dynamic stall vortex starts to evolve. Due to three-dimensional effects the effective angle of attack at stall is reduced by $\varDelta \alpha \approx$5$^\circ$ and the gradient of the slope is reduced ($\varDelta$C$_{L}$/$\varDelta \alpha$ = 0.07/$^\circ$ for the three-dimensional case and $\varDelta$C$_{L}$/$\varDelta \alpha$ = 0.11/$^\circ$ for the two-dimensional case).

Fig. 4

Comparison of lift for 3D dynamic DLR-TAU computations using Menter SST between y/s = 0.36 and y/s = 0.5

Figure 5 showed that the effective angle of attack is reduced by $\varDelta \alpha \approx$5$^\circ$, therefore two-dimensional URANS computations with the same settings as in the three-dimensional case, but with mean angles of attack reduced by $\varDelta \alpha = 4-6^\circ$, were performed to obtain the same effective angle of attack. In Fig. 6 large differences occur between the computations. The computations with lowest mean angle of attack $\alpha _{mean} = 11.0^\circ$ shows only a small hysteresis in lift, whereas at $\alpha _{mean} =12.0^\circ$ a significant drop in lift at $\alpha =15^\circ \downarrow$ on the downstroke occurs, Fig. 6 (left). For the three highest mean angles of attack ($\alpha _{mean} = 12.2^\circ$, $\alpha _{mean} =12.5^\circ$, $\alpha _{mean} =13.0^\circ$) stall occurs earlier with an additional overshoot in lift.

Fig. 5

Comparison of lift for static DLR-TAU computations using Menter SST between the two-dimensional case and the three-dimensional case at y/s = 0.36

The strong sensitivity becomes even clearer when looking at the pitching moment, Fig. 6 (right). The computation with $\alpha _{mean} = 11.0^\circ$ results in a counterclockwise rotating curve, whereas the curve of $\alpha _{mean} = 12.0^\circ$ exhibit a pronounced pitching moment peak of C$_{M_{P}} = -0.15$ at $\alpha = 15.1^\circ \downarrow$ on the downstroke. The higher the mean angle the larger the pitching moment peak becomes: C$_{M_{P}} = -0.21$ at $\alpha = 15.2^\circ \downarrow$ for $\alpha _{mean} = 12.1^\circ$, C$_{M_{P}}=-0.40$ at $\alpha = 14.7^\circ \downarrow$ for $\alpha _{mean} = 12.2^\circ$, C$_{M_{P}}=-0.52$ at $\alpha = 15.9^\circ \downarrow$ for $\alpha _{mean} = 12.5^\circ$ and C$_{M_{P}}=-0.54$ at $\alpha = 17.2^\circ \downarrow$ for $\alpha _{mean} = 13.0^\circ$. Especially, the large change from $\alpha _{mean} = 12.1^\circ$ to $\alpha _{mean} = 12.2^\circ$ where the pitching moment peak increases by 90 % is significant. In contrast the pitching moment between $\alpha _{mean} = 12.5^\circ$ and $\alpha _{mean} = 13.0^\circ$ does not increase significantly (+4 %), but the pitching moment peak is moved to a higher angle of attack (+1.3$^\circ$).

Fig. 6

Comparison between two-dimensional computations using different mean angles of attack. Left lift. Right pitching moment

Figure 7 shows the comparison between three-dimensional dynamic stall computations at y/s = 0.36 and two-dimensional dynamic stall computations with $\alpha _{mean} = 12.1^\circ$. For clarity the three-dimensional data was shifted by $\varDelta \alpha = -4.9^\circ$ to display approximately the effective angle of attack for the three-dimensional case. This two-dimensional case provides the most comparable integrated values with the three-dimensional dynamic stall case at the section of the origin of the dynamic stall vortex, both for the lift (left) and for the pitching moment (right). For other sections of the three-dimensional case the results differ from the two-dimensional case, because stall is triggered by the formation of the dynamic stall vortex at y/s = 0.36. The lift gradient is $\varDelta$C$_{L}$/$\varDelta \alpha = 0.03/^\circ$ higher and the pitching moment peak is 11 % stronger and 0.9$^\circ$ earlier with respect to the changed effective angle of attack in the two-dimensional case.

Fig. 7

Comparison between two-dimensional computations with $\alpha _{mean} = 12.1^{\circ }$ and the three-dimensional computations at y/s = 0.36 shifted by $\varDelta \alpha = -4.9^\circ$ to display approximately the effective angle of attack. Left lift. Right pitching moment

Although the integrated values of these two cases are comparable, the aerodynamic behavior is completely different as Figs. 8 and 9 show. Figure 8 shows snapshots of the $C_P$ distribution and the streamlines around the finite wing at y/s = 0.36 for angles of attack around stall. At $\alpha _{max} = 22^\circ$ the flow starts to separate at the trailing edge, at $\alpha = 20.8^{\circ }$ $\downarrow$ on the downstroke the dynamic stall vortex is already formed around the leading edge and moves downstream and spreads in the further process, $\alpha = 20.2^{\circ }$ $\downarrow$ and $\alpha = 19.4^{\circ }$ $\downarrow$.

In contrast to the three-dimensional case the flow in 2D (Fig. 9) shows a less pronounced stall region. At $\alpha = 16.9^{\circ }$ $\downarrow$ the flow is separated at the trailing edge, this subsequently enlarges and a vortex is formed within the separated region at $\alpha = 14.2^\circ$ $\downarrow$ leading to the pitching moment peak seen in Fig. 7.

The aerodynamic behavior of the two-dimensional computations using $\alpha _{mean} = 12.5^{\circ }$ is shown in Fig. 10. For this case the beginning of the flow separation is comparable to the three-dimensional case as a vortex is formed at the leading edge at $\alpha = 16.9^{\circ }$ $\downarrow$ (Fig. 10b), which then spreads as it moves downstream. The reason for the differences between the three-dimensional case and the two-dimensional case with $\alpha _{mean} = 12.5^{\circ }$ is due to the different strength of the vortex as it reaches the trailing edge, where in the two-dimensional case the vortex is much more pronounced and in the three-dimensional case the vortex loses it’s strength while moving downstream.

Fig. 8

Stall behavior of the three-dimensional computation at y/s = 0.36

Fig. 9

Stall behavior of the two-dimensional computation 12.1$^{\circ }\pm$5$^{\circ }$

Fig. 10

Stall behavior of the two-dimensional computation 12.5$^{\circ }\pm$5$^{\circ }$

Fig. 11

Non-dimensional spanwise velocity $V_y = V_{y_{local}}/U_{\infty }$ of the three-dimensional case at x/c = 0.25

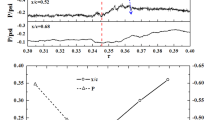
The big difference between two-dimensional and three-dimensional flow is of course the additional degree of freedom in the spanwise direction. Spanwise velocities in the two-dimensional case are nonexistent. To investigate this influence and the process of the dynamic stall evolution in the spanwise direction, the non-dimensional spanwise velocities $V_y = V_{y_{local}}/U_{\infty }$ and streamlines over the finite wing with the wing root on the left and the wing tip on the right are plotted in Fig. 11 at x/c = 0.25 for $\alpha = 12.5^{\circ }$ $\uparrow$, $\alpha = 21.8^{\circ }$ $\uparrow$, $\alpha = 21.2^{\circ }$ $\downarrow$, $\alpha = 20.7^{\circ }$ $\downarrow$, $\alpha = 19.6^{\circ }$ $\downarrow$ and $\alpha = 18.0^{\circ }\downarrow$. During attached flow (Fig. 11a), $V_y$ is close to zero in the middle region of the wing. The flow becomes more three-dimensional when moving towards the wing’s tip or the wing’s root, with velocities towards the middle of the wing on the suction side and outboard on the pressure side of the wing. With increasing angles of attack this effect increases, see Fig. 11b. In Fig. 11c, the dynamic stall vortex evolves and the flow field is split into two parts, left and right of the spanwise position of the starting point of dynamic stall. Figure 11d–f show that large spanwise velocities occur on the suction side of the finite wing, which temporarily exceed the inflow velocity (not shown). Rootward of the starting point of dynamic stall the velocity is pointed towards the wing’s root and tipward of the starting point of dynamic stall the velocity is pointed towards the wing’s tip. Figure 11d shows that the spanwise velocity is initially reduced to a small area close to the evolution point of dynamic stall at $\alpha = 20.7^{\circ }$ $\downarrow$, but then spreads fast and covers almost the whole area on the suction side of the wing as the airfoil pitches down, see Fig. 11e, f. Due to this velocity the dynamic stall vortex is deflected out of the plane where it occurs first and is weakened in the plane at y/s = 0.36.

4 Conclusion

Two-dimensional and three-dimensional numerical simulations were performed using DLR-TAU. The analysis of the static computations showed that the effective angle of attack is reduced by $\varDelta \alpha \approx$-5$^\circ$. Two-dimensional URANS computations with the variation of the mean angle of attack from $\alpha _{mean} = 11^\circ$ to $\alpha _{mean} = 13^\circ$ revealed the strong sensitivity of the dynamic stall behavior in this range, resulting in trailing edge separation only at $\alpha _{mean} = 11^\circ$ and in deep dynamic stall at $\alpha _{mean} = 13^\circ$. The change of the mean angle of attack from $\alpha _{mean} = 12.1^\circ$ to $\alpha _{mean} = 12.2^\circ$ resulted in an increase of the pitching moment of 90 %.

The analysis of the three-dimensional dynamic stall computations revealed the flow field is separated into two parts with high spanwise velocities moving towards the root in the inner part and high spanwise velocities moving towards the blade tip in the outer part. These velocities result in the deflection of the dynamic stall vortex out of the section where it evolves and a reduced pitching moment in this section.

Further investigations on the influence of the amplitude and the frequency on the dynamic stall behavior will be carried out.