Dynamic Resource Provision for Cloud Broker with Multiple Reserved Instance Terms

Abstract

Relying on the knowledge of the pricing benefit of long-term reserved resource and multiplexing gains, cloud broker strives to minimize its cost by utilizing infrastructure resources from public cloud service provider. Different reserved instance terms accompanied by different prices are provisioned by the provider. How to choose the appropriate ones from various terms to meet the dynamic user demands at the least cost is a great challenge. This paper addresses the challenge by two algorithms. Extensive real world traces driven evaluations show that the heuristic algorithm runs about twice as fast as the approximation one, while both algorithms can save almost the same resource cost up to 27 %.

1 Introduction

Many public cloud service providers (CSPs) deliver infrastructure as a service (IaaS) to users. Each provider differentiates itself in terms of service area, virtual machine (VM) instance types (each instance with a fixed CPU, memory and storage etc.), prices of different sources and performance guaranteed. Especially, there are various pricing mechanisms for VM instances. The instance can be provisioned on-demand and billed at a cycle of hour (Amazon EC2 [3]), minute (Microsoft Azure [16]) or 15 min (Elasthosts [6]). Optionally, the instance can be reserved at any time in advance and then launched at any time as required [21]. The reserved instance is charged a total cost whenever it is active. For example, Amazon EC2 provides a choice of two reserved instance terms, 1 year and 3 years [3] and the terms are charged differently. VMware vCloud Air permits a more flexible subscription term from 1 month to 36 months [21]. Normally, the average price for reservation at each billing cycle is far lower than that of the on-demand one. Furthermore, the longer the term, the lower the price. For instance, the saving over on-demand price of Amazon m3.media instance can be up to 29 % and 60 %, for 1-year and 3-year terms, respectively [3].

Users can rent instances from the provider directly. But limited by their knowledge of the cloud IaaS market, it is a great pain for users to make a selection from various instances with various prices to cut their cost. Even sometimes, they have to bargain with more than one provider to meet the different services or service area requirements, thus incurring more overhead. Subjectively, these requirements drive users to seek the help of the third party and lead to the emergence of cloud broker in recent years [11].

A cloud broker can provide on-demand instance to users with lower price. On one hand, the broker can choose infrastructures among providers for their “expertise and experience” offering the service. On the other hand, based on multiplexing of relatively small requirements of individual users, the broker can make a bulk reservation in advance at a much lower reservation price. Then offer users on-demand instances at an intermediate price. Huge profit space exists and entices the broker to render brokerage services objectively.

Fig. 1.

Broker multiplexes the time-varying dynamic requests of four users. Then delivers on-demand services to users at a lower intermediate price by leveraging proper reserved and on-demand instances. The left user request bar is served by the instance bar with the same setting on the right CSP side.

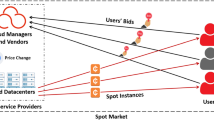
Figure 1 depicts the service delivery scheme. Different users apply for on-demand instances from time 1 to 6 (step 1). The broker tries to rent instances from CSP to meet the requests at the least cost (step 2). CSP provides on-demand and reserved instances with different prices and terms $\tau$. The price for on-demand instance is charged at each hour (billing cycle). For the reserved scenario, the price is the total cost of $\tau$ billing cycles. Based on the number and the lifetime of the aggregated request, the broker can exploit the pricing benefit of long-term resource reservation and multiplexing gains (step 3). This enables the broker to offer users with a price of only 0.9$ which is lower than the on-demand prices of CSP (step 4). In reality, the broker can earn 1.9$, because he can charge 9.9$ and only need to pay 8$.

The challenge for the broker is how to exploit the price differences of on-demand and reserved resources from a cloud, so as to reduce his cost. Because every user dynamically submits his request, the aggregated request fluctuates with time. Policies for broker to rent instances from providers should be adapted accordingly. It is necessary to make the following decisions about renting instances, such as, on-demand launching or selecting an appropriate instance to reserve? How many instances and at what time to launch?

This paper aims to answer these questions. The main contributions are as follows:

• 1. We formulate the dynamic resource provision problem where the broker rents resources from a cloud service provider with multiple reserved instance terms.

• 2. A heuristic and an approximation algorithms are presented for the problem.

• 3. Extensive real world traces driven simulations demonstrate the effectiveness of both the algorithms. Significant resource cost saving can be achieved by using the algorithms.

The remainder of the paper is organized as follows. In Sect. 2 related work is reviewed. Section 3 formulates the problem. Section 4 and Sect. 5 present a heuristic and an approximation algorithms, respectively. They are evaluated in Sect. 6 and concluded in Sect. 7.

2 Related Work

Cloud Brokering has been proposed as a service and attracted plenty of attention in recent years [1, 15]. Cost minimization and profit maximization are two main topics being explored. To minimize cost, the authors of [18] explore the possibility to optimally place VMs across multiple clouds. The capacity of each cloud and the load balance are considered. Eight heuristic algorithms which differ in diverse criteria for assigning priorities to VMs requests are presented in [17]. The authors try to maximize the profit of a broker who sublets on demand resources to customers. It is extended in [10] and a distributed simulated annealing algorithm is recommended. Different from the granularity of VMs, data center based graph clustering algorithm is presented to minimize the cost of the broker, including nodes (data centers), intra-cloud bandwidth and inter-cloud bandwidth [4]. Broker mechanism is also recommended to make cooperation decisions so as to maximize the cooperated CSPs [19].

In addition to cost and profit, quality of service is another main concern. Aiming to meet the requirements of users, a multi-objective decision strategy [2] sorts CSPs by scoring all kinds of constraints, especially on the technology heterogeneity, and then chooses the CSP with the maximum score. Reaction time minimizing and profit maximizing are explored in [13]. Based on Pareto optimum theory, the author formalizes the broker scheduling problem as a multi-objective programming and solves it by a simplified multi-objective genetic algorithm. The placement of latency sensitive application in multiple CSPs environment is also studied [5]. The problem is formulated as a mixed-integer programming subject to the resource capacity, load balance and latency. Furthermore, two policies are given to address the faulty scenario of CSP. Based on different criteria, such as performance optimization, cost minimization and energy efficiency, the scheduling function of the broker is equipped with 0-1 integer programming based algorithm to select the optimal cloud to deploy a service. Modern portfolio theory is leveraged to choose an efficient broker policy so that the tradeoff between satisfying uncertain demand and risk of not delivering satisfied services is balanced [8]. A framework is proposed to select CSPs so that the quality of service is achieved by combining their trustworthiness and competence [9]. Trustworthiness is estimated by the historical record of quality or reputation. While competence is the claimed service level. However, the aforementioned works do not take into account the price difference between on-demand and reserved resources. The dynamic property of the request is also not captured.

Reserved resources provide a great opportunity for the broker to reduce his cost. A dynamic resource reservation strategy is recommended for broker to minimize cost [22, 23]. A dynamic programming is used to characterize the optimal solution. The original combinatorial problem is decomposed into a number of subproblems by using a set of recursive bellman equations and each is solved more efficiently. Two approximation algorithms are proposed for off-line and online scenarios, respectively. Especially, the off-line algorithm is proved as 2-approximate. Broker federation is explored in [14]. But all of them deem that there is only one reserved instance term. It is inconsistent with the practice of the cloud computing industry. This work explores dynamic resource provision with multiple reserved instance terms and just fills the gap.

3 Formulation

3.1 User Demand and CSP Pricing

User demand. Suppose a broker has an estimation of aggregated request up to a rather long period T. For any $t\in [1,T]$, the aggregated request at t is $d_t$. It is reasonable for each user should have a plan for the future request. The aggregation can be estimated based on the users’ plans [14, 23], or based on the historical requests. Let $L=max_t(d_t)$ is the peak request. We divide the demand $d_t$ into L levels. Define indicator $d_t^l$ to represent whether there is a demand at level l at billing cycle t, i.e., $d_t^l = 1$ if $d_t \ge l$, and 0 otherwise. For example, a demand curve is depicted in Fig. 2. $d_3^4 = 0$ because there is no demand at billing cycle 3 at level 4. This billing cycle is called as a vacant billing cycle. $d_5^5=1$, because there is a demand at billing cycle 5 at level 5. Obviously, $\sum \nolimits _{l=1}^{d_t}{d_t^l}=d_t$.

Fig. 2.

Demand curve and level by level reservation with three reserved instance terms, where $\{\tau _0,\tau _1,\tau _2\,\tau _3\}=\{1,3,6,10\}$, $\{c_0,c_1,c_2,c_3\}=\{1,2.5,3.8,6\}$. $T=9$. At level 1, $\tau _1$ and $\tau _2$ will be replaced by $\tau _3$ at last because $c_1+c_2>c_3$.

A demand curve is called convex if for any $t_0 \in [1,T]$, there is no other $t_1 \in [1,T], t_2 \in [1,T]$, such that $t_1<t_0<t_2$, $\sum \nolimits _{l = 1}^L{d_{t_1}^l} > \sum \nolimits _{l = 1}^L{d_{t_0}^l}$ and $\sum \nolimits _{l = 1}^L{d_{t_2}^l} > \sum \nolimits _{l = 1}^L{d_{t_0}^l}$. For example, in Fig. 2, the curve between time 1, 3 is convex.

CSP pricing. Suppose a CSP provides J increasing reserved instance terms $\tau _1,\tau _2,...,\tau _J$ (an instance with term $\tau _j$ is also called instance $\tau _j$ or term $\tau _j$ when there is no ambiguity, $j=1,...,J$), and all terms are longer than one billing cycle. The corresponding costs are $c_1,c_2,...,c_J$, respectively. Specifically, let $c_0$ denotes the on-demand price, hence $\tau _0$ is 1 which means one billing cycle. Then we have

(1) $c_0<c_1<...<c_J$. Namely, the longer the term, the bigger the cost. Otherwise, the short term with bigger cost can be replaced by the long term with smaller cost. It is unnecessary to set the shorter one.

(2) $c_0/\tau _0>c_1/\tau _1>...>c_J/\tau _J$. Namely, the longer the term, the cheaper the average price at each billing cycle. Otherwise, suppose for $i,j, (i<j)$, $c_i/\tau _i < c_j/\tau _j$. Then users can reserve $\tau _i$ by $\lceil \tau _j/\tau _i \rceil$ times to achieve the same resource with less cost and more capital flexibility.

3.2 Problem Formulation

Let $y_{ljt}$ is a boolean variable which indicates whether to allocate an instance $\tau _j$ at time t to serve the demand at this time at level l. It equals 1 if this demand is served by an instance $\tau _j$ rather than $\tau _0$, and 0 otherwise. For example, at level 2 in Fig. 2, $y_{223}=1$ because $\tau _2$ is reserved at time 3. All other $y_{2jt} = 0$. This problem can be formulated from the point view of levels.

$$\begin{aligned} \min&\sum \limits _{l=1}^L {{\sum \limits _{t=1}^T}{\sum \limits _{j=0}^J}{y_{ljt}c_j}}&\qquad \qquad \;\;\text {(0-1ILP)}&\nonumber \\ \text{ s.t. }&\sum \limits _{l = 1}^{d_t} ({\sum \limits _{j = 1}^J {\sum \limits _{i = t-\tau _j+1}^t{y_{lji}}}+y_{l0t}}) \ge d_t&{}{}t = 1, 2, \cdots ,T&\end{aligned}$$

(1)

$$\begin{aligned}&y_{ljt} \in \{0,1\}{}{} l = 0, 1, \cdots ,L, j = 0, 1, \cdots ,J,t= 1,2,\cdots ,T.&\end{aligned}$$

(2)

The objective is the total cost because whenever $\tau _j$ is reserved at any level, it should be charged $c_j$. In constraint (1), $\sum \nolimits _{j = 1}^J {\sum \nolimits _{i = t-\tau _j+1}^t{y_{lji}}}$ is the number of instances which remain effective until time t at level l. $y_{l0t}$ is the number of on-demand instances allocated at time t at level l. After calculating the sum of all levels, the left part of the constraint represents the number of all instances which can be used at time t. It should not be smaller than the demand $d_t$.

Programming 0-1ILP is a 0-1 integer programming and it belongs to one of the Karp’s 21 NP-complete problems [12]. Hence it is also NP-hard.

Now, for each level l ($l=1,2,...,L$), considering the following single level programming:

$$\begin{aligned} \min&{\sum \limits _{t=1}^T}{\sum \limits _{j=0}^J}{y_{ljt}c_j}&\qquad \qquad \qquad \,\text {(0-1ILPForLevel)}&\nonumber \\ \text{ s.t. }&\sum \limits _{j = 1}^J {\sum \limits _{i = t-\tau _j+1}^t{y_{lji}}}+y_{l0t} \ge d_t^l&{}{}t = 1, 2, \cdots ,T&\end{aligned}$$

(3)

$$\begin{aligned}&y_{ljt} \in \{0,1\}{}{}{}{}{}{}{}{}{}{}{}{} j = 0, 1, \cdots ,J, t= 1,2,\cdots ,T.&\end{aligned}$$

(4)

It is easy to check the feasible set of programming 0-1ILP and the intersection of the feasible set of all programming 0-1ILPForLevel are just the same. Let f(y) denotes ${\sum \nolimits _{t=1}^T}{\sum \nolimits _{j=0}^J}{y_{ljt}c_j}$. Suppose $y^*$ is the optimal solution for all programming 0-1ILPForLevel. That means, for any feasible solution of all 0-1ILPForLevel y, which is also feasible for 0-1ILP, we have $f(y) \ge f(y^*)$. So $\sum \nolimits _{l=1}^L{f(y)} \ge \sum \nolimits _{l=1}^L{f(y^*)}$. Thus

$$\begin{aligned} min \sum \nolimits _{l=1}^L{f(y)} \ge min \sum \nolimits _{l=1}^L{f(y^*)}=\sum \nolimits _{l=1}^L{f(y^*)}. \end{aligned}$$

(5)

The left part is just the optimal value of programming 0-1ILP. This motivates us to find the optimal solution of programming 0-1ILP level by level.

4 Heuristic Algorithm

4.1 Reservation Heuristic

With One Reserved Instance Term. We define $u^l=\sum \nolimits _{t = 1}^{T}{d_t^l}$, is the number of non-vacant billing cycles during period T at level l. In Fig. 2 $u^1$ = 8 because there is no demand at time 4. $u^5$ =1.

When there is only one reserved instance term $\tau _1$ with cost $c_1$, the periodic reservation mechanism is recommended [23]. Considering the simplest scenario where $T \le \tau _1$, because any reservation remains effective in T, the problem becomes trying to reserve instances as many as possible at time 1. At level 1, if $u^1c_0 \ge c_1$, that means compared to reserved instance with lower cost $c_1$, more expense is necessary if to launch $u^1$ on-demand instances. So we should reserve an instance $\tau _1$. Suppose $l-1$ instances have been reserved at bottom $l-1$ levels, then the l-th instance should be reserved only if $u^lc_0 \ge c_1$, i.e., $u^l \ge c_1/c_0$. Note that $u^l$ is non-increasing in l, we obtain a useful heuristic: reserve l instance at time 1 only if $u^l \ge c_l/c_0 > u^{l+1}$, if insufficient, launch other instances on demand. Because this heuristic finds the maximum l, for any level which is bigger than l, it is not economical any longer if adopting reservation policy.

In Fig. 3, considering the first scenario, where $T=3 < \tau$, $d_3^3 = 0$ because there is no demand at billing cycle 3 at level 3, so even there is a reservation, it will not be used. $d_2^5=1$, because there is a demand at billing cycle 2 at level 5. $u^2=3$, $u^3=2$, $c_1/c_0=2.5$, $u^2>c_1/c_0>u^3$, so we reserve 2 instances at time 1.

Fig. 3.

Periodic reservation mechanism.

If $T>\tau _1$, T is divided into intervals and each with a length of $\tau _1$. The upper heuristic is used in each intervals. In the upper figure, the demand curve where $T=7$ is divided into 3 intervals.

With Multiple Reserved Instance Terms. When there are multiple reserved instance terms, it is impossible to find an appropriate term in advance to facilitate the periodic reservation. A new mechanism is necessary to address the problem. First, we give some notions to facilitate the mechanism presentation.

Length of each level. Note that the length of each level may be different. For level l, the length of this level is the number of billing cycles between the first demand time and the last demand time at level l, i.e.,

$$\begin{aligned} T^l=b_l-e_l+1, \end{aligned}$$

(6)

where $b_l=min\{t|d_t^l = 1\}, e_l=max\{t|d_t^l = 1\}$ are the first demand time and the last demand time, respectively. In Fig. 2, $[b_1,e_1]=[1,9],T^1=9$, $[b_2,e_2]=[3,9],T^2=7$.

Residue length of each level. For level l, let $b'$ denotes the current non-vacant beginning time, then the residue length of this level is

$$\begin{aligned} T^{Rl}=e_l-b'+1. \end{aligned}$$

(7)

If beginning from $b^l$, $T^{Rl}=T^l$.

Note that given a level l, it is still economical to reserve a $\tau _j$ instance if

$$\begin{aligned} u_I^lc_0 \ge c_j, \end{aligned}$$

(8)

where $u_I^l = \sum \nolimits _{t \in I} {d_t^l}$, $I=[b,b+\tau _j]$. b is any given beginning time in the residue interval at this level and its initial value equals 1.

Feasible term. Given a level l with residue length $T^{Rl}$, a term $\tau _j$ $(j \ge 1)$ is called feasible if $\tau _j \le T^{Rl}$ and inequation (8) holds.

Beginning time update. At each level, we try to find the longest feasible term from the beginning of the level, i.e., $b_l$. Let $b'$ denotes the current beginning. Suppose the longest feasible term is $\tau _h$ ($h \ge 1$) if it is found, or even $\tau _1$ is still not feasible, then the beginning time is moved backward to find the next longest feasible term. The next beginning time can be determined as follows:

$$\begin{aligned} b = min\{t| d_t^l = 1, t \ge b'+\tau _h\}, \end{aligned}$$

(9)

where $h=1$ if there is no feasible term or $\tau _1$ is the longest feasible term. Namely, the first demand time after the current interval. For example, in Fig. 2, at level 1, the first beginning time is 1 and the second beginning time is 7.

4.2 Level by Level Reservation Algorithm

We adopt a level by level reservation mechanism. Of course, every time the term with the lowest average price (i.e., the longest term) is preferred to others which also meet (8). If this longest term is shorter than the length of this level $T^l$, then the upper mechanism is repeated in the residue interval. It is detailed in Algorithm 1.

The first For loop (Lines 1–31) checks the demand level by level. At each level, If the residue length of the level is bigger than $\tau _1$, the While loop (Lines 3–15) tries to reserve the longest term. The second For loop checks all the terms which are shorter than the residue length in a decreasing order (Lines 5–14). If a longer term is feasible, then we reserve such an instance and the related parameters are updated. Otherwise, we try the shorter instance, until we find one (Lines 7–10) or all the reservations are not economical (Lines 11–13). The beginning time is moved backward to begin a new interval try. For example, in Fig. 2, a $\tau _2$ and then a $\tau _1$ instance are reserved at level 1. The process is repeated until $T^{Rl}$ is shorter than the shortest term $\tau _1$. Then we decide whether to reserve $\tau _1$ or serve the residue demands by on-demand instances (Lines 16–23). In Fig. 2, the demand at time 9 can only be served by an on-demand instance since there is no feasible term.

Suppose at level l, $\tau _j$ is the shortest term which is bigger than $T^l$. Then it is possible that the cost of $\tau _j$ is smaller than the current total cost at this level. Since it can meet the demand at this level, we will check it so as find a lower cost (Lines 24–27). As in Fig. 2, $\tau _1$ and $\tau _2$ at level 1 are replaced by $\tau _3$ finally.

Because $u_I^l$ is non-increasing of l, if no term is feasible in interval I at level l, then there is no feasible term in interval I at upper levels. It is necessary to check so that the program terminates in time (Lines 28–30), or after all levels are traversed. Any demand which cannot be served by reserved instance should be served by the on-demand instance.

It is easy to show the time complexity of 3LTPD is O(LTJ). If bisearch is used to seek the longest feasible term, then O(LT log J) time is required.

The next theorem demonstrates that for the convex demand, this algorithm can find a 2-approximation solution.

Lemma 1

For each level, algorithm 3LTPD finds a 2-approximation solution when the demand is convex.

Proof

Suppose there are J reserved instances with increasing terms $\tau _1,\tau _2,...,\tau _J$ and increasing cost $c_1,c_2,...,c_J$, where $c_1/\tau _1 > c_2/\tau _2 > ... > c_J/\tau _J$. $c_0$ is the on-demand price. $T^l$ is the length of this level. Let j is the biggest one for which $\tau _j \le T^l$. $C^{Al}$ is the cost of level l incurred by algorithm 3LTPD and $opt^l$ is the optimal cost of level l. When the demand is convex, then the algorithm tries to fill the level by $\tau _j$ because it is the cheapest. Suppose $o^l$ is the number of on-demand instances to be launched. We have $C^{Al} = \lfloor T^l/\tau _j \rfloor c_j + min\{o^lc_0,c_j\}$, $opt^l \ge \lfloor T^l/\tau _j \rfloor c_j$. So $\frac{C^{Al}}{opt^l} \le \frac{min\{\lfloor T^l/\tau _j \rfloor c_j + min\{o^l c_0,c_j\},c_{j+1}\}}{\lfloor T^l/\tau _j \rfloor c_j} \le \frac{min\{(\lfloor T^l/\tau _j \rfloor +1)*c_j,c_{j+1}\}}{\lfloor T^l/\tau _j \rfloor *c_j} \le \frac{(\lfloor T^l/\tau _j \rfloor +1)*c_j}{\lfloor T^l/\tau _j \rfloor *c_j} \le \frac{2\lfloor T^l/\tau _j \rfloor *c_j}{\lfloor T^l/\tau _j \rfloor *c_j} =2$. The fourth inequality is due to $T^l/\tau _j \ge 1$.

Theorem 1

For the brokering problem, algorithm 3LTPD finds a 2-approximation solution when the demand is convex.

Proof

Let $C^{A}$ is the cost of 0-1ILP incurred by 3LTPD, opt is the optimal cost of 0-1ILP and $opt^l$ is the optimal cost of level l. Based on inequality (5), for any feasible solution y for 0-1ILP, $\sum \nolimits _{l=1}^L{f(y)} \ge \sum \nolimits _{l=1}^L{f(y^*)}$. So $opt \ge \sum \nolimits _{l=1}^L{opt^l}$. We have $\frac{C^A}{opt} = \frac{\sum \nolimits _{l=1}^L{C^{Al}}}{opt} \le \frac{2\sum \nolimits _{l=1}^L{opt^l}}{\sum \nolimits _{l=1}^L{opt^l}} =2$where the inequality is due to Lemma 1.

5 Set Cover Based Approximation Algorithm

Given a level l, denote all non-vacant billing cycles at this level as set $S^l$ whose element is the single non-vacant billing cycle. Taking all reserved and on-demand instances as a subset family $\tau =\{\tau _0,...,\tau _J\}$, where each subset $\tau _j$ is attached with a cost $c_j$, then the cost minimization resource provision can be viewed as a cost minimization set cover problem. In this set cover problem, subset from $\tau$ can be repeatedly selected to cover $S^l$. Define the cost effectiveness for each $\tau _j$ at interval I as $e_j=c_j/u_I^l$ (I and $u_I^l$ are as in inequation (8)). Then a simple algorithm based on set cover greedy algorithm (Chap. 1 of [20]) is adapted as follows. Each time it selects the feasible term (Sect. 4.1) with the lowest $e_j$ from $\tau$ until $S^l$ is covered. We call such term as the cheapest feasible term.

Suppose that the optimal cost of level l is $opt^l$. Obviously, if the optimal term is longer than $T^l$ then cost found by Algorithm 2 is the same as $opt^l$. Thus Lemma 3 is established. So we only consider the case where the optimal terms are all smaller than $T^l$. Similar to the corresponding proof in Chap. 1 of [20], it is easy to prove the following theorems. Number the billing cycles at level l in the sequence of covering as $1^l,...,u^l$, we have

Lemma 2

Given level l, for any $k \in {1^l,...,u^l}$, $e_k \le opt^l/(u^l-k+1)$ if the solution is not a term which is longer than $T^l$.

Proof

Note that the optimal term must be feasible term, otherwise it can be replaced by any feasible ones and thus lead to a smaller cost.

Suppose $opt^l$ is the optimal cost of level l. Because $S^l$ can be covered by the optimal terms, during any iteration of Algorithm 2, the residue subset must can be covered by some terms with cost at most $opt^l$. Suppose the number of residue non-vacant billing cycles is r, then the average cost effective of the optimal terms is $opt^l/r$. So there must exists terms with cost effectiveness at most $opt^l/r$, during the iteration when k is covered, and the number of residue non-vacant billing cycles must be at most $u^l-k+1$ elements, i.e. $r \ge u^l-k+1$. Because in this iteration, the smallest cost effectiveness is selected, we have $e_k \le opt^l/r \le opt^l/(u^l-k+1)$.

Lemma 3

Algorithm SCBA gets a $H(u^l)-$ approximation for each level, where $H(u^l)=1+1/2+...+1/{u^l}$.

Proof

If the solutions are some feasible terms, the cost incurred by Algorithm 2 is $\sum \nolimits _{k=1}^{u^l}{e_k}$. Based on Lemma 2, we know the cost is at most $(1+1/2+...+1/{u^l}) opt^l$. If the solution is a term which is longer than $T^l$, the cost is smaller than that of feasible terms found by the algorithm, and we get it.

Based on Lemma 3, similar to the proof of Theorem 1, it is easy to get

Theorem 2

Algorithm SCBA finds a $H(m)-$ approximation for problem 0-1ILP, where $m = max_l{H(u^l)}$.

Note that the only difference between 3LTPD and SCBA is the criterion to select the feasible term every time. The former selects the longest feasible term and the latter need to calculate the cost effectiveness for all feasible terms and then choose the smallest one. So SCBA will not run faster than 3LTPD as shown in experiments. For a general cost minimization set cover problem, it is proved that the greedy algorithm is tight. But maybe it is not true for the brokering problem where the set has a special structure. The next experiment demonstrates that 3LTPD can perform as well as SCBA.

6 Experimental Evaluation

6.1 Experiments Setup

Since public cloud workloads are often confidential, no real IaaS data trace is released so far. So we use Parallel Workloads Archive [7], a repository of job-level usage data from large scale parallel supercomputers, clusters and grids, to evaluate the performance of our algorithms. Four traces logs corresponding to four Intel Netbatch grid clusters, three on the west coast in the US and one in Israel, are used. Each log file contains one month’s (i.e., November 2012) accounting records. The original logs are available as Intel-NetbatchX-2012-0 (where “X” is A, B, C, or D for the four different clusters). In experiments, we use A, B, C and D to represent the four data sources, respectively.

User demand and data preprocessing. Since the billing cycle is an hour, the demand at each billing cycle is rounded up, i.e., only when the lifetime of the request falling within the billing cycle is longer than 30 min, the request is counted as one demand.

Fig. 4.

Demand curves of four data sources.

Fig. 5.

Demand volume and fluctuation.

The four data sources have different demand volumes and fluctuations. The corresponding demand curves are depicted in Fig. 4. The peak hourly demands are more than 13k, 23k, 16k and 25k for the four data, respectively. Figure 5 demonstrates the mean values and standard deviations. Generally speaking, data A has the smallest demand and D has the biggest demand. B and C have modest demand and B requests more than C. The fluctuation has almost the same tendency.

Parameter setting. The duration of the data trace is a month. Because there are no data at the beginning and end time of the month, we set T as the duration in which data are available, i.e., $T=712$ h.

Table 1. Two groups of resources

Suppose there are two groups of resources represented by CSP 1 and CSP 2, each with the following terms and prices as demonstrated in Table 1. The on-demand price is borrowed from that of Amazon E2C m3.media with Windows operation system. Limited by the duration of data source, the reserved instance term is shortened accordingly. The cost discount is within the range of business CSP (about 60 % discount for 3-year term for Amazon). For convenience of comparison of the saving cost, the same on-demand price is adopted for the two groups. Note that the terms of CSP 2 are relatively longer than that of CSP 1. This setting can reveal the factors affecting the resource cost¹.

The simulation environment is set up in a Java platform. The platform is running on a PC (Lenovo Think Centre M4350t-N020Intel(R) Core(TM) i5-3470 CPU @ 3.20GHz8G RAM).

6.2 Experimental Results

To evaluate the cost saving of the broker and the proposed algorithms, five different schemes, including the proposed two algorithms are compared. For the scenario without broker, (1) longest preference for each user’s request (abbreviated as N/B LP): select the longest reserved instance term for a continuous demand every time and traversing vacant demand is prohibited. The feasible longest term is used because obviously that the shorter term will incur more cost; (2) all demand is served by on-demand instances (abbreviated as N/B OnD). In the scenario with a broker, (1) similar as N/B LP except that it operates on the aggregated demand curve (abbreviated as W/B LP); (2) 3LTPD; (3) SCBA.

Performance Evaluation. We exploit resources from CSP 1 or CSP 2 to serve the requests from data source A, B, C and D. The resource cost is depicted in Fig. 6. In Fig. 6(b) and (d), the cost of on-demand is used as the baseline to calculate the saving percentage.

Fig. 6.

Cost efficiency when exploiting resources from different CSP.

Since the demand volumes of four data differ, the total costs are also different. From Fig. 6(a) and (c) we can find whichever group of resources is exploited, the total costs demonstrate the similar tendency as that of the demand volume in Fig. 5. Overall, more demand incurs more cost for all five schemes.

Even when there is no broker and the demands are not multiplexed, it is still efficient to use the reserved instances as more as possible. As illustrated in Fig. 6(b) and (d), the scheme that tries the longest term (N/B LP) saves more cost. For CSP 1, it leads to an average saving up to 3.81 %. While 2.30 % for CSP 2. The reason lies in that the terms of CSP 1 are relatively shorter than that of CSP 2. When the demands are not multiplexed, the lifetime of single user’s request is shorter, so the relatively longer terms of CSP 2 cannot be fully used. It reveals the effect of terms on resource cost.

However, after multiplexing by a broker, it demonstrates a contrary situation when the proposed 3LTPD is leveraged. On average, 27.23 % and 24.26 % cost are saved for CSP 2 and CSP 1, respectively. This is because that the aggregated request becomes longer and 3LTPD prefers the feasible longest term every time. Thus the relatively longer terms of CSP 2 can do better. Although W/B LP scheme also prefers the longest term, it does not use the heuristic. So, though it saves more than N/B LP, it is still not more efficient than 3LTPD. This also shows that 3LTPD can enable economical utilization of longer terms across vacant billing cycles.

The fluctuation of demand has an effect on the cost as well. Because the more volatile the demand is, the more demand valleys exist, fluctuation hinders the utilization of longer terms. It is detailed in Table 2. Note that the cost saving has the same tendency as that of the standard deviation curve in Fig. 5 when the W/B LP scheme is used: the more fluctuant, the more cost is saved. But 3LTPD can mitigate the negative effect of fluctuation. In total, the gap between cost saving for different data is reduced, though most cost is saved for data D.

Table 2. Saving percentage with broker relevant to fluctuation

Fig. 7.

Cost efficiency when more reserved instance terms are exploited.

Figure 7 further justifies the benefit of exploiting multiple terms for 3LTPD. Herein all the terms of CSP 1 and CSP 2 are viewed as available for the algorithm and hence more candidate terms can be chosen. Figure 7(a) and (b) plot the cost and saving percentage when all terms are used. Comparing with Fig. 6, it is shown that more terms lead to more cost saving. Especially, we compare the resource cost efficiency for 3LTPD in Fig. 7(c) and (s). When all terms of both CSPs are used, up to 46 thousand dollars (5 %) are saved compared with that when only the terms of CSP 1 are used, and 19 thousand dollars (2 %) are saved compared with CSP 2. This is due to that more terms lead to higher applicability to dynamic demands.

It is noteworthy that for all data sources, although we can only prove 3LDPP is 2-approximation for the convex demand curve, 3LDPP performs almost exactly the same as SCBA for all data sources.

Fig. 8.

Time efficiency when exploiting resources from different CSP.

Running Time Efficiency Evaluation. Running time of the algorithms is compared in Fig. 8. The running time of algorithms which exploit terms from CSP 1, CSP 2 and both of them are depicted in Fig. 8(a), (b) and (c), respectively. All the three figures show a common pattern. The on-demand algorithm takes the least time. N/B LP takes more time because it seeks the longest term each time for each user. But after multiplexing the demand of each user by the broker, the longest preference scheme (W/B LP) runs faster than N/B LP. This lies in that the broker aggregates users’ request and thus reduces the number of times to find the longest term. SCBA and 3LTPD run slower than the former three schemes. Since SCBA computes the cost effectiveness for each feasible term and then selects the smallest one, 3LTPD only selects the longest feasible term, 3LTPD runs almost twice as fast as SCBA. Recall that 3LTPD and SCBA exhibit almost the same performance (Figs. 6 and 7), the superiority of 3LTPD is demonstrated.

7 Conclusion

Considering the multiple reserved instance terms, two algorithms are presented to facilitate broker to utilize infrastructure resources from public CSP at the least cost. One is heuristic and another is an approximation algorithm. Extensive traces driven evaluation demonstrates the effectiveness of both the algorithms. Our future work aims to exploit resources from multiple CSPs. In this scenario, though there are more candidate terms, there is also interoperability which impedes the multiplexing effect. How to balance the contradiction to achieve an efficient scheme is a great challenge.