Heat Transfer in Suspension Plasma Spraying

Abstract

Suspension plasma spraying (SPS) is an emerging thermal spray processes. Its specific feature is to use a suspension that is a heterogeneous mixture of very fine particles in an aqueous or organic solvent, to achieve finely structured coatings. The latter have a great potential for demanding applications like solid-oxide fuel cells or thermal barriers in gas turbines. The suspension feedstock is injected radially or axially into a DC plasma jet in the form of a spray of droplets with size of 20–200 μm or a continuous jet. The interaction of the suspension drops/jet with the high-temperature high-velocity plasma jet results in their fragmentation into small droplets and vaporization of solvent in a few microseconds. Subsequently, the solid particles are accelerated, heated, and melted by the plasma jet and rapidly flatten and solidify after impact on the substrate. Although this process has been investigated for about 20 years, the effect of process operation parameters and mechanisms are not fully understood yet. In this chapter, the phenomena involved in suspension plasma spraying process, the basic aspects in the simulation of this process, as well as the main technological challenges are described in detail. Different correlations for suspension properties, liquid penetration height in gaseous crossflow, effervescent atomizers, droplet/particle drag coefficient, and Nusselt number, as well as the importance of coating particles’ Stokes number are discussed. Moreover, various methods for plasma jet modeling, the specific volume of fluid approach for modeling the liquid-plasma jet interaction, the commonly used secondary breakup models, and an approach for modeling suspension droplet based on a multicomponent assumption are reviewed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Conventional plasma spraying uses powders of particle size between 10 and 100 μm to produce coatings with a characteristic microstructural dimension in the micrometer range. This dimension corresponds to the thickness of the lamellae formed by the impact of the molten particles on the substrate. If it were possible to spray nano- and submicron-sized particles, the resulting coatings would have a smaller characteristic length scale, and this would result in improved wear resistance, enhanced thermal insulation and thermal shock resistance, and superior superhydrophobicity and catalytic behavior (Killinger et al. 2011; Fauchais et al. 2011; Aghasibeig et al. 2014). However, the use of nano- and submicron-sized particles in conventional plasma spray techniques is challenging for the following reasons:

• 1. Possible clogging of the feed line because of the natural tendency of fine particles to agglomerate

• 2. The difficulty of injecting fine particles in the core of a high-temperature high-velocity gas jet because the injection force of particles has to be of the same order of magnitude as the force imparted by the gas flow (S.ρ.v², where S is the cross section of the injected particle, ρ the specific mass of the plasma, and v the particle velocity)

• 3. The low inertia of the fine particles that may result in their following the gas streamlines instead of impacting on the substrate (Jadidi et al. 2015a)

There are two techniques called suspension and solution precursor plasma spray used to address the two first issues stated above (Fauchais et al. 2011; Pawlowski 2009). The basic idea of these techniques is to use a conventional plasma spray system but replace the powder carrier gas by a liquid whose density is about 1000 times greater than that of the gas.

Suspensions are a combination of nano−/submicron-sized particles, a liquid carrier (e.g., water or alcohol), and usually a dispersant (Pawlowski 2009). Solutions are made by dissolving metal salts, organometallic precursors, or liquid metal precursors in a solvent so that the submicronic particles are formed in flight. This chapter will be limited to suspension plasma spraying that, a priori, does not involve chemistry in the in-flight treatment of the suspension particles. Detailed information about solution precursor plasma spray can be found in the following review papers (Gell et al. 2008; Killinger et al. 2011; Jordan et al. 2015; Vardelle et al. 2016).

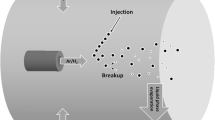
Suspensions are commonly injected into the plasma flow issuing from a plasma torch in the form of fine droplets by using spray atomization (Fig. 1a) or in the form of a continuous liquid jet by using mechanical injection (Fig. 1b). In this second injection method, the high-velocity plasma crossflow causes the atomization of the liquid jet. Depending on the type of plasma torch used, the liquid feedstock can be injected into the plasma jet either radially or axially (Fauchais et al. 2008; Curry et al. 2014).

Fig. 1

Radial external injection of a suspension into a high-temperature high-velocity plasma flow: (a) spray atomization and (b) mechanical injection (Fauchais et al. 2008; Curry et al. 2014)

The suspension droplet evolution in a high-temperature high-velocity gas flow is shown schematically in Fig. 2 (Pawlowski 2009). When the droplets or liquid jet penetrate into the plasma flow, they are subjected to a strong shear stress by the plasma flow and a very high heat flux. The former causes the fragmentation of the liquid feedstock and the latter its vaporization. However, the characteristic time scales of fragmentation and vaporization differ by at least two orders of magnitude: the liquid feedstock is first atomized by the jet (primary and secondary breakup) and then the liquid evaporation becomes dominant freeing the fine solid particles or agglomerates which are then accelerated, heated up, and melted by the gas flow before impact on the substrate (Fazilleau et al. 2006; Pawlowski 2009; Fauchais et al. 2010). It is worth mentioning that, the suspension vaporization includes complex phenomena and different scenarios such as shell formation, and micro-explosion may happen as comprehensively discussed in Jadidi et al. (2015a).

Fig. 2

A schematic of a suspension droplet evolution in a high-temperature high-velocity gas flow (Pawlowski 2009)

The microstructure of the coating and its properties depend on the distributions of temperature, velocity, and size of the particles impacting on the substrate which in turn depend on the trajectory of the suspension droplets in the plasma jet and therefore on the primary and eventually secondary breakup of the suspension (Fazilleau et al. 2006; Pawlowski 2009). These phenomena strongly depend on the injector type, and angle and location of the injector. Moreover, the suspension properties and injection velocity combined with the characteristics of the plasma jet control the penetration of the suspension into the gas flow and ensuing breakup and evaporation phenomena (Jadidi et al. 2015a). In the following sections, the suspension properties, primary and secondary breakup, and suspension evaporation phenomena are explained in more details.

2 Suspension Properties

The key properties of a suspension are its density, viscosity, surface tension, specific heat, thermal conductivity, and heat of evaporation of the solvent. They control to a great extent, the behavior of the suspension in the plasma jet. These properties depend on the solid particle concentration, type, size and shape, solvent type, surfactant concentration and composition, suspension acidity (pH), and temperature (Schramm 1996; Litchfield and Baird 2006; Gadow et al. 2008; Yu et al. 2008; Ghadimi et al. 2011; Tanvir and Qiao 2012).

The most used solvents are distilled/deionized water, alcohols, or water-alcohol mixtures. Empirical correlations as well as a few theoretical equations allow the prediction of suspension properties. However, these correlations are usually developed for particular conditions, for example, for a given solid particle concentration and size (Schramm 1996; Litchfield and Baird 2006; Yu et al. 2008; Ghadimi et al. 2011; Tanvir and Qiao 2012). The most prominent correlations for predicting the suspension properties are presented below.

The density (ρ) and specific heat (C) are defined,

$$ \uprho =\left(1-{\alpha}_p\right){\uprho}_l+{\alpha}_p{\uprho}_p $$

(1)

$$ C=\left(1-{\alpha}_p\right){C}_l+{\alpha}_p{C}_p $$

(2)

$$ \uprho C=\left(1-{\alpha}_p\right){\uprho}_l{C}_l+{\alpha}_p{\uprho}_p{C}_p $$

(3)

where α_p, ρ_p, and C_p are the solid particle volume fraction, density, and specific heat, respectively, and, ρ_land C_l are the liquid density and specific heat, respectively (Ghadimi et al. 2011; Fan and Zhu 1998). Equations 2 and 3 are both widely used in the literature to calculate the suspension specific heat.

The suspension viscosity is generally higher than the solvent viscosity. Moreover, a Newtonian-base liquid can exhibit a non-Newtonian behavior at low to high particle concentrations (i.e., the suspension is usually pseudoplastic at low to moderate particle concentration and can be dilatant at high particle concentration). However, when the base liquid is Newtonian and particle concentration is very low (i.e., dilute suspension), the suspension behaves as a Newtonian fluid (Schramm 1996). The following correlations are used to calculate the suspension viscosity (μ) as a function of the solid particle volume fraction (α_p) and base liquid viscosity μ₀ (Schramm 1996; Litchfield and Baird 2006),

$$ \upmu ={\upmu}_0\left(1+2.5{\upalpha}_{\mathrm{p}}\right) $$

(4)

$$ \upmu ={\upmu}_0\left(1+2.5{\upalpha}_p+10.5{\upalpha_p}^2+0.00273\exp \left(16.6{\upalpha}_{\mathrm{p}}\right)\right) $$

(5)

For anisometric particles,

$$ \upmu ={\upmu}_0\left(1+a{\upalpha}_p/1.47b\right) $$

(6)

where a and b are the major and minor dimensions of the particle. Equations 4–6 are applied to dilute Newtonian suspensions (i.e., α_p < 1%) where the particle size is in the range of submicron and micron and no strong electrostatic interactions exist between particles.

To estimate the viscosity of dilute and dense suspensions, the Kitano et al.’s (1981), Krieger-Dougherty, and the modified Krieger-Dougherty equations are generally used (Krieger and Thomas 1957; Chen et al. 2007),

$$ \upmu ={\upmu}_0{\left(\frac{1}{1-{\upalpha}_p/{\upalpha}_{pm}}\right)}^2 $$

(7)

$$ \upmu ={\upmu}_0{\left(\frac{1}{1-{\upalpha}_p/{\upalpha}_{pm}}\right)}^{\eta {\upalpha}_{pm}} $$

(8)

$$ \upmu ={\upmu}_0{\left(\frac{1}{1-{\upalpha}_p{\left({\mathrm{r}}_{\mathrm{a}}/\mathrm{r}\right)}^{1.2}/{\upalpha}_{pm}}\right)}^{2.5{\upalpha}_{pm}} $$

(9)

where α_pm is the maximum packing volume fraction (it generally ranges between 0.495 and 0.54 and can reach 0.605 and 0.3 for spherical and rodlike particles, respectively), η is the intrinsic viscosity (which is equal to 2.5 for monodispersed hard spherical particles), and r and r_a are the radii of primary and aggregated particles, respectively (Pabst 2004; Mishra et al. 2014). Using α_pm, the particle properties such as size distribution, shape, and porosity can all be considered (Pabst 2004; Litchfield and Baird 2006). Although the above correlations are applicable for a wide range of α_p, they are not accurate when the particle size is less than 100 nm (Mishra et al. 2014).

The thermal conductivity of a suspension is generally greater than that of the solvent. The Maxwell correlation can be used to predict the suspension thermal conductivity (Kleinstreuer and Feng 2011),

$$ \kappa ={\kappa}_l+{\kappa}_l\frac{3{\upalpha}_p\left({\kappa}_p-{\kappa}_l\right)}{\kappa_p+2{\kappa}_l-{\upalpha}_p\left({\kappa}_p-{\kappa}_l\right)} $$

(10)

where κ_l and κ_p are the thermal conductivity of the liquid and solid phases, respectively. However, this correlation is only appropriate for dilute suspensions (i.e., α_p < 1%) of relatively large particles. If the particle size is less than 100 nm, other empirical correlations should be used (Yu et al. 2008; Ghadimi et al. 2011).

The Hamilton-Crosser model makes possible to take the particle shape into account (Tavman et al. 2008),

$$ \frac{\kappa }{\kappa_l}=\frac{\kappa_p+\left(n-1\right){\kappa}_l-\left(n-1\right)\left({\kappa}_l-{\kappa}_p\right){\upalpha}_p}{\kappa_p+\left(n-1\right){\kappa}_l+\left({\kappa}_l-{\kappa}_p\right){\upalpha}_p}, \quad n=\frac{3}{\psi } $$

(11)

where ψ is a sphericity factor (i.e., ψ = 1 for spherical particles). When the particle size is less than 100 nm, the Hamilton-Crosser model is modified as follows (Chen et al. 2009),

$$ \frac{\kappa }{\kappa_l}=\frac{\kappa_a+\left(n-1\right){\kappa}_l-\left(n-1\right)\left({\kappa}_l-{\kappa}_a\right){\upalpha}_p{\left({r}_a/r\right)}^{1.2}}{\kappa_a+\left(n-1\right){\kappa}_l+\left({\kappa}_l-{\kappa}_a\right){\upalpha}_p{\left({r}_a/r\right)}^{1.2}} $$

(12)

where κ_a is the aggregate thermal conductivity calculated with the following correlation,

$$ \begin{array}{ll}& \frac{\kappa_a}{\kappa_l} = \frac{1}{4} \left\{\left(3{\alpha}_{in}-1\right)\frac{\kappa_p}{\kappa_l}+\left(3\left(1-{\alpha}_{in}\right)-1\right)+\sqrt{{\left(\left(3{\alpha}_{in}-1\right)\frac{\kappa_p}{\kappa_l}+\left(3\left(1-{\alpha}_{in}\right)-1\right)\right)}^2+8\frac{\kappa_p}{\kappa_l}}\right\}, \\ & \qquad \quad {\alpha}_{in}={\left(\frac{r_a}{r}\right)}^{-1.2}\end{array} $$

(13)

The suspension surface tension depends on the solid particle volume fraction, material and size, and surfactant type and concentration, base liquid, and temperature (Tanvir and Qiao 2012). The experimental data proposed in the literature present inconsistencies regarding whether it decreases or increases compared to that of the base liquid (Brian and Chen 1987; Tanvir and Qiao 2012; Bhuiyan et al. 2015; Chinnam et al. 2015) and therefore, the suspension surface tension should be experimentally determined. Although the effect of particles on the suspension surface tension is not clear yet, it was found that adding surfactant resulted in a reduction of surface tension compared to that of the pure-liquid value (Kihm and Deignan 1995; Tanvir and Qiao 2012). In addition, the surface tension of surfactant solution is time dependent because the surfactant molecules require a certain time to reach the gas-liquid interface and change the surface tension. Depending on the concentration and composition of surfactants, this time can vary from a few milliseconds to days. Therefore, the static (equilibrium) and dynamic surface tensions are generally defined for surfactant solutions (Kihm and Deignan 1995; Jadidi et al. 2015a). By increasing the concentration of surfactant, the static surface tension decreases and reaches its minimum value at a certain surfactant concentration named as the critical micelle concentration (CMC) (Kihm and Deignan 1995). As the surfactant concentration goes further than the CMC, the static surface tension remains relatively constant. The dynamic rather than the static surface tension is involved in the breakup of suspensions (Kihm and Deignan 1995). To determine the dynamic surface tension, a simple, accurate, and inexpensive method is measuring the characteristics (e.g., interface shape and wavelength) of an oscillating free jet emerging from an elliptical injector, and inputting the experimental data in an analytical model (Ronay 1978; Bechtel et al. 1995, 1998, 2002; Howell et al. 2004).

Finally, an important characteristic of the suspension is the enthalpy of vaporization of the solvent as the liquid vaporization cooled down the plasma jet according to its heat of vaporization; for example, the latter is 2260 kJ/kg for water and 841 kJ/kg for ethanol.

3 Plasma Jet Modeling

The suspension plasma spray (SPS) process can be considered to consist of the following subsystems: plasma jet formation in the plasma torch, liquid feedstock injection in the plasma jet, suspension treatment and formation of the coating on the substrate.

Conventional plasma spray uses a direct current nontransferred plasma torch to produce a high temperature and high-velocity plasma jet by conversion of electrical energy into chemical and thermal energy. The most used plasma torches consist of a rod-shaped doped-tungsten cathode with a conical tip and a concentric water-cooled copper anode. The arc issuing from the tip of the cathode attaches to the anode by at least one high-temperature, low-density gas column through the cold gas boundary layer that develops on the water-cooled anode wall. The cold gas flow in the boundary layer exerts a pulling down drag force on the hot column while the Lorentz forces may act in the same or opposite direction depending on the curvature of the arc attachment column. Under the combined actions of these forces but also effect of thermal and acoustic phenomena, the arc root moves on the anode surface. This movement brings about variations in the arc length and, therefore, in arc voltage that result in variations in the enthalpy input to the gas, velocity of the plasma jet and the way it mixes with the ambient gas when issuing from the torch.

The plasma jet produced by a conventional DC plasma torch has a specific enthalpy between 5 MJ/kg and 35 MJ/kg. Its maximum temperature at the nozzle exit is around 10,000–12,000 K and its maximum velocity between 400 m/s and 2600 m/s. The plasma-forming gas is either a gas with a high-atomic weight (Ar, N₂) or a mixture of these gases with a gas of higher thermal conductivity (H₂, He) or viscosity (He). The use of diatomic gases (N₂, H₂) results in an increase in the plasma enthalpy with the addition of molecule dissociation energy.

The time-evolution of the voltage difference between the electrodes (Δϕ) makes it possible to investigate the arc behavior inside the plasma torch. The arc operation mode is commonly referred as steady, takeover, and restrike mode depending on the transient features of Δϕ (Trelles et al. 2006; Meillot et al. 2009). These modes are schematically depicted in Fig. 3. The steady mode is characterized by a relatively small voltage difference between the electrodes (Δϕ) with negligible time fluctuations. The takeover mode is characterized by larger values of Δϕ and presents periodic or quasi-periodic voltage fluctuations, while the restrike mode is characterized by more chaotic, large amplitude voltage fluctuations with a characteristic saw-tooth shaped voltage evolution (Trelles et al. 2006; Meillot et al. 2009).

Fig. 3

Classification of DC plasma arc modes based on the time-evolution of the voltage difference between the electrodes (Δϕ) (Trelles et al. 2006)

The steady arc mode is characteristic of a stable plasma jet issuing from the nozzle but causes rapid erosion of the anode, whereas the restrike mode results in a highly fluctuating plasma jet which enhances turbulence development in the plasma jet and its mixing with the surrounding cold gas. This mode is promoted by the use of diatomic gases and high gas flow rate. The ensuing fluctuations of the plasma jet issuing from the torch affect the injection and processing of the suspension and in particular when the suspension is injected radially in the plasma jet. Indeed, the low density of the liquid and small inertia of the fine particles makes them very sensitive to the space- and time-variations of the plasma jet.

The modeling of the suspension plasma process is generally based on the modeling of the plasma jet issuing from the plasma torch and the treatment of the suspension within the plasma jet. However, at least two questions arise: (i) is it necessary to model the plasma formation in the plasma torch and (ii) does the plasma jet model need to take into account the time and space fluctuations of the plasma jet?

The prediction of arc behavior and plasma jet formation in the plasma torch is based on the simultaneous solution of the Navier-Stokes equations (gas mass, momentum, and species), energy conservation equation (gas temperature), and the Maxwell equations (electric and magnetic fields). The more advanced models take into account the nonlocal thermal equilibrium (NLTE) that prevails close to the electrodes by using two energy equations, for electrons and heavy species, respectively (Trelles et al. 2007). The set of equations is described in details in Trelles et al. (2006, 2009) and Moreau et al. (2006). If the current arc models are useful tools for plasma torch parametric studies and geometry improvement, their predictions should be carefully validated against experimental data obtained under well-defined torch operating conditions and geometry as they are not fully predictive. A fully predictive model of plasma spray torch operation that can reproduce the effect of the process parameters on the arc behavior without the need of adjustable model parameters requires further developments that involve the use of chemical and thermodynamic nonequilibrium plasma model (NCTE) and inclusion of the electrodes in the computational domain along with the sheath model (Vardelle et al. 2015; Chazelas et al. 2017). If a complete arc model is not necessary for works dealing with plasma torch operation and geometry improvement, simpler models can be used to set the plasma jet conditions at the exit of the torch nozzle for investigation of the suspension in the plasma jet whose predictions of interest are the characteristics of the particles and eventually droplets impacting on the substrate. The first model consists in solving the Navier-Stokes equations in a domain upstream of the nozzle exit (lower part of the nozzle) and adds a source term in the energy equation to take into account the conversion of electrical energy to gas enthalpy. For a nonfluctuating arc, this volumetric heat source can be expressed,

$$ P=\frac{\eta_t\phi I}{V} $$

(14)

where P, η_t,ϕ, I, and V are the volumetric heat source, torch thermal efficiency, arc voltage, current, and, anode volume, respectively (Pourang et al. 2016).

For a fluctuating plasma flow (i.e., arc operating in the takeover and restrike modes), the energy conversion can be considered as effective in a volume whose dimensions vary with time in order to model the time-variation of the arc length (Mariaux and Vardelle 2005; Meillot et al. 2008; Dalir 2016). For example, this volume can consist of a cone (V₁) followed by a cylinder (V₂) as shown in Fig. 4 (Meillot et al. 2008; Dalir 2016); the volume of the conical shape is constant, while the length of the cylinder L₂ varies with time according to the following expression (Dalir 2016),

$$ {L}_2(t)= a\phi (t)+b $$

(15)

where the constant a and b are determined from the actual minimum and maximum values of the arc voltage ϕ_min and ϕ_max. The heat sources P₁ and P₂ in V₁ and V₂ respectively are then calculated by,

$$ {P}_1=\frac{P_m}{L_m}\frac{L_1}{V_1}=\mathrm{constant}, \, {P}_2=\frac{P_m}{L_m}\frac{L_2(t)}{V_2(t)}=\mathrm{constant} $$

(16)

where L_m is the average length of V₂ drawn from the comparison of the predicted torch thermal efficiency in steady-state calculations with the actual thermal efficiency corresponding to the mean electric power P_m (Meillot et al. 2008; Dalir 2016).

Fig. 4

Example of volumes used to model the conversion of electrical energy in enthalpy inside the plasma torch (Dalir 2016)

A second model consists in using transient boundary conditions for the velocity and temperature (or enthalpy) profiles imposed at the nozzle exit assuming their time-variation is modeled on arc fluctuations (Dussoubs et al. 1999). For example, for a plasma torch operating in the restrike mode, the local velocity and temperature of the gas can be assumed to vary continuously about a mean value over a time period corresponding to the typical time τ of an arc attachment spot. The instantaneous gas velocity at the nozzle exit can be then expressed,

$$ {u}_t={u}_s\left(1+\frac{\beta }{100}\sin \omega t\right) $$

(17)

where the subscript s represents the stationary value drawn from steady-state calculations or experiments, and ω = 2πf, where f is the arc fluctuation frequency, t the time, and β the arc fluctuation percentage.

The most common assumptions of the model of the plasma jet issuing from the torch are the following:

• The local thermodynamic equilibrium (LTE) prevailed in the whole calculation domain even though departures from equilibrium may occur in regions with steep temperature gradients.

• The medium is considered as a continuum.

• The fluid is Newtonian.

• The plasma is optically thin.

• No demixion and chemical reactions occurred in the gas phase. The thermodynamic (specific heat and specific enthalpy) and transport properties (viscosity and thermal conductivity) are expressed in terms of temperature and composition. Figure 5 shows the temperature-variation of these properties for argon, hydrogen, and helium (Boulos et al. 1994; Remesh et al. 2003; Trelles et al. 2009; Fauchais et al. 2014).

  Fig. 5

  

  Thermophysical and transport properties of plasma gases (Boulos et al. 1994)

For a compressible gas flow, the continuity, momentum, species mass fractions (Y_k), energy, and state equations are expressed (Echekki and Mastorakos 2010; Jadidi et al. 2015a):

Continuity equation

$$ \frac{\mathrm{\partial \uprho }}{\partial t}+\nabla \cdotp \uprho u=0 $$

(18)

where u is the gas velocity vector, ρ is the gas density, and t is the time.

Momentum equation

$$ \uprho \frac{\partial u}{\partial t}+\uprho u\cdotp \nabla u=-\nabla P+\nabla \cdotp \uptau +\uprho \sum \limits_{k=1}^N{Y}_k{f}_k $$

(19)

where P is the pressure, τ is the tensor of viscous shear stress, and f_k is the body force related to the k^th species.

Species conservation equation (k = 1,…,N)

$$ \uprho \frac{\partial {Y}_k}{\partial t}+\uprho u\cdotp \nabla {Y}_k=\nabla \cdotp \left(-\uprho {V}_k{Y}_k\right)+{\dot{\upomega}}_k $$

(20)

where ${\dot{\omega}}_k$ is the k^th species reaction rate and V_k is the diffusive speed of the k^th species.

Energy equation

$$ \uprho \frac{\partial e}{\partial t}+\uprho u\cdotp \nabla e=-\nabla \cdotp q-P\nabla \cdotp u+\uptau :\nabla u+\uprho \sum \limits_{k=1}^N{Y}_k{f}_k\cdotp {V}_k $$

(21)

where e and q stand for the gas mixture internal energy and the heat flux, respectively.

State equation under ideal gas assumption

$$ P=\uprho RT=\uprho {R}_uT\sum \limits_{k=1}^N\left(\frac{Y_k}{W_k}\right) $$

(22)

where W_k stands for the k^th species molecular weight.

The tensor of viscous shear stress for a Newtonian fluid is given by

$$ \uptau =\upmu \left[\left(\nabla u\right)+{\left(\nabla u\right)}^T\right]-\left(\frac{2}{3}\upmu -\gamma \right)\left(\nabla \cdotp u\right)I $$

(23)

where μ, γ, and I are the dynamic viscosity, bulk viscosity, and identity matrix, respectively. The term ρY_kV_k in Eq. 20 shows the species transport by the molecular diffusion phenomenon. Using Fick’s law, V_k is related to the molar (X_k) or mass fraction gradients (Echekki and Mastorakos 2010; Jadidi et al. 2015a),

$$ {X}_k{V}_k=-{D}_k^m\nabla {X}_k $$

(24)

where ${D}_k^m$ stands for the mixture-averaged mass diffusivity (mass diffusion coefficient) for species k. Furthermore, the term q in Eq. 21 consists of conduction heat transfer, radiation heat transfer, and heat diffusion by the mass diffusion of the various species (Echekki and Mastorakos 2010; Jadidi et al. 2015a),

$$ q=-\uplambda \mathrm{\nabla}T+{q}_{\mathrm{rad}}+\uprho \sum \limits_{i=1}^N{h}_i{Y}_i{V}_i $$

(25)

The rates of diffusion of heat, momentum, and species in the plasma flow are determined to a great extent, by the level of turbulence and the way this turbulence is modeled. The arc fluctuations enhance the development of the turbulence that starts at the jet border where it comes into contact with the ambient gas at rest.

Three approaches are commonly used to model gas flow turbulence: direct numerical simulation (DNS), large eddy simulation (LES), and Reynolds-averaged Navier-Stokes (RANS) (Echekki and Mastorakos 2010; ANSYS 2011; Jadidi et al. 2015a). DNS consists in solving the Navier-Stokes equations on a fine grid using a small time-step and so it captures all eddy sizes, including the smallest turbulence scales. If the predictions are accurate, the overall computation cost is proportional to Re³ and therefore the model is not suited to multiphase plasma flows with the current computing power. Large eddy simulation (LES) retains only the largest and most important eddies and predicts their motion uncoupled from the small eddies that are modeled using a subgrid-scale model (Garnier et al. 2009; Echekki and Mastorakos 2010; Jadidi et al. 2015a).

The RANS approach is based on the Reynolds decomposition and the time averaging of Navier-Stokes equations. In this approach, further terms including the Reynolds stresses and fluxes exist in the transport equations and all the turbulence scales are simulated (Echekki and Mastorakos 2010; ANSYS 2011; Jadidi et al. 2015a). To simulate the Reynolds stresses and fluxes, two approaches namely the eddy viscosity models and the Reynolds stress model (RSM) are commonly used. In the eddy viscosity models, an eddy-viscosity constitutive relation is used to make a correlation between the Reynolds stress term and mean velocity profiles (e.g., Boussinesq equation). In this relation, a parameter called eddy viscosity, μ_t, exists that should be calculated. To predict μ_t, many models such as standard k-ε and RNG k-ε (where k is the turbulent kinetic energy and ε is the viscous dissipation rate of turbulent kinetic energy) are frequently used (Echekki and Mastorakos 2010; ANSYS 2011; Jadidi et al. 2015a). In the RSM, each component of Reynolds stress tensor has an individual transport equation and a scale-determining equation (e.g., viscous dissipation rate of turbulent kinetic energy (ε) equation) is considered. Compared to the eddy viscosity models, the RSM usually predicts more accurate results, particularly for the swirling flows and flows with strong streamline curvature (ANSYS 2011; Jadidi et al. 2015a). To model the thermal spray processes, the eddy viscosity as well as the RSM models available in commercial software packages such as ANSYS Fluent and open source CFD softwares as Code_Saturne (2017) are extensively used. Using ANSYS Fluent (2011), Jabbari et al. (2014) showed that, under the conditions of their study, the RSM model predicted the plasma jet behavior more accurately than the eddy viscosity model.

4 Suspension/Plasma Jet Interaction

4.1 Suspension/Liquid Breakup

Figure 6 illustrates the radial injection of a suspension in the form of a liquid jet (mechanical injection) into a plasma jet issuing from a dc plasma spray torch. The spray field can be divided into three zones: (1) liquid column jet, (2) disintegration of liquid column subjected to the action of the plasma crossflow and formation of ligaments, and (3) droplets (Marchand et al. 2008). When the liquid is injected in the form of drops (spray injection), only ligaments and droplets are present in the plasma flow (see Fig. 1). After fine droplets are produced, the liquid evaporation becomes dominant. The interactions between the plasma flow and liquid control the final size of droplets, their trajectories and heating and acceleration in the plasma flow, and finally the coating quality. Therefore, the penetration height of the suspension in the gas flow, droplet size distribution, and momentum flux should be carefully controlled. In the following sections, liquid jet breakup in the plasma crossflow and droplet breakup phenomena are discussed in more details.

Fig. 6

The suspension atomization in plasma crossflow is divided into three zones: (1) cylindrical liquid jet, (2) disintegration of liquid column and formation of ligaments, (3) droplets (Marchand et al. 2008)

4.1.1 Fundamental Studies on Breakup Phenomena

The breakup is defined as a process in which the surface-to-volume ratio of liquid augments (Dumouchel 2008). It happens when the liquid flow interacts with a high-momentum gas flow. The breakup process is generally divided into three parts namely as liquid flow ejection, primary breakup, and secondary breakup. In general, after initiation of liquid flow from the orifice, the deformations/perturbations appear on the liquid-gas interface. By the growth of the perturbations in space and time, liquid fragments eject from the main flow eventually. The initial flow perturbations and subsequent liquid fragment formation are known as the primary breakup mechanism. The secondary breakup mechanism results from the distortion of the liquid fragments and their breakdown into smaller elements. At last, stable drops are formed when the surface tension force is strong enough to ensure the liquid fragment cohesion (Dumouchel 2008; Jadidi et al. 2015a). Different atomizers and various techniques for injecting the suspension in the plasma jet are designed and applied in industry. They involve either cylindrical liquid jets interacting with the plasma crossflow or two-fluid atomizers (Ashgriz 2011a).

4.1.1.1 Primary Breakup

4.1.1.1.1 Liquid Jet in Crossflow

As shown in Fig. 6, after cylindrical jet formation, the jet interacts with the plasma crossflow (zones 2 and 3). The liquid column bends in the direction of the plasma gas flow due to the dynamic pressure exerted by the gas flow (see Fig. 7). The perturbations and instabilities that develop on the liquid column bring about the formation of ligaments and drops (i.e., column breakup). The ligaments break up further into smaller drops. The location where the liquid column ceases to exist is called the column breakup point (CBP). On the lower surface of the liquid jet (leeward), waves with short wavelengths are detected. As a result, drops are sheared off the leeward surface, which is referred to as surface breakup. The size of drops formed by surface breakup is smaller than drops produced from ligaments (Wu et al. 1997; Inamura and Nagai 1997; Inamura 2000; Becker and Hassa 2002; Cavaliere et al. 2003; Lubarsky et al. 2012; Jadidi et al. 2015a, 2016b)

Fig. 7

Breakup of liquid jets in transverse subsonic gas flow (Jadidi et al. 2015a)

In general, six nondimensional numbers are defined to characterize the behavior of liquid jets in crossflows: the gaseous Reynolds number, Re_G; liquid Reynolds number, Re_L; gaseous Weber number, We_G; momentum flux ratio, q (or liquid Weber number, We_L); liquid-to-gas density ratio; and ratio of duct width (L) to orifice diameter (D) (Jadidi et al. 2015a),

$$ {\mathit{\operatorname{Re}}}_G=\frac{\uprho_G{U}_GL}{\upmu_G},{\mathit{\operatorname{Re}}}_L=\frac{\uprho_L{U}_LD}{\upmu_L},{We}_G=\frac{\uprho_G{U}_G^2D}{\upsigma},q=\frac{\uprho_L{U}_L^2}{\uprho_G{U}_G^2},\upvarepsilon =\frac{\uprho_G}{\uprho_L},\updelta =\frac{D}{L} $$

(26)

where ρ_G and ρ_L are the density of the gas and liquid phase, respectively, μ_G and μ_L are the viscosity of the gas and liquid phase, respectively, and σ the liquid surface tension. Wu et al. (1997) showed that the gaseous Weber number and momentum flux ratio are the main parameters that control the spray characteristics. They also established a map based on these nondimensional numbers to evaluate the breakup regimes of liquid jets in crossflows (see Figs. 8, and 9) (Wu et al. 1997; Sallam et al. 2004; Ashgriz 2011b). As shown in Figs. 8, and 9, based on the gaseous Weber number, four breakup regimes named as enhanced capillary, bag, multimode, and shear breakup are observed. In addition, the map shows that for low values of We_G and q, the drops are formed from the ligaments and the column breakup mechanism is dominant. However, for high values of We_G and q, drops can be sheared off the leeward surface and the surface breakup becomes important as well. In other words, as the Weber numbers increase, the surface breakup extent grows gradually (Wu et al. 1997; Sallam et al. 2004; Tambe et al. 2005). In addition to the mentioned parameters, the injection angle and injector internal design have significant influence on the liquid jet behavior in crossflows. Fuller et al. (2000) and Costa et al. (2006) found that the injection angle can affect the spray characteristics (e.g., breakup mechanisms and spray trajectory) even more than q. Ahn et al. (2006) indicated that cavitation and hydraulic flip of the injector internal flow cause the breakup mechanisms and the observed trajectories to be considerably different from the ones reported by Wu et al. (1997). In the suspension plasma spray process, the gas Weber number is high and the surface/column breakup regime can be reached (Fazilleau et al. 2006).

Fig. 8

Different modes of liquid jets breakup in subsonic gaseous crossflows: (a) enhanced column breakup, (b) bag breakup, (c) bag/shear (multimode) breakup, (d) shear breakup (Sallam et al. 2004; Ashgriz 2011b)

Fig. 9

Breakup regime map of liquid jets in subsonic crossflows (Wu et al. 1997)

The spray trajectory or liquid penetration height, and the location of liquid column breakup point (CBP) are considered as the main parameters that characterize the near field behavior of liquid jets in crossflows (Lubarsky et al. 2012). In general, the liquid penetration height increases as q increases and is independent of the gaseous Weber number (noting that in a few studies, it is reported that the liquid penetration height slightly decreases when We_G increases) (Wu et al. 1997; Becker and Hassa 2002; Lubarsky et al. 2012). Furthermore, the liquid penetration height decreases with the increase of liquid viscosity, liquid temperature, and gas temperature (Stenzler et al. 2003; Lakhamraju 2005). In the literature, there are many experimental and theoretical studies that attempt to link the liquid penetration height and CBP location with q, We_G, and gas temperature and pressure. Although numerous correlations have been developed, their results are significantly different from each other due to dissimilar injector shape, different turbulence intensity, and measurements methods (Lubarsky et al. 2012). The most used correlations for spray trajectory and CBP location are the following (x and y show the crossflow and liquid jet directions, respectively):

Spray trajectory proposed by Wu et al. (1997) for nonturbulent liquid jets in uniform crossflow:

$$ \frac{y}{D}=1.37\sqrt{q\left(x/D\right)} $$

(27)

CBP height for nonturbulent liquid jets in uniform crossflow (Wu et al. 1997):

$$ \frac{y_b}{D}=3.44\sqrt{q} $$

(28)

CBP axial distance for nonturbulent liquid jets in uniform crossflow (Wu et al. 1997):

$$ \frac{x_b}{D}=8.06 $$

(29)

Lee et al. (2007) found that for turbulent liquid jets in uniform crossflow, x_b/D = 5.2 and the spray trajectory correlation was similar to Eq. 27. In the following correlation, the effect of gas temperature, T_∞, on the spray trajectory is included (Lakhamraju 2005),

$$ \frac{y}{D}=1.8444{q}^{0.546}\mathit{\ln}\left(1+1.324\left(\frac{x}{D}\right)\right){\left(\frac{T_{\infty }}{T_0}\right)}^{-0.117}, \quad {T}_0=294\ K $$

(30)

In the SPS process, the plasma crossflow is fluctuating both in length and width; it also exhibits steep radial gradients of properties (enthalpy, density, and velocity) which are time dependent. The effect of air crossflow oscillation on the liquid jet penetration was fundamentally studied by changing the crossflow oscillation frequency between 0 and 450 Hz, and it was found that the strength of the response of the liquid jet decreases as the oscillation frequency of the crossflow increases that is the spray oscillation was reduced by the increase of crossflow frequency (Sharma 2015). In addition, it was found that the crossflow velocity gradient (i.e., nonuniform/shear-laden crossflow) had significant effects on the spray trajectory (Tambe et al. 2007; Tambe 2010). Jadidi et al. (2017) found that the spray trajectory (y/D) in nonuniform crossflow is equal to $A\sqrt{q\left(x/D\right)}$ where A is a function of the slope of gas velocity profile, and q is defined from the gas average velocity. Furthermore, when the crossflow is swirling, it was observed that the liquid jet follows a path close to the crossflow helical trajectory. In the case of swirling crossflow, the liquid penetration is also dependent on the swirl number (Tambe 2010; Tambe and Jeng 2010).

4.1.1.1.2 Two-Fluid Atomizers

Most practical atomiz ers are of the pressure, rotary, or twin-fluid type. The latter use the kinetic energy of a gas flow to break a liquid into ligaments and then drops. This type is generally used in suspension plasma spraying and essentially includes airblast, air-assist, and effervescent atomizers (Kassner et al. 2008; Esfarjani and Dolatabadi 2009; Fauchais and Montavon 2010; Aubignat et al. 2016). They differ in the amount of gas employed and its flow velocity. Figure 1-a shows the injection of a suspension in the plasma jet using an effervescent atomizer. This type of atomizer is shown in Fig. 10. It involves four components: the liquid supply port, gas supply port, mixing chamber, and an exit orifice (Sovani et al. 2001). By injecting the atomizing gas (the gas supply pressure is slightly higher than the liquid supply pressure) into the liquid, a bubbly two-phase mixture is formed upstream of the exit orifice (see Fig. 11). Then, this bubbly mixture is ejected through the discharge orifice (Roesler 1988; Roesler and Lefebvre 1988; Sovani et al. 2001). It is worth mentioning that, compared to the single phase flow, a two-phase flow through a nozzle chokes at considerably lower velocity. In other words, a two-phase flow with relatively low injection pressures and low flow velocities can experience a steep pressure jump at the nozzle exit (Sovani et al. 2001). In effervescent atomizer, the bubbles experience a sudden pressure relaxation and expand quickly on leaving the nozzle. Due to the presence of expanding bubbles, the liquid is shattered into drops (see Fig. 11a) (Roesler 1988; Roesler and Lefebvre 1988; Sovani et al. 2001). In addition, as shown in Fig. 11b, the liquid can form an annular sheath within the orifice of the atomizer when gas/liquid mass ratio (GLR) is high. In this case, the rapidly expanding gas core causes the liquid breaks up into thin ligaments (Buckner et al. 1990; Lund et al. 1993; Santangelo and Sojka 1995; Sutherland et al. 1997; Sovani et al. 2001). At high gas/liquid mass ratios (GLRs > 0.4), drops suspended in the atomizing gas discharge from the orifice (Chin and Lefebvre 1993; Sovani et al. 2001).

Fig. 10

A schematic of a typical effervescent nozzle (Roesler 1988; Roesler and Lefebvre 1988; Sovani et al. 2001)

Fig. 11

Schematic representation of the atomization mechanism in effervescent nozzle: (a) bubbly flow (Roesler 1988; Roesler and Lefebvre 1988), (b) annular flow (Buckner et al. 1990; Santangelo and Sojka 1995)

In general, the drop sizes obtained from effervescent atomizer are smaller than those generated by other conventional atomizers. The injection pressures and the gas flow rates are much lower than those required by other twin-fluid atomizers. Using this atomizer, the clogging problem can be alleviated and the orifice erosion can be reduced (Lefebvre 1989; Sovani et al. 2001). Furthermore, the effect of liquid viscosity on the mean drop size is relatively negligible (Buckner and Sojka 1991; Lund et al. 1993; Sutherland et al. 1997). However, the mean drop size is significantly affected by the length/diameter ratio of the orifice. The mean drop size decreases as the length/diameter ratio reduces (Chin and Lefebvre 1995). As the gas to liquid ratio (GLR) increases from zero to around 0.03, the Sauter mean diameter (SMD), i.e., the mean diameter of spheres that have the same volume/surface area ratio, decreases rapidly. For higher GLR, the mean diameter reduces slightly (Whitlow and Lefebvre 1993). In general, as the GLR increases, the drop velocity and the spray momentum flux increase, and the spray cone angle widens (Chen and Lefebvre 1994; Bush et al. 1996; Panchagnula and Sojka 1999).

4.1.1.2 Numerical Modeling of Primary Breakup of the Liquid jet

In order to identify the location of the liquid phase and topology of the liquid-gas interface, the interface tracking methods are usually applied. These methods are based on the Eulerian approach and can be categorized into two classes: fixed-grid methods and moving-grid methods (Jiang et al. 2010; Jadidi et al. 2015a). In fixed-grid methods, the grid is predefined and does not move with the interface. The fixed-grid methods are the most commonly used due to their simple description and ease of programming. Among various fixed-grid methods, the volume of fluid (VOF) method is perhaps the most commonly used interface tracking to simulate the primary atomization of the liquid jet (Jiang et al. 2010; Jadidi et al. 2015a).

In VOF method, an indicator function (called also as volume fraction and color function) is defined to implicitly calculate the liquid-gas interface location, its curvature and normal. The indicator function, α, denotes the fractional volume of the cell occupied by liquid: α = 0 and α = 1 correspond to a cell full of gas and a cell full of liquid, respectively. In addition, a cell with α value between zero and one represents the location of the liquid-gas interface (see Fig. 12). In this method, the set of the Navier-Stokes equations is solved for both gas and liquid phases as well as the volume fraction advection equation (Hirt and Nichols 1981; Prosperetti and Tryggvason 2009; Tryggvason et al. 2011). Furthermore, the surface tension force is usually included in the momentum equation and it is determined by the interface curvature (Brackbill et al. 1992). The main advantages and disadvantages of the VOF methods are the mass conservation and grid dependency, respectively (Jadidi et al. 2015a; Prosperetti and Tryggvason 2009; Tryggvason et al. 2011).

Fig. 12

Distribution of the indicator function, α, which represents the fractional volume of the cell occupied by liquid (Jadidi et al. 2015a)

To model the liquid primary breakup in the crossflow plasma jet, a specific compressible VOF method was recently developed (Vincent et al. 2009; Meillot et al. 2013). It assumes that the plasma behaves like a perfect gas, and the conservation equations of continuity, momentum, volume fraction, energy, and species (Eqs. 31–35) are formulated (Vincent et al. 2009; Meillot et al. 2013),

$$ \frac{\partial P}{\partial t}+\frac{1}{\chi_T}\nabla \cdotp u=0 $$

(31)

$$ \uprho \frac{\partial u}{\partial t}+\uprho u\cdotp \nabla u=\uprho \mathrm{g}-\nabla \left(P-\frac{\tau }{\chi_T}\nabla .u\right)+\nabla \cdotp \left(\mu \left(\nabla u+{\nabla}^Tu\right)\right)+{F}_{TS} $$

(32)

$$ \frac{\mathrm{\partial \upalpha }}{\partial t}+\left(\nabla \cdotp u\right)\upalpha =0 $$

(33)

$$ \rho {C}_p\left(\frac{\partial T}{\partial t}+\left(\nabla \cdotp u\right)\mathrm{T}\right)=\nabla \cdotp \left(\lambda \nabla T\right)+{\Phi}_{\mathrm{rad}} $$

(34)

$$ \frac{\partial {\psi}_i}{\partial t}+u\cdotp \nabla {\psi}_i=\nabla \cdotp \left({D}_i{\psi}_i\right) $$

(35)

$$ \uprho =\upalpha {\rho}_L+\left(1-\alpha \right)\left[{\psi}_a{\rho}_a+\left(1-{\psi}_a\right){\rho}_p\right] $$

(36)

$$ \mu ={\upalpha \upmu}_L+\left(1-\alpha \right)\left[{\psi}_a{\mu}_a+\left(1-{\psi}_a\right){\mu}_p\right] $$

(37)

$$ \uplambda ={\upalpha \uplambda}_L+\left(1-\alpha \right)\left[{\psi}_a{\uplambda}_a+\left(1-{\psi}_a\right){\uplambda}_p\right] $$

(38)

$$ {C}_p=\upalpha {C}_{pL}+\left(1-\alpha \right)\left[{\psi}_a{C}_{pa}+\left(1-{\psi}_a\right){C}_{pp}\right] $$

(39)

$$ D=\upalpha {D}_L+\left(1-\alpha \right)\left[{\psi}_a{D}_a+\left(1-{\psi}_a\right){D}_p\right] $$

(40)

$$ {F}_{TS}=\sigma \kappa {\mathrm{n}}_i{\delta}_i $$

(41)

where P, ρ, u, g, μ, and T stand for pressure, density, local velocity vector, gravitational acceleration, viscosity, and temperature, respectively. χ_T = (∂ρ/∂P)/ρ is the adiabatic compressibility, τ the characteristic time assumed to be equal to the numerical dynamic time step, C_p the specific heat, λ the thermal conductivity, ψ_i the concentration of species i, D_i the mass diffusion coefficient of species i, and Φ_rad represents the radiative effects. F_TS, σ, κ, n_i, and δ_i are the surface tension force, surface tension coefficient, local interface curvature, interface normal, and Dirac function, respectively. In addition, the index L, a, and p stand for liquid, air, and plasma, respectively (Vincent et al. 2009; Meillot et al. 2013). The results of this method will be discussed in the next paragraphs.

The interaction of a train of spherical water droplets with a plasma flow was numerically studied by Meillot et al. (2013). The droplet diameter was assumed to be 360 μm. Moreover, a new droplet was injected every 0.1 μs. Figure 13 shows the behavior of the first three droplets in a steady Ar/H₂ plasma crossflow as well as the temperature isotherms. Predictions show that droplet deformation began as soon as it reached the plasma flow. Furthermore, in actual plasma condition the droplet fragmentation started faster and large fragments were quickly destroyed (Meillot et al. 2013), compared to the case of a uniform temperature plasma flow (gas temperature was fixed to 3200 K).

Fig. 13

Behavior of 360-μm water droplets injected in a steady Ar/H₂ (45/15 SLM) plasma flow (the lines represent the gas isotherms) (Meillot et al. 2013)

Meillot et al. (2013) also numerically studied the primary breakup of continuous water jets in Ar/He and Ar/H₂ plasma crossflows exhibiting different fluctuation levels: the Ar/He plasma jet was supposed to fluctuate according to the take-over mode and the Ar/H₂ jet according to the restrike mode. For the Ar/He plasma flow, the arc current, mean voltage, and gas flow rates were 700 A, 40 V, and 30/30 SLM, respectively, while for the Ar/H₂ flow, they were 500 A, 76 V, and 45/15 SLM, respectively. The liquid (water) jet velocity and diameter, right before the interaction point with the plasma flow, were assumed equal to 22 m/s and 200 μm, respectively. Figure 14 shows the penetration and breakup of the continuous water jet injected in a steady Ar/H₂ plasma flow: the surface waves are developed on the liquid column, and arm-shaped filaments are formed and break up into droplets. Predictions showed that the water penetration in Ar/He is much less than in Ar/H₂. The model was also applied to the breakup of a continuous liquid jet injected into a time-dependent Ar/H₂ plasma jet. Figure 15 compares the liquid behavior at two different times (60 and 70 μs) and confirms that the liquid penetration height depends on time since the gas velocity and temperature fields change with time (Meillot et al. 2013).

Fig. 14

Interaction of a continuous water jet with a steady Ar/H₂ (45/15 SLM) plasma flow (Meillot et al. 2013)

Fig. 15

Behavior of water jet in a time-dependent Ar/H₂ (45/15 SLM) plasma flow at 60 μs (left image) and 70 μs (right image) (Meillot et al. 2013)

4.1.1.3 Secondary Breakup

As the drops enter the disruptive flow field, a secondary breakup process may initiate. An unequal pressure distribution is created around the drop by the acceleration of the ambient fluid and, the initial spherical drop is deformed. The viscous and interfacial tension forces resist the deformation. However, when the aerodynamic forces are large enough, the drop fragmentation happens (Guildenbecher et al. 2009). The following nondimensional numbers are used in secondary breakup analysis,

$$ We=\frac{\uprho_G{U}_0^2{d}_0}{\upsigma}, Oh=\frac{\upmu_L}{\sqrt{\uprho_L{d}_0\upsigma}},{\mathit{\operatorname{Re}}}_G=\frac{\uprho_G{U}_0{d}_0}{\upmu_{\mathrm{G}}},\upvarepsilon =\frac{\uprho_L}{\uprho_G},N=\frac{\upmu_L}{\upmu_G}, Ma=\frac{U_0}{c} $$

(42)

where d₀ is the initial diameter of the drop, U₀ the initial relative speed between the gas and drop, and c the speed of sound (Shraiber et al. 1996; Guildenbecher et al. 2009).

In secondary breakup analysis, the Weber number, We, and Ohnesorge number, Oh, are the most effective parameters. As We increases, the tendency toward disintegration enhances. In contrast, the tendency toward disintegration decreases when Oh increases. A schematic of different breakup regimes for Newtonian drops is shown in Fig. 16. From top to bottom, the figure illustrates vibrational, bag, multimode, sheet-thinning, and catastrophic breakup regimes (Guildenbecher et al. 2009). The transition between two breakup regimes depends on We and Oh (see Fig. 17). When Oh < 0.1, the transition Weber numbers are constant and reported in Table 1. Figure 17 shows that the transition Weber numbers increase as Oh increases (Hsiang and Faeth 1995).

Fig. 16

A schematic of the secondary breakup regimes of a Newtonian drop. From top to bottom: vibrational, bag, multimode, sheet-thinning, and catastrophic breakup regimes (Guildenbecher et al. 2009)

Fig. 17

Map of secondary breakup regimes (Hsiang and Faeth 1995)

Table 1 Secondary breakup regimes of a Newtonian drop as a function of Weber number when Oh < 0.1 (Pilch and Erdman 1987; Hsiang and Faeth 1992; Guildenbecher et al. 2009)

During vibrational breakup, a few fragments with sizes comparable to the size of the parent drop are generated. Pilch and Erdman (1987) explained that the vibrational breakup does not always happen and does not result in small final fragment sizes. Therefore, most authors ignore the vibrational breakup and consider bag breakup as the first secondary breakup regime. In the bag breakup regime, a thin hollow bag attached to a thicker toroidal rim is observed. The bag breaks up first, producing a large number of small drops. Then the toroidal rim breaks up generating a small number of large fragments. As We increases, a stamen oriented anti-parallel to the drop motion direction is added to bag breakup. This breakup regime is known as multimode. After bag disintegration, the rime and the stamen breakup. In sheet-thinning regime, a film is unceasingly eroded from the drop surface and breaks up after being detached. Consequently, a small drop plethora, and sometimes a core with a size that is comparable to the size of the parent drop, is generated. In the catastrophic breakup regime, large amplitude waves with long wavelengths cause the drop surface to corrugate. As a result, a small number of large fragments are formed. Then, these fragments disintegrate into smaller units (Guildenbecher et al. 2009).

The breakup regime in the SPS process strongly depends on the plasma flow properties at the instant the drops penetrate the gas flow, drop size, and injection velocity. In other words, in plasma spray condition, due to time and space variations of the plasma flow properties, temperature, and velocity, the drops may experience different breakup regimes (Vardelle et al. 2008). Figure 18 shows the images of 250-μm-diameter water drops penetrating a transverse Ar/H₂ (45/15 NLM) plasma jet. As clearly shown, depending on the time when the drops penetrate the gas flow, different breakup regimes can be observed (Vardelle et al. 2008).

Fig. 18

Various secondary breakup regimes of 250-μm-dimeter water drops penetrating the transverse Ar/H₂ plasma jet (Vardelle et al. 2008)

4.2 Droplet/Particle Phase Modeling

Today, the Eulerian-Lagrangian approach is mostly used to model multiphase spray flows. In this approach, the gas phase is modeled as a continuum while Lagrangian particle tracking (LPT) models are used to evaluate the trajectory, velocity, and temperature of droplets/particles. This approach is appropriate for simulating dilute flows. One-way coupling and two-way coupling are the main assumptions in the Eulerian-Lagrangian approach. In one-way coupling, the effect of the gas phase on droplets/particles is only considered and there are no reverse effects contrarily to the two-way coupled assumption (Crowe et al. 1998; Fan and Zhu 1998; Jiang et al. 2010; Jadidi et al. 2015a).

4.2.1 Droplet/Particle Motion

The overall mass conservation of the droplet/ particle is expressed,

$$ \frac{dm_d}{dt}=-{\rho}_s wS $$

(43)

where m_d is the droplet/particle mass, ρ_s is density at droplet/particle surface, w is the gas velocity at the droplet/particle surface, and S is the droplet/particle surface area (Crowe et al. 1998; Fan and Zhu 1998; Jiang et al. 2010).

The droplet/particle velocity v is calculated by solving the droplet/particle motion equation in the gas flow,

$$ F={m}_d\frac{dv}{dt} $$

(44)

where F is the fluid forces acting on the droplet /particle of mass m_d. The drag force is the most important force acting on a droplet/particle in plasma spray. It is expressed,

$$ {F}_D=\frac{1}{2}{\uprho}_G{C}_DA\left|u-v\right|\left(u-v\right) $$

(45)

where ρ_G, C_D, A, and u are the gas density, drag coefficient, droplet/particle projected area, and gas velocity, respectively. The drag coefficient, C_D, depends on the Reynolds (Re) relating to particle, Mach (M) and Knudsen (Kn) numbers (Crowe et al. 1998; Fan and Zhu 1998). However, for relatively large particles (micrometer sized) with low Mach number, Oberkampf and Talpallikar (1994) utilized the correlation,

$$ {C}_D=\left\{\begin{array}{cc}24/\mathit{\operatorname{Re}},& \mathit{\operatorname{Re}}<1\hfill \\ {}24\left(1+0.15{\mathit{\operatorname{Re}}}^{0.687}\right)/\mathit{\operatorname{Re}},& 1<\mathit{\operatorname{Re}}<1000\hfill \\ {}0.44,& \mathit{\operatorname{Re}}>1000\hfill \end{array}\right. $$

(46)

Under plasma condition, a steep temperature gradient exists across the gas boundary layer surrounding the particle, which results in severe variations of the gas transport properties (Fauchais et al. 2014). To account for this temperature gradient, Lewis and Gauvin (1973) recommended that the drag coefficient for a particle immersed in an Ar plasma jet should be corrected,

$$ {C}_D={C}_{DF}{\left({\nu}_f/{\nu}_{\infty}\right)}^{0.15} $$

(47)

where C_DF is the drag coefficient where the fluid properties are calculated at the arithmetic mean film temperature across the boundary layer (T_f = (T_s + T_∞)/2 where T_s and T_∞ are the particle surface temperature and gas stream temperature, respectively), and ν_f and ν_∞ are the kinematic viscosities estimated at the mean film temperature and the free stream temperature, respectively.

Another correction factor for the plasma condition was proposed by Lee et al. (1981),

$$ {C}_D={C}_{DF}{\left({\rho}_{\infty }{\mu}_{\infty }/{\rho}_s{\mu}_s\right)}^{-0.45} $$

(48)

where the index “s” stands for the plasma properties at the droplet/particle surface temperature.

Also, to estimate the transport of relatively small particles (particle diameter less than 10 μm) in plasma flow, another correction factor for the noncontinuum effect (i.e., Knudsen effect) should be taken into account. Chen and Pfender (1983) proposed the following correction for the drag coefficient,

$$ \begin{array}{ll} & {C}_D={C}_{DF}{\left({\rho}_{\infty }{\mu}_{\infty }/{\rho}_s{\mu}_s\right)}^{-0.45}{\left[\frac{1}{1+\left(\frac{2-a}{a}\right)\left(\frac{\gamma }{1+\gamma}\right)\frac{4}{\Pr_s}{Kn}^{\ast }}\right]}^{0.45} \\ & {Kn}^{\ast }={\lambda}^{\ast }/{d}_0,{\lambda}^{\ast }=\left(2,\overline{k},/,{\rho}_s,{\overline{v}}_s,{\overline{c}}_p\right){\Pr}_s \end{array}$$

(49)

where γ = c_p/c_v, a is the thermal accommodation coefficient, and Pr_s is the gas Prandtl number at the droplet/particle surface temperature, ${\overline{v}}_s$ is the average molecular speed at the particle/droplet surface temperature, and $\overline{k}$ and ${\overline{c}}_p$ are the average thermal conductivity and specific heat between the true droplet/particle surface temperature and the gas temperature at the droplet/particle surface (due to temperature jump condition). ${Kn}^{\ast }$is the Knudsen number based on an effective mean free path length.

Another phenomenon which an affect the droplet/particle dynamics, especially when the particle size is small, is thermophoresis. This effect arises due to steep temperature gradients in the gas phase. To estimate the thermophoresis force, F_T, the following empirical correlation which is valid for a wide range of thermal conductivity ratios and Knudsen numbers is extensively used,

$$ {F}_T=\frac{-6{\uppi \upmu}_G^2{d}_0{C}_s}{\uprho_G{m}_d}\frac{1}{1+6{C}_m Kn}\frac{k_G/{k}_d+2{C}_t Kn}{1+2{k}_G/{k}_d+4{C}_t Kn}\frac{\nabla T}{T} $$

(50)

where μ_G is the gas viscosity, k_G is the gas thermal conductivity, d₀ is the droplet/particle diameter, and k_d is the droplet/particle thermal conductivity. C_s, C_t, and C_m are 1.17, 2.18, and 1.14, respectively (Crowe et al. 1998).

4.2.2 Droplet Breakup

In Eulerian-Lagrangian approach, two droplet breakup models named as the Taylor analogy breakup (TAB) and the wave breakup models have been extensively applied (Taylor 1963; Reitz 1987; Patterson and Reitz 1999; Jiang et al. 2010). In general, TAB and wave models are appropriate for low and high Weber conditions, respectively. The TAB model is based on the analogy between the oscillating-distorting droplet and a spring-mass system. In this model, the liquid viscosity, liquid surface tension, and aerodynamic force are similar to the damping force, spring restoring force, and external force in the spring-mass system, respectively (Taylor 1963; Jiang et al. 2010). The following equation is solved to calculate the distortion parameter, y,

$$ \ddot{y}+\frac{5{\mu}_L}{\rho_L{r}^2}\dot{y}+\frac{8\sigma }{\rho_L{r}^3}y=\frac{2}{3}\frac{\rho_G}{\rho_L}\frac{{\left(v-u\right)}^2}{r^2} $$

(51)

where r is the droplet radius. The droplet breaks up when y > 1 (Taylor 1963; Jiang et al. 2010).

The unstable growth of Kelvin-Helmholtz waves at the liquid-gas interface is considered in the wave breakup model (Reitz 1987; Patterson and Reitz 1999). A dispersion equation which relates the perturbation growth rate, Ω, to the wavelength, Λ, and physical parameters is obtained from the stability analysis. The following correlations are developed for estimating the maximum growth rate and its wavelength,

$$ \Omega {\left(\frac{\rho_L{a}^3}{\sigma}\right)}^{0.5}=\frac{0.34+0.38{We_G}^{1.5}}{\left(1+ Oh\right)\left(1+1.4{J}^{0.6}\right)} $$

(52)

$$ \frac{\Lambda}{a}=9.02\frac{\left(1+0.45{Oh}^{0.5}\right)\left(1+0.4{J}^{0.7}\right)}{{\left(1+0.87{We_G}^{1.67}\right)}^{0.6}} \, ,\kern0.75em J=1/{\left(\frac{\uprho_L}{\uprho_G}{\left(\frac{{\mathit{\operatorname{Re}}}_L}{We_L}\right)}^2\right)}^2 $$

(53)

where We_G and Oh are calculated from the parent droplet radius, a. In this model, the child droplets with radius r are formed from a parent droplet with,

$$ r={B}_0\Lambda \kern2.00em \mathrm{where} \, \left({B}_0\Lambda \le a\right)\kern1.5em \mathrm{or} $$

$$ r=\min \left[{\left(3\pi {a}^2{U}_G/2\Omega \right)}^{1/3},{\left(3{a}^2\Lambda /4\right)}^{1/3}\right]\kern2.50em \mathrm{where}\ \, \left({B}_0\Lambda >a\right) $$

(54)

where B₀ = 0.61. In this model, the child droplet size is assumed to be proportional to the wavelength of the fastest-growing wave. In recent works, the Kelvin-Helmholtz Rayleigh-Taylor (KHRT) breakup model which is a combination of wave (Kelvin-Helmholtz) breakup model with the Rayleigh-Taylor breakup model is used. In this model, the mechanism (KH vs. RT) that has the shorter breakup time results in the droplet breakup (Reitz 1987; Patterson and Reitz 1999; ANSYS 2011).

4.2.3 Droplet/Particle Heat Transfer (in-Flight Heating and Cooling of Particles)

If the thermal conductivity of the droplet/particle material, k_d, is much higher than that of the gas k_g and the droplet/particle is homogenous, the particle/droplet energy equation can be calculated by using the lumped capacity method (for droplet Biot numbers less than 0.1) (Crowe et al. 1998; Fan and Zhu 1998),

$$ {m}_d{C}_p\frac{dT_d}{dt}=\dot{Q}+{\dot{m}}_d{h}_{fg} $$

(55)

where $\dot{Q}$ is the convective and radiative heat transfer, T_d is the droplet/particle temperature, C_p is the particle phase specific heat, and h_fg is the vaporization latent heat.

The convection heat transfer is formulated,

$$ {\dot{Q}}_c= hS\left(T-{T}_d\right) $$

(56)

where h is the heat transfer coefficient, which is usually calculated from the Nusselt number, Nu, by using the Ranz-Marshall correlation,

$$ Nu=\frac{hd}{k_G}=2+0.6{\mathit{\operatorname{Re}}}_p^{1/2}{\mathit{\Pr}}^{1/3},\kern1em \mathit{\operatorname{Re}}<200\ \mathrm{and}\ 0.5<\mathit{\Pr}<1.0 $$

(57)

where Pr and Re are the Prandtl number of the gas phase and Reynolds number, respectively (Crowe et al. 1998; Fan and Zhu 1998).

Under plasma conditions, due to the steep temperature gradient across the thermal boundary layer surrounding the particle and the strong variations of the gas thermal conductivity with temperature, a question arises about the temperature at which the gas thermal conductivity should be evaluated (e.g., it can be the film temperature or any other temperature). Based on the theoretical analysis of the problem of pure conduction (assuming a Nusselt number of 2.0), Bourdin et al. (1983) suggested that the gas thermal conductivity can be evaluated as an integrated mean value defined by,

$$ \begin{array} {lll} {\overline{k}}_G & =\frac{1}{\left({T}_{\infty }-{T}_s\right)}\left[\underset{T_s}{\overset{T_{\infty }}{\int }}{k}_G(T) dT\right] \\ & =\frac{1}{\left({T}_{\infty }-{T}_s\right)}\left[\underset{T_{300}}{\overset{T_{\infty }}{\int }}{k}_G(T) dT-\underset{T_{300}}{\overset{T_s}{\int }}{k}_G(T) dT\right] \\ & =\frac{1}{\left({T}_{\infty }-{T}_s\right)}\left[I\left({T}_{\infty}\right)-I\left({T}_s\right)\right] \end{array}$$

(58)

where I(T) is the heat conduction potential and is given in the literature (Bourdin et al. 1983). It should be noted that if k_G is a linear function of temperature, the above equation reduces to $\overline{k_G}={k}_G\left({T}_f\right)$ where T_f is the mean film temperature.

Lewis and Gauvin (1973) developed the following correlation for plasma flow,

$$ Nu=\left(2+0.515{\mathit{\operatorname{Re}}}_p^{1/2}\right){\left({\nu}_f/{\nu}_{\infty}\right)}^{0.15} $$

(59)

where Re is evaluated at film temperature. Lee et al. (1981) developed the correlation,

$$ Nu=\left(2+0.6{\mathit{\operatorname{Re}}}_p^{1/2}{\mathit{\Pr}}^{1/3}\right){\left(\frac{\rho_{\infty }{\mu}_{\infty }}{\rho_s{\mu}_s}\right)}^{0.6}{\left(\frac{c_{p\infty }}{c_{ps}}\right)}^{0.38} $$

(60)

where Re and Pr are evaluated at film temperature. Chen et al. (1982) also proposed the correlation,

$$ Nu=2\left(1+0.63{\mathit{\operatorname{Re}}}_{\infty }{\mathit{\Pr}}_{\infty}^{0.8}{\left(\frac{{\mathit{\Pr}}_s}{{\mathit{\Pr}}_{\infty }}\right)}^{0.42}{\left(\frac{\rho_{\infty }{\mu}_{\infty }}{\rho_s{\mu}_s}\right)}^{0.52}{\left(\frac{1-{\left(\frac{h_s}{h_{\infty }}\right)}^{1.1}}{1-{\left(\frac{h_s}{h_{\infty }}\right)}^2}\right)}^2\right) $$

(61)

where h_s and h_∞ are the specific enthalpy of plasma at the particle surface temperature and plasma temperature, respectively.

To account for noncontinuum effects in plasma conditions, Chen and Pfender (1983) developed the following correlation using the temperature jump concept,

$$ q={(q)}_{\mathrm{cont}.}\left[\frac{1}{1+\left(\frac{2-a}{a}\right)\left(\frac{\gamma }{1+\gamma}\right)\frac{4}{\Pr_s}{Kn}^{\ast }}\right] $$

(62)

where (q)_cont. is the heat flux obtained from continuum assumption, and Kn^∗ as well as other parameters are defined in equation (49).

If the particle phase is assumed to be a diffuse-gray surface, the radiation heat transfer equation would be,

$$ {\dot{Q}}_r=S{\upalpha \upsigma}_b\left({T}_{\infty}^4-{T}_d^4\right) $$

(63)

where α is the absorptivity (from Kirchhoff’s law ε = α where ε is the emissivity), T_∞ is the ambient temperature, and σ_b = 5.6704 × 10⁻⁸W/(m² . K⁴) is the Stefan-Boltzmann constant (Siegel and Howell 1981; Crowe et al. 1998).

When the droplet/particle temperature is between the melting and boiling temperatures (T_melt ≤ T_d < T_boil), the vaporization phenomenon should be modeled. In the case of slow vaporization rate, it can be assumed that the process is only controlled by diffusion (ANSYS 2011; Jadidi et al. 2015a),

$$ {N}_i={h}_m\left({C}_{i,s}-{C}_{i,\infty}\right) $$

(64)

where N_i is the vapor molar flux, h_m is the mass transfer coefficient, C_i, s is the vapor concentration at the droplet surface, and C_i, ∞ is the vapor concentration in the bulk gas. h_m is usually calculated using the Sherwood number correlation,

$$ Sh=\frac{h_m{d}_0}{D_{i,j}}=2+0.6{\mathit{\operatorname{Re}}}^{1/2}{Sc}^{1/3} $$

(65)

where D_i, j is the binary diffusion coefficient, Re is the droplet/particle Reynolds number, and Sc is the Schmidt number (ratio of kinematic viscosity (i.e., momentum diffusivity) and mass diffusivity, Sc = ν/D_i, j). The parameter C_i, s in Eq. 64 is usually calculated by,

$$ {C}_{i,s}=\frac{P_{\mathrm{sat}}}{R_u{T}_d} $$

(66)

where P_sat is the saturated vapor pressure at the droplet/particle temperature, and R_u is the universal gas constant. In addition, C_i, ∞ is calculated by solving the transport equation for species.

In the case of high vaporization rate, vapor diffusion and convection from the droplet/particle surface to the surrounding gas should be considered. The following correlation is suggested to estimate the vaporization rate (Sazhin 2006),

$$ \frac{dm_d}{dt}={h}_mS{\uprho}_G\mathit{\ln}\left(1+{B}_m\right), \, {B}_m=\frac{Y_{i,s}-{Y}_{i,\infty }}{1-{Y}_{i,s}} $$

(67)

where Y_i, s and Y_i, ∞ are the vapor mass fraction at the droplet/particle surface and in the bulk gas, respectively, and B_m is the Spalding mass number. When the boiling temperature is reached, the droplet/particle energy equation becomes,

$$ -\frac{dm_d}{dt}{h}_{fg}= hS\left(T-{T}_d\right)+S{\upalpha \upsigma}_b\left({T}_{\infty}^4-{T}_d^4\right) $$

(68)

In the case of high vaporization rate, the convection heat transfer coefficient can be computed by,

$$ Nu=\frac{hd}{k_G}=\frac{\mathit{\ln}\left(1+{B}_T\right)}{B_T}\left(2+0.6{\mathit{\operatorname{Re}}}^{1/2}{\mathit{\Pr}}^{1/3}\right) $$

(69)

where B_T is the Spalding heat transfer number. It is usually assumed that B_T = B_m (ANSYS 2011; Jadidi et al. 2015a).

4.2.4 An Approach to Model the Suspension Droplets

Jabbari et al. (2014) used an Eulerian-Lagrangian approach with two-way coupling assumption to model the suspension plasma spray processes. The suspension droplets (containing nickel (15 wt.%) and ethanol) were radially injected into an atmospheric plasma jet. The injector diameter was 0.15 mm. Suspension with a given particle concentration (i.e., slurry droplet) was modeled as a multicomponent droplet carrying properties of solid particles and base liquid (see Fig. 19). In other words, one component is the base liquid (e.g., ethanol) and another one includes the particle properties such as density and latent heat of evaporation. The KHRT breakup model was used to simulate the droplet breakup. After completion of the suspension breakup and evaporation, the solid particles were tracked through the computational domain to determine the characteristics of the coating particles (see Fig. 19). To evaluate the particle temperature before its melting point, the specific heat of solid particle was used. The particle melting phenomenon was approximated by the following formula:

$$ {\mathrm{C}}_p\Delta T={H}_f $$

(70)

where C_p is the estimated particle specific heat, ΔT is assumed to be 10 K, and H_f is the heat of fusion. After melting, the specific heat of molten particle was used (see also Jadidi et al. 2015b, 2016a; Pourang et al. 2016; Dalir 2016).

Fig. 19

Suspension droplet evolution in realistic and model cases (Jabbari et al. 2014)

The temperature evolution of a 40 μm suspension droplet (containing zirconia (10 wt.%) and ethanol) in a steady undisturbed plasma flow (argon and hydrogen (10% volume fraction) jet with mass flow rate of 1.48 g/s and arc current and voltage of 500 A and 65 V, respectively) was analyzed using the abovementioned model (Pourang 2015). The droplet was located at the center of the nozzle exit plane and the breakup phenomenon was not considered. Figure 20 illustrates the evolution of suspension droplet and particle as a function of time while it is traveling inside the plasma flow. It is shown that after ethanol evaporation, the particle temperature increases and then decreases due to its trajectory along the jet centerline. Figure 20b shows that the melting state of the particle can be captured by the above assumption.

Fig. 20

Evolution of the overall temperature of a suspension droplet (containing zirconia (10 wt.%) and ethanol) as function of time (Pourang 2015)

The velocity, location, and angle of injection of the suspension have an important effect on its penetration in the plasma jet and ensuing particle inflight behavior. For example, Jabbari et al. (2014) showed that the penetration of suspension containing nickel (10 wt.%) and ethanol increases as the injection momentum increases. However, when the liquid/gas momentum ratio was too high, the plasma jet cooled down severely, and the resulting number of high-temperature particles decrease. Figure 21 illustrates the effect of injection angle and location on the suspension penetration and plasma temperature. If the injector is near the torch exit and its angle is toward the torch, the suspension penetrates more efficiently the plasma jet resulting eventually in higher particle velocity and temperature (Jabbari et al. 2014).

Fig. 21

Effects of injector location and angle on the suspension penetration and plasma temperature (the suspension injection velocity is 25.7 m/s) (Jabbari et al. 2014)

5 Heat Transfer to the Substrate

Heat is transferred to the substrate during spraying due to the impingement of the hot gas jet and spray particles. The heat transfer mechanisms are similar in SPS to that in air plasma spray (APS) and other thermal spray processes (Mariaux et al. 2003). However, the heat transfer to the substrate from the hot gas jet is much higher in SPS than APS because of the shorter spray distances used in SPS (3–5 cm) as compared to APS (7–12 cm). The heat flux brought by the plasma jet is generally higher than 10 MW/m² in SPS while it is below 2 MW/m² at the spraying distances used in APS.

In all spray processes, the molten or semi-molten particles transfer energy to the substrate from their kinetic energy upon impact, specific heat and heat of solidification. Although the size of the spray particles is smaller in SPS than that in APS, the energy transfer is expected to be in the same range as their spray rate and impact velocity are comparable. One distinctive characteristic of SPS is the actual particle trajectories around the substrate as discussed below.

5.1 Particle Trajectories Around the Substrate

In SPS, the diameter of molten particles is in the range of 0.1–4 μm. Due to their low inertia, these particles tend to be decelerated and deflected by the presence of the substrate (Oberste-Berghaus et al. 2005). To provide detailed information on the coating particles upon impact, the influence of flat substrates located at various standoff distances from the torch exit was investigated by Jadidi et al. (2015b) (suspension droplet containing nickel (15 wt.%) and ethanol, and particles in the range of 0.5–3.5 μm were considered). In this study, it was assumed that when particles hit the substrate, they stick on it. It was found that, by adding the substrate in the domain, the Ar plasma temperature near the substrate location increases due to less mixing of air and plasma. Moreover, it was shown that many small particles are decelerated and get diverted by the stagnation region near the substrate location. Noting that the particles that move close to the plasma jet centerline are less affected by the stagnation region (see Fig. 22). The effect of Stokes number on the particle inflight behavior near the substrate was also investigated (see Fig. 23). It was revealed that particles with low Stokes number (St = 0.1) follow the gas streamlines and decelerate dramatically. On the other hand, particles with high Stokes number (St = 2.1) decelerate gradually. They concluded that, particles with low Stokes number coat the substrate at large radial distance from the centerline, with low velocity (Jadidi et al. 2015b).

Fig. 22

Nickel particle velocity and trajectory at different standoff distances (D) (Jadidi et al. 2015b)

Fig. 23

Effects of Stokes number on particle inflight behavior near the substrate (using normalized diameter and velocity, D is the distance between the torch exit and the substrate, d is the distance from the substrate, d_i = 7.88 mm, and v₀ = 1800 m/s) (Jadidi et al. 2015b)

The effect of substrate shape and curvature on particle inflight behavior was studied by Pourang et al. (2016). They developed the works of Jabbari et al. (2014) and Jadidi et al. (2015b) by adding a constant volumetric heat source (Eq. 14) in the plasma flow energy equation. Flat and cylindrical substrates at different standoff distances were considered. They showed that the substrate shape has significant influences on the particles trajectory and velocity near the substrate (see Fig. 24). Based on the assumed operating conditions, it was revealed that, in a fixed time interval, particles struck the flat substrate 2.2 times more often than observed on the cylindrical substrate (Pourang et al. 2016). Therefore, they introduced a new parameter called catch rate, which shows the maximum possible deposition rate, as follows:

$$ \mathrm{Catch}\ \mathrm{rate}\ \left(\%\right)=\frac{\mathrm{mass}\ \mathrm{of}\ \mathrm{landed}\ \mathrm{particles}\ \mathrm{in}\ \Delta t}{\mathrm{mass}\ \mathrm{of}\ \mathrm{in}\mathrm{jected}\ \mathrm{particles}\ \mathrm{in}\ \Delta t}\times 100 $$

(71)

Fig. 24

The effect of cylindrical substrate on Yttria-stabilized zirconia particle temperature and trajectory (standoff distance is 40 mm) (Pourang et al. 2016)

Based on the operating conditions assumed in their paper, they explained that catch rates on the flat and cylindrical substrates were 23 and 11%, respectively. In other words, the deposition rate on the curved substrates was found to be lower (Pourang et al. 2016).

The model presented by Jabbari et al. (2014) as well as the approach of variable conical/cylindrical zones (Eqs. 15, and 16) was employed by Dalir (2016) to study the effect of plasma fluctuations on the particle trajectory, velocity, and temperature in the suspension plasma spray processes. It was found that the suspension penetration height significantly changes due to the plasma jet fluctuations. It was also shown that as the injection velocity increases, the changes of suspension penetration height become more severe. Moreover, it was found that particle trajectory, temperature, and velocity are strongly dependent on time since the gas temperature and velocity change with time due to plasma fluctuations (Dalir 2016).

6 Conclusion

Suspension plasma spray (SPS) is an innovative process in which a suspension of submicron size particles is injected in a DC plasma jet. The suspension is rapidly atomized by the high speed plasma jet forming suspension droplets that, in turn, are heated by the plasma freeing the suspended particles that are then molten and propelled toward a substrate by the plasma jet. The atomization of the suspension plays a fundamental role in the final spray particle characteristics as it directly influences the droplet size and trajectories in the plasma jet and then the heat and momentum transfer to the spray particles.

This chapter focused on the mechanical and thermal interactions of the injected suspension with a DC plasma jet. 3D modeling of these interactions makes it possible to develop a better understanding of the influence of the spray parameters on the spray particle characteristics that combined with the substrate properties (material, surface roughness and cleanliness, temperature, standoff distance, etc.) determine the coating characteristics. This is an ongoing journey as the physical and chemical transformations occurring during spraying are complex.

7 Cross-References

• A Prelude to the Fundamentals and Applications of Radiation Transfer

• Analytical Methods in Heat Transfer

• Droplet Impact and Solidification in Plasma Spraying

• Electrohydrodynamically Augmented Internal Forced Convection

• Full-Coverage Effusion Cooling in External Forced Convection: Sparse and Dense Hole Arrays

• Fundamental Equations for Two-Phase Flow in Tubes

• Heat Transfer in DC and RF Plasma Torches

• Macroscopic Heat Conduction Formulation

• Plasma-Particle Heat Transfer

• Radiative Plasma Heat Transfer

• Radiative Properties of Gases

• Radiative Properties of Particles

• Synthesis of Nanosize Particles in Thermal Plasmas

• Thermophysical Properties Measurement and Identification

• Turbulence Effects on Convective Heat Transfer