Compressive Data Recovery in Wireless Sensor Networks—A Matrix Completion Approach

Abstract

Energy-consumption of the wireless sensor networks(WSNs) is proportional to the sampling rate. The need for more energy-efficient methods for WSNs data gathering is greater demand since most of the energy is consumed in sampling and transmission. Recently, compressive sensing (CS) and matrix completion (MC) have been earning increasing interests in the area of WSNs. Both of CS and MC exploit the sparsity presents in sensing environment to reduce sampling rate needed for data acquisition and processing. In this paper, a new scheme based on MC is proposed to reduce such sampling rate. The new scheme is evaluated in a real-data domain and its performance is compared with CS techniques in unified framework. The results show the superiority of MC over the CS techniques in the accuracy of data recovery with different sampling rate.

The original version of this chapter was revised: Two of the authors names were excluded in the chapter. The erratum to this chapter is available at DOI 10.1007/978-3-319-26690-9_47

An erratum to this chapter can be found at http://dx.doi.org/10.1007/978-3-319-26690-9_47

1 Introduction

In recent years, the development of WSNs has received much attention both in the academia and in the industry. Due to its ability to operate at inaccessible areas. While WSNs are equipped to handle some of complex functions and in-network processing, these sensor nodes are required to use their energies efficiently in order to extend their effective network lifetime [1–3]. It has recognized the sparseness in signal structures in a surplus of applications where, various signals of interest may be sparsely modelled and that sparse modelling is often beneficial, or even essential to signal recovery. The rich theory of sparse and compressible signal recovery has recently been developed under the name compressed sensing (CS). This revolutionary research has demonstrated that many signals can be recovered from severely under-sampled measurements by taking advantage of their inherent low-dimensional structure. More recently, an offshoot of compressive sensing has been a focus of research on other low-dimensional signal structures such as matrices of low rank. A subclass of low rank matrices problems called matrix completion (MC). To further extend the sparse problem from the vector to the matrix, the matrix completion can complete a matrix from a small set of corrupted entries based on the assumption that the matrix is essentially of low rank. The compressive sensing involves in the vectors $l_{1}$-norm minimization, which is the number of non-zero items of a vector. In matrix recovery problem, the signal to be recovered is a low-rank matrix $M \in R^{m \times n}$, about which we have information supplied by means of a linear operator $P_{\varOmega }: R^{m \times n} \rightarrow R^{m \times n}$. In this paper, a new method based on the matrix completion for WSNs is proposed to reduce such sampling rate based on non pre-defined probability (i.e., random-distribution). The purposed method is evaluated in a real-data WSNs domain and its performance is compared to two compressive sensing methods in unified framework. The key contributions of this paper are concluded as follows: (1) We propose MC technique for data recovery to improve the lifetime of wireless sensor networks by reduce such sampling rate, (2) We evaluate the proposed techniques accuracy through experimental results, and (3) We demonstrate the superiority of our MC data recovery scheme through experiments on extensive datasets compared with other CS-algorithms, our MC-scheme achieves significant energy-saving while delivering data to the end with high fidelity.

The rest of the paper is organized in the following manner. In Sect. 2, the related works are surveyed. In Sect. 3, we describe a brief mathematical introduction on CS and MC theory that will be applied in this paper. In Sect. 4, a new algorithm is proposed for data aggregation and recovery in WSNs. Detailed experiments results are provided in Sect. 5. Finally, Sect. 6 concludes the paper and discuss the future work.

2 Related Works

The traditional approach to data recovery in WSNs is to collect data from each sensor to one central server, and then process and compress the data centrally. However, WSNs sensing data often have high spatial or temporal correlation [4]. These sparsity in structure of the signals, channels and sensors can be explored and utilized by many techniques such as distributed source coding techniques [5], in-network collaborative wavelet transform methods [6] and clustered data aggregation methods [7]. Recently, both compressive sensing and matrix completion help to significantly reduce the number of transmissions required to have an efficient and reliable data communications [8]. This is because, the compressive sensing (CS) [9]; is compressing the sensed data in each sensor prior to transmission to the fusion center [10, 11]. Recently, Candes and Recht [12] describes the matrix completion (MC) which has emerged as an extend to compressive sensing and promising technology to enable efficient data gathering in WSNs [10, 11, 13, 14]. The matrix representations have many advantages over vector representations. The matrix completion proposed approaches are taking the advantage of the intra-temporal correlation of the sensor measurements and the data matrix filled by sensory readings exhibits low rank feature [15]. Therefore, the fusion center can only collect part of the sensory readings and use matrix completion algorithm to recover the missing data, due to data communication losses results from bandwidth limitations and the resource-constrained nature of the sensors, by using the matrix completion principles [16]. Both compressive sensing and matrix completion based data compression are moves most computation from sensor nodes to the fusion center, which makes it a good fit for in-network data suppression and compression. Cheng et al. [17] are proposed an Efficient Data Gathering Approach (EDCA) which takes advantage of the low-rank feature to achieve both less traffic and high-level accuracy. However, suffer from a low sampling rate tends to result in insufficient measurements, leading to large recovery errors. Recently, a Spatio-Temporal Compressive Data Collection (STCDG) is an extend to (EDCA) data gathering scheme which takes advantage of both the low-rank and short-term stability features to reduce the amount of traffic in WSNs and achieves a reasonable recovery accuracy [18]. One of the major disadvantages of these previously successful attempts to implement the matrix completion for WSNs, is to forward its readings to the fusion center according to a pre-set probability. Another issue is does not evaluate its performance against compressive sensing-based approaches in low level sampling rate.

3 Preliminaries

3.1 Compressive Sensing Technique

Compressive sensing has emerged as a new framework for signal acquisition and sensor design that enables a potentially large reduction in the sampling and computation costs for sensing signals that have a sparse or compressible representation. The concept of compressive sensing is based on the fact that there is a difference between the rate of change of a signal and the rate of information in the signal [19]. A conventional compression algorithm would then be applied to all of these samples taken to remove any redundancy present, giving a reduced number of bits that represent the signal. In contrast, compressive sensing exploits the information rate within a particular signal. In the context of a WSN, suppose that $\mathbf {x} \in R^{N}$ is a signal referred to the sensed data of an individual sensor. compressive sensing theory proves that if $\mathbf {x}$ is sparse in some domain, it can be reconstructed exactly with high probability from $\mathbf {M}$ randomized linear projections of signal $\mathbf {x}$ into a measurement matrix $\varPhi \in R^{M\times N}$, where $M\ll N$. When a signal is sparse in the domain it is samples in, e.g. a high sample-rate time-series sampling infrequently occurring events, one can make a condensed representation of this signal by simple dimensionality reduction.

$$\begin{aligned} \mathbf {y} = \varPhi \mathbf {x} \end{aligned}$$

(1)

where in (1) $\mathbf {x}$ is an N-dimensional K-sparse vector of the original signal, $\varPhi$ is an $M \times N$ dimensionality reduction matrix and $\mathbf {y}$ is an M-dimensional dense vector containing a condensed representation of $\mathbf {x}$, where:

$$\begin{aligned} K \le M \ll N \end{aligned}$$

(2)

It can then be proven that using random projection i.e. using a random dimensionality reduction matrix $\varPhi$, will allow for recovery of $\mathbf {x}$ with little to no information loss, with overwhelming probability. When a signal is sparse in a domain different from the sampled domain, one can make a transformation, by way of a transformation matrix.

$$\begin{aligned} \mathbf {y} = \varPhi \varPsi \mathbf {b} \end{aligned}$$

(3)

where in (3) $\varPsi$ is an $N \times N$ transformation matrix e.g. Wavelets, Discrete Fourier Transform (DFT) or Discrete Cosine Transform (DCT). The dimensionality reduction matrix and the transformation matrix can be combined to an augmented dimensionality reduction matrix.

$$\begin{aligned} \mathbf {y} = \varPhi \varPsi \mathbf {x} = \varTheta \mathbf {b} \end{aligned}$$

(4)

where $\varTheta$ = $\varPhi \varPsi$. This, combined with the fact that random projection is an option negates the need for a transformation matrix, as a random projection of any matrix is just another random matrix. It is then only necessary to be aware of the domain in which the signal is sparse when one is reconstructing the signal, not when sampling or transmitting. One needs only to be able to know or construct the random projection matrix used to compress the signal. This can be done by using pseudo-random generator with a known or predictable seed. Essentially, each sensor instead of transmitting a signal $\mathbf {x} \in R^{N}$, it performs compressive sensing, and it finally transmits a smaller signal $\mathbf {y} \in R^{M}$. The original vector b and consequently the sparse signal $\mathbf {x}$ is estimated by solving the following $\ell _{1}-norm$ constrained optimization problem:

$$\begin{aligned} \min _{\mathbf b} \; \parallel \mathbf {b} \parallel _{1} \qquad \text {subject to } \;\; \mathbf {y} = \varTheta \mathbf {b} \end{aligned}$$

(5)

3.2 Matrix Completion Technique

The job of matrix completion is to recover a matrix $\mathbf {M}$ from only a small sample of its entries. Let $\mathbf {M} \in R^{m \times n}$ be the matrix we would like to know as precisely as possible while only observing a subset of its entries $(i, j) \in \varOmega$. It is assumed that observed entries in $\varOmega$ are uniform randomly sampled. Low-rank matrix completion is a variant that assumes that $\mathbf {M}$ is low-rank. The tolerance for “low” is dependant upon the size of $\mathbf {M}$ and the number of sampled entries. For further explanation let us define the sampling operator $P_{\varOmega }: R^{m \times n} \rightarrow R^{m \times n}$ as

$$\begin{aligned} P_{\varOmega }(\mathbf {A}) = \left\{ \begin{array}{lr} A_{ij} &{} : (i,j) \in \varOmega \\ 0 &{} : \mathrm {otherwise} \end{array} \right. \end{aligned}$$

(6)

Let an opposite operator $P_{\varOmega }$ is defined which keeps those outside $\varOmega$ unchanged and sets values inside $\varOmega$ (i.e. $\bar{\varOmega }$) to 0. Since we assume that the matrix to recover is low-rank, one could find the unknown matrix by solving

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{} \text{ rank }(\mathbf {M})\\ \text{ subject } \text{ to } &{} M_{ij} = A_{ij} \qquad (i,j)\in \varOmega \end{array} \end{aligned}$$

(7)

where matrix $\mathbf {M}$ is the partially observed matrix. Unfortunately, this optimization problem has been shown to be NP-hard and all known algorithms which provide exact solutions require exponential time complexity in the dimension of the matrix both in theory and in practice [12]. Also, the $rank(\mathbf {M})$ makes the problem non-convex and several approximations to the problem exists. One, the tightest convex relaxation of $rank(\mathbf {M})$ [20] is the following problem

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{} \tau \Vert \mathbf {M}\Vert _* :=\sum \nolimits _{i=1}^r \sigma _i(\mathbf {M}) \\ \text{ subject } \text{ to } &{} P_{\varOmega }(\mathbf {M}) = P_{\varOmega }(\mathbf {A}) \end{array} \end{aligned}$$

(8)

where $\sigma _i(\mathbf {M})$ denotes the ith largest singular value of M and $\Vert M\Vert _*$ is called the nuclear norm. The main point of this relaxation is that the nuclear norm is a convex function and thus can be optimized efficiently via semi-definite programming or by iterative soft thresholding algorithms [21, 22]. The case where observed entries may contain a limited amount of noise $\mathbf {E}$ is considered. The corresponding objective is considered as following:

$$\begin{aligned} \min _{\mathbf {M}} \; \tau \Vert \mathbf {M} \Vert _* + \frac{\lambda }{2} \Vert P_{\varOmega } (\mathbf {E}) \Vert _F^2 \qquad \text {subject to } \; P_{\varOmega } (\mathbf {A}) = P_{\varOmega } (\mathbf {M}) + P_{\varOmega } (\mathbf {E}) \end{aligned}$$

(9)

where $\tau$ and $\lambda$ are regularisation parameters. The matrix completion theory proves that if this matrix (denoted by $\mathbf {M} \in R^{m \times n}$ ) has a low rank, it can be recovered with high probability. More interestingly, one can recover $(\mathbf {M})$ from $s \geqslant C d^{6/5}rlog(d)$ random measurements, where C is a positive constant, $d = max(m, n)$, and r is the rank of the matrix [23].

4 Proposed Approach

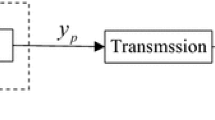
In this section, a new data aggregation method for WSNs which is based on matrix completion is proposed. Consider a sensor network consisting of N nodes. Each node samples at a fixed rate and forwards the data to the fusion center through a single-hop way. Where at the fusion center an $N\times T$ matrix can be constructed, where T means the maximum number of samples at each node, i.e., $M \in R^{N\times T}$. However, due to the sampling scheduling or lossy transmission and the failure of sensor nodes, some data are missing and the matrix is incomplete and only S samples are received by fusion center. Thus adopting a linear operator $P_{\varOmega }(\cdot )$ to represent such lossy or selection effect(s) (see Sect. 3). The implemented matrix completion algorithm using the Interest-Zone Matrix-Approximation [24]. The representation of the operations of proposed system is shown below in Fig. 1 and the proposed procedure is listed in Algorithm 1. As demonstrated in Fig. 1, the data sampled or collected and transmitted to the fusion center which recovers the missing or lost samples based on the linear operator $P_{\varOmega }(\cdot )$.

Fig. 1

Representation of the operations of matrix completion system in a WSN. The sensor nodes send the measured data to the fusion center based on the sampling or lossy communication, then the fusion center complete these entries using matrix completion algorithm

By applying the same concept using the compressive sensing theory for both the orthogonal matching pursuit (OMP) algorithm and adaptive principle component analysis (PCA) [14], where the signal model is learned from the measurements.

5 Implementation and Evaluation

In this section, the performance of discussed methods are evaluated and compared empirically; the applied algorithms is verified in the multi-sensor case where nearby sensor nodes measure spatially correlated signals and a real-world meteorological datasets are used as the ground truth, namely Valais [14]. The Valais is provided by a micro-climate monitoring service provider [25]. A total of six stations are deployed in a mountain valley, covering an area of around $18\,\mathrm{km}^{2}$. The deployments were started in March 2012 and collected 125 days of continuous temperature measurements. The data set is 144 uniformly sampled data points for each day. The real world trace forms a $144 \times 6$ matrix which represents the temperature values sampled. A key issue regarding the evaluation of performance of different techniques, is related to the specific metric that we use in order to quantify the results. The commonly used root mean squared error (RMSE) is employed which given by,

$$\begin{aligned} \mathbf {RMSE} = \frac{1}{\sqrt{m\times n}}\parallel \mathbf M - {\hat{\mathbf {M}}} \parallel _{l_{2}} \end{aligned}$$

(10)

defined as the root mean squared error between the fully populated and the reconstructed measurements matrix, normalized with respect to the $l_{2}$ norm. where, $\mathbf M$ is the actual data matrix, ${\hat{\mathbf {M}}}$ is the recovered data matrix and $m \times n$ are the dimensions of the matrices. In our paper, we implemented the proposed data recovery methods using MATLAB. Table 1 summarize the reconstruction error under a fixed data selection or sampling rate ($\eta$) with respect to the estimation error of SNR, whereas the true SNR is $30\,\mathrm{dB}$. According to results given in Table 1 and Fig. 2, MC is both more accurate and robust when compared to the state-of-the-art CS methods.

Table 1 Evaluation of different approaches at sampling rate $\eta =20\,\%$

Fig. 2

The recovery of the last day for first sensor using orthogonal matching pursuit (OMP), adaptive principle component analysis (PCA) and matrix completion (MC) algorithms

Fig. 3

The sampling rate ($\eta$) versus RMSE of each algorithm

Fig. 4

Recovery error (RMSE) versus SNR (dB) of the measurements under sampling rate ($\eta =20\,\%$)

Then, we analyze the influence of the sampling rate. Figure 3, comparing the recovery error (RMSE) against different sampling rate ($\eta$) shows that the MC-scheme has the minimum error value compared to other techniques. The experiments have been carried out with $5{-}50\,\%$ of the samples. It has been empirically observed that if the number of samples is higher, it slightly reduces the error of the recovered value. The results shows that both of MC and PCA recovery rate is more accurate in low sampling rate than OMP algorithm. However, at higher sampling rate the OMP algorithm converges nearly to the MC and PCA results. An estimations of the SNR for the noisy measurement is necessary to avoid degradations of the recovery quality. Figure 4 shows the comparison results of the three algorithms. In the high SNR regime $({\geqslant }30\,\mathrm{dB})$, the three algorithms tend to perform the similar trend and are stable w.r.t. errors in the SNR estimation. However, it can be noted that MC generally performs better than the two compressive sensing-based schemes, in high and low SNR regime. also, it can be see that matrix completion performs the best and is more accurate and robust when compared to the other sparse sensing methods.

6 Conclusions and Future Work

In this paper, a new data aggregation technique for WSNs based on MC is proposed, which obtains successful results with a uniform random selection of samples. The detailed algorithm is explained, and experiments are carried out to show its effectiveness. The potential of both CS and MC techniques are investigated by using real sensor data. The results of our simulations on real data is promising and confirming that utilizing spatio-temporal correlation in MC increases the performance, which is introduced in terms of reconstruction error and the number of measurements taken. The fact that a minimum mutual coherence between the measurement matrix $\varPhi$ and representing matrix $\varPsi$ in CS-schemes is not guaranteed which is a requirement for achieving a successful CS recovery even with the using of adaptive PCA scheme. The main contribution is to show the feasibility of employing the MC for WSN data aggregation purposes in the under-sampled case which achieves significant energy-saving while delivering data to the end with high fidelity. In the future, the studies will be aimed to improve the performance of proposed method and study the effect of different parameters such as communication loss and increasing number of sensors for very large-scale WSN problems.