Opinion Formation Dynamics Under the Combined Influences of Majority and Experts

Abstract

Opinion formation modelling is still poorly understood due to the hardness and complexity of the abstraction of human behaviours under the presence of various types of social influences. Two such influences that shape the opinion formation process are: (i) the expert effect originated from the presence of experts in a social group and (ii) the majority effect caused by the presence of a large group of people sharing similar opinions. In real life when these two effects contradict each other, they force public opinions towards their respective directions. Existing models employed the concept of confidence levels associated with the opinions to model the expert effect. However, they ignored the majority effect explicitly, and thereby failed to capture the combined impact of these two influences on opinion evolution. Our model explicitly introduces the majority effect through the use of a concept called opinion consistency, and captures the opinion dynamics under the combined influence of majority supported opinions as well as experts’ opinions. Simulation results show that our model properly captures the consensus, polarization and fragmentation properties of public opinion and reveals the impact of the aforementioned effects.

1 Introduction

Opinion formation dynamics captures the evolution of individual’s opinion in a social group to a collective opinion under social influences. Repeated interactions among the group members due to social influences enforce individuals to revise their thoughts, adopt new ideas, or refine beliefs. Modelling such dynamics ensures the better realization of individual behaviours and peer influences that encourage the group members to change their initial opinions and thereby helps better understanding of the nature and composition of the final opinion.

Opinion formation modelling has been established as an active research area, thanks to the seminal works of DeGroot [3], Clifford and Sudbury [4], Hegselmann and Krause [5], Deffuant and Weisbuch [6], and Sznajd [2] that have attracted researchers from multiple disciplines afterwards. The models either represent opinions using continuous values in a range [3, 5, 6] or consider discrete opinions [1, 4]. Though a group of discrete opinion models have exploited majority effects [2] and some continuous models have considered expert effect to an extent, but none of the modelling approaches have considered majority and expert effects jointly. As both effects are concurrently present in the society with possible contradiction between them, we need to model their joint influence on an agent’s opinion to better capture the dynamics.

Continuous opinion dynamics encode the expert effect by incorporating the concept of confidence of an agent on its expressed opinion [8, 9]. Moussaid et al. [8] used confidence level in their modelling to distinguish experts as agents with high confidence levels. However, the efficacy of the approach is limited due to the use of: (i) a few intuitively defined rules considering a particular context and (ii) interactions are limited to pair-wise between agents. Consequently, this approach fails to capture the impact of the overall confidence levels of a group of agents having similar opinions. On the other hand, Cho et al. [9] uses uncertainty in beliefs to model the confidence of agents. Likewise [8], this model only considers pairwise interactions between the agents. As a result, both models fail to consider the conformity of an agent to a group with majority of them sharing similar opinions (majority effect) while in Asch experiment [10] conformity to majority group is exhibited as a strong social influencing factor. Consequently, their models ignore the presence of the joint influence of the majority and expert effects. Motivated by these research gaps, we assimilate the conformation to majority opinions in a group and the joint influence of the majority effect and the expert effect in continuous opinion formation modelling.

2 Proposed Opinion Formation Model

Consider a social network $G=(V,E)$ with $\vert V \vert = n$ agents forming a collective opinion. An agent $i \in V$ interacts to all its neighbours, $N_i=\lbrace j|j\in V \wedge (i,j)\in E \rbrace$ in each iteration. At time t, the opinion is denoted by $O_{i}(t) \in [0,1]$ for agent i. The range is called the Opinion Space (OS). Every agent also expresses a confidence level $C_{i}(t) \in [0,1]$ on its own opinion $O_{i}(t)$. A highly confident agent can be considered an expert whom other people can rely on. In contrast, individuals with very low confidence level represents lay people having poor knowledge and thus, very hard to be relied on. To jointly integrate the majority and expert effects, in our model an agent is usually influenced by four influencing factors: (i) its own opinion $O_{i} (t)$, (ii) its own confidence $C_{i}(t)$, (iii) neighbours’ opinions $O_{N_{i}} (t)= \lbrace O_{j} (t)| j\in N_{i} \rbrace$, and (iv) neighbours’ confidences $C_{N_{i}}(t)=\lbrace C_{j} (t)| j \in N_{i}\rbrace$. According to the literature [1, 8], in real life opinion update process considers one of the three possible heuristics: (i) keep own opinion, (ii) make a compromise by averaging with neighbours’ opinions and (iii) adopt neighbour’s opinion. To make opinion update as realistic as possible, our model considers all of them. Our model captures the combined effects of majority and expert as described below.

2.1 Formulation of Majority and Expert Effects

To measure the combined impact of the majority and expert effect, an agent computes the credibility of its neighbours’ opinions using the aforementioned four types of information. Here, the credibility score determines how much an agent can rely on its neighbours. To compute credibility, we use a particular measure called consistency for both opinions and confidence levels. Consistency ($\xi (A)$) of a set (A) of values indicates the overall similarity present in the set. The Shannon’s entropy from information theory properly represents the consistency as a set with similar values results in a small entropy whereas diverge valued set has a large entropy. Consequently, a set’s entropy normalized with the maximum possible entropy ($e_{m}$) [11] is a reasonable realization of its consistency.

Opinion Consistency (Majority Effect): Opinion consistency of a neighbourhood is calculated from the entropy value as per Eq. (1).

$$\begin{aligned} \xi (O_{N_{i}}(t)) = 1 - \frac{e(O_{N_{i}}(t))}{e_{m}} \text { where}, \end{aligned}$$

(1)

$$\begin{aligned} e(O_{N_{i}}(t)) = \mathrm {entropy}(O_{N_{i}}(t)) = - \sum \nolimits _{O(t) \in O_{N_{i}}(t)} p(O(t)) \times \log (p(O(t))) \end{aligned}$$

Here, p(O(t)) is the probability of opinion O(t) in neighbours’ opinion set $O_{N_{i}}(t)$. A high $\xi (O_{N_{i}}(t))$ indicates the presence of a large group of agents holding similar opinions, thus captures the majority effect.

Confidence Consistency (Expert Effect): We take into account the possibility of forming different opinion clusters and measure individual groups’ expert effects because experts are likely to share similar thoughts. For simplicity, we assume the OS to be composed of a set $B=\{b_{1}, b_{2}, \cdots , b_{z}\}$ of equal sized blocks constructed from i’s neighbourhood, and opinions inside a block form a cluster. We compute the confidence consistency of a block $b \in B$ as per Eq. (2).

$$\begin{aligned} \xi (C_{ib}(t)) = \log (\mathcal {E}(C_{ib}(t)) \times E(C_{ib}(t))+\eta )/\log (1+\eta ) \text { where, } \end{aligned}$$

(2)

$$\begin{aligned} \mathcal {E}(C_{ib}(t)) = 1- \frac{e(C_{ib}(t))}{e_{m}}, e(C_{ib}(t)) = -\sum \nolimits _{C(t) \in C_{ib}(t)} p(C(t)) \times \log (p(C(t))), \end{aligned}$$

$$\begin{aligned} E(C_{ib}(t)) = \sum \nolimits _{C(t) \in C_{ib}(t)} p(C(t)) \times (C(t)) \end{aligned}$$

Here, $C_{ib}(t)$ is the set of confidence values within the block b and $E(C_{ib}(t))$ is its expected value. Unlike Eq. (1), normalized entropy $\mathcal {E}(C_{ib}(t))$ of the confidence of a block is further multiplied by its expected confidence $E(C_{ib}(t))$ to neutralize any undue impact of expert effect such as a group having similar but very low confidence levels. $\eta$ is used to keep the values in a specific range. The expected confidence consistency as evaluated in Eq. (3) further validates the presence of such expert groups.

$$\begin{aligned} E(\xi (C_{ib}(t))) = \sum \nolimits _{b \in B} \xi (C_{ib}(t)) \times p_{ib}((t)) \text { where, } p_{ib}((t)) = \frac{\vert O_{ib}(t)\vert }{\vert O_{N_{i}}(t)\vert } \end{aligned}$$

(3)

Here, $O_{ib}(t)$ is the opinion set within b and $\vert . \vert$ computes the cardinality of a set.

So far, we have defined the theoretical underpinnings to capture majority and expert effects separately. However to realize their effects in opinion dynamics, Eqs. (2) and (3) can be used to represent the three major mutually exclusive real-world scenarios of opinion update process that are described below:

Scenario 1 (Joint Consideration of Majority and Expert Effects): This scenario captures the influence of a large group consisting of the majority neighbouring agents who are also experts. To represent the majority effect, the majority of the neighbouring agents have to possess similar opinions which yields high opinion consistency, while for the concurrent expert effect, their confidence levels are to be high and consistence. Therefore, their joint effects termed as the credibility score of neighbours can be calculated as the product of opinion and confidence consistencies, which is defined as:

$$\begin{aligned} \chi _{N_{i}}(t) = \xi (O_{N_{i}}(t)) \times E(\xi (C_{ib}(t))) \end{aligned}$$

(4)

Scenario 2 (Influence of Small Groups Consisting of Experts): In the absence of such joint effects, an emerging group of expert agents in the neighbourhood having similar opinions influences the agent to update its opinion. The group exerts more influence as it grows larger, which is a characteristic reflecting majority phenomenon. The larger confidence consistency within group ensures greater influence according to the expert effect. Finally, based on the homophily principle [5], closer distant group have more impacts. Therefore, the influence of a group on an agent opinion is formulated as in Eq. (5).

$$\begin{aligned} \chi _{ib}(t) = \underset{b \in B}{\mathrm {argmax}} (\frac{\xi (C_{ib}(t)) \times p_{ib}(t)}{1+abs(O_{i}(t)-\overline{O_{ib}(t)})}) \end{aligned}$$

(5)

Here, abs() denotes absolute value and $\overline{O_{ib}(t)}$ is the average opinion of block, b. $p_{ib}(t)$, $\xi (C_{ib}(t))$ and $abs(O_{i}(t)-\overline{O_{ib}(t)})$ represent the relative group size, its expert influence and the homophily principle, respectively.

Scenario 3 (Individual Expert’s Influence): When there is no such group in the neighbour opinions, it is only the individual experts that influence an agent. In this situation, the amount of influence depends on their opinion distances [5] and relative confidence level [8] of an expert to an agent as captured by Eq. (6).

$$\begin{aligned} \zeta _{ij}(t) = \frac{ C_{j}(t) - C_{i}(t) }{1+abs(O_{j}(t) - O_{i}(t))}, \text {where } j \in N_{i} \text { and } C_{j}(t) - C_{i}(t) \ge \zeta _{th}(t) \end{aligned}$$

(6)

Here, $\zeta _{th}(t)$ determines the minimum level of confidence that an expert should be higher than an agent to impact on its decision. How an opinion be updated in our proposed model are presented in the following sections.

2.2 Model Description

While revising an agent’s opinion at time t, it looks for the presence of majority and expert effects in the neighbourhood as measured by the neighbours’ credibility score $\chi _{N_{i}}(t)$, small expert group influence $\chi _{ib}(t)$, and individual expert impact $\zeta _{ij}(t)$ and applies the opinion update process for each scenario. Here, the scenarios are confined using three bounding functions that are computed by applying bounding conditions on $\chi _{N_{i}}(t)$ and $\chi _{ib}(t)$ of Eqs. (4) and (5) respectively. The bounding conditions are: (i) $\chi _{N_{i}}(t)\ge \mathcal {F}_{1}(B, \eta )$ for Scenario 1 with $\overline{C_{N_{i}}(t)}\ge C_{i}(t)$, (ii) $\chi _{N_{i}}(t) < \mathcal {F}_{1}(B, \eta )$ and $\chi _{ib}(t)\ge \mathcal {F}_{2}(B,\eta )$ for Scenario 2 with $\overline{C_{ib}(t)}\ge C_{i}(t)$, (iii) $\mathcal {F}_{3}(B,\eta ) \le \chi _{N_{i}}(t)$ for Scenario 3 with not satisfying the conditions for Scenario 1 and 2 and (iv) $\chi _{N_{i}}(t) < \mathcal {F}_{3}(B,\eta )$ for others. The derivations of the bounding functions $\mathcal {F}_{1}(B,\eta )$, $\mathcal {F}_{2}(B,\eta )$ and $\mathcal {F}_{3}(B,\eta )$ are well formulated, however due to the page limitation, it have been presented in https://rajkumardas.files.wordpress.com/2015/08/iconip2015.pdf.

Here, we adopt weighted averaging as the compromise method. An agent choose from one of the following three compromise options:

• Compromising with whole neighbourhood (Scenario 1): As with the condition (i) for Scenario 1 defined above, the collective influence of neighbours is very strong and its average confidence level $\overline{C_{N_{i}}(t)}$ is higher than agent’s own confidence. Thus, the neighbours are as good as one information source and agent i compromises with whole neighbourhood as per Eq. (7).

  $$\begin{aligned} O_{i}(t+1) = (C_{i}(t)\times O_{i}(t)+ \chi _{N_{i}}(t) \times \overline{O_{N_{i}}(t)})/(C_{i}(t)+\chi _{N_{i}}(t)) \end{aligned}$$

  (7)

  Here, the neighbourhood opinion is represented as the average of their opinions, $\overline{O_{N_{i}}(t)}$ and the credibility score is as weight.

• Compromising with a block (Scenario 2): With $\chi _{N_{i}}(t) < \mathcal {F}_{1}(B, \eta )$, neighbours don’t form one overall strong group. However, in absence of such larger block, there may exist some blocks consisting of experts that can influence an agent. $\chi _{ib}(t)\ge \mathcal {F}_{2}(B,\eta )$ and $\overline{C_{ib}(t)}\ge C_{i}(t)$ indicate the presence of such a group with higher average confidence than i, and enforce to compromise with that block as in Eq. (8).

  $$\begin{aligned} O_{i}(t+1) = (C_{i}(t)\times O_{i}(t)+ \chi _{ib}(t) \times \overline{O_{ib}(t)})/(C_{i}(t)+\chi _{ib}(t)) \end{aligned}$$

  (8)

  where, $\overline{O_{ib}(t)}$ is the average opinion of block b.

• Compromising with an expert (Scenario 3): Condition (iii) implies that there is no majority block consisting of experts in the neighbourhood. In such scenario, an agent may search for individual experts to compromise its opinion with one of them chosen with probability $\zeta _{ij}(t)$ using Eq. (9).

  $$\begin{aligned} O_{i}(t+1) = (C_{i}(t)\times O_{i}(t)+ \zeta _{ij}(t) \times O_{j}(t))/(C_{i}(t)+\zeta _{ij}(t)) \end{aligned}$$

  (9)

As alluded at the beginning of Sect. 2, in addition to compromise, opinion update process also allows an agent either to keep own opinion or to adopt one of the neighbours’ opinions which is discussed in the following section.

• Other Scenarios: $\chi _{N_{i}}(t) <\mathcal {F}_{3}(B,\eta )$ means neither a majority nor an expert effect is present. Therefore, the agent ignores them by keeping its opinion. However, we incorporate the free-will concept [7] in our model by making a probabilistic choice between the keep and adoption heuristic.

  $$\begin{aligned} O_{i}(t+1) = \text {Choose randomly with probability p, } \lbrace O_{i}(t),O_{k}(t)\rbrace \end{aligned}$$

  (10)

  Here, $O_{k}(t) \in O_{N_{i}}(t)$ is chosen randomly from the neighbourhood.

3 Simulation Results and Analysis

We adopted the Erdos-Renyi random graph with 1000 nodes to represent a social group in our simulation. Both the agents’ initial opinions and their declared confidence levels were randomly distributed in the range [0, 1]. We experimented with two random distributions for the initial values: (i) uniform random and (ii) normal random with particular mean ($\mu$) and standard deviation ($\sigma$). We considered 10 equal length opinion blocks as per the options in a survey in a scale from 1 to 10. Initial confidence levels were assigned in one of the two ways: (i) uniformly random across the agents and (ii) separately for each block to differentiate their expertise level. To balance the randomness present in the free-will of human decisions, the probability p of selecting between keep and adoption heuristics was set with 0.5. Finally, $\lbrace d_{th}, \lambda _{th}\rbrace$ was assigned with $\lbrace 0.1, 0.85\rbrace$ to make the confidence change condition more stringent.

3.1 Majority vs. Expert Effect

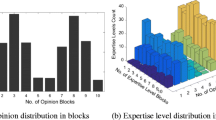
We examined the majority vs. expert effect through a controlled experiment. Agents started with a bimodal initial opinion distribution having two modes at $\mu _{1}=0.25$ (A) and $\mu _{2}=0.75$ (B) with a small standard deviation ($\sigma _{1}=\sigma _{2}=0.05$) for both. The majority effect was created by increasing the number of opinions in mode A from 50 % to 95 %. However, their confidence was confined within [0–0.2] to make them lay people. However, the agents in mode B were assigned confidence levels from 0.1 (very low) to 1 (very high) in experiment with all agents having the same confidence level for each assignment to reflect the expert effect. Figure 1 illustrates the findings by showing the predominant effects in the converged opinions. From Fig. 1 it is clear that consistent agents with high confidence level (0.8 or higher) can be considered experts and drive the majority towards them. As the confidence level decreases, majority effect becomes more prominent. However, there is another region of parameters where both the effects are exerted together which is identified as ‘C’ (combined). Figure 1(b) shows the results of Moussaid et al. [8] model for the same parameters. Their method fails to separate the majority and expert effects as indicated by the large number of grids with ’C’. It also couldn’t accurately capture the expert effect as for very high confidence levels of 0.8–1 only 6 out of 18 cases i.e., ($33.33\,\%$ cases) show the expert influences. In contrast, for confidence level 0.8–1, our model produces $94.44\,\%$ expert effect. Moreover, our model more accurately captures the majority impacts as $75\,\%$ agents having the same initial opinion has produced majority effect in the absence of high confident agents. However, in such cases none of them has shown majority impact in their model.

Fig. 1.

Majority vs. expert effects observed at the end of opinion evolution. (a): Our model, (b): Moussaid et al. [8] Model. Here, E: Expert, M: Majority, and C: Combined.

Fig. 2.

Fraction adopting stubborn opinion

3.2 Effect of Stubborn Agents

Stubborn agents don’t change their opinions under any social influences. In Biased Voter Model [1], the proportion of agents adopting stubborn opinion is increased with the increase of the initial fraction of stubborn agents as shown in Fig. 2. In contrast, in our model this proportion remains steady. In society, stubbornness is not always viewed as an acceptable behaviour to others and is not conducive to influence people. Since our model captures expert effects, people are influenced by informative and reliable sources. Therefore, the effect of stubbornness is minimal, which is expected in a knowledge based society.

3.3 Consensus, Polarization and Fragmentation

Our model captures consensus, polarization, and fragmentation of opinion dynamics as shown in Fig. 3. From the figures we observe that a single confident group leads others to consensus around it (Fig. 3(a)) whereas the presence of more than one confident groups cause polarization (Fig. 3(b)) or fragmentation (Fig. 3(c)). Here, the reason behind the fragmentation of opinions is that the two confident groups reside at the two opposite end of the OS. Therefore, due to their distances and opposite forces, agents in the middle are not convinced by them, thus form their own groups. Without any experts, all agents are grouping in the middle which is an expected outcome of the dynamics (Fig. 3(d)). However, a majority group attract agents towards them in the absence of experts. The polarization around the group depends on the majority proportion. A group of $60\,\%$ majority attracts many agents to it (Fig. 3(e)), whereas a group of $70\,\%$ majority leads to consensus on its opinion (Fig. 3(f)).

Fig. 3.

The initial and final opinion distributions of all agents. Expert blocks are highlighted within rectangle. (a) Consensus (b) Polarization (c) Fragmentation (d) Big cluster in the middle of OS, (e)–(f) Majority effect in absence of experts

4 Conclusion

In this paper we introduce an opinion formation model by considering the combined impact of majority and expert effects. We for the first time introduce the concept of consistency in opinion and associated confidence level of neighbouring agents and embed metrics derived from those to update own opinion as well as confidence level. The performance of our model is analysed through simulation and compared with recent existing opinion formation models. Results show that our model captures the effect of majority, expert and stubbornness more accurately compared to other models. Our future works include the mining of confidence level of agents from online social networks data and incorporation of thereof in our model.