Rapid Reconnection and Field Line Topology

Abstract

Rapid reconnection of magnetic fields arises where the magnetic stresses push the plasma and field so as to increase the field gradient without limit. The intent of the present writing is to show the larger topological context in which this commonly occurs. Consider an interlaced field line topology as commonly occurs in the bipolar magnetic regions on the Sun. A simple model is constructed starting with a strong uniform magnetic field B ₀ in the z-direction through an infinitely conducting fluid from the end plate z = 0 to z = L with the field lines tied at both end plates. Field line interlacing is introduced by smooth continuous random turbulent mixing of the footpoints at the end plates. This configuration is well suited to be modeled with the reduced magnetohydrodynamic (MHD) equations, with the equilibria given by the solutions of the 2D vorticity equation in this case. The set of continuous solutions to the “vorticity” equation have greatly restricted topologies, so almost all interlaced field topologies do not have continuous solutions. That infinite set represents the “weak” solutions of the vorticity equation, wherein there are surfaces of tangential discontinuity (current sheets) in the field dividing regions of smooth continuous field. It follows then that current sheets are to be found throughout interlaced fields, providing potential sites for rapid reconnection. That is to say, rapid reconnection and nanoflaring are expected throughout the bipolar magnetic fields in the solar corona, providing substantial heating to the ambient gas. Numerical simulations provide a direct illustration of the process, showing that current sheets thin on fast ideal Alfvén timescales down to the smallest numerically resolved scales. The asymmetric structure of the equilibria and the interlacing threshold for the onset of singularities are discussed. Current sheet formation and dynamics are further analyzed with dissipative and ideal numerical simulations.

5.1 Introduction

Rapid reconnection of magnetic field arises where the magnetic stresses drive the plasma and field toward increasing field gradients, so that the current density becomes large without bound. In the real world the increasing field gradients are limited by the slight resistivity of the plasma, of course. That is to say, the gradient increases to the point where resistive dissipation eats up the field fast enough to prevent further gradient increase. This quasi-steady dissipation progresses across the field at a speed at least as fast as the Alfvén speed C divided by the square root of the Lundquist number R _L for the overall field (Parker 1957; Sweet 1958a,b). In other words the rapid reconnection phenomenon is a mechanical process, driven by the magnetic forces so as to increase the field gradients and enhance the resistive dissipation. It occurs where two nonparallel field components are actively squashed together, expelling plasma and field from between them and approaching more closely so as to increase the field gradient and current density. The plasma dynamics and the kinetics of the thin intense current sheet control the rate of reconnection of the fields.

Note then that the basic resistive reconnection rate $C/R_{L}^{1/2}$ is nowhere near the explosive field reconnection rate in a solar flare or in a substorm in the geomagnetic tail, motivating serious consideration of the precise form of the reconnection site and the effective rate of dissipation. Petschek (1964) made the important point that the dissipation and reconnection site need not extend the full width of the field. He provided plausible arguments for the reconnection speed to be as large as $C/\ln R_{L}$ and comparable to the reconnection rates in nature. Others noted that the electron conduction speeds in the current sheet may be as large as the ion thermal velocity or greater, exciting plasma turbulence and creating “anomalous resistivity”. Then it became clear that the expected central concentration of anomalous resistivity favored the shortening of the current sheet, automatically providing the Petschek mode. It was recognized that the current sheet may be subject to island formation, with the Hall effect involved to further enhance the dissipation rate. And then it was realized that the current sheet is often so thin at the large Lundquist numbers encountered in tenuous plasmas that the ions may decouple from the magnetic field. So the simple resistive MHD current sheet must be replaced by a treatment in plasma kinetics (Biskamp and Drake 1994; Drake et al. 1994, 2005; Biskamp et al. 1997). The result is a further enhancement of the theoretical dissipation rate with a central concentration that automatically favors the Petschek mode. The reader is referred to the review by Yamada (2011) to fill in some of the details of this fundamental work. One can expect reconnection in nature at the observed rates of 0.01–0.1 C at active moments, interspersed with quiet periods of ongoing reconnection perhaps as slow as the basic resistive rate $C/R_{L}^{1/2}$. Remote observations generally pick up only the active moments, of course.

Finally, Yamada and coworkers have set up the rapid reconnection phenomenon in the laboratory for quantitative measurements. In particular, they have studied conditions for reconnection at the basic rate $C/R_{L}^{1/2}$ compared to conditions for the faster Petschek reconnection mode, reviewed in Yamada et al. (2010) and Yamada (2011). The reader is referred to the several papers (and references therein) on the reconnection rate presented in this Volume and to the alternative approach developed by Ng and Bhattacharjee (1998).

Fig. 5.1

Sketch of interlaced magnetic field line topology of a bipolar solar magnetic field rooted in the convective solar photosphere

The present writing considers where and how the local rapid reconnection phenomenon arises in the overall topology of the surrounding magnetic field. The vigorous convective motions and very large Lundquist numbers found in astrophysical settings suggest that field line topology may be complicated. To consider a basic example, note the common bipolar magnetic fields arching above the solar photosphere. Both ends of the bipolar field are rooted in the turbulent convective photosphere, so the photospheric footpoints of the field are continually intermixed on scales of a few hundred km by the convective granules. It follows that the field lines connecting between the two ends of the bipolar field are interlaced in random patterns along their length, sketched in Fig. 5.1. We investigate the final equilibrium of such a common interlaced field line topology, starting from an initial smooth, continuous, and bounded interlaced field with no further deformations introduced from outside the region, and letting the magnetic stresses in the field topology alone determine the final equilibrium state. The result is that current sheets, i.e., internal sites for rapid reconnection, are intrinsic to interlaced field line topologies wherever they occur (Parker 2012a,b).

In particular it has long been proposed that with vanishing electrical resistivity the current sheets reduce to true mathematical tangential discontinuities. The investigation of singularities in fluid equations poses grand mathematical, physical and computational challenges (Gibbon 2008). While there is no doubt that from a variety of initial conditions of interest to solar and stellar coronae the electric current will in general grow rapidly forming current sheets, a mathematically rigorous proof of the development of a singularity (that remains open also for the 3D Euler and Navier-Stokes equations) may require new methods (e.g., see Tao 2015), while numerical simulations cannot currently follow the unlimited steepening of the field gradients below the numerical resolution set by computational power and machine precision. It seems that a clearer understanding may be attained by a combination of analytical and numerical investigations, and the development of novel computational and mathematical techniques.

5.2 2D Neutral Points

We begin with a brief review of the field line topology associated with the ongoing field gradient increase and rapid reconnection, so that we can better understand the physical ramifications of the general mathematics of the interlaced field line topology.

It is well known (Parker 1957, 1979; Syrovatskii 1971, 1978, 1981) that a 2D X-type neutral point is the setting for rapid reconnection. Pick a point P in the field B(r). Set up a Cartesian coordinate system with its origin at P and the z-axis tangent to B(P). The x and y-axes are perpendicular to B(P) of course, so $B_{x}(P) = B_{y}(P) = 0$. Thus the transverse field in the xy-plane has a 2D neutral point at P. The neutral point is either X-type or O-type.

A pure X-type neutral point arises in the absence of torsion (B ⋅ ∇×B = 0), i.e., in a 2D potential field. With suitable orientation of the xy coordinates, the local field in the near neighborhood of P can be written as

$$\displaystyle{ B_{x} \simeq \beta y,\quad B_{y} \simeq \beta x,\quad }$$

(5.1)

where β is a constant and the scalar potential is β x y. This field can be expressed in terms of the local vector potential in the z-direction,

$$\displaystyle{ A \simeq \frac{1} {2}\beta \left (y^{2} - x^{2}\right ). }$$

(5.2)

The hyperbolic field lines are given by A = constant, sketched in Fig. 5.2 (left).

The pure O-type neutral point is represented by the field

$$\displaystyle{ B_{x} \simeq +\gamma y,\quad B_{y} \simeq -\gamma x, }$$

(5.3)

where γ is a constant. This field can be expressed in terms of the vector potential

$$\displaystyle{ A \simeq \frac{1} {2}\gamma \left (x^{2} + y^{2}\right ) }$$

(5.4)

in the z-direction. The field lines form concentric circles and the curl of the field is − 2γ.

When both fields are present,

$$\displaystyle{ B_{x} \simeq (\beta +\gamma )y,\quad B_{y} \simeq (\beta -\gamma )x, }$$

(5.5)

with

$$\displaystyle{ A \simeq \frac{1} {2}\left [(\beta +\gamma )y^{2} - (\beta -\gamma )x^{2}\right ]. }$$

(5.6)

Thus the field lines A = constant are a family of hyperbolas when $(\beta +\gamma )(\beta -\gamma )> 0$ and ellipses when $(\beta +\gamma )(\beta -\gamma ) <0$. That is to say, we have an oblique X-type neutral point when β ² > γ ² and an elliptical O-type neutral point when β ² < γ ². For $\beta = +\gamma$ the magnetic field is $B_{x} \simeq 2\beta y$, $B_{x} \simeq 0$, while $\beta = -\gamma$ gives $B_{x} \simeq 0$, $B_{y} \simeq 2\beta x$. Obliquity is generally expected in nature.

Fig. 5.2

Left: 2D X-type neutral point in a curl-free magnetic field. Center: Current sheet $N^{{\prime}}N$ formed by squashing the X-type neutral point. Right: Resistive reconnection of magnetic field across the current sheet $N^{{\prime}}N$

Reconnection is associated with the X-type neutral point. For if the field in y > 0 in Fig. 5.2 (left panel) is pushed downward and the field in y < 0 is pushed upward, the field sectors in x > 0 and x < 0 are squeezed right and left out of the picture. The field sectors in y > 0 and y < 0 squash together at the x-axis, sketched in Fig. 5.2 (center panel). The X-type neutral point has been split into two opposite facing Y-type neutral points, marked N and $N^{{\prime}}$ in Fig. 5.2 (center panel). The tails of the Y-type neutral points join to form a current sheet $N^{{\prime}}N$ between the opposite fields in y > 0 and y < 0. In an infinitely conducting fluid the field at the current sheet is B _y  = 0 while B _x is discontinuous, reversing sign across the current sheet.

Field line reconnection requires the introduction of some slight resistive diffusivity η. If the fluid did not move, the width of the current sheet profile across the x-axis would evolve with the characteristic thickness (4η t)^1∕2 in a time t, increasing at the declining rate $(\eta /t)^{1/2}$. Figure 5.2 (right panel) is a sketch of the field after a small time t, showing the reconnection of field across the segment $N^{{\prime}}N$ of the x-axis. It is obvious from the figure that the tension in the field ejects fluid out each end of the current layer $N^{{\prime}}N$. What is more, B _x changes sign across the x-axis and therefore vanishes on the x-axis, thereby reducing the total magnetic pressure. So pressure equilibrium, $p + B^{2}/8\pi = constant$, across the current sheet is maintained with enhanced fluid pressure. The enhanced fluid pressure, together with the magnetic tension, eject field and fluid out each end of the current sheet. The ejection of fluid thins the current sheet and increases the field gradient, so that the rate at which resistivity dissipates magnetic field is maintained at the greatly elevated rate $C/R_{L}^{1/2}$ or more that we call rapid reconnection.

The next step is to look at the 3D picture of the simple 2D rapid reconnection described so far. The tension in B(P), i.e. B _z , plays no role in the 2D picture, but in 3D the variation with z puts B _z in a central role. To explore the variation in the z-direction along the field B(P) we turn to the optical analogy.

5.3 The Optical Analogy

The optical analogy applies to potential fields, $B_{i} = \partial \varphi /\partial x_{i}$. The direction cosines of a field line are given by

$$\displaystyle{ \frac{dx_{i}} {ds} = \frac{1} {B} \frac{\partial \varphi } {\partial x_{i}}, }$$

(5.7)

where B is the field magnitude and ds is an element of length along the field line.

Consider an electromagnetic wave $\exp \,i\psi$ in a medium with index of refraction n. The direction cosines of a ray path are

$$\displaystyle{ \frac{dx_{i}} {ds} = \frac{\partial \psi /\partial x_{i}} {\left \vert \partial \psi /\partial x_{k}\right \vert }. }$$

(5.8)

The Eikonal equation, $\left \vert \partial \psi /\partial x_{k}\right \vert ^{2} = n^{2}$, reduces this to

$$\displaystyle{ \frac{dx_{i}} {ds} = \frac{1} {n} \frac{\partial \psi } {\partial x_{i}}. }$$

(5.9)

Comparing Eqs. (5.7) and (5.9) it is evident that a field line in a potential field follows the same path as an optical ray in a medium with index of refraction n proportional to the field magnitude B.

We apply this to a field in force-free equilibrium, for which

$$\displaystyle{ \nabla \times \mathbf{B} =\alpha \mathbf{B}. }$$

(5.10)

Consider, then, a field line in a flux surface S. The 2D field in the flux surface is a potential field, hence the optical analogy is applicable to the field lines in every flux surface in a force-free field (Parker 1989a,b, 1991, 1994).

Given the optical analogy, it follows that the field line extending between points J and K is subject to Fermat’s principle, that the optical path length is an extremum, and usually a minimum. Thus

$$\displaystyle{ \delta \int \limits _{J}^{K}ds\ B(s) = 0, }$$

(5.11)

along with the associated Euler equations. It follows that in the neighborhood of a local maximum, the field lines are concave toward the maximum. That is to say, the field lines tend to pass around, rather than through, a region of increased field in order to minimize the “optical” path length. In other words the field lines tend to be squeezed out of regions of high magnetic pressure. The increased magnetic pressure displaces the field line away from the high pressure, while the tension in the displaced field line tends to pull the field line back. The net effect is described by the optical analogy. Figure 5.2 (center panel) shows a 2D cross section through the region of maximum field.

Fig. 5.3

Sketch of a region (scale λ) of enhanced magnetic pressure B ⋅ Δ B∕4π midway between the anchor points J and K of a field line of length $2\varLambda$

Figure 5.3 is a sketch of a simple example, wherein a local increase Δ B in field strength above the ambient B has a characteristic scale λ. The example treats a field line extending a large distance $2\varLambda$ between two anchor points ($\varLambda \gg \lambda$). For simplicity the local maximum is placed at the center point of the line connecting the anchor points. Thus a field line skirting the maximum is inclined to the line by an angle of the order of $\lambda /\varLambda$, and the optical path length between anchor points J and K is $2B\varLambda (1 +\lambda ^{2}/2\varLambda ^{2})$ to lowest order in $\lambda ^{2}/\varLambda ^{2}$. On the other hand, the optical path length straight over the top of the maximum is of the order of $2B\varLambda [1 + (\varDelta B/B)(\lambda /\varLambda )]$. It follows that the optical path length around the maximum is shorter than the path length through the maximum when

$$\displaystyle{ \frac{\varDelta B} {B}> \frac{\lambda } {2\varLambda }. }$$

(5.12)

Thus an increase Δ B∕B of this amount squeezes the field out of the region of Δ B, creating a gap in the flux surface S. The gap appears as $N^{{\prime}}N$ in Fig. 5.2 (center panel), where magnetic flux on one side of $N^{{\prime}}N$ comes into contact with magnetic flux on the other side. The two fluxes are oppositely inclined to the z-axis so they produce the current sheet $N^{{\prime}}N$. The resistive rapid reconnection across $N^{{\prime}}N$ is maintained as fluid is ejected out both ends of the current sheet. Figure 5.4 is a sketch of the whole 3D picture, including the cross section sketched in Fig. 5.2 (center panel).

Fig. 5.4

Cutaway sketch of expulsion of magnetic field from magnetic pressure region, including the cross section sketched in the center panel of Fig. 5.2

It should be noted that the essential fluid motions creating the current sheet are the transverse displacements of the field, pushing the quadrants RNQ and $R^{{\prime}}N^{{\prime}}Q^{{\prime}}$ (Fig. 5.2, center panel) aside so that the field in $R^{{\prime}}N^{{\prime}}NR$ comes in contact with the oppositely directed field in $Q^{{\prime}}N^{{\prime}}NQ$.

Incidentally, we note that the discontinuity of the magnetic field across $N^{{\prime}}N$ slightly displaces the fields extending away from the region along the separatrices dividing the four sectors. The displacements are not the same on the two sides of each separatrix, resulting in surfaces of discontinuity (current sheets) along the separatrices shown in Fig. 5.2 (center and right panels).

Thus far we have considered the effect of local squeezing of the magnetic field to provide the current sheets, sketched in Fig. 5.2 (center and right panels). In fact there are initial field line topologies in continuous fields wherein the magnetic stresses create current sheets as an intrinsic part of the equilibrium of that field topology. As already noted, the commonly occurring interlaced field, sketched in Fig. 5.1, represents an important astrophysical example of the formation of current sheets as a direct consequence of the field topology.

5.4 Interlaced Field Line Topology

To show the universal formation of current sheets in interlaced fields we turn to the equilibrium equation (5.10) to show that almost all of the interlaced field line topologies naturally form internal surfaces of field discontinuity, i.e. current sheets, thereby providing rapid reconnection sites as an intrinsic part of their equilibria.

Consider, then, the mathematics of the static equilibrium of an interlaced topology. The interlacing topology is best defined relative to the topology of a uniform field. So consider a uniform magnetic field B extending in the z-direction through an infinitely conducting (dissipationless) cold plasma extending from an infinitely conducting end plate at z = 0 to another such end plate at z = L. At time t = 0 the fluid is set in motion with the transverse 2D incompressible form

$$\displaystyle{ v_{x} = +kz \frac{\partial \psi } {\partial y},\quad v_{y} = -kz \frac{\partial \psi } {\partial x},\quad v_{z} = 0, }$$

(5.13)

where ψ = ψ(x, y, kzt) represents a bounded, continuous, differentiable function of its arguments. It is readily shown from the MHD induction equation that this fluid motion deforms the magnetic field into

$$\displaystyle{ B_{x} = +Bkt \frac{\partial \psi } {\partial y},\quad B_{y} = -Bkt \frac{\partial \psi } {\partial x},\quad B_{z} = B. }$$

(5.14)

This deformation corresponds to holding the footpoints of the field fixed at z = 0 while introducing an arbitrary swirling and mixing of the footpoints at z = L, thereby creating an interlaced field line topology throughout 0 < z < L, sketched in Fig. 5.5. The function ψ(x, y, kzt) defines the interlaced topology. Note that the interlaced field is everywhere bounded, continuous, and differentiable.

Fig. 5.5

Sketch of the interlaced magnetic field extending between the end plates z = 0 and z = L

Switch off the swirling ψ(x, y, kzt) at time t = τ, when the interlacing is well developed on a characteristic scale l ( < < L) in the transverse x and y-directions, and wound up tightly enough that the scale in the z-direction (along the mean field) is comparable to l. That is to say, the field components B _x , B _y , B _z are comparable in magnitude. Then hold fixed the footpoints of the field at z = 0, L while releasing the fluid throughout 0 < z < L to move in response to the Lorentz force exerted by the interlaced field. Introduce a small viscosity into the fluid (plasma) so that the motions decline asymptotically to zero as the magnetic field relaxes to the lowest available magnetic energy state.

It is important to note that, with the magnetic field attached at both ends z = 0 and z = L, the field cannot escape. Escape would mean stretching the field in opposition to the tension along the field lines. So with the passage of time the magnetic field, no matter what its interlaced topology, has no choice but to settle into a stable equilibrium. That is to say, there exists a formal mathematical solution to Eq. (5.10) for each and every interlaced field line topology. This fact plays a basic role in the interpretation of the equilibrium equations for the field.

5.5 Equilibrium of the Interlaced Field

In the absence of plasma pressure variations, the final equilibrium conforms to the familiar force-free field equation (5.10)

$$\displaystyle{ \nabla \times \mathbf{B} =\alpha \mathbf{B} }$$

where the scalar function α is the torsion coefficient, given by

$$\displaystyle{ \alpha = \frac{\oint d\mathbf{s} \cdot \mathbf{B}} {\int d\mathbf{S} \cdot \mathbf{B}} }$$

(5.15)

at any point P. Here the integration is over a small circle around B(P) centered on P, d s is an element of arc length along the circle, and d S is an element of area enclosed by the circle. The torsion coefficient is equal to the magnetic circulation around any small circle divided by the magnetic flux enclosed by that circle.

The force-free equation (5.10), having mixed characteristics, is unlike other field equations with which we are familiar. This may be seen from the curl of Eq. (5.10),

$$\displaystyle{ \mathbf{B} \times \nabla \alpha = \nabla ^{2}\mathbf{B} +\alpha ^{2}\mathbf{B}, }$$

(5.16)

wherein the Laplacian operator indicates two families of complex characteristics. Equation (5.16) is a quasilinear elliptic equation. In contrast the divergence of Eq. (5.10) yields

$$\displaystyle{ \mathbf{B} \cdot \nabla \alpha = 0, }$$

(5.17)

asserting that α is constant along each individual field line. Thus the field lines represent a family of real characteristics, so that the topology of the field enters directly into the solution of Eq. (5.10), that has both real and complex characteristics, and we may expect solutions of unfamiliar form.

The first point to consider is the assertion that the torsion coefficient α is constant along each field line regardless of how the interlacing topology involves field lines writhing their way from z = 0 to z = L through the surrounding interlaced magnetic field. It is not obvious how a constant α can be accomplished along the line, particularly if the line writhes in opposite senses at different locations along the field. And yet there must be a resolution of this seeming contradiction because, as already noted, a solution to Eq. (5.10) exists for every interlacing topology.

To explore the question, reduce the mathematics to its basic form for the given field line topology by dilating the system, stretching the region 0 < z < L in the z-direction by a large factor 1∕ε, with ε ≪ 1. The dilatation preserves the topology, of course, and reduces the transverse field components to the order of ε B, while the z-component is not much affected. So write

$$\displaystyle{ B_{x} =\epsilon Bb_{x},\quad B_{y} =\epsilon Bb_{y},\quad B_{z} = B\left (1 +\epsilon ^{2}b_{ z}\right ),\quad \alpha =\epsilon a, }$$

(5.18)

with

$$\displaystyle{ \nabla \cdot \mathbf{B} = 0. }$$

(5.19)

The term first order in ε in B _z can be included but turns out to be zero, as we would expect from the fact that the magnetic pressure fluctuations associated with b _x , b _y and b _z are all comparable and, hence, second order in ε.

Equation (5.17) becomes

$$\displaystyle{ \frac{\partial a} {\partial z} +\epsilon \left (b_{x}\frac{\partial a} {\partial x} + b_{y}\frac{\partial a} {\partial y}\right ) = 0. }$$

(5.20)

So to lowest order in ε we have

$$\displaystyle{ \frac{\partial a} {\partial z} = 0. }$$

(5.21)

This proclaims that the torsion coefficient a is constant along the unperturbed field lines. It is a highly restrictive condition on the magnetic field topology (Parker 1972, 1979) and foreshadows the more precise result worked out by van Ballegooijen (1985), who noted that ∂∕∂ z is small to O(ε) compared to ∂∕∂ x and ∂∕∂ y in the stretched field. Take this into account by introducing the coordinate ζ = ε z, so that

$$\displaystyle{ \frac{\partial } {\partial z} =\epsilon \frac{\partial } {\partial \zeta }, }$$

(5.22)

and ∂∕∂ ζ is of the same order as the transverse derivatives ∂∕∂ x and ∂∕∂ y. Equation (5.20) becomes

$$\displaystyle{ \frac{\partial a} {\partial \zeta } + \left (b_{x}\frac{\partial a} {\partial x} + b_{y}\frac{\partial a} {\partial y}\right ) = 0, }$$

(5.23)

representing Eq. (5.17) computed along the perturbed field lines, i.e., the actual field lines when expressed in terms of Eq. (5.18).

Now Eq. (5.16) provides the three equations for the local relations between a and the three field components, with

$$\displaystyle\begin{array}{rcl} -\frac{\partial a} {\partial y} = \frac{\partial ^{2}b_{x}} {\partial x^{2}} + \frac{\partial ^{2}b_{x}} {\partial y^{2}},& &{}\end{array}$$

(5.24)

$$\displaystyle\begin{array}{rcl} +\frac{\partial a} {\partial x} = \frac{\partial ^{2}b_{y}} {\partial x^{2}} + \frac{\partial ^{2}b_{y}} {\partial y^{2}},& &{}\end{array}$$

(5.25)

$$\displaystyle\begin{array}{rcl} \epsilon \left (b_{x}\frac{\partial a} {\partial y} - b_{y}\frac{\partial a} {\partial x}\right ) = \frac{\partial ^{2}b_{z}} {\partial x^{2}} + \frac{\partial ^{2}b_{z}} {\partial y^{2}} +\epsilon a^{2}.& &{}\end{array}$$

(5.26)

to lowest order in ε. For present purposes however it is easier to work with the components of Eq. (5.10) because they are one order lower in spatial derivatives. Again neglecting terms second order in ε compared to one, we have

$$\displaystyle\begin{array}{rcl} & & \frac{\partial b_{z}} {\partial y} -\frac{\partial b_{y}} {\partial \zeta } = ab_{x},{}\end{array}$$

(5.27)

$$\displaystyle\begin{array}{rcl} & & \frac{\partial b_{x}} {\partial \zeta } -\frac{\partial b_{z}} {\partial x} = ab_{y},{}\end{array}$$

(5.28)

$$\displaystyle\begin{array}{rcl} & & \frac{\partial b_{y}} {\partial x} -\frac{\partial b_{x}} {\partial y} = a.{}\end{array}$$

(5.29)

Equation (5.19) reduces to

$$\displaystyle{ \frac{\partial b_{x}} {\partial x} + \frac{\partial b_{y}} {\partial y} = 0, }$$

(5.30)

neglecting terms second order in ε compared to one.

Now, it follows from Eq. (5.30) that there exists a function $\varTheta (x,y,\zeta )$ such that

$$\displaystyle{ b_{x} = + \frac{\partial \varTheta } {\partial y},\quad b_{y} = - \frac{\partial \varTheta } {\partial x}. }$$

(5.31)

Equation (5.30) is automatically satisfied, and Eq. (5.23) becomes

$$\displaystyle{ \frac{\partial a} {\partial \zeta } = \frac{\partial \varTheta } {\partial x} \frac{\partial a} {\partial y} - \frac{\partial \varTheta } {\partial y} \frac{\partial a} {\partial x}. }$$

(5.32)

Equation (5.29) is written

$$\displaystyle{ a = -\left ( \frac{\partial ^{2}} {\partial x^{2}} + \frac{\partial ^{2}} {\partial y^{2}}\right )\varTheta. }$$

(5.33)

Equations (5.32) and (5.33) together determine the possible variations of a and Θ. It is obvious by inspection that Eq. (5.26) provides an equation for b _z once a and Θ are known.

Van Ballegooijen (1985) pointed out that the two Eqs. (5.32) and (5.33) are the exact mathematical analog of the 2D time dependent vorticity (Euler) equation for an inviscid incompressible fluid with time t replaced by ζ. The torsion coefficient a corresponds to the vorticity ω, and the field components b _x and b _y correspond to the fluid velocity components v _x and v _y , the stream function being Θ in both realizations. Unfortunately van Ballegooijen misinterpreted the mathematics, failing to recognize that the infinitely many solutions to the vorticity equation form a topological set only of zero measure compared to all possible field line topologies (see the penultimate paragraph of Appendix B, Janse et al. 2010). So he concluded that all topologies can be accommodated by the vorticity solutions and there is no reason to expect discontinuities. Nonetheless his analogy with vorticity is correct and important. The fact is that ψ(x, y, kzt) represents all possible interlacing field line topologies, and, with all field lines anchored at both ends, every topology has a stable equilibrium. On the other hand, the only continuous equilibrium solutions are the solutions to the vorticity equation (5.23), representing 2D turbulence with the enstrophy analog cascading toward small scales and the kinetic energy analog cascading toward large-scales along the field. But almost all interlaced topologies lack such unique cascading topology. That is to say, a member of the topological set of continuous solutions is a rarity within the set of all topologies. It follows that almost all interlaced field line topologies fail to have continuous equilibrium solutions, i.e., almost all solutions contain one or more surfaces of tangential discontinuity (current sheets). The spaces between the discontinuities are filled with continuous vorticity solutions.

5.6 Structure of Reduced MHD Equilibria and Dynamics

Further insight into the dynamics and the structure of the equilibria has been recently gained with numerical simulations and a quantitative analysis of the equilibria axial asymmetry (Rappazzo and Parker 2013; Rappazzo 2015). A coronal loop is modeled, as in previous work (Rappazzo et al. 2007, 2008), with a simplified cartesian geometry, uniform density ρ, and a strong and homogeneous axial magnetic field $\mathbf{B}_{0} = B_{0}\,\mathbf{\hat{e}}_{z}$ threading the system: a configuration well suited to be studied in the reduced MHD regime (Zank and Matthaeus 1992). At leading order the dynamic velocity and magnetic fields are solenoidal ($\nabla \cdot \mathbf{u} = \nabla \cdot \mathbf{b} = 0$) and have only orthogonal components $\mathbf{u} \cdot \mathbf{B}_{0} = \mathbf{b} \cdot \mathbf{B}_{0} = 0$. They are linked to the corresponding potentials φ and ψ by $\mathbf{u} = \nabla \varphi \times \mathbf{\hat{e}}_{z}$, and $\mathbf{b} = \nabla \psi \times \mathbf{\hat{e}}_{z}$, while vorticity and current density are given by $\omega = -\nabla _{\perp }^{\,2}\varphi$ and $j = -\nabla _{\perp }^{\,2}\psi$ ( pointing in the z direction, where $\nabla _{\perp }^{\,2} = \partial _{x}^{2} + \partial _{y}^{2}$). With this notation the nondimensional reduced MHD equations (Kadomtsev and Pogutse 1974; Strauss 1976) are written as:

$$\displaystyle\begin{array}{rcl} & & \frac{\partial \psi } {\partial t} = \left [\varphi,\psi \right ] + B_{0}\, \frac{\partial \varphi } {\partial z} +\eta _{_{n}}\nabla _{_{\!\!\perp }}^{2n}\psi,\quad {}\end{array}$$

(5.34)

$$\displaystyle\begin{array}{rcl} & & \frac{\partial \omega } {\partial t} = \left [\,j,\psi \right ] -\left [\omega,\varphi \right ] + B_{0}\, \frac{\partial j} {\partial z} +\nu _{_{\!n}}\nabla _{_{\!\!\perp }}^{2n}\omega,{}\end{array}$$

(5.35)

where the Poisson bracket of functions g and h is defined as $[g,h] = \partial _{x}g\,\partial _{y}h - \partial _{y}g\,\partial _{x}h$ (e.g., [ j, ψ] = b ⋅ ∇j). To render the equations nondimensional the magnetic field has been first expressed as an Alfvén velocity ($b \rightarrow b/\sqrt{4\pi \rho }$), and then all velocities have been normalized with u ^∗ = 1 km s⁻¹, a typical value in photospheric convective granules. The domain spans 0 ≤ x, y ≤ L _⊥ and 0 ≤ z ≤ L _z , with L _⊥ = 1 and L _z  = 10 in all calculations. Magnetic field lines are line-tied to a motionless photosphere at the top and bottom plates (z = 0 and 10), where a vanishing velocity u = 0 is in place. In the perpendicular (x-y) directions a pseudo-spectral scheme with periodic boundary conditions and isotropic truncation de-aliasing is used (2∕3-rule) (Canuto et al. 2006), while along z a second-order finite difference scheme is implemented. The CFL (Courant-Friedrichs-Levy) condition is satisfied through an adaptive time-step (for a more detailed description of the model and numerical code see Rappazzo et al. 2007, 2008).

Reduced MHD equilibria are given by B ⋅ ∇j = 0, obtained by neglecting velocity and diffusion terms in Eqs. (5.34)–(5.35). Since the total magnetic field is given by $\mathbf{B} = B_{0}\mathbf{\hat{e}}_{z} + \mathbf{b}(x,y,z)$, the equilibrium condition can be written as:

$$\displaystyle{ \frac{\partial j} {\partial z} = - \frac{\mathbf{b}} {B_{0}} \cdot \nabla j, }$$

(5.36)

where both sides correspond to different Lorentz force components orthogonal to B ₀: the right-hand side term corresponds to b ⋅ ∇b, and the left hand side to the B ₀ ∂ _z b field line tension. Assigned b in an x-y plane, e.g., at the boundary z=0 $\mathbf{b}(x,y,z = 0) = \mathbf{b}_{bd}(x,y)$, the integration of this equation for z > 0 allows to compute the corresponding equilibrium in the whole computational box 0 ≤ z ≤ L _z .

The reduced MHD equilibrium equation (5.36) is identical to the 2D Euler equation

$$\displaystyle{ \frac{\partial \omega } {\partial t} = -\mathbf{u} \cdot \nabla \omega, }$$

(5.37)

(with ∇⋅ u = 0, $\mathbf{u}(x,y,t) = \nabla \phi (x,y,t) \times \mathbf{\hat{e}}_{z}$, and vorticity $\omega = -\nabla ^{2}\phi$, with ϕ the velocity potential) under the mapping

$$\displaystyle{ t \rightarrow z,\qquad \mathbf{u} \rightarrow \frac{\mathbf{b}} {B_{0}}, }$$

(5.38)

and consequently $\omega \rightarrow j/B_{0}$.

The physics and solutions of the 2D Euler equation have been studied extensively, including in the laboratory, in the framework of 2D hydrodynamic turbulence (Kraichnan and Montgomery 1980; Tabeling 2002; Boffetta and Ecke 2012). It is among the few partial differential equations for which a theorem proves the existence and uniqueness of its solutions: given a smooth initial condition u ₀(x, y) at time t = 0, the 2D Euler equation admits a unique and regular solution at t > 0 (Rose and Sulem 1978; Chemin 1993; Bertozzi and Constantin 1993; Majda and Bertozzi 2001).

The dynamics of its solutions differ substantially from those of MHD and 3D hydrodynamics. In 2D besides energy also enstrophy $\varOmega =\int \mathrm{ d}a\ \omega ^{2}$ (i.e., integrated square vorticity) is conserved. The presence of this additional ideal invariant strongly limits the development of a direct energy cascade (a transfer of energy toward smaller scales), since the conservation of both $E =\int \mathrm{ d}k\ E(k)$ and $\varOmega =\int \mathrm{ d}k\ k^{2}E(k)$ favors the transfer of energy at larger scales (corresponding to smaller k), i.e., an inverse cascade. Kraichnan (1967) and Batchelor (1969) first proposed this inverse energy cascade phenomenology (now supported also by numerical simulations and laboratory experiments, see Boffetta and Ecke (2012) and references therein), where energy develops a spectrum $E_{k} \propto k^{-5/3}$ following a phenomenology similar to that proposed by Kolmogorov (1941) (that does not depend on the direction of the cascade; Rose and Sulem 1978), with eddy turnover time approximately given by

$$\displaystyle{ t_{\ell} \sim \frac{\ell} {u_{\ell}}, }$$

(5.39)

with a possible logarithmic correction that we neglect (Kraichnan 1971). For a configuration made of vortices of scale ℓ and velocity u _ℓ , t _ℓ is the timescale over which such a vortex (eddy) experiences significant distortions due to the relative motion of its components, transferring its energy approximately from the scale ℓ to the scale of double size 2ℓ (schematically drawn in the left panel of Fig. 5.6).

Fig. 5.6

Left: Diagram of the inverse energy cascade in time of the solution of the 2D Euler equation, characterized by the eddy turnover time $t_{\ell} \sim \ell /u_{\ell}$ (Eq. (5.39)).  Right: Structure of the reduced MHD equilibria in space. Its asymmetry in the axial direction z is measured by the variation length-scale $z_{\ell} \sim B_{0}\ell/b$ (Eq. (5.40)). Images adapted from Rappazzo (2015)

The mapping (5.38) between the solutions of the 2D Euler equation and the reduced MHD equilibria allows to connect the inverse energy cascade in time of the solutions of the 2D Euler equation to the asymmetric structure in space of the reduced MHD equilibria along the axial direction z (Fig. 5.6), with the caveat that eddies are vortices in the hydrodynamic case and magnetic islands in reduced MHD. In particular given a magnetic field b _bd (x, y) at the boundary z = 0, made of magnetic islands of scale $\sim \ell$, the unique and regular reduced MHD equilibrium solution b _eq (x, y, z) for which $\mathbf{b}_{eq}(x,y,z = 0) = \mathbf{b}_{bd}(x,y)$ undergoes an increasingly stronger inverse cascade in space in the x-y planes for higher values of z (see Fig. 5.6, right panel), with the orthogonal magnetic field length-scale ℓ getting progressively larger up to doubling its value in the plane $z \sim z_{\ell}$, with

$$\displaystyle{ z_{\ell} \sim \frac{B_{0}} {b_{bd}}\,\ell. }$$

(5.40)

The variation length-scale z _ℓ is derived from Eq. (5.39) through the mapping (5.38). If the magnetic field is characterized by a scale of order ℓ at z = 0 it will have its energy at scale $\sim 2\ell$ at z = z _ℓ , corresponding respectively to magnetic islands of scales ℓ and 2ℓ in the x-y planes z = 0 and z = z _ℓ .

Therefore the reduced MHD equilibria can be strongly asymmetric in the axial direction if the variation length-scale (Eq. (5.40)) is small compared to the loop length z _ℓ  < L _z , or quasi-invariant if the variation lenght-scale is larger than the loop length $z_{\ell} \gtrsim L_{z}$.

On the other hand the dynamic solutions of the reduced MHD equations (5.34)–(5.35) do not generally develop strong spatial variations along the axial direction, particularly in the case of interest here of footpoint shuffling at the boundaries z = 0 and L _z . Indeed the linear terms $\propto B_{0}\partial _{z}$ in Eqs. (5.34)–(5.35) give rise to a Alfvén wave propagation at the fast speed B ₀ of any perturbation along the axial direction. Consequently the fields do not develop strong variations along z, as confirmed by numerical simulations (e.g., Galsgaard and Nordlund 1996; Dmitruk and Gómez 1999; Rappazzo et al. 2008; Wilmot-Smith et al. 2011; Dahlburg et al. 2012). Since in general the magnetic field rms is approximately invariant along z, we will drop the “boundary” subscript in Eq. (5.40) hereafter, indicating the variation length-scale simply as $z_{\ell} \sim \ell B_{0}/b$.

As discussed in the next section, numerical simulations suggest that the loop length L _z is a critical length for the variation scale z _ℓ . For initial configurations with magnetic fields invariant along z and intensities stronger than b > ℓ B ₀∕L _z , the corresponding equilibria have variation length-scales z _ℓ  < L _z and therefore are strongly asymmetric and cannot be accessed dynamically. The strong initial deviation from equilibrium sets the plasma in motion, with nonlinear dynamics generating quickly current sheets (Rappazzo and Parker 2013). In the dissipative case energy is then dissipated, and in this relaxation process energy continues to be dissipated and decrease until the variation length-scale grows up to the critical length $z_{\ell} \sim L_{z}$, when an equilibrium quasi-invariant along z can be asymptotically accessed. Hence magnetic fields for which z _ℓ  < L _z necessarily have to dissipate energy, requiring current sheets to form and magnetic reconnection to occur. On the contrary, for magnetic fields with intensities approximately smaller than $b \lesssim \ell B_{0}/L_{z}$, the corresponding equilibria have variation length-scales larger than approximately the loop length $z_{\ell} \gtrsim L_{z}$, the equilibria are then quasi-invariant along z at the loop scale. The initial magnetic field can in this case adapt quasi-statically to the very close equilibrium with a negligible, if any, energy dissipation.

In summary an initial magnetic field invariant along z will always decay toward an equilibrium. But for intensities larger than b > ℓ B ₀∕L _z the corresponding equilibrium cannot be accessed because it is strongly asymmetric (z _ℓ  < L _z ), therefore current sheets will form and magnetic reconnection occur so that a lower energy equilibrium quasi-invariant along z, with variation length-scale $z_{\ell} \sim L_{z}$ and magnetic field intensity $b \sim \ell B_{0}/L_{z}$, can be accessed.

In the aforementioned discussion we have always considered initial magnetic fields not in equilibrium, i.e., that do not satisfy Eq. (5.36). Solar photospheric motions have a very low frequency (1∕t _c , with $t_{c} \sim$ 5–8 m) compared to the fast crossing time of Alfvén waves along the loop axis t _c  ≫ t _A , where for typical values of L _z and B ₀, e.g., with $L_{z} \sim$ 4 × 10⁴ km and $B_{0} \sim$ 2 × 10³ km/s, we obtain $t_{A} = L_{z}/B_{0} \sim$ 20 s. The configurations most of interest to the Sun are those with $\partial _{z}j \sim 0$, but with b ⋅ ∇j ≠ 0, i.e., with the orthogonal component of the magnetic field out-of-equilibrium in the x–y planes due to the disordered and turbulent nature of photospheric convection. Therefore it is important to remark that the configurations considered here are not unstable. Classic unstable equilibria, e.g., kink (other unstable configurations can be found in Parker (1983); Longcope and Strauss (1993) and references therein), can be recovered in the limit $\mathbf{b} \cdot \nabla j \rightarrow 0$ with b ≠ 0 in Eq. (5.36), that implies also $\partial _{z}j \rightarrow 0$. In this limit the highly symmetric fields of unstable configurations are recovered, but they are outside the scope of this paper.

Since the dynamics are not driven by instabilities, but rather by nonlinear dynamics developing as soon as photospheric motions twist the field lines beyond the critical intensity threshold b > ℓ B ₀∕L _z (see also Eq. (5.12)), current sheets formation clearly stems from the nonlinear dynamics developing due to the magnetic field striving to relax while continuously set out of equilibrium by photospheric motions at its footpoints.

An alternative model for coronal heating had been proposed by van Ballegooijen (1986). Because in his view the magnetic field evolution should be restricted to a continuous quasi-static relaxation to nearby equilibria, he conjectured that successive uncorrelated steps of the magnetic field line footpoints random walk would shred the coronal magnetic field thus producing small-scale current sheets (necessary to heat the corona) uniformly distributed in the loop volume. This kinematic “cascade” of magnetic energy would originate from magnetic field lines passively tracing their footpoints shuffled in random directions by photospheric motions. This mechanism would lead to current sheet formation on timescale longer than photospheric convection (several random walk steps would be required). The relaxation simulations by Rappazzo and Parker (2013) unquestionably rule out this mechanism, since current sheets form on ideal timescales while the footpoints are fixed at the photospheric plates where no motions are in place (and therefore no footpoint random walk occurs).

On the other hand earlier 2D (Einaudi et al. 1996; Dmitruk and Gómez 1997) and later reduced MHD numerical simulations (Dmitruk and Gómez 1999; Dmitruk et al. 2003; Rappazzo et al. 2007, 2008) have pointed out the connection of the dynamics of this system with MHD turbulence (with similar dynamics also shown in the cold plasma regime (Hendrix and van Hoven 1996) and fully compressible MHD simulations (Galsgaard and Nordlund 1996; Dahlburg et al. 2012)) such as the formation of energy spectra with power-law behavior, the formation of current sheets distributed intermittently in space and time, and the power-law behavior in total energy, peak dissipation and duration of the bursts of dissipation, that correspond to the formation and dissipation of current sheets, that exhibit indexes not far from those determined observationally in X-rays (Georgoulis et al. 1998; Dmitruk et al. 1998). Nevertheless the turbulent regime for this system is very distinct from the corresponding 3D hydrodynamic case (Frisch 1995), and it is overall best characterized as magnetically dominated MHD turbulence. Indeed not only velocity fluctuations u are generally smaller than magnetic fluctuations b, but energy transfers across scales are determined by the magnetic field. Energy flows between different scales have long been tracked for the hydrodynamic Navier-Stokes equations (Frisch 1995), and more recently they have been studied numerically also in MHD at relatively high resolutions (Dar et al. 2001; Alexakis et al. 2005). A recent investigation of the energy flows toward small scales in a high-resolution boundary driven reduced MHD simulation (Rappazzo and Velli 2011) has allowed to determine which nonlinear terms drive the nonlinear cascade and thus the formation of current sheets. As schematically drawn in Fig. 5.7 energy across different scales of the velocity field (indicated with T _uu ) have been found to be negligible. In other words the term u ⋅ ∇u (corresponding to the term $[\omega,\varphi ]$ in Eq. (5.35)), that generates all nonlinear dynamics in the Navier-Stokes equations, gives a negligible contributions to the energy fluxes in this problem.

Fig. 5.7

Diagram of energy flows between fields and scales in the inertial range (at scales intermediate between the larger scales where photospheric convection injects energy into the corona and the smaller scales where dissipation occurs). Spectral fluxes are indicated with, e.g., T _bu for the flux between different scales of magnetic and velocity fields, and analogously for other fields permutations. Image adapted from Rappazzo and Velli (2011)

As a result, the magnetic field is in “dynamical non-equilibrium” (Parker 1972, 1988, 1994, 2012b) at all scales, and it creates and shapes the small velocity field along the inertial range (through the Lorentz force terms b ⋅ ∇b and B ₀ ∂ _z b), that in turn create small scales in the magnetic field by distorting it and pushing field lines together, with an overall energy flux toward smaller scales akin to that put forward by Kolmogorov (1941) but for which the eddies that get distorted are magnetic islands.

5.6.1 Numerical Simulations (Dissipative)

In this section we briefly summarize the dissipative numerical simulations carried out in Rappazzo and Parker (2013) and Rappazzo (2015). Initial conditions at t = 0 have a vanishing velocity u = 0 everywhere in the computational box, and a uniform and homogeneous guide field B ₀ = 10³. The initial perpendicular magnetic field component b ₀, with several intensities b ₀ considered, consists of large-scale Fourier modes, with orthogonal wave-numbers in the range 3 ≤ n _⊥ ≤ 4, and example of which is shown in Fig. 5.10 (top left panel). In the parallel direction z initial magnetic fields differ for the number of parallel Fourier modes present at time t = 0. Since the photospheric convection frequency is low compared to the fast Alfvén transit time along coronal loops, the magnetic field is not expected to have strong variations along the loop axis, therefore we consider at first initial conditions invariant along z with ∂ _z  = 0, that have only the parallel mode m=0. Additionally we consider also initial magnetic fields with only the parallel mode m = 1, apt for longer loops on the Sun and other active stars where the Alfvén crossing time becomes of the order of the convective timescale or faster, and finally also initial conditions with all parallel modes m ∈ [0, 4] with a dominant m=0 mode are considered. As remarked in the previous section all magnetic fields at time t = 0 are out of equilibrium, in particular for all simulations b ₀ ⋅ ∇j ≠ 0 initially, because the magnetic field brought about by the turbulent and disordered solar convection lacks the symmetry required to make the corresponding Lorentz force component vanish.

Fig. 5.8

Reduced MHD simulations with initial magnetic field invariant along z (∂ _z b = 0, only parallel mode m = 0 present). Left: Total energy vs. time (in logarithmic scale in the inset) for line-tied simulations with different values of b ₀∕B ₀ and a 2D simulation with $b_{0}/B_{0} = 10\,\%$. Right: Taylor microscale $\lambda _{T}$ and normalized energy dissipation rate ε∕E ($\epsilon = dE/dt$) vs. time. Images adapted from Rappazzo and Parker (2013)

Results of numerical simulations with initial magnetic field invariant along z are shown in Fig. 5.8. All simulations have line-tying boundary conditions in the photospheric-mimicking plates z=0 and 10 (where field lines are rooted in a motionless plasma where u = 0), and periodic boundary conditions in the orthogonal x–y planes. Additionally also results from a 2D simulation are shown (in dotted-continuous black line). As discussed more in detail in Rappazzo and Parker (2013) and Rappazzo (2015) the 2D simulation corresponds to use periodic boundary conditions also in the axial direction z (because the initial condition is invariant along z, no variations are developed in this direction in time), and is used here as a reference case to compare with line-tied simulations. Furthermore the 2D case is appropriate to model the central part of long loops far from the boundaries, where line-tying has a weak influence.

As shown in Fig. 5.8 (left panel) the relaxation of the 2D magnetic field is similar to 2D turbulence decay simulations (Hossain et al. 1995; Galtier et al. 1997; Biskamp 2003), decaying in time approximately as the power-law t ⁻¹, even though no velocity field is present in the initial condition and the velocity developed by the out-of-equilibrium magnetic field remains much smaller than magnetic fluctuations the entire time (while in turbulence simulations the velocity field is in approximate equipartition with the magnetic field the whole time). As shown in the right panel of Fig. 5.8 the energy decay corresponds to the rapid formation of small scales, as indicated by the initial sharp decrease of the Taylor micro-scale $\lambda _{T} = \left (\langle b^{2}\rangle /\langle \,j^{2}\rangle \right )^{1/2}$ that measures the average length-scale of magnetic gradients (Matthaeus et al. 2005), while magnetic reconnection leads to coalescence of magnetic islands that become increasingly larger (corresponding to an inverse cascade of magnetic energy in Fourier space). As detailed in Rappazzo and Parker (2013) and Rappazzo (2015) the solutions of the 2D equations with different initial magnetic field intensities b ₀ are self-similar in time, i.e., $\mathbf{b}^{{\prime}}(t) = \mathbf{b}(t \cdot b_{0}^{{\prime}}/b_{0})\ b_{0}^{{\prime}}/b_{0}$. While the time evolution is rescaled with the relative intensity $b_{0}^{{\prime}}/b_{0}$, the decay exhibits the same power-law behavior t ⁻¹ with same index for all intensities, current sheets will form and the inverse cascade occur at rescaled times as for $b_{0}/B_{0} = 10\,\%$, as shown in Fig. 5.8 (see Rappazzo 2015 for corresponding snapshots of the fields in physical space).

Line-tied simulations with differing intensities of the initial magnetic field (Fig. 5.8) depart from the 2D behavior more substantially the smaller the ratio b ₀∕B ₀. For $b_{0}/B_{0} = 10\,\%$ the dynamics are similar, although less small scales are formed, as shown by the slightly larger value of the Taylor micro-scale and smaller dissipative peak, so that a smaller fraction of energy is dissipated (see inset in the left panel of Fig. 5.8). For increasingly smaller values of b ₀∕B ₀ Taylor microscale becomes increasingly larger, while the peak in the dissipation rate strongly decreases, so that increasingly less energy is dissipated and a smaller inverse cascade of magnetic energy occurs. In particular for $b_{0}/B_{0} \lesssim 3\,\%$ barely any dynamics are detected.

The results of these numerical simulations are consistent with the heuristic phenomenology and the structure of the equilibria summarized in the previous section and described in greater detail in Rappazzo and Parker (2013); Rappazzo (2015). The asymmetry along z of the solutions of the reduced MHD equilibrium equation (5.36) can be estimated with the axial variation length-scale $z_{\ell} \sim \ell B_{0}/b$ (Eq. (5.40), see also Fig. 5.6), where ℓ is the perpendicular characteristic scale (in the x–y plane) of the magnetic field component b. The dynamical solutions of the reduced MHD equations (5.34)–(5.35) generally do not exhibit strong asymmetries along z. On the other hand the equilibria are strongly asymmetric for z _ℓ  < L _z or quasi-invariant for $z_{\ell} \gtrsim L_{z}$, depending on the relative value of the axial variation scale z _ℓ respect to the loop axial length L _z , with the critical length given by $z_{\ell} \sim L_{z}$ (corresponding to the critical intensity $b \sim \ell B_{0}/L_{z}$). As shown in Fig. 5.8 below the threshold $b_{0}/B_{0} \lesssim 3\,\%$ no substantial energy is dissipated for the line-tied 3D runs, minimal dynamics occurs as the field slightly readjusts to the close equilibrium quasi-invariant along z. In this case the initial magnetic field has a perpendicular scale $\ell\sim L_{\perp }/3.87 \sim 1/3.87$ (the averaged wavenumber of the initial condition is 3.87 and L _⊥ = 1), so that the threshold corresponds to a variation length-scale for the initial magnetic field of about $z_{\ell} =\ell B_{0}/b_{0} \gtrsim 100/(3 \times 3.87)$, i.e., $z_{\ell} \gtrsim L_{z}$ since L _z  = 10.

On the contrary for larger intensities of the initial magnetic field b ₀∕B ₀ > 3 % the corresponding equilibria, computed from Eq. (5.36) have a small variation length-scale z _ℓ  < L _z and are therefore strongly asymmetric along z. Since the initial magnetic field has only the parallel m=0 mode, it is invariant along z and it cannot therefore access the strongly asymmetric equilibrium. Nonlinear dynamics must develop current sheets and dissipate energy via magnetic reconnection for the system to decay to a lower energy state close to an accessible equilibrium quasi-invariant along z. As confirmed by the simulations shown in Fig. 5.8, in the cases when decay occurs, i.e., for initial conditions with b ₀∕B ₀ > 3 %, the magnetic field relaxes to a new equilibrium that approximately satisfies the condition $b/B_{0} \sim 3\,\%$ and $z_{\ell} \sim L_{z}$.

Initial conditions with only the parallel mode m = 1 decay for any value of the magnetic field intensity b ₀∕B ₀ no matter how small its value (see Rappazzo 2015 for a more extended discussion), in stark contrast with the evolution of initial magnetic field with only parallel mode m=0 for which no decay is observed for $b_{0}/B_{0} \lesssim 3\,\%$ (Fig. 5.8). This behavior is consistent with the structure of the equilibria outlined previously. Indeed since the only equilibria accessible dynamically must be quasi-invariant along z, i.e., the parallel mode m=0 is the larger parallel mode, if the initial magnetic field has only the mode m = 1 it can only decay. Furthermore the nonlinear dynamics developing during the decay must transfer a fraction of the energy into a parallel m=0 mode for the system to relax to a non-vanishing equilibrium with b ≠ 0. In fact this is what happens, and in Fig. 5.9 (middle) the relaxed magnetic field with a structure strongly elongated in the axial direction is shown for the numerical simulation with $b_{0}/B_{0} = 10\,\%$.

Initial magnetic fields with all modes m ∈ [0, 4] excited, where m=0 is the largest mode, show a behavior similar to that of initial fields with only the mode m=0 (shown in Fig. 5.8), but with a higher fraction of energy dissipated while decaying, and a small but clearly discernible energy dissipation occurs also for very small ratios of b ₀∕B ₀. Again, in agreement with the structure of the equilibria discussed above the magnetic field must decay to a configuration quasi-invariant along z. Therefore all excess energy, particularly in modes higher than zero (m ≥ 1), must be dissipated and/or partially transferred to the parallel mode m=0, so that the system decays to a lower energy configuration quasi-invariant along z with magnetic field intensity $b \lesssim \ell B_{0}/L_{z}$ ($\lesssim 3\,\%$ in this case) and variation length-scale larger than the loop length $z_{\ell} \gtrsim L_{z}$.

Finally Fig. 5.9 shows that no matter what the exact structure of the initial magnetic field is (the initial magnetic field has only the modes m=0 in the top panel, only m = 1 in the middle panel, and all modes m ∈ [0, 4] in the bottom panel), the relaxed magnetic field is quasi-invariant along the axial direction z with its structure dominated by the m=0 mode.

Fig. 5.9

Isosurfaces of the magnetic potential ψ in the asymptotic regime, when the magnetic field has relaxed. The initial magnetic field has intensity $b_{0}/B_{0} = 10\,\%$, and it has a different structure along the z direction for the three simulations. This is determined by the parallel modes present at t = 0, respectively only the single parallel modes m = 0, m = 1 and all modes m  ∈ [0, 4]. The elongated structure of ψ along z in the asymptotic regime shows that the fields relax into an equilibrium with a strong parallel m = 0 mode for all the initial conditions considered, including the initial condition with only parallel mode m = 1 (where no m = 0 mode is initially present). The computational box has been rescaled for an improved visualization, but the axial length is ten times longer that the perpendicular cross section length. During the decay energy decreases considerably for the initial conditions with $b_{0}/B_{0} = 10\,\%$, as shown in Fig. 5.8 for the initial condition with m = 0, and in Rappazzo (2015) for initial conditions with m = 1 and m  ∈ [0, 4] (than display a similar decay rate). Images adapted from Rappazzo (2015)

5.7 Continuous Solutions and Weak Solutions

The mathematical studies of the vorticity equation (5.32) have established two important restrictive principles associated with the vorticity ω being constant along each streamline, i.e., the torsion coefficient a being constant along each field line. First, the enstrophy ω ² cascades to small scales with the passage of time, while the kinetic energy cascades to large scales. That is to say, a ² cascades with increasing ζ to small scales, while the magnetic energy density b _x ² + b _y ² cascades to large scales.

The essential point here is that the field line interlacing topology, described by the choice of ψ(x, y, kzt), does not generally exhibit the topology associated with the cascading properties prescribed by the vorticity equation (5.32). That is to say, the special topologies required by the continuous vorticity solutions are contained somewhere within the set of all possible topologies prescribed by ψ(x, y, kzt), but their special nature, necessary to maintain a constant torsion coefficient along each field line, makes them a topological set of measure zero compared to the set of all possible interlacing topologies. Thus almost all topologies prescribed by ψ(x, y, kzt) do not have the very special evolution toward larger or smaller characteristic lengths associated with a continuous solution to Eq. (5.32).

So the vorticity equation (5.32) provides the set of all continuous equilibrium solutions for which the torsion coefficient is constant along each field line, and the continuous solutions exist only for that set of restricted field line topologies. Yet as already noted there is equilibrium for all field line topologies described by the function ψ(x, y, kzt). Thus almost all of the equilibrium solutions are not to be found among the continuous solutions. Recall that specification of the unknown function—the torsion α in this case—on any one characteristic curve of Eq. (5.10), i.e., on any one field line, in no way affects the unknown function on any of the neighboring characteristic curves, i.e., field lines. Thus there may be a discontinuous jump in the unknown function between two contiguous characteristic curves, in the present case a discontinuous jump in the torsion coefficient and in the field between two contiguous field lines. In particular one expects a surface of tangential discontinuity (TD) along a flux surface, with the field direction jumping discontinuously across the TD where the field magnitude is continuous. Neither the field nor the torsion coefficient is defined on the TD, so the troublesome equation (5.10) is inapplicable on the TD. Thus, when the constant torsion along a field line does not fit continuously against the contiguous flux bundles, there is created a TD. Almost all interlaced topologies fail to conform to the requirements dictated by the vorticity equation (5.32). So almost all field line topologies possess one or more TD’s as an intrinsic part of their equilibrium (Parker 1972, 1994, 2007). These solutions to the field equation (5.10) are the so called weak solutions (Courant and Hilbert 1980), analogous to the shock solutions familiar in hydrodynamics.

Now conservation (∇⋅ j = 0) of current that is everywhere parallel to B implies that a TD can terminate only at the end plates, z = 0, L. Thus a TD created by the field line interlacing at one location extends through successive uncorrelated interlacing patterns elsewhere along the field (Parker 1994). So a succession of independent interlacing patterns provides TD’s with diverse orientations. TD’s intersect laterally, generally forming an irregular cell structure with continuous solutions of the vorticity equation (5.32) filling the spaces between the TD’s.

We emphasize that TDs are an intrinsic part of the mathematics of the equilibrium equation (5.10); they do not arise arbitrarily or independently. They are subject to the field line topology and they form the cell structure into which the continuous vorticity-like solutions are fitted. Each cell writhes along with the field lines, and the solution of Eq. (5.32) fits within its writhing TD boundaries. In this connection note that Eq. (5.16) determines the variation of α in the direction perpendicular to B, while Eq. (5.17) states that α does not vary in the direction of B. These two conditions are made mathematically compatible by the fact that Eq. (5.16) is a quasi-linear elliptic equation, indicated by the linear position of the Laplacian in the equation. Hence, there is a solution of Eq. (5.16) for every possible simply-connected boundary shape. The formal mathematical solution of Eqs. (5.16) and (5.17) is difficult because the precise form and location of the TD’s must be worked out simultaneously with the construction of the continuous field that fits within those TD’s. Low (2015) has explored the mathematical structure of the equilibrium equations, providing a formal view far beyond the brief remarks given here.

5.8 Formation of TD’s and Rapid Reconnection

The initial interlacing of the magnetic field, described by ψ(x, y, kzt) provides a field, Eq. (5.14), that is everywhere continuous, but not in equilibrium. The TD’s form as the asymptotic limit of the relaxation to equilibrium, driven by the Lorentz force of the initial nonequilibrium field, while preserving the field line topology of course. The field gradient is caused to steepen as the Lorentz force squeezes plasma and field out from between two regions of nonparallel field. It is the diminishing separation of the two fields that provides the increasing field gradient and current density. The ultimate equilibrium, with its TD’s, arises only in an infinitely conducting (dissipationless) fluid of course. The slightest resistive dissipation prevents the fields reaching that ultimate equilibrium state. We recognize the relaxation process as the formation of rapid reconnection sites. Rapid reconnection, then, is a ubiquitous phenomenon in actively interlacing magnetic fields, e.g., the bipolar magnetic fields of active regions on the Sun and other stars.

Following this proof of existence of the ubiquitous rapid reconnection, the next step in the theoretical development of rapid reconnection in interlaced topologies is to follow the dynamical relaxation of the initial nonequilibrium magnetic field described by Eq. (5.14). So far we have described only the final equilibrium state, made up of weak solutions, in which the continuous solutions of the vorticity equation (5.32) are fitted in among the TD’s. Noting that the equilibrium state involves the mathematics of the 2D vorticity equation, for which there are only a few limited analytic solutions (Kraichnan and Montgomery 1980), it is evident that the dynamical evolution toward that state must be pursued by numerical methods. Numerical efforts have been made using the seemingly plausible algorithm that the velocity of the plasma is everywhere equal to a constant times the Lorentz force. Those numerical experiments found no evident trend toward forming TD’s. More recently Low (2013) has pointed out that the algorithm is unphysical, i.e., unable to hold the field fixed at the end plates because vanishing plasma velocity requires vanishing Lorentz force. There is also the unphysical effect that neutral points do not move because the Lorentz force vanishes there.

Fig. 5.10

Midplane section through interlaced magnetic field, reproduced from Rappazzo and Parker (2013), showing the initial continuous current density j and then the subsequent concentrated current sheets at time t = 0. 1993 t _A in the relaxation toward stable static equilibrium. Top panels show j and the magnetic field lines of the orthogonal magnetic field component b

Fig. 5.11

Left: Fits of total energy spectra at selected times to Eq. (5.41) in linear-logarithmic scale (top panel) and double logarithmic scale (bottom panel). Right: Linear-logarithmic plot vs. time of the analyticity strip width δ (top panel) and of the sum of the current density and vorticity (moduli) maxima (bottom panel), for two ideal simulations with respectively only mode m = 0 and all modes m = 0–4 present. The dashed line is the resolution scale set at 2∕k _max . Right panel image adapted from Rappazzo and Parker (2013)

The preferred algorithm assumes a uniform viscosity, so that ∇² v is equal to a small constant times the Lorentz force, and the velocity can be maintained at zero at the end plates. The formation of current layers of monotonically declining thickness is immediately evident in the relaxation of the initial non-equilibrium magnetic field in the reduced MHD regime, illustrated in Fig. 5.10, reprinted from Rappazzo and Parker (2013). In this case an initial magnetic field invariant in the axial direction was considered, and the analyticity-strip method (Sulem et al. 1983; Frisch et al. 2003; Krstulovic et al. 2011; Bustamante and Brachet 2012; Brachet et al. 2013) used to track current sheet thinning. Indicating with δ the distance from the real domain of the nearest complex space singularity, this corresponds to an exponential fall-off in Fourier space at large k for the total energy spectrum power-law (of the real solutions):

$$\displaystyle{ E(k,t) = C(t)\,k^{-n(t)}\,e^{-2\delta (t)k}. }$$

(5.41)

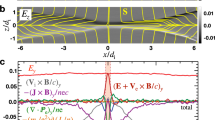
The width in time of the thinnest current sheet is therefore measured by δ(t), determined by fitting the total energy spectra with Eq. (5.41) at different times (Fig. 5.11, left panels). The intensification of the current sheets proceeds to the limit of the numerical resolution, as shown in Fig. 5.11 (right panels), where δ decreases down to the smallest admissible scale (fixed at 2 meshes: 2∕k _max, with k _max = 1364), while the current and vorticity maxima increase exponentially. One can see the formation of the rapid reconnection site from the beginning. Figure 5.12 shows the current density and field lines of the orthogonal magnetic field for the ideal simulations with initial magnetic field made of all parallel modes m ∈ [0, 4]. It shows that the strongest current in the mid-plane does not overlap with an X-point, a result present also in line-tied dissipative reduced MHD simulations (Rappazzo et al. 2008, 2010), for which it has been shown that the X-points of the orthogonal magnetic field are often displaced from current sheets both in periodic and line-tied systems (Zhdankin et al. 2013; Wan et al. 2014), with the higher reconnection rates occurring when both overlap. Linear and nonlinear investigations (Pucci and Velli 2014; Tenerani et al. 2015; Landi et al. 2015) have shown that an exponentially thinning current sheet is unstable to tearing, with its growth rate increasing for smaller thicknesses, reaching fast “ideal” Alfvén values ($\gamma \tau _{A} \sim 1$) for thicknesses $\delta /L \sim S^{-1/3}$ (where L is the current sheet length, and S the Lundquist number), leading to the formation of many magnetic islands and X-points and developing the complex dynamics of so-called super-tearing or plasmoid instability (Bulanov et al. 1978; Biskamp 1986; Loureiro et al. 2007; Lapenta 2008; Bhattacharjee et al. 2009).

Fig. 5.12

Current density j in the mid-plane z = 5 for the simulation with m = 0–4, at t = 0 (top left panel) and at $t \sim 0.125\ \tau _{A}$ (all other panels). The color scale reveals thin sheets with strong current enhancements, just before δ crosses the resolution scale (see Fig. 5.11). Field lines of the orthogonal magnetic field are overdrawn as continuous lines

Several authors have pursued the formation of current sheets in diverse initial field line topologies, finding the formation of current sheets, TD’s, to be ubiquitous in complex topologies. Rappazzo has pursued an interlaced field three “stitches” long to obtain a first estimate of the threshold for the onset of TD’s. Kumar et al. (2013, 2014) have investigated periodic fields containing 3D nulls. Kumar et al. (2014) use a novel representation of B in terms of Euler potentials, so that the computation follows flux surfaces rather than the field itself, to some advantage. They show that TD’s are ubiquitous, but do not originate at 3D null points.

This success with numerical methods opens up the possibility to pursue a variety of questions. For instance, in the reduced MHD regime it has been shown that intense current sheets form only above the magnetic field intensity $b \gtrsim \ell B_{0}/L_{z}$, corresponding to an equilibrium axial variation scale smaller than the coronal loop length $z_{\ell} \lesssim L_{z}$ (Sects. 5.6 and 5.6.1). What is the precise threshold for the strength of the interlacing if it is to develop TD’s for magnetic configuration not limited to the reduced MHD regime? Then what is the number of TD’s that might form as a consequence of each independent stitch in the interlacing along the field. With the local correlation length l it follows that a field line extends through O(L∕l) independent eddies along its path from z = 0 to z = L. So are there as many as O(L∕l) TD’s in each characteristic area $/x/$ at the end plate? On the other hand, TD’s can join laterally (Parker 1994) reducing the number of separate TD’s. It would be interesting to have a look at the irregular cell structure formed by the TD’s. Each cell is filled with a solution of the vorticity equation (5.32).

Then there are questions about the final asymptotic field line topology arising from the ongoing rapid reconnection in an arbitrary initial topology ψ(x, y, kzt). Presumably reconnection ceases when the topology is reduced to the threshold for the formation of TD’s.

Turning to the Sun consider the interlaced magnetic fields arching up over the convective photosphere into the corona of the Sun. We expect that there is ongoing coronal heating by the basic minimum rapid reconnection rate, of the order of $C/R_{L}^{1/2}$. This minimum rate is maintained indefinitely along each TD by the active convective interlacing to provide an ongoing low level heating of the ambient plasma. Evidently the minimum rapid reconnection does not always keep up with the active interlacing of the field, with the result that the interlacing may increase in intensity with the passage of time, providing stronger TD’s. The growth in the strength of the magnetic TD’s in a tenuous gas would be expected occasionally to push the local reconnection rate toward the explosive speed 0.01–0.1 C, producing nanoflares along the TD. The flaring soon dissipates the local interlacing and is sustained for a time by the propagation of interlacing (as Alfvén waves) into the flaring region from the interlacing elsewhere along the field. The individual flare is estimated to be small, of course, perhaps of the order of 10²⁴ ergs or less (Parker 1988, and references therein). One can only turn to solar observations of flares, microflares, nanoflares and perhaps picoflares (Katsukawa 2003) for quantitative information. We have suggested (Parker 1988, 1994) that it is such localized small-scale flaring in the interlaced topology of bipolar magnetic filaments that heats the transient filaments of X-ray emitting gas on the Sun, and we expect that most late main sequence stars produce X-rays through the same process.