Distance-Based 3D Face Reconstruction Using Regularization

Abstract

This study addresses the problem of reconstructing 3D face shapes from a small set of 2D facial points. By using Maximum Posterior Probability estimation, prior information modeled by PCA is connected to Tikhonov regularization method in order to solve the ill-posed problem of 3D face reconstruction. The prior information is learned from 3D faces of a standard 3D database. However, the optimal value of the regularization parameter λ is usually not available in advance. To overcome this problem, we restrict the distance between the reconstructed 3D face and the average 3D face close to the average of the distances between sample 3D faces and the average 3D face. This is due to the fact that the sample data are mostly located at the boundary of the data space for high dimensional and low sample size problems, which is the case for 3D faces. The optimal regularization parameter is then obtained to reconstruct the 3D face shape of a given 2D near frontal image using limited number of feature. The solution is plausible while not over-smoothing. By warping the 2D texture to the reconstructed face shape, 3D face reconstruction is achieved. Our experimental results justify the robustness of the proposed approach with respect to the reconstruction of realistic 3D face shapes from a small set of 2D facial coordinates.

1 Introduction

The objective of 3D facial reconstruction systems is to recover the three dimensional shape of individuals from their 2D pictures or video sequences. Until now, in most popular commercially available tools, the 3D facial models are obtained not directly from images but by laser-scanning of the people’s faces [1]. The problem of 3D facial modeling remains as a partially solved problem in the field of computer vision in terms of the accuracy and speed of reconstruction algorithms.

In this paper we present an approach for reconstructing the 3D face of an individual given the 2D face image, in which prior knowledge based on exemplar 3D faces is acquired. With help of the prior knowledge, the 3D face shape is estimated using a set of 2D control points while the 2D texture is registered with the texture model and warped to the reconstructed 3D face shape. Example based modeling allows more realistic face reconstruction than other methods [2, 3]. In the simplest form, example-based 3D face reconstruction methods have two main stages: The model building stage and the model fitting stage. In this paper, Principal Component Analysis (PCA) based 3D face model is used for model building and the regularized algorithm is used for model fitting. For texture, similar to [4], the 2D image texture has been registered to the reference texture model using Thin Plate Splines (TPS) [5] and then warped on the reconstructed shape. We therefore focus on shape modeling.

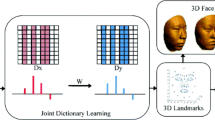
When shapes are considered, the reconstruction of 3D face from 2D images using shape models is relatively simple. One of the reconstruction methods that uses prior knowledge to estimate the shape coefficients from a set of facial points is regularization [4]. In [4], Jiang et al. use a regularization equation that estimate the geometry coefficient in an iterative procedure. Alternatively regularization method has also been presented in [6]. Figure 1 shows how a given input face is reconstructed via 3D face shape estimation using a prior shape model. It also shows the process of warping 2D texture to the reconstructed 3D face shape.

Fig. 1.

Proposed scheme for 3D face reconstruction from single 2D image

Our 3D shape learning model relies on examples of 3D scans which mean that missing information can be inferred using correlation between the model shape vectors. For robust, plausible and stable results, the regularization mechanism needs to find a tradeoff between fitting 3D shape to the given 2D facial landmarks and producing plausible solution in terms of prior knowledge [7]. The Standard Tikhonov Regularization method (STR), which uses the identity matrix as a regularization matrix, is used to estimate the model parameters by solving the inverse problem and preventing the overfitting. However, the quality of the reconstructed face shapes is very similar to the mean face shape (excessive smoothness) which leads to loss of information about the reconstructed images [8]. Eigenvalue Tikhonov Regularization (ETR) [9] replaces the identity matrix with the eigenvalue matrix in order to utilize the prior information that is modeled by PCA. It has been shown that using ETR reduces the reconstruction error significantly when compared with STR. Furthermore, by using Tikhonov regularization, the problem of choosing an appropriate regularization parameter arises. Choosing too large regularization parameter causes the solution to be over-smoothed. Otherwise, too small regularization parameter leads to overfitting. In other words, the regularization parameter balances the tradeoff between the excessive smoothing of the reconstruction and the data misfit.

There are numerous strategies for determining the regularization parameter [10]. Some mathematical methods such as the discrepancy principle, the Tikhonov prior estimation, the Engl criteria, and Arcangeli criteria method need prior information about the data noise [8]. In practice, however, such prior information cannot be easily acquired and it is highly impractical to obtain the noise characteristic in real time [11]. Other methods including L-curve and generalized Cross Validation need less prior information but are time consuming. In addition, some factors can influence the parameter selection. These factors include e.g. diffusion of errors in the process of numerical computation, and the random fluctuation of errors in the input data [8]. Furthermore, these methods have also its limitations. For example, although in the last decade, L-curve gained attention for determining optimal regularization parameters, yet, however, its limitation is of having asymptotic property which means it is non convergent [12].

A different strategy is to select the regularization parameter in a straightforward way and setting its value as constant for all images [13]. For example, in [8] the range of the regularization parameter was determined empirically by solving typical cases in advance. However, empirically determination of regularization parameter leads to an unwanted bias in the solution. Furthermore, it varies for different problems and requires prior information on the target images as well as the noise in the data.

In this paper, we use a different strategy for optimal selection of the regularization parameter for 3D face shape estimation. A distance-based approach that utilizes the distance from the average 3D face and the reconstructed face through an optimization function is proposed. The only prior knowledge required for the new strategy is the average of training face shapes, which is very easy to obtain. The distance from the average face is used to control the regularization process in order to obtain a plausible 3D face shape for any given 2D face image. This method ensures that the obtained 3D face shape is plausible and not over-soothing. The proposed method is backed up by the fact that for high dimensional and low sample size problems, which is the case for the 3D faces in this paper, most of the sample data are located at the boundary of the data space [14]. The histogram of the distances between sample faces and the average face in Fig. 2(b) has demonstrated this effect.

Fig. 2.

(a) A scheme representing the model boundary: The mean face (middle) and the training faces with their distances D _m. (b) Histogram for the distance between sample faces and the mean face. For example, the first bin 0.0047 means the frequency >=0.0047 and <0.0066 and so on.

For the texture, we use TPS techniques to register the input image texture with the model texture and then warp the interpolated texture to the reconstructed 3D shape face [15]. Our reconstructed results from real 2D face images show good reconstruction and retains real characteristic of the given 2D face images.

The rest of the paper is organized as follows: Sect. 2 demonstrates the modelling of 3F face shapes. Section 3 describes the fitting process of 3D shape model to new faces. Section 4 deals with the experimental results and associated discussions. Section 5 concludes our research.

2 Modeling 3D Face Shape

The characteristic shape properties of the 3D face shape are derived from a dataset of 3D scans. The 3D shapes are aligned with each other in such a way that 3D-3D correspondence for all vertices are obtained [16]. The p number of vertices corresponding to each face is defined by concatenating the x, y, z coordinates of the face surface to a single vector $s_{i}$ with the dimension $n = 3 \times p$ as:

$$ \varvec{s}_{i} = (x_{i1} ,y_{i1} ,z_{i1} , \ldots ,x_{ip} ,y_{ip} ,z_{ip} )^{T} . $$

(1)

where i = 1, …, m (number of face shapes). The dimensions of the shape vectors are very large compared to the sample size, whereas the number of vertices n is equal to 75972 and the sample size m comprises 100 face shapes. If we apply PCA on the data, the covariance matrix will be n × n which is very huge. However, the same eigenvectors and eigenvalues can be derived from a smaller m × m matrix.

Let

$$ \varvec{s}_{0} = \frac{1}{m}\sum\limits_{i = 1}^{m} {\varvec{s}_{i} } . $$

(2)

where s ₀ be the average face shape of m exemplar face shapes and S = [s ₁ , s ₂ , …, s _m ] ∈ R ^n×m. Each vector is centered around the mean in a new vector x such that

$$ \varvec{x}_{i} = \varvec{s}_{i} - \varvec{s}_{0} , \, \quad \, i = 1,2, \ldots m . $$

(3)

Let the data matrix $X = [x_{1} ,x_{2} , \ldots ,x_{m} ] \in R^{n \times m}$. Then the covariance matrix C can be written as

$$ C = \frac{1}{m}X^{T} X = \frac{1}{m}\sum\limits_{i = 1}^{m} {x_{i} } x_{i}^{T} \in R^{n \times n} . $$

(4)

The Covariance matrix C has only (m-1) eigenvectors v _i with nonzero corresponding eigenvalues w _i , and all remaining eigenvectors of C have zero eigenvalues. It can be shown that the vectors X ^T v _i are all eigenvectors of $C \in R^{n \times n}$ with corresponding eigenvalues w _i . Let $C^{T} = XX^{T} \in R^{m \times m}$, then the matrix ${\mathbf{C}}^{T}$ can be decomposed into:

$$ C^{T} = XX^{T} = UWV^{T} VWU^{T} = UW^{2} U^{T} . $$

(5)

where U and V are orthogonal matrices and $W^{2}$ is the diagonal m × m matrix with diagonal elements being the eigenvalues. $\varvec{C}^{T}$ is symmetric, so it can be written as

$$ C^{T} = UW'U^{T} . $$

(6)

$U = [u_{1} ,u_{2, \ldots ,} u_{m} ]$ is the set of orthonormal eigenvectors and $W' = diag(w'_{i} )$ is a diagonal matrix containing the associated eigenvalues. The set of vectors $X^{T} u_{i}$ form an orthogonal basis, where each vector has the length $\sqrt {w'_{i} }$. The scaled basis vectors of the covariance matrix $C \in R^{n \times n}$ are derived as follows:

$$ E = X^{T} U(\sqrt {W'} )^{ - 1} . $$

(7)

where E = (e ₁ , e ₂ , …, e _m ) is the matrix of scaled basis vectors of unit length ($||e_{i} ||_{2} = 1$) and $\sqrt {w_{i}^{'} }$ represents the standard deviation within the face shapes along the basis vectors $X^{T} U$. A new shape vector $s_{rec} \in R^{n}$ can be expressed as

$$ s_{rec} = s_{0} + E\alpha = s_{0} + \sum\limits_{i = 1}^{m} {\varvec{\alpha}_{i} } \varvec{e}_{i} $$

(8)

where e _i represent the i ^th scaled basis vector of the covariance matrix C and α _i is the coefficient of the scaled basis vector e _i .

Since E is an orthonormal matrix, the PCA-coefficients α of a vector $x = \varvec{s} - \varvec{s}_{0} \in R^{n}$ can be derived from Eq. (8). as

$$ \alpha = E^{T} x . $$

(9)

2.1 Model Boundary

As mentioned in [17], the Representational Power (RP) of the PCA-based model is its capability to depict a new 3D face of a given face image. It depends on the exemplar faces in the training data set. The common factors that are generally concerned are the size of the training dataset and the selection of different examples in the training set. Even if a more powerful model, trained with more examples or a different dataset, generates a better representation of the true face, the generated face remains within the boundaries of the PCA-model. In this paper, the Euclidean distances between all training face shapes and the average face were utilized to determine the mode boundary (interval). The Euclidean distance weighted by the number of vertices can be computed between the mean face vector s ₀ and any other face vector s in the dataset as follows:

$$ D{}_{m} = \frac{1}{n}\sum\limits_{i = 1}^{n} {||\;s_{0i,} - s_{i.} \;||} . $$

(10)

Where D _m is the weighted Euclidean distance and n is the dimension of the face shape vector. Accordingly, we assume that any new reconstructed face shape will have a distance that does not goes beyond the model’s boundary. The assumption is backed up by the fact that for the high dimensional and low sample size problem, which is the case for the 3D faces in this paper, most of the sample data are located at the boundary of the data space [9]. Figure 2(a) demonstrates some exemplar face shapes from the training data set and their distances D _m from the mean face. Figure 2(b) is the distribution of the distances between sample faces and the mean face. Accordingly any new reconstructed face shape can be only plausible and not over-smoothing if it has a distance D _m that locates in the model boundary (between the minimum and maximum D _m of all training faces).

3 3D Shape Model Fitting to New Faces

Learning models are trained from a set of examples to reach a state where the model will be able to predict the correct output for other examples. However, the available training data set (number of 3D faces) is much smaller than the dimension (number of vertices) and there are too many missing features in the testing data (real 2D face images). Therefore, overfitting can easily occur [7]. The goal of robust fitting algorithms is to reduce the chance of fitting noise and increase the accuracy in predicting new data. Noise in such cases may occur due to intricacies in selecting input feature points, which depends on the acquisition systems or the uncertainties imposed by the used alignment methods. Fitting the shape model to a given 2D image is formulated as an optimization problem to solve the linear system in Eq. (9), which can be written as

$$ x = E\alpha . $$

(11)

The goal of this inverse problem is to find the PCA-coefficients α, rapidly and efficiently, given E and the shape vector $\varvec{x} = \varvec{s} - \varvec{s}_{0}$, where s is the given shape vector and s ₀ is the mean face shape. The direct solution of α is by the projection of the vector x onto E using Eq. (9), whereas E is an orthonormal matrix with $E^{T} E = I$, the identity matrix. However, the inverse problem of Eq. (11) is ill-posed and ill-conditioned. It causes the solution to be unstable and very sensitive to noise in the input data. Thus constraints or prior information shall be employed to get a meaningful reconstruction results. Given a number of feature points $f < < p$, the problem is to find the 3D coordinates of all other vertices. In case of limited feature points, overfitting may occur by using approximation methods. In addition, using a holistic model such as PCA based model, the model cannot be adapted to the particular set of feature points resulting in overfitting. Therefore, regularization can be used to enforce the result to be plausible according to the prior knowledge [18].

Assume that $s_{f} \in R^{l} (l = 2f)$ contains f feature points on a given 2D face image for which a 3D shape will be estimated, s _0f is the corresponding points on s ₀ (the average 3D face shape) and $x_{f} = s_{f} - s_{0f}$ is related to r such that

$$ x_{f} = Ar + \varepsilon , \, \quad \quad A:R^{m} \mapsto R^{l} , \, \quad \quad x_{f} \in R^{l} , $$

(12)

where $A \in R^{l \times m}$ is the matrix of corresponding scaled basis vectors in $E^{T} \in R^{n \times m}$, $r$ is the model parameter, and ${\varvec{\upvarepsilon}} \in R^{l}$ can be considered as measurement errors with unknown properties.

Ultimately the goal is to estimate r as accurate as possible, given A and x _f . Because A is not a square matrix which leads to non-invertible matrix, the model cannot be solved directly as an inverse problem. Instead, we consider the problem as an optimization problem which has the following objective function:

$$ \varphi = ||\;x_{f} - Ar\;||_{2}^{2} . $$

(13)

Minimizing $\varphi$ is to minimize the difference between the original and the predicted data. A simple least square technique can be used to minimize $\varphi$ by solving the inverse problem to

$$ r = (A^{T} A)^{ - 1} A^{T} x_{f} = A^{ + } x_{f} , $$

(14)

where $A^{ + }$ is the Moore-Penrose Pseudoinverse of A. It is considered as an optimal solution of the L2-optimization problem but not necessary the best solution. Moreover, in addition to the measuring errors, the measured feature points $x_{f}$ captures only a small portion of the original image x, which introduces errors in the recovered model. To solve this ill-posed problem, regularization can be used as a constraint that utilizes the possible features in the holistic model to produce plausible results. One of the most popular regularization methods for the linear least square problem is due to Tikhonov. A general Tikhonov regularization with desirable properties has the following minimization

$$ ||\;Ar - x_{f} \;||_{2}^{2} + \lambda ||\;Lr\;||_{2}^{2} , $$

(15)

where $||\;Lr\;||_{2}^{2}$ is the stabilizing item with some suitably chosen L (Tikhonov matrix) and $\lambda > 0$ is called the regularization parameter. This regularization enables a numerical solution by improving the conditioning of the problem. If L is chosen to be the identity matrix, the Tikhonov regularization has the following standard form

$$ (A^{T} A + \lambda L^{T} L)r = A^{T} x_{f} . $$

(16)

For each $\lambda > 0$, and replacing $L^{T} L$ with I (identity matrix), the above equation has the following unique solution

$$ r_{reg} = (A^{T} A + \lambda I)^{ - 1} A^{T} x_{f} . $$

(17)

The solution of Eq. (17) is influenced by the variety of $\lambda > 0$, where r _reg is more sensitive to the error ε, the smaller $\lambda > 0$ is. On the other hand, as $\lambda$ increases the solution r _reg converges to 0. However, when $\lambda > 0$, r _reg is reduced to the least squares solution r ₀ of Eq. (14 ) with no regularisation. Mathematically, this means that

$$ \mathop {\lim }\limits_{\lambda \to 0} r_{reg} = r_{0} , \, \quad \mathop {\lim }\limits_{\lambda \to \infty } r_{reg} = 0 \, . $$

(18)

These restrictions limit the possibility of obtaining a meaningful approximation of r. Hence, it is essential to choose a suitable value of $\lambda > 0$ which determines the sensitivity of the solution r _reg of Eq. (17) to the error ε and how close r _reg to the desired solution α of Eq. ( 9 ).

In our case, the original data matrix $X = S - S_{0}$ is a multivariate normal distribution whereas the means are zero and the principle components are independent and have the same standard deviation. We also assume that the errors in x _f are independent with zero mean and same standard deviation of the original data. By Bayes’ theorem, under these assumptions, the Tikhonov-regularized solution is the most probable solution [19].

According to the maximum posterior probability, the case in Eq. (17) can be reformulated to minimize

$$ ||\;\;Ar - x_{f} \;||_{2}^{2} + \lambda ||\;\;r^{T} C_{r}^{ - 1} r\;||_{2}^{2} , $$

(19)

where C _r is the covariance matrix of the coefficient r. Equation (19) amounts to the Maximum-A-Posterior (MAP) estimation.

3.1 Generalized Tikhonov Regularization

The Tikhonov regularization (Eq. (15)) of the linear system of Eq. (12) is

$$ \mathop {\hbox{min} }\limits_{r} ||\;Ar - x_{f} \;||_{2}^{2} + \lambda ||\;r\;||_{2}^{2} , $$

(20)

Compared with the MAP estimation (Eq. (19)) of our linear problem, the second term is $\lambda ||\;r\;||_{2}^{2}$ rather than $\lambda r^{T} C_{r}^{ - 1} r$. $C_{r}^{ - 1}$ is the inverse covariance matrix of r which can be factorized as $C_{r}^{ - 1} = L^{T} L$. Thus, the optimal solution r ^* can be estimated by Tikhonov as

$$ r^{*} = (A^{T} A + \lambda C_{r}^{ - 1} )^{ - 1} A^{T} x_{f} . $$

(21)

Moreover, the covariance matrix C _r of the model coefficients is equivalent to the diagonal eigenvalue matrix Wʹ of C = XX^T. Let L be the matrix containing all model coefficient vectors, and according to Eq. (7) $E = X^{T} U(\sqrt {W'} )^{ - 1}$, then

$$ L = XE = XX^{T} U(\sqrt {W'} )^{ - 1} . $$

(22)

Since $XX^{T} = UW'U^{T}$(Eq. (6)) and Wʹ is a diagonal matrix, we see that

$$ L = UW'U^{T} U(\sqrt {W'} )^{ - 1} = UW'(\sqrt {W'} )^{ - 1} = U\sqrt {W'} . $$

(23)

Let $C_{r} = L^{T} L$ be the covariance matrix of the model coefficient vectors, then

$$ C_{r} = \sqrt {W'} U^{T} U\sqrt {W'} = W' . $$

(24)

Since $W' = C_{r}$, which means that the coefficient r has variance that follows eigenvalues, the stabilizing item can be chosen to be the inverse of the diagonal eigenvalue matrix Wʹ to solve the minimization problem of Eq. (19). This ensures that the solution will be in the boundary of the learning model. Hence, the model parameter α can be estimated as

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha } = (A^{T} A + \lambda W'^{ - 1} )^{ - 1} A^{T} x_{f} . $$

(25)

Then, a new face shape s _rec can be obtained by applying ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha } }}$ to Eq. (8) Jiang et al. [4] have used the same regularization equation in an iterative procedure in order to converge to a stable solution. In this work, the shape coefficients are calculated directly using Eq. (25).

3.2 Distance Based Reconstruction

Usually, a good value of the regularization parameter λ cannot be known in advance and the optimal λ can be only found if the original 3D face is available. The case for real 2D face images does not exist. On the other hand, increasing λ makes the solution more stable but may result in over-smoothing when λ is increased excessively. Conversely, when λ is too small, unstable behaviour of the solution occurs resulting in a huge variation of the trained model. Hence, to avoid this problem, the distance between the reconstructed face and the mean face (s ₀ ) is used to compute the face parameter α. The Euclidean distance was computed between the reconstructed face shape and the mean face (Eq. (10)) to determine how close the solution is to the mean face.

By calculating D _m, we can avoid the over-smoothing of the solution (the highly closeness to the mean face) whereas D _m can be considered as a measure of the smoothness. D _m has to be not close to 0 to avoid successive smoothness and not so large to avoid overfitting. Furthermore, D _m was used to control the regularization through the assumed model’s boundary (Sect. 3.1). First, the average distance $D_{vag}$ for all training face shapes was computed as follows:

$$ D_{vag} = \frac{1}{m}\sum\nolimits_{j = 1}^{m} {\left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {||\;s_{ji,0} - s_{ji,reconst} \;||} } \right)} . $$

(26)

With reference to Sect. 3.1, new reconstructed faces have a distance which is similar to training face distances, as any new reconstructed face is assumed to be within model’s boundary. In this situation, the distance of the new reconstructed face can be selected to be equal to $D_{vag}$. Depending on $D_{vag}$, the minimization problem can be represented as follows:

Recall that (Eqs. (11) and (25))

$$ x_{{}} = E\alpha . $$

(27)

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha } = (A^{T} A + \lambda W'^{ - 1} )^{ - 1} A^{T} x_{f} . $$

(28)

$$ x_{new} = E(A^{T} A + \lambda W'^{ - 1} )^{ - 1} A^{T} x_{f} . $$

(29)

The problem is simplified to find λ that satisfy the following equation

$$ f(\lambda ) = ||\;E(A^{T} A + \lambda W'^{ - 1} )^{ - 1} A^{T} x_{f} - s_{0} \;||^{2} , $$

(30)

where $D_{vag} - \varepsilon < f(\lambda ) < D_{avg} + \varepsilon$ and ε is a very small value. Choosing f(λ) to be close to $D_{vag}$ guarantees that the solution is in the model’s boundary and therefore is plausible and not over-smooth.

4 Experiments and Discussion

This paper aims at reconstructing 3D faces from their 2D source images using a distance based approach. By reconstructing 3D faces from real 2D images using Tikhonov regularization, the quality of reconstruction depends on selecting the regularization parameter λ which works as tradeoff between the prior probability and the accurate selection of feature points. The proposed method automatically determines the regularization parameter by using a predefined value of the distance from the prior average face. The experimental evaluation aspects of the proposed methods are reported in comparison with reconstructed testing faces produced by optimal λ which has the smallest reconstruction error. In addition, reconstructed 3D face shapes from input 2D face images were visualized for different values of D _m . The experiments were categorized in terms of the following three phases:

• 1. Evaluating the reconstruction of 3D faces through different values of λ. At the same time, D _m was computed for every testing face. The interval of distance D _m that meets the best interval of λ-values was determined.

• 2. Visualizing reconstructed 3D faces for input 2D face images through different values D _m .

• 3. Reconstructing 3D faces from real 2D images for D _m  = D _avg using the proposed method.

Noticeably, D _m is the distance between the reconstructed face and the mean face.

In the first phase, as reported in our previous work [9], the interval of D _m that meets the best interval of λ was determined. This interval was compared with the training face distances D _m to justify our assumption of this study that every new reconstructed face shape will have a distance from the mean face that is similar to the training face distances. In order to test the proposed approach, 3D faces were randomly selected from the testing set to visualize the reconstructed faces through different values of λ including the optimal λ. In the second phase, three examples of 2D face images were randomly selected from the CMU-PIE database to visualize the reconstruction results among different value of D _m . In the third phase, the proposed method is qualitatively evaluated through reconstructing 3D faces from their 2D faces images for D _m  = D _avg .

The USF Human ID 3D Face database [16] which contains 100 3D faces has been used. The proposed model has been trained with the 100 3D face shapes. Each face shape has coordinates of 75972 vertices. They are aligned with each other as explained by [3]. Figure 3 shows 3D face examples from the 3D database including shape and texture.

Fig. 3.

3D face examples from the USF Human ID 3D database [15].

To evaluate the proposed Distance-based reconstruction method on 3D face reconstruction, the current 100 face shapes were divided into a training set of m = 80 faces and a testing set of 20 faces. The testing set was used to evaluate the performance of the proposed method through different distances from the mean face. From the vertices of each test face vector, 25 XY feature point coordinates were selected. The 25 points are salient points such as nose, eye corners, eyebrows, mouth corners, and face contours. Similar to Eq. (10), the evaluation was based on determining the average distance between the points of the original and the reconstructed face shape vectors

$$ E_{r} = \frac{1}{n}\sum\limits_{i = 1}^{n} {||\;s_{i,orig.} - s_{i,reconst.} \;||} . $$

(31)

In order to qualitatively evaluate the distance-based approach, 3D face shapes were reconstructed from real 2D face images where the PCA-based model was trained with the 100 3D face shapes. The evaluation was achieved pertaining to the visualization aspect of the reconstructed faces using two sets of feature points with different sizes.

Fig. 4.

The effect of λ on the average reconstruction errors $E{}_{r}$ and the distance from the mean face for 20 test faces for a given set of 25 feature points, left: noise free feature points and right: noisy feature points [9].

4.1 Reconstruction of Testing 3D Face Shapes

Similar to our previous work in [9], the testing faces were reconstructed from 25 feature points through different values of λ. Then, the average reconstruction error of all reconstructed testing faces was determined. The reconstruction error for every testing face was determined by using the weighted Euclidean distance in Eq. (31). The reconstruction error was calculated for f = 25 as the ultimate goal of this study is to reconstruct 3D faces from a limited number of feature points. To see the effect of noise on the proposed method, random noises in the range (−5, 5) were added to the 2D point coordinates. Figure 4 shows the average reconstruction error and average distance D _m of 20 testing 3D face shapes at different values of λ.

The best interval of λ that produces the best solution in terms of minimum E _r were observed from Fig. 4(left) and (right) for noise and noise free respectively. Furthermore, as shown in Fig. 4, the opposite interval of D _m to the best interval of λ was determined. Regarding the noise free feature points, the values of λ in the interval (10, 1000) produce the best average of values for all 20 test faces with slight convergence to the average face as λ increases (Fig. 4, left). However, with regard to noisy feature points, the best interval was (100, 10000) whereas the average reconstruction errors has the minimum values and D _m is large enough for non-successive smooth solution (Fig. 4, right). For both noisy and noise free feature points, a value of D _m was located between 0.006 and 0.011 produced an appropriate λ that belonged to the best interval. Furthermore, the interval (0.006, 0.01) was also included in the interval of all training face distances which is (0.0050, 0.0210). This justified the assumption that any new reconstructed face shape will be in the model’s boundary. Figure 5 visualizes six reconstructed face shapes for the same four testing face shapes with different values of λ.

Fig. 5.

Reconstructed testing face shapes from 25 feature points. Every testing face has 6 different reconstructed shapes through different λ and different distances D _m . The bolded λ shows optimal distance from the ground truth and the bolded D _m shows the nearest distance to D_avg.

For smaller values of λ, the face shape became far from the original shape, D _m is large, and the face was distorted when λ converged to 0. In contract, D _m decreased, the shape becomes smoother and closer to the mean face, when λ converged to infinity. It was clear that the reconstructed faces with distances close to the average distance $D_{vag}$ were closer to the ground truth. This is illustrated in Fig. 5 where D _m for the optimal λ is equal to 0.0096, 0.0094, 0.0094 and 0.0101 for the four visualized testing faces.

To statistically test if the value of $D_{vag}$ can be used to determine an appropriate λ for all new faces, the Chi Square (X²) test was applied on the all 100 face distances. The Chi Square is a statistical test used to test if there are differences between the observations and the expected value. According to the Chi Square test results in Table 1, there are no differences between the training set distances and the average distance $D_{vag}$ where Chi P-value is greater than α = 0.05. It was, thus, concluded that $D_{vag}$ is appropriate choice to find an appropriate λ for any new input face.

Table 1. Chi Square result

4.2 Reconstruction of 3D Face Shapes from 2D Face Images for Variety of Distances D _m

The visual effects of the proposed model have been tested using the CMU-PIE database [18]. 3D models for the 2D images have been reconstructed through different distances D _m . Two sets of 25 and 78 of 2D facial landmarks were used for reconstruction. Using different sizes of landmarks sets helped to test the robustness of the proposed technique against variety in landmark number. The input 2D images are in near frontal pose with most of their expression being neutral. The selected feature points were aligned with the reference 3D model using Procrustes Analysis, which is the usual preliminary step before the reconstruction stage. The aligned feature points were used through the optimization function (Eq. (30)) to compute an optimal regularization parameter λ for different distances D _m including $D_{avg}$. Then, λ was used to compute the face coefficient α through Eq. (28). Finally, α was used to reconstruct the 3D shape using Eq. (27).

Figure 6 shows reconstructed faces from 25 feature points selected from real 2D images through different values of D _m. As shown by the values of D _m = $D_{avg}$ = 0.0100 and those close to $D_{avg}$ such as 0.0080 and 0.0120, the reconstructed face is plausible and not over-smoothing. However, the reconstructed faces with distances much less than $D_{avg}$ are very smooth (e.g., D _m = 0.0040) and those with distances much greater that $D_{avg}$ are damaged (e.g., Figure 6 the right most column, D _m = 0.0160). This finding is also consistent with the results shown in Fig. 7 where the 3D faces were reconstructed from a different number of feature points equal to 78.

Fig. 6.

Given 25 feature points of 2D images (left), 3D face shapes among different distances D _m were reconstructed. The fifth columns (D _m = 0.0100) shows reconstructed face shapes that have the distance D _m which is equal to D _avg.

Fig. 7.

Reconstructed face shapes from 78 feature points of 2D images (left). Every 2D image has 7 different reconstructed shapes among different distances D _m . The fifth columns (D _m  = 0.0100) shows reconstructed face shapes that has the distance D _m which is equal to D _avg .

This indicates that the distance D _m between the reconstructed face shape and the mean face shape can be used as guidance for a new reconstruction from real 2D face images. Furthermore, the finding in Figs. 6 and 7 show that the best solutions are those which have a distance D _m equal or closer to $D_{avg}$ = 0.0100.

On the other hand, λ can be affected by some factors such as the input face and the number of feature points. For example, optimal λ becomes smaller if the number of feature points increases. However, using D_m instead of λ for regularization shows stability against the number of feature points and the different input faces. Figures 6 and  7 show that while the reconstructed face shapes can be affected by using similar λ among the two sets of feature points, the solution is plausible by the same D _m for the two sets of feature points, i.e., 25 in Fig. 6 and 78 in Fig. 7.

4.3 Reconstruction of 3D Face Shapes from Real 2D Face Images for D _avg

The results in Sects. 4.1 and 4.2 show that setting D _m = 0.0100 (D _avg) or any close value to D _avg is reliable and can produce a good solution for all input faces with different selection of feature points. An appropriate λ was automatically determined using Eq. (30) for D _m  = $D_{avg}$. Moreover, the original 2D texture was registered with the reference texture and warped on the reconstructed 3D face shapes. Figure 8 shows reconstructed faces for three different input faces by D _m = $D_{avg}$. It can be seen that, interestingly the proposed model is capable of reconstructing 3D face shapes and warp the original texture of the input image on the reconstructed 3D face shape by retaining realistic facial features.

Fig. 8.

From real near frontal images, the 3D shapes have been reconstructed from 78 feature points for distance D _m = 0.0100 (D _avg). The 2D input textures are first mapped on the model textures and then warped on the reconstructed shapes [15].

5 Conclusion

In this contribution, the standard Tikhonov regularization method has been extended by replacing the identity matrix with the eigenvalue matrix in order to solve the ill-posed problem of reconstructing complete 3D face shapes from 2D face images. The proposed approach has been used to reconstruct the 3D face shape for the given input 2D near frontal image. However, by using Tikhonov regularization, it is unattainable to identify an optimal value of the regularization parameter λ in advance, and solving the linear system for every λ is time consuming. Hence, we have proposed an approach that automatically determines an appropriate regularization parameter, which is based on the distance from the average face due to the fact that sample faces are mostly located at the boundary of the data space for high dimensional low sample size problems. The proposed method has been evaluated using appropriate training and testing 3D faces and real 2D face images by visualizing the reconstructed results. Our reconstruction results clearly demonstrate the effectiveness of the proposed method. Further we have shown that the proposed method is able to intuitively retain real characteristic of the given 2D face images. However, the experiments were carried out on near frontal 2D face images. In future, we plan to investigate the approach by considering face images that are subjected to pose and expression variations. Also a good future direction could be to explore the possibility of applying bio-inspired approaches to tackle the problem under consideration.