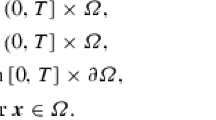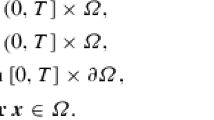Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We consider the time-dependent incompressible flow model for velocity u and pressure p according to

$$\displaystyle\begin{array}{rcl} \partial _{t}\mathbf{u} -\nu \varDelta \mathbf{u} + (\mathbf{a} \cdot \nabla )\mathbf{u} + \nabla p& =& \mathbf{f}\quad \mbox{ in}\ \ (0,T)\times \varOmega,{}\end{array}$$
(1)
$$\displaystyle\begin{array}{rcl} \nabla \cdot \mathbf{u}& =& 0\quad \mbox{ in}\ \ (0,T)\times \varOmega,{}\end{array}$$
(2)
$$\displaystyle\begin{array}{rcl} \mathbf{u} = \mathbf{0}\quad \mbox{ on}\ \partial \varOmega,& & \mathbf{u}\vert _{t=0} = \mathbf{u}_{0}\quad \mbox{ on}\ \varOmega,{}\end{array}$$
(3)

with bounded T > 0, bounded polygonal or polyhedral Lipschitz domain \(\varOmega \subset \mathbb{R}^{d},d \in \{2,3\}\), f ∈ L 1(0, T; L 2(Ω)), \(\mathbf{u}_{0} \in L^{2}(\varOmega )\) and a constant ν. Model (1)–(2) covers the Stokes problem (\(\mathbf{a} \equiv \mathbf{0}\)), the Oseen problem (\(\mathbf{a} \in L^{\infty }(0,T;[W^{1,\infty }(\varOmega )]^{d})\) with ∇⋅ a = 0) and the Navier-Stokes problem (a ≡ u). The weak form of problem (1), (2), and (3) reads:

Find \(\mathcal{U}:= (\mathbf{u},p): (0,T) \rightarrow V \times Q:= [W_{0}^{1,2}(\varOmega )]^{d} \times L_{0}^{2}(\varOmega )\), s.t.

$$\displaystyle\begin{array}{rcl} (\partial _{t}\mathbf{u},\mathbf{v}) + a_{G}(\mathbf{a};\mathcal{U},\mathcal{V})& = (\mathbf{f},\mathbf{v}),&{}\end{array}$$
(4)
$$\displaystyle\begin{array}{rcl} \mathbf{u}\vert _{t=0} = \mathbf{u}_{0}& &{}\end{array}$$
(5)

for all \(\mathcal{V}:= (\mathbf{v},q) \in V \times Q\) and with

$$\displaystyle\begin{array}{rcl} a_{G}(\mathbf{a};\mathcal{U},\mathcal{V}):= (\nu \nabla \mathbf{u},\nabla \mathbf{v}) + c(\mathbf{a};\mathbf{u},\mathbf{v}) - (\,p,\nabla \cdot \mathbf{v}) + (q,\nabla \cdot \mathbf{u}),& &{}\end{array}$$
(6)
$$\displaystyle\begin{array}{rcl} c(\mathbf{a};\mathbf{u},\mathbf{v}):= \frac{1} {2}[(\mathbf{a} \cdot \nabla \mathbf{u},\mathbf{v}) - (\mathbf{a} \cdot \nabla \mathbf{v},\mathbf{u})].& &{}\end{array}$$
(7)

Let \(\mathcal{T}_{h}\) be a suitable finite element (FE) mesh giving an exact decomposition of the domain Ω. The standard Galerkin-FEM to problem (4), (5), and (6) with conforming subspaces \(V _{h} \times Q_{h} \subset V \times Q\) reads:

Find \(\mathcal{U}_{h}:= (\mathbf{u}_{h},p_{h}): (0,T) \rightarrow V _{h} \times Q_{h}\) s.t. for all \(\mathcal{V}_{h}:= (\mathbf{v}_{h},q_{h}) \in V _{h} \times Q_{h}\)

$$\displaystyle\begin{array}{rcl} (\partial _{t}\mathbf{u}_{h},\mathbf{v}_{h}) + a_{G}(\mathbf{a};\mathcal{U}_{h},\mathcal{V}_{h}) = (\mathbf{f},\mathbf{v}_{h}),& &{}\end{array}$$
(8)
$$\displaystyle\begin{array}{rcl} \mathbf{u}_{h}\vert _{t=0} = \mathbf{u}_{0h},& &{}\end{array}$$
(9)

with an appropriate approximation u 0h of the initial condition u 0.

In this paper, we consider stabilized FE approximations of problem (1), (2), and (3). In particular, inf-sup stable velocity-pressure FE pairs are chosen together with local projection stabilization (LPS). For the linear Oseen problem Matthies and Tobiska [20] provide a comprehensive overview on stabilized FE methods, in particular in the case of LPS methods for inf-sup stable FE methods. (For a corresponding review and presentation of LPS methods with equal-order interpolation of velocity and pressure see [23].) To our knowledge there are not many results available in the literature for the nonlinear problem. For the case of small data, the stationary case was considered in [1, 25]. Some results for the time-dependent case can be found in [18, 22] where LPS-based subgrid models of Smagorinsky type were considered.

Some challenges of numerical methods for problem (1), (2), and (3) to be considered in this paper are: (i) a stable velocity-pressure interpolation (Sect. 2), (ii) local mass conservation (Sect. 3), (iii) high Reynolds numbers \(Re_{\varOmega }:=\| \mathbf{u}\|_{L^{\infty }(\varOmega )}\mbox{ diam}(\varOmega )/\nu \ \gg 1\), (Sects. 3 and 4), and (iv) fast and scalable numerical algorithms (Sect. 5). A fast FEM with inf-sup stable element pairs, minimal stabilization and robust estimates w.r.t. Re Ω is a desired goal of current research. In this paper, we will give some recent results often referring to [2].

2 Finite Element Setting

2.1 Finite Element Spaces

For a measurable subset G of Ω, the usual Sobolev spaces W m, p(G) with norm \(\|\cdot \|_{W^{m,p}(G)}\) and semi-norm \(\vert \cdot \vert _{W^{m,p}(G)}\) are used. In the case p = 2, we set H m(G) = W m, 2(G). The L 2 inner product on G is denoted by (⋅ , ⋅ ) G . For G = Ω we will usually omit the index G. This notation of norms, semi-norms and inner products is also applied in the vector-valued case. For time-dependent problems we use the notation L p(0, T; X) for vector-valued functions in the Sobolev space X with bounded norm \((\int _{0}^{T}\| \cdot (s)\|_{X}^{p}ds)^{\frac{1} {p} },1 \leq p <\infty\) and standard modification for \(p = \infty\).

Let \(\{\mathcal{T}_{h}\}_{h}\) be a family of exact shape-regular decompositions of Ω. For a simplex \(T \in \mathcal{T}_{h}\) or a quadrilateral/hexahedron T in \(\mathbb{R}^{d}\), let \(\hat{T }\) be the reference unit simplex or the unit cube (−1, 1)d. Let the reference mapping \(F_{T}: \hat{T }\rightarrow T\) be bijective and satisfy

$$\displaystyle\begin{array}{rcl} ch_{T}^{d} \leq \vert \mathop{\mathrm{det}}\nolimits DF_{ T}(\hat{x})\vert \leq Ch_{T}^{d}\quad \forall \hat{x} \in \hat{T }&& {}\\ \end{array}$$

with constants c and C independent of the cell diameter h T . This mapping is affine for simplices and multi-linear for quadrilaterals/hexahedra. Let \(\mathbb{P}_{l}\) resp. \(\mathbb{Q}_{l}\) with \(l \in \mathbb{N}_{0}\) be the set of polynomials of degree ≤ l resp. of polynomials of degree ≤ l in each variable separately and let

$$\displaystyle{\mathbb{R}_{l}(\hat{T } ):= \left \{\begin{array}{ll} \mathbb{P}_{l}(\hat{T } ) &\text{on simplices}\ \hat{T } \\ \mathbb{Q}_{l}(\hat{T } )&\text{on quadrilaterals/hexahedra}\ \hat{T }. \end{array} \right.}$$

We define

$$\displaystyle{Y _{h,-l}:= \{v_{h} \in L^{2}(\varOmega ):\ v_{ h}\vert _{T} \circ F_{T} \in \mathbb{R}_{l}(\hat{T } )\ \forall T \in \mathcal{T}_{h}\},\quad Y _{h,l}:= Y _{h,-l} \cap W^{1,2}(\varOmega ).}$$

For convenience, we write \(V _{h} = [\mathbb{R}_{k}]^{d}\) instead of \(V _{h} = [Y _{h,k}]^{d} \cap V\) and \(Q_{h} = \mathbb{R}_{\pm (k-1)}\) instead of \(Q_{h} = Y _{h,\pm (k-1)} \cap Q\).

Let us assume the following inverse and approximation properties in FE spaces.

Assumption (A.1)

Let the FE space Y h,k satisfy the local inverse inequality

$$\displaystyle{\|\nabla v_{h}\|_{L^{2}(T)} \leq Ch_{T}^{-1}\|v_{ h}\|_{L^{2}(T)}\quad \forall v_{h} \in Y _{h,k},\ \forall T \in \mathcal{T}_{h}.}$$

Assumption (A.2)

There are interpolation operators j u : V → V h and j p : Q → Q h such that for all \(T \in \mathcal{T}_{h}\) , for all \(\mathbf{w} \in V \cap [W^{l,2}(\varOmega )]^{d}\) with 2 ≤ l ≤ k + 1:

$$\displaystyle{\|\mathbf{w} - j_{u}\mathbf{w}\|_{L^{2}(T)} + h_{T}\|\nabla (\mathbf{w} - j_{u}\mathbf{w})\|_{L^{2}(T)} \leq Ch_{T}^{l}\|\mathbf{w}\|_{ W^{l,2}(\omega _{T})}}$$

and for all \(q \in Q \cap W^{l,2}(\varOmega )\) with 2 ≤ l ≤ k:

$$\displaystyle{\|q - j_{p}p\|_{L^{2}(T)} + h_{T}\|\nabla (q - j_{p}q)\|_{L^{2}(T)} \leq Ch_{T}^{l}\|q\|_{ W^{l,2}(\omega _{T})}}$$

on a suitable patch \(\omega _{T} \supset T\) .

2.2 Inf-Sup Stable and Stabilized Velocity-Pressure Interpolation

Let us consider for simplicity here (and in Sect. 3.1) the stationary Stokes problem with a ≡ 0:

Find \(\mathcal{U}:= (\mathbf{u},p) \in V \times Q\), s.t. for all \(\mathcal{V}:= (\mathbf{v},q) \in V \times Q\)

$$\displaystyle{ (\nu \nabla \mathbf{u},\nabla \mathbf{v}) - (\,p,\nabla \cdot \mathbf{v}) + (q,\nabla \cdot \mathbf{u}) = (\mathbf{f},\mathbf{v}). }$$
(10)

The Galerkin-FEM simplifies to:

Find \(\mathcal{U}_{h}:= (\mathbf{u}_{h},p_{h}) \in V _{h} \times Q_{h} \subset V \times Q\), s.t. for all \(\mathcal{V}_{h}:= (\mathbf{v}_{h},q_{h}) \in V _{h} \times Q_{h}\)

$$\displaystyle{ (\nu \nabla \mathbf{u}_{h},\nabla \mathbf{v}_{h}) - (\,p_{h},\nabla \cdot \mathbf{v}_{h}) + (q_{h},\nabla \cdot \mathbf{u}_{h}) = (\mathbf{f},\mathbf{v}_{h}). }$$
(11)

An inf-sup stable interpolation according to

Assumption (A.3) (Discrete inf-sup condition)

$$\displaystyle{ \exists \beta \neq \beta (h)> 0\ \ s.t.:\ \ \ \sup _{\mathbf{v}\in V _{h}\setminus \{0\}}\frac{(\nabla \cdot \mathbf{v},q)} {\|\nabla \mathbf{v}\|_{L^{2}(\varOmega )}} \geq \beta \| q\|_{L^{2}(\varOmega )}\ \forall q \in Q_{h} }$$
(12)

implies a compatibility condition between V h and Q h . Otherwise spurious pressure modes may occur. Condition (12) is valid, e.g., for Taylor-Hood elements \([\mathbb{R}_{k}]^{d}/\mathbb{R}_{k-1}\) with k ≥ 2 and FE spaces \(\mathbb{R}_{k} \in \{\mathbb{P}_{k}, \mathbb{Q}_{k}\}\) on \(\mathcal{T}_{h}\).

For inf-sup stable Galerkin-FEM, we define

$$\displaystyle{ V _{h}^{div}:= \{\mathbf{v}_{ h} \in V _{h}:\ (\nabla \cdot \mathbf{v}_{h},q_{h}) = 0\ \forall q_{h} \in Q_{h}\}\ \neq \ \{\mathbf{0}\}. }$$
(13)

The convergence result for the Stokes problem with (a ≡ 0) reads:

$$\displaystyle\begin{array}{rcl} \begin{array}{ll} \|\nabla (\mathbf{u} -\mathbf{u}_{h})\|_{L^{2}(\varOmega )} \leq &\,C_{1}\inf _{\mathbf{v}_{h}\in V _{h}}\|\nabla (\mathbf{u} -\mathbf{v}_{h})\|_{L^{2}(\varOmega )} \\ & + \frac{C_{2}} {\nu } \inf _{q_{h}\in Q_{h}}\sup _{\mathbf{v}_{h}\in V _{h}^{div}\setminus \{0\}}\frac{(\,p-q_{h},\nabla \cdot \mathbf{v}_{h})} {\|\nabla \mathbf{v}_{h}\|_{L^{2}(\varOmega )}}.\end{array} & &{}\end{array}$$
(14)

Condition (12) is not valid for equal-order interpolation, e.g. \([\mathbb{Q}_{k}]^{d}/\mathbb{Q}_{k}\). To circumvent this, Franca/Hughes [14] introduced a pressure gradient stabilization via a consistent residual-based method

$$\displaystyle{ a_{G}(\mathbf{0};\mathcal{U}_{h},\mathcal{V}_{h}) +\sum _{T\in \mathcal{T}_{h}}\tau _{T}(-\nu \varDelta \mathbf{u}_{h} + \nabla p_{h} -\mathbf{f},\nabla q_{h})_{T} = (\mathbf{f},\mathbf{v}_{h}). }$$
(15)

The additional control of \(\sum _{T\in \mathcal{T}_{h}}\tau _{T}\|\nabla p_{h}\|_{L^{2}(T)}^{2}\) allows a convenient error analysis for the practically interesting case of equal-order interpolation of velocity/pressure. A relevant drawback of such residual-based methods in applications to time-dependent coupled incompressible flow problems is the bulk of additional non-symmetric terms leading to an expensive implementation.

Methods based on local projection stabilization [6] provide a potential remedy. Here, a scale separation into small and large scales is performed via local orthogonal L 2-projection onto appropriate discontinuous discrete function spaces. Details are given later on in Sect. 4. In a sparse symmetric stabilization (here: pressure gradient or PSPG) stabilization terms are added only on small scales:

$$\displaystyle{ a_{G}(\mathbf{0};\mathcal{U}_{h},\mathcal{V}_{h}) +\sum _{M\in \mathcal{M}_{h}}\tau _{M}(\kappa _{M}\nabla p_{h},\kappa _{M}\nabla q_{h})_{M} = (\mathbf{f},\mathbf{v}_{h}), }$$
(16)

where κ M : id |  M −π M denotes the fluctuation operator with the local L 2-projector π M . Later on, we will extend method (16) to the original nonlinear problem (1), (2), and (3).

3 Inf-Sup Stable Galerkin FEM with Grad-Div Stabilization

In this section, we consider the application of inf-sup stable Galerkin FEM with grad-div stabilization. For convenience, we start in Sect. 3.1 with grad-div stabilization for the Stokes problem. Then, in Sect. 3.2, we extend the approach to the Navier-Stokes problem.

3.1 Local Mass Conservation for Stokes Problem

In the convergence result (14) for the Stokes problem (10) with inf-sup stable Galerkin-FEM, the second error term is disastrous in case of 0 < ν ≪ 1. It leads to a strong error penetration for large external gradient forces in coupled problems. This can be seen in Example 1 (Fig. 1) with γ = 0. There one observes a very strong influence of the gradient force leading to a completely wrong physical solution. In fact, the velocity error in the H 1 semi-norm scales with ν −1.

Fig. 1
figure 1

No-flow test for \(\mathbb{Q}_{2}/\mathbb{Q}_{1}\) and \(\nu \in \{1,10^{-3},10^{-6}\}\) without (γ = 0) and with (γ = 1) grad-div-stabilization: (i) distorted mesh, (ii) undistorted mesh

Full size image

Let us follow an important argument given by A. Linke in [16]: For the continuous Stokes problem we observe

$$\displaystyle{\nu (\nabla \mathbf{u},\nabla \mathbf{v}) - (\,p_{\psi },\nabla \cdot \mathbf{v}) = (\mathbf{f} + \nabla \psi,\mathbf{v}) = (\mathbf{f},\mathbf{v}) - (\psi,\nabla \cdot \mathbf{v}).}$$

Setting \(p:= p_{\psi }-\psi\) we get \(\nu (\nabla \mathbf{u},\nabla \mathbf{v}) - (\,p,\nabla \cdot \mathbf{v}) = (\mathbf{f},\mathbf{v})\) and we obtain an invariance property for incompressible flows:

$$\displaystyle{\mathbf{f} \rightarrow \mathbf{f} + \nabla \psi \ \ \Rightarrow\ \ (\mathbf{u},p) \rightarrow (\mathbf{u},p+\psi ).}$$

Unfortunately, nearly all inf-sup stable discretizations for incompressible flows violate the discrete version of the invariance property, i.e.,

$$\displaystyle{\mathbf{f} \rightarrow \mathbf{f} + \nabla \psi \ \ \not \Longrightarrow\ \ ({\mathbf{u}_{h},p_{h}}) \rightarrow (\mathbf{u}_{h},p_{h}+\psi ).}$$

One exception are pointwise divergence-free velocity spaces V h , e.g. Scott-Vogelius elements \([\mathbb{P}_{k}]^{d}/\mathbb{P}_{-(k-1)},\ k \geq d\) on barycentrically refined simplicial meshes \(\mathcal{T}_{h}\).

As a remedy, grad-div stabilization provides an improved local mass conservation for inf-sup stable FE methods for the Stokes problem with a ≡ 0. Let us consider, e.g., Taylor-Hood type pairs \([\mathbb{R}_{k}]^{d} \times \mathbb{R}_{k-1}\) with k ≥ 2. Then one adds a consistent symmetric penalty term to the Galerkin method such that

$$\displaystyle{ a_{G}(\mathbf{0};\mathcal{U}_{h},\mathcal{V}_{h}) +\sum _{T\in \mathcal{T}_{h}}\gamma _{T}(\nabla \cdot \mathbf{u}_{h},\nabla \cdot \mathbf{v}_{h})_{T} = (\mathbf{f},\mathbf{v}_{h}). }$$
(17)

As a result one obtains the error estimate

$$\displaystyle\begin{array}{rcl} & & \nu \|\nabla (\mathbf{u} -\mathbf{u}_{h})\|_{L^{2}(\varOmega )}^{2} +\ \sum _{ T\in \mathcal{T}_{h}}\gamma _{T}\|\nabla \cdot \mathbf{u}_{h}\|_{L^{2}(T)}^{2} {}\\ & & \leq C\sum _{T\in \mathcal{T}_{h}}\Big((\nu +\gamma _{T})\inf _{\mathbf{v}_{h}\in V _{h}}\|\nabla (\mathbf{u} -\mathbf{v}_{h})\|_{L^{2}(T)}^{2} +\min \Big (\frac{1} {\nu }; \frac{d} {\gamma _{T}}\Big)\inf _{q_{h}\in Q_{h}}\|p - q_{h}\|_{L^{2}(T)}^{2}\Big). {}\\ \end{array}$$

An essential problem is the choice of grad-div parameter γ T which allows to remove the ν −1-dependence of the pressure interpolation term in case of 0 < ν ≪ 1. An equilibration of the right-hand side terms in the error estimate gives

$$\displaystyle{\gamma _{T} =\gamma _{0}\max \Big(0; \frac{\vert p\vert _{W^{k,2}(\omega _{T})}} {\vert \mathbf{u}\vert _{W^{k+1,2}(\omega _{T})}}-\nu \Big)}$$

This choice is unfeasible in practical problems, e.g. for time-dependent Navier-Stokes problem. Some numerical experiments for Stokes problem can be found in [15]. A reasonable compromise is given by γ T  ≡ γ = O(1) with possibly problem-dependent parameter γ. This leads to methods of order k such that

$$\displaystyle{\nu \|\nabla (\mathbf{u}-\mathbf{u}_{h})\|_{L^{2}(\varOmega )}^{2}+\sum _{ T\in \mathcal{T}_{h}}\gamma _{T}\|\nabla \cdot \mathbf{u}_{h}\|_{L^{2}(T)}^{2} \leq C\sum _{ T\in \mathcal{T}_{h}}h_{T}^{2k}\Big[\vert \mathbf{u}\vert _{ W^{k+1,2}(\omega _{T})}^{2}+\vert p\vert _{ W^{k,2}(\omega _{T})}^{2}\Big]}$$

where the constant C is independent on ν −1 and ω T denotes an appropriate element patch around element T.

Example 1 (No-flow test)

We consider the Stokes problem in the domain Ω = [0, 1]2 with given forcing term \(\mathbf{f} = (3x_{1}^{2} + 1,3x_{2}^{2})^{T}\) as gradient field and the analytical solution \((\mathbf{u},p)(x) = (\mathbf{0},x_{1}^{3} + x_{1} + x_{2}^{3} - 1)\). We apply the grad-div stabilized Galerkin scheme with the \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\) pair on a distorted mesh \(\mathcal{T}_{h}\).

Comparing the cases γ T  = 0 and γ T  = 1 we observe for the latter case with decreasing ν an essential improvement in the H 1(Ω)-error. Instead of a scaling like ν −1 we observe a dependence like \(\nu ^{-1/2}\) in the velocity error. On a structured mesh one observes even superconvergence. The L 2(Ω)-error of the pressure is not influenced by grad-div stabilization. □ 

We may draw the conclusion that a grad-div stabilization can be very important for coupled flow problems with large external gradient forces compared to the diffusion term (like thermally coupled problems or resistive magnetohydrodynamics).

Finally, we mention the very recent approach by Linke et al. [17] to modify inf-sup stable FE pairs for incompressible flows in such a way that a pointwise divergence-free discrete velocity field can be obtained. The essential idea is to replace the test function v h in (f, v h ) by Π h v h with a projector Π h : V + V h  → X h to an appropriate FE subspace of \(H(\mbox{ div};\varOmega ):= \{\mathbf{v} \in [L^{2}(\varOmega )]^{d}: \nabla \cdot \mathbf{v} \in L^{2}(\varOmega )\}\). Potentially this allows to omit the grad-div stabilization.

3.2 Extension to the Nonlinear Problem

Consider now the weak form of the time-dependent Navier-Stokes problem (1), (2), and (3): Find \(\mathcal{U}:= (\mathbf{u},p): (0,T) \rightarrow V \times Q\), such that

$$\displaystyle{ (\partial _{t}\mathbf{u},\mathbf{v}) + a_{G}(\mathbf{u};\mathcal{U},\mathcal{V}) = (\mathbf{f},\mathbf{v}) }$$
(18)

for all \(\mathcal{V}:= (\mathbf{v},q) \in V \times Q\) and with a G (⋅ ; ⋅ , ⋅ ) as in (6). The grad-div stabilized Galerkin-FEM scheme with inf-sup stable interpolation in \(V _{h} \times Q_{h} \subseteq [\mathbb{R}_{k}]^{d} \times \mathbb{R}_{k-1}\) reads:

Find \(\mathcal{U}_{h} = (\mathbf{u}_{h},p_{h}): (0,T) \rightarrow V _{h} \times Q_{h}\) such that

$$\displaystyle{ (\partial _{t}\mathbf{u}_{h},\mathbf{v}_{h}) + a_{G}(\mathbf{u}_{h};\mathcal{U}_{h},\mathcal{V}_{h}) + t_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{v}_{h}) = (\mathbf{f},\mathbf{v}_{h}) }$$
(19)

for all \(\mathcal{V}_{h} = (\mathbf{v}_{h},q_{h}) \in V _{h} \times Q_{h}\) with grad-div stabilization

$$\displaystyle{t_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{v}_{h}):=\sum _{T\in \mathcal{T}_{h}}\gamma _{T}(\mathbf{u}_{h})(\nabla \cdot \mathbf{u}_{h},\nabla \cdot \mathbf{v}_{h})_{T}.}$$

For the semidiscrete grad-div stabilized FEM we want to improve the results of [20] for the Oseen problem with given solenoidal flow field a in problem (18) towards the nonlinear problem with a = u. Moreover, we want to obtain a realistic growth of Gronwall constants following Burman and Fernandez [8]. One basic idea in the discrete stability analysis is to treat u h and p h separately since \(V _{h}^{div}\neq \ \{\mathbf{0}\}\), see (13), and to apply interpolation estimates in V h div following Girault and Scott [11]. Symmetric testing in V h div yields

$$\displaystyle{\frac{1} {2} \frac{d} {dt}\|\mathbf{u}_{h}\|_{L^{2}(\varOmega )}^{2} +\mathop{\underbrace{ \nu \|\nabla \mathbf{u}_{ h}\|_{L^{2}(\varOmega )}^{2} + t_{ h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{u}_{h})}}\limits _{=:\vert \vert \vert \mathbf{u}_{h}\vert \vert \vert ^{2}} = (\mathbf{f},\mathbf{u}_{h}),}$$

leading to the stability estimate (for details see [2], Section 3.2)

$$\displaystyle{ \|\mathbf{u}_{h}(t)\|_{L^{2}(\varOmega )}^{2} +\int _{ 0}^{t}\vert \vert \vert \mathbf{u}_{ h}(\tau )\vert \vert \vert ^{2}\ d\tau \leq \|\mathbf{u}_{ h}(0)\|_{L^{2}(\varOmega )}^{2} + 3\|\mathbf{f}\|_{ L^{2}(0,T;L^{2}(\varOmega ))}^{2}. }$$
(20)

This result allows to apply the generalized Peano theorem and to prove existence of the semidiscrete velocity u h : [0, T] → V h div. Under the stronger condition of a Lipschitz-continuous force term f one obtains uniqueness of u h . Existence of the unique discrete pressure p h is a consequence of the discrete inf-sup condition.

We are now in the position to derive error estimates of the semidiscrete grad-div stabilized Galerkin scheme (19). First of all, for solutions \(\mathbf{u} \in [L^{\infty }(0,T;W^{1,\infty }(\varOmega ))]^{d}\), p ∈ L 2(0, T; Q) and ∂ t u ∈ [L 2(0, T; L 2(Ω))]d one can show (via density arguments) strong convergence of the discrete velocity in \([L^{\infty }(0,T;L^{2}(\varOmega )) \cap L^{2}(0,T;V )]^{d}\). For details we refer to Corollary 4.1 in [2].

In case of sufficiently smooth solutions of problem (18), we obtain the following error estimate:

Theorem 1

Let Assumptions  (A.1) , (A.2) , and (A.3) be valid. Assume for the solution of (1) , (2) , and (3) that \(\mathbf{u} \in [L^{\infty }(0,T;W^{1,\infty }(\varOmega )) \cap L^{2}(0,T;W^{k+1,2}(\varOmega ))]^{d}\) , \(\partial _{t}\mathbf{u} \in [L^{2}(0,T;W^{k,2}(\varOmega ))]^{d}\) and \(p \in L^{2}(0,T;Q \cap W^{k,2}(\varOmega )).\) Moreover, let j u u be the divergence-preserving interpolant [11] of the velocity u and set u h (0) = j u u 0 . Then we obtain

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} &\|\mathbf{u}_{h} - j_{u}\mathbf{u}\|_{L^{\infty }(0,T;L^{2}(\varOmega ))}^{2} +\int _{ 0}^{t}\vert \vert \vert (\mathbf{u}_{h} - j_{u}\mathbf{u})(\tau )\vert \vert \vert ^{2}\ d\tau \\ & \leq C\sum _{T\in \mathcal{T}_{h}}h_{T}^{2k}\int _{0}^{t}e^{C_{G}(\mathbf{u})(t-\tau )}\,\Big[(1 +\nu Re_{T}^{2} + d\gamma _{T})\vert \mathbf{u}(\tau )\vert _{W^{k+1,2 }(\omega _{T})}^{2} \\ & \quad + \vert \partial _{t}\mathbf{u}(\tau )\vert _{W^{k,2}(\omega _{T})}^{2} +\min \Big ( \frac{d} {\gamma _{T}}; \frac{1} {\nu } \Big)\vert p(\tau )\vert _{W^{k,2}(\omega _{T})}^{2}\Big]d\tau \end{array} & &{}\end{array}$$
(21)

with the local Reynolds number \(Re_{T}:= \frac{h_{T}\|\mathbf{u}\|_{L^{\infty }(T)}} {\nu }\) and Gronwall constant

$$\displaystyle{ C_{G}(\mathbf{u}):= 1 +\| \mathbf{u}\|_{L^{\infty }(0,T;W^{1,\infty }(\varOmega ))} + Ch\|\mathbf{u}\|_{L^{\infty }(0,T;W^{1,\infty }(\varOmega ))}^{2}. }$$
(22)

Sketch of proof

The proof is a special case of Theorem 4.1 in [2]. Set

$$\displaystyle{\mathcal{U}-\mathcal{U}_{h} = (\mathcal{U}- J\mathcal{U}) + (J\mathcal{U}-\mathcal{U}_{h}) \equiv (\eta _{u},\eta _{p}) + (\mathbf{e}_{h},r_{h}).}$$

Here the interpolant J consists of a standard interpolator for the pressure and the divergence-preserving velocity interpolator j u : V h  → V h div, see [11]. The latter choice implies \(\mathbf{e}_{h} \in V _{h}^{div}.\) Then the approximate Galerkin orthogonality in V h div, coercivity of a G (u h ; ⋅ , ⋅ ) and use of (r h , ∇⋅ e h ) = 0 thanks to e h  ∈ V h div yield

$$\displaystyle\begin{array}{rcl} \frac{1} {2}\partial _{t}\|\mathbf{e}_{h}\|_{L^{2}(\varOmega )}^{2} + \vert \vert \vert \mathbf{e}_{ h}\vert \vert \vert ^{2}& =& -(\partial _{ t}\eta _{u},\mathbf{e}_{h}) -\nu (\nabla \eta _{u},\nabla \mathbf{e}_{h}) + (\eta _{p},\nabla \cdot \mathbf{e}_{h}) {}\\ & & -t_{h}(\mathbf{u}_{h};\eta _{u},\mathbf{e}_{h}) + c(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{e}_{h}) - c(\mathbf{u};\mathbf{u},\mathbf{e}_{h}). {}\\ \end{array}$$

Careful estimates of the convective terms give

$$\displaystyle\begin{array}{rcl} & & c(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{e}_{h}) - c(\mathbf{u};\mathbf{u},\mathbf{e}_{h}) {}\\ & & \leq \frac{1} {4\epsilon }\sum _{T\in \mathcal{T}_{h}}\frac{1 +\nu Re_{T}^{2}} {h_{T}^{2}} \|\eta _{u}\|_{L^{2}(T)}^{2} + 3\vert \vert \vert \eta _{ u}\vert \vert \vert ^{2} + 4\epsilon \vert \vert \vert \mathbf{e}_{ h}\vert \vert \vert ^{2} {}\\ & & \quad +\Big [\vert \mathbf{u}\vert _{W^{1,\infty }(\varOmega )} +\Big (\epsilon h^{2} + C\max _{ T\in \mathcal{T}_{h}}h_{T}\Big)\vert \mathbf{u}\vert _{W^{1,\infty }(\varOmega )}^{2}\Big]\|\mathbf{e}_{ h}\|_{L^{2}(\varOmega )}^{2}. {}\\ \end{array}$$

Finally, an application of the Gronwall Lemma to \(\|\mathbf{e}_{h}\|_{L^{2}(\varOmega )}^{2}\) with u h (0) = j u u 0 gives the desired result with Gronwall constant (22). □ 

Corollary 1

Under the assumptions of Theorem 1 assume the mesh restriction

$$\displaystyle{ Re_{T} = \frac{h_{T}\|\mathbf{u}\|_{L^{\infty }(T)}} {\nu } \leq \frac{C} {\sqrt{\nu }} }$$
(23)

Then we obtain the error estimate of order \(\mathcal{O}(h^{k})\)

$$\displaystyle\begin{array}{rcl} & & \|\mathbf{u}_{h} - j_{u}\mathbf{u}\|_{L^{\infty }(0,T;L^{2}(\varOmega ))}^{2} +\int _{ 0}^{t}\vert \vert \vert (\mathbf{u}_{ h} - j_{u}\mathbf{u})(\tau )\vert \vert \vert ^{2}\ d\tau {}\\ & & \leq C\sum _{T\in \mathcal{T}_{h}}h_{T}^{2k}\int _{ 0}^{t}e^{(t-\tau )C_{G} }\Big[\vert \partial _{t}\mathbf{u}(\tau )\vert _{W^{k,2}(\omega _{T})}^{2} + \vert \mathbf{u}(\tau )\vert _{ W^{k+1,2}(\omega _{T})}^{2} + \vert p(\tau )\vert _{ W^{k,2}(\omega _{T})}^{2}\Big]d\tau {}\\ \end{array}$$

in the sense that all constants are uniformly bounded w.r.t. the data. In particular, the Gronwall constant (22) does not explicitly depend on ν −1 .

We proceed with some numerical examples. The first example is to check Corollary 1 whereas the following examples may give an impression of a certain robustness of grad-div stabilized Galerkin schemes with inf-sup stable elements for laminar flow problems.

Example 2

For the numerical verification let us consider the Couzy test problem [9] in Ω = (0, 1)2. The solution of problem (4), (5), and (6) with a = u is

$$\displaystyle\begin{array}{rcl} \mathbf{u}(x)& =& \sin (\pi t)\left (-\cos \left (\frac{1} {2}\pi x_{1}\right )\sin \left (\frac{1} {2}\pi x_{2}\right ),\sin \left (\frac{1} {2}\pi x_{1}\right )\cos \left (\frac{1} {2}\pi x_{2}\right )\right )^{T}, {}\\ p(x)& =& \pi \sin \left (\frac{1} {2}\pi x_{1}\right )\sin \left (\frac{1} {2}\pi x_{2}\right )\sin \left (\pi t\right ). {}\\ \end{array}$$

The forcing term f, the initial and the Dirichlet boundary data are deduced from the exact solution. For the \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\)-pair we obtain on a sequence of equidistant meshes and for globally constant grad-div parameter γ T convergence results as in Fig. 2. The significant influence of grad-div stabilization is observed for a wide range of Re Ω . The L 2-errors of the divergence and of pressure show optimal rates of \(\mathcal{O}(h^{2})\) robust w.r.t. Re Ω . On the other hand, for the W 1, 2- and L 2-errors of the velocity we see a deviation from the optimal error rate for increasing Re Ω . □ 

Fig. 2
figure 2

Couzy test with optimized grad-div parameter γ for \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\): Dependence on Re Ω ; (i) W 1, 2-velocity error, (ii) L 2-velocity error

Full size image

Example 3 (Driven cavity problem)

Next we consider the standard driven cavity flow with stationary solutions in the range up to Re Ω  = 7. 500 in Ω = (0, 1)2.

In Fig. 3 we show exemplarily cross-sections of the discrete velocity at Re Ω  = 5 ⋅ 103 at x 1 = 0. 5 and x 2 = 0. 5 for the \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\)-pair. The results on moderately fine meshes are in very good agreement, even in the boundary layers, with the results given by Erturk et al. [10] on a much finer 601 × 601 mesh. Interestingly, the results are very similar to an equal-order approximation with \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{2}\) pair. In [19] a non-stationary approach with moderately large time steps was applied showing that just grad-div stabilization was required in experiments up to Re Ω  = 7. 5 ⋅ 103.

Fig. 3
figure 3

Driven cavity problem with Re Ω  = 5 ⋅ 103: Cross-sections of the solutions for \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\) without SUPG-LPS and \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{2}\) with SUPG/PSPG-LPS

Full size image

Moreover, we considered the time-accurate simulation of the driven cavity problem in the transient regime at Re Ω  = 104 where only grad-div stabilization was required. In Fig. 4 a snapshot of the time-periodic velocity solution for Re Ω  = 104 is shown. Secondary and tertiary vortices are well-resolved. □ 

Fig. 4
figure 4

Time-dependent driven cavity problem at Re Ω  = 104 with \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\) pair; whole domain (left) and zoom into corners (right)

Full size image

Example 4 (Time-dependent 3D-flow around cylinder at Re Ω  = 100)

The benchmark problem of the time-dependent 3D-flow around a cylinder in a channel at ν = 0. 01 (corresponding to Re Ω  = 100), see [24], is shown in Fig. 4 (left). \([\mathbb{Q}_{2}]^{3}/\mathbb{Q}_{1}\) elements with 0. 7 × 106 degrees of freedom were applied with a globally constant grad-div stabilization.

In Fig. 4 (right) the convergence of the (maximal) lift coefficient is compared to a reference solution with 12 ⋅ 106 degrees of freedom. □ 

The given examples show that grad-div stabilization is very often sufficient for academic examples and simple laminar flow problems. In order to show that grad-div stabilization is not always sufficient, we found the following example of boundary layer flow.

Example 5 (Flow over a horizontal plate)

Consider the flow over a infinitely thin horizontal plate at Re Ω  = 103, see Fig. 5. The attached laminar boundary layer developing along the plate can be quite well described by the Blasius profile as exact solution of Prandtl’s boundary layer equations, see Fig. 5 (right).

Fig. 5
figure 5

Snapshot of flow at Re Ω  = 100 (left). Development and convergence of lift coefficient (right)

Full size image
Fig. 6
figure 6

Flow over a horizontal plate at Re Ω  = 103

Full size image

Using \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\)-interpolation of velocity-pressure on a structured rectangular mesh, we observed spurious wiggles of the velocity in front of the plate, see Fig. 5 (left). It seems that an additional stabilization mechanism is required to remove such wiggles. □ 

Let us summarize some pros and cons of Galerkin schemes with inf-sup stable velocity-pressure interpolation. We observed a certain robustness of such methods for laminar flows. In the semidiscrete analysis we obtained no explicit dependence of the Gronwall constant on ν −1 if \(\mathbf{u} \in L^{\infty }(0,T;[W^{1,\infty }(\varOmega )]^{d})\). In case of smooth solutions and under a mesh width restriction we obtained error estimates of order \(\mathcal{O}(h^{k})\). For problems with minimal regularity we proved in [2] strong convergence of the discrete velocity for h → 0 and fixed ν > 0. Interestingly, a result by Guermond [12] clarified that the Galerkin-FEM converges for h → 0 to a “suitable” Navier-Stokes solution. This result should remain valid for the grad-div stabilized Galerkin scheme. Such results provide some mathematical justification for direct numerical simulation (DNS) for h → 0.

Nevertheless, the mentioned mesh width restriction \(h_{T}\|\mathbf{u}_{h}\|_{L^{\infty }(T)} \leq C\sqrt{\nu }\) disturbs the robustness of the method w.r.t. Re Ω . In the following section, we want to obtain better control of the convective terms by introducing a velocity subgrid model for large Re Ω . This is important as the W 1, 2-control disappears in case of ν → 0. As a by-product, we can remove the mentioned mesh width restriction.

4 Subgrid Models for Inf-Sup Stable Galerkin Schemes

An appropriate and efficient numerical simulation of high Reynolds number flow is only possible if the small scales of velocity and pressure which cannot be resolved by a given mesh \(\mathcal{T}_{h}\) are modeled (see Fig. 7, left). So far any stabilization or subgrid modeling of the unresolved velocity scales in the grad-div stabilized Galerkin schemes is missing.

Fig. 7
figure 7

Left: Resolved and unresolved velocity scales in the energy cascade, Right: Two-grid LPS-mesh

Full size image

It is well-known that the standard subgrid model, the Smagorinsky model, is too dissipative. The combination of the Smagorinsky model with local projection stabilization (LPS) techniques had been considered for the Navier-Stokes model in, e.g., [18, 22]. Sometimes grad-div stabilization is considered as model of the unresolved pressure scales whereas a combination of streamline upwind stabilization (SUPG) with LPS provides a potential model of the unresolved velocity scales, see Fig. 7 (left). Let us remark that the application of standard stabilization schemes as subgrid model can be seen as implicit large eddy simulation (ILES).

Now we introduce the framework of local projection stabilization. Consider a two-level ansatz with a coarse grid \(\mathcal{M}_{h} = \{M\}\) consisting of elements M as union of cells \(T \in \mathcal{T}_{h}\) of the primary mesh \(\mathcal{T}_{h}\), see Fig. 7 (right), or a one-level method with \(\mathcal{M}_{h} = \mathcal{T}_{h}\). One selects an appropriate projection space \(D_{M} \subset L^{\infty }(M)\) for all coarse grid cells \(M \in \mathcal{M}_{h}\). The local orthogonal L 2-projector: π M : L 2(M) → D M defines the global projector π h : L 2(Ω) → D h by (π h w) |  M : = π M (w |  M ) and the fluctuation operator κ M : id |  M −π M . In a LPS model of velocity, the scale separation is given via local L 2-projection.

Assumption (A.4)

The fluctuation operator \(\kappa _{M} = id -\pi _{M}\) provides the approximation property (depending on D M and s ∈ {0,⋯ ,k }):

$$\displaystyle{ \|\kappa _{M}\mathbf{w}\|_{L^{2}(M)} \leq Ch_{M}^{l}\|\mathbf{w}\|_{ W^{l,2}(M)},\ \forall w \in W^{l,2}(M),\ M \in \mathcal{M}_{ h},\ l = 0,\ldots,s. }$$
(24)

A sufficient condition for Assumption (A.4) is \(\mathbb{P}_{s-1} \subset D_{M}\) .

Furthermore, consider a piecewise constant approximation \(\mathbf{u}_{M} \approx \mathbf{u}_{h}\vert _{M}\) with

Assumption (A.5)

$$\displaystyle{\|\mathbf{u}_{M} -\mathbf{u}_{h}\|_{L^{\infty }(M)} \leq Ch_{M}\|\nabla \mathbf{u}_{h}\|_{L^{\infty }(M)}}$$

and a symmetric LPS-stabilization of \((\mathbf{u}_{M} \cdot \nabla )\mathbf{u}_{h}\) according to

$$\displaystyle{ s_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{v}_{h}):=\sum _{M\in \mathcal{M}_{h}}\tau _{M}(\kappa _{M}(\mathbf{u}_{M} \cdot \nabla )\mathbf{u}_{h},\kappa _{M}(\mathbf{u}_{M} \cdot \nabla )\mathbf{v}_{h})_{M}. }$$
(25)

The inf-sup stable Galerkin-FEM with grad-div stabilization and SUPG-LPS subgrid model reads: Find \(\mathcal{U}_{h} = (\mathbf{u}_{h},p_{h}): (0,T) \rightarrow V _{h} \times Q_{h}\), such that

$$\displaystyle{ (\partial _{t}\mathbf{u}_{h},\mathbf{v}_{h})+a_{G}(\mathbf{u}_{h};\mathcal{U}_{h},\mathcal{V}_{h})+s_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{v}_{h})+t_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{v}_{h})+i_{h}(\,p_{h},q_{h}) = (\mathbf{f},\mathbf{v}_{h}) }$$
(26)

for all \(\mathcal{V}_{h} = (\mathbf{v}_{h},q_{h}) \in V _{h} \times Q_{h}\). Here a G (⋅ ; ⋅ , ⋅ ) is the Galerkin form defined in (6). Besides the grad-div stabilization term t h (u h ; ⋅ , ⋅ ) and the SUPG-LPS term s h (u h ; ⋅ , ⋅ ), the following stabilization of pressure jumps over edges E ∈ ∂ M is defined by

$$\displaystyle{i_{h}(\,p_{h},q_{h}):=\sum _{E\in \partial M,M\in \mathcal{M}_{h}}\phi _{E}([p_{h}]_{E},[q_{h}]_{E})_{E}.}$$

Let us briefly consider the semidiscrete numerical analysis of scheme (26). Regarding the stability of discrete solutions, we obtain the following improved estimate

$$\displaystyle{ \|\mathbf{u}_{h}(t)\|_{L^{2}(\varOmega )}^{2} +\int _{ 0}^{t}\vert \vert \vert \mathcal{U}_{ h}(\tau )\vert \vert \vert _{LPS}^{2}\ d\tau \leq \|\mathbf{u}_{ h}(0)\|_{L^{2}(\varOmega )}^{2} + 3\|\mathbf{f}\|_{ L^{2}(0,T;L^{2}(\varOmega ))}^{2} }$$
(27)

with

$$\displaystyle{ \vert \vert \vert \mathcal{V}\vert \vert \vert _{LPS}:=\Big (\nu \|\nabla \mathbf{v}\|_{L^{2}(\varOmega )}^{2} + t_{ h}(\mathbf{u}_{h};\mathbf{v},\mathbf{v}) + s_{h}(\mathbf{u}_{h};\mathbf{v},\mathbf{v}) + i_{h}(q,q)\Big)^{\frac{1} {2} }. }$$
(28)

The existence of a solution (u h , p h ): (0, T) → V h div × Q h of the LPS-model (26) follows as in Sect. 3.2.

Theorem 2

Let the assumptions of Theorem 1 be valid and assume \(\tau _{M}(\mathbf{u}_{M})\vert \mathbf{u}_{M}\vert ^{2} \leq C = \mathcal{O}(1)\) . Then the semidiscrete convergence results of Theorem 1 and Corollary 1 remain valid with norm |||⋅||| replaced by the LPS-norm (28) .

The proof is very similar to Theorem 1, but one takes advantage of the approximation property of the fluctuation operator \(\|\kappa _{M}\mathbf{w}\|_{L^{2}(M)} \leq ch_{M}^{k}\|\mathbf{w}\|_{W^{k,2}(M)}\). For further details of the analysis, we refer to Theorem 1 in [2].

Henceforth, we want to remove the mesh width restriction \(h_{T}\|\mathbf{u}_{h}\|_{L^{\infty }(T)}/\nu \leq C/\sqrt{\nu }\) and to refine the analysis of the SUPG-LPS scheme. The essential step is based on an additional inf-sup condition on projection space D M .

Assumption (A.6)

There exists β > 0 independent of h such that

$$\displaystyle{\sup _{v\in V _{M}}\frac{(v,q)_{M}} {\|v\|_{L^{2}(M)}} \geq \beta \| q\|_{L^{2}(M)}\qquad \forall q \in D_{M}}$$

for all \(M \in \mathcal{M}_{h}\) where \(V _{M}:= \{\mathbf{v}_{h}\vert _{M}:\ \mathbf{v}_{h} \in V _{h},\ \mathbf{v}_{h} = 0\ \mbox{ on}\ \varOmega \setminus M\}.\)

Matthies et al. [21] proved the following technical result.

Lemma 1

Select projection spaces D M such that Assumption  (A.6) is valid. Then there exists an interpolator i: V → V h with optimal interpolation estimates in W 1,2 (M) and the orthogonality condition

$$\displaystyle{(\mathbf{v} - i\mathbf{v},\mathbf{w}_{h}) = 0\qquad \forall \mathbf{w}_{h} \in \bigoplus _{M\in \mathcal{M}_{h}}D_{M},\ \forall \mathbf{v} \in V.}$$

The assumptions of Lemma 1 can be realized for two- and one-level methods. Let \(\mathbb{R}_{k}(\hat{T } ) = \mathbb{P}_{k}(\hat{T } )\ \mbox{ or}\ \mathbb{Q}_{k}(\hat{T } )\). For two-level methods set \(D_{M}:= \mathbb{P}_{k-1}(M)\) and select

$$\displaystyle{V _{h}:= V \cap \{v_{h} \in C(\overline{\varOmega }):\ v_{h}\vert _{T} \circ F_{T} \in \mathbb{R}_{k}(\hat{T } )\ \forall T \in \mathcal{T}_{h}\}.}$$

For one-level methods set \(D_{M}:= \mathbb{P}_{k-1}(T)\) and define enriched velocity spaces by

$$\displaystyle{V _{h}:= V \cap \{v_{h} \in C(\overline{\varOmega }):\ v_{h}\vert _{T} \circ F_{T} \in \mathbb{R}_{k}(\hat{T } ) + b_{\hat{T } } \cdot \mathbb{R}_{k-1}(\hat{T } )\ \forall T \in \mathcal{T}_{h}\}}$$

with polynomial (cubic or d-quadratic) bubble function \(b_{\hat{T } } \in W_{0}^{1,2}(\hat{T } )\), see Fig. 8.

Fig. 8
figure 8

One-level method: Enrichment of velocity space V h via bubble functions

Full size image

Please note that in the error splitting

$$\displaystyle{\mathcal{U}-\mathcal{U}_{h} = (\mathcal{U}- J\mathcal{U}) + (J\mathcal{U}-\mathcal{U}_{h}) \equiv (\eta _{u},\eta _{p}) + (\mathbf{e}_{h},r_{h})}$$

we cannot apply the divergence-preserving interpolant in V h div, hence e h  ∉ V h div. The approximate Galerkin orthogonality in V h and coercivity of a G (u h ; ⋅ , ⋅ ) yield

$$\displaystyle\begin{array}{rcl} & & \frac{1} {2}\partial _{t}\|\mathbf{e}_{h}\|_{L^{2}(\varOmega )}^{2} + \vert \vert \vert (\mathbf{e}_{ h},r_{h})\vert \vert \vert _{LPS}^{2} {}\\ & & = -(\partial _{t}\eta _{u},\mathbf{e}_{h}) -\nu (\nabla \eta _{u},\nabla \mathbf{e}_{h}) + (\eta _{p},\nabla \cdot \mathbf{e}_{h}) - (r_{h},\nabla \cdot \eta _{u}) - i_{h}(\eta _{p},r_{h}) {}\\ & & \quad - t_{h}(\mathbf{u}_{h};\eta _{u},\mathbf{e}_{h}) - s_{h}(\mathbf{u}_{h};\eta _{u},\mathbf{e}_{h}) + s_{h}(\mathbf{u}_{h};\mathbf{u},\mathbf{e}_{h}) + c(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{e}_{h}) - c(\mathbf{u};\mathbf{u},\mathbf{e}_{h}). {}\\ \end{array}$$

Furthermore, we have to estimate the non-vanishing term \(-(r_{h},\nabla \cdot \eta _{u}) - i_{h}(\eta _{p},r_{h})\) for discrete pressure spaces \(Q_{h} \in \{\mathbb{P}_{k-1}, \mathbb{P}_{-(k-1)}\}\). Careful estimates of the convective terms lead to the improved bound

$$\displaystyle\begin{array}{rcl} & & c(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{e}_{h}) - c(\mathbf{u};\mathbf{u},\mathbf{e}_{h}) {}\\ & & \leq \frac{1} {2\epsilon }\sum _{M\in \mathcal{M}_{h}}\left ( \frac{1} {\tau _{M}} + \frac{1} {2h_{M}^{2}}\right )\|\eta _{u}\|_{L^{2}(M)}^{2} + 3\vert \vert \vert \eta _{ u}\vert \vert \vert _{LPS}^{2} + 4\epsilon \vert \vert \vert \mathbf{e}_{ h}\vert \vert \vert _{LPS}^{2} {}\\ & & \quad + C\Big(\vert \mathbf{u}\vert _{W^{1,\infty }(\varOmega )} +\max _{M}h_{M}\vert \mathbf{u}\vert _{W^{1,\infty }(\varOmega )}^{2}\Big)\|\mathbf{e}_{ h}\|_{L^{2}(\varOmega )}^{2} {}\\ \end{array}$$

provided Assumption (A.6) is valid.

We are now in the position to derive improved error estimates for smooth solutions where any mesh width restriction could be avoided. For a detailed proof of the result we refer to Theorem 2 in [2].

Theorem 3

Let Assumptions (A.1) , (A.2) , (A.3) , (A.4) , (A.5) , and (A.6) be valid. Moreover, let \(Q_{h} = \mathbb{P}_{k-1}\) or \(Q_{h} = \mathbb{P}_{-(k-1)}\)  and select the stabilization parameters as

$$\displaystyle{\tau _{M}(\mathbf{u}_{M}) \leq C \frac{1} {\vert \mathbf{u}_{M}\vert ^{2}};\qquad \quad \gamma _{M}(\mathbf{u}_{M}) \sim 1,\qquad \quad \phi _{E} =\phi _{0} \sim 1.}$$

Then we obtain an \(\mathcal{O}(h^{k})\) -estimate uniformly w.r.t. data:

$$\displaystyle\begin{array}{rcl} & & \|\mathbf{u}_{h} - i\mathbf{u}\|_{L^{\infty }(0,T;L^{2}(\varOmega ))}^{2} +\int _{ 0}^{t}\vert \vert \vert (\mathbf{u}_{ h} - i\mathbf{u},\ p_{h} - j_{p}p)(\tau )\vert \vert \vert _{LPS}^{2}\ d\tau {}\\ & & \qquad \ \leq C\sum _{M\in \mathcal{M}_{h}}h_{M}^{2k}\int _{ 0}^{t}e^{C_{G}(\mathbf{u})(t-\tau )}\Big[\vert \partial _{ t}\mathbf{u}(\tau )\vert _{W^{k,2}(\omega _{M})}^{2} + \vert \mathbf{u}(\tau )\vert _{ W^{k+1,2}(\omega _{M})}^{2} {}\\ & & \phantom{vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv} + \vert p(\tau )\vert _{W^{k,2}(\omega _{M})}^{2}\Big]\ d\tau {}\\ \end{array}$$

with Gronwall constant C G as in Theorem 1 .

For the numerical verification let us consider again Example 2.

Example 6

The data are given as in Example 2. For the \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\)-pair we obtain on a sequence of equidistant meshes and globally constant grad-div parameter γ T convergence results as in Fig. 9. The significant influence of grad-div stabilization is observed for a wide range of Re Ω . Compared to the results in Example 2, we observe with the enriched one-level method in Fig. 9 W 1, 2- and L 2-errors of the velocity without any deviation from the optimal error rate for increasing Re Ω . □ 

Fig. 9
figure 9

Couzy test for Re Ω  = 106 with grad-div stabilization: Comparison of \([\mathbb{Q}_{2}]^{2}/\mathbb{Q}_{1}\) and \([\mathbb{Q}_{2}^{+}]^{2}/\mathbb{Q}_{1}\); (i) W 1, 2-velocity error, (ii) L 2-velocity error

Full size image

Let us now look at problems with boundary layers and separation.

Example 7 (Flow over a horizontal plate)

We consider again the situation of Example 5 with boundary layer flow over a infinitely thin horizontal plate at Re Ω  = 103. In Fig. 10 we see the Blasius boundary layer flow at Re Ω  = 103 without (left) and with SUPG stabilization (right). Spurious wiggles in front of the leading edge appear without SUPG-LPS (left), but SUPG-LPS allows to suppress these wiggles (right). Moreover, we obtain the correct Blasius profile with an adapted choice of the parameter set τ M  = 1. Then the stabilization vanishes at the surface of the plate, which seems to be essential. Otherwise, the stabilization influences the thickness of the boundary layer especially on coarse meshes and leads to wrong boundary profiles. □ 

Fig. 10
figure 10

Blasius boundary layer flow, Re Ω  = 103, global mesh size \(h = 2^{-5}\) without (left) and with (right) SUPG stabilization

Full size image

Example 8 (Flow over an inclined plate)

Here we consider the flow over an inclined (infinitely thin) plate at Re Ω  = 106 and an angle of attack of 18. 43∘ in the domain Ω = (0, 16) × (0, 10). 

The parameters are selected as γ T  ≡ γ = 1 and \(\tau _{M} = 1/\vert \mathbf{u}_{M}\vert ^{2}\). In both cases we apply an isotropic mesh refinement based on a residual jump indicator of the form \(\eta _{T}^{2} = h_{T}\sum _{E\in \partial T}\|[\nabla \mathbf{u}_{h} \cdot \mathbf{n}]\|_{L^{2}(E)}^{2}\). Figure 11 shows snapshots of the flow. Differences between both variants are clearly visible above the plate. Due to the high Reynolds number, the wake should be closely attached to the plate. Without SUPG-LPS stabilization the trailing edge vortex is suppressed by a leading edge vortex of high intensity. Compared to the grad-div stabilized case the flow with additional SUPG-LPS stabilization seems to be more appropriate for the numerical simulation. □ 

Fig. 11
figure 11

Different strong separation for grad-div stabilization (left) vs. grad-div + SUPG-LPS (right)

Full size image

Let us summarize some first experiences with the SUPG-LPS as subgrid model. Away from boundary layers one should apply SUPG-LPS with \(\tau _{M} =\tau _{0}/\mathbf{u}_{M}^{2}\) and \(\tau _{0} \sim 1\). Rewriting the stabilization yields

$$\displaystyle\begin{array}{rcl} s_{h}(\mathbf{u}_{h};\mathbf{u}_{h},\mathbf{u}_{h})& =& \sum _{M\in \mathcal{M}_{h}} \frac{\tau _{0}} {\vert \mathbf{u}_{M}\vert ^{2}}\left (\kappa _{M}\left (\mathbf{u}_{M} \cdot \nabla \mathbf{u}_{h}\right ),\kappa _{M}\left (\mathbf{u}_{M} \cdot \nabla \mathbf{v}_{h}\right )\right )_{M} {}\\ & =& \sum _{M\in \mathcal{M}_{h}}\tau _{0}\left (\kappa _{M}\left ( \frac{\mathbf{u}_{M}} {\vert \mathbf{u}_{M}\vert }\cdot \nabla \mathbf{u}_{h}\right ),\kappa _{M}\left ( \frac{\mathbf{u}_{M}} {\vert \mathbf{u}_{M}\vert }\cdot \nabla \mathbf{v}_{h}\right )\right )_{M}. {}\\ \end{array}$$

This means that just directional information is used for the stabilization.

In boundary layer regions a combination of (anisotropic) local refinement and near-wall modeling with an appropriate choice of the SUPG-LPS parameter set τ M (u h ) as in Example 7 is required.

5 Robust and Fast Solvers

For the numerical implementation the C++-FEM library deal.II [3, 5] is used. Here the goal is to construct an efficient, i.e. robust and fast, solver for the semidiscrete system. In particular, one has to decide whether a fully coupled or a segregated approach w.r.t. velocity and pressure is applied.

A fully coupled parallel approach to the preconditioned saddle-point problems appearing in each time step had been considered by Bangerth et al. in [4] in the FE simulation of mantle convection problems. The model is a Stokes/Fourier model for velocity, pressure and temperature. They applied algebraic multigrid preconditioners which showed robustness w.r.t. ν, the mesh size h and time step Δ t. In particular, very good weak and strong scaling properties for the Stokes/Fourier model were obtained on unstructured adapted grids with up to 109 unknowns, cf. Fig. 12.

Fig. 12
figure 12

Weak and strong scaling properties of the mantle convection problem (Results by Bangerth et al. [4])

Full size image

Unfortunately, the extension of the fully coupled solver to Navier-Stokes simulations proved to be too less robust and to have unacceptable CPU times, mostly for Large-Eddy simulations of weakly turbulent flows. Due to these reasons we used a segregated approach with velocity/pressure decoupling with a Chorin/Temam-type splitting:

$$\displaystyle\begin{array}{rcl} \begin{array}{llll} \frac{3\tilde{\mathbf{u}}^{k+1}-4\mathbf{u}^{k}+\mathbf{u}^{k-1}} {2\varDelta t} -\nu \varDelta \tilde{\mathbf{u}}^{k+1} +\tilde{ \mathbf{u}}^{k+1} \cdot \nabla \tilde{\mathbf{u}}^{k+1} + \nabla p^{k}& = \mathbf{f}(t^{k+1})&&\mbox{ in}\ \varOmega, \\ \tilde{\mathbf{u}}^{k+1} & = 0 &&\mbox{ on}\ \partial \varOmega,\end{array} & &{}\end{array}$$
(29)
$$\displaystyle\begin{array}{rcl} \begin{array}{rlll} \frac{3\mathbf{u}^{k+1}-3\tilde{\mathbf{u}}^{k+1}} {2\varDelta t} + \nabla \phi ^{k+1} & = 0 &&\mbox{ in}\ \varOmega, \\ \nabla \cdot \mathbf{u}^{k+1} & = 0 &&\mbox{ in}\ \varOmega, \\ \mathbf{u}^{k+1} \cdot \mathbf{n}& = 0 &&\mbox{ on}\ \partial \varOmega, \\ \phi ^{k+1} - p^{k+1} + p^{k}& =\nu \nabla \cdot \tilde{\mathbf{u}}^{k+1} & & \mbox{ in}\ \varOmega.\end{array} & &{}\end{array}$$
(30)

A BDF(2) time discretization is applied together with a rotational incremental pressure correction scheme [13]. In the first step (29) solving a reaction-diffusion-advection problem for the velocity is required and we use a GMRES solver in conjunction with an algebraic multigrid (AMG) preconditioner. The second step (30) consists simply of a pressure-Poisson problem that is solved by a CG solver and again AMG preconditioner.

In Fig. 13 we observe a convincing strong scaling of the used algorithm. All the major parts apart from solving the Poisson equation behave optimally in this regime. In particular, the total time is inversely proportional to the number of processes used.

Fig. 13
figure 13

Strong scaling results for the Couzy problem (Example 2)

Full size image

6 Summary and Outlook

In this paper, we considered the numerical simulation of time-dependent incompressible flow problems via inf-sup stable Galerkin-FEM with minimal stabilization. In practice, the classical grad-div stabilization leads to improved local mass conservation, but a rigorous theoretical foundation is missing even for the Stokes problem.

For grad-div stabilized Galerkin schemes with inf-sup stable velocity-pressure interpolation and sufficiently smooth solutions of the time-dependent Navier-Stokes problem we can prove error estimates of order \(\mathcal{O}(h^{k})\) uniformly w.r.t. the data. Moreover, the Gronwall constant does not depend explicitly on ν. Unfortunately, a mesh-width restriction is required, see Theorem 1. For laminar flows, numerical experiments show a certain robustness of grad-div stabilized Galerkin schemes with inf-sup stable velocity-pressure interpolation.

The results extend to grad-div stabilized Galerkin schemes with a subgrid model for the unresolved velocity scales. The subgrid model consists of local projection stabilization of an approximate streamline derivative of the velocity, see Theorem 3. Under an additional compatibility condition on the projection space, one can remove the mentioned mesh width restriction while maintaining the features of the previous analysis, see Theorem 3. We considered some basic problems with boundary layers and flow separation.

A velocity-pressure segregation based on BDF(2)-approximation in time and the rotational incremental pressure-correction scheme was parallelized within the C++-FEM package deal.II. First reasonable scaling results for up to 512 processors are reported.

An extension of the results is possible in the following directions:

  • An extension to problems with in- and outflow, in particular based on the so-called directional do-nothing condition by Braack and Mucha [7], is desirable.

  • The approach by Linke et al. [17] with enhancement of inf-sup stable elements to exactly divergence-preserving schemes will eventually allow to remove grad-div stabilization.

  • Further improvement of the velocity subgrid model based on local projection of the streamline derivative is required for boundary layer problems, flows with separation and for weakly turbulent flows.

  • Finally, an extension of the approach to coupled flow models like nonisothermal incompressible flows and resistive incompressible magnetohydrodynamics is in preparation.