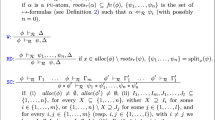On Automated Lemma Generation for Separation Logic with Inductive Definitions

Abstract

Separation Logic with inductive definitions is a well-known approach for deductive verification of programs that manipulate dynamic data structures. Deciding verification conditions in this context is usually based on user-provided lemmas relating the inductive definitions. We propose a novel approach for generating these lemmas automatically which is based on simple syntactic criteria and deterministic strategies for applying them. Our approach focuses on iterative programs, although it can be applied to recursive programs as well, and specifications that describe not only the shape of the data structures, but also their content or their size. Empirically, we find that our approach is powerful enough to deal with sophisticated benchmarks, e.g., iterative procedures for searching, inserting, or deleting elements in sorted lists, binary search tress, red-black trees, and AVL trees, in a very efficient way.

Zhilin Wu is supported by the NSFC projects (No. 61100062, 61272135, and 61472474), and the visiting researcher program of China Scholarship Council. This work was supported by the ANR project Vecolib (ANR-14-CE28-0018).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Program verification requires reasoning about complex, unbounded size data structures that may carry data ranging over infinite domains. Examples of such structures are multi-linked lists, nested lists, trees, etc. Programs manipulating such structures perform operations that may modify their shape (due to dynamic creation and destructive updates) as well as the data attached to their elements. An important issue is the design of logic-based frameworks that express assertions about program configurations (at given control points), and then to check automatically the validity of these assertions, for all computations. This leads to the challenging problem of finding relevant compromises between expressiveness, automation, and scalability.

An established approach for scalability is the use of Separation logic (SL) [18, 24]. Indeed, its support for local reasoning based on the “frame rule” leads to compact proofs, that can be dealt with in an efficient way. However, finding expressive fragments of SL for writing program assertions, that enable efficient automated validation of the verification conditions, remains a major issue. Typically, SL is used in combination with inductive definitions, which provide a natural description of the data structures manipulated by a program. Moreover, since program proofs themselves are based on induction, using inductive definitions instead of universal quantifiers (like in approaches based on first-order logic) enables scalable automation, especially for recursive programs which traverse the data structure according to their inductive definition, e.g., [22]. Nevertheless, automating the validation of the verification conditions generated for iterative programs, that traverse the data structures using while loops, remains a challenge. The loop invariants use inductive definitions for fragments of data structures, traversed during a partial execution of the loop, and proving the inductiveness of these invariants requires non-trivial lemmas relating (compositions of) such inductive definitions. Most of the existing works require that these lemmas be provided by the user of the verification system, e.g., [8, 17, 22] or they use translations of SL to first-order logic to avoid this problem. However, the latter approaches work only for rather limited fragments [20, 21]. In general, it is difficult to have lemmas relating complex user-defined inductive predicates that describe not only the shape of the data structures but also their content.

To illustrate this difficulty, consider the simple example of a sorted singly linked list. The following inductive definition describes a sorted list segment from the location E to F, storing a multiset of values M:

$$\begin{aligned} lseg (E,M,F)&\,{:}{:}{=}\, E = F \wedge M=\emptyset \wedge \mathtt {emp}\end{aligned}$$

(1)

$$\begin{aligned} lseg (E,M,F)&\,{:}{:}{=}\, \exists X,v,M_1.\ E\mapsto \{(\mathtt {next},X),(\mathtt {data},v)\}* lseg (X,M_1,F)\nonumber \\&\qquad \qquad \qquad \!\!\wedge \ v \le M_1\wedge M=M_1\cup \{v\} \end{aligned}$$

(2)

where $\mathtt {emp}$ denotes the empty heap, $E\mapsto \{(\mathtt {next},X),(\mathtt {data},v)\}$ states that the pointer field $\mathtt {next}$ of E points to X while its field $\mathtt {data}$ stores the value v, and $*$ is the separating conjunction. Proving inductive invariants of typical sorting procedures requires such an inductive definition and the following lemma:

$$\begin{aligned} \exists E_2.\, lseg (E_1,M_1,E_2) * lseg (E_2,M_2,E_3) \wedge M_1\le M_2\Rightarrow \exists M.\, lseg (E_1,M,E_3). \end{aligned}$$

The data constraints in these lemmas, e.g., $M_1\le M_2$ (stating that every element of $M_1$ is less or equal than all the elements of $M_2$), which become more complex when reasoning for instance about binary search trees, are an important obstacle for trying to synthesize them automatically.

Our work is based on a new class of inductive definitions for describing fragments of data structures that (i) supports lemmas without additional data constraints like $M_1 \le M_2$ and (ii) allows to automatically synthesize these lemmas using efficiently checkable, almost syntactic, criteria. For instance, we use a different inductive definition for $lseg$, which introduces an additional parameter $M'$ that provides a “data port” for appending another sorted list segment, just like F does for the shape of the list segment:

$$\begin{aligned} lseg (E,M,F,M')&\,{:}{:}{=}\, E = F \wedge M = M' \wedge \mathtt {emp}\end{aligned}$$

(3)

$$\begin{aligned} lseg (E,M,F,M')&\,{:}{:}{=}\,\exists X,v,M_1.\ E\mapsto \{(\mathtt {next},X),(\mathtt {data},v)\}* lseg (X,M_1,F,M')\nonumber \\&\qquad \qquad \qquad \!\!\!\wedge \ v \le M_1\wedge M=M_1\cup \{v\} \end{aligned}$$

(4)

The new definition satisfies the following simpler lemma, which avoids the introduction of data constraints:

$$\begin{aligned} \exists E_2,M_2.\, lseg (E_1,M_1,E_2,M_2) * lseg (E_2,M_2,E_3,M_3) \Rightarrow lseg (E_1,M_1,E_3,M_3). \end{aligned}$$

(5)

Besides such “composition” lemmas (formally defined in Sect. 4), we define (in Sect. 5) other classes of lemmas needed in program proofs and we provide efficient criteria for generating them automatically. Moreover, we propose (in Sect. 6) a proof strategy using such lemmas, based on simple syntactic matchings of spatial atoms (points-to atoms or predicate atoms like $lseg$) and reductions to SMT solvers for dealing with the data constraints. We show experimentally (in Sect. 7) that this proof strategy is powerful enough to deal with sophisticated benchmarks, e.g., the verification conditions generated from the iterative procedures for searching, inserting, or deleting elements in binary search trees, red-black trees, and AVL trees, in a very efficient way. The proofs of theorems and additional classes of lemmas are provided in [12].

2 Motivating Example

Figure 1 lists an iterative implementation of a search procedure for binary search trees (BSTs). The property that E points to the root of a BST storing a multiset of values M is expressed by the following inductively-defined predicate:

$$\begin{aligned} bst (E,M)&{:}{:}{=}\, E = \mathsf{nil}\wedge M = \emptyset \wedge \mathtt {emp} \end{aligned}$$

(6)

$$\begin{aligned} bst (E,M)&{:}{:}{=}\, \exists X,Y,M_1,M_2,v.\, E \mapsto \{(\mathtt {left},X), (\mathtt {right},Y),(\mathtt {data},v)\} \\&\qquad \qquad \qquad *\ bst (X,M_1)* bst (Y,M_2) \nonumber \\&\qquad \qquad \qquad \wedge \ M=\{v\} \cup M_1 \cup M_2 \wedge M_1 < v < M_2\nonumber \end{aligned}$$

(7)

Fig. 1.

Searching a key in BST

The predicate $bst (E,M)$ is defined by two rules describing empty (Eq. (6)) and non-empty trees (Eq. (7)). The body (right-hand side) of each rule is a conjunction of a pure formula, formed of (dis)equalities between location variables (e.g. $E = \mathsf{nil}$) and data constraints (e.g. $M= \emptyset$), and a spatial formula describing the structure of the heap. The data constraints in Eq. (7) define M to be the multiset of values stored in the tree, and state the sortedness property of BSTs.

The precondition of search is $bst ({\texttt {root}},M_0)$, where $M_0$ is a ghost variable denoting the multiset of values stored in the tree, while its postcondition is $bst ({\texttt {root}},M_0) \wedge ({\texttt {key}} \in M_0 \rightarrow ret = 1) \wedge ({\texttt {key}} \not \in M_0 \rightarrow ret = 0)$, where $ret$ denotes the return value.

The while loop traverses the BST in a top-down manner using the pointer variable t. This variable decomposes the heap into two domain-disjoint sub-heaps: the tree rooted at t, and the truncated tree rooted at root which contains a “hole” at t. To specify the invariant of this loop, we define another predicate $bsthole (E,M_1,F,M_2)$ describing “truncated” BSTs with one hole F as follows:

$$\begin{aligned} bsthole (E,M_1,F,M_2)&{:}{:}{=}\, E = F \wedge M_1 = M_2 \wedge \mathtt {emp} \end{aligned}$$

(8)

$$\begin{aligned} bsthole (E,M_1,F,M_2)&{:}{:}{=}\, \exists X,Y,M_3,M_4,v.\, E \mapsto \{(\mathtt {left},X), (\mathtt {right},Y),(\mathtt {data},v)\} \nonumber \\&\qquad \qquad \qquad *\ bst (X,M_3) * bsthole (Y,M_4,F,M_2) \\&\qquad \qquad \qquad \wedge \ M_1=\{v\} \cup M_3 \cup M_4 \wedge M_3 < v < M_4\nonumber \end{aligned}$$

(9)

$$\begin{aligned} bsthole (E,M_1,F,M_2)&{:}{:}{=}\,\exists X,Y,M_3,M_4, v.\, E \mapsto \{(\mathtt {left},X),(\mathtt {right},Y),(\mathtt {data},v)\} \nonumber \\&\qquad \qquad \qquad *\ bsthole (X,M_3,F,M_2) * bst (Y,M_4) \\&\qquad \qquad \qquad \wedge \ M_1=\{v\} \cup M_3 \cup M_4 \wedge M_3 < v < M_4\nonumber \end{aligned}$$

(10)

Intuitively, the parameter $M_2$, interpreted as a multiset of values, is used to specify that the structure described by $bsthole (E,M_1,F,M_2)$ could be extended with a BST rooted at F and storing the values in $M_2$, to obtain a BST rooted at E and storing the values in $M_1$. Thus, the parameter $M_1$ of $bsthole$ is the union of $M_2$ with the multiset of values stored in the truncated BST represented by $bsthole (E,M_1,F,M_2)$.

Using $bsthole$, we obtain a succinct specification of the loop invariant:

$$\begin{aligned} \textit{Inv}\, {:}{:}{=}\, \exists M_1.\ bsthole ({\texttt {root}},M_0,\texttt {t},M_1) * bst (\mathtt{t},M_1) \wedge ({\texttt {key}} \in M_0 \Leftrightarrow {\texttt {key}} \in M_1). \end{aligned}$$

(11)

We illustrate that such inductive definitions are appropriate for automated reasoning, by taking the following branch of the loop: assume(t != NULL); assume(t->data > key); t ${'}$ = t->left (as usual, if statements are transformed into assume statements and primed variables are introduced in assignments). The postcondition of ${ Inv}$ w.r.t. this branch, denoted ${ post}({ Inv})$, is computed as usual by unfolding the $bst$ predicate:

$$\begin{aligned} \nonumber \exists M_1, Y, v ,M_2, M_3.\,&bsthole (\mathtt{root},M_0,\mathtt{t},M_1) *\mathtt{t}\mapsto \{(\mathtt {left},\mathtt{t}'), (\mathtt {right}, Y), (\mathtt {data},v)\}\\ \nonumber&*\ bst (\mathtt{t}',M_2) * bst (Y,M_3)\wedge M_1 = \{v\} \cup M_2 \cup M_3 \wedge M_2 < v < M_3\\&\wedge \ (\mathtt{key} \in M_0 \Leftrightarrow \mathtt{key} \in M_1) \wedge v > \mathtt{key}. \end{aligned}$$

(12)

The preservation of ${ Inv}$ by this branch is expressed by the entailment ${ post}({ Inv})\Rightarrow { Inv}'$, where ${ Inv}'$ is obtained from ${ Inv}$ by replacing $\mathtt{t}$ with $\mathtt{t}'$.

Based on the lemmas, this paper also proposes a deterministic proof strategy for proving the validity of entailments of the form $\varphi _1\Rightarrow \exists \vec {X}.\varphi _2$, where $\varphi _1,\varphi _2$ are quantifier-free and $\vec {X}$ contains only data variables¹. The strategy comprises two steps: (i) enumerating spatial atoms A from $\varphi _2$, and for each of them, carving out a sub-formula $\varphi _A$ of $\varphi _1$ that entails A, where it is required that these subformulas do not share spatial atoms (due to the semantics of separation conjunction), and (ii) proving that the data constraints from $\varphi _A$ imply those from $\varphi _2$ (using SMT solvers). The step (i) may generate constraints on the variables in $\varphi _A$ and $\varphi _2$ that are used in step (ii). If the step (ii) succeeds, then the entailment holds.

For instance, by applying this strategy to the entailment ${ post}({ Inv})\Rightarrow { Inv}'$ above, we obtain two goals for step (i) which consist in computing two sub-formulas of ${ post}({ Inv})$ that entail $\exists M_1'.\ bsthole (\mathtt{root},M_0,\mathtt{t}',M_1')$ and respectively, $\exists M_1''.\ bst (\mathtt{t}',M_1'')$. This renaming of existential variables requires adding the equality $M_1=M_1'=M_1''$ to ${ Inv}'$. The second goal, for $\exists M_1''.\ bst (\mathtt{t}',M_1'')$, is solved easily since this atom almost matches the sub-formula $bst (\mathtt{t}',M_2)$. This matching generates the constraint $M_1''=M_2$, which provides an instantiation of the existential variable $M_1''$ useful in proving the entailment between the data constraints in step (ii).

Computing a sub-formula that entails $\exists M_1'.\ bsthole (\mathtt{root},M_0,\mathtt{t}',M_1')$ requires a non-trivial lemma. Thus, according to the syntactic criteria defined in Sect. 4, the predicate $bsthole$ enjoys the following composition lemma:

$$\begin{aligned} \big (\exists F,M.\ bsthole (\mathtt{root},M_0, F, M)\ *&\ bsthole (F,M,\mathtt{t}',M_1')\big ) \\ \nonumber&\Rightarrow bsthole (\mathtt{root},M_0,\mathtt{t}',M_1'). \end{aligned}$$

(13)

Intuitively, this lemma states that composing two heap structures described by $bsthole$ results in a structure that satisfies the same predicate. The particular relation between the arguments of the predicate atoms in the left-hand side is motivated by the fact that the parameters F and M are supposed to represent “ports” for composing $bsthole (\mathtt{root},M_0,F, M)$ with some other similar heap structures. This property of F and M is characterized syntactically by the fact that, roughly, F (resp. M) occurs only once in the body of each inductive rule of $bsthole$, and F (resp. M) occurs only in an equality with $\mathtt{root}$ (resp. $M_0$) in the base rule (we are referring to the rules (8)–(10) with the parameters of $bsthole$ substituted by $(\mathtt{root},M_0,F, M)$).

Therefore, the first goal reduces to finding a sub-formula of ${ post}({ Inv})$ that implies the premise of (13) where $M_1'$ remains existentially-quantified. Recursively, we apply the same strategy of enumerating spatial atoms and finding sub-formulas that entail them. However, we are relying on the fact that all the existential variables denoting the root locations of spatial atoms in the premise of the lemma, e.g., F in lemma (13), occur as arguments in the only spatial atom of the conclusion whose root location is the same as that of the consequent, i.e., $bsthole (\mathtt{root},M_0, F, M)$ in lemma (13). Therefore, the first sub-goal, $\exists F,M.\ bsthole (\mathtt{root},M_0, F, M)$ matches the atom $bsthole (\mathtt{root},M_0,\mathtt{t},M_1)$, under the constraint $F=\mathtt{t}\wedge M=M_1$. This constraint is used in solving the second sub-goal, which now becomes $\exists M_1'.\ bsthole (\mathtt{t},M_1,\mathtt{t}',M_1')$.

The second sub-goal is proved by unfolding $bsthole$ twice, using first the rule (10) and then the rule (8), and by matching the resulting spatial atoms with those in ${ post}({ Inv})$ one by one. Assuming that the existential variable $M_1$ from ${ Inv}'$ is instantiated with $M_2$ from ${ post}({ Inv})$ (fact automatically deduced in the first step), the data constraints in ${ post}({ Inv})$ entail those in ${ Inv}'$. This completes the proof of ${ post}({ Inv})\Rightarrow { Inv}'$.

3 Separation Logic with Inductive Definitions

Let $\mathsf{LVar}$ be a set of location variables, interpreted as heap locations, and $\mathsf{DVar}$ a set of data variables, interpreted as data values stored in the heap, (multi)sets of values, etc. In addition, let $\mathsf {Var}=\mathsf{LVar}\cup \mathsf{DVar}$. The domain of heap locations is denoted by ${\mathbb L}$ while the domain of data values stored in the heap is generically denoted by ${\mathbb D}$. Let $\mathcal {F}$ be a set of pointer fields, interpreted as functions ${\mathbb L}\rightharpoonup {\mathbb L}$, and $\mathcal {D}$ a set of data fields, interpreted as functions ${\mathbb L}\rightharpoonup {\mathbb D}$. The syntax of the Separation Logic fragment considered in this paper is defined in Table 1.

Formulas are interpreted over pairs (s, h) formed of a stack s and a heap h. The stack s is a function giving values to a finite set of variables (location or data variables) while the heap h is a function mapping a finite set of pairs $(\ell ,{ pf})$, where $\ell$ is a location and ${ pf}$ is a pointer field, to locations, and a finite set of pairs $(\ell ,{ df})$, where ${ df}$ is a data field, to values in ${\mathbb D}$. In addition, h satisfies the condition that for each $\ell \in {\mathbb L}$, if $(\ell ,{ df}) \in \mathsf{dom}(h)$ for some ${ df} \in \mathcal {D}$, then $(\ell ,{ pf}) \in \mathsf{dom}(h)$ for some ${ pf} \in \mathcal {F}$. Let $\mathsf{dom}(h)$ denote the domain of h, and $\mathsf{ldom}(h)$ denote the set of $\ell \in {\mathbb L}$ such that $(\ell , { pf}) \in \mathsf{dom}(h)$ for some ${ pf} \in \mathcal {F}$.

Table 1. The syntax of the Separation Logic fragment

Formulas are conjunctions between a pure formula $\varPi$ and a spatial formula $\varSigma$. Pure formulas characterize the stack s using (dis)equalities between location variables, e.g., a stack models $x=y$ iff $s(x)=s(y)$, and constraints $\varDelta$ over data variables. We let $\varDelta$ unspecified, though we assume that they belong to decidable theories, e.g., linear arithmetic or quantifier-free first order theories over multisets of values. The atom $\mathtt {emp}$ of spatial formulas holds iff the domain of the heap is empty. The points-to atom $E \mapsto \{ (f_i,x_i) \}_{i\in \mathcal {I}}$ specifies that the heap contains exactly one location E, and for all $i\in \mathcal {I}$, the field $f_i$ of E equals $x_i$, i.e., $h(s(E),f_i)=s(x_i)$. The predicate atom $P(E,\vec {F})$ specifies a heap segment rooted at E and shaped by the predicate P; the fragment is parameterized by a set $\mathcal {P}$ of inductively defined predicates, formally defined hereafter.

Let $P \in \mathcal {P}$. An inductive definition of P is a finite set of rules of the form $P(E,\vec {F})\,{:}{:}{=}\,\exists \vec {Z}. \varPi \wedge \varSigma$, where $\vec {Z} \in \mathsf {Var}^*$ is a tuple of variables. A rule R is called a base rule if $\varSigma$ contains no predicate atoms. Otherwise, it is called an inductive rule. A base rule R is called spatial-empty if $\varSigma =\mathtt {emp}$. Otherwise, it is called a spatial-nonempty base rule. For instance, the predicate $bst$ in Sect. 2 is defined by one spatial-empty base rule and one inductive rule.

We consider a class of restricted inductive definitions that are expressive enough to deal with intricate data structures (see Sect. 7) while also enabling efficient proof strategies for establishing the validity of the verification conditions (see Sect. 6). For each rule $R: P(E,\vec {F})\,{:}{:}{=}\,\exists \vec {Z}. \varPi \wedge \varSigma$ in the definition of a predicate $P(E,\vec {F}) \in \mathcal {P}$, we assume that:

• If R is inductive, then $\varSigma = \varSigma _1 *\varSigma _2$ and the following conditions hold:

  • the root atoms: $\varSigma _1$ contains only points-to atoms and a unique points-to atom starting from E, denoted as $E \mapsto \rho$. Also, all the location variables from $\vec {Z}$ occur in $\varSigma _1$. $\varSigma _1$ is called the root of R and denoted by root(R).

  • connectedness: the Gaifman graph of $\varSigma _1$, denoted by $G_{\varSigma _1}$, is a connected DAG (directed acyclic graph) with the root E, that is, every vertex is reachable from E,

  • predicate atoms: $\varSigma _2$ contains only atoms of the form $Q(Z,\vec {Z'})$, and for each such atom, Z is a vertex in $G_{\varSigma _1}$ without outgoing arcs.

• If R is a spatial-nonempty base rule, then $\varSigma$ contains exactly one points-to atom $E \mapsto \rho$, for some $\rho$.

The classic acyclic list segment definition [24] satisfies these constraints as well as the first rule below; the second rule below falsifies the “root atoms” constraint:

$$\begin{aligned} lsegeven (E,F)&\,{:}{:}{=}\,\exists X,Y.\ E \mapsto (\mathtt {next}, X) *X \mapsto (\mathtt {next},Y) * lsegeven (Y,F) \\ lsegb (E,F)&\,{:}{:}{=}\,\exists X.\ lsegb (E,X) *X \mapsto (\mathtt {next},F). \end{aligned}$$

Since we disallow the use of negations on top of the spatial atoms, the semantics of the predicates in $\mathcal {P}$ is defined as usual as a least fixed-point. The class of inductive definitions defined above is in general undecidable, since with data fields, inductive definitions can be used to simulate two-counter machines.

A variable substitution $\eta$ is a mapping from a finite subset of $\mathsf {Var}$ to the set of terms over the respective domains. For instance, if $X \in \mathsf{LVar}$ and $v,v_1 \in \mathsf{DVar}$ be integer variables then the mapping $\eta =\{X \rightarrow \mathsf{nil}, v \rightarrow v_1 + 5\}$ is a variable substitution. We denote by $\mathtt {free}(\psi )$ the set of free variables of a formula $\psi$.

4 Composition Lemmas

As we have seen in the motivating example, the predicate $bsthole (E,M_1,F,M_2)$ satisfies the property that composing two heap structures described by this predicate results in a heap structure satisfying the same predicate. We call this property a composition lemma. We define simple and uniform syntactic criteria which, if they are satisfied by a predicate, then the composition lemma holds.

The main idea is to divide the parameters of inductively defined predicates into three categories: The source parameters $\vec {\alpha }=(E,C)$, the hole parameters $\vec {\beta }=(F,H)$, and the static parameters $\vec {\xi }\in \mathsf {Var}^*$, where $E,F \in \mathsf{LVar}$ are called the source and resp., the hole location parameter, and $C,H \in \mathsf{DVar}$ are called the cumulative and resp., the hole data parameter².

Let $\mathcal {P}$ be a set of inductively defined predicates and $P \in \mathcal {P}$ with the parameters $(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$. Then P is said to be syntactically compositional if the inductive definition of P contains exactly one base rule, and at least one inductive rule, and the rules of P are of one of the following forms:

• Base rule: $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\,{:}{:}{=}\,\alpha _{1} = \beta _{1} \wedge \alpha _2 = \beta _2 \wedge \mathtt {emp}$. Note that here the points-to atoms are disallowed.

• Inductive rule: $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\,{{:}{:}=}\,\exists \vec {Z}. \ \varPi \wedge \varSigma$, with (a) $\varSigma \triangleq \varSigma _1 *\varSigma _2 *P(\vec {\gamma },\vec {\beta },\vec {\xi }\,)$, (b) $\varSigma _1$ contains only and at least one points-to atoms, (c) $\varSigma _2$ contains only and possibly none predicate atoms, (d) $\vec {\gamma } \subseteq \vec {Z}$, and (d) the variables in $\vec {\beta }$ do not occur elsewhere in $\varPi \wedge \varSigma$, i.e., not in $\varPi$, or $\varSigma _1$, or $\varSigma _2$, or $\vec {\gamma }$. Note that the inductive rule also satisfies the constraints “root atom” and “connectedness” introduced in Sect. 3. In addition, $\varSigma _2$ may contain P atoms.

One may easily check that both the predicate $lseg (E,M,F,M')$ in Eqs. (3)–(4) and the predicate $bsthole (E,M_1,F,M_2)$ in Eqs. (8)–(10) are syntactically compositional, while the predicate $lseg (E,M,F)$ in Eqs. (1)–(2) is not.

A predicate $P \in \mathcal {P}$ with the parameters $(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$ is said to be semantically compositional if the entailment $\exists \vec {\beta }.\ P(\vec {\alpha },\vec {\beta },\vec {\xi }\,) *P(\vec {\beta },\vec {\gamma },\vec {\xi }\,) \Rightarrow P(\vec {\alpha }, \vec {\gamma },\vec {\xi }\,)$ holds.

Theorem 1

Let $\mathcal {P}$ be a set of inductively defined predicates. If $P \in \mathcal {P}$ is syntactically compositional, then P is semantically compositional.

The Proof of Theorem 1 is done by induction on the size of the domain of the heap structures. Suppose $(s,h) \models P(\vec {\alpha },\vec {\beta },\vec {\xi }\,) *P(\vec {\beta },\vec {\gamma },\vec {\xi }\,)$, then either $s(\vec {\alpha })=s(\vec {\beta })$ or $s(\vec {\alpha }) \ne s(\vec {\beta })$. If the former situation occurs, then $(s,h) \models P(\vec {\alpha }, \vec {\gamma },\vec {\xi }\,)$ follows immediately. Otherwise, the predicate $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$ is unfolded by using some inductive rule of P, and the induction hypothesis can be applied to a sub-heap of smaller size. Then $(s,h) \models P(\vec {\alpha }, \vec {\gamma },\vec {\xi }\,)$ can be deduced by utilizing the property that the hole parameters occur only once in each inductive rule of P.

Remark 1

The syntactically compositional predicates are rather general in the sense that they allow nestings of predicates, branchings (e.g. trees), as well as data and size constraints. Therefore, composition lemmas can be obtained for complex data structures like nested lists, AVL trees, red-black trees, and so on. In addition, although lemmas have been widely used in the literature, we are not aware of any work that uses the composition lemmas as simple and elegant as those introduced above, when data and size constraints are included.

5 Derived Lemmas

Theorem 1 provides a mean to obtain lemmas for one single syntactically compositional predicate. In the following, based on the syntactic compositionality, we demonstrate how to derive additional lemmas describing relationships between different predicates. We present here two categories of derived lemmas: “completion” lemmas and “stronger” lemmas; more categories are provided in [12]. Based on our experiences in the experiments (cf. Sect. 7) and the examples from the literature, we believe that the composition lemmas as well as the derived ones are natural, essential, and general enough for the verification of programs manipulating dynamic data structures. For instance, the “composition” lemmas and “completion” lemmas are widely used in our experiments, the “stronger” lemmas are used to check the verification conditions for rebalancing AVL trees and red-black trees.

5.1 The “Completion” Lemmas

We first consider the “completion” lemmas which describe relationships between incomplete data structures (e.g., binary search trees with one hole) and complete data structures (e.g., binary search trees). For example, the following lemma is valid for the predicates $bsthole$ and $bst$:

$$\begin{aligned}&\exists F,M_2.\ bsthole (E,M_1, F, M_2) * bst (F,M_2) \Rightarrow bst (E,M_1). \end{aligned}$$

Notice that the rules defining $bst (E,M)$ can be obtained from those of $bsthole (E_1,M_1,F,M_2)$ by applying the variable substitution $\eta =\{F \rightarrow \mathsf{nil}, M_2 \rightarrow \emptyset \}$ (modulo the variable renaming $M_1$ by M). This observation is essential to establish the “completion lemma” and it is generalized to arbitrary syntactically compositional predicates as follows.

Let $P \in \mathcal {P}$ be a syntactically compositional predicate with the parameters $(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$, and $P' \in \mathcal {P}$ a predicate with the parameters $(\vec {\alpha },\vec {\xi }\,)$. Then $P'$ is a completion of P with respect to a pair of constants $\vec {c}=c_1c_2$, if the rules of $P'$ are obtained from the rules of P by applying the variable substitution $\eta =\{\beta _1 \rightarrow c_1, \beta _2 \rightarrow c_2\}$. More precisely,

• let $\alpha _1 = \beta _1 \wedge \alpha _2 = \beta _2 \wedge \mathtt {emp}$ be the base rule of P, then $P'$ contains only one base rule, that is, $\alpha _1 = c_1 \wedge \alpha _2 = c_2 \wedge \mathtt {emp}$,

• the set of inductive rules of $P'$ is obtained from those of P as follows: Let $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\,{:}{:}{=}\,\exists \vec {Z}.\ \varPi \wedge \varSigma _1 *\varSigma _2 *P(\vec {\gamma },\vec {\beta },\vec {\xi }\,)$ be an inductive rule of P, then $P'(\vec {\alpha },\vec {\xi }\,)\,{:}{:}{=}\,\exists \vec {Z}.\ \varPi \wedge \varSigma _1 *\varSigma _2 *P'(\vec {\gamma },\vec {\xi }\,)$ is an inductive rule of $P'$ (Recall that $\vec {\beta }$ does not occur in $\varPi ,\varSigma _1,\varSigma _2,\vec {\gamma }$).

Theorem 2

Let $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,) \in \mathcal {P}$ be a syntactically compositional predicate, and $P'(\vec {\alpha },\vec {\xi }\,) \in \mathcal {P}$. If $P'$ is a completion of P with respect to $\vec {c}$, then $P'(\vec {\alpha },\vec {\xi }\,) \Leftrightarrow P(\vec {\alpha },\vec {c},\vec {\xi }\,)$ and $\exists \vec {\beta }.\ P(\vec {\alpha },\vec {\beta },\vec {\xi }\,) *P'(\vec {\beta },\vec {\xi }\,) \Rightarrow P'(\vec {\alpha }, \vec {\xi }\,)$ hold.

5.2 The “Stronger” Lemmas

We illustrate this class of lemmas on the example of binary search trees. Let ${ natbsth}(E,M_1, F, M_2)$ be the predicate defined by the same rules as $bsthole (E,M_1,F,M_2)$ (i.e., Eqs. (8)–(10)), except that $M_3 \ge 0$ ($M_3$ is an existential variable) is added to the body of each inductive rule (i.e., Eqs. (9) and (10)). Then we say that ${ natbsth}$ is stronger than $bsthole$, since for each rule $R'$ of ${ natbsth}$, there is a rule R of $bsthole$, such that the body of $R'$ entails the body of R. This “stronger” relation guarantees that the following lemmas hold:

$$\begin{aligned} { natbsth}(E,M_1,F,M_2)&\Rightarrow bsthole (E,M_1,F,M_2)\\ \exists E_2,M_2.\ { natbsth}(E_1, M_1, E_2, M_2) * bsthole (E_2, M_2, E_3, M_3)&\Rightarrow bsthole (E_1,M_1, E_3, M_3). \end{aligned}$$

In general, for two syntactically compositional predicates $P,P' \in \mathcal {P}$ with the same set of parameters $(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$, $P'$ is said to be stronger than P if for each inductive rule $P'(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\,{:}{:}{=}\,\exists \vec {Z}. \ \varPi ' \wedge \varSigma _1 *\varSigma _2 *P'(\vec {\gamma },\vec {\beta },\vec {\xi }\,)$, there is an inductive rule $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\,{:}{:}{=}\,\exists \vec {Z}. \ \varPi \wedge \varSigma _1 *\varSigma _2 *P(\vec {\gamma },\vec {\beta },\vec {\xi }\,)$ such that $\varPi ' \Rightarrow \varPi$ holds. The following result is a consequence of Theorem 1.

Theorem 3

Let $P(\vec {\alpha },\vec {\beta },\vec {\xi }\,),P'(\vec {\alpha },\vec {\beta },\vec {\xi }\,) \in \mathcal {P}$ be two syntactically compositional predicates. If $P'$ is stronger than P, then the entailments $P'(\vec {\alpha },\vec {\beta },\vec {\xi }\,)\Rightarrow P(\vec {\alpha },\vec {\beta },\vec {\xi }\,)$ and $\exists \vec {\beta }.\ P'(\vec {\alpha },\vec {\beta },\vec {\xi }\,) *P(\vec {\beta },\vec {\gamma },\vec {\xi }\,) \Rightarrow P(\vec {\alpha },\vec {\gamma },\vec {\xi }\,)$ hold.

The “stronger” relation defined above requires that the spatial formulas in the inductive rules of P and $P'$ are the same. This constraint can be relaxed by only requiring that the body of each inductive rule of $P'$ is stronger than a formula obtained by unfolding an inductive rule of P for a bounded number of times. This relaxed constraint allows generating additional lemmas, e.g., the lemmas relating the predicates for list segments of even length and list segments.

6 A Proof Strategy Based on Lemmas

We introduce a proof strategy based on lemmas for proving entailments $\varphi _1\Rightarrow \exists \vec {X}.\varphi _2$, where $\varphi _1$, $\varphi _2$ are quantifier-free, and $\vec {X} \in \mathsf{DVar}^*$. The proof strategy treats uniformly the inductive rules defining predicates and the lemmas defined in Sects. 4 and 5. Therefore, we call lemma also an inductive rule. W.l.o.g. we assume that $\varphi _1$ is quantifier-free (the existential variables can be skolemized). In addition, we assume that only data variables are quantified in the right-hand side ³.

W.l.o.g., we assume that every variable in $\vec {X}$ occurs in at most one spatial atom of $\varphi _2$ (multiple occurrences of the same variable can be removed by introducing fresh variables and new equalities in the pure part). Also, we assume that $\varphi _1$ and $\varphi _2$ are of the form $\varPi \wedge \varSigma$. In the general case, our proof strategy checks that for every disjunct $\varphi _1'$ of $\varphi _1$, there is a disjunct $\varphi _2'$ of $\varphi _2$ s.t. $\varphi _1'\Rightarrow \exists \vec {X}.\varphi _2'$.

We present the proof strategy as a set of rules in Fig. 2. For a variable substitution $\eta$ and a set $\mathcal {X} \subseteq \mathsf {Var}$, we denote by $\eta |_{\mathcal {X}}$ the restriction of $\eta$ to $\mathcal {X}$. In addition, $\mathtt{EQ}(\eta )$ is the conjunction of the equalities $X=t$ for every X and t such that $\eta (X)=t$. Given two formulas $\varphi _1$ and $\varphi _2$, a substitution $\eta$ with $\mathsf{dom}(\eta )=\vec {X}$, the judgement $\varphi _1\models _{\eta } \exists \vec {X}.\varphi _2$ denotes that the entailment $\varphi _1 \Rightarrow \eta (\varphi _2)$ is valid. Therefore, $\eta$ provides an instantiation for the quantified variables $\vec {X}$ which witnesses the validity.

Fig. 2.

The proof rules for checking the entailment $\varphi _1 \Rightarrow \exists \vec {X}.\ \varphi _2$

The rules $\textsc {Match1}$ and $\textsc {Match2}$ consider a particular case of $\models _{\eta }$, denoted using the superscript $\textit{SUB}$, where the spatial atoms of $\varphi _2$ are syntactically matched⁴ to the spatial atoms of $\varphi _1$ modulo a variable substitution $\theta$. The substitution of the existential variables is recorded in $\eta$, while the substitution of the free variables generates a set of equalities that must be implied by $\varPi _1\wedge \mathtt{EQ}(\eta )$. For example, let $\varPi _1 \wedge \varSigma _1 {:}{:}{=}\, w=w'\wedge E\mapsto \{(f,Y),(d_1,v),(d_2,w)\}$, and $\exists \vec {X}.\ \varSigma _2\ {:}{:}{=}\ \exists X,v'.\ E\mapsto \{(f,X),(d_1,v'),(d_2,w')\}$, where $d_1$ and $d_2$ are data fields. If $\theta =\{X \rightarrow Y, v' \rightarrow v, w' \rightarrow w\}$, then $\varSigma _1 = \theta (\varSigma _2)$. The substitution of the free variable $w'$ from the right-hand side is sound since the equality $w=w'$ occurs in the left-hand side. Therefore, $\varPi _1 \wedge \varSigma _1 \models ^{SUB}_{\theta |_{\{X,v'\}}} \exists X, v'.\ \varSigma _2$ holds.

The rule $\textsc {Lemma}$ applies a lemma $L\ {:}{:}{=}\ \exists \vec {Z}.\ \varPi \wedge root(L) *\varSigma \Rightarrow A$. It consists in proving that $\varphi _1$ implies the LHS of the lemma where the variables in $\vec {X}$ are existentially quantified, i.e., $\exists \vec {X}\exists \vec {Z}.\ \varPi \wedge root(L) *\varSigma$. Notice that $\vec {Z}$ may contain existential location variables. Finding suitable instantiations for these variables relies on the assumption that ${ root}(L)$ in the LHS of L is either a unique predicate atom or a separating conjunction of points-to atoms rooted at E (the first parameter of A) and ${ root}(L)$ includes all the location variables in $\vec {Z}$. This assumption holds for all the inductive rules defining predicates in our fragment (a consequence of the root and connectedness constraints) and for all the lemmas defined in Sects. 4 and 5. The proof that $\varphi _1$ implies $\exists \vec {X}\exists \vec {Z}.\ \varPi \wedge root(L) *\varSigma$ is split into two sub-goals (i) proving that a sub-formula of $\varphi _1$ implies $\exists \vec {X}\exists \vec {Z}.\ root(L)$ and (ii) proving that a sub-formula of $\varphi _1$ implies $\exists \vec {X}\exists \vec {Z}.\ \varPi \wedge \varSigma$. The sub-goal (i) relies on syntactic matching using the rule $\textsc {Match1}$, which results in a quantifier instantiation $\eta _1$. The substitution $\eta _1$ is used to instantiate existential variables in $\exists \vec {X} \exists \vec {Z}.\ \varPi \wedge \varSigma$. Notice that according to the aforementioned assumption, the location variables in $\vec {Z}$ are not free in $\eta _1(\varPi \wedge \varSigma )$. Let $\eta _2$ be the quantifier instantiation obtained from the second sub-goal. The quantifier instantiation $\eta$ is defined as the extension of $\eta _1 \cup \eta _2$ to the domain $\vec {X} \cup \vec {Z}$ by utilizing the pure constraints $\varPi$ from the lemma⁵. This extension is necessary since some existentially quantified variables may only occur in $\varPi$, but not in root(L) nor in $\varSigma$, so they are not covered by $\eta _1 \cup \eta _2$. For instance, if $\varPi$ contains a conjunct $M=M_1 \cup M_2$ such that $M_1\in \mathsf{dom}(\eta _1)$, $M_2 \in \mathsf{dom}(\eta _2)$, and $M \not \in \mathsf{dom}(\eta _1 \cup \eta _2)$, then $\eta _1 \cup \eta _2$ is extended to $\eta$ where $\eta (M)=\eta _1(M_1) \cup \eta _2(M_2)$.

The rule $\textsc {Slice}$ chooses a spatial atom A in the RHS and generates two sub-goals: (i) one that matches A (using the rules $\textsc {Match2}$ and $\textsc {Lemma}$) with a spatial sub-formula of the LHS ($\varSigma _1$) and (ii) another that checks that the remaining spatial part of the RHS is implied by the remaining part of the LHS. The quantifier instantiations $\eta _1$ and $\eta _2$ obtained from the two sub-goals are used to check that the pure constraints in the RHS are implied by the ones in LHS. Note that in the rule $\textsc {Slice}$, it is possible that $\varSigma _2=\varSigma =\mathtt {emp}$.

The rules in Fig. 2 are applied in the order given in the figure. Note that they focus on disjoint cases w.r.t. the syntax of the RHS. The choice of the atom A in $\textsc {Slice}$ is done arbitrary, since it does not affect the efficiency of proving validity.

We apply the above proof strategy to the entailment $\varphi _1\Rightarrow \exists M.\ \varphi _2$ where:

$$\begin{aligned} \varphi _1&\, {:}{:}{=}\, x_1\ne \mathsf{nil}\wedge x_2\ne \mathsf{nil}\wedge v_1 < v_2\wedge x_1 \mapsto \{(\mathtt {next},x_2),(\mathtt {data},v_1)\} \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \!\!\!\!\!\!*\ x_2 \mapsto \{(\mathtt {next},\mathsf{nil}), (\mathtt {data},v_2)\} \\ \varphi _2&\, {:}{:}{=}\, lseg (x_1, M, \mathsf{nil},\emptyset ) \wedge v_2\in M, \end{aligned}$$

and $lseg$ has been defined in Sect. 1 (Eqs. (3) and (4)). The entailment is valid because it states that two cells linked by $\mathtt {next}$ and storing ordered data values form a sorted list segment. The RHS $\varphi _2$ contains a single spatial atom and a pure part so the rule $\textsc {Slice}$ is applied and it generates the sub-goal $\varphi _1\models _{\eta }\exists M.\ lseg (x_1, M, \mathsf{nil},\emptyset )$ for which the syntactic matching (rule Match1) can not be applied. Instead, we apply the rule $\textsc {Lemma}$ using as lemma the inductive rule of $lseg$, i.e., Eq. (4) (page II). We obtain the RHS $\exists M,X,M_1,v.\ x_1 \mapsto \{(\mathtt {next},X), (\mathtt {data},v)\} * lseg (X,M_1,\mathsf{nil},\emptyset ) \wedge M=\{v\}\cup M_1 \wedge v \le M_1$, where $x_1 \mapsto \{(\mathtt {next},X), (\mathtt {data},v)\}$ is the root. The rule $\textsc {Match1}$ is applied with $\varPi _1 \wedge \varSigma _1\ {:}{:}{=}\ x_1\ne \mathsf{nil}\wedge x_2\ne \mathsf{nil}\wedge v_1 < v_2\wedge x_1 \mapsto \{(\mathtt {next},x_2),(\mathtt {data},v_1)\}$ and it returns the substitution $\eta _1=\{X \rightarrow x_2, v \rightarrow v_1\}$. The second sub-goal is $\varPi _1 \wedge \varSigma _2 \models _{\eta _2} \exists M,M_1. \psi '$ where $\varPi _1 \wedge \varSigma _2 {:}{:}{=}\, x_1\ne \mathsf{nil}\wedge x_2\ne \mathsf{nil}\wedge v_1 < v_2 \wedge x_2 \mapsto \{(\mathtt {next},\mathsf{nil}), (\mathtt {data},v_2)\}$ and $\psi '\ {:}{:}{=}\ M=\{v_1\} \cup M_1 \wedge v_1 \le M_1 \wedge lseg (x_2,M_1,\mathsf{nil},\emptyset )$. For this sub-goal, we apply the rule $\textsc {Slice}$, which generates a sub-goal where the rule $\textsc {Lemma}$ is applied first, using the same lemma, then the rule Slice is applied again, and finally the rule Lemma is applied with a lemma corresponding to the base rule of $lseg$, i.e., Eq. (3) (page II). This generates a quantifier instantiation $\eta _2=\{M \rightarrow \{v_1,v_2\}, M_1 \rightarrow \{v_2\}\}$. Then, $\eta _1 \cup \eta _2$ is extended with the constraints from the pure part of the lemma, i.e., $M=\{v\}\cup M_1 \wedge v_1 \le M_1$. Since $M \in \mathsf{dom}(\eta _1 \cup \eta _2)$, this extension has no effect. Finally, the rule $\textsc {Slice}$ checks that $\varPi _1 \wedge \mathtt{EQ}(\eta |_{\{M\}}) \models \varPi _2$ holds, where $\mathtt{EQ}(\eta |_{\{M\}})\ {:}{:}{=}\ M = \{v_1,v_2\}$ and $\varPi _2\ {:}{:}{=}\ v_2 \in M$. The last entailment holds, so the proof of validity is done.

The following theorem states the correctness of the proof rules. Moreover, since we assume a finite set of lemmas, and every application of a lemma L removes at least one spatial atom from $\varphi _1$ (the atoms matched to ${ root}(L)$), the termination of the applications of the rule $\textsc {Lemma}$ is guaranteed.

Theorem 4

Let $\varphi _1$ and $\exists \vec {X}.\varphi _2$ be two formulas such that $\vec {X}$ contains only data variables. If $\varphi _1 \models _{\eta } \exists \vec {X}.\varphi _2$ for some $\eta$, then $\varphi _1\Rightarrow \exists \vec {X}.\varphi _2$.

7 Experimental Results

We have extended the tool spen [25] with the proof strategy proposed in this paper. The entailments are written in an extension of the SMTLIB format used in the competition SL-COMP’14 for separation logic solvers. It provides as output SAT, UNSAT or UNKNOWN, and a diagnosis for all these cases.

The solver starts with a normalization step, based on the boolean abstractions described in [11], which saturates the input formulas with (dis)equalities between location variables implied by the semantics of separating conjunction. The entailments of data constraints are translated into satisfiability problems in the theory of integers with uninterpreted functions, discharged using an SMT solver dealing with this theory.

We have experimented the proposed approach on two sets of benchmarks⁶:

• RDBI: verification conditions for proving the correctness of iterative procedures (delete, insert, search) over recursive data structures storing integer data: sorted lists, binary search trees (BST), AVL trees, and red black trees (RBT).

• SL-COMP’14: problems in the SL-COMP’14 benchmark, without data constraints, where the inductive definitions are syntactically compositional.

Table 2. Experimental results on benchmark RDBI

Table 2 provides the experiment results⁷ for RDBI. The column #VC gives the number of verification conditions considered for each procedure. The column Lemma provides statistics about the lemma applications as follows: #b and #r are the number of the applications of the lemmas corresponding to base resp. inductive rules, #c and #d are the number of the applications of the composition resp. derived lemmas, and #p is the number of predicates matched syntactically, without applying lemmas. Column $\Rightarrow _\mathbb {D}$ gives the number of entailments between data constraints generated by spen. Column Time- spen gives the “system” time spent by spen on all verification conditions of a function⁸ excepting the time taken to solve the data constraints by the SMT solver, which is given in the column Time-SMT.

Table 3 provides a comparison of our approach (column spen ) with the decision procedure in [11] (column spen -TA) on the same set of benchmarks from SL-COMP’14. The times of the two decision procedures are almost the same, which demonstrates that our approach, as an extension of that in [11], is robust.

Table 3. Experimental results on benchmark SL-COMP’14

8 Related Work

There have been many works on the verification of programs manipulating mutable data structures in general and the use of separation logic, e.g., [1–5, 7–11, 13–17, 21, 23, 26]. In the following, we discuss those which are closer to our approach.

The prover SLEEK [7, 17] provides proof strategies for proving entailments of SL formulas. These strategies are also based on lemmas, relating inductive definitions, but differently from our approach, these lemmas are supposed to be given by the user (SLEEK can prove the correctness of the lemmas once they are provided). Our approach is able to discover and synthesize the lemmas systematically, efficiently, and automatically.

The natural proof approach DRYAD [19, 22] can prove automatically the correctness of programs against the specifications given by separation logic formulas with inductive definitions. Nevertheless, the lemmas are still supposed to be provided by the users in DRYAD, while our approach can generate the lemmas automatically. Moreover, DRYAD does not provide an independent solver to decide the entailment of separation logic formulas, which makes difficult to compare the performance of our tool with that of DRYAD. In addition, the inductive definitions used in our paper enable succinct lemmas, far less complex than those used in DRYAD, which include complex constraints on data variables and the magic wand.

The method of cyclic proofs introduced by [5] and extended recently in [9] proves the entailment of two SL formulas by using induction on the paths of proof trees. They are not generating the lemma, but the method is able to (soundly) check intricate lemma given by the user, even ones which are out of the scope of our method, e.g., lemmas concerning the predicate RList which is defined by unfolding the list segments from the end, instead of the beginning. The cyclic proofs method can be seen like a dynamic lemma generation using complex reasoning on proof trees, while our method generates lemma statically by simple checks on the inductive definitions. We think that our lemma generator could be used in the cyclic proof method to cut proof trees.

The tool SLIDE [14, 15] provides decision procedures for fragments of SL based on reductions to the language inclusion problem of tree automata. Their fragments contain no data or size constraints. In addition, the EXPTIME lower bound complexity is an important obstacle for scalability. Our previous work [11] introduces a decision procedure based on reductions to the membership problem of tree automata which however is not capable of dealing with data constraints.

The tool GRASShopper [21] is based on translations of SL fragments to first-order logic with reachability predicates, and the use of SMT solvers to deal with the latter. The advantage is the integration with other SMT theories to reason about data. However, this approach considers a limited class of inductive definitions (for linked lists and trees) and is incapable of dealing with the size or multiset constraints, thus unable to reason about AVL or red-black trees.

The truncation point approach [13] provides a method to specify and verify programs based on separation logic with inductive definitions that may specify truncated data structures with multiple holes, but it cannot deal with data constraints. Our approach can also be extended to cover such inductive definitions.

9 Conclusion

We proposed a novel approach for automating program proofs based on Separation Logic with inductive definitions. This approach consists of (1) efficiently checkable syntactic criteria for recognizing inductive definitions that satisfy crucial lemmas in such proofs and (2) a novel proof strategy for applying these lemmas. The proof strategy relies on syntactic matching of spatial atoms and on SMT solvers for checking data constraints. We have implemented this approach in our solver spen and applied it successfully to a representative set of examples, coming from iterative procedures for binary search trees or lists.

In the future, we plan to investigate extensions to more general inductive definitions by investigating ideas from [9, 22] to extend our proof strategy. From a practical point of view, apart from improving the implementation of our proof strategy, we plan to integrate it into the program analysis framework Celia [6].