The Trojan Problem from a Hamiltonian Perturbative Perspective

Abstract

The study of the Trojan problem (i.e. the motion in the vicinity of the equilateral Lagrangian points L ₄ or L ₅) has a long history in the literature. Starting from a representation of the Elliptic Restricted 3-Body Problem in terms of modified Delaunay variables, we propose a sequence of canonical transformations leading to a Hamiltonian decomposition in the three degrees of freedom (fast, synodic and secular). From such a decomposition, we introduce a model called the ‘basic Hamiltonian’ H _b , corresponding to the part of the Hamiltonian independent of the secular angle. Averaging over the fast angle, the 〈H _b 〉 turns to be an integrable Hamiltonian, yet depending on the value of the primary’s eccentricity e′. This allows to formally define action-angle variables for the synodic degree of freedom, even when e′ ≠ 0. In addition, we introduce a method for locating the position of secondary resonances between the synodic libration frequency and the fast frequency, based on the use of the normalized 〈H _b 〉. We show that the combination of a suitable normalization scheme and the representation by the H _b is efficient enough so as to allow to accurately locate secondary resonances as well as higher order resonances involving also the very slow secular frequencies.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent years, the equilateral Lagrangian points L ₄ and L ₅ have become the subject of several mission proposals, as a privileged position for solar observatories (see Gopalswamya et al. 2011 and references therein). While these studies show the high feasibility of a mission towards the equilateral points, a deep understanding of the Trojan dynamics (i.e. the motion in the vicinity of the equilateral Lagrangian points) is mandatory for the success of such missions.

From a theoretical point of view, many studies faced the problem of the Trojan motion by using the circular approximation of the Restricted 3-Body Problem (CR3BP). In this framework, the linear stability around L ₄ or L ₅ is guaranteed for values of the mass parameter $\mu \leq \mu _{R} = \frac{27-\sqrt{621}} {54} \approx 0.0385$, known as the Routh criterion (Gascheau 1843). The linearized orbits, in the vicinity of L ₄ and L ₅, are given by the composition of two different oscillatory motions, with frequencies $\omega _{f} = 1 -\frac{27} {8} \mu + \mathcal{O}(\mu ^{2})$ and $\omega _{s} = \sqrt{\frac{27} {4} \mu } + \mathcal{O}(\mu )$, where the subscripts f and s stand for ‘fast’ and ‘synodic’ respectively. These two oscillations have very different timescales. On one hand, ω _f is approximately equal to 1, i.e. it gives an oscillation of period similar to the mean motion of the primary. On the other hand, ω _s is proportional to the square root of the mass parameter μ, which is a small parameter itself. Thus, the motion of the test particle can be decomposed in two different contributions (Murray and Dermott 1999): the slow motion, associated to a guiding center motion around the position of equilibrium, with period 2π∕ω _s (known as synodic libration), and the fast one, attributed to the short period motion of the particle around the guiding center.

Besides the 1:1 mean motion resonance between the primary and the Trojan object, there may exist secondary resonances, corresponding to commensurabilities between the fast and the synodic frequency of the type ω _f  ≈ nω _s , with n integer. These resonances generate periodic orbits forming n epicyclic oscillations (e.g. loops) while they accomplish one full synodic libration. The presence of the secondary resonances affects the quasiperiodic orbital solutions in terms of the two main frequencies ω _f and ω _s (e.g. Deprit and Delie 1965), as it gives rise to so-called critical terms, i.e., terms depending on a resonant combination of the angles. These resonant terms in the series require a special treatment (e.g. Garfinkel 1977). On the other hand, in the Trojan problem it can be shown that their effect on the slow (secular) motions is rather limited (Namouni 1999). Let us mention, finally, that the use of averaging techniques allows to simplify the study of the synodic librations by finding a simplified form of the equation of motion for the so-called critical argument $\tau =\lambda -\lambda '$, with λ, λ′ the mean longitude of the test particle and the primary, respectively.

Whereas the CR3BP may be a good first model for developing the theory of Trojan orbits, it clearly does not suffice to represent more realistic problems. As a natural extension, there exist several approximations to the analytical solution of the Trojan problem in the framework of the Elliptic Restricted 3-Body problem (ER3BP). This generalization brings new interesting features to the formulation. While most works on the CR3BP consider two time scales (associated to ω _f and ω _s ), in the ER3BP three times scales are necessary (Érdi 1977), associated to the fast, synodic and secular frequency. From the physical point of view, these three scales are associated to the epicyclic oscillation (fast, $\mathcal{O}(1)$), the libration around the libration center (synodic, $\mathcal{O}(\sqrt{\mu })$) and the slow precession of the perihelion of the orbit of the Trojan body (secular, $\mathcal{O}(\mu )$) (Érdi 1978).

In the present work, we obtain a Hamiltonian decomposition individualizing the three time scales, starting from the ER3BP. From this decomposition, we introduce a model called the ‘basic Hamiltonian’ H _b , representing only the fast and synodic d.o.f. of the elliptic problem. Averaging over the fast angle, the 〈H _b 〉 turns to be an integrable Hamiltonian, yet depending on the value of the primary’s eccentricity e′. From the latter, we can define action-angle variables for the synodic degree of freedom, even when e′ ≠ 0. We introduce a method, based on the use of the normalized 〈H _b 〉, for locating the position of the secondary resonances between the synodic libration frequency and the fast frequency. We show that the H _b normalized under a suitable scheme is efficient enough to accurately locate both secondary resonances and higher order resonances involving also the secular frequency.

2 The Basic Hamiltonian H _b

We start the construction of the H _b from the Hamiltonian corresponding to the planar ER3BP.

$$\displaystyle{ H_{ell} =\, \frac{\|\mathbf{p}\|^{2}} {2} -\frac{1} {\|\mathbf{r}\|} -\mathcal{G}m'\left (\frac{1} {\varDelta } -\frac{1} {\|\mathbf{r}\|} -\frac{\mathbf{r} \cdot \mathbf{r}'} {\|\mathbf{r}'\|^{3}} \right )\, }$$

(1)

where r′ and r are the heliocentric position vectors for the planet and for the massless body, respectively, $\varDelta =\| \mathbf{r} -\mathbf{r}'\|$, $\mathbf{p} =\dot{ \mathbf{r}}$ and $\mathcal{G}m' =\mu$. We introduce modified Delaunay variables (x, y, λ, ϖ), independent of the mass parameter μ (Brown and Shook 1933; Morais 2001), given by

$$\displaystyle{ x = \sqrt{a} - 1\,\quad \lambda \,\quad y = \sqrt{a}\left (\sqrt{1 - e^{2}} - 1\right )\,\quad \varpi \, }$$

(2)

where λ, ϖ, a and e are the mean longitude, longitude of the pericenter, major semiaxis and eccentricity of the orbit of the Trojan body (primed symbols correspond to the primary). The Hamiltonian (1) in the new variables reads

$$\displaystyle{ H_{ell} = - \frac{1} {2(1 + x)^{2}} + I -\mu R(x,y,\lambda,\varpi,\lambda ';\varpi ',e') }$$

(3)

where we introduce a ‘dummy’ action variable I conjugate to λ′, and λ′ = nt. The present expression of the Hamiltonian corresponds to an autonomous system of 3 d.o.f.

For the study of the Trojan dynamics, we define two new angles. The angle $\tau =\lambda -\lambda '$ is the resonant angle corresponding to the 1:1 MMR resonance, with value $\tau =\pi /3$ at the Lagrangian point L ₄. The angle $\delta \varpi =\varpi -\varpi '$ expresses the relative position of the pericenter of the Trojan body from the pericenter of the planet. We introduce these new angles through a generating function S ₂ depending on the old angles (λ, λ′, ϖ) and the new actions (X ₁, X ₂, X ₃),

$$\displaystyle{ S_{1} = (\lambda -\lambda ')X_{1} +\lambda 'X_{2} + (\varpi -\varpi ')X_{3}\, }$$

(4)

yielding the following transformation rules

$$\displaystyle{ \tau =\lambda -\lambda '\,\quad \tau _{2} =\lambda '\,\quad \delta \varpi =\varpi -\varpi '\,\quad x = X_{1}\,\quad I = X_{2} - X_{1}\,\quad y = X_{3}. }$$

(5)

We keep the old notation for all variables involved in an identity transformation (X ₁ = x, τ ₂ = λ′, X ₃ = y). The Hamiltonian then reads:

$$\displaystyle{ H_{ell} = - \frac{1} {2(1 + x)^{2}} - x + X_{2} -\mu R(x,y,\tau,\delta \varpi,\lambda ';e',\varpi '). }$$

(6)

This expression can be recast under the form

$$\displaystyle{ H_{ell} =\langle H\rangle + H_{1} }$$

(7)

where

$$\displaystyle{ \langle H\rangle = - \frac{1} {2(1 + x)^{2}} - x + X_{2} -\mu \langle R\rangle (\tau,\delta \varpi,x,y;e',\varpi ') }$$

(8)

and

$$\displaystyle{ H_{1} = -\mu \tilde{R}(\tau,\delta \varpi,x,y,\lambda ';e',\varpi ')\, }$$

with

$$\displaystyle{ \langle R\rangle = \frac{1} {2\pi }\int _{0}^{2\pi }R\text{d}\lambda ',\ \ \ \ \tilde{R} = R -\langle R\rangle \ . }$$

The action X ₂ is an integral of motion under the Hamiltonian flow of 〈H _ell 〉. Thus, 〈H _ell 〉 represents a system of two d.o.f. We call position of the forced equilibrium (τ ₀, δ ϖ ₀, x ₀, y ₀) the solution of the system of equations

$$\displaystyle{ \dot{\tau }= \frac{\partial \langle H\rangle } {\partial x} = 0,\ \ \ \dot{\delta \varpi } = \frac{\partial \langle H\rangle } {\partial y} = 0,\ \ \ \dot{x} = -\frac{\partial \langle H\rangle } {\partial \tau } = 0,\ \ \ \dot{y} = -\frac{\partial \langle H\rangle } {\partial \delta \varpi } = 0\ \ . }$$

(9)

We find

$$\displaystyle{ (\tau _{0},\delta \varpi _{0},x_{0},y_{0}) =\big (\pi /3,\pi /3,0,\sqrt{1 - e'^{2}} - 1\big)\ . }$$

(10)

Let us note that the equilibrium point given by (10) does not represent a fixed point in the synodic frame of reference, as in the circular case, but a short-period epicyclic loop around L ₄, corresponding to a fixed ellipse of eccentricity e = e′ in the inertial frame.

We now introduce local action-angle variables around the point of forced equilibrium. To this end, we consider the ‘shift of center’ canonical transformation given by¹:

$$\displaystyle{ v = x - x_{0},\ \ u =\tau -\tau _{0},\ \ Y = -(W^{2} + V ^{2})/2,\ \ \phi =\arctan (V,W) }$$

(11)

where

$$\displaystyle{ V = \sqrt{-2y}\sin \delta \varpi -\sqrt{-2y_{0}}\sin \delta \varpi _{0},\ \ \ \ W = \sqrt{-2y}\cos \delta \varpi -\sqrt{-2y_{0}}\cos \delta \varpi _{0}\ \, }$$

where Y is defined negative so as to keep the canonical structure with respect to ϕ. Re-organising terms, the Hamiltonian (6) takes the form:

$$\displaystyle\begin{array}{rcl} H_{ell}& =& - \frac{1} {2(1 + v)^{2}} - v + X_{2} -\mu \left (\mathcal{F}^{(0)}(u,\lambda '-\phi,v,Y;e',\varpi ')\right. \\ & & \left.+\mathcal{F}^{(1)}(u,\phi,\lambda ',v,Y;e',\varpi ')\right ) {}\end{array}$$

(12)

where $\mathcal{F}^{(0)}$ contains terms depending on the angles λ′ and ϕ only through the difference λ′ −ϕ, and $\mathcal{F}^{(1)}$ contains terms dependent on non-zero powers of e′. The part of the Hamiltonian corresponding to $\mathcal{F}^{(0)}$ can be formally reduced to a system of 2 d.o.f. through the generating function

$$\displaystyle{ S_{2}(u,\lambda ',\phi,Y _{u},Y _{s},Y _{p}) = uY _{u} + (\lambda '-\phi )Y _{f} +\phi Y _{p} }$$

(13)

yielding

$$\displaystyle{ \phi _{u} = u\,\quad \phi _{f} =\lambda ' -\phi \,\quad \phi _{p} =\phi \,\quad v = Y _{u}\,\quad X_{2} = Y _{f}\,\quad Y = Y _{p} - Y _{f}. }$$

(14)

The subscripts ‘f’ and ‘p’ stand for ‘fast’ and ‘proper’ respectively. As before, we keep the old notation for the variables transforming by the identity $\phi _{u} = u,\phi _{p} =\phi$, and Y _u  = v, except for the action Y _f  ≡ X ₂. The Hamiltonian (12) in the new canonical variables reads

$$\displaystyle\begin{array}{rcl} H_{ell}& =& \,- \frac{1} {2(1 + v)^{2}} - v + Y _{f} -\mu \mathcal{F}^{(0)}(v,Y _{ p} - Y _{f},u,\phi _{f};e',\varpi ') \\ & & \,-\mu \mathcal{F}^{(1)}(v,Y _{ p} - Y _{f},u,\phi _{f},\phi;e',\varpi ')\ \ . {}\end{array}$$

(15)

Collecting terms linear in (Y _p − Y _f ), we find:

$$\displaystyle{ \omega _{f} \equiv \dot{\phi _{f}} = \frac{\partial H_{ell}} {\partial Y _{f}} = 1 - 27\mu /8 + \mathcal{O}(\mu ^{2})\ldots,\ \ \ g \equiv \dot{\phi }= \frac{\partial H_{ell}} {\partial Y _{p}} = 27\mu /8 + \mathcal{O}(\mu ^{2})\ldots \ \ \ }$$

(16)

We identify ω _f and g as the short-period and secular frequencies, respectively, of the Trojan body. Therefore, the set of variables constructed in (13) allows to separate the three time-scales by the corresponding 3 d.o.f. in the Hamiltonian, and it allows to consider various ‘levels’ of perturbation. We call basic model the one of Hamiltonian

$$\displaystyle{ H_{b} = - \frac{1} {2(1 + v)^{2}} - v + Y _{f} -\mu \mathcal{F}^{(0)}(v,Y _{ p} - Y _{f},u,\phi _{f};e',\varpi ')\ \ . }$$

(17)

The total Hamiltonian takes the form $H_{ell} = H_{b} + H_{sec}$, where

$$\displaystyle{ H_{sec} = -\mu \mathcal{F}^{(1)}(v,Y _{ p} - Y _{f},u,\phi _{f},\phi;e',\varpi ') }$$

(18)

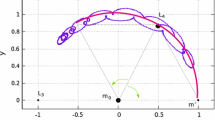
contains terms of at least order $\mathcal{O}(e'\,\mu )$. Figure 1 summarizes the physical meaning of the action-angle variables (ϕ _f , u, ϕ, Y _f , v, Y _p ).

Fig. 1

Schematic representation of the physical meaning of the action-angle variables used for the H _ell in Eq. (15). The plane (u, v) corresponds to the ‘synodic’ motion of the Trojan body. Under the Hamiltonian H _b , the phase portrait can be represented by a Poincaré section corresponding to every time when the angle ϕ _f accomplishes a full cycle. The left panel shows schematically the form of the projection of this section on the plane (u, v). The central point P represents a stable fixed point corresponding to the short-period periodic orbit around L4. The orbit has frequency ω _f , while its amplitude increases monotonically with Y _f . The forced equilibrium corresponds to u ₀ = 0, Y _f  = 0. The point P, however, has in general a shift to positive values u ₀ > 0 for proper eccentricities larger than zero [see later Eq. (24)]. Far from resonances, the invariant curves around P are labeled by a constant action variable J _s , and its associated angle (phase of the oscillation) ϕ _s . Resonances, and their island chains correspond to rational relations between the frequencies ω _f and ω _s . Within the resonant islands, J _s is no longer preserved, but we have, instead, the preservation of a resonant integral J _s, res . The plane (W, V ) (right panel) depicts the evolution of the Trojan body’s eccentricity vector under the Hamiltonian H _b . The motion of the endpoint of the eccentricity vector can be decomposed to a circulation around the forced equilibrium, with angular frequency g, and a fast (of frequency ω _f ) ‘in-and-out’ oscillation with respect to a circle of radius e _p , of amplitude which is of order $\mathcal{O}(Y _{f})$. Under H _b alone, the quantities Y _p , J _s , or Y _p , J _s, res are quasi-integrals for all the regular orbits. Furthermore, all extra terms with respect to H _b in the Hamiltonian (6) depend on the slow angles ϕ. Thus, all these terms can only slowly modulate the dynamics under H _b , and this modulation can produce a long-term drift of the values of (Y _p , J _s ), or Y _p , J _s, res

In a first approximation, the quasi-integral of the proper eccentricity (Érdi 1996) can be defined as

$$\displaystyle{ e_{p,0} = \sqrt{V ^{2 } + W^{2}} = \sqrt{-2Y}\ . }$$

(19)

However, Y is subject to fast variations due to its dependence on Y _f $\omega _{f} \sim \mathcal{O}(1)$. The time variations of Y _f become particularly important when one of the following two conditions holds: i) e′ < μ, or ii) the orbit of the Trojan body is subject to a low-order resonance. On the other hand, since ϕ is ignorable, Y _p remains an exact integral of the Hamiltonian (17) even in the cases (i) or (ii). We thus adopt the following definition of the proper eccentricity:

$$\displaystyle{ e_{p} = \sqrt{-2Y _{p}}\ . }$$

(20)

Since $\mathcal{F}^{(1)}$ is at least $\mathcal{O}(e')$, $\dot{Y _{p}} = \mathcal{O}(e')$ under the full Hamiltonian (15). Thus, e _p remains a good quasi-integral for not very high values of the primary’s eccentricity (Páez and Efthymiopoulos 2015).

A second averaging over the fast angle ϕ _f yields the Hamiltonian

$$\displaystyle{ \overline{H_{b}}(u,v;Y _{f},Y _{p},e',\varpi ') = - \frac{1} {2(1 + v)^{2}} - v + Y _{f} -\mu \overline{\mathcal{F}^{(0)}}(u,v,Y _{p} - Y _{f};e',\varpi ')\ \ }$$

(21)

with

$$\displaystyle{ \overline{\mathcal{F}^{(0)}} = \frac{1} {2\pi }\int _{0}^{2\pi }\mathcal{F}^{(0)}\text{d}\phi _{ f}\ . }$$

The Hamiltonian $\overline{H_{b}}(u,v;Y _{f},Y _{p},e',\varpi )$ represents a system of one degree of freedom, all three quantities Y _f , Y _p , e′ serving now as parameters, i.e. constants of motion under the dynamics of $\overline{H_{b}}$. The Hamiltonian $\overline{H_{b}}$ describes the synodic (guiding-center) motions of the Trojan body, with the additional point that, since it depends on e′, it does not correspond to the averaged (over fast angles) Hamiltonian of the circular RTBP. Thus, it allows to find an integrable approximation to synodic motions even when e′ ≠ 0.

The equilibrium point (u ₀, v ₀) given by

$$\displaystyle{ \frac{\partial \overline{\mathcal{F}^{(0)}}} {\partial u} = \frac{\partial \overline{\mathcal{F}^{(0)}}} {\partial v} = 0 }$$

corresponds to a short-period periodic orbit of the Hamiltonian H _b around the forced equilibrium point. We define the action variable

$$\displaystyle{ J_{s} = \frac{1} {2\pi }\int _{C}(v - v_{0})\text{d}(u - u_{0}) }$$

(22)

where the integration is over a closed invariant curve C around (u ₀, v ₀) and ‘s’ stands for ‘synodic’ (see Fig. 1). The angular variable ϕ _s , conjugate to J _s , evolves in time according to the synodic frequency ω _s given by [see Eq. (28)]

$$\displaystyle{ \omega _{s} =\dot{\phi } _{s} = -\sqrt{\frac{27\mu } {4}} +\ldots }$$

(23)

Some manipulation of Eq. (21) allows to find a first order approximation to the values of the frequencies ω _s and g. We deduce the shift in position, with respect to L4, of the fixed point of $\overline{\mathcal{F}^{(0)}}$, corresponding to the short-period orbit around L4 (Namouni and Murray 2000). The shift is given by $u_{0} =\tau _{0} -\pi /3$, where τ ₀ is the solution of $\partial \overline{\mathcal{F}^{(0)}}/\partial \tau = 0$. We find:

$$\displaystyle{ u_{0} = \frac{29\sqrt{3}} {24} e_{p,0}^{2}+\ldots }$$

(24)

where the error is of order 4 in the eccentricities e _p, 0, e′.

We introduce the following canonical transformation to analyze the motion around the position of the periodic orbit given by u ₀, v ₀

$$\displaystyle{ S_{3}(\phi _{f},u,\phi,V,J_{f},J_{p}) = (u - u_{0})V +\phi _{f}\,J_{f} +\phi J_{p}\, }$$

(25)

where, in terms of the new actions, we have $u_{0} = \frac{29\sqrt{3}} {12} \,(J_{f} - J_{p})$, yielding

$$\displaystyle{ v = V \,\:\:\:\:Y _{f} = J_{f}\,\quad Y _{p} = J_{p}\,\quad \delta u = u - u_{0}\,\quad q_{f} =\phi _{f} -\frac{29\sqrt{3}} {12} \,V \quad q_{p} =\phi +\frac{29\sqrt{3}} {12} \,V . }$$

Since $\overline{H}_{b}$ in Eq. (21) does not explicitly depend on the angles q _p and q _f , the conjugated actions J _p  = Y _p and J _f  = Y _f remain integrals of motion. We keep the notation for Y _f , Y _p and v. Taylor-expanding $\overline{H}_{b}$, around u ₀ up to terms of order $\mathcal{O}(\delta u^{2})$, we find (up to terms of first order in μ and second order in the eccentricities):

$$\displaystyle\begin{array}{rcl} \overline{H}_{b,ell}& =& -\frac{1} {2} + Y _{f} -\mu \left (\frac{27} {8} +\ldots \right )\frac{e_{p,0}^{2}} {2} -\frac{3} {2}x^{2} +\ldots \\ & & -\mu \left (\frac{9} {8} + \frac{63e'^{2}} {16} + \frac{129e_{p,0}^{2}} {64} +\ldots \right )\delta u^{2}+\ldots {}\end{array}$$

(26)

where $\frac{e_{p,0}^{2}} {2} = Y _{f} - Y _{p}$. Since Y _f is of order $\mathcal{O}(\mu )$, up to terms linear in μ the part

$$\displaystyle{ H_{syn} = -\frac{3} {2}v^{2} -\mu \left (\frac{9} {8} + \frac{63e'^{2}} {16} + \frac{129e_{p}^{2}} {64} +\ldots \right )\delta u^{2} }$$

(27)

defines a harmonic oscillator for the synodic degree of freedom. The corresponding synodic frequency is

$$\displaystyle{ \omega _{s} = -\sqrt{6\mu \left (\frac{9} {8} + \frac{63e'^{2}} {16} + \frac{129e_{p}^{2}} {64} +\ldots \right )}\ . }$$

(28)

On the other hand, the secular frequency is given by $g = \partial \overline{H}_{b}/\partial Y _{p}$. Assuming a harmonic solution $\delta u =\delta u_{0}\cos (\omega _{s}t +\phi _{0s})$, and averaging over the synodic period $\langle \delta u^{2}\rangle =\delta u_{0}^{2}/2$, we find

$$\displaystyle{ g =\mu \left (\frac{27} {8} + \frac{129} {64} \delta u_{0}^{2}+\ldots \right )\ \, }$$

(29)

completing the estimation of the frequencies.

2.1 Secondary Resonances in the ER3BP

The Trojan domain describes itself a resonant regime, defined by the 1:1 commensurability of the mean motions of the Trojan body and the primary. In addition, within this domain, we can find secondary resonances of the form

$$\displaystyle{ m_{f}\omega _{f} + m_{s}\omega _{s} + mg = 0 }$$

(30)

with m _f , m _s , m integers. The most important resonances are those involving low order conmensurabilities between ω _f and ω _s , which exist also in the pCR3BP (e′ = 0). They are of the form

$$\displaystyle{ \omega _{f} + n\omega _{s} = 0 }$$

(31)

with n = m _s . We refer to (31), as the ‘1:n’ resonance. For m _f  = 1 and μ in the range 0. 001 ≤ μ ≤ 0. 01, n is in the range 4 ≤ n ≤ 12. In the frequency space (ω _f , ω _s , g), the relations (31) represent planes normal to the plane (ω _f , ω _s ) which intersect each other along the g–axis. We refer to the resonances with m ≠ 0 as ’transverse’, since they intersect tranversally such planes. In the numerical examples below, we use the notation (m _f , m _s , m), for the integers of the resonant condition (30).

Figure 2 presents stability maps produced by the computation of the chaotic indicator Ψ FLI (Froeschlé et al. 2000), in the space of proper elements e _p, 0 [given in Eq. (19)] and $\varDelta u = u - u_{0}$, with u ₀ given in Eq. (24), (for a conspicuous discussion of the initial conditions, see Páez and Efthymiopoulos 2015). In color scale, we differentiate chaotic orbits (yellow) from regular orbits (dark purple). For the different combinations of μ and e′ considered, we can distinguish the structures of the resonances 1:m _s and (1,m _s ,m), for m _s  = 6, 7, 8, 10 and m = ±1, ±2, 3. A validation of the resonant nature of the orbits within these structures is done by means of Frequency Analysis (Laskar 2004).

Fig. 2

Stability maps in terms of the FLI chaotic indicator. Light colors (yellow) correspond to chaotic orbits, while dark colors (dark purple) correspond to regular orbits. The maps show different resonances appearing for different combinations of physical parameters: μ = 0. 0016 and e′ = 0 (a ), μ = 0. 0024 and e′ = 0. 06 (b ), μ = 0. 0031 and e′ = 0. 04 (c ), μ = 0. 0016 and e′ = 0. 02 (d )

3 The Normalized Basic Hamiltonian 〈H _b 〉

As already emphasized, the Trojan motion in the ER3BP has three well separated temporal scales. The most basic form of Hamiltonian normalization stems from averaging the Hamiltonian over the fast angles. Independently of the formalism used, what remains after such averaging gives the synodic motion around the libration center. However, the Hamiltonian of the ER3BP has a real singularity corresponding to close encounters of the massless body with the primary m′. This singularity corresponds to a = a′, $\tau =\lambda -\lambda ' = 0$ and it is inherited by the H _b . The key remark is that any polynomial series expansion of the equations of motion (or the Hamiltonian) with respect to τ around a fixed value is convergent in a disk of radius equal to the distance between the fixed point and the singularity. In the literature, it has been common to consider such polynomial expansions around the position of equilibrium ($\tau _{L_{4},L_{5}} = \pm \frac{\pi }{3}$). Due to the asymmetry of the librations (Érdi 1996), it is easy to see that the above limited convergence affects severely the representation of the orbits mainly in the opposite direction to the primary.

Following Páez and Locatelli (2015), we average the H _b over the short period without making expansions affected by the singular behavior of the Hamiltonian at $\vert \tau -\pi /3\vert =\pi /3$. We start by expressing the basic model H _b in variables appropriate for introducing the normalization scheme of Páez and Locatelli (2015). Hence, the synodic degree of freedom is re-expressed by the variables

$$\displaystyle{ x = v + x_{0},\quad \tau = u +\tau _{0}\ \, }$$

(32)

where x ₀ and τ ₀ are given in Eq. (10). We introduce new canonical pairs, though the transformation

$$\displaystyle{ \mathcal{S}_{3} = (Y _{f} - Y _{p})\theta _{1} + Y _{p}\theta _{2} + x\theta _{3}\, }$$

(33)

yielding

$$\displaystyle{ \mathcal{Y} = Y _{f} - Y _{p}\,\quad Y _{p} =\, Y _{2}\,\quad x = Y _{3}\,\quad \theta _{1} =\phi _{f}\,\quad \theta -\theta _{1} =\phi \,\quad \theta _{3} =\tau . }$$

(34)

Keeping the previous notation for Y _p , x, ϕ _f , τ, the basic model H _b reads

$$\displaystyle{ H_{b} = - \frac{1} {2(1 + x)^{2}} - x + \mathcal{Y} + Y _{p} -\mu \mathcal{F}^{(0)}(x,\mathcal{Y},\tau,\phi _{ f};e')\ . }$$

(35)

In terms of these variables, the dependence of H _b on τ is of the form $\frac{\cos ^{k_{1}}\tau } {(2-2\cos \tau )^{\,j/2}}$ or $\frac{\cos ^{k_{2}}\tau } {(2-2\cos \tau )^{\,j/2}}$, $j = 2n - 1$ with k ₁, k ₂ and n integers. Additionally, we express the Hamiltonian in terms of modified Poincaré variables,

$$\displaystyle{ x\,\quad \tau \,\quad \xi =\, \sqrt{2\mathcal{Y}}\cos \phi _{f}\,,\quad \eta =\, \sqrt{2\mathcal{Y}}\sin \phi _{f}\,\ . }$$

(36)

The new expression for the Hamiltonian reads

$$\displaystyle{ H_{b}(x,\tau,\xi,\eta,Y _{p}) = - \frac{1} {2(1 + x)^{2}} - x + Y _{p} + \frac{\xi ^{2} +\eta ^{2}} {2} -\mu \mathcal{F}^{(0)}(\tau,x,\xi,\eta;Y _{ p},e')\ . }$$

(37)

Finally, we expand the Hamiltonian in terms of every variable except τ, obtaining

$$\displaystyle\begin{array}{rcl} & & H_{b}(x,\tau,\xi,\eta,Y _{p}) = -x +\sum _{ i=0}^{\infty }\,(-1)^{i-1}(i + 1)\,\frac{x^{i}} {2} \, +\, \frac{\xi ^{2} +\eta ^{2}} {2} \, +\, Y _{p} \\ & & \phantom{H_{b}(x,\tau,\xi,\eta,}+\,\mu \sum _{\begin{array}{c}m_{1},m_{2},m_{3} \\ k_{1},k_{2},k_{3},j \end{array}}a_{m_{1},m_{2},m_{3},k_{1},k_{2},j}\,e'^{k_{3} }x^{m_{1} }\,\xi ^{m_{2} }\,\eta ^{m_{3} }\,\cos ^{k_{1} }(\tau )\,\sin ^{k_{2} }(\tau )\,\beta ^{j}(\tau )\ \,{}\end{array}$$

(38)

where the $a_{m_{1},m_{2},m_{3},k_{1},k_{2},j}$ are constant coefficients and $\beta (\tau ) = \frac{1} {\sqrt{2-2\cos \tau }}$. The Hamiltonian H _b in (38) corresponds to the ‘zero-th’ step in the normalizing scheme, i.e., before any normalization. This is denoted as H ^(1, 0).

3.1 Normalization Scheme

The normalizing algorithm defines a sequence of Hamiltonians by an iterative procedure. Let us first introduce the following definition

Definition 1

A generic function g = g(x, ξ, τ, η) belongs to the class $\mathcal{P}_{l,s}\,$, if its expansion is of the type:

$$\displaystyle{ \sum _{2m_{1}+m_{2}+m_{3}=l}\ \sum _{{ k_{1}+k_{2}\leq l+4s-3 \atop j\leq 2l+7s-6} }c_{m_{1},m_{2},m_{3},k_{1},k_{2},j}\,\mu ^{s}\,\rho ^{m_{1} }\xi ^{m_{2} }\eta ^{m_{3} }\,(\cos \tau )^{k_{1} }(\sin \tau )^{k_{2} }\,\big(\beta (\tau )\big)^{j}\, }$$

where the real coefficients $c_{m_{1},m_{2},m_{3},k_{1},k_{2},j}$ gather also the dependence on the primary’s eccentricity e′.

At a generic normalizing step (r ₁,r ₂), the expansion of the Hamiltonian is given by

$$\displaystyle\begin{array}{rcl} & & H^{(r_{1},r_{2})}(x,\xi,\tau,\eta,Y _{ p}) =\, Y _{p} + \frac{\xi ^{2} +\eta ^{2}} {2} +\sum _{l\geq 4}Z_{l}^{(0)}\left (x,(\xi ^{2} +\eta ^{2})/2\right ) \\ & & \phantom{H^{(r_{1},}} +\,\sum _{ s=1}^{r_{1}-1}\left (\sum _{ l=0}^{R_{2} }\mu ^{s}Z_{ l}^{(s)}\left (x,(\xi ^{2} +\eta ^{2})/2,\tau \right ) +\sum _{ l>R_{2}}\mu ^{r_{1} }f_{l}^{(r_{1},r_{2}-1;s)}(x,\xi,\eta,\tau )\right ) \\ & & \phantom{H^{(r_{1},}} +\,\sum _{ l=0}^{r_{2} }\mu ^{r_{1} }Z_{l}^{(r_{1})}(x,(\xi ^{2} +\eta ^{2})/2,\tau ) +\sum _{ l\geq r_{2}+1}\mu ^{r_{1} }f_{l}^{(r_{1},r_{2}-1;r_{1})}(x,\tau,\xi,\eta ) \\ & & \phantom{H^{(r_{1},}} +\,\sum _{ s>r_{1}}\sum _{l\geq 0}\mu ^{s}f_{ l}^{(r_{1},r_{2}-1;s)}(x,\tau,\xi,\eta )\ . {}\end{array}$$

(39)

All the terms Z _l ^(s) and $f_{l}^{(r_{1},r_{2};s)}$ appearing in (39) are produced by expansions including a finite number of monomials of the type given by the class $\mathcal{P}_{l,s}$. More specifically $Z_{l}^{(0)} \in \mathcal{P}_{l,0}\ \forall \ l \geq 4$, $Z_{l}^{(s)} \in \mathcal{P}_{l,s}\ \forall \ 0 \leq l \leq R_{2}\,,\ 1 \leq s < r_{1}\,$, $Z_{l}^{(r_{1})} \in \mathcal{P}_{l,r_{ 1}}\ \forall \ 0 \leq l < r_{2}\,$, $f_{l}^{(r_{1},r_{2}-1;r_{1})} \in \mathcal{P}_{l,r_{ 1}}\ \forall \ l \geq r_{2}\,$, $f_{l}^{(r_{1},r_{2}-1;s)} \in \mathcal{P}_{l,s}\ \forall \ l > R_{2}\,,\ 1 \leq s < r_{1}\,$ and $\forall \ l \geq 0,\ s > r_{1}\,$. We can distinguish the terms in normal form Z (i.e. the terms depending on ξ and η exclusively through $(\xi ^{2} +\eta ^{2})/2$), of order up to r ₁ and r ₂, from those that still keep a generic dependence on these variables.

The (r ₁, r ₂)th step of the algorithm formally defines the latter Hamiltonian $H^{(r_{1},r_{2})}$ by

$$\displaystyle{ H^{(r_{1},r_{2})} =\exp \left (\mathcal{L}_{\mu ^{ r_{1}}\chi _{r_{ 2}}^{(r_{1})}}\right )H^{(r_{1},r_{2}-1)}\ \, }$$

(40)

where the Lie series operator is

$$\displaystyle{ \exp \mathcal{L}_{\chi }\:\cdot = \mathbb{I}\: \cdot +(\mathcal{L}_{\chi }\:\cdot \:) + \frac{1} {2}(\mathcal{L}_{\chi }^{2}\:\cdot \:)+\ldots }$$

(41)

and

$$\displaystyle{ \mathcal{L}_{\chi }\equiv \{\:\cdot \:,\chi \}, }$$

(42)

is the Poisson bracket with χ. The generating function $\mu ^{r_{1}}\chi _{r_{ 2}}^{(r_{1})}$ is determined by solving the following homological equation with respect to the unknown $\chi _{r_{2}}^{(r_{1})} =\chi _{ r_{ 2}}^{(r_{1})}(x,\xi,\tau,\eta )$:

$$\displaystyle{ \mathcal{L}_{\mu ^{r_{1}}\chi _{r_{ 2}}^{(r_{1})}}Z_{2}^{(0)} + f_{ r_{2}}^{(r_{1},r_{2}-1;r_{1})} = Z_{ r_{2}}^{(r_{1})}\ \, }$$

(43)

where $Z_{r_{2}}^{(r_{1})}$ is the new term in the normal form, and Z ₂ ⁽⁰⁾ represents the kernel of the homological equation. By construction, the Hamiltonian produced at ever step inherits the structure presented in (39). From the latter, we point out that the splitting of the Hamiltonian in sub-functions of the form $\mathcal{P}_{l,s}$, organizes the terms in groups with the same order of magnitude μ ^s and total degree l∕2 (possibly semi-odd) in the variables x and $\mathcal{Y} = \frac{\xi ^{2}+\eta ^{2}} {2}$.

Let R ₁ and R ₂ be the maximum orders considered for the normalization scheme, thus the algorithm requires R ₁ ⋅ R ₂ normalization steps, constructing the finite sequence of Hamiltonians $H^{(1,0)} = H_{b},H^{(1,1)},\,\ldots,H^{(R_{1},R_{2})}$. We remark here that $H^{(r_{1}+1,0)} = H^{(r_{1},R_{2})}\,\forall \,1 \leq r_{1} \leq R_{1}$. Hence, the final Hamiltonian, reads

$$\displaystyle{ H^{(R_{1},R_{2})}(x,\xi,\tau,\eta,Y _{ p}) = Z^{(R_{1},R_{2})}\left (x, \frac{(\xi ^{2} +\eta ^{2})} {2},\tau,Y _{p}\right ) + R^{(R_{1},R_{2})}(x,\xi,\tau,\eta )\ \, }$$

(44)

where we distinguish the normal form $Z^{(R_{1},R_{2})}$ from the remainder $R^{(R_{1},R_{2})}$. While the dependence of $Z^{(R_{1},R_{2})}$ on x and τ remains generic, it depends on ξ and η only though the form $\frac{\xi ^{2}+\eta ^{2}} {2}$. Thus, we have

$$\displaystyle{ H^{(R_{1},R_{2})}(x,\tau,\mathcal{Y},\phi _{ f},Y _{p}) = Z^{(R_{1},R_{2})}\left (x,\tau,\mathcal{Y},Y _{ p}\right ) + R^{(R_{1},R_{2})}(x,\tau,\mathcal{Y},\phi _{ f})\ . }$$

(45)

The key remark is that ϕ _f becomes ignorable in the normal form and, therefore, $\mathcal{Y}$ becomes an integral of motion of $Z^{(R_{1},R_{2})}$. Then, the normal form can be viewed as a Hamiltonian of one d.o.f. depending on two constant actions $\mathcal{Y}$ and Y _p , i.e. $Z^{(R_{1},R_{2})}$ represents now a formally integrable dynamical system. In all subsequent computations, we fixed the values R ₁ = 2 and R ₂ = 4, corresponding to a second order expansion and truncation on the mass parameter μ and fourth order for the polynomial degree of ξ and η (second order expansion in the eccentricity e; note also that the expansion is of second order as well in the primary’s eccentricity e′). In the following, these normalization orders are shown to be sufficient for the normal form to provide a good representation of the original Hamiltonian in the domain of regular motions.

4 Application: Location of the Resonances by Means of the 〈H _b 〉

The obtention of a normal form by averaging the basic Hamiltonian allows to extract information of the resonant structure by pure analytical means. In this section, we focus on the use of the normal form approximation $Z^{(R_{1},R_{2})}$ in (45) for the computation of the values of the three main frequencies of motion. With these values, it is possible to locate the position of the most important resonances for a certain combination of physical parameters.

Consider an orbit with initial conditions as specified in terms of the two parameters Δ u and e _p, 0 as in the stability map of Fig. 2. The computation proceeds by the following steps.

• 1) We first evaluate the synodic frequency ω _s , i.e., the frequency of libration of the synodic variables τ and x. The normal form $Z^{(R_{1},R_{2})}$ leads to Hamilton’s equations:

  $$\displaystyle{ \frac{\text{d}x} {\text{d}t} = f(x,\tau;\mathcal{Y}) = -\frac{\partial Z^{(R_{1},R_{2})}} {\partial \tau } \ \ }$$

  (46)

  and

  $$\displaystyle{ \frac{\text{d}\tau } {\text{d}t} = g(x,\tau;\mathcal{Y}) = \frac{\partial Z^{(R_{1},R_{2})}} {\partial x} \ . }$$

  (47)

  For every orbit we can define the constant energy

  $$\displaystyle{ Z^{(R_{1},R_{2})}(x,\tau;\mathcal{Y},Y _{ p}) - Y _{p} \equiv \zeta ^{(R_{1},R_{2})}(x,\tau;\mathcal{Y}) = \mathcal{E}\ . }$$

  (48)

  Note that since Y _p appears only as an additive constant in $Z^{(R_{1},R_{2})}$, the function $\zeta ^{(R_{1},R_{2})}$ does not depend on Y _p . Also, according to (19) and (36), we have $\mathcal{Y} = \frac{e_{p,0}^{2}} {2}$. Then, for a fixed value of $\mathcal{E}$, if $\frac{\partial \zeta ^{(R_{1},R_{2})}} {\partial \tau } \neq 0$, we can express τ as an explicit function of x,

  $$\displaystyle{ \zeta ^{(R_{1},R_{2})}(x,\tau;\mathcal{Y}) = \mathcal{E}\quad \Longrightarrow\quad \tau =\tau (\mathcal{E},x;\mathcal{Y})\ . }$$

  (49)

  Thus, replacing in (46),

  $$\displaystyle{ \frac{\text{d}x} {\text{d}t} = f(x,\tau (\mathcal{E},x;\mathcal{Y});\mathcal{Y})\quad \Longrightarrow\quad \text{d}t = \frac{\text{d}x} {f(x,\tau (\mathcal{E},x;\mathcal{Y});\mathcal{Y})}\ \, }$$

  (50)

  by which we can derive an expression for the synodic period T _syn

  $$\displaystyle{ T_{syn} =\oint \frac{\text{d}x} {f(x,\tau (\mathcal{E},x;\mathcal{Y});\mathcal{Y})}\ \, }$$

  (51)

  and thus the synodic frequency is $\omega _{s} = \frac{2\pi } {T_{syn}}$. In practice, (49) is hard to invert analytically, and likewise, the integral (51) cannot be explicitly computed. We thus compute both expressions numerically on grids of points of the associated invariant curves on the plane (τ, x), or by integrating numerically (50) as a first order differential equation (we found that the latter method is more precise than the former).

• 2) We now compute the fast and secular frequencies ω _f , g. From Eq. (48), we find $\dot{\theta }= \frac{\partial \mathcal{Z}^{(R_{1},R_{2})}} {\partial Y _{p}} = 1$, implying $g = 1 -\omega _{f}$. To compute ω _f , we use the equation

  $$\displaystyle{ \omega _{f} =\, \frac{1} {T_{syn}}\int _{0}^{T_{syn} }\frac{\text{d}\phi _{f}} {\text{d}t} \,\text{d}t =\, \frac{1} {T_{syn}}\int _{0}^{T_{syn} }\frac{\partial Z^{(R_{1},R_{2})}(x,\tau;\mathcal{Y})} {\partial \mathcal{Y}} \,\text{d}t\ . }$$

  (52)

  Replacing (50) in (52), we generate an explicit formula for the fast frequency

  $$\displaystyle{ \omega _{f} = \frac{1} {T_{syn}}\oint \frac{1} {f(x,\tau (\mathcal{E},x;\mathcal{Y});\mathcal{Y})}\,\frac{\partial Z^{(R_{1},R_{2})}(x,\tau (\mathcal{E},x;\mathcal{Y});\mathcal{Y})} {\partial \mathcal{Y}} \,\text{d}x\ . }$$

  (53)

Both frequencies ω _f and ω _s are functions of the labels $\mathcal{E}$ and $\mathcal{Y}$, which, in the integrable normal form approximation, label the proper libration and the proper eccentricity of the orbits. In the normal form approach one has $e_{p,0} = e_{p} =$ const, implying $\mathcal{Y} = e_{p}^{2}/2$. If, as for the FLI maps in Fig. 2 (see Páez and Efthymiopoulos 2015), we fix a scanning line of initial conditions of the form $x_{in} = B\,u_{in} = B\,(\tau _{in} -\tau _{0})$, with B a constant, the energy $\mathcal{E}$, for fixed e _p , becomes a function of the initial condition u _in only. Thus, u _in represents an alternative label of the proper libration (Érdi 1978). With these conventions, all three frequencies become functions of the labels (u _in , e _p ). A generic resonance condition then reads

$$\displaystyle{ \varPhi _{m_{f},m_{s},m} = m_{f}\omega _{f}(e_{p},u_{in}) + m_{s}\omega _{s}(e_{p},u_{in}) + mg(e_{p},u_{in}) = 0\ . }$$

(54)

For fixed resonance vector (m _f , m _s , m), (54) can be solved by root-finding, thus specifying the position of the resonance in the plane of the proper elements (u _in , e _p ).

In order to test the accuracy of the above method, we compare the results of the analytical estimation with the position of the resonances extracted from the FLI map. Under the assumption that the local minimum of the FLI in the vicinity of a resonance gives a good approximation of the resonance center, we study the curves of the FLI Ψ as a function of the libration amplitude Δ u, for a fixed value of e _p, 0. The confirmation of the resonant nature of the candidate initial conditions is done by means of Frequency Analysis (Laskar 2004). By changing the value of e _p, 0 along the interval [0, 0. 1], we can depict the centers of the resonances on top of the FLI map.

Figure 3 shows an example of these computations, for the parameters μ = 0. 0024 and e′ = 0. 06. The normal form predictions are superposed as yellow lines upon the underlying the FLI stability map (panel (B), Fig. 2) and the resonant candidates extracted from the FLI maps denote the green curves. Due to the noise in the FLI curves, it is not possible to clearly extract the position of the resonance centers for all values of e _p, 0, while an analytic estimation (with varying levels of accuracy) is always possible. At any rate, in Fig. 3 we plot the values of the centers only in the cases when both methods provide clear results.

Fig. 3

Location of the center of different resonances by means of the normal form 〈H _b 〉 (yellow) and the minima of the FLI indicator (green), on top of the corresponding FLI stability map for μ = 0. 0024 and e′ = 0. 06

Table 1 summarizes the results for the location of the centers ($u_{\mathcal{Z}}$, u _Ψ ) and the relative errors ($\delta u_{in} = \frac{\vert u_{\mathcal{Z}}-u_{\varPsi }\vert } {u_{\varPsi }}$), on average, for the resonances shown in the figure. We can note that the level of approximation is very good for relatively low values of u _in , while the error in the predicted position of the resonance increases to a few percent for greater values. Nevertheless, we demonstrate the overall efficiency of the normal form approach in order to analytically determine the locus of resonances in the space of proper elements. More detailed presentations of the above methods will be given in forthcoming publication.

Table 1 Averaged values of $u_{\mathcal{Z}}$, u _Ψ and δ u _in for the resonances in Fig. 3 for μ = 0. 0024 and e′ = 0. 06