The Simulation Powers and Limitations of Hierarchical Self-Assembly Systems

Abstract

In this paper, we extend existing results about simulation and intrinsic universality in a model of tile-based self-assembly. Namely, we work within the 2-Handed Assembly Model (2HAM), which is a model of self-assembly in which assemblies are formed by square tiles that are allowed to combine, using glues along their edges, individually or as pairs of arbitrarily large assemblies in a hierarchical manner, and we explore the abilities of these systems to simulate each other when the simulating systems have a higher “temperature” parameter, which is a system wide threshold dictating how many glue bonds must be formed between two assemblies to allow them to combine. It has previously been shown that systems with lower temperatures cannot simulate arbitrary systems with higher temperatures, and also that systems at some higher temperatures can simulate those at particular lower temperatures, creating an infinite set of infinite hierarchies of 2HAM systems with strictly increasing simulation power within each hierarchy. These previous results relied on two different definitions of simulation, one (strong simulation) seemingly more restrictive than the other (standard simulation), but which have previously not been proven to be distinct. Here we prove distinctions between them by first fully characterizing the set of pairs of temperatures such that the high temperature systems are intrinsically universal for the lower temperature systems (i.e. one tile set at the higher temperature can simulate any at the lower) using strong simulation. This includes the first impossibility result for simulation downward in temperature. We then show that lower temperature systems which cannot be simulated by higher temperature systems using the strong definition, can in fact be simulated using the standard definition, proving the distinction between the types of simulation.

J. Hendricks, M.J. Patitz, and T.A. Rogers—Supported in part by National Science Foundation Grant CCF-1422152.

T.A. Rogers—This author’s research was supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1450079.

1 Introduction

In computational theory, a powerful and widely used tool for determining the relative powers of systems is simulation. For instance, in order to prove the equivalence (in terms of computational power) of Turing machines and various abstract models (such as tag systems, counter machines, cellular automata, and tile-based self-assembly models), systems have been developed in each which demonstrate their abilities to simulate arbitrary Turing machines, and vice versa. This has been used to prove that whatever can be computed by a system within one model can also be computed by a system in another. Additionally, the notion of a universal Turing machine is based upon the fact that there exist Turing machines which can simulate others.

The methods of simulation which are typically employed involve mappings of behaviors and states in one model or system to those in another, often following some “natural” mapping function, and also often in such a way that the simulation is guaranteed to generate the same final result as the simulated system, and maybe even some or all of its intermediate states. Nonetheless, there is usually no requirement that the simulator “do it the same way,” i.e. the dynamical behavior of the simulator need not mirror that of the simulated. For instance, as one Turing machine A simulates another, B, its head movements may be in a significantly different pattern than B’s since, for instance, it may frequently move to a special portion of the tape which encodes B’s transition table, then back to the “data” section.

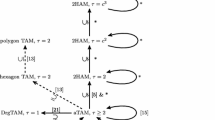
While such types of simulation can be informative when asking questions about the equivalence of computational powers of systems, oftentimes it is the behavior of a system which is of interest, not just its “output.” Self-assembling systems, which are those composed of large numbers of relatively simple components which autonomously combine to form structures using only local interactions, often fall into this category since the actual ways in which they evolve and build structures are of key importance. In this paper, we focus our attention on tile-based self-assembling systems in a model known as the 2-Handed Assembly Model (2HAM) [3], which is a generalization of the abstract Tile Assembly Model (aTAM) [19] in which the basic components are square tiles which are able to bind to each other when they possess matching glues on their edges. In the aTAM, assembly occurs as tiles autonomously combine, with one tile at a time attaching to a growing assembly. In the 2HAM, similar growth can occur, but it is possible for pairs of arbitrarily large assemblies (a.k.a. supertiles) to combine as well. Because the dynamical behaviors of these systems are of such importance, work in these models (e.g. [8, 9, 12, 13, 16, 20]) has turned to a notion of simulation developed within the domain of cellular automata, whose dynamical behaviors are also often of central importance. This notion of simulation, called intrinsic universality (see [1, 2, 5, 6, 10, 11, 15, 17, 18] for some examples related to various models such as cellular automata), is defined in such a way that the simulations performed are essentially “in place” simulations which mirror the dynamics of the simulated systems, modulo a scale factor allowed the simulator. Intrinsic universality has been used to show the existence of “universal” systems, somewhat analogous to universal Turing machines, which can simulate all other systems within a given model or class of systems, but in a dynamics-preserving way. Previous work [9] has shown that there exists a single aTAM tile set which is capable of simulating any arbitrary aTAM system, and thus that tile set is intrinsically universal (IU) for the aTAM (and we also say that the aTAM is IU). Further work in [8] showed that the 2HAM is much more complicated in terms of IU, with there existing hierarchies of 2HAM systems with strictly-increasing power of simulation. These simulations are performed by scaled blocks of tiles known as macrotiles in the simulator used to simulate individual tiles in the simulated systems. The simulation hierarchy in the 2HAM is based on a classification of systems separated by a system parameter known as the temperature, which is the global threshold that specifies the minimum strength of glue bindings required for pairs of tiles or supertiles to combine. It was proven in [8] that for every temperature $\tau \ge 2$, there exists a system at temperature $\tau$ such that no system at temperature $\tau ' < \tau$ can simulate it. However, they also showed that for each $\tau \ge 2$, the class of 2HAM systems at $\tau$ is IU.

The motivation of the current paper is to extend and further develop the results of [8], especially Theorem 4 which states: “There exists an infinite number of infinite hierarchies of 2HAM systems with strictly-increasing power (and temperature) that can simulate downward within their own hierarchy.” Our results elucidate more details about this hierarchy, including proving important differences between different notions of simulation used to characterize intrinsically universal systems. More specifically, different definitions of simulation have been used even within the IU results of [8], with one referred to as strong simulation and one as (standard) simulation. Strong simulation is a stricter notion essentially stating that whenever two supertiles in the simulated system $\mathcal {T}$ can combine, every pair of macrotiles that represents them in the simulator $\mathcal {S}$ must be able to (eventually) combine. However, standard simulation simply requires that for each half of such a pair in the simulator, there must exist some mate with which it can eventually combine. While both notions of simulation were utilized in [8], no concrete distinction was proven in terms of what is or isn’t possible between them. Here, we first prove that higher temperature systems can strongly simulate lower temperature systems if and only if there is a relationship between the temperature values which we call a uniform mapping. We show that it is easy to find whether such a mapping exists between two temperatures and, if so, what one is, and prove that for each pair of temperatures $2 < \tau < \tau '$ where a uniform mapping exists from $\tau$ to $\tau '$, that there exists a tile set which, at temperature $\tau '$, is IU for the class of 2HAM systems at $\tau$. We then prove that if no uniform mapping exists from $\tau$ to $\tau '$, then there exist systems at $\tau$ which cannot be strongly simulated by any system at $\tau '$, which is the first impossibility result for simulating downward in temperature that we are aware of, and is of interest because a natural intuition is that higher temperature systems are strictly more powerful. (However, we also show that for any given $\tau$ there are only a finite number of $\tau ' > \tau$ to which a uniform mapping does not exist.) Finally, we show that some systems which cannot be strongly simulated by higher temperature systems when no uniform mapping exists between temperatures can in fact be simulated from the higher temperature using the standard definition of simulation. This shows the first clear distinction between what is possible under the various definitions, and that the notion of strong simulation is provably more restrictive than that of (standard) simulation since the set of systems which can be simulated by a higher temperature system is strictly greater than that which can be strongly simulated.

In the next section we provide the definitions of the model and framework for our results, then provide an overview of our results in the following sections. Please note that due to space constraints, proofs can be found in an extend version of the paper [14].

2 Definitions

2.1 Informal Definition of the 2HAM

Here we give a brief, informal, sketch of the 2HAM. Please see [14] for a more formal definition. The 2HAM [4, 7] is a generalization of the aTAM [19], and in both the basic components are “tiles”. A tile type is a unit square with four sides, each having a glue consisting of a label (a finite string) and strength (a non-negative integer). We assume a finite set T of tile types, but an infinite number of copies of each tile type, each copy referred to as a tile. A supertile is (the set of all translations of) a positioning of tiles on the integer lattice $\mathbb {Z}^2$. Two adjacent tiles in a supertile interact if the glues on their abutting sides are equal and have positive strength. Each supertile induces a binding graph, a grid graph whose vertices are tiles, with an edge between two tiles if they interact. The supertile is $\tau$-stable if every cut of its binding graph has strength at least $\tau$, where the weight of an edge is the strength of the glue it represents. That is, the supertile is stable if at least energy $\tau$ is required to separate the supertile into two parts. A 2HAM tile assembly system (TAS) is a triple $\mathcal {T}= (T,S,\tau )$, where T is a finite tile set, S is a set of seed supertiles over T, and $\tau$ is the temperature, usually 1 or 2. When S is solely an infinite number of each of the singleton tiles of T, we call that the default initial state, and for shorthand notion refer to a TAS with a default initial state simply as a pair $\mathcal {T}= (T,\tau )$. Given a TAS $\mathcal {T}=(T,S,\tau )$, a supertile is producible, written as $\alpha \in \mathcal {A}[\mathcal {T}]$ if either it is a (super)tile in S, or it is the $\tau$-stable result of translating two producible assemblies without overlap. That is, any $\tau$-stable supertile which can result from some positioning of two producible supertiles, so that they do not overlap and they bind with at least strength $\tau$, is itself a producible supertile. This potentially allows for the combination of pairs of arbitrary large supertiles. A supertile $\alpha$ is terminal, written as $\alpha \in \mathcal {A}_{\Box }[\mathcal {T}]$ if for every producible supertile $\beta$, $\alpha$ and $\beta$ cannot be $\tau$-stably attached.

2.2 Definitions for Simulation

In this subsection, we formally define what it means for one 2HAM TAS to “simulate” another 2HAM TAS. The definitions presented in this (and the next) subsection are based on the simulation definitions from [3, 9, 16] and are included here for the sake of completeness. We will be describing how the assembly process followed by a system $\mathcal {T}$ is simulated by a system $\mathcal {U}$, which we will call the simulator. The simulation performed by $\mathcal {U}$ will be such that the assembly process followed by $\mathcal {U}$ mirrors that of the simulated system $\mathcal {T}$, but with the individual tiles of $\mathcal {T}$ represented by (potentially large) square blocks of tiles in $\mathcal {U}$ called macrotiles. We now provide the definitions necessary to define $\mathcal {U}$ as a valid simulator of $\mathcal {T}$. For a tileset T, let $A^T$ and $\tilde{A}^T$ denote the set of all assemblies over T and all supertiles over T respectively. Let $A^T_{< \infty }$ and $\tilde{A}^T_{< \infty }$ denote the set of all finite assemblies over T and all finite supertiles over T respectively.

In what follows, let U be a tile set. An m-block assembly, or macrotile, over tile set U is a partial function $\gamma : \mathbb {Z}_m \times \mathbb {Z}_m \dashrightarrow U$, where $\mathbb {Z}_m = \{ 0,1,\ldots m-1 \}$. Let $B^U_m$ be the set of all m-block assemblies over U. The m-block with no domain is said to be $empty$. For an arbitrary assembly $\alpha \in A^U$ define $\alpha ^m_{x,y}$ to be the m-block defined by $\alpha ^m_{x,y}(i,j) = \alpha (mx+i,my+j)$ for $0\le i,j < m$.

For a partial function $R: B^{U}_m \dashrightarrow T$, define the assembly representation function $R^*: A^{U} \dashrightarrow A^T$ such that $R^*(\alpha ) = \beta$ if and only if $\beta (x,y) = R(\alpha ^m_{x,y})$ for all $x,y \in \mathbb {Z}^2$. Further, $\alpha$ is said to map cleanly to $\beta$ under $R^*$ if either (1) for all non empty blocks $\alpha ^m_{x,y}$, $(x+u,y+v) \in \mathrm{dom} \;{\beta }$ for some $u,v \in \{-1,0,1\}$ such that $u^2+v^2 < 2$, or (2) $\alpha$ has at most one non-empty m-block $\alpha ^m_{x,y}$. In other words, we allow for the existence of simulator “fuzz” directly north, south, east or west of a simulator macrotile, but we exclude the possibility of diagonal fuzz.

For a given assembly representation function $R^*$, define the supertile representation function $\tilde{R}: \tilde{A}^{U} \dashrightarrow \mathcal {P}(A^T)$ such that $\tilde{R}(\tilde{\alpha }) = \{R^*(\alpha ) | \alpha \in \tilde{\alpha }\}$. $\tilde{\alpha }$ is said to map cleanly to $\tilde{R}(\tilde{\alpha })$ if $\tilde{R}(\tilde{\alpha })\in \tilde{A}^T$ and $\alpha$ maps cleanly to $R^*(\alpha )$ for all $\alpha \in \tilde{\alpha }$.

In the following definitions, let $\mathcal {T} = \left( T,S,\tau \right)$ be a 2HAM TAS and, for some initial configuration $S_{\mathcal {T}}$, that depends on $\mathcal {T}$, let $\mathcal {U} = \left( U,S_{\mathcal {T}},\tau '\right)$ be a 2HAM TAS, and let R be an m-block representation function $R: B^U_m \dashrightarrow T$.

Definition 1

We say that $\mathcal {U}$ and $\mathcal {T}$ have equivalent productions (at scale factor m), and we write $\mathcal {U} \Leftrightarrow _R \mathcal {T}$ if the following conditions hold:

• 1. $\left\{ \tilde{R}(\tilde{\alpha }) | \tilde{\alpha }\in \mathcal {A}[\mathcal {\mathcal {U}}]\right\} = \mathcal {A}[\mathcal {\mathcal {T}}]$.

• 2. $\left\{ \tilde{R}(\tilde{\alpha }) | \tilde{\alpha }\in \mathcal {A}_{\Box }[\mathcal {\mathcal {U}}]\right\} = \mathcal {A}_{\Box }[\mathcal {\mathcal {T}}]$.

• 3. For all $\tilde{\alpha }\in \mathcal {A}[\mathcal {\mathcal {U}}]$, $\tilde{\alpha }$ maps cleanly to $\tilde{R}(\tilde{\alpha })$

Equivalent production tells us that a simulating system $\mathcal {U}$ produces exactly the same set of assemblies as the simulated system $\mathcal {T}$, modulo scale factor (with the representation function providing the mapping of assemblies between the systems). While this is a powerful set of conditions ensuring that the simulator makes the same assemblies, it does not provide a guarantee that the simulator makes them in the same way. Namely, we desire a simulator to make the same assemblies, but also by following the same assembly sequences (again modulo scale and application of the representation function). We call this the dynamics of the systems and capture the necessary equivalence in the next few definitions. It is notable that the conditions required for the dynamics of the systems to be equivalent, following and modeling, are strong enough that equivalent production follows in a straightforward way from them, and therefore is redundant. However, we include it for completeness and clarity. We require some notation pertaining to assembly sequences.

For two supertiles $\tilde{\alpha }$ and $\tilde{\beta }$, and temperature $\tau \in \mathbb {N}$, define the combination set $C^\tau _{\tilde{\alpha },\tilde{\beta }}$ to be the set of all supertiles $\tilde{\gamma }$ such that there exist $\alpha \in \tilde{\alpha }$ and $\beta \in \tilde{\beta }$ such that (1) $\alpha$ and $\beta$ are disjoint (steric protection), (2) $\gamma \equiv \alpha \cup \beta$ is $\tau$-stable, and (3) $\gamma \in \tilde{\gamma }$. That is, $C^\tau _{\tilde{\alpha },\tilde{\beta }}$ is the set of all $\tau$-stable supertiles that can be obtained by “attaching” $\tilde{\alpha }$ to $\tilde{\beta }$ stably, with $|C^\tau _{\tilde{\alpha },\tilde{\beta }}| > 1$ if there is more than one position at which $\beta$ could attach stably to $\alpha$.

Given a TAS $\mathcal {T}=(T,S,\tau )$, define an assembly sequence of $\mathcal {T}$ to be a sequence of states $\mathbf {S} = (S_i \mid 0 \le i < k)$ (where $k = \infty$ if $\mathbf {S}$ is an infinite assembly sequence), and $S_{i+1}$ is constrained based on $S_i$ in the following way: There exist supertiles $\tilde{\alpha },\tilde{\beta },\tilde{\gamma }$ such that (1) $\tilde{\gamma }\in C^\tau _{\tilde{\alpha },\tilde{\beta }}$, (2) $S_{i+1}(\tilde{\gamma }) = S_{i}(\tilde{\gamma }) + 1$,¹ (3) if $\tilde{\alpha }\ne \tilde{\beta }$, then $S_{i+1}(\tilde{\alpha }) = S_{i}(\tilde{\alpha }) - 1$, $S_{i+1}(\tilde{\beta }) = S_{i}(\tilde{\beta }) - 1$, otherwise if $\tilde{\alpha }= \tilde{\beta }$, then $S_{i+1}(\tilde{\alpha }) = S_{i}(\tilde{\alpha }) - 2$, and (4) $S_{i+1}(\tilde{\omega }) = S_{i}(\tilde{\omega })$ for all $\tilde{\omega } \not \in \{\tilde{\alpha },\tilde{\beta },\tilde{\gamma }\}$. That is, $S_{i+1}$ is obtained from $S_i$ by picking two supertiles from $S_i$ that can attach to each other, and attaching them, thereby decreasing the count of the two reactant supertiles and increasing the count of the product supertile.

The result of a supertile assembly sequence $\mathbf {\tilde{\alpha }}$ is the unique supertile $\text {res}(\mathbf {\tilde{\alpha }})$ such that there exist an assembly $\alpha \in \text {res}(\mathbf {\tilde{\alpha }})$ and, for each $0 \le i < k$, assemblies $\alpha _i \in \tilde{\alpha }_i$ such that $\mathrm{dom} \;{\alpha } = \bigcup _{0 \le i < k}{\mathrm{dom} \;{\alpha _i}}$ and, for each $0 \le i < k$, $\alpha _i \sqsubseteq \alpha$. For all supertiles $\tilde{\alpha },\tilde{\beta }$, we write $\tilde{\alpha }\rightarrow _\mathcal {T}\tilde{\beta }$ (or $\tilde{\alpha }\rightarrow \tilde{\beta }$ when $\mathcal {T}$ is clear from context) to denote that there is a supertile assembly sequence $\mathbf {\tilde{\alpha }} = ( \tilde{\alpha }_i \mid 0 \le i < k )$ such that $\tilde{\alpha }_0 = \tilde{\alpha }$ and $\text {res}(\mathbf {\tilde{\alpha }}) = \tilde{\beta }$. We write $\tilde{\alpha }\rightarrow _\mathcal {T}^1 \tilde{\beta }$ ($\tilde{\alpha }\rightarrow ^1 \tilde{\beta }$) to denote an assembly sequence of length 1 from $\tilde{\alpha }$ to $\tilde{\beta }$ and $\tilde{\alpha }\rightarrow _\mathcal {T}^{\le 1} \tilde{\beta }$ ($\tilde{\alpha }\rightarrow ^{\le 1} \tilde{\beta }$) to denote an assembly sequence of length 1 from $\tilde{\alpha }$ to $\tilde{\beta }$ if $\tilde{\alpha }\ne \tilde{\beta }$ and an assembly sequence of length 0 otherwise.

Definition 2

We say that $\mathcal {T}$ follows $\mathcal {U}$ (at scale factor m), and we write $\mathcal {T} \dashv _R \mathcal {U}$ if, for any $\tilde{\alpha }, \tilde{\beta }\in \mathcal {A}[\mathcal {\mathcal {U}}]$ such that $\tilde{\alpha }\rightarrow _{\mathcal {U}}^1 \tilde{\beta }$, $\tilde{R}(\tilde{\alpha }) \rightarrow _\mathcal {T}^{\le 1} \tilde{R}\left( \tilde{\beta }\right)$.

Definition 3

We say that $\mathcal {U}$ weakly models $\mathcal {T}$ (at scale factor m), and we write $\mathcal {U} \,\models ^-_R \mathcal {T}$ if, for any $\tilde{\alpha }, \tilde{\beta }\in \mathcal {A}[\mathcal {\mathcal {T}}]$ such that $\tilde{\alpha }\rightarrow _\mathcal {T}^1 \tilde{\beta }$, for all $\tilde{\alpha }' \in \mathcal {A}[\mathcal {\mathcal {U}}]$ such that $\tilde{R}(\tilde{\alpha }')=\tilde{\alpha }$, there exists an $\tilde{\alpha }'' \in \mathcal {A}[\mathcal {\mathcal {U}}]$ such that $\tilde{R}(\tilde{\alpha }'')=\tilde{\alpha }$, $\tilde{\alpha }' \rightarrow _{\mathcal {U}} \tilde{\alpha }''$, and $\tilde{\alpha }'' \rightarrow _{\mathcal {U}}^1 \tilde{\beta }'$ for some $\tilde{\beta }' \in \mathcal {A}[\mathcal {\mathcal {U}}]$ with $\tilde{R}\left( \tilde{\beta }'\right) =\tilde{\beta }$.

Definition 4

We say that $\mathcal {U}$ strongly models $\mathcal {T}$ (at scale factor m), and we write $\mathcal {U} \,\models ^+_R \mathcal {T}$ if for any $\tilde{\alpha }$, $\tilde{\beta }\in \mathcal {A}[\mathcal {\mathcal {T}}]$ such that $\tilde{\gamma } \in C^{\tau }_{\tilde{\alpha }, \tilde{\beta }}$, then for all $\tilde{\alpha }', \tilde{\beta }' \in \mathcal {A}[\mathcal {\mathcal {U}}]$ such that $\tilde{R}(\tilde{\alpha }')=\tilde{\alpha }$ and $\tilde{R}\left( \tilde{\beta }'\right) =\tilde{\beta }$, it must be that there exist $\tilde{\alpha }'', \tilde{\beta }'', \tilde{\gamma }' \in \mathcal {A}[\mathcal {\mathcal {U}}]$, such that $\tilde{\alpha }' \rightarrow _{\mathcal {U}} \tilde{\alpha }''$, $\tilde{\beta }' \rightarrow _{\mathcal {U}} \tilde{\beta }''$, $\tilde{R}(\tilde{\alpha }'')=\tilde{\alpha }$, $\tilde{R}\left( \tilde{\beta }''\right) =\tilde{\beta }$, $\tilde{R}(\tilde{\gamma }')=\tilde{\gamma }$, and $\tilde{\gamma }' \in C^{\tau '}_{\tilde{\alpha }'', \tilde{\beta }''}$.

Definition 5

Let $\mathcal {U} \Leftrightarrow _R \mathcal {T}$ and $\mathcal {T} \dashv _R \mathcal {U}$.

• 1. $\mathcal {U}$ simulates $\mathcal {T}$ (at scale factor m) if $\mathcal {U} \,\models ^-_R \mathcal {T}$.

• 2. $\mathcal {U}$ strongly simulates $\mathcal {T}$ (at scale factor m) if $\mathcal {U} \,\models _R^+ \mathcal {T}$.

For simulation, we require that when a simulated supertile $\tilde{\alpha }$ may grow, via one combination attachment, into a second supertile $\tilde{\beta }$, then any simulator supertile that maps to $\tilde{\alpha }$ must also grow into a simulator supertile that maps to $\tilde{\beta }$. The converse should also be true. For strong simulation, in addition to requiring that all supertiles mapping to $\tilde{\alpha }$ must be capable of growing into a supertile mapping to $\tilde{\beta }$ when $\tilde{\alpha }$ can grow into $\tilde{\beta }$ in the simulated system, we further require that this growth can take place by the attachment of $any$ supertile mapping to $\tilde{\gamma }$, where $\tilde{\gamma }$ is the supertile that attaches to $\tilde{\alpha }$ to get $\tilde{\beta }$.

Note that, by these definitions, strong simulation implies simulation. That is, if system $\mathcal {T}_1$ strongly simulates $\mathcal {T}_2$, then it also simulates $\mathcal {T}_2$.

2.3 Intrinsic Universality

Let $\mathsf {REPR}$ denote the set of all m-block (or macrotile) representation functions. Let $\mathfrak {C}$ be a class of tile assembly systems, and let U be a tile set. We say U is intrinsically universal for $\mathfrak {C}$ if there are computable functions $\mathcal {R}:\mathfrak {C}\rightarrow \mathsf {REPR}$ and $\mathcal {S}:\mathfrak {C}\rightarrow \left( A^U_{< \infty } \rightarrow \mathbb {N} \cup \{\infty \}\right)$, and a $\tau '\in \mathbb {Z}^+$ such that, for each $\mathcal {T} = (T,S,\tau ) \in \mathfrak {C}$, there is a constant $m\in \mathbb {N}$ such that, letting $R = \mathcal {R}(\mathcal {T})$, $S_\mathcal {T}=\mathcal {S}(\mathcal {T})$, and $\mathcal {U}_\mathcal {T} = (U,S_\mathcal {T},\tau ')$, $\mathcal {U}_\mathcal {T}$ simulates $\mathcal {T}$ at scale m and using macrotile representation function R. That is, $\mathcal {R}(\mathcal {T})$ gives a representation function R that interprets macrotiles (or m-blocks) of $\mathcal {U}_\mathcal {T}$ as assemblies of $\mathcal {T}$, and $\mathcal {S}(\mathcal {T})$ gives the initial state used to create the necessary macrotiles from U to represent $\mathcal {T}$ subject to the constraint that no macrotile in $S_{\mathcal {T}}$ can be larger than a single $m \times m$ square.

3 Uniform Mappings

In this section, we define uniform mapping and almost linear uniform mapping, which will provide the basis for our results related to strong simulation. We then prove a set of facts about pairs of temperatures and these mappings, most notably that it is “easy” to find a uniform mapping between temperatures if one exists.

Definition 6

Let $E = \{n | n \in \mathbb {N} \,and\, n \le Q\}$ and $F = \{n | n \in \mathbb {N} \,and\, n \le R\}$ for some $Q, R \in \mathbb {Z}^+$ with $Q \le R$. Let S be a multiset consisting of members from E. Then we say that there is a uniform mapping M from E to F if there exists a function $M:E \rightarrow F$ such that $\sum \limits _{x \in S} M(x) \ge R$ if and only if $\sum \limits _{x \in S} x \ge Q$.

We say that there is a uniform mapping from $\tau$ to $\tau '$ provided that there exists a uniform mapping from $\{1, 2, ..., \tau \}$ to $\{1, 2, ..., \tau '\}$.

Definition 7

Let $E = \{n | n \in \mathbb {N} \,and\, n \le Q\}$ and $F = \{n | n \in \mathbb {N} \,and\, n \le R\}$ for some $Q, R \in \mathbb {Z}^+$ with $Q \le R$, and let $M:E \rightarrow F$ be a uniform mapping from E to F. We say that M is almost linear if there exists a $c \in \mathbb {N}$ such that for all $e \in (E - \{Q\})$, $M(e) = ce$, and $M(Q) = R$.

If a uniform mapping is almost linear, that means that other than for the greatest value in the domain of the mapping, the mapping of a number x is simply x times some constant c, where c is constant for the mapping.

Lemma 1

There exists a uniform mapping from $E = \{1, ..., \tau \}$ to $F\!=\!\{1, ..., \tau '\}$ if and only if there exists an almost linear uniform mapping from E to F.

Corollary 1

For $\tau , \tau ' \in \mathbb {Z}^+$ where $\tau \le \tau '$, a uniform mapping from $\tau$ to $\tau '$ exists if and only if there exists a constant $c \in \mathbb {N}$ such that $c(\tau -1) < \tau ' \le c\tau$.

Corollary 2

Let $\tau \in \mathbb {Z}^+$ and suppose that $\tau < \tau ' < 2\tau - 1$ for some $\tau ' \in \mathbb {Z}^+$. Then there does not exist a uniform mapping from $\{1, 2, ... \tau \}$ to $\{1, 2, ..., \tau '\}$.

Corollary 3

For any $\tau \in \mathbb {Z}^+$, there are a finite number of $\tau ' \in \mathbb {Z}^+$ with $\tau ' > \tau$ such that a uniform mapping cannot be found from $\tau$ to $\tau '$.

Theorem 1

Given $\tau ,\tau ' \in \mathbb {Z}^+$ with $\tau \le \tau '$, there exists an algorithm which runs in time $O(\log ^2 \tau ')$ and (1) determines whether or not a uniform mapping from $\tau$ to $\tau '$ exists, and (2) if so, produces that mapping.

The following corollary will be used later in the proof of Lemma 3.

Corollary 4

Given $\tau ,\tau ' \in \mathbb {N}$ such that $1 < \tau < \tau '$, if no uniform mapping exists from $\tau$ to $\tau '$, then $(\tau -1)\lceil \frac{\tau '}{\tau } \rceil \ge \tau '$.

4 Strong Simulation via Uniform Mappings

In this section, we provide positive results showing that for any pair of temperatures $\tau ,\tau ' \in \mathbb {Z}^+$ such that $\tau < \tau '$ and there is a uniform mapping from $\tau$ to $\tau '$, then there exists a tile set $U_{\tau '}$ which is intrinsically universal at temperature $\tau '$ for the class of all 2HAM systems at temperature $\tau$.

Lemma 2

Let $\tau ,\tau ' \in \mathbb {Z}^+$ with $\tau < \tau '$, such that there exists a uniform mapping M from $\tau$ to $\tau '$, and let $\mathcal {T}= (T,S,\tau )$, be an arbitrary 2HAM system at temperature $\tau$. Then, there exists $\mathcal {T}' = (T',S',\tau ')$ such that $\mathcal {T}'$ strongly simulates $\mathcal {T}$.

To prove Lemma 2, we show how to create $T'$ from T by using the mapping M. $T'$ is essentially identical to T, but for each glue g on a tile in T, if its strength is given by the function $\mathtt{str }(g)$, then the strength of that glue in $T'$ is equal to $M(\mathtt{str }(g))$. Due to the properties of a uniform mapping, we show that if and only if a multiset of glues on a pair of supertiles over T allow those supertiles to bind in $\mathcal {T}$, the mapped glues over supertiles in $T'$ will allow the equivalent supertiles in $\mathcal {T}'$ to bind. Thus, $\mathcal {T}'$ will correctly strongly simulate $\mathcal {T}$.

Lemma 2 shows that as long as there is a uniform mapping between two temperatures, for each system at the lower temperature there exists a system at the higher temperature which can strongly simulate it. Furthermore, Corollaries 2 and 3 show us that there are only a very few temperatures greater than a given $\tau$ for which a uniform mapping does not exist. Theorem 1 tells us that we can efficiently find a uniform mapping M if one exists, and by the proof of Lemma 2 we can also see that the generation of the simulating system merely requires M and time linear in the size of the system to be simulated. We now show that such a strongly simulating system can be created for a tile set which is intrinsically universal for systems at $\tau$, resulting in a tile set which is IU for systems at temperature $\tau$ while strongly simulating them at $\tau '$.

Theorem 2

Let $\tau ,\tau ' \in \mathbb {Z}^+$ with $1 < \tau < \tau '$, such that there exists a uniform mapping M from $\tau$ to $\tau '$. Then there exists a tile set $U_{\tau '}$ which is intrinsically universal for the class of all 2HAM systems at temperature $\tau$, such that the simulating systems using $U_{\tau '}$ are at temperature $\tau '$.

The proof of Theorem 2 simply makes use of the result of [8] showing that for the class of systems at each temperature $\tau \ge 2$, there exists a tile set which is IU for that class. That IU tile set simulates at temperature $\tau$, so we use Lemma 2 to show that for $\tau ' > \tau$ where a uniform mapping exists from $\tau$ to $\tau '$, we can make a strongly simulating tile set at temperature $\tau '$ for the tile set which is IU for $\tau$ systems.

Note that the results of [8] provide for a variety of tile sets for each $\tau > 1$ such that each is IU for that $\tau$. These tile sets provide for a variety of tradeoffs in scale factor, tile set size, and number of seed assemblies. Any such tile set $U_{\tau }$ can be used to create the tile set $U_{\tau '}$ from Theorem 2 to achieve the same tradeoffs since the simulation of $U_{\tau }$ by $U_{\tau '}$ is at scale factor 1 and there is a bijective mapping of tile types from $U_{\tau '}$ to whichever $U_{\tau }$ is chosen. Furthermore, an IU tile set at temperature $\tau$ can be chosen which is IU in terms of either strong simulation or standard simulation, and by those definitions the result still holds.

5 Impossibility of Strong Simulation at Higher Temperatures

Intuitively, it may appear that the class of systems at higher temperatures is more “powerful” than the class of systems at lower temperatures. In this section, we show that this is not strictly the case. Here we present a sketch of the proof by giving an example of a tile set U such that there exists a 2HAM TAS $\mathcal {T} = (T, S, 3)$ such that for any initial configuration $S_{\mathcal {T}}$ over U, the 2HAM TAS $\mathcal {U} = (U, S_{\mathcal {T}}, 4)$ does not strongly simulate $\mathcal {T}$. This gives an intuitive idea of the general proof which can be found in [14].

Theorem 3

Let $\tau , \tau ' \in \mathbb {N}$ be such that (1) $2 < \tau < \tau '$ and (2) there does not exist a uniform mapping from $\tau$ to $\tau '$. For every tile set U, there exists a 2HAM TAS $\mathcal {T} = (T, S, \tau )$ such that for any initial configuration $S_{\mathcal {T}}$ over U, the 2HAM TAS $\mathcal {U} = (U, S_{\mathcal {T}}, \tau ')$ does not strongly simulate $\mathcal {T}$.

Proof: As in [8], the idea behind this proof is to use Definitions 2 and 4 in order to show two producible supertiles in $\mathcal {T}$ which cannot bind due to insufficient strength, but whose simulating supertiles in $\mathcal {U}$ can combine. This will contradict the definition of simulation. A large part of the terminology and notation in this proof are borrowed from [8].

Fig. 1.

The tile set for the proof of Theorem 3. Black rectangles represent strength-$\tau$ glues (labeled 1–8), and black squares represent the strength-1 glue (labeled 0).

Our proof is by contradiction. Therefore, suppose, for the sake of obtaining a contradiction, that there exists an intrinsically universal tile set U such that, for any 2HAM TAS $\mathcal {T} = (T,S,\tau )$, there exists an initial configuration $S_{\mathcal {T}}$ and $\tau '\ge \tau$, such that $\mathcal {U} = \left( U, S_{\mathcal {T}}, \tau '\right)$ strongly simulates $\mathcal {T}$ and there does not exist a uniform mapping from $\tau$ to $\tau '$. Define $\mathcal {T} = (T, \tau )$ where T is the tile set defined in Fig. 1, the default initial state is used, and $\tau > 2$. Let $\mathcal {U} = \left( U, S_{\mathcal {T}}, \tau '\right)$ be the temperature $\tau '\ge \tau$ 2HAM system, which uses tile set U and initial configuration $S_{\mathcal {T}}$ (depending on $\mathcal {T}$) to strongly simulate $\mathcal {T}$ at scale factor m. Let $\tilde{R}$ denote the supertile representation function that testifies to the fact that $\mathcal {U}$ strongly simulates $\mathcal {T}$.

Fig. 2.

(a) gives an example half-ladders with $\tau$ rungs. The squares in (b) and (c) depict macrotiles which assemble in $\mathcal {U}$ and simulate tiles $\mathcal {T}$ when $\tau '=4$ and $\tau = 3$.

We say that a supertile $\tilde{l} \in \mathcal {A}[\mathcal {\mathcal {T}}]$ is a d-rung left half-ladder of height $h \in \mathbb {N}$ if it contains h tiles of the type $A_2$ and $h-1$ tiles of type $A_3$, arranged in a vertical column, plus d tiles each of the types $A_1$ and $A_0$ for $d \in \mathbb {N}$. (An example of a $\tau$-rung left half-ladder is shown on the left in Fig. 2a. The dotted lines show positions at which tiles of type $A_1$ and $A_0$ could potentially attach, but since a $\tau$-rung half-ladder has exactly $\tau$ of each, only $\tau$ such locations have tiles.) Essentially, a d-rung left half-ladder consists of a single-tile-wide vertical column of height $2h-1$ with an $A_2$ tile at the bottom and top, and those in between alternating between $A_2$, $A_3$, and $A_4$ tiles. To the east of exactly d of the $A_2$ tiles an $A_1$ tile is attached and to the east of each $A_1$ tile an $A_0$ tile is attached. These $A_1$-$A_0$ pairs, collectively, form the $\tau$ rungs of the left half-ladder. We enumerate the $A_2$ tiles appearing in $\tilde{l}$ from north to south and denote the $i^{th}$ $A_2$ tile by $A_{2,i}$. Thus, $A_{2,0}$ denotes the northernmost $A_2$ tile in $\tilde{l}$ and $A_{2,(d-1)}$ denotes the southernmost tile in $\tilde{l}$. We can define d-rung right half-ladders similarly. A d-rung right half-ladder of height h is defined exactly the same way but using the tile types $B_3$, $B_2$, $B_1$, and $B_0$ and with rungs growing to the left of the vertical column. The east glue of $A_0$ is a strength-1 glue matching the west glue of $B_0$.

We say that a supertile consisting only of tiles of type $A_2$, $A_3$, and $A_4$ is a left bar provided that the northernmost tile in the supertile is $A_4$ and the southernmost tile in the supertile is $A_3$. The height of a bar is the number of $A_2$ tiles appearing in the bar. We define a right bar similarly. In the case where $\tau = 3$ and $\tau ' = 4$, note that there does not exist a uniform mapping from $\tau$ to $\tau '$. Also, in this case, Fig. 2 shows the main idea of the proof of Theorem 3.

Consider the left half-ladder shown in Fig. 2b. We show that for sufficiently many rungs, some macrotile (labeled x) must repeat an arbitrary number of times. Therefore, for strong simulation, there must be a left half-ladder, $\tilde{l}'$, with rungs that contain these macrotiles. $\tilde{l}'$ is depicted by yellow tiles. By assumption, $\mathcal {T}$ is strongly simulated by $\mathcal {U}$, therefore, there must be a 3 rung right half-ladder which we call $r_p'$ that binds to exactly three of the rungs of $\tilde{l}'$. $\tilde{r_p}'$ is depicted by red tiles. Note that because $\tau ' > \tau$, it must be the case that some rung binds with strength at least $\lceil \frac{\tau '}{\tau }\rceil$ (we say that such a rung “over-binds”.) Moreover, we show that we can choose x such that x belongs to an “over-binding” rung and such that the distance between each consecutive macrotile x is increasing. Then, as depicted in Fig. 2c, we use the assumption of strong simulation to construct a right half-ladder which we call $\tilde{r}_{bar}'$ that consists of $\tau - 1$ copies of the supertile $\tilde{r}_p'$ bound to spacer macrotiles such that each copy of $\tilde{r}_p'$ is precisely and appropriately spaced. The tiles which bind between copies of $\tilde{r}_p'$ supertiles are depicted by blue tiles. Note that each $\tilde{r}_p'$ contains an “over-binding” rung. Then, the spacings of the $\tilde{r}_p'$ supertiles of $\tilde{r}_{bar}'$ are chosen so that only “over-binding” rungs attach to $\tilde{l}'$ and each “over-binding” rung attaches to a rung of $\tilde{l}'$ with at least strength $\lceil \frac{\tau '}{\tau }\rceil$. Finally, given the assumption that there is not a uniform mapping from $\tau$ to $\tau '$, it follows from Corollary 4 that $(\tau -1)\lceil \frac{\tau '}{\tau } \rceil \ge \tau '$. We then show that this implies that $\tilde{l}'$ and $\tilde{r}_{bar}'$ can bind in $\mathcal {U}$, but that $\tilde{R}(\tilde{l}')$ cannot stably bind to $\tilde{R}(\tilde{r}_{bar}')$. Thus, we arrive at a contradiction. It should be noted that the proof is not merely combinatorial and relies on arguing about the dynamics of $\mathcal {U}$, though we have not indicated that here. Please see [14] for more detail.

6 Simulating Arbitrary Lower Temperature Ladder Systems

We now prove that, even though higher temperature systems can only strongly simulate lower temperature ladder systems (the 2HAM system described in Sect. 5 consisting of the tile depicted in Fig. 1) if a uniform mapping exists between the temperatures, a uniform mapping is not required for (standard) simulation.

Fig. 3.

Intuitive sketch of the set of half-ladders possible in the high temperature system $\mathcal {S}$ which simulates a low temperature ladder system $\mathcal {T}$, shown without scaling. Yellow: B-type half-ladders, Blue: C-type half-ladders, Red: A-type half-ladders, Green: D-type half-ladders. Each type of half-ladder is shown once with no special rung and once with one special rung (the most possible), and each is paired with the type of half-ladder with which it could bind if each had at least $\tau$ rungs in matching locations (after translating appropriately). Note that the spacing and ordering of rungs can be arbitrary, and also that spacing tiles are left out for compactness, so rungs are closer together and shorter than they would actually be. All pairs of rungs of different types bind with each other with strength 1 (due to the H glues on their bottom tiles - not shown), and all pairs of rungs of the same type bind with strength $\tau ' - \tau + 1$ due to the sum of the H glue (strength 1) and “type” glue (strength $\tau ' - \tau$) bindings (Color figue online).

Theorem 4

For $\tau , \tau ' \in \mathbb {N}$ where $1<\tau <\tau '$, let $\mathcal {T}$ be the ladder system at temperature $\tau$. Then, there exists a system $\mathcal {S}$ at temperature $\tau '$ which simulates $\mathcal {T}$.

At a high-level, the construction which proves Theorem 4 works by leveraging nondeterminism and the fact that for each pair of supertiles $\tilde{\alpha },\tilde{\beta }\in \mathcal {A}[\mathcal {\mathcal {T}}]$ which are able to $\tau$-stably combine, for each $\tilde{\alpha }' \in \mathcal {A}[\mathcal {\mathcal {S}}]$ where $\tilde{R}(\tilde{\alpha }') = \tilde{\alpha }$, there simply must exist some $\tilde{\beta }' \in \mathcal {A}[\mathcal {\mathcal {S}}]$ where $\tilde{R}(\tilde{\beta }') = \tilde{\beta }$ and $\tilde{\alpha }'$ and $\tilde{\beta }'$ can $\tau '$-stably combine, but there may be many other $\tilde{\beta }'' \in \mathcal {A}[\mathcal {\mathcal {S}}]$ where $\tilde{R}(\tilde{\beta }'') = \tilde{\beta }$ such that $\tilde{\alpha }'$ and $\tilde{\beta }''$ cannot $\tau '$-stably combine. Specifically, for each side of half-ladder, there are multiple types which can form, each with exactly 0 or 1 “special” rungs. (See Fig. 3 for a schematic example.) All rungs on a left half-ladder can combine with all rungs on a right half-ladder with strength 1, but whenever rungs of the same type combine, they do so with strength $\tau ' - \tau + 1$. The formation of all half-ladder supertiles guarantees that any pair of oppositely facing half-ladders can have no more than one pair of rungs with matching types, and for each half-ladder with $\tau$ or more rungs there exists a producible oppositely facing half-ladder with rungs in matching locations and one of them matching in type. (Note that $\mathcal {S}$ simulates at scale factor 2.) In such a way, $\tau$ rungs in matching locations of two oppositely facing half-ladders all guaranteed to be sufficient and necessary to form a ladder, and all possible half-ladder and ladder representing supertiles are producible, making $\mathcal {S}$ correctly simulate $\mathcal {T}$.