Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

By analysing magnetic resonance (MR) images of the brain, surgeons can make an appropriate decision for diagnosing many neurological diseases, such as Parkinsons disease, Alzheimers disease, brain tumors, and stroke. However, MR images are affected by several artifacts and noise sources. One of them is the random fluctuation of the MR signal which is mainly due to thermal noise. Such a noise seriously degrades the acquisition of any quantitative measurements from the MR images, such as registration, segmentation, classification, and visualization. To obtain reliable analysis results, denoising MR image is vital before further analysis steps can be conducted. MR images are computed from both real and imaginary images, which are assumed to contain Gaussian distribution noises with zero means. Thus, noise is image dependent, which follows a Rician distribution, and makes removing noises difficult [12].

Postprocessing filtering techniques have the advantage of not increasing the acquisition time and, hence have been extensively used in MR image denoising. Most denoising methods are based on the signal averaging principle by using the spatial pattern redundancy in the image. However, there are other filtering techniques that use other statistical estimates such as the Median [10], Gaussian [1] and Anisotropic Diffusion [16] that have received considerable attention due to their simplicity. Although these denoising methods can significantly remove noise, they tend to cause blurring and erase small features if there are high peaks in the histogram, often resulting a mask effect in uniform regions and other artifacts in the output image.

One way to approaching this problem is to use multi-scale image decomposition, that is, processing images in each scale independently and recombining each processed image to obtain the final image. Advances in wavelet theory combined with multi-scale analysis applied to image contrast enhancement can achieve promising results. The decomposition of images into different frequency ranges permits the isolation of the frequency components introduced by intrinsic deformations or extrinsic factors in certain subbands [18].

In [13], the undecimated wavelet transform is employed to provide effective representation of the noisy coefficients information. However, the 2D wavelet transform used is a separable extension of the 1D wavelet transform, which does not work well in capturing the geometry of image edges [14].

We propose a new image enhancement method based on the nonsubsampled contourlet transform (NSCT) [6]. The proposed algorithm enhances the MR image while amplifying weak edges and suppressing noise by modifying the NSCT coefficients using a nonlinear mapping function in each directional subband.

The rest of this paper is organized as follows. In Sect. 2, we explain the intrinsic geometrical information based methodology for image denoising. A variety of experimental results are presented in Sect. 3. Finally, the conclusions are given in Sect. 4.

2 Methodology

Existing image-denoising methods amplify noise when they amplify weak edges since they cannot distinguish noise from weak edges. In the frequency domain, both weak edges and noise produce low-magnitude coefficients. Since weak edges are geometric structures and noise is not, we can use the NSCT to distinguish them [17].

2.1 Nonsubsampled Countourlet Transform

In [7], Do and Vetterli proposed the contourlet transform (CT), which is a multiscale directional representation constructed in the discrete grid by combining the Laplacian pyramid and the directional filter bank. Due to its directionality and anisotropy CT can represent curve more sparsely. NSCT, based on the theory of CT, is a kind of multi-scale, multi-directional computation framework of discrete images. The main difference lies in that, in the course of decomposition and reconstruction, traditional upsamplers and downsamplers in CT do not exist in NSCT any more, so that the NSCT is a fully multi-scale, multi-directional, good time-frequency property and shift invariant expansion.

Fig. 1
figure 1

Three-stage NSP decomposition

Full size image

NSCT falls into two phases, including nonsubsampled pyramid (NSP) and nonsubsampled directional filter bank (NSDFB). The former phase ensures the multi-scale property by using two-channel nonsubsampled filter bank, and a low-pass image with a band-pass one can be produced at each NSP decomposition stage. The subsequent NSP decomposition stages are carried out to decompose the low-pass component available iteratively to capture the singularities in the image. As a result, NSP can result in \(k+1\) subband images including one low-pass image and k band-pass images, whose sizes are all the same as that of the source image, where k denotes the number of decomposition stages. Figure 1 gives the NSP decomposition with \(k = 3\) stages with a 2-D low-pass filter is represented by its z-transform \(H_0(z)\) where \(z=[z_1,z_2]^T\) and \(H_1(z)=1-H_0(z)\). The filters for subsequent stages are obtained by upsampling the filters of the first stage. This gives the multi-scale property without the need for additional filter design. The NSDFB, constructed by combining the directional fan filter banks devised by Bamberger and Smith [2], is two-channel nonsubsampled filter banks. NSDFB allows the direction decomposition with l stages in band-pass images from NSP at each scale and produces 2l directional subband images which have the same size as the source image. Thus, the NSDFB endows the NSCT with the multi-direction property and we can benefit a lot from the NSDFB because it provides us with more precise directional detail information. A four-channel NSDFB, constructed with two-channel fan filter banks and parallelogram filters without downsamplers and upsamplers, is illustrated in Fig. 2. Note that in the second level, the upsampled fan filters \(U_i(z^Q), i=0,1\) have checker-board frequency support, and when combined with the filters in the first level give the four directional frequency decomposition. We use the ‘maxat’ filters and ‘dmaxat7’ filters for NSP and NSDFB, respectively. The concrete filter banks constuction methods and more NSCT details can be found in [6].

Fig. 2
figure 2

Four-channel nonsubsampled DFB

Full size image

2.2 Proposed Image Denoising Using Intrinsic Geometrical Information

NSCT differs from other multi-scale analysis methods in that contourlet transform allows for different and flexible number of directions at each scale. According the direction information contours are obtained by directional filter bank concatenated the neighbouring singular points into local contours in the frequency domain. By combination of NSP and NSDFB, NSCT is constructed as a fully shift invariant, multi-scale, and multi-direction expansion that has better directional frequency localization and a fast implementation. It is worth noting that shift invariance is very important. Being shift invariant, each pixel of the transform subbands corresponds to that of the original image in the same spatial location. Therefore, we gather the geometrical information pixel by pixel from the NSCT coefficients. All directional contour subbands can be expressed as:

$$\begin{aligned} \begin{array}{r} \lbrace C_{m,d} \rbrace , \ m=1,2,\ldots k, \ d=1,2,\ldots l_m, \\ k\in (1,2,\ldots N),\ l_m=2^N. \end{array} \end{aligned}$$
(1)

where m and d are the scale and direction of the decomposition respectively, k is the number of contour decomposition scale, \(l_m\) is the number of contour decomposition directions of mth scale and \(\lbrace C_{m,d} \rbrace \) is the coefficient at the dth directional subband of the mth scale. We observe that in the NSCT domain, the Rician noise corresponds to those pixels with small magnitude coefficients in all directional subbands at a specific pyramidal level. Based on this observation, we can classify pixels into two categories by analysing the distribution of their coefficients in different subbands. One simple way is to compute the mean (denoted by mean) and the maximum (denoted by max) magnitude of the coefficients for each pixel across directional subbands, and then classify it by:

$$\begin{aligned} \text {pixel}={\left\{ \begin{array}{ll} \text {noise}, &{} \text {if} \big (({{mean}}<\alpha \sigma \gamma )\;\text {and}\;({{max}}<\alpha \sigma \gamma )\big )\\ \text {edge}, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(2)

where \(\alpha \) is the amplifying gain of the subbands at a specific pyramidal level (3), \(\sigma \) is the noise variance of the input MR image and \(\gamma \) is the noise standard deviation of the subbands at a specific pyramidal level.

$$\begin{aligned} \alpha = \dfrac{\log \bigg (\dfrac{\text {mean}\big (|C_{m,d}|\big )}{\max \big (|C_{m,d}|\big )}\bigg )}{\log \bigg (\sin \bigg (\dfrac{\pi }{2}\dfrac{\text {mean}\big (|C_{m,d}|\big )}{\max \big (|C_{m,d}|\big )}\bigg )\bigg )} \end{aligned}$$
(3)

We first estimate the noise variance of the input MR image, \(\hat{\sigma }\), with the robust median operator defined in [4] and then compute the noise variance of each subband, \(\hat{\gamma }\), by using [18]. The core requirement for image denoising by multi-scale transforms is to suppressing noise while amplifying weak edges. To this end we modify the NSCT coefficients, \(\tilde{C}_{m,d}\), by a nonlinear mapping function in each scale and direction where \(m>1\):

$$\begin{aligned} \tilde{C}_{m,d} = {\left\{ \begin{array}{ll} {\bigg (\dfrac{\max \big (|C_{m,d}|\big )}{\text {sgn}\big (C_{m,d}\big )}}\bigg ) \sin \bigg (\dfrac{\pi }{2}\sin \bigg (\dfrac{\pi }{2}\dfrac{|C_{m,d}|}{\max \big (|C_{m,d}|\big )}\bigg )^{\alpha }\bigg )^{\sqrt{\alpha }}, &{} \text {edge}\\ \text {0}, &{} \text {noise}. \end{array}\right. } \end{aligned}$$
(4)

We summarize our denoising method in the following algorithm.

  1. 1.

    Compute the NSCT of the input MR image for k levels according to (1).

  2. 2.

    Estimate the noise standard deviation \((\hat{\sigma })\) of the input image.

  3. 3.

    For each level of the pyramid where \(m>1\):

    1. a.

      Estimate the noise variance \((\hat{\gamma })\).

    2. b.

      At each pixel location, compute the mean and the maximum magnitude of the corresponding coefficients in all directional subbands at this level, and classify each pixel according to (2) and (3) into “edges” or “noise”.

    3. c.

      For each directional subband, use the nonlinear mapping function given in (4) to modify the NSCT coefficients according to the classification.

  4. 4.

    Reconstruct the denoised MR image from the modified NSCT coefficients.

Fig. 3
figure 3

Visual quality comparison: Top row; from left to right: a Ground truth T1-weighted image. b Ground truth corrupted with Rician noise of 13 %. Denoised with c NLM, d SURELET and e the proposed method. Middle row; and bottom row: same results for a simulated T2- and PD-weighted images

Full size image

3 Experimental Results

We have compared the performance of our proposed image denoising using intrinsic geometrical information with two state-of-the-art denoising algorithms, the non-local mean (NLM) algorithm [3] and a modern wavelet-based denoising algorithm (SURELET) [11] using the 3D-simulated MR images downloaded from the BrainWeb database [5]. The simulated T1-, T2-, and PD-weighted synthetic noise-free MR images are downloaded where the size of each image is \(181 \times 217 \times 181\) and the intensity is 256 bins.

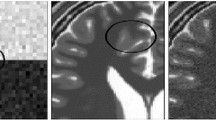
Visual quality comparison of the MR images denoised with the NLM, the SURELET and the proposed method was conducted on the simulated T1-, T2-, and PD-weighted synthetic noise-free MR images after corrupting the images by Rician noise [8] with 13 %. It can be observed from Fig. 3 that the images denoised with the proposed method are more closer to the ground truth than the images denoised with the other approaches.

Fig. 4
figure 4

Quantitative comparison of the proposed NSTC based denoising method with NLM and SURELET methods based on a PSNR, b SSIM and c MAD for simulated T1 images corrupted with Rician noise varying from 5 to 21

Full size image

For a quantitative analysis, MR images were degraded with Rician noise for a wide range of noise levels and the denoising efficiency of the algorithms was evaluated based on the Peak Signal to Noise Ratio (PSNR) [9], the mean Structural Similarity Index Matrix (SSIM) [19] and the Mean Absolute Difference (MAD) [15]. A higher PSNR, MSSIM and a lower MAD correspond to a higher performance. Figures 4, 5 and 6 show the quantitative analysis of of the denoising methods in terms of PSNR, mean SSIM and MAD. It can be observed from the plots that the proposed method performs better than the NLM and SURELET based on the quality metrics used for the evaluation. Furthermore, proposed methodology does not require any parameter selection and on a PC with 2.5 GHz Intel Core i5 CPU and 8 GB RAM, NSCT costs on average of 5.23 s to decompose a 181\(\,\times \,\)217 MR image into directional subbands and to reconstruct denoised MR image using MatlabFootnote 1 hence, can be easily applied for a clinical application.

Fig. 5
figure 5

Quantitative comparison of the proposed NSTC based denoising method with NLM and SURELET methods based on a PSNR, b SSIM and c MAD for simulated T2 images corrupted with Rician noise varying from 5 to 21

Full size image
Fig. 6
figure 6

Quantitative comparison of the proposed NSTC based denoising method with NLM and SURELET methods based on a PSNR, b SSIM and c MAD for simulated PD images corrupted with Rician noise varying from 5 to 21

Full size image

4 Conclusion

We have proposed a novel multi-scale image denoising algorithm to remove Rician noise from MR images based on the NSCT. We have shown that the new algorithm can sufficiently remove Rician noise, while simultaneously preserving edges and fine structures in a given noisy MR image. Experimental results on the BrainWeb database verified that the intrinsic geometrical information extracted from directional contour coefficients is quite efficient, speedy and can be effectively applied to T1-, T2-, and PD-weighted MR images without any parameter tuning under diverse noise levels.