The Use of Digital Technology in Extending Mathematical Problem Solving Reasoning

Abstract

The incorporation of digital technologies (both multiple purpose and mathematics action technologies) in mathematical learning environments can foster and extend discussions among learners and teachers even beyond class time. That is, learners not only keep reflecting on mathematical ideas or problems; but also they can review or consult related online resources. Similarly, the use of dynamic geometry systems provides affordances to construct dynamic models of tasks where learners can analyse how objects move within the configuration and formulate mathematical relations. In this report, we discuss three exemplars to characterize ways in which the use of technology extends mathematical reasoning in problem solving approaches. This information becomes important for teachers to value and frame the incorporation of technology in learning environments. At the end, some limitations of this approach are discussed.

1 Introduction

School systems worldwide face a challenge to consistently incorporate the coordinated use of digital technologies in curriculum proposals and learning environments. In this context, it is important to discuss what changes the use of technology brings into contents, structure, and ways of reasoning that learners could develop about concepts and problems solving competencies. For example, with the use of a dynamic geometry system, students can construct models where parameters or elements can be moved to visualize and explore behaviours of mathematical objects. Similarly, learners can access online information that includes concept definitions and explanations (https://www.khanacademy.org), problem examples, and in some cases solutions of typical course problems. As results, teaching/learning environments should not only guide students to select and analyse pertinent online resources; but also to incorporate that information into the learning activities. Mobile devices such as tablets o smart phones can extend learning environments to support peers communication or interaction almost anytime. That is, the use of technology becomes important to structure extended conversations among students and teachers to frame and foster problems solving experiences. Walling [1] pointed out “this Digital Age shift in schools is not, or should not be, about hardware and software. It should be about teaching and learning in new and exciting ways that expand learning opportunities for all students” (p. xiii). How can mathematics teachers design and implement learning activities where students rely on the use different technologies to develop mathematical knowledge and problem solving experiences? To delve into this question, we review the role played by the coordinated use of digital technology in students’ development of mathematical knowledge. Furthermore, we present and discuss exemplars that illustrate ways in which learners could formulate problems, transform routine tasks into a set of opportunities to develop deep mathematical knowledge and engage in collaboration projects to comprehend, refine, and apply mathematical concepts.

2 Background and Conceptual Framework

In the traditional teaching/learning environments the teacher is the only responsible to select mathematics tasks and to coordinate the implementation of learning activities. In general terms, the way teachers and students interact during class activities has remained consistent over the years. This model has been criticized in terms that its success depends mainly on the teacher’s individual competencies to select and implement learning activities, the lack of motivation that students often experience during the development of the course, and the limited options for students to discuss curriculum contents beyond syllabus and courses goals. What type of innovations should learning environments incorporate in order for students to rely on online resources and technologies to develop mathematical thinking? Alagic and Alagic [2] pointed out that digital technologies offer teachers and learners affordances to provide a learning environment that fosters collaboration and direct interaction with peers. Thus, teaching environments need to be adjusted to take into account and incorporate the use of diverse technologies in students learning of mathematics. Barbeau [3] argues that in the process of learning, students face challenges that “often involve explanation, questioning and conjecturing, multiple approaches, evaluation of solutions for effectiveness and elegance, and construction and evaluation examples” (p. 5). Nowadays, it is recognized that learning involves a maturation process that requires time for students to develop an increasingly complex network of connections of concepts and problem solving strategies. “To learn mathematics more meaningfully, students need to build connections over time through a coherent learning progression with adequate support for the affective challenges of maintaining interest and engagement” [4] (p. 34). Mathematical tasks play a crucial role for students to develop awareness of technology affordances as a means to comprehend and develop problem-solving competencies. Tasks are given to students to engage them in thinking in order to experience shifts in their focus and structure of their attention. Mason [5] stated: …“Tasks are provided for students to initiate activity, which provides experience and, in order to learn effectively from experience, it helps to adopt a reflexive stance” (p. 12). With the use of technologies students continuously reflect on what ways of reasoning about concepts and problems that are important to detect invariance and to support mathematical relationships. It is recognized that different digital technologies offer distinct opportunities for learners to engage in mathematical thinking. Thus, the existence of several types of technologies makes necessary to identify what a particular technology can offer to learners during the process of comprehending mathematical ideas and solving problems.

Artigue and Mariotti [6] characterize a conceptual framework as a structured but dynamic entity that articulates research questions, methods to address those questions, data collection, and interpretation of research results. In this perspective, our research inquiry is framed around three related fields: mathematical problem solving, digital technologies, and subjects’ construction of mathematical knowledge [7]. In the problem solving domain, our interest lies on orienting and discussing learners behaviours and activities in terms of three constructs: (i) the importance of goals (what do mathematics learning and problem solving activities involve?), (ii) orientations (what do learning experiences, beliefs, values, and resources teachers or learners bring into learning environments?) and (iii) the decision making process involved in dealing with mathematical tasks [8]. In the field of digital technologies, we identify changes to the content and learning environments that the use of technology brings to the students’ construction of mathematical knowledge. In particular, we emphasize and make explicit the potential and opportunities that the coordinated use of digital technologies offer to subjects to reason about mathematical concepts and problems. Furthermore, the subjects’ comprehension of mathematical ideas and the development of problem solving competencies can be framed and structured around a problematizing principle. Problematizing means that students develop and practice an inquisitive or inquiring approach to delve into concepts, to identify relationships among data and to solve mathematical tasks. Likewise, the coordinated use of digital technologies appears relevant throughout all problem-solving episodes that include problem formulation, comprehension, representation, exploration, generalization, and communication of results. In this perspective, learners engage in continuous problem solving activities that involve:

• Looking for information related to the themes or contents in study through online books, Wikipedia and WolframAlpha computational knowledge machine. In this process, students rely on methods and strategies that help them select, analyse, summarize and contrast the use of available information.

• Learning and fostering several ways to work on problems within a community that shares and discusses ideas as a part of a group or teams where it is important for students to listen to others during problem solving approaches.

• Using different digital tools to represent, explore, solve and communicate results, in particular, the construction and analysis of dynamic models of problems.

• Identifying and discussing partial results that might appear during the solution process of tasks and share them with other students.

• Looking for different and novel ways to represent and explore problems. In this process, students are encouraged to find creative solutions to problems.

3 Exemplars

We present three exemplars to illustrate how the use of technology becomes important to construct dynamic models of problems in order to engage learners in the process of recognizing patterns, in looking for arguments to support mathematical relations and in presenting and communicating results. For each exemplar, we comment on features of mathematical reasoning that emerges during the solution process of the task. It is important to mention that the tasks are part of the activities that we have been implementing in a problem-solving seminar with high school teachers. One goal of the seminar is to analyse the process that teachers get involved during the tool appropriation and to examine ways of reasoning that they exhibit to represent, explore and solve the tasks. In this report, we focus on identifying features of mathematical reasoning that appear during the solution of the tasks associated with the use of the tools. We argue that teachers themselves need to get involved in problem solving experiences in order for them to develop resources and strategies to efficiently use technology affordances in the problem solving approaches. Although the approaches the problems represent part of the work that high school teachers have shown during the problem solving sessions, we do not intend to analyse in detail how teachers individually contributed to each task solution; rather, we aim at characterizing what types of reasoning became involved during those approaches as a group.

3.1 The Construction of Dynamic Models

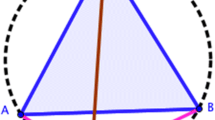
The goal is to represent mathematical tasks dynamically. To this end, learners are guided to develop resources and strategies to construct or build dynamic configurations of tasks where objects can be moved within the model. Thus, moving points or objects orderly becomes a crucial strategy to construct dynamic models. Güçler et al. [9] argue that the use of a dynamic geometry system “allows students to reason quickly from the specific to the general, from concrete to abstract, from example or illustration to concept and idea (p. 99). Figure 1 shows triangle ABC and a perpendicular bisector of side BC. Circle centred at A is a heuristic strategy to move side AC on the plane by moving point P along the circle. It is observed that a family of triangles is generated when point P is moved along the circle. What is the locus of point Q when point P is moved along the circle?

Fig. 1.

Triangle ABC and the perpendicular bisector of side BC.

Figure 2 shows that the locus of point Q seems to be a hyperbola. It also shows that for different positions of point Q it is true that |d(A, Q) – d(Q, B)| is a constant (2.37). That is, it holds the definition of the hyperbola with foci points A and B. Another argument to show that the locus is hyperbola involves recognizing that point Q is on the perpendicular bisector of side BC, then, d(Q, C) = d(Q, B) and d(A, Q) = d(A, C) + d(C, Q). Therefore, d(A, Q) – d(Q, B) = d(A, C) which is constant (side AC).

Fig. 2.

An empirical argument to show that the locus of Q is a hyperbola.

What happens if point B is moved along line AB? Figure 3 shows that at one position the hyperbola becomes an ellipse. Point Q generates de locus and is on the perpendicular bisector of BC. Then, d(A, Q) + d(Q, B) = d(A, Q) + d(Q, C) = d(A, C). That is, the sum of the distances from Q to foci A and B is constant (definition of ellipse).

Fig. 3.

The generation of an ellipse within the dynamic model.

Comment:

A key activity in mathematical practice is to examine objects or models in order to identify patterns or invariants. To this end, the use of a dynamic geometry system (such as GeoGebra) offers affordances for learners to explore the behaviour of mathematical objects as a result of moving others elements within the model or dynamic configuration. In this case, a triangle is a model or platform to identify objects that appear in an analytic geometric course. The construction of a perpendicular bisector becomes instrumental to generate and justify properties the conic sections. The objects dynamic exploration involves examining a family of triangles by moving a particular point (P) and looking for arguments to explain relationships among the objects. Similarly, finding loci of points is another important strategy to find mathematical relations.

3.2 Patterns’ Recognition

In general terms, a pattern is a rule or way to describe certain type of behaviour of a finite or infinity family of objects. It can be described verbally or via a formula or symbolic expressions. There are different types of patterns that might appear in the study of numbers, shapes, motion, or mathematical objects behaviours. Steen [10] points out that mathematics is an exploratory science that aims to identify different types of patterns found in nature phenomena or even patterns created by analysing the behaviours of other patterns.

…[Thus] patterns can be either real of imagined, visual or mental, static or dynamic, qualitative or quantitative…They can arise from the world around us, from the depths of space and time, or from the inner working of the human mind [11] (p. 3).

The process involved in the identification of patterns includes ways to observe what is important in the situation or phenomenon and to think of what mathematical resources are need to express it. What tools or resources and ways of thinking do students need to develop in order to identify and explore different types of mathematical patterns? What type of problems or tasks should teachers discuss with their students in order to explore, identify, and communicate mathematical patterns? Addressing these types of questions implies analysing and reflecting on what features of mathematical thinking are relevant in the process of looking for and examining the behaviours of mathematical objects. We argue that students not only should deal with a variety of situations to find and explore patterns; but also teachers should discuss overly with students what tools and questions become important to recognize and analyse how the patter behaves.

Within a variety of patterns, the concept of recursion is essential in mathematics, computers science, biology and even language. Recursion definitions are used to characterize something in terms of itself. For example, the factorial function is defined as 1! = 1 and N! = (N − 1)!(N) for N ≥ 2, N integer. Cuoco [12] pointed out that recursive thinking is a key problem solving approach to build spreadsheet analysis to explain how banks figure out the monthly payment on a house or car loan. What types of resources and ways of reasoning should students develop and exhibit to approach recursive tasks? We use a task that involves a recursive sequence to illustrate that the use of GeoGebra provides a means for learners to make sense of the task and to initially explore the sequence behaviour.

The task: Let the real numbers $a_{0}$ and $a_{1}$ be given. Define the sequence $\left\{ {a_{n} } \right\}$ by $a_{n} = \frac{{a_{n - 2} + a_{n - 1} }}{2}$ for each $n \ge 2$. Prove that $\mathop {\lim }\limits_{n \to \infty } a_{n}$ exists and determine its value [13] (p. 77).

To focus on particular cases in order to make sense of and explore the sequence behaviour is a common strategy in pattern recognition. The issue is then how the problem solver decides and implements what a special case to consider or try in order to shed light on its solution. In this problem, Schoenfeld recommends to evaluate the sequence for $a_{0} = 0$ and $a_{1} = 1$ and (as special case) to observe the involved pattern. Figure 4 shows a dynamic model of the sequence where $a_{0} = 0$ and $a_{1} = 1$. In http://www.geogebratube.org/student/m139246 the initial values are associated with two sliders whose values can be changed by moving the points on the sliders. Visually, the behaviour of the sequence, for $a_{0} = 0$ and $a_{1} = 1$, converges to $0.666 \ldots = {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}$. How can we get a closed form for the general term $a_{n}$?

Fig. 4.

Visualizing the behaviour of some elements of the sequence

We can also begin by finding some of its particular values. The list of terms of the sequence includes both rational and decimal representations.

$$ a_{n} = \frac{{a_{n - 2} + a_{n - 1} }}{2} $$

The initial conditions are $a_{0} = 0$ and $a_{1} = 1$, then, some terms of the sequence are:

$$ 0,1,\frac{1}{2},\frac{3}{4},\frac{5}{8},\frac{11}{16},\frac{21}{32},\frac{43}{64},\frac{85}{128}, \ldots $$

These terms expressed in decimal form are:

$$ 0,\;1,\;0.5,\;0.75,\;0.625,\;0.6875,\;0.65625,\;0.671875,\;0.6640625,\; \ldots $$

If we continue writing more terms, we can observe that after certain number of terms of the decimal part includes the digit 6 (looking for patterns). That is, we get expressions such as 0.666…Here are some examples:

$$ a_{10} = \frac{341}{512} \approx 0.666015625 $$

Or

$$ a_{20} = \frac{349525}{5124288} \approx 0.6666660308 $$

Examining the behaviour of the decimal expression let us to conjecture that the limit of the sequence is $0.666 \ldots = {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}$.

Comment:

Exploring dynamically the sequence behavior via the use of digital technologies (GeoGebra) offers students not only a way to visualize graphically the behavior of the sequence elements associated with the special case; but also (through the use of sliders) others cases can be visualized. In addition, the use of others technologies (CAS) became important to carry out numeric and symbolic calculations to delve into the pattern sequence. Making sense of task statements is essential to recognize and express patterns that are involved in recursive tasks. Cases that are easy to handle ($a_{0} = 0$ and $a_{1} = 1$) often provide useful information to recognize and explore patterns. Rational and decimal representations of results offer different angles to detect invariance. For instance, the decimal representation of the generated elements for the special case led us to visualize the limit; while the rational form led us to focus on the differences $a_{n + 1} - a_{n}$. Looking at the difference is also an important strategy to detect patterns. Similarly, expressing the sequence terms in different manners is another useful to identify interesting behaviors. Table 1 shows some patterns that emerged from the list of some element of the initial sequence.

Table 1. Some patterns involved in the terms of the sequence.

3.3 Making Sense and Conjecturing

The task involves analysing properties and relationships associated with linear and quadratic functions.

The task: Based on a given linear function $f$, find another linear function $g$, such as the graph of the product function $h=f.g$ is tangent to both linear functions. The task is an adjusted version of a problem used by Wilson and Barnes and it can be found in: http://jwilson.coe.uga.edu/Texts.Folder/tangent/f(x).g(x)%3Dh(x).html

.

To make sense of the task, we can begin with a particular case, that is, “given the function $f(x) = x + \frac{1}{2}$, find a linear function $g$ such as the graph of $h=f.g$ is tangent to $f$ and $g$”. Some questions might help learners understand the task: What does it mean two linear functions are each tangent to its product? Can we sketch some examples? Is it always possible to find those functions holding the condition? What properties or how the product of two linear function behave? The use of GeoGebra provides affordances to represent and explore graphically a family of linear functions and their product by changing through a slider the slope and y-intercept point. Figure 5a shows a visual solution to the task, and Fig. 5b shows others examples that satisfy the conditions.

Fig. 5.

(a) Finding function $g$. (b) Examples of some solutions.

Based on this empirical information, some conjectures emerge:

• (i) For two given linear functions $f(x) = m_{1} x + b_{1}$ and $g(x) = m_{2} x + b_{2}$ when the graph of the product $f(x).g(x)$ is tangent to both $f$ and $g$ then $m_{1} = - m_{2}$ (same slope with opposite sign) and also $b_{1} + b_{2} = 1$.

• (ii) The function $f$ intersects the quadratic function $h=h(f(x).g(x))$ at one or two points and one them (in case that there are two) $B(x_{1} ,f(x_{1} ))$ also holds that $g(x_{1} ) = 1$. This is because at the intersection point it is true that $f(x_{1} ) = h(x_{1} ) = f(x_{1} )$ and therefore $g(x_{1} ) = 1$ . Likewise, when a linear function became tangent to the parabola, then intersection points between the product function and the linear function coincide (Fig.  6 ).

  Fig. 6.

  

  The intersection points of the linear functions and the product function coincide when the lines are tangent to the product function.

• (iii) When both lines are tangent to the parabola, then the parabola vertex and the intersection point of both lines (point H) are on the axis of symmetry of the parabola and the point H, intersection of $f$ and $g$ , is located at the intersection point of the axis of symmetry and line $y = 0.5$ (Fig.  7 ). Furthermore, the intersection of function product and the axis of symmetry is the vertex (V) of the parabola.

  Fig. 7.

  

  Identifying the axis of symmetry and the intersection of $f$ and $g$.

Comment:

Making sense of the task is a crucial step for learners to represent and explore possible ways to solve it. The use of GeoGebra, in this case, became instrumental to associate the sliders with the graphic representation of the linear and quadratic functions. In this process, the analysis of a particular case provides useful information to formulate a set of conjectures not only to solve the task, but also to explore others related properties. In addition, the graphic and empirical information can be used to construct an algebraic approach to the task.

4 Discussion and Final Remarks

A powerful mathematical activity that get heightened with the use of digital technology, such as a dynamic geometry system, is making explicit the implicit dynamism of reasoning about mathematical objects behaviours. The first exemplar illustrates how a dynamic model of a simple figure (triangle) can be used to generate and explore properties of the conic sections. Likewise, the dynamic exploration not only involves analysing family of objects via dragging; but also the identification of new concepts such as the perpendicular bisector and loci to generate those conic sections. In this context, a new route to study and structure an analytic course emerges. Furthermore, the use of the tool affordances could play an important role to explore visually the behaviour of recursive sequence, second exemplar, and this exploration again provides useful information to analyse both decimal and rational representation of the sequence values. In addition, the visual representation can easily be extended to analyse a family of cases where the initial values can be modified. It is observed that problem solving strategies such as “examining special cases” or “assuming the problem as solved” can be implemented and enhanced with the use of the tool because it is possible to coordinate visual and numeric information about parameter behaviours. The third exemplar illustrates that a dynamic geometry system allows learners to explore graphically properties of functions (linear and quadratic, in this case) through changing slider values that represent main parameters. This exploration can lead learners to formulate a set of conjectures and patterns to explain relations between linear functions and their product. In general terms, the systematic use of technology offers learners not only a set of affordances to make sense and explore concepts or objects embedded in mathematical tasks; but also offer them an opportunity to identify new mathematical results. It is also important to recognize that teachers need to develop some kind of expertise in the use of digital technologies and a possible path to develop it is to engage themselves in problem solving activities as a part of a community that recognize and value strengths and limitations in the use of technologies. In addition, teachers should also discuss what new heuristic strategies (dragging, finding foci, quantification of attributes, etc.) emerge during the construction of tasks dynamic models. It is clear that a limitation in a technology problem solving approach is to work on and follow up a well-structured curriculum that often includes course and contents sequences. In this context, a new flexible proposal to organize contents and fundamental concepts in which the systematic use of digital technologies appears as important in fostering students’ mathematical thinking and peer collaboration.

Finally, all approaches to the tasks can be put online and all students can access and continue their analysis and discussion anytime. Thus the tools are used to keep the discussion alive even outside of classrooms.