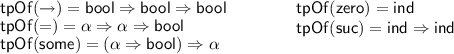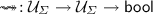Abstract
The interactive theorem prover Isabelle/HOL is based on the well understood Higher-Order Logic (HOL), which is widely believed to be consistent (and provably consistent in set theory by a standard semantic argument). However, Isabelle/HOL brings its own personal touch to HOL: overloaded constant definitions, used to achieve Haskell-like type classes in the user space. These features are a delight for the users, but unfortunately are not easy to get right as an extension of HOL—they have a history of inconsistent behavior. It has been an open question under which criteria overloaded constant definitions and type definitions can be combined together while still guaranteeing consistency. This paper presents a solution to this problem: non-overlapping definitions and termination of the definition-dependency relation (tracked not only through constants but also through types) ensures relative consistency of Isabelle/HOL.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Polymorphic HOL, more precisely, Classic Higher-Order Logic with Infinity, Hilbert Choice and Rank-1 Polymorphism, endowed with a mechanism for constant and type definitions, was proposed in the nineties as a logic for interactive theorem provers by Mike Gordon, who also implemented the seminal HOL theorem prover [12]. This system has produced many successors and emulators known under the umbrella term “HOL-based provers” (e.g., [2, 3, 5, 14, 27]), launching a very successful paradigm in interactive theorem proving.
A main strength of HOL-based provers is a sweet spot in expressiveness versus complexity: HOL on the one hand is sufficient for most mainstream mathematics and computer science applications, and on the other is a well-understood logic. In particular, the consistency of HOL has a standard semantic argument, comprehensible to any science graduate: one interprets its types as sets, in particular the function types as sets of functions, and the terms as elements of these sets, in a natural way; the rules of the logic are easily seen to hold in this model. The definitional mechanism has two flavors:
-
New constants c are introduced by equations \(c \equiv t\), where t is a closed term not containing c.
-
New types \(\tau \) are introduced by “typedef” equations \(\tau \equiv t\), where \(t : \sigma \Rightarrow \mathsf{bool}\) is a predicate on an existing type \(\sigma \) (not containing \(\tau \) anywhere in the types of its subterms)—intuitively, the type \(\tau \) is carved out as the t-defined subset of \(\sigma \).
Again, this mechanism is manifestly consistent by an immediate semantic argument [30]; alternatively, its consistency can be established by regarding definitions as mere abbreviations (which here are non-cyclic by construction).
Polymorphic HOL with Ad Hoc Overloading. Isabelle/HOL [26, 27] adds its personal touch to the aforementioned sweet spot: it extends polymorphic HOL with a mechanism for (ad hoc) overloading. As an example, consider the following Nominal-style [33] definitions, where \({{\mathsf {prm}}}\) is the type of finite-support bijections on an infinite type \({{\mathsf {atom}}}\), and where we write \({{\mathsf {apply}}}\;\mathsf pi \;\mathsf a \) for the application of a bijection pi to an atom a:
Example 1

Above, the constant \({{\mathsf {perm}}}\) is declared using the keyword “consts”—its intended behavior is the application of a permutation to all atoms contained in an element of a type \(\alpha \). Then, using the keyword “defs”, several overloaded definitions of \({{\mathsf {perm}}}\) are performed for different instances of \(\alpha \). For atoms, \({{\mathsf {perm}}}\) applies the permutation; for numbers (which don’t have atoms), \({{\mathsf {perm}}}\) is the identity function; for \(\alpha \;\mathsf{list}\), the instance of \({{\mathsf {perm}}}\) is defined in terms of the instance for the component \(\alpha \). All these definitions are non-overlapping and their type-based recursion is terminating, hence Isabelle is fine with them.
Inconsistency. Of course, one may not be able to specify all the relevant instances immediately after declaring a constant like \({{\mathsf {perm}}}\)—at a later point, a user may define their own atom-container type, such asFootnote 1

and instantiate \({{\mathsf {perm}}}\) to this type. (In fact, the Nominal package automates instantiations for user-requested datatypes, including terms with bindings.) To support such delayed instantiations, which are also crucial for the implementation of type classes [13, 35], Isabelle/HOL allows intermixing definitions of instances of an overloaded constant with definitions of other constants and types. Unfortunately, the improper management of the intermixture leads to inconsistency: Isabelle/HOL accepts the following definitionsFootnote 2.
Example 2

which immediately yield a proof of False:

The inconsistency argument takes advantage of the circularity \(T \rightsquigarrow c_\mathsf{bool}\rightsquigarrow T\) in the dependency relation introduced by the definitions: one first defines T to contain only one element just in case \(c_\mathsf{bool}\) is \(\mathsf {{True}}\), and then defines c to be \(\mathsf {{True}}\) just in case T contains more than one element.
Our Contribution. In this paper, we provide the following, in the context of polymorphic HOL extended with ad hoc overloading (Sect. 3):
-
A definitional dependency relation that factors in both constant and type definitions in a sensible fashion (Sect. 4.1).
-
A proof of consistency of any set of constant and type definitions whose dependency relation satisfies reasonable conditions, which accept Example 1 and reject Example 2 (Sect. 4).
-
A new semantics for polymorphic HOL (Sect. 4.4) that guides both our definition of the dependency relation and our proof of consistency.
More details on our constructions and proofs can be found in the technical report [20]. We hope that our work settles the consistency problem for Isabelle/HOL’s extension of HOL, while showing that the mechanisms of this logic admit a natural and well-understandable semantics. We start with a discussion of related work, including previous attempts to establish consistency (Sect. 2). Later we also show how this work fits together with previous work by the first author (Sect. 5).
2 Related Work
Type Classes and Overloading. Type classes were introduced in Haskell by Wadler and Blott [34]—they allow programmers to write functions that operate generically on types endowed with operations. For example, assuming a type \(\alpha \) which is a semigroup (i.e., comes with a binary associative operation \(+\)), one can write a program that computes the sum of all the elements in an \(\alpha \)-list. Then the program can be run on any concrete type T that replaces \(\alpha \) provided T has this binary operation \(+\). Prover-powered type classes were introduced by Nipkow and Snelting [28] in Isabelle/HOL and by Sozeau and Oury [32] in Coq—they additionally feature verifiability of the type-class conditions upon instantiation: a type T is accepted as a member of the semigroup class only if associativity can be proved for its \(+\) operation.
Whereas Coq implements type classes directly by virtue of its powerful type system, Isabelle/HOL relies on arbitrary ad hoc overloading: to introduce the semigroup class, the system declares a “global” constant \(+ : \alpha \Rightarrow \alpha \Rightarrow \alpha \) and defines the associativity predicate; then different instance types T are registered after defining the corresponding overloaded operation \(+ : T \Rightarrow T \Rightarrow T\) and verifying the condition. Our current paper focuses not on the Isabelle/HOL type classes, but on the consistency of the mechanism of ad hoc overloading which makes them possible.
Previous Consistency Attempts. The settling of this consistency problem has been previously attempted by Wenzel [35] and Obua [29]. In 1997, Wenzel defined a notion of safe theory extension and showed that overloading conforms to this notion. But he did not consider type definitions and worked with a simplified version of the system where all overloadings for a constant c are provided at once. Years later, when Obua took over the problem, he found that the overloadings were almost completely unchecked—the following trivial inconsistency was accepted by Isabelle2005:
Example 3

Obua noticed that the rewrite system produced by the definitions has to terminate to avoid inconsistency, and implemented a private extension based on a termination checker. He did consider intermixing overloaded constant definitions and type definitions but his syntactic proof sketch misses out inconsistency through type definitions.
Triggered by Obua’s observations, Wenzel implemented a simpler and more structural solution based on work of Haftmann, Obua and Urban: fewer overloadings are accepted in order to make the consistency/termination check decidable (which Obua’s original check is not). Wenzel’s solution has been part of the kernel since Isabelle2007 without any important changes—parts of this solution (which still misses out dependencies through types) are described by Haftmann and Wenzel [13].
In 2014, we discovered that the dependencies through types are not covered (Example 2), as well as an unrelated issue in the termination checker that led to an inconsistency even without exploiting types. Kunčar [19] amended the latter issue by presenting a modified version of the termination checker and proving its correctness. The proof is general enough to cover termination of the definition dependency relation through types as well. Our current paper complements this result by showing that termination leads to consistency.
Inconsistency Club. Inconsistency problems arise quite frequently with provers that step outside the safety of a simple and well-understood logic kernel. The various proofs of False in the early PVS system [31] are folklore. Coq’s [8] current stable versionFootnote 3 is inconsistent in the presence of Propositional Extensionality; this problem stood undetected by the Coq users and developers for 17 years; interestingly, just like the Isabelle/HOL problem under scrutiny, it is due to an error in the termination checker [11]. Agda [10] suffers from similar problems [23]. The recent Dafny prover [21] proposes an innovative combination of recursion and corecursion whose initial version turned out to be inconsistent [9].
Of course, such “dangerous” experiments are often motivated by better support for the users’ formal developments. The Isabelle/HOL type class experiment was practically successful: substantial developments such as the Nominal [17, 33] and HOLCF [24] packages and Isabelle’s mathematical analysis library [16] rely heavily on type classes. One of Isabelle’s power users writes [22]: “Thanks to type classes and refinement during code generation, our light-weight framework is flexible, extensible, and easy to use.”
Consistency Club. Members of this select club try to avoid inconsistencies by impressive efforts of proving soundness of logics and provers by means of interactive theorem provers themselves. Harisson’s pioneering work [15] uses HOL Light to give semantic proofs of soundness of the HOL logic without definitional mechanisms, in two flavors: either after removing the infinity axiom from the object HOL logic, or after adding a “universe” axiom to HOL Light; a proof that the OCaml implementation of the core of HOL Light correctly implements this logic is also included. Kumar et al. [18] formalize in HOL4 the semantics and the soundness proof of HOL, with its definitional principles included; from this formalization, they extract a verified implementation of a HOL theorem prover in CakeML, an ML-like language featuring a verified compiler. None of the above verified systems factor in ad-hoc overloading, the starting point of our work.
Outside the HOL-based prover family, there are formalizations of Milawa [25], Nuprl [4] and fragments of Coq [6, 7].
3 Polymorphic HOL with Ad Hoc Overloading
Next we present syntactic aspects of our logic of interest (syntax, deduction and definitions) and formulate its consistency problem.
3.1 Syntax
In what follows, by “countable” we mean “either finite or countably infinite.” All throughout this section, we fix the following:
-
A countably infinite set \(\mathsf {{TVar}}\), of type variables, ranged over by \(\alpha ,\beta \)
-
A countably infinite set \(\mathsf {{Var}}\), of (term) variables, ranged over by x, y, z
-
A countable set K of symbols, ranged over by k, called type constructors, containing three special symbols: “\(\mathsf{bool}\)”, “\(\mathsf{ind}\)” and “\(\Rightarrow \)” (aimed at representing the type of booleans, an infinite type and the function type constructor, respectively)
We also fix a function \(\mathsf {arOf}: K \rightarrow \mathbb {N}\) associating an arity to each type constructor, such that \(\mathsf {arOf}(\mathsf{bool}) = \mathsf {arOf}(\mathsf{ind}) = 0\) and \(\mathsf {arOf}(\Rightarrow ) = 2\). We define the set \(\mathsf {{Type}}\), ranged over by \(\sigma ,\tau \), of types, inductively as follows:
-
\(\mathsf {{TVar}}\subseteq \mathsf {{Type}}\)
-
\((\sigma _1,\ldots ,\sigma _n)k \in \mathsf {{Type}}\) if \(\sigma _1,\ldots ,\sigma _n \in \mathsf {{Type}}\) and \(k \in K\) such that \(\mathsf {arOf}(k) = n\)
Thus, we use postfix notation for the application of an n-ary type constructor k to the types \(\sigma _1,\ldots ,\sigma _n\). If \(n=1\), instead of \((\sigma )k\) we write \(\sigma \;k\) (e.g., \(\sigma \;\mathsf{list}\)).
A typed variable is a pair of a variable x and a type \(\sigma \), written \(x_\sigma \). Given \(T \subseteq \mathsf {{Type}}\), we write \(\mathsf {{Var}}_T\) for the set of typed variables \(x_\sigma \) with \(\sigma \in T\). Finally, we fix the following:
-
A countable set \({{\mathsf {Const}}}\), ranged over by c, of symbols called constants, containing five special symbols: “\(\rightarrow \)”, “\(=\)”, “\({{\mathsf {some}}}\)” “\({{\mathsf {zero}}}\)”, “\({{\mathsf {suc}}}\)” (aimed at representing logical implication, equality, Hilbert choice of “some” element from a type, zero and successor, respectively).
-
A function \({{\mathsf {tpOf}}}: {{\mathsf {Const}}}\rightarrow \mathsf {{Type}}\) associating a type to every constant, such that:
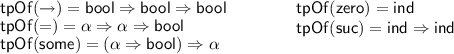
We define the type variables of a type, \({{\mathsf {TV}}}: \mathsf {{Type}}\rightarrow {{\mathcal {P}}}(\mathsf {{TVar}})\), as expected. A type \(\sigma \) is called ground if \({{\mathsf {TV}}}(\sigma ) = \emptyset \). We let \(\mathsf {{GType}}\) be the set of ground types.
A type substitution is a function \(\rho : \mathsf {{TVar}}\rightarrow \mathsf {{Type}}\); we let \({{\mathsf {TSubst}}}\) denote the set of type substitutions. Each \(\rho \in {{\mathsf {TSubst}}}\) extends to a homonymous function \(\rho : \mathsf {{Type}}\rightarrow \mathsf {{Type}}\) by defining \(\rho ((\sigma _1,\ldots ,\sigma _n)k) = (\rho (\sigma _1),\ldots ,\rho (\sigma _n))k\). We let \(\mathsf {GTSubst}\) be the set of all ground type substitutions \(\theta : \mathsf {{TVar}}\rightarrow \mathsf {{GType}}\), which again extend to homonymous functions \(\theta : \mathsf {{Type}}\rightarrow \mathsf {{GType}}\).
We say that \(\sigma \) is an instance of \(\tau \), written \(\sigma \le \tau \), if there exists \(\rho \in {{\mathsf {TSubst}}}\) such that \(\rho (\tau ) = \sigma \). Two types \(\sigma \) and \(\tau \) are called orthogonal, written \(\sigma \, {\#}\,\tau \), if they have no common instance.
Given \(c \in {{\mathsf {Const}}}\) such that \(\sigma \le {{\mathsf {tpOf}}}(c)\), we call the pair \((c,\sigma )\), written \(c_{\sigma }\), an instance of c. A constant instance is therefore any such pair \(c_\sigma \). We let \({{\mathsf {CInst}}}\) be the set of all constant instances, and \({{\mathsf {GCInst}}}\) the set of constant instances whose type is ground. We extend the notions of being an instance (\(\le \)) and being orthogonal (\({\#}\)) from types to constant instances, as follows:

We also define \({{\mathsf {tpOf}}}\) for constant instances by \({{\mathsf {tpOf}}}(c_\sigma ) = \sigma \).
The tuple \((K,\mathsf {arOf},C,{{\mathsf {tpOf}}})\), which will be fixed in what follows, is called a signature. This signature’s pre-terms, ranged over by s, t, are defined by the grammar:
Thus, a pre-term is either a typed variable, or a constant instance, or an application, or an abstraction. As usual, we identify pre-terms modulo alpha-equivalence.
Typing of pre-terms is defined in the expected way (by assigning the most general type possible); a term is a well-typed pre-term, and \({{\mathsf {Term}}}\) denotes the set of terms. Given \(t \in {{\mathsf {Term}}}\), we write \({{\mathsf {tpOf}}}(t)\) for its (uniquely determined, most general) type and \({{\mathsf {FV}}}(t)\) for the set of its free (term) variables. We call t closed if \({{\mathsf {FV}}}(t) = \emptyset \).
We let \({{\mathsf {TV}}}(t)\) denote the set of type variables occurring in t. A term t is called ground if \({{\mathsf {TV}}}(t) = \emptyset \). Thus, closedness refers to the absence of free (term) variables in a term, whereas groundness refers to the absence of type variables in a type or a term. Note that, for a term, being ground is a stronger condition than having a ground type: \((\lambda x_\alpha .\,c_\mathsf{bool})\,x_\alpha \) has the ground type \(\mathsf{bool}\), but is not ground.
We can apply a type substitution \(\rho \) to a term t, written \(\rho (t)\), by applying \(\rho \) to all the type variables occurring in t; and similarly for ground type substitutions \(\theta \); note that \(\theta (t)\) is always a ground term.
A formula is a term of type \(\mathsf{bool}\). We let \({{\mathsf {Fmla}}}\), ranged over by \(\varphi \), denote the set of formulas. The formula connectives and quantifiers are defined in the standard way, starting from the implication and equality primitives.
When writing concrete terms or formulas, we often omit indicating the type in occurrences of bound variables—e.g., we may write \(\lambda x_\alpha .\,x\) instead of \(\lambda x_\alpha .\,x_\alpha \).
3.2 Built-Ins and Non-Built-Ins
The distinction between built-in and non-built-in types and constants will be important for us, since we will employ a slightly non-standard semantics only for the latter.
A built-in type is any type of the form \(\mathsf{bool}\), \(\mathsf{ind}\), or \(\sigma _1 \Rightarrow \sigma _2\) for \(\sigma _1,\sigma _2\in \mathsf {{Type}}\). We let \({{\mathsf {Type}^{\bullet }}}\) denote the set of types that are not built-in. Note that a non-built-in type can have a built-in type as a subtype, and vice versa; e.g., if \(\mathsf{list}\) is a type constructor, then \(\mathsf{bool}\,\mathsf{list}\) and \((\alpha \Rightarrow \beta )\,\mathsf{list}\) are non-built-in types, whereas \(\alpha \Rightarrow \beta \;\mathsf{list}\) is a built-in type. We let \(\mathsf {{GType}}^\bullet = \mathsf {{GType}}\cap {{\mathsf {Type}^{\bullet }}}\) denote the set of ground non-built-in types.
Given a type \(\sigma \), we define \({{\mathsf {types^\bullet }}}(\sigma )\), the set of non-built-in types of \(\sigma \), as follows:
-
\({{\mathsf {types^\bullet }}}(\mathsf{bool}) = {{\mathsf {types^\bullet }}}(\mathsf{ind}) = \emptyset \)
-
\({{\mathsf {types^\bullet }}}((\sigma _1,\ldots ,\sigma _n)\,k) = \{(\sigma _1,\ldots ,\sigma _n)\,k\}\), if k is different from \(\Rightarrow \)
-
\({{\mathsf {types^\bullet }}}(\sigma _1 \Rightarrow \sigma _2) = {{\mathsf {types^\bullet }}}(\sigma _1)\,\cup \,{{\mathsf {types^\bullet }}}(\sigma _2)\)
Thus, \({{\mathsf {types^\bullet }}}(\sigma )\) is the smallest set of non-built-in types that can produce \(\sigma \) by repeated application of the built-in type constructors. E.g., if the type constructors \({{\mathsf {prm}}}\) (0-ary) and \(\mathsf{list}\) (unary) are in the signature and if \(\sigma \) is \((\mathsf{bool}\Rightarrow \alpha \;\mathsf{list}) \Rightarrow {{\mathsf {prm}}}\Rightarrow (\mathsf{bool}\Rightarrow \mathsf{ind})\;\mathsf{list}\), then \({{\mathsf {types^\bullet }}}(\sigma )\) has three elements: \(\alpha \;\mathsf{list}\), \({{\mathsf {prm}}}\) and \((\mathsf{bool}\Rightarrow \mathsf{ind})\;\mathsf{list}\).
A built-in constant is a constant of the form \(\rightarrow \), \(=\), \({{\mathsf {some}}}\), \({{\mathsf {zero}}}\) or \({{\mathsf {suc}}}\). We let \({{\mathsf {CInst}}}^\bullet \) be the set of constant instances that are not instances of built-in constants, and \({{\mathsf {GCInst}}}^\bullet \subseteq {{\mathsf {CInst}}}^\bullet \) be its subset of ground constants.
As a general notation rule: the prefix “G” indicates ground items, whereas the superscript \(\bullet \) indicates non-built-in items, where an item can be either a type or a constant instance. In our semantics (Sect. 4.4), we will stick to the standard interpretation of built-in items, whereas for non-built-in items we will allow an interpretation looser than customary. The standardness of the \(\mathsf{bool}\), \(\mathsf{ind}\) and function-type interpretation will allow us to always automatically extend the interpretation of a set of non-built-in types to the interpretation of its built-in closure.
Given a term t, we let \({{\mathsf {consts^\bullet }}}(t) \subseteq {{\mathsf {CInst}}}^\bullet \) be the set of all non-built-in constant instances occurring in t and \({{\mathsf {types^\bullet }}}(t) \subseteq {{\mathsf {Type}^{\bullet }}}\) be the set of all non-built-in types that compose the types of non-built-in constants and (free or bound) variables occurring in t. Note that the \({{\mathsf {types^\bullet }}}\) operator is overloaded for types and terms.
Note that the \({{\mathsf {consts^\bullet }}}\) and \({{\mathsf {types^\bullet }}}\) operators commute with ground type substitutions (and similarly with type substitutions, of course):
Lemma 4
(1) \({{\mathsf {consts^\bullet }}}(\theta (t)) = \{c_{\theta (\sigma )} \mid c_\sigma \in {{\mathsf {consts^\bullet }}}(t)\}\)
(2) \({{\mathsf {types^\bullet }}}(\theta (t)) = \{\theta (\sigma ) \mid \sigma \in {{\mathsf {types^\bullet }}}(t)\}\).
3.3 Deduction
If D is a finite set of closed formulas, a.k.a. a theory, and \(\varphi \) is a closed formula, we write \(D \vdash \varphi \) for the deducibility of \(\varphi \) from D according to the standard deduction rules of polymorphic HOL [12, 27].Footnote 4 A theory D is called consistent if there exists \(\varphi \) such that \(D \not \vdash \varphi \) (or equivalently if \(D \not \vdash \mathsf {{False}}\), where the formula \(\mathsf {{False}}\) is defined in a standard way from the built-in constants).
3.4 Definitional Theories
We are interested in the consistency of theories arising from constant-instance and type definitions, which we call definitional theories.
Given \(c_\sigma \in {{\mathsf {CInst}}}^\bullet \) and a closed term \(t \in {{\mathsf {Term}}}_\sigma \), we let \(c_\sigma \equiv t\) denote the formula \(c_\sigma =t\). We call \(c_\sigma \equiv t\) a constant-instance definition provided \({{\mathsf {TV}}}(t) \subseteq {{\mathsf {TV}}}(c_\sigma )\) (i.e., \({{\mathsf {TV}}}(t) \subseteq {{\mathsf {TV}}}(\sigma )\)).
Given the types \(\tau \in {{\mathsf {Type}^{\bullet }}}\) and \(\sigma \in \mathsf {{Type}}\) and the closed term t whose type is \(\sigma \Rightarrow \mathsf{bool}\), we let \(\tau \equiv t\) denote the formula
We call \(\tau \equiv t\) a type definition, provided \({{\mathsf {TV}}}(t) \subseteq {{\mathsf {TV}}}(\tau )\) (which also implies \({{\mathsf {TV}}}(\sigma ) \subseteq {{\mathsf {TV}}}(\tau )\)).
Note that we defined \(\tau \equiv t\) not to mean:
as customary in most HOL-based systems, but rather to mean:
Moreover, note that we do not require \(\tau \) to have the form \((\alpha _1,\ldots ,\alpha _n)k\), as is currently required in Isabelle/HOL and the other HOL provers, but, more generally, allow any \(\tau \in {{\mathsf {Type}^{\bullet }}}\). (To ensure consistency, we will also require that \(\tau \) has no common instance with the left-hand side of any other type definition.) This enables an interesting feature: ad hoc overloading for type definitions. For example, given a unary type constructor \(\mathsf{tree}\), we can have totally different definitions for \(\mathsf{nat}\;\mathsf{tree}\), \(\mathsf{bool}\;\mathsf{tree}\) and \(\alpha \;\mathsf{list}\;\mathsf{tree}\).
In general, a definition will have the form \(u \equiv t\), where u is either a constant instance or a type and t is a term (subject to the specific constraints of constant-instance and type definitions). u and t are said to be the left-hand and right-hand sides of the definition. A definitional theory is a finite set of definitions.
3.5 The Consistency Problem
An Isabelle/HOL development proceeds by:
-
1.
declaring constants and types,
-
2.
defining constant instances and types,
-
3.
stating and proving theorems using the deduction rules of polymorphic HOL.
Consequently, at any point in the development, one has:
-
1.
a signature \((K,\mathsf {arOf}: K \rightarrow \mathbb {N},{{\mathsf {Const}}},{{\mathsf {tpOf}}}: {{\mathsf {Const}}}\rightarrow \mathsf {{Type}})\),
-
2.
a definitional theory D,
-
3.
other proved theorems.
In our abstract formulation of Isabelle/HOL’s logic, we do not represent explicitly point 3, namely the stored theorems that are not produced as a result of definitions, i.e., are not in D. The reason is that, in Isabelle/HOL, the theorems in D are not influenced by the others. Note that this is not the case of the other HOL provers, due to the type definitions: there, \(\tau \equiv t\), with \({{\mathsf {tpOf}}}(t) = \sigma \Rightarrow \mathsf{bool}\), is introduced in the unconditional form (*), and only after the user has proved that t gives a nonempty subset (i.e., that \(\exists x_\sigma .\; t\;x\) holds). Of course, Isabelle/HOL’s behavior converges with standard HOL behavior since the user is also required to prove nonemptiness, after which (*) is inferred by the system—however, this last inference step is normal deduction, having nothing to do with the definition itself. This very useful trick, due to Wenzel, cleanly separates definitions from proofs. In summary, we only need to guarantee the consistency of D:
The Consistency Problem: Find a sufficient criterion for a definitional theory D to be consistent (while allowing flexible overloading, as discussed in the introduction).
4 Our Solution to the Consistency Problem
Assume for a moment we have a proper dependency relation between defined items, where the defined items can be types or constant instances. Obviously, the closure of this relation under type substitutions needs to terminate, otherwise inconsistency arises immediately, as shown in Example 3. Moreover, it is clear that the left-hand sides of the definitions need to be orthogonal: defining \(c_{\alpha \times \mathsf{ind}\Rightarrow \mathsf{bool}}\) to be \(\lambda x_{\alpha \times \mathsf{ind}}.\mathsf {{False}}\) and \(c_{\mathsf{ind}\times \alpha \Rightarrow \mathsf{bool}}\) to be \(\lambda x_{\mathsf{ind}\times \alpha }.\mathsf {{True}}\) yields \(\lambda x_{\mathsf{ind}\times \mathsf{ind}}.\mathsf {{False}}= c_{\mathsf{ind}\times \mathsf{ind}\Rightarrow \mathsf{bool}} = \lambda x_{\mathsf{ind}\times \mathsf{ind}}.\mathsf {{True}}\) and hence \(\mathsf {{False}}= \mathsf {{True}}\).
It turns out that these necessary criteria are also sufficient for consistency. This was also believed by Wenzel and Obua; what they were missing was a proper dependency relation and a transparent argument for its consistency, which is what we provide next.
4.1 Definitional Dependency Relation
Given any binary relation R on \({{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \), we write \(R^+\) for its transitive closure, \(R^*\) for its reflexive-transitive closure and \(R^\downarrow \) for its (type-)substitutive closure, defined as follows: \(p \,R^\downarrow \, q\) iff there exist \(p',q'\) and a type substitution \(\rho \) such that \(p = \rho (p')\), \(q = \rho (q')\) and \(p' \,R\, q'\). We say that a relation R is terminating if there exists no sequence \((p_i)_{i \in \mathbb {N}}\) such that \(p_i\,R\,p_{i+1}\) for all i.
Let us fix a definitional theory D. We say D is orthogonal if for all distinct definitions \(u \equiv t\) and \(u' \equiv t'\) in D, we have one of the following cases:
-
either one of \(\{u,u'\}\) is a type and the other is constant instance,
-
or both u and \(u'\) are types and are orthogonal (\(u\, {\#}\, u'\)),
-
or both u and \(u'\) are constant instances and are orthogonal (\(u\, {\#}\,u'\)).
We define the binary relation \(\rightsquigarrow \) on \({{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \) by setting \(u \rightsquigarrow v\) iff one of the following holds:
-
1.
there exists a (constant-instance or type) definition in D of the form \(u \equiv t\) such that \(v \in {{\mathsf {consts^\bullet }}}(t) \,\cup \, {{\mathsf {types^\bullet }}}(t)\),
-
2.
there exists \(c \in {{\mathsf {Const}}}^{\bullet }\) such that \(u=c_{{{\mathsf {tpOf}}}(c)}\) and \(v \in {{\mathsf {types^\bullet }}}({{\mathsf {tpOf}}}(c))\).
We call \(\rightsquigarrow \) the dependency relation (associated to D).
Thus, when defining an item u by means of t (as in \(u \equiv t\)), we naturally record that u depends on the constants and types appearing in t (clause 1); moreover, any constant c should depend on its type (clause 2). But notice the bullets! We only record dependencies on the non-built-in items, since intuitively the built-in items have a pre-determined semantics which cannot be redefined or overloaded, and hence by themselves cannot introduce inconsistencies. Moreover, we do not dig for dependencies under any non-built-in type constructor—this can be seen from the definition of the \({{\mathsf {types^\bullet }}}\) operator on types which yields a singleton whenever it meets a non-built-in type constructor; the rationale for this is that a non-built-in type constructor has an “opaque” semantics which does not expose the components (as does the function type constructor). These intuitions will be made precise by our semantics in Sect. 4.4.
Consider the following example, where the definition of \(\alpha \;k\) is omitted:
Example 5

We record that \(c_{\mathsf{ind}\;k \Rightarrow \mathsf{bool}}\) depends on the non-built-in constants \(d_{\mathsf{bool}\;k\;k \Rightarrow \mathsf{ind}\;k \Rightarrow \mathsf{bool}}\) and \(d_{\mathsf{bool}\;k\;k}\), and on the non-built-in types \(\mathsf{bool}\;k\;k\) and \(\mathsf{ind}\;k\). We do not record any dependency on the built-in types \(\mathsf{bool}\;k\;k \Rightarrow \mathsf{ind}\;k \Rightarrow \mathsf{bool}\), \(\mathsf{ind}\;k \Rightarrow \mathsf{bool}\) or \(\mathsf{bool}\). Also, we do not record any dependency on \(\mathsf{bool}\;k\), which can only be reached by digging under k in \(\mathsf{bool}\;k\;k\).
4.2 The Consistency Theorem
We can now state our main result. We call a definitional theory D well-formed if it is orthogonal and the substitutive closure of its dependency relation, \(\rightsquigarrow ^\downarrow \), is terminating.
Note that a well-formed definitional theory is allowed to contain definitions of two different (but orthogonal) instances of the same constant—this ad-hoc overloading facility is a distinguishing feature of Isabelle/HOL among the HOL provers.
Theorem 6
If D is well-formed, then D is consistent.
Previous attempts to prove consistency employed syntactic methods [29, 35]. Instead, we will give a semantic proof:
-
1.
We define a new semantics of Polymorphic HOL, suitable for overloading and for which standard HOL deduction is sound (Sect. 4.4).
-
2.
We prove that D has a model according to our semantics (Sect. 4.5).
Then 1 and 2 immediately imply consistency.
4.3 Inadequacy of the Standard Semantics of Polymorphic HOL
But why define a new semantics? Recall that our goal is to make sense of definitions as in Example 1. In the standard (Pitts) semantics [30], one chooses a “universe” collection of sets \(\mathcal {U}\) closed under suitable set operations (function space, an infinite set, etc.) and interprets:
-
1.
the built-in type constructors and constants as their standard counterparts in \(\mathcal {U}\):
-
\([\mathsf{bool}]\) and \([\mathsf{ind}]\) are some chosen two-element set and infinite set in \(\mathcal {U}\)
-
\([\Rightarrow ] : \mathcal {U}\rightarrow \mathcal {U}\rightarrow \mathcal {U}\) takes two sets \(A_1,A_2 \in \mathcal {U}\) to the set of functions \(A_1 \rightarrow A_2\)
-
\([\mathsf {{True}}]\) and \([\mathsf {{False}}]\) are the two distinct elements of \([\mathsf{bool}]\), etc.
-
-
2.
the non-built-in type constructors similarly:
-
a defined type \({{\mathsf {prm}}}\) or type constructor \(\mathsf{list}\) as an element \([{{\mathsf {prm}}}] \in \mathcal {U}\) or operator \([\mathsf{list}] : \mathcal {U}\rightarrow \mathcal {U}\), produced according to their “typedef”
-
a polymorphic constant such as \({{\mathsf {perm}}}: {{\mathsf {prm}}}\rightarrow \alpha \rightarrow \alpha \) as a family \([{{\mathsf {perm}}}] \in \prod _{A \in \mathcal {U}} [{{\mathsf {prm}}}] \rightarrow A \rightarrow A\).
-
In standard polymorphic HOL, \({{\mathsf {perm}}}\) would be either completely unspecified, or completely defined in terms of previously existing constants—this has a faithful semantic counterpart in \(\mathcal {U}\). But now how to represent the overloaded definitions of \({{\mathsf {perm}}}\) from Example 1? In \(\mathcal {U}\), they would become:
-
\([{{\mathsf {perm}}}]_{[{{\mathsf {atom}}}]}\;\textit{pi}\;a = [{{\mathsf {apply}}}]\;\textit{pi}\;a\)
-
\([{{\mathsf {perm}}}]_{[\mathsf{nat}]}\;\textit{pi}\;n = n\)
-
\([{{\mathsf {perm}}}]_{[\mathsf{list}](A)}\;\textit{pi}\;\textit{xs} = [\mathsf {{map}}]_{A}\;([{{\mathsf {perm}}}]_{A}\;\textit{pi})\;\textit{xs}\)
There are two problems with these semantic definitions. First, given \(B \in \mathcal {U}\), the value of \([{{\mathsf {perm}}}]_B\) varies depending on whether B has the form \([{{\mathsf {atom}}}]\), or \([\mathsf{nat}]\), or \([\mathsf{list}](A)\) for some \(A \in \mathcal {U}\); hence the interpretations of the type constructors need to be non-overlapping—this is not guaranteed by the assumptions about \(\mathcal {U}\), so we would need to perform some low-level set-theoretic tricks to achieve the desired property. Second, even though the definitions are syntactically terminating, their semantic counterparts may not be: unless we again delve into low-level tricks in set theory (based on the axiom of foundation), it is not guaranteed that decomposing a set \(A_0\) as \([\mathsf{list}](A_1)\), then \(A_1\) as \([\mathsf{list}](A_2)\), and so on (as prescribed by the third equation for \([{{\mathsf {perm}}}]\)) is a terminating process.
Even worse, termination is in general a global property, possibly involving both constants and type constructors, as shown in the following example where c and k are mutually defined (so that a copy of \(e_{\mathsf{bool}\;k^n}\) is in \(\mathsf{bool}\;k^{n+1}\) iff n is even):
Example 7

The above would require a set-theoretic setting where such fixpoint equations have solutions; this is in principle possible, provided we tag the semantic equations with enough syntactic annotations to guide the fixpoint construction. However, such a construction seems excessive given the original intuitive justification: the definitions are “OK” because they do not overlap and they terminate. On the other hand, a purely syntactic (proof-theoretic) argument also seems difficult due to the mixture of constant definitions and (conditional) type definitions.
Therefore, we decide to go for a natural syntactic-semantic blend, which avoids stunt performance in set theory: we do not semantically interpret the polymorphic types, but only the ground types, thinking of the former as “macros” for families of the latter. For example, \(\alpha \Rightarrow \alpha \;\mathsf{list}\) represents the family \((\tau \Rightarrow \tau \;\mathsf{list})_{\tau \in \mathsf {{GType}}}\). Consequently, we think of the meaning of \(\alpha \Rightarrow \alpha \;\mathsf{list}\) not as \(\prod _{A \in \mathcal {U}} A \rightarrow [\mathsf{list}](A)\), but rather as \(\prod _{\tau \in \mathsf {{GType}}} [\tau ] \rightarrow [\tau \;\mathsf{list}]\). Moreover, a polymorphic formula \(\varphi \) of type, say, \((\alpha \Rightarrow \alpha \;\mathsf{list}) \Rightarrow \mathsf{bool}\), will be considered true just in case all its ground instances of types \((\tau \Rightarrow \tau \;\mathsf{list}) \Rightarrow \mathsf{bool}\) are true.
Another (small) departure from standard HOL semantics is motivated by our goal to construct a model for a well-formed definitional theory. Whereas in standard semantics one first interprets all type constructors and constants and only afterwards extends the interpretation to terms, here we need to interpret some of the terms eagerly, before some of the types and constants. Namely, given a definition \(u \equiv t\), we interpret t before we interpret u (according to t). This requires a straightforward refinement of the notion of semantic interpretation: to interpret a term, we only need the interpretations for a sufficient fragment of the signature containing all the items appearing in t.
4.4 Ground, Fragment-Localized Semantics for Polymorphic HOL
Recall that we have a fixed signature \((K,\mathsf {arOf}, {{\mathsf {Const}}}, {{\mathsf {tpOf}}})\), that \(\mathsf {{GType}}^\bullet \) is the set of ground non-built-in types and \({{\mathsf {GCInst}}}^\bullet \) the set of ground non-built-in constant instances.
Given \(T \subseteq \mathsf {{Type}}\), we define \({{\mathsf {Cl}}}(T) \subseteq \mathsf {{Type}}\), the built-in closure of T, inductively:
-
\(T \cup \{\mathsf{bool},\mathsf{ind}\} \subseteq {{\mathsf {Cl}}}(T)\)
-
\(\sigma _1 \Rightarrow \sigma _2 \;\in \; {{\mathsf {Cl}}}(T)\) if \(\sigma _1 \in {{\mathsf {Cl}}}(T)\) and \(\sigma _2 \in {{\mathsf {Cl}}}(T)\).
I.e., \({{\mathsf {Cl}}}(T)\) is the smallest set of types built from T by repeatedly applying built-in type constructors.
A (signature) fragment is a pair (T, C) with \(T \subseteq \mathsf {{GType}}^\bullet \) and \(C \subseteq {{\mathsf {GCInst}}}^\bullet \) such that \(\sigma \in {{\mathsf {Cl}}}(T)\) for all \(c_\sigma \in C\).
Let \(F = (T,C)\) be a fragment. We write:
-
\(\mathsf {{Type}}^F\), for the set of types generated by this fragment, namely \({{\mathsf {Cl}}}(T)\)
-
\({{\mathsf {Term}}}^F\), for the set of terms that fall within this fragment, namely \(\{t \in {{\mathsf {Term}}}\mid {{\mathsf {types^\bullet }}}(t) \subseteq T \,\wedge \, {{\mathsf {consts^\bullet }}}(t) \subseteq C\}\)
-
\({{\mathsf {Fmla}}}^F\!\), for \({{\mathsf {Fmla}}}\cap {{\mathsf {Term}}}^F\).
Lemma 8
The following hold:

The above straightforward lemma shows that fragments F include only ground items (points (1) and (2)) and are “autonomous” entities: the type of a term from F is also in F (3), and similarly for the free (term) variables (4), subterms (5) and substituted terms (6). This autonomy allows us to define semantic interpretations for fragments.
For the rest of this paper, we fix the following:
-
a singleton set \(\{*\}\)
-
a two-element set \(\{\mathsf {{true}},\mathsf {{false}}\}\)
-
a global choice function, \({{\mathsf {choice}}}\), that assigns to each nonempty set A an element \({{\mathsf {choice}}}(a) \in A\).
Let \(F = (T,C)\) be a fragment. An F-interpretation is a pair \(\mathcal {I}= (([\tau ])_{\tau \in T}, ([c_\tau ])_{c_\tau \in C})\) such that:
-
1.
\(([\tau ])_{\tau \in T}\) is a family such that \([\tau ]\) is a non-empty set for all \(\tau \in T\). We extend this to a family \(([\tau ])_{\tau \in {{\mathsf {Cl}}}(T)}\) by interpreting the built-in type constructors as expected:
-
\([\mathsf{bool}] = \{\mathsf {{true}},\mathsf {{false}}\}\)
-
\([\mathsf{ind}] = \mathbb {N}\) (the set of natural numbers)Footnote 5
-
\([\sigma \Rightarrow \tau ] = [\sigma ] \rightarrow [\tau ]\) (the set of functions from \([\sigma ]\) to \([\tau ]\))
-
-
2.
\(([c_\tau ])_{c_\tau \in C}\) is a family such that \([c_\tau ] \in [\tau ]\) for all \(c_\tau \in C\).
(Note that, in condition 2 above, \([\tau ]\) refers to the extension described at point 1.)
Let \(\mathsf {{GBI}}^F\) be the set of ground built-in constant instances \(c_\tau \) with \(\tau \in \mathsf {{Type}}^F\). We extend the family \(([c_\tau ])_{c_\tau \in C}\) to a family \(([c_\tau ])_{c_\tau \in \, C \;\cup \; \mathsf {{GBI}}^F}\), by interpreting the built-in constants as expected:
-
\([\rightarrow _{\mathsf{bool}\Rightarrow \mathsf{bool}\Rightarrow \mathsf{bool}}]\) as the logical implication on \(\{\mathsf {{true}},\mathsf {{false}}\}\)
-
\([=_{\tau \Rightarrow \tau \Rightarrow \mathsf{bool}}]\) as the equality predicate in \([\tau ] \rightarrow [\tau ] \rightarrow \{\mathsf {{true}},\mathsf {{false}}\}\)
-
\([{{\mathsf {zero}}}_\mathsf{ind}]\) as 0 and \([{{\mathsf {suc}}}_{\mathsf{ind}\Rightarrow \mathsf{ind}}]\) as the successor function for \(\mathbb {N}\)
-
\([{{\mathsf {some}}}_{(\tau \Rightarrow \mathsf{bool})\Rightarrow \tau }]\) as the following function, where, for each \(f : [\tau ] \rightarrow \{\mathsf {{true}},\mathsf {{false}}\}\), we let \(A_f = \{a \in [\tau ] \mid f(a) = \mathsf {{true}}\}\): \([{{\mathsf {some}}}_{(\tau \Rightarrow \mathsf{bool})\Rightarrow \tau }](f) = \left\{ \begin{array}{ll} {{\mathsf {choice}}}(A_f) &{} \text{ if } A_f \text{ is } \text{ non-empty } \\ {{\mathsf {choice}}}([\tau ]) &{} \text{ otherwise } \end{array}\right. \)
In summary, an interpretation \(\mathcal {I}\) is a pair of families \((([\tau ])_{\tau \in T}, ([c_\tau ])_{c_\tau \in C})\), which in fact gives rise to an extended pair of families \((([\tau ])_{\tau \in {{\mathsf {Cl}}}(T)},([c_\tau ])_{c_\tau \in \, C \;\cup \; \mathsf {{GBI}}^F})\).
Now we are ready to interpret the terms in \({{\mathsf {Term}}}^F\) according to \(\mathcal {I}\). A valuation  is called \(\mathcal {I}\)
-compatible if \(\xi (x_\sigma ) \in [\sigma ]^\mathcal {I}\) for each \(x_\sigma \in \mathsf {{Var}}_\mathsf {{GType}}\). We write \({{\mathsf {Comp}}}^\mathcal {I}\) for the set of compatible valuations. For each \(t \in {{\mathsf {Term}}}^F\), we define a function \([t] : {{\mathsf {Comp}}}^\mathcal {I}\rightarrow [{{\mathsf {tpOf}}}(t)]\) recursively over terms as expected:
is called \(\mathcal {I}\)
-compatible if \(\xi (x_\sigma ) \in [\sigma ]^\mathcal {I}\) for each \(x_\sigma \in \mathsf {{Var}}_\mathsf {{GType}}\). We write \({{\mathsf {Comp}}}^\mathcal {I}\) for the set of compatible valuations. For each \(t \in {{\mathsf {Term}}}^F\), we define a function \([t] : {{\mathsf {Comp}}}^\mathcal {I}\rightarrow [{{\mathsf {tpOf}}}(t)]\) recursively over terms as expected:

(Note that this recursive definition is correct thanks to Lemma 8.(5).)
If t is a closed term, then [t] does not truly depend on \(\xi \), and hence we can assume \([t] \in [{{\mathsf {tpOf}}}(t)]\). In what follows, we only care about the interpretation of closed terms.
The above concepts are parameterized by a fragment F and an F-interpretation \(\mathcal {I}\). If \(\mathcal {I}\) or F are not clear from the context, we may write, e.g., \([t]^{\mathcal {I}}\) or \([t]^{F,\mathcal {I}}\). If \(\varphi \in {{\mathsf {Fmla}}}^F\), we say that \(\mathcal {I}\) is a model of \(\varphi \), written \(\mathcal {I}\models \varphi \), if \([\varphi ]^{\mathcal {I}} = \mathsf {{true}}\).
Note that the pairs \((F,\mathcal {I})\) are naturally ordered: Given fragments \(F_1 = (T_1,C_1)\) and \(F_2 = (T_2,C_2)\), \(F_1\)-interpretation \(\mathcal {I}_1\) and \(F_2\)-interpretation \(\mathcal {I}_2\), we define \((F_1,\mathcal {I}_1) \le (F_2,\mathcal {I}_2)\) to mean \(T_1 \subseteq T_2\), \(C_1 \subseteq C_2\) and \([u]^{\mathcal {I}_1} = [u]^{\mathcal {I}_2}\) for all \(u \in T_1 \cup C_1\).
Lemma 9
If \((F_1,\mathcal {I}_1) \le (F_2,\mathcal {I}_2)\), then the following hold:

The total fragment \({{\mathsf {\top }}}= (\mathsf {{GType}}^\bullet ,{{\mathsf {GCInst}}}^\bullet )\) is the top element in this order. Note that \(\mathsf {{Type}}^{{\mathsf {\top }}}= \mathsf {{GType}}\) and \({{\mathsf {Term}}}^{{\mathsf {\top }}}= \mathsf {G Term}\).
So far, \(\mathcal {I}\models \varphi \), the notion of \(\mathcal {I}\) being a model of \(\varphi \), was only defined for formulas \(\varphi \) that belong to \({{\mathsf {Term}}}^F\), in particular, that are ground formulas. As promised, we extend this to polymorphic formulas by quantifying universally over all ground type substitutions. We only care about such an extension for the total fragment: Given a polymorphic formula \(\varphi \) and a \({{\mathsf {\top }}}\)-interpretation \(\mathcal {I}\), we say \(\mathcal {I}\) is a model of \(\varphi \), written \(\mathcal {I}\models \varphi \), if \(\mathcal {I}\models \theta (\varphi )\) for all ground type substitutions \(\theta \). This extends to sets E of (polymorphic) formulas: \(\mathcal {I}\models E\) is defined as \(\mathcal {I}\models \varphi \) for all \(\varphi \in E\).
Theorem 10
(Soundness). Let E be a set of formulas that has a total-fragment model, i.e., there exists a \({{\mathsf {\top }}}\)-interpretation \(\mathcal {I}\) such that \(\mathcal {I}\models E\). Then E is consistent.
Proof
It is routine to verify that the deduction rules for polymorphic HOL are sound w.r.t. our ground semantics. \(\square \)
4.5 The Model Construction
The only missing piece from the proof of consistency is the following:
Theorem 11
Assume D is a well-formed definitional theory. Then it has a total-fragment model, i.e., there exists a \({{\mathsf {\top }}}\)-interpretation \(\mathcal {I}\) such that \(\mathcal {I}\models D\).
Proof
For each \(u \in \mathsf {{GType}}^\bullet \cup {{\mathsf {GCInst}}}^\bullet \), we define [u] by well-founded recursion on \(\rightsquigarrow ^{{\downarrow } +}\), the transitive closure of \(\rightsquigarrow ^\downarrow \); indeed, the latter is a terminating (well-founded) relation by the well-formedness of D, hence the former is also terminating.
We assume [v] has been defined for all \(v \in \mathsf {{GType}}^\bullet \cup {{\mathsf {GCInst}}}^\bullet \) such that \(u \rightsquigarrow ^{{\downarrow }+} v\). In order to define [u], we first need some terminology: We say that a definition \(w \equiv s\) matches u if there exists a type substitution \(\theta \) with \(u = \theta (w)\). We distinguish the cases:
-
1.
There exists no definition in D that matches u. Here we have two subcases:
-
\(u \in \mathsf {{GType}}^\bullet \). Then we define \([u] = \{*\}\).
-
\(u \in {{\mathsf {GCInst}}}^\bullet \). Say u has the form \(c_\sigma \). Then \(u \rightsquigarrow ^\downarrow \sigma \), and hence \([\sigma ]\) is defined; we define \([u] = {{\mathsf {choice}}}([\sigma ])\).
-
-
2.
There exists a definition \(w \equiv s\) in D that matches u. Then let \(\theta \) be such that \(u = \theta (w)\), and let \(t = \theta (s)\). Let \(V_u = \{v \mid u \rightsquigarrow ^{{\downarrow }+} v\}\), \(T_u = V_u \cap \mathsf {{Type}}\) and \(C_u = V_u \cap {{\mathsf {CInst}}}\). It follows from the definition of \(\rightsquigarrow \) that \(F_u = (T_u,C_u)\) is a fragment; moreover, from the definition of \(\rightsquigarrow \) and Lemma 4, we obtain that \({{\mathsf {types^\bullet }}}(t) \subseteq T_u\) and \({{\mathsf {consts^\bullet }}}(t) \subseteq C_u\), which implies \(t \in {{\mathsf {Term}}}^{F_u}\); hence we can speak of the value \([t]^{F_u,\mathcal {I}_u}\) obtained from the \(F_u\)-interpretation \(\mathcal {I}_u = (([v])_{v \in T_u},([v])_{v \in C_u})\). We have two subcases:
-
\(u \in {{\mathsf {GCInst}}}^\bullet \). Then we define \([u] = [t]^{F_u,\mathcal {I}_u}\).
-
\(u \in \mathsf {{GType}}^\bullet \). Then the type of t has the form \(\sigma \Rightarrow \mathsf{bool}\); and since \(\sigma \in {{\mathsf {types^\bullet }}}(t) \subseteq \mathsf {{Type}}^{F_u}\), it follows that \([\sigma ]^{F_u,\mathcal {I}_u}\) is also defined. We have two subsubcases:
-
\([\exists x_\sigma .\;t\,x] = \mathsf {{false}}\). Then we define \([u] = \{*\}\).
-
\([\exists x_\sigma .\;t\,x] = \mathsf {{true}}\). Then we define \([u] = \{a \in [\sigma ]^{F_u,\mathcal {I}_u} \mid [t](a) = \mathsf {{true}}\}\).
-
-
Having defined the \({{\mathsf {\top }}}\)-interpretation \(\mathcal {I}= (([u])_{u \in \mathsf {{GType}}^\bullet },([u])_{u \in {{\mathsf {GCInst}}}^\bullet })\), it remains to show that \(\mathcal {I}\models D\). To this end, let \(w \equiv s\) be in D and let \(\theta '\) be a ground type substitution. We need to show \(\mathcal {I}\models \theta '(w \equiv s)\), i.e., \(\mathcal {I}\models \theta '(w) \equiv \theta '(s)\).
Let \(u = \theta '(w)\); then u matches \(w \equiv s\), and by orthogonality this is the only definition in D that it matches. So the definition of [u] proceeds with case 2 above, using \(w \equiv s\)—let \(\theta \) be the ground type substitution considered there. Since \(\theta '(w) = \theta (w)\), it follows that \(\theta '\) and \(\theta \) coincide on the type variables of w, and hence on the type variables of s (because, in any definition, the type variables of the right-hand side are included in those of the left-hand side); hence \(\theta '(s) = \theta (s)\).
Now the desired fact follows from the definition of \(\mathcal {I}\), by a case analysis matching the subcases of the above case 2. (Note that the definition operates with \([t]^{F_u,\mathcal {I}_u}\), whereas we need to prove the fact for \([t]^{{{\mathsf {\top }}},\mathcal {I}}\); however, since \((F_u,\mathcal {I}_u) \le ({{\mathsf {\top }}},\mathcal {I})\), by Lemma 9 the two values coincide; and similarly for \([\sigma ]^{F_u,\mathcal {I}_u}\) vs. \([\sigma ]^{{{\mathsf {\top }}},\mathcal {I}}\).) \(\square \)
5 Deciding Well-Formedness
We proved that every well-formed theory is consistent. From the implementation perspective, we can ask ourselves how difficult it is to check that the given theory is well-formed. We can check that D is definitional and orthogonal by simple polynomial algorithms. On the other hand, Obua [29] showed that a dependency relation generated by overloaded definitions can encode the Post correspondence problem and therefore termination of such a relation is not even a semi-decidable problem.
Kunčar [19] takes the following approach: Let us impose a syntactic restriction, called compositionality, on accepted overloaded definitions which makes the termination of the dependency relation decidable while still permitting all use cases of overloading in Isabelle. Namely, let

be the substitutive and transitive closure of the dependency relation \(\rightsquigarrow \) (which is in fact equal to \(\rightsquigarrow ^{{\downarrow } +}\)). Then D is called composable if for all \(u, u'\) that are left-hand sides of some definitions from D and for all v such that

, it holds that either \(u' \le v\), or \(v \le u'\), or \(u'\, {\#}\, v\). Under composability, termination of

is equivalent to acyclicity of \(\rightsquigarrow \), which is a decidable condition.Footnote 6
Theorem 12
The property of D of being composable and well-formed is decidable.
Proof
The above-mentioned paper [19] presents a quadratic algorithm (in the size of \(\rightsquigarrow \)), Check, that checks that D is definitional, orthogonal and composable, and that

terminates.Footnote 7 Notice that

terminates iff \(\rightsquigarrow ^\downarrow \) terminates. Thus, Check decides whether D is composable and well-formed. \(\square \)
For efficiency reasons, we optimize the size of the relation that the quadratic algorithm works with. Let \(\rightsquigarrow _1\) be the relation defined like \(\rightsquigarrow \), but only retaining clause 1 in its definition. Since \(\rightsquigarrow ^\downarrow \) is terminating iff \(\rightsquigarrow _1^\downarrow \) is terminating, it suffices to check termination of the latter.
6 Conclusion
We have provided a solution to the consistency problem for Isabelle/HOL’s logic, namely, polymorphic HOL with ad hoc overloading. Consistency is a crucial, but rather weak property—a suitable notion of conservativeness (perhaps in the style of Wenzel [35], but covering type definitions as well) is left as future work. Independently of Isabelle/HOL, our results show that Gordon-style type definitions and ad hoc overloading can be soundly combined and naturally interpreted semantically.
Notes
- 1.
In Isabelle/HOL, as in any HOL-based prover, the “datatype” command is not primitive, but is compiled into “typedef.”
- 2.
- 3.
Namely, Coq 8.4pl5; the inconsistency is fixed in Coq 8.5 beta.
- 4.
The deduction in polymorphic HOL takes place using open formulas in contexts. In addition, Isabelle/HOL distinguishes between theory contexts and proof contexts. We ignore these aspects in our presentation here, since they do not affect our consistency argument.
- 5.
Any infinite (not necessarily countable) set would do here; we only choose \(\mathbb {N}\) for simplicity.
- 6.
Composability reduces the search space when we are looking for the cycle—it tells us that there exist three cases on how to extend a path (to possibly close a cycle): in two cases we can still (easily) extend the path (\(v \le u'\) or \(u' \le v\)) and in one case we cannot (\(v \, {\#}\, u'\)). The fourth case (v and \(u'\) have a non-trivial common instance; formally \(u' \not \le v\) and \(v \not \le u'\) and there exists w such that \(w\le u'\), \(w\le v\)), which complicates the extension of the path, is ruled out by composability. More about composability can be found in the original paper.
- 7.
The correctness proof is relatively general and works for any
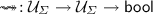
on a set \(\mathcal {U}_\varSigma \) endowed with a certain structure—namely, three functions \(= \,: \mathcal {U}_\varSigma \rightarrow \mathcal {U}_\varSigma \rightarrow \mathsf{bool}\), \(\mathsf {App}: (\mathsf {{Type}}\rightarrow \mathsf {{Type}}) \rightarrow \mathcal {U}_\varSigma \rightarrow \mathcal {U}_\varSigma \) and \({\mathsf {size}}: \mathcal {U}_\varSigma \rightarrow \mathbb {N}\), indicating how to compare for equality, type-substitute and measure the elements of \(\mathcal {U}_\varSigma \). In this paper, we set \(\varSigma = (K,\mathsf {arOf},C,{{\mathsf {tpOf}}})\) and \(\mathcal {U}_\varSigma = {{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \). The definition of \(=, \mathsf {App}\) and \({\mathsf {size}}\) is then straightforward: two elements of \({{\mathsf {Type}^{\bullet }}}\cup {{\mathsf {CInst}}}^\bullet \) are equal iff they are both constant instances and they are equal or they are both types and they are equal; \(\mathsf {App}\,\rho \,\tau = \rho (\tau )\) and \(\mathsf {App}\,\rho \,c_{\tau } = c_{\rho (\tau )}\); finally, \({\mathsf {size}}(\tau )\) counts the number of type constructors in \(\tau \) and \({\mathsf {size}}(c_\tau ) = {\mathsf {size}}(\tau )\).
References
The HOL4 Theorem Prover. http://hol.sourceforge.net/
Adams, M.: Introducing HOL Zero. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 142–143. Springer, Heidelberg (2010)
Anand, A., Rahli, V.: Towards a formally verified proof assistant. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 27–44. Springer, Heidelberg (2014)
Arthan, R.D.: Some mathematical case studies in ProofPower-HOL. In: TPHOLs 2004 (2004)
Barras, B.: Coq en Coq. Technical report 3026, INRIA (1996)
Barras, B.: Sets in Coq, Coq in Sets. J. Formalized Reasoning 3(1), 29–48 (2010)
Bertot, Y., Casteran, P.: Interactive Theorem Proving and Program Development: Coq’Art: The Calculus of Inductive Constructions. Springer, Heidelberg (2004)
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion. In: ICFP 2015. ACM (2015)
Bove, A., Dybjer, P., Norell, U.: A brief overview of Agda – a functional language with dependent types. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 73–78. Springer, Heidelberg (2009)
Dénès, M.: [Coq-Club] Propositional extensionality is inconsistent in Coq, archived at https://sympa.inria.fr/sympa/arc/coq-club/2013-12/msg00119.html
Gordon, M.J.C., Melham, T.F. (eds.): Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press, New York (1993)
Haftmann, F., Wenzel, M.: Constructive type classes in Isabelle. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 160–174. Springer, Heidelberg (2007)
Harrison, J.: HOL Light: a tutorial introduction. In: Srivas, M., Camilleri, A. (eds.) FMCAD 1996. LNCS, vol. 1166, pp. 265–269. Springer, Heidelberg (1996)
Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 177–191. Springer, Heidelberg (2006)
Hölzl, J., Immler, F., Huffman, B.: Type classes and filters for mathematical analysis in Isabelle/HOL. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 279–294. Springer, Heidelberg (2013)
Huffman, B., Urban, C.: Proof pearl: a new foundation for Nominal Isabelle. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 35–50. Springer, Heidelberg (2010)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: HOL with definitions: semantics, soundness, and a verified implementation. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 308–324. Springer, Heidelberg (2014)
Kunčar, O.: Correctness of Isabelle’s cyclicity checker: implementability of overloading in proof assistants. In: CPP 2015. ACM (2015)
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. Technical report (2015). www.eis.mdx.ac.uk/staffpages/andreipopescu/pdf/IsabelleHOL.pdf
Leino, K.R.M., Moskal, M.: Co-induction simply–automatic co-inductive proofs in a program verifier. In: FM 2014 (2014)
Lochbihler, A.: Light-Weight Containers for Isabelle: Efficient, Extensible, Nestable. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 116–132. Springer, Heidelberg (2013)
McBride, C., et al.: [HoTT] Newbie questions about homotopy theory and advantage of UF/Coq, archived at http://article.gmane.org/gmane.comp.lang.agda/6106
Müller, O., Nipkow, T., von Oheimb, D., Slotosch, O.: HOLCF = HOL + LCF. J. Funct. Program. 9, 191–223 (1999)
Myreen, M.O., Davis, J.: The reflective Milawa theorem prover is sound. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 421–436. Springer, Heidelberg (2014)
Nipkow, T., Klein, G.: Concrete Semantics - With Isabelle/HOL. Springer, New York (2014)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002)
Kang, J., Adibi, S.: Type classes and overloading resolution via order-sorted unification. In: Doss, R., Piramuthu, S., ZHOU, W. (eds.) Functional Programming Languages and Computer Architecture. LNCS, vol. 523, pp. 1–14. Springer, Heidelberg (1991)
Obua, S.: Checking conservativity of overloaded definitions in higher-order logic. In: Pfenning, F. (ed.) RTA 2006. LNCS, vol. 4098, pp. 212–226. Springer, Heidelberg (2006)
Pitts, A.: Introduction to HOL: a theorem proving environment for higher order logic. Chapter The HOL Logic, pp. 191–232. In: Gordon and Melham [12] (1993)
Shankar, N., Owre, S., Rushby, J.M.: PVS Tutorial. Computer Science Laboratory, SRI International (1993)
Sozeau, M., Oury, N.: First-class type classes. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 278–293. Springer, Heidelberg (2008)
Urban, C.: Nominal techniques in Isabelle/HOL. J. Autom. Reason. 40(4), 327–356 (2008)
Wadler, P., Blott, S.: How to make ad-hoc polymorphism less ad-hoc. In: POPL (1989)
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A.P. (eds.) TPHOLs 1997. LNCS, vol. 1275, pp. 307–322. Springer, Heidelberg (1997)
Acknowledgments
We thank Tobias Nipkow, Larry Paulson and Makarius Wenzel for inspiring discussions and the anonymous referees for many useful comments. This paper was partially supported by the DFG project Security Type Systems and Deduction (grant Ni 491/13-3) as part of the program Reliably Secure Software Systems (RS3, priority program 1496).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Kunčar, O., Popescu, A. (2015). A Consistent Foundation for Isabelle/HOL. In: Urban, C., Zhang, X. (eds) Interactive Theorem Proving. ITP 2015. Lecture Notes in Computer Science(), vol 9236. Springer, Cham. https://doi.org/10.1007/978-3-319-22102-1_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-22102-1_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22101-4
Online ISBN: 978-3-319-22102-1
eBook Packages: Computer ScienceComputer Science (R0)