Spectrum Sublet Game Among Secondary Users in Cognitive Radio Networks

Abstract

Dynamic spectrum sharing can improve the efficiency of spectrum utilization. Spectrum trading between primary users (PUs) and secondary users (SUs) is a popular and efficient way to fulfill this kind of spectrum sharing. In this paper we present a novel spectrum trading mechanism which operate among secondary users. More specifically, some secondary users which has leased spectrum from PUs can sublet it to other SUs to reduce their own leasing cost. Then all of the SUs can share these spectrum bands to conduct data transmission respectively. This leads to a new multi-leader multi-follower (MLMF) game which is different from existing works. The existence of Nash equilibrium of this formulated game is proven by redefining it as a shared MLMF constraint game. A decentralized algorithm is then proposed to find Nash equilibrium of this two tiers game with only local information. Simulations are provided to illustrate the convergence and effectiveness of the proposed algorithm.

1 Introduction

Wireless spectrum can be shared by primary users (PUs) and secondary users (SUs) through dynamic trading in cognitive radio networks (CRNs) to achieve more efficient spectrum utilization [1]. PU dynamically trade the usage right of temporarily unused part of its licensed spectrum to SUs in exchange for monetary compensation. SUs are price takers who lease the licensed spectrum for their own data transmissions. Various spectrum trading mechanisms have been proposed along this direction in literature. The common mode of these works assume that each SU occupies the leased bands alone regardless of the behaviors of owners so long as it’s under the interference constraint. PU sells its spectrum bands to SUs and charge them respectively without considering who buys its channel.

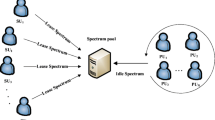
However, wireless spectrum is often considered as scarce resource, thus the rent of spectrum could be very high for SUs even they only lease them temporarily. Existing works deal with the spectrum trading of separate purchase mode in which each SU buys a channel independently and is charged separately, which may restrict the spectrum market. Multiple SUs form a group purchasing the same spectrum band together could reduce the burden of everyone. There could be two schemes to enforce this kind of spectrum trading. One is that a group of SUs purchase the same spectrum band with PU concurrently and joint funding the trade. Another one is that one SU buy a spectrum band at first, and then it sublets it to others and share it with them. We focus on the latter one in this paper, and the former will be left as our future work.

We call the users that can’t afford the spectrum alone but still need frequency bands as hungry users (HUs). The users who have bought spectrum and want to share the leasing cost by subletting spectrum to HUs are called full users (FUs). The spectrum trade between FU and PU is called primary market, while the spectrum trade between HU and FU is called secondary market. FU needs to make leasing and pricing decision in primary market based on its own demand and the demand from secondary market to maximize its payoff which is the sum of its own data rate and sublet profits. After perceiving the prices of FUs, each HU sets appropriate communication power on the channel of the selected FU and pay the rent. So they need deal with FU selection and power allocation problem jointly. We focus on the interaction in secondary market in this paper, where FU and HUs share the same channel and interfere with each other. On the FU’s side, more HUs purchasing with itself, lower cost it will pay for its leased channel, but higher interference from HUs would lead to lower data rate. More FUs coexisting in the network will complicate this problem due to the competition among these FUs, which makes the pricing strategy more challenging.

This paper studies the spectrum sublet problem in the secondary market and model the interaction between FUs and HUs as a multi-leader multi-follower (MLMF) game. A similar problem related to the joint price decision of leader and resource selection of follower has been addressed in CRNs and femtocell networks. All these works consider the problem of spectrum trade between PU and SU in primary market, not the trade among different SUs. These two kinds of trade have much in common, but there are specific features in the later one and can not be solved using existing schemes.

There exists a rich body of related literature on spectrum trading in primary market. [2, 3] tackled the problem of pricing strategy of PUs and power allocation of SUs by model it as a stackelberg game. These works only consider interference among SUs which are charged with fixed price. In [4, 5], a single PU prices interference power from SUs under the interference power constraint, so the communication rate is not influenced by the strategies of SUs. All SUs works on the same single channel based on CDMA, and the channel selection is not considered in this paper. In [6], authors studied the trade between macrocell base station and femtocell users. The former controls the received interference from femtocell users through pricing the interference from later. However, all of above works resolve the two-tier resource trading with single leader multiple followers game, while the problem considered in this paper is a MLMF scenario.

Competition of multiple wireless providers to sell spectrum is studied in related works, which uses MLMF game to model the two stages decision problem. Reference [7] considered multiple-seller and multiple-buyer spectrum trading in CRNs using MLMF game, where PUs compete by setting price to attract SUs. The profit of each PU is the product of price and number of users who purchase spectrum with it. There is no interference between PU and SU. More SUs making trade with it produce higher profits in this model. Reference [8] studied spectrum leasing from owners and trading with end users for two secondary operators whose profits are functions of bandwidths sold to users. The operators profit from a price discrepancy when they buy spectrum from owners and sell it to end users.

All of these works above do not consider how spectrum is exploited and only treat it as ordinary commodity. A seller doesn’t care about whom it sells the spectrum resource to, only care about how much sold. However, in the secondary market where spectrum is shared by FUs and HUs, interference plays a more important role. FUs hope to sublet spectrum to the harmless HUs who produce minimum interference. This interference aware spectrum sublet in secondary market has not been studied before. This problem is challenging when there is competition among FUs in the first stage and among HUs in the second stage, especially the optimal decision of these users are made dynamically.

The key results and contributions of this paper are summarized as follows.

• We proposed a novel spectrum trading mechanism which is conducted among secondary users. The two kinds of secondary users can improve their payoff by spectrum sublet. The interaction of SUs is formulated as a MLMF game with a new defined utility function.

• Due to the challenge that there is no closed form best response function of the leader optimization problem in the MLMF game, we present a new method to prove the existence of the Nash equilibrium.

• We provide a distributed algorithm that results in an equilibrium of the spectrum sublet game. The participants only need local information during the execution of this algorithm.

We organize the paper as follows. In Sect. 2, we present the system model and formulate the problem into a multi-leader multi-follower game. In Sect. 3, we analyze the properties of the NE. In Sect. 4, we provide our main algorithm and its convergence properties. We present simulation results in Sect. 5 and conclude the paper in Sect. 6.

2 System Model and Problem Formulation

Suppose there are a set $F=\{1,...,M\}$ of FUs and a set $H=\{1,...,N\}$ of HUs in CRNs. Each user (a FU or HU) consists of a transmitter and receiver forming a data link. FU j has leased a channel from primary user with bandwidth of size $B_j$ and it would like to sublet the leased channel to HUs to share cost. Each HU can access multiple channels of FUs simultaneously. Assume that the channels of each FU are orthogonal. A FU and the HUs purchased with it share the channel equally and take the interference caused by others as noises.

There are two levels of competition in this multiple-seller multiple-buyer secondary market. The competition in the first level is among FUs to conduct price war. FU j charges HU $\mu _j$ per unit interference power and all the price are set simultaneously. Lower price could make a FU attract more HUs thus boost its profits, but the increased interference will reduce its own transmission rate. In the second level, after perceiving the price vector ${\{ {\mu _j}\} _{j \in F}}$, HUs allocate power to all channels to maximize their own utility. In this case, if many HUs choose to buy channel offered by the same FU or put more power on this it, the corresponding channel becomes congested, which may result in an increased spectrum price and/or performance degradation.

Let $p_{ij}$ represent the amount of power HU i transmits on the channel of FU j when it purchases with j. $p_{ij}=0$ means i doesn’t purchase with j. Let $p_i=(p_{i1},...,p_{iM})$ denotes the power profile of HU i and $p_{-i}$ be the joint power profiles of all the HUs other than i. The power profiles of the HUs must also satisfy the following two constraints: (1) Total power constraints: $\sum \limits _{j = 1}^M {{p_{ij}} \le {{\overline{p} }_i}}$, $\forall i \in H$, where ${\overline{p} }_i$ is the power limit for HU i; (2) Positivity constraints: $p_{ij}\ge 0$.

The aggregated received transmission power of FU j on its own channel is ${I_j} = \sum \limits _{i = 1}^N {{{\left| {{h_{ji}}} \right| }^2}{p_{ij}}}$, where $h_{ji}$ is the channel gain of the transmitter of HU i to the receiver of FU j. We assume that the link gains will be fixed for the duration of the sublet game as [6, 9]. This indicates that the fading rate of the channel is slow in comparison to the rate of power control algorithm.

The FUs objective is to maximize its utility obtained from selling the interference quota to femtocell users and its own transmission rate. Mathematically, the utility function of FU j can be defined as

$$\begin{aligned} {U_j}({\mu _j},{\mu _{ - j}},\mathrm{P}) = {\beta _j}{B_j}\log (1 + \frac{{{{\left| {{h_j}} \right| }^2}{p_j}}}{{w + {I_j}}}) + {\mu _j}{I_j} - \varphi ({B_j}) \end{aligned}$$

(1)

where $p_j$ is the transmission power of FU j, w is the variance of noise, $\beta _i$ is predefined coefficient that transforms the ith FUs transmission rate to a monetary utility. We refer to $\beta _i$ as the preference factor of FU j. If FU j prefers to achieve higher data rate, it can set $\beta _i$ to a large value. $\varphi (B_j)$ is the cost of spectrum leasing from PU. $B_j$ is a constant in this paper since we focus on the interaction of users in secondary market. $P={p_1,...,p_N}$ is the power profile of all HUs, which is actually a function of $(\mu _j, \mu _{-j})$ under the stackelberg game formulation. This indicates that the amount of the interference quota that the HUs are willing to buy is dependent on the interference price. Each FU j has to find the optimal interference price $\mu _j$ to maximize its utility.

At the second competition level, the aggregated received transmission power of HU i on the channel of FU j can be written as

$$\begin{aligned} {I_{ij}} = \sum \limits _{k = 1,k \ne i}^N {{{\left| {{h_{ki}(j)}} \right| }^2}{p_{kj}}} + {\left| {{h_{ji}}} \right| ^2}{p_j} \end{aligned}$$

(2)

where $h_{ki}(j)$ is the channel gain from k to i on the channel of FU j, $h_{ji}$ is the channel gain from j to i. Then the utility of HU i can be defined as

$$\begin{aligned} {U_i}({p_i},{p_{ - i}},\mu ) = \sum \limits _{j = 1}^M {[{\beta _i}{B_j}\log (1 + \frac{{{{\left| {{h_{ij}}} \right| }^2}{p_{ij}}}}{{w + {I_{ij}}}})} - {\mu _j}{\left| {{h_{ji}}} \right| ^2}{p_{ij}}] \end{aligned}$$

(3)

where $h_{ij}$ is the channel gain of HU i on FU jth channel, $\mu =(\mu _i,...,\mu _M)$. It is observed from (3) that the utility function of HU consist of two parts: profit and cost. If the HU increases its transmit power, the transmission rate will increase, and thus the profit will increase. On the other hand, with the increasing of the transmit power, the HU will definitely cause more interference to FUs. Then, it has to buy more interference quota from FUs, and this will increase the cost. Therefore, power allocation strategies are needed at the HUs to maximize their utilities. Mathematically, for each user i, the problem can be formulated as

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{p_i}} {U_i}({p_i}, {p_{ - i}}, \mu ) \\ s.t. \sum \limits _{j = 1}^M {{p_{ij}} \le {{\overline{p} }_i}} , {p_{ij}} \ge 0, \forall i \in H \\ \end{array} \end{aligned}$$

(4)

where ${\overline{p}}_i$ is the maximum allowable transmission power. Based on the discussion above, we are now ready to define a multi-leader stackelberg game $\Gamma =(F,H,\{\mu _j\}_{j\in F},\{P_i\}_{i\in H},\{U_j\}, \{U_i\})$ The utility functions of leader $U_i$ and $U_j$ are given in (1) and (3). The objective of such a Stackelberg game is to find the subgame perfect equilibrium (SPE) point(s) where neither the leader (FUs) nor the followers (HUs) have incentive to deviate unilaterally from that point(s). More specifically, the point $(\mu ^{*}, p^*)$ is a SPE for the proposed Stackelberg game if for any $(\mu , p)$ , the following conditions are satisfied:

$$\begin{aligned} \begin{array}{l} {U_j}(\mu _j^*, \mu _{ - j}^*,{p^\mathrm{{*}}}) \ge {U_j}({\mu _j}, \mu _{ - j}^*,{p^\mathrm{{*}}}) \\ {U_i}(p_i^*, p_{ - i}^*, {\mu ^*}) \ge {U_i}(p_i^{}, p_{ - i}^*, {\mu ^*}) \\ \end{array} \end{aligned}$$

(5)

3 Property of the Sublet Game

A common approach of analyzing multiple layers game is backward induction to characterize the subgame perfect equilibrium. We start with the second stage game and analyze the HUs’ behaviors given the FUs’ pricing decisions. In order to maximize its utility, each HU competes with each other to allocates limited power to the channels with lower price and little interference. We prove this subgame among HUs has only one NE by showing that it belong to a potential game, which is defined as

Definition 1

(Potential Game [10]): A game is called a potential game if it admits a potential function $\varPhi (x)$ such that for every $i \in H$ and $p_{-i}$,

$$\begin{aligned} \varPhi (p^*_i, {p_{ - i}},\mu ) - \varPhi ({p_i}, {p_{ - i}},\mu ) = {U_i}(p^*_i, {p_{ - i}},\mu ) - {U_i}({p_i}, {p_{ - i}},\mu ) \end{aligned}$$

(6)

Based on this definition, we can give the conclusion as follows.

Theorem 1

Given any pricing strategy $\mu$, the low-tier game among HUs is a potential game and there is only one NE $p^*$ which is the maximum of the potential function, i.e., $p^* \in \mathop {\arg }\limits _{p \in P} \max \varPhi (p, \mu )$. The upper-tier game among FUs also possess at least one pure strategy Nash equilibrium.

Proof

The potential function of subgame among HUs is

$$\begin{aligned} \varPhi ({p_i},{p_{ - i}},\mu ) = \sum \limits _{j = 1}^M {[{\beta _i B_j}\log (w + \sum \limits _{i = 1}^N {{{\left| {{h_{ij}}} \right| }^2}{p_{ij}} + } {{\left| {{h_{ji}}} \right| }^2}{p_j})} - \sum \limits _{i = 1}^N {{\mu _j}{{\left| {{h_{ji}}} \right| }^2}{p_{ij}}]} \end{aligned}$$

(7)

We can readily observe that the following identity is true for all $i \in H$:

$$\begin{aligned} \begin{array}{l} \varPhi ({p_i}, {p_{ - i}},\mu ) - \varPhi (p{'_i}, {p_{ - i}},\mu ) \\ = \sum \limits _{j = 1}^M {[{\beta _i}{B_j}\log (\frac{{w + {{\left| {{h_{ji}}} \right| }^2}{p_j} + \sum \limits _{i = 1}^N {{{\left| {{h_{ij}}} \right| }^2}{p_{ij}}} }}{{w + {{\left| {{h_{ji}}} \right| }^2}{p_j} + \sum \limits _{i = 1}^N {{{\left| {{h_{ij}}} \right| }^2}p{'_{ij}}} }}) - } \sum \limits _{i = 1}^N {{\mu _j}{{\left| {{h_{ij}}} \right| }^2}({p_{ij}} - p{'_{ij}})]} \\ = {U_i}({p_i}, {p_{ - i}},\mu ) - {U_i}(p{'_i}, {p_{ - i}},\mu ) \\ \end{array} \end{aligned}$$

(8)

Thus, based on Definition 1 we can get that $\varPhi (p_i,p_{-i},\mu )$ is a potential function and the subgame posses a pure-strategy NE. Observing that $\varPhi (p,\mu )$ is concave and the domain of which is convex, thus there is only one extreme value which corresponding to the unique NE of the subgame.

The competition among FUs belongs to equilibrium problem with equilibrium constraints (EPECs) in which a collection of FUs compete in a game constrained by the equilibrium conditions of another Nash game amongst the HUs. The resulting equilibrium problem is complicated by nonconvex constrainted deduced by the follower game, thus the Kakutani’s fixed point theorems can’t be used to prove the existence of NE of the up tier game. In this paper we adopt another method to bypass this challenge. Note that the low-tier game among HUs is potential game and the NE of it is the maximization of potential function (8), then we can redefine the optimization problem of each FU as follows:

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{{\mu _j},{p_j}} {U_j}({\mu _j},{p_j};{\mu _{ - j}}) \\ s.t. {p_j} \in \mathop {\arg \max }\limits _{{p_i}} = \varPhi ({p_i}, {p_{ - i}},\mu ) \\ {\mu _j} \ge 0, for \ \forall j \in F \\ \end{array} \end{aligned}$$

(9)

where $p_j$ is conjecture about HU’s equilibria seen by FU j, which could be different from $p_{-j}$ if there are multiple NE in the low-tier game. The constraint of each FU’s optimization problem is identical since the function $\varPhi$ is the same to each one. Based on discussion above, there is unique extreme value of $\varPhi$. In another word, FUs as leaders of the two level game share all equilibrium constraints. This lead to that the new defined optimization problem of FUs belong to shared constraint EPECs and based on the Theorem 4.4 of [11], we can deduce that the up tire game possess at least one pure strategy Nash equilibrium.

4 Iterative Algorithm to Approach Subgame Nush Equilibrium

To obtain the subgame Nash equilibrium of the prices set by the FUs, information on the net utility function of all HUs would be required. Also, the power allocation profile of HUs at the equilibrium would be required. However, these information may not be available in a practical cognitive radio environment. Therefore, we propose that a FU iteratively adjusts the price and observe the received net utility. A FU adjusts the price in a direction that results in a higher payoff. The relationship between the strategies in the current and the future iteration can be expressed as follows:

$$\begin{aligned} {\mu _j}(t + 1) = {\mu _j}(t) + {\alpha _j}\frac{{\partial {U_j}({\mu _j},{\mu _{ - j}},p)}}{{\partial {\mu _j}}} \end{aligned}$$

(10)

where $\alpha _j$ is the speed of adjustment for the spectrum price of FU j. Since the closed form solution of the best response function of FUs can’t be obtained, the partial derivative has no closed form neither. But the marginal payoff can be estimated by a FU by observing the variations in utilities for small variation $\varepsilon$ in $\mu _j$. That is,

$$\begin{aligned} \frac{{\partial {U_j}({\mu _j},{\mu _{ - j}},p)}}{{\partial {\mu _j}}} \approx \frac{{{U_j}({\mu _j} + \varepsilon ,{\mu _{ - j}},p) - {U_j}({\mu _j} - \varepsilon ,{\mu _{ - j}},p)}}{{2\varepsilon }} \end{aligned}$$

(11)

After the price of each FU is adjusted, the HUs will select the best FU(s) and trade spectrum with it(them). There are multiple factors that influence the decision of each HU. Generally speaking, a HU would like to choose the FU with lower price and furthest distance. It also need to avoid the interference from other HUs which select the same FU, since other HUs could impact received signal and the pricing of FU. We present an iterative algorithm that enables the HUs to distributedly compute the subgame NE among HUs under a given price profile from FUs.

(1) Calculate the best reply power allocation:

$$\begin{aligned} {\varPhi _{ij}}({\mu _j}, {I_{ij}}) = \max [0, \frac{{{\beta _i}{B_j}}}{{\lambda _i + {\mu _j}{{\left| {{h_{ji}}} \right| }^2}}} - \frac{{{w_j} + {I_{ij}}}}{{{{\left| {{h_{ji}}} \right| }^2}}}] \end{aligned}$$

(12)

where $\lambda _i$ ensures $\sum \limits _{j = 1}^M {{p_{ij}} = {{\overline{p} }_i}}$, and let $\varPhi _i = \{\varPhi _{ij}\}_{j\in F}$.

(2) Adjust their power profiles according to:

$$\begin{aligned} p_{ij}^{t + 1}({\mu _j}, {I_{ij}}) = p_{ij}^t({\mu _j}, {I_{ij}}) + {\alpha ^t}{\varPhi _{ij}}({\mu _j}, {I_{ij}}) \end{aligned}$$

(13)

where the sequence $\{\alpha ^t\}^\infty _{t=1}$ satisfy $\alpha ^t\in (0,1)$ and:

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } {\alpha ^t} = 0, \mathop {\lim }\limits _{T \rightarrow \infty } \sum \limits _{t = 1}^T {{\alpha ^t}} = \infty , \mathop {\lim }\limits _{T \rightarrow \infty } \sum \limits _{t = 1}^T {{{({\alpha ^t})}^2}} < \infty \end{aligned}$$

Then the HUs’ individual power profiles converge to a NE power allocation profile, i.e., $\mathop {\lim }\limits _{t \rightarrow \infty } p_{ij}^t({\mu _j}, {I_{ij}}) = p_{ij}^*({\mu _j}, {I_{ij}}), \forall i \in H, j \in F$, where $p_{ij}^*({\mu _j}, {I_{ij}})$ is a NE power allocation of HU i on then channel of FU j given price $\mu _j$.

All HUs are able to decide on their NE power allocation profiles distributedly by running this algorithm. In order to calculate ${\varPhi _{ij}}({\mu _j}, {I_{ij}})$ in each iteration, each HU i only needs to know the sublet rent of channel j and the aggregated interference plus noise contributed by all other HUs and FU j, and this information can be fed back to HU i by FU j.

This algorithm includes two processes of iteration which corresponding to upper-tier inter-FU game and lower-tier inter-HU game respectively. FUs update their pricing decision after the all HUs iterate to reach a equilibrium. The convergence of this algorithm can be proved easily by exploiting the feature of utility functions of users (including HUs and FUs). As it’s shown in last section, both tiers of subgame belong to potential game. It means it possess the finite improvement property. The update rule (10) and (13) of each player in this algorithm is also a better response to opponents, thus the convergence can be guaranteed.

5 Numerical Results

5.1 Parameter Setting

We now evaluate the proposed algorithms by simulations. We have the following general settings for the simulation. Consider a cognitive radio environment with three full users (i.e., $M=3$) and five hungry users (i.e., $N=5$) which are placed randomly in a $200\,m\,\times \,200\,m$ area. We let $d_{ij}$ denote the distance between user i and user j (including FUs and SUs). We consider a Rayleigh fading channel environment. The channel gain amplitudes $h_{ij}=\varepsilon _{ij}/ d^{\alpha /2}_ij$ follow Rayleigh fading, where $\varepsilon _{ij}$ is a Rayleigh distributed random variable with parameter 1, and $\alpha = 1.7$. The total bandwidth of each FU is 25 MHz (i.e., $B_j=25$) and the maximum allowable transmission power ${\overline{p}}_i$ is $100\,mW$. The cost of spectrum leasing $\varphi (B_j)$ for each FU is assumed to be constant for simplicity. The coefficients $\beta _i$ that transforms the ith user’s transmission rate to a monetary utility is randomly chosen between 1 and 20 for each user.

Fig. 1.

Dynamics of FUs’ sublet game

Fig. 2.

Average time of convergence for different numbers of users.

We first show the results regarding to the convergence of the algorithm with the parameters presented above, as shown in Fig. 1. Each FU updates its price after the low-tier spectrum sharing game converging to subgame nash equilibrium. Thus every iteration in this figure represents a time period for the evolution of HUs. However, it is seen that the up-tier pricing game converges to an equilibrium $(\mu ^*_j, \mu ^*_{-j})$ in less than 50 iterations, and no user has the incentive to deviate its channel selection and price decision unilaterally.

In Fig. 2, we compare the average convergence time for different number of users. As its illustrated that as the increase of number of users, more iterations are needed to converge to mixed NE.

Fig. 3.

Spectrum sublet results under different FUs’ prefer coefficients

To characterize the influence of the prefer coefficient $\beta _j$ of each FU on the spectrum trading between FUs and HUs, we show the power allocation profiles of each HU at the subgame Nash equilibrium in Fig. 3. The prefer coefficients $\{\beta _j\}_{j\in F}$ are set to satisfy ${\beta _1} > {\beta _2} > {\beta _3}$ in this simulation. The three bars in this figure correspond to the channels of three FUs and the height of each bar stands for the amount of power allocated on each channel by HUs. There are two points to be noted about this results. At first, not every HU consumes all of its power at the NE. HU 2 only use 63.7 mW on the channel of FU 1 because the later prefer to achieve higher data rate and would not like to share its channel with other users. Second, the channel selection is not orthogonal due to the price regulation of FUs. HUs balance the profit from higher data rate and the cost of spectrum leasing. These two results are different from related works. Therefore, it’s interest and challenging to study the interaction of different kinds of secondary users to improve spectrum sharing efficiency.

6 Conclusion

We have studied the spectrum sublet game among secondary users and modeled this interaction as a two-tier multi-leader multi-follower game. Then we characterized its subgame Nash equilibrium and proposed a decentralized algorithm which can converge to the equilibrium. In the future work, we will study this problem along with the spectrum trading between full user and primary user, which forms a three-tier trading. The competition among PUs and FUs will appear to attract more HUs and the problem will be more challenging.