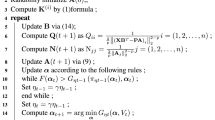IKLTSA: An Incremental Kernel LTSA Method

Abstract

Since 2000, manifold learning methods have been extensively studied, and demonstrated excellent performance in dimensionality reduction in some application scenarios. However, they still have some drawbacks in approximating real nonlinear relationships during the dimensionality reduction process, thus are unable to retain the original data’s structure well. In this paper, we propose an incremental version of the manifold learning algorithm LTSA based on kernel method, which is called IKLSTA, the abbreviation of Incremental Kernel LTSA. IKLTSA exploits the advantages of kernel method and can detect the explicit mapping from the high-dimensional data points to their low-dimensional embedding coordinates. It is also able to reflect the intrinsic structure of the original high dimensional data more exactly and deal with new data points incrementally. Extensive experiments on both synthetic and real-world data sets validate the effectiveness of the proposed method.

1 Introduction

Dimensionality reduction is one of important tasks in machine learning. Manifold learning aims at constructing the nonlinear low-dimensional manifold from sampled data points embedded in high-dimensional space, is a class of effective nonlinear dimension reduction algorithms. Typical manifold learning algorithms include Isomap [16] and LLE [14] etc. These algorithms are easy to implement and can obtain satisfactory mapping results in some application scenarios. However, they also have some limitations. When projecting complicate high-dimensional data to low-dimensional space, they can keep only some characteristics of the original high-dimensional data. For example, the local neighborhood construction in Isomap is quite different from that of the original dataset, and the global distance between data points cannot be maintained well by the LLE method.

Kernel methods are a kind of approaches that use kernel functions to project the original data as inner product to high dimensional eigen-space where subsequent learning and analysis are done. Kernel functions are used to approximate real data’s non-linear relations. From either global or local viewpoint [17], the low dimensional mapping can reflect the intrinsic structure of the original high dimensional data more accurately after dimension reduction. It is significant in many fields such as pattern recognition and so on.

Research works in recent years indicate the close inherent relationship between manifold learning and dimension reduction algorithms based on kernel method [2, 8]. Ham [4] studied the relationships between several manifold learning algorithms including Isomap, LLE and Laplacian Eigenmap (LE) [1] etc. and kernel method. These algorithms all can be seen as the problem of calculating eigenvectors of a certain matrix, which satisfies the kernel matrix’s conditions and reveals the characteristics to be preserved of the dataset. So all these methods can be regarded as kernel methods that keep the geometric characteristics of the original dataset after dimension reduction under the kernel framework.

For the out-of-sample learning problems, the key point lies in that most manifold learning algorithms find low-dimensional coordinates by optimizing a certain cost function, while the mappings of data points in high dimensional space to their low dimensional coordinates lack explicit formulation. When new samples are added into the dataset, it is unable to get its corresponding low dimensional coordinates directly by the obtained mappings, so the re-running of the algorithm is required. If some specific mapping function can be obtained, we can get newly-added data points’ low dimensional coordinates through the mapping function directly. Then the processing efficiency can be significantly improved for the new-coming data.

So if we bring the mapping function from high-dimensional input data to the corresponding low-dimensional output coordinates into manifold learning methods under the kernel framework, given the explicit mapping relationships of kernel methods, we can combine the advantages of kernel methods and the explicit mapping function. As a result, the learning complexity can be reduced, and new data points’ low dimensional coordinates can be calculated more efficiently, which makes the algorithms suitable for incremental manifold learning. In addition, dimensionality reduction algorithms served as a kind of feature extraction methods have attracted wide attention in applications. If we can apply the new method into these scenarios, human cost can be cut off greatly.

The rest of the paper is organized as follows. We review related work in Sect. 2. We present the proposed method in detail in Sect. 3. In Sect. 4, experiments on synthetic and real datasets are carried out to evaluate the proposed method. Finally, we conclude the paper in Sect. 5.

2 Related Work

As Liu and Yan pointed out [10], linear manifold learning algorithms that can extract local information, such as locality preserving projection (LPP) [5], neighborhood preserving embedding (NPE) [6], orthogonal neighborhood preserving projection (ONPP) [7] have sprung up in recent years. Recently, Zheng et al. used a kind of nonlinear implicit representation as a nonlinear polynomial mapping, and applied it to LLE and thus proposed the neighborhood preserving polynomial embedding algorithm (NPPE) [20]. This algorithm can keep the nonlinear characteristics of high dimensional data. Although these algorithms can detect the local characteristics very well [11], they cannot deal with noise effectively. Considering that real-world datasets inevitably contain outliers and noise, it is challenging for these manifold learning algorithms to process real-world data effectively.

Manifold learning algorithms based on kernel method are effective to solve the out-of-sample learning problem. Considering that data inseparable in the linear space may be separable in a nonlinear space, people tend to study manifold learning methods based on kernel functions (or kernel methods). Here, the selection of kernel function is the key step. Kernel function describes the dataset’s characteristics. By doing eigen-decomposition on the kernel matrix, we can get the original dataset’s characteristics, which improves the learning ability of the out-of-sample problem. Furthermore, the compute cost can be decreased consequently by doing eigen-decomposition on the kernel matrix instead of in high dimensional eigen-space.

2.1 LLE Under the Kernel Framework

Several works combining kernel functions and manifold learning methods appear in recent years. Take kernel LLE [4] for example, the last step of LLE is to search the low dimensional embedding coordinates Y that can maintain the weight matrix W optimally. The cost function is as follows:

$$\begin{aligned} {\varPhi }(Y)= & {} \sum \limits _i {||{Y_i}} - \sum \limits _j {{w_{ij}}} {Y_j}|| = ||Y(I - W)|{|^2} = Trace(Y(I - W){(I - W)^T}{Y^T})\nonumber \\= & {} Trace(YM{Y^T}),where M = (I - W){(I - W)^T}. \end{aligned}$$

(1)

We try to find the coordinates Y minimizing the cost function, which are d-dimensional embedding coordinates, i.e., the d eigenvectors according to the d smallest eigenvalues of matrix M. Ham [4] supposed that LLE’s kernel matrix can be represented as $K = ({\lambda _{\max }}I - M)$, ${\lambda _{\max }}$ is the largest eigenvalue of M. Because M is positive definite, it can be proved that K is also positive definite, which satisfies the requirement of kernel matrix consequently. The original cost function can be rewritten as ${\varPhi }(Y) = Trace({Y^T}KY)$. Then, the first d largest eigenvectors of kernel matrix K that minimize the cost function are proved to be the low dimensional embedding coordinates.

The LTSA [18, 19] algorithm is similar to LLE in essence, both come down to the eigen-decomposition of a matrix, which can be described as the kernel matrix form. We put LTSA under the framework of kernel method to pursue dimension reduction based on kernel technique.

2.2 Manifold Learning Based on Explicit Mapping

The mapping relationship F between a high-dimensional dataset and its low dimensional representation is usually nonlinear and cannot be represented in an exact form [13]. One commonly used method is to use a linear function [3] to approximate the real nonlinear mapping F in order to get the mapping between the high dimensional input dataset and its low dimensional coordinates. For example, in the locality preserving projection (LPP) [5] method, a linear function $Y = {A^T}X$ is used, where $X \in {\mathbb {R}^D}$, $Y \in {\mathbb {R}^d}$, $A \in {\mathbb {R}^{D \times d}}$, X and Y represent the input and output data respectively, and A represents the linear transformation matrix. This linear function is then substituted into the manifold learning method’s optimization objective function and we can get $\arg \min ({a^T}X)L{({a^T}X)^T}$. The optimal linear transformation matrix $A = [{a_i}]$ can be solved by minimizing the cost function $Trace({Y^T}LY) = Trace({a^T}XL{X^T}a)$. The mapping representation ${y_i} = {A^T}{x_i}$ gotten from the linear transformation matrix A reflects the nonlinear mapping relationship from X to Y. So we can get a newly-added data point’s corresponding low dimensional coordinates according to the explicit mapping formula.

In the neighborhood preserving projections (NPP) [12] algorithm, based on the LLE method, the authors used a linear transformation matrix to build the linear connection ${y_i} = {U^T}{x_i}$ between the input dataset $X = [{x_1},{x_2},...,{x_N}]$ and the corresponding output $Y = [{y_1},{y_2},...,{y_N}]$ after dimension reduction by LLE. Then, the linear connection is put to a generic procedure of dimension reduction of manifold learning to calculate the optimal linear transformation matrix U, so as to minimize the cost function ${\varPhi }(Y) = Trace(Y(I - W){(I - W)^T}{Y^T}) = Trace(YM{Y^T})$. After that, we can get $Trace(YM{Y^T}) = Trace({U^T}XM{X^T}U)$. By doing eigen-decomposition on matrix $XM{X^T}$, we get the d smallest eigenvectors ${u_1},{u_2},...,{u_d}$, which can be represented as a matrix $U = [{u_1},{u_2},...,{u_d}]$. Finally, the low dimensional output coordinates Y are computed directly from the linear function $Y = {U^T}X$.

3 Incremental Kernel LTSA

3.1 LTSA Under Kernel Framework

For dimensionality reduction, both LTSA and LLE do eigen-decomposition on a certain cost function to determine the low dimensional output coordinates of a high-dimensional dataset. So we can use kernel in the third step of LTSA to align the global coordinates. The optimization objective of the original cost function $\mathop {\min }\limits _U tr(YM{Y^T})$ with $M = W{W^T}$ can be formulated as $\mathop {\min }\limits _U tr(YK{Y^T})$. Now we define the kernel matrix as $K = {\lambda _{\max }}I - M$, where ${\lambda _{\max }}$ is M’s largest eigenvalue. K is positive definite because $M = W{W^T}$ is positive definite, which can be proved as follows.

The eigen-decomposition on matrix M is $YM = Y\lambda$, multiplying both sides by ${Y^T}$, we get $YM{Y^T} = Y{Y^T}\lambda = \lambda$, substituting $M = {\lambda _{\max }}I - K$ into the equation above, we can get

$$\begin{aligned} Y({\lambda _{\max }}I - K){Y^T} = \lambda \Rightarrow Y{\lambda _{\max }}I{Y^T} - YK{Y^T} = \lambda \Rightarrow {\lambda _{\max }}I - \lambda = YK{Y^T} \end{aligned}$$

(2)

Considering that M is positive definite, we know M’s eigenvalues $\lambda$ are positive by $YM = Y\lambda$. While ${\lambda _{\max }}$ is M’s largest eigenvalue, so it is positive and ${\lambda _{\max }}I - \lambda > 0$. So Eq. (2) is positive on both sides. That is, K is positive definite, which satisfies the condition of kernel matrix.

3.2 Putting Explicit Mapping Function into the Kernel Framework

On the other hand, LTSA assumes that the coordinates of the input data points’ neighbors in the local tangent space can be used to reconstruct the global embedding coordinates’ geometric structure. So there exist one-to-one correspondences between global coordinates and local coordinates. We put the explicit mapping function $Y = {U^T}X$ into the optimization function by kernel: $\min tr(YK{Y^T})$ where $K = {\lambda _{\max }}I - M$, $M = W{W^T} = \sum \limits _{i = 1}^N {{W_i}} W_i^T$, ${W_i} = (I - \frac{1}{k}e{e^T})(I - {\varTheta }_i^\dag {{\varTheta }_i})$. The constraint on Y is $Y{Y^T} = I$. So the optimization function turns to $\mathop {\min }\limits _U tr({U^T}XK{({U^T}X)^T}) = \mathop {\min }\limits _U tr({U^T}(XK{X^T})U)$. Rewriting the constraint as $Y{Y^T} = {U^T}X{({U^T}X)^T} = I$, i.e., ${U^T}X{X^T}U = I$. Then, we put the constraint into the optimization function and apply the Lagrangian multiplier to get the following equation:

$$\begin{aligned} L(U)= & {} {U^T}(XK{X^T})U + \lambda (I - {U^T}X{X^T}U) \nonumber \\\Rightarrow & {} \frac{{\partial L(U)}}{{\partial U}} = 2(XK{X^T})U - 2\lambda X{X^T}U = 0 \Rightarrow (XK{X^T})U = \lambda X{X^T}U \end{aligned}$$

(3)

The problem can be transformed to eigen-decomposition on matrix $XK{X^T}$. The solution of the optimization problem $\mathop {\min }\limits _U tr({U^T}(XK{X^T})U)$ is U = [$u_1$,$u_2$,...,$u_d$], where ${u_1},{u_2},...,{u_d}$ are corresponding eigenvectors of the d largest eigenvalues ${\lambda _1},{\lambda _2},$ $...,{\lambda _d}$. With the coefficient matrix U, we can work out the low dimensional output coordinates Y according to the function $Y = {U^T}X$ between the local coordinates and the low-dimensional global coordinates. With the explicit mapping function, a newly-added point ${x_{new}}$’s low-dimensional coordinates can be obtained by ${y_{new}} = {U^T}{x_{new}}$. This is the key point of incremental manifold learning in this paper.

3.3 Procedure of the IKLTSA Algorithm

In this paper, the kernel method with an explicit mapping formulation $Y = {U^T}X$ has the ability of processing newly-added data points incrementally. The kernel matrix can be used to recover the original high-dimensional data’s intrinsic structure effectively. We call the method Incremental Kernel LTSA — IKLTSA in short. The procedure of IKLSTA is outlined as follows.

Input: Dataset X, neighborhood parameter k

Output: Low-dimensional coordinates Y

Procedure:

• Step 1 (Extract local information): Use the k-nearest neighbor method to evaluate each data point ${x_i}$’s neighborhood ${X_i}$. Compute the eigenvectors ${v_i}$ corresponding to the d largest eigenvalues of the covariance matrix ${({X_i} - \mathop {{x_i}}\limits ^\_ {e^T})^T}({X_i} - \mathop {{x_i}}\limits ^\_ {e^T})$ with respect to point ${x_i}$’s neighborhood, and construct matrix ${V_i}$, then get each point’s coordinates in the local tangent space ${{\varTheta }_i} = V_i^T{X_i}(I - \frac{1}{k}e{e^T})$.

• Step 2 (Align local coordinates): Minimize the following local reconstruction error to align the global embedding coordinates ${Y_i}$ corresponding to the coordinates in the local tangent space: ${E_i} = {Y_i}(I - \frac{1}{k}e{e^T})(I - {\varTheta }_i^\dag {{\varTheta }_i})$. Let ${W_i} = (I - \frac{1}{k}e{e^T})(I - {\varTheta }_i^\dag {{\varTheta }_i})$, $M = \sum \limits _{i = 1}^N {{W_i}W_i^T}$.

• Step 3 (Obtain the kernel function): Construct the kernel function by $K = {\lambda _{\max }}I - M$, ${\lambda _{\max }}$is M’s largest eigenvalue.

• Step 4 (Use the explicit mapping function): Do eigen-decomposition on matrix $XK{X^T}$ and get the eigenvectors ${u_1},{u_2},...,{u_d}$ corresponding to the d largest eigenvalues by using the explicit mapping function $Y = {U^T}X$.

• Step 5 (Compute the low dimensional output coordinates): After getting the coefficient matrix $U = [{u_1},{u_2},...,{u_d}]$, calculate the low dimensional output coordinates Y in accordance with the function $Y = {U^T}X$. For a newly-added point ${x_{new}}$, the corresponding low dimensional coordinate are evaluated directly by ${y_{new}} = {U^T}{x_{new}}$.

4 Experimental Results

We conduct a series of experiments in this section to validate the proposed algorithm. Tested datasets include both simulated benchmarks and real world datasets of face images, handwritten digits etc.

4.1 Performance of Dimensionality Reduction

Here we show the dimensionality reduction effect of IKLTSA on datasets Swiss Roll and Twin Peaks [15]. We compare a series of manifold learning algorithms: LTSA [18], LE [1], LLE [14], ISOMAP [16], LPP [5], NPP [12], and the proposed method IKLTSA.

We first use these methods to reduce the dimensionality of 1000 points in the Swiss Roll dataset and map the points to two-dimensional space with k=14. The results are shown in Fig. 1. We can see clearly that our algorithm preserves best the mutual spatial relationships among data points after dimensionality reduction, which indicates that our method can reflect the intrinsic structure of the original high-dimensional data accurately. We then test these methods on dataset Twin Peaks, and the two-dimensional results after dimensionality reduction are demonstrated in Fig. 2. We can see that the proposed algorithm is still superior to the other methods.

Fig. 1.

Dimensionality reduction results of several manifold learning methods on Swiss Roll dataset. (a) The original dataset (1000 points), (b) Result of LTSA, (c) Result of LE, (d) Result of LLE, (e) Result of ISOMAP, (f) Result of LPP, (g) Result of NPP, (h) Result of IKLTSA.

Fig. 2.

Dimensionality reduction results of several manifold learning methods on twin peaks dataset. (a) The original dataset (1000 points), (b) Result of LTSA (c) Result of LE (d) Result of LLE (e) Result of ISOMAP (f) Result of LPP (g) Result of NPP (h) Result of IKLTSA.

One major advantage of the proposed algorithm IKLTSA is that we can use it to evaluate the low dimensional coordinates of a newly-added point by the explicit formulation directly. To show this, we use three datasets: Swiss Roll, Punctured Sphere [15] and Twin Peaks [15], each of which contains 1000 points. Each dataset is divided into a testing subset (containing 20 points) and a training subset (containing 980 points). First, we reduce the dimensionality of points in the training subset, then compute the corresponding low dimensional coordinates of points in the testing subset by using the mapping function from the original high dimensional data to the low dimensional coordinates. Furthermore, we reduce the dimensionality of each dataset by using kernel function. All results are shown in Fig. 3.

Fig. 3.

Comparison between the low dimensional coordinates obtained by explicit mapping function and the coordinates obtained by direct dimension reduction on the whole dataset. (a, d, g) The original datasets; (b, e, h) Results of dimension reduction in training subset and the coordinates of points in the testing subset obtained by mapping function directly; (c, f, i) The low dimensional coordinates obtained by dimension reduction over the whole dataset.

From Fig. 3, we can see that the coordinates of testing points computed by the mapping function are close to the coordinates obtained by dimension reduction on the whole dataset. This means that our algorithm is able to process new data incrementally. For a new point, we can compute the corresponding low dimensional coordinates directly by the explicit mapping function. Our method has an obvious advantage in processing high dimensional data streams over the other methods.

4.2 Classification Performance

Dimension reduction is often used as a preprocessing step of classification task. So dimension reduction outputs play an important role in classification. In this section we first do dimension reduction on two real-world datasets using different algorithms, then classify the low dimensional outputs using kNN (k-nearest neighborhood) classifier. Finally, we compare the classification performance to validate the effectiveness of our algorithm.

First, we use a human face image dataset sampled from Olivetti Faces [21] as input. This dataset contains 8 individuals’ face images of size 64 by 64 pixels; each individual has 10 face images of different expressions, from which 5 images are used for training and the others for testing. The results are shown in Fig. 4, where the horizontal axis represents the dimensionality of face images after dimension reduction. From Fig. 4, we can see that our method IKLTSA performs better than the other algorithms. Then we do the same experiments with major incremental manifold learning methods, including incremental LE, incremental LTSA, incremental Isomap, incremental LLE and incremental HLLE [9]. The results are shown in Fig. 5. Again we can see that our algorithm achieves the best performance. This indicates that our algorithm can detect the intrinsic structure hidden in the dataset well.

Fig. 4.

Classification performance comparison on the Olivetti Faces dataset with major manifold learning algorithms.

Fig. 5.

Classification performance comparison on the Olivetti Faces dataset with major incremental manifold learning algorithms.

Fig. 6.

Classification performance comparison on the MNIST Handwritten Digits dataset with major manifold learning algorithms.

The second real-world dataset used here is the MNIST Handwritten Digits dataset [21], which contains images of hand-written digits 0–9. Here we select only 5 digits 0, 1, 3, 4 and 6, each of which has 980 images of size 28 by 28 pixels. These images are divided training set and testing set. We reduce the dimensionality of each image to 1–8 dimensions using different manifold learning algorithms, and then classify the low-dimensional images using kNN classifier. The classification results are shown in Fig. 6. We can see that our algorithm achieves a higher accuracy than the other algorithms. Similarly, we compare IKLTSA with major incremental methods on the same dataset, and get roughly similar results, which are shown in Fig. 7.

Fig. 7.

Classification performance comparison on the MNIST Handwritten Digits dataset with major incremental manifold learning algorithms.

Fig. 8.

Dimensionality reduction results on the Rendered face dataset.

Fig. 9.

Time cost comparison on the Swiss Roll dataset

Fig. 10.

Time cost comparison on the Rendered face dataset

4.3 Dimensionality Reduction Performance on the Rendered Face Dataset

Here we check the dimensionality reduction performance on the rendered face dataset [16]. The results are shown in Fig. 8. The dataset contains 698 facial sculpture images of $64 \times 64$ pixels. These images have 2 groups of pose parameters: up to down and left to right. All images are transformed to 4096-dimension vectors. We reduce the 698 high dimensional images to 2D using IKLTSA, and are shown in Fig. 8. Here, each point represents a facial image. 10 images are selected randomly and marked as red points in Fig. 8. We can see that the facial poses are from right to left along the horizontal axis, and from look-up to look-down along the vertical axis (posture is from up to down). So the low dimensional projections obtained by our algorithm keep the original data’s intrinsic structure very well. The selected images are mapped to the low dimensional space accurately in accordance with their positions and poses in the original data. This shows that the proposed algorithm is effective in detecting the implicit structures of high dimensional images.

4.4 Time Cost

Here we compare time cost on dimension reduction of our IKLTSA method with three existing incremental manifold learning algorithms, including incremental LE, incremental LTSA and incremental HLLE, over the Swiss Roll and the Rendered face datasets. Figures 9 and 10 show the time cost as the number of data points or images processed increases. On the Swiss Roll dataset, although IKLTSA consumes more time than incremental LE, it is faster than the other incremental manifold learning algorithms to process the whole dataset. On the Rendered face datasets. our algorithm is always faster than the other algorithms.

5 Conclusion

In this paper, we propose a new manifold learning algorithm based on kernel that combines an explicit mapping function from the high dimensional data to its low dimensional coordinates. Compared with existing batch and incremental manifold learning algorithms, the new method can directly compute newly-added data points’ low dimensional coordinates by the explicit mapping function. This enables the proposed method to process new data incrementally, which has extensive applications in processing data streams.