Efficient Mining of High-Utility Sequential Rules

Abstract

High-utility pattern mining is an important data mining task having wide applications. It consists of discovering patterns generating a high profit in databases. Recently, the task of high-utility sequential pattern mining has emerged to discover patterns generating a high profit in sequences of customer transactions. However, a well-known limitation of sequential patterns is that they do not provide a measure of the confidence or probability that they will be followed. This greatly hampers their usefulness for several real applications such as product recommendation. In this paper, we address this issue by extending the problem of sequential rule mining for utility mining. We propose a novel algorithm named HUSRM (High-Utility Sequential Rule Miner), which includes several optimizations to mine high-utility sequential rules efficiently. An extensive experimental study with four datasets shows that HUSRM is highly efficient and that its optimizations improve its execution time by up to 25 times and its memory usage by up to 50 %.

1 Introduction

Frequent Pattern Mining (FPM) is a fundamental task in data mining, which has many applications in a wide range of domains [1]. It consists of discovering groups of items appearing together frequently in a transaction database. However, an important limitation of FPM is that it assumes that items cannot appear more than once in each transaction and that all items have the same importance (e.g. weight, unit profit). These assumptions do not hold in many real-life applications. For example, consider a database of customer transactions containing information on quantity of purchased items and their unit profit. If FPM algorithms are applied on this database, they may discover many frequent patterns generating a low profit and fail to discover less frequent patterns that generate a high profit. To address this issue, the problem of FPM has been redefined as High-utility Pattern Mining (HUPM) [2, 5, 7, 9, 12, 13]. However, these work do not consider the sequential ordering of items in transactions. High-Utility Sequential Pattern Mining (HUSP) was proposed to address this issue [14, 15]. It consists of discovering sequential patterns in sequences of customer transactions containing quantity and unit profit information. Although, this definition was shown to be useful, an important drawback is that it does not provide a measure of confidence that patterns will be followed. For example, consider a pattern $\langle \{milk\},\{bread\},\{champagne\} \rangle$ meaning that customers bought milk, then bread, and then champagne. This pattern may generate a high profit but may not be useful to predict what customers having bought milk and bread will buy next because milk and bread are very frequent items and champagne is very rare. Thus, the probability or confidence that milk and bread is followed by champagne is very low. Not considering the confidence of patterns greatly hampers their usefulness for several real applications such as product recommendation.

In FPM, a popular alternative to sequential patterns that consider confidence is to mine sequential rules [3]. A sequential rule indicates that if some item(s) occur in a sequence, some other item(s) are likely to occur afterward with a given confidence or probability. Two main types of sequential rules have been proposed. The first type is rules where the antecedent and consequent are sequential patterns [10, 11]. The second type is rules between two unordered sets of items [3, 4]. In this paper we consider the second type because it is more general and it was shown to provide considerably higher prediction accuracy for sequence prediction in a previous study [4]. Moreover, another reason is that the second type has more applications. For example, it has been applied in e-learning, manufacturing simulation, quality control, embedded systems analysis, web page prefetching, anti-pattern detection, alarm sequence analysis and restaurant recommendation (see [4] for a survey). Several algorithms have been proposed for sequential rule mining. However, these algorithms do not consider the quantity of items in sequences and their unit profit. But this information is essential for applications such as product recommendation and market basket analysis. Proposing algorithms that mine sequential rules while considering profit and quantities is thus an important research problem.

However, addressing this problem raises major challenges. First, algorithms for utility mining cannot be easily adapted to sequential rule mining. The reason is that algorithms for HUPM and HUSP mining such as USpan [14], HUI-Miner [8] and FHM [5] use search procedures that are very different from the ones used in sequential rule mining [3, 4]. A distinctive characteristics of sequential rule mining is that items may be added at any time to the left or right side of rules to obtain larger rules and that confidence needs to be calculated. Second, the proposed algorithm should be efficient in both time and memory, and have an excellent scalability.

In this paper, we address these challenges. Our contributions are fourfold. First, we formalize the problem of high-utility sequential rule mining and its properties. Second, we present an efficient algorithm named HUSRM (High-Utility Sequential Rule Miner) to solve this problem. Third, we propose several optimizations to improve the performance of HUSRM. Fourth, we conduct an extensive experimental study with four datasets. Results show that HUSRM is very efficient and that its optimizations improve its execution time by up to 25 times and its memory usage by up to 50 %.

The rest of this paper is organized as follows. Sections 2, 3, 4 and 5 respectively presents the problem definition and related work, the HUSRM algorithm, the experimental evaluation and the conclusion.

2 Problem Definition and Related Work

Table 1. A sequence database

Table 2. External utility values

We consider the definition of a sequence database containing information about quantity and unit profit, as defined by Yin et al. [14].

Definition 1

(Sequence Database). Let $I = \{i_1, i_2, ..., i_l\}$ be a set of items (symbols). An itemset $I_x = \{i_1, i_2, ..., i_m\} \subseteq I$ is an unordered set of distinct items. The lexicographical order $\succ _{lex}$ is defined as any total order on I. Without loss of generality, it is assumed in the following that all itemsets are ordered according to $\succ _{lex}$. A sequence is an ordered list of itemsets $s = \langle I_1, I_2, ..., I_n$ $\rangle$ such that $I_k \subseteq I$ $(1 \le k \le n)$. A sequence database SDB is a list of sequences $SDB = \langle s_1, s_2, ..., s_p\rangle$ having sequence identifiers (SIDs) 1, 2... p. Note that it is assumed that sequences cannot contain the same item more than once. Each item $i \in I$ is associated with a positive number p(i), called its external utility (e.g. unit profit). Every item i in a sequence $s_c$ has a positive number $q(i, s_c)$, called its internal utility (e.g. purchase quantity).

Example 1

Consider the sequence database shown in Table 1, which will be the running example. It contains four sequences having the SIDs 1, 2, 3 and 4. Each single letter represents an item and is associated with an integer value representing its internal utility. Items between curly brackets represent an itemset. When an itemset contains a single item, curly brackets are omitted for brevity. For example, the first sequence $s_1$ contains five itemsets. It indicates that items a and b occurred at the same time, were followed by c, then f, then g and lastly e. The internal utility (quantity) of a, b, c, e, f and g in that sequence are respectively 1, 2, 2, 3, 2 and 1. The external utility (unit profit) of each item is shown in Table 2.

The problem of sequential rule mining is defined as follows [3, 4].

Definition 2

(Sequential Rule). A sequential rule $X \rightarrow Y$ is a relationship between two unordered itemsets $X, Y \subseteq I$ such that $X \cap Y = \emptyset$ and $X,Y \not = \emptyset$. The interpretation of a rule $X \rightarrow Y$ is that if items of X occur in a sequence, items of Y will occur afterward in the same sequence.

Definition 3

(Sequential Rule Size). A rule $X \rightarrow Y$ is said to be of size $k*m$ if $|X| = k$ and $|Y| = m$. Note that the notation $k*m$ is not a product. It simply means that the sizes of the left and right parts of a rule are respectively k and m. Furthermore, a rule of size $f*g$ is said to be larger than another rule of size $h*i$ if $f > h$ and $g \ge i$, or alternatively if $f \ge h$ and $g > i$.

Example 2

The rules $r = \{a, b, c\} \rightarrow \{e, f, g\}$ and $s = \{a\} \rightarrow \{e, f\}$ are respectively of size $3*3$ and $1*2$. Thus, r is larger than s.

Definition 4

(Itemset/Rule Occurrence). Let $s = \langle I_1, I_2 ... I_n \rangle$ be a sequence. An itemset I occurs or is contained in s (written as $I \sqsubseteq s$ ) iff $I \subseteq \bigcup _{i=1}^{n} I_i$. A rule $r = X \rightarrow Y$ occurs or is contained in s (written as $r \sqsubseteq s$ ) iff there exists an integer k such that $1 \le k < n$, $X\subseteq \bigcup _{i=1}^{k} I_i$ and $Y \subseteq \bigcup _{i=k+1}^{n} I_i$. Furthermore, let seq(r) and ant(r) respectively denotes the set of sequences containing r and the set of sequences containing its antecedent, i.e. $seq(r) = \{s | s \in SDB \wedge r \sqsubseteq s \}$ and $ant(r) = \{s | s \in SDB \wedge X \sqsubseteq s \}$.

Definition 5

(Support). The support of a rule r in a sequence database SDB is defined as $sup_{SDB}(r) = |seq(r)| / |SDB|$.

Definition 6

(Confidence). The confidence of a rule $r = X \rightarrow Y$ in a sequence database SDB is defined as $conf_{SDB}(r) = |seq(r)| / |ant(r)|$.

Definition 7

(Problem of Sequential Rule Mining). Let minsup,  minconf $\in$ [0, 1] be thresholds set by the user and SDB be a sequence database. A sequential rule r is frequent iff $sup_{SDB}(r) \ge minsup$. A sequential rule r is valid iff it is frequent and $conf_{SDB}(r) \ge minconf$. The problem of mining sequential rules from a sequence database is to discover all valid sequential rules [3].

We adapt the problem of sequential rule mining to consider the utility (e.g. generated profit) of rules as follows.

Definition 8

(Utility of an Item). The utility of an item i in a sequence $s_c$ is denoted as $u(i, s_c)$ and defined as $u(i, s_c)$ = $p(i) \times q(i, s_c)$.

Definition 9

(Utility of a Sequential Rule). Let be a sequential rule $r: X \rightarrow Y$. The utility of r in a sequence $s_c$ is defined as $u(r, s_c) = \sum _{i \in X \cup Y} u(i, s_c)$ iff $r \sqsubseteq s_c$. Otherwise, it is 0. The utility of r in a sequence database SDB is defined as $u_{SDB}(r) = \sum _{s \in SDB} u(r, s)$ and is abbreviated as u(r) when the context is clear.

Example 3

The itemset $\{a, b, f \}$ is contained in sequence $s_1$. The rule $\{a, c\} \rightarrow \{e, f\}$ occurs in $s_1$, whereas the rule $\{a, f\} \rightarrow \{c\}$ does not, because item c does not occur after f. The profit of item c in sequence $s_1$ is $u(c,s_1) = p(c) \times q(c, s_1) = 5 \times 2 = 10$. Consider a rule $r = \{c, f\} \rightarrow \{g\}$. The profit of r in $s_1$ is $u(r, s_1) = u(c,s_1) + u(f,s_1) + u(g,s_1) = (5 \times 2 )+ (3 \times 3 ) + (1 \times 2 ) = 18$. The profit of r in the database is $u(r) = u(r,s_1) + u(r,s_2) + u(r,s_3) + u(r,s_4) = 18 + 0 + 0 + 9 = 27$.

Definition 10

(Problem of High-Utility Sequential Rule Mining). Let $minsup, minconf \in [0,1]$ and $minutil \in \mathbf {R}^{+}$ be thresholds set by the user and SDB be a sequence database. A rule r is a high-utility sequential rule iff $u_{SDB}(r) \ge minutil$ and r is a valid rule. Otherwise, it is said to be a low utility sequential rule. The problem of mining high-utility sequential rules from a sequence database is to discover all high-utility sequential rules.

Example 4

Table 3 shows the sequential rules found for $minutil = 40$ and $minconf = 0.65$. In this example, we can see that rules having a high-utility and confidence but a low support can be found (e.g. $r_7$). These rules may not be found with regular sequential rule mining algorithms because they are rare, although they are important because they generate a high profit.

Table 3. Sequential rules found for $minutil = 40$ and $minconf = 0.65$

Algorithms for mining sequential rules explore the search space of rules by first finding frequent rules of size $1*1$. Then, they recursively append items to either the left or right sides of rules to find larger rules [3]. The left expansion of a rule $X \rightarrow Y$ with an item $i \in I$ is defined as $X \cup \{i \} \rightarrow Y$, where $i \succ _{lex} j, \forall j \in X$ and $i \not \in Y$. The right expansion of a rule $X \rightarrow Y$ with an item $i \in I$ is defined as $X \rightarrow Y \cup \{i \}$, where $i \succ _{lex} j, \forall j \in Y$ and $i \not \in X$. Sequential rule mining algorithms prune the search space using the support because it is anti-monotonic. However, this is not the case for the utility measure, as we show thereafter.

Property 1

(antimonotonicity of utility). Let be a rule r and a rule s, which is a left expansion of r. It follows that $u(r) < u(s)$ or $u(r) \ge u(s)$. Similarly, for a rule t, which is a right expansion of r, $u(r) < u(t)$ or $u(r) \ge u(t)$.

Example 5

The rule $\{a\} \rightarrow \{b\}$, $\{a\} \rightarrow \{b,g\}$ and $\{a\} \rightarrow \{b,e\}$ respectively have a utility of 10, 7 and 12.

In high-utility pattern mining, to circumvent the problem that utility is not anti-monotonic, the solution has been to use anti-monotonic upper-bounds on the utility of patterns to be able to prune the search space. Algorithms such as Two-Phase [9], IHUP [2] and UP-Growth [12] discover patterns in two phases. During the first phase, an upper-bound on the utility of patterns is calculated to prune the search space. Then, during the second phase, the exact utility of remaining patterns is calculated by scanning the database and only high-utility patterns are output. However, an important drawback of this method is that too many candidates may be generated and may need to be maintained in memory during the first phase, which degrades the performance of the algorithms. To address this issue, one-phase algorithms have been recently proposed such as FHM [5], HUI-Miner [8] and USpan [14] to mine high-utility patterns without maintaining candidates. These algorithms introduces the concept of remaining utility. For a given pattern, the remaining utility is the sum of the utility of items that can be appended to the pattern. The main upper-bound used by these algorithms to prune the search space is the sum of the utility of a pattern and its remaining utility. Since one-phase algorithms were shown to largely outperform two-phase algorithms, our goal is to propose a one-phase algorithm to mine high-utility sequential rules.

3 The HUSRM Algorithm

In the next subsections, we first present important definitions and data structures used in our proposal, the HUSRM algorithm. Then, we present the algorithm. Finally, we describe additional optimizations.

3.1 Definitions and Data Structures

To prune the search space of sequential rules, the HUSRM algorithm adapts the concept of sequence estimated utility introduced in high-utility sequential pattern mining [14] as follows.

Definition 11

(Sequence Utility). The sequence utility (SU) of a sequence $s_c$ is the sum of the utility of items from $s_c$ in $s_c$. i.e. $SU(s_c) = \sum _{\{x\} \sqsubseteq s_c}{u(x, s_c)}$.

Example 6

The sequence utility of sequences $s_1, s_2, s_3$ and $s_4$ are respectively 27, 40, 15 and 16.

Definition 12

(Sequence Estimated Utility of an Item). The sequence estimated utility (SEU) of an item x is defined as the sum of the sequence utility of sequences containing x, i.e. $SEU(x) = \sum _ {s_c \in SDB \wedge \{x\} \sqsubseteq s_c} {SU(s_c)}$.

Definition 13

(Sequence Estimated Utility of a Rule). The sequence estimated utility (SEU) of a sequential rule r is defined as the sum of the sequence utility of sequences containing r, i.e. $SEU(r) = \sum _ {s_c \in seq(r)} {SU(s_c)}$.

Example 7

The SEU of rule $\{a\} \rightarrow \{b\}$ is $SU(s_1) + SU(s_2) + SU(s_3) = 27 + 40 + 15 = 82.$

Definition 14

(Promising Item). An item x is promising iff $SEU(x) \ge minutil$. Otherwise, it is unpromising.

Definition 15

(Promising Rule). A rule r is promising iff $SEU(r) \ge minutil$. Otherwise, it is unpromising.

The SEU measure has three important properties that are used to prune the search space.

Property 2

(Overestimation). The SEU of an item/rule w is higher or equal to its utility, i.e. $SEU(w) \ge u(w)$.

Property 3

(Pruning Unpromising Items). Let x be an item. If x is unpromising, then x cannot be part of a high-utility sequential rule.

Property 4

(Pruning unpromising rules). Let r be a sequential rule. If r is unpromising, then any rule obtained by transitive expansion(s) of r is a low utility sequential rule.

We also introduce a new structure called utility-table that is used by HUSRM to quickly calculate the utility of rules and prune the search space. Utility-tables are defined as follows.

Definition 16

(Extendability). Let be a sequential rule r and a sequence s. An item i can extend r by left expansion in s iff $i \succ _{lex} j, \forall j \in X, i \not \in Y$ and $X \cup \{i\} \rightarrow Y$ occurs in s. An item i can extend r by right expansion in s iff $i \succ _{lex} j, \forall j \in Y, i \not \in X$ and $X \rightarrow Y \cup \{i\}$ occurs in s. Let onlyLeft(r, s) denotes the set of items that can extend r by left expansion in s but not by right expansion. Let onlyRight(r, s) denotes the set of items that can extend r by right expansion in s but not by left expansion. Let leftRight(r, s) denotes the set of items that can extend r by left and right expansion in s.

Definition 17

(Utility-Table). The utility-table of a rule r in a database SDB is denoted as ut(r), and defined as a set of tuples such that there is a tuple (sid,  iutil,  lutil,  rutil,  lrutil) for each sequence $s_{sid}$ containing r (i.e. $\forall s_{sid} \in seq(r)$). The iutil element of a tuple is the utility of r in $s_{sid}$. i.e., $u(r,s_{sid})$. The lutil element of a tuple is defined as $\sum u(i,s_{sid})$ for all item i such that i can extend r by left expansion in $s_{sid}$ but not by right expansion, i.e. $\forall i \in onlyLeft(r, s_{sid})$. The rutil element of a tuple is defined as $\sum u(i,s_{sid})$ for all item i such that i can extend r by right expansion in $s_{sid}$ but not by left expansion, i.e. $\forall i \in onlyRight(r, s_{sid})$. The lrutil element of a tuple is defined as $\sum u(i,s_{sid})$ for all item i such that i can extend r by left or right expansion in $s_{sid}$, i.e. $\forall i \in leftRight(r, s_{sid})$.

Example 8

The utility-table of $\{a\} \rightarrow \{b\}$ is $\{ (s_1, 5, 12, 3, 20), (s_2, 5, 0, 10, 0) \}$. The utility-table of $\{a\} \rightarrow \{b,c\}$ is $\{ (s_1, 25, 12, 3, 0) \}$. The utility-table of the rule $\{a,c\} \rightarrow \{b\}$ is $\{ (s_1, 25, 12, 3, 0) \}$.

The proposed utility-table structure has the following nice properties to calculate the utility and support of rules, and for pruning the search space.

Property 5

Let be a sequential rule r. The utility u(r) is equal to the sum of iutil values in ut(r).

Property 6

Let be a sequential rule r. The support of r in a database SDB is equal to the number of tuples in the utility-table of r, divided by the number of sequences in the database, i.e. $sup_{SDB}(r) = |ut(r)| / |SDB|$.

Property 7

Let be a sequential rule r. The sum of iutil, lutil, rutil and lrutil values in ut(r) is an upper bound on u(r). Moreover, it can be shown that this upper bound is tighter than SEU(r).

Property 8

Let be a sequential rule r. The utility of any rule t obtained by transitive left or right expansion(s) of r can only have a utility lower or equal to the sum of iutil, lutil, rutil and lrutil values in ut(r).

Property 9

Let be a sequential rule r. The utility of any rule t obtained by transitive left expansion(s) of r can only have a utility lower or equal to the sum of iutil, lutil and lrutil values in ut(r).

Now, an important question is how to construct utility-tables. Two cases need to be considered. For sequential rules of size $1*1$, utility-tables can be built by scanning the database once. For sequential rules larger than size $1*1$, it would be however inefficient to scan the whole database for building a utility-table. To efficiently build a utility-table for a rule larger than size $1*1$, we propose the following scheme.

Consider the left or right expansion of a rule with an item i. The utility-table of the resulting rule $r'$ is built as follows. Tuples in the utility-table of r are retrieved one by one. For a tuple (sid, iutil, lutil, rutil, lrutil), if the rule $r'$ appears in sequence $s_{sid}$ (i.e. $r \sqsubseteq s_{sid}$), a tuple $(sid, iutil', lutil', rutil', lrutil')$ is created in the utility-table of $r'$. The value $iutil'$ is calculated as $iutil + u(\{i\}, s_{sid})$. $lutil'$ is calculated as $lutil - u(j, s_{sid}) \forall j \not \in onlyLeft(r',s_{sid})$ $\wedge j \in onlyLeft(r,s_{sid}) - [u(i, s_{sid})$ if $i \in onlyLeft(r, s_{sid})]$. The value $rutil'$ is calculated as $rutil - u(j, s_{sid}) \forall j \not \in onlyRight(r',s_{sid})$ $\wedge j \in onlyRight(r,s_{sid}) - [u(i, s_{sid})$ if $i \in onlyRight(r,s_{sid})]$. Finally, the value $lrutil'$ is calculated as $lrutil - u(j, s_{sid}) \forall j \not \in leftRight(r',s_{sid})$ $\wedge j \in leftRight(r,s_{sid}) - [ u(i, s_{sid})$ if i $\in$ $leftRight(r,s_{sid}) ]$. This procedure for building utility-tables is very efficient since it requires to scan each sequence containing the rule r at most once to build the utility-table of $r'$ rather than scanning the whole database.

Example 9

The utility-table of $r: \{a\} \rightarrow \{e\}$ is $\{ (s_1, 2, 14, 0, 11),$ $(s_2, 2, 36, 2, 0),$ $(s_3, 2, 4, 0, 9) \}$. By adding the iutil values of this table, we find that $u(r) = 6$ (Property 5). Moreover, by counting the number of tuples in the utility-table and dividing it by the number of sequences in the database, we find that $sup_{SDB}(r) = 0.75$ (Property 6). We can observe that the sum of iutil, lutil, rutil and lrutil values is equal to 82, which is an upper bound on u(r) (Property 7). Furthermore, this value tells us that transitive left/right expansions of r may generate high-utility sequential rules (Property 8). And more particularly, because the sum of iutil, lutil and lrutil values is equal to 80, transitive left expansions of r may generate high-utility sequential rules (Property 9). Now, consider the rule $r': \{a,b\} \rightarrow \{e\}$. The utility-table of $r'$ can be obtained from the utility-table of r using the aforementioned procedure. The result is $\{ (s_1, 6, 10, 0, 11), (s_2, 6, 32, 2, 0), (s_3, 6, 0, 0, 9) \}$. This table, can then be used to calculate utility-tables of other rules such as $\{a,b,c\} \rightarrow \{e\}$, which is $\{ (s_1, 16, 0, 0, 11), (s_2, 26, 12, 2, 0) \}$.

Up until now, we have explained how the proposed utility-table structure is built, can be used to calculate the utility and support of rules and can be used to prune the search space. But a problem remains. How can we calculate the confidence of a rule $r:X \rightarrow Y$? To calculate the confidence, we need to know |seq(r)| and |ant(r)|, that is the number of sequences containing r and the number of sequences containing its antecedent X. |seq(r)| can be easily obtained by counting |ut(r)|. However, |ant(r)| is more difficult to calculate. A naive solution would be to scan the database to calculate |ant(r)|. But this would be highly inefficient. In HUSRM, we calculate |ant(r)| efficiently as follows. HUSRM first creates a bit vector for each single item appearing in the database. The bit vector bv(i) of an item i contains |SDB| bits, where the j-th bit is set to 1 if $\{i\} \sqsubseteq s_j$ and is otherwise set to 0. For example, $bv(a) = 1111$, $bv(b) = 1011$ and $bv(c) = 1101$. Now to calculate the confidence of a rule r, HUSRM intersects the bit vectors of all items in the rule antecedent, i.e. $\bigwedge _{i \in X} bv(i)$. The resulting bit vector is denoted as bv(X). The number of bits set to 1 in bv(X) is equal to |ant(r)|. By dividing the number of lines in the utility-table of the rule |ut(r)| by this number, we obtain the confidence. This method is very efficient because intersecting bit vectors is a very fast operation and bit vectors does not consume much memory. Furthermore, an additional optimization is to reuse the bit vector bv(X) of rule r to more quickly calculate $bv(X \cup \{i\})$ for any left expansions of r with an item i (because $bv(X \cup \{i\})$ $= bv(X)$ $\wedge$ $bv(\{i\})$).

3.2 The Proposed Algorithm

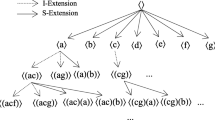
HUSRM explores the search space of sequential rules using a depth-first search. HUSRM first scans the database to build all sequential rules of size $1*1$. Then, it recursively performs left/right expansions starting from those sequential rules to generate larger sequential rules. To ensure that no rule is generated twice, the following ideas have been used.

First, an important observation is that a rule can be obtained by different combinations of left and right expansions. For example, consider the rule $r: \{a,b\} \rightarrow \{c,d\}$. By performing a left and then a right expansion of $\{a\} \rightarrow \{c\}$, one can obtain r. But this rule can also be obtained by performing a right and then a left expansion of $\{a\} \rightarrow \{c\}$. A simple solution to avoid this problem is to not allow performing a left expansion after a right expansion but to allow performing a right expansion after a left expansion. Note that an alternative solution is to not allow performing a left expansion after a right expansion but to allow performing a right expansion after a left expansion.

Second, another key observation is that a same rule may be obtained by performing left/right expansions with different items. For example, consider the rule $r_9: \{b, c\} \rightarrow \{e\}$. A left expansion of $\{b\} \rightarrow \{e\}$ with item c results in $r_9$. But $r_9$ can also be found by performing a left expansion of $\{c\} \rightarrow \{e\}$ with item b. To solve this problem, we chose to only add an item to a rule by left (right) expansion if the item is greater than each item in the antecedent (consequent) according to the total order $\succ _{lex}$ on items. By using this strategy and the previous one, no rules is considered twice.

Figure 1 shows the pseudocode of HUSRM. The HUSRM algorithm takes as parameters a sequence database SDB, and the minutil and minconf thresholds. It outputs the set of high-utility sequential rules. HUSRM first scans the database once to calculate the sequence estimated utility of each item and identify those that are promising. Then, HUSRM removes unpromising items from the database since they cannot be part of a high-utility sequential rule (Property 3). Thereafter, HUSRM only considers promising items. It scans the database to create the bit vectors of those items, and calculate seq(r) and SEU(r) for each rule r of size $1*1$ appearing in the database. Then, for each promising rule r, HUSRM scans the sequences containing r to build its utility-table ut(r). If r is a high-utility sequential rule according to its utility-table and the bit-vector of its antecedent, the rule is output. Then, Property 8 and 9 are checked using the utility-table to determine if left and right expansions of r should be considered. Exploring left and right expansions is done by calling the leftExpansion and rightExpansion procedures.

The leftExpansion procedure (Algorithm 2) takes as input a sequential rule r and the other parameters of HUSRM. It first scans sequences containing the rule r to build the utility-table of each rule t that is a left-expansion of r. Note that the utility-table of r is used to create the utility-table of t as explained in Sect. 3.1. Then, for each such rule t, if t is a high-utility sequential rule according to its utility-table and the bit-vector of its antecedent, the rule is output. Finally, the procedure leftExpansion is called to explore left-expansions of t if Property 9 is verified. The rightExpansion procedure (Algorithm 3) is very similar to leftExpansion and is thus not described in details here. The main difference is that rightExpansion considers right expansions instead of left expansions and can call both leftExpansion and rightExpansion to search for larger rules.

3.3 Additional Optimizations

Two additional optimizations are added to HUSRM to further increase its efficiency. The first one reduces the size of utility-tables. It is based on the observations that in the leftExpansion procedure, (1) the rutil values of utility-tables are never used and (2) that lutil and lrutil values are always summed. Thus, (1) the rutil values can be dropped from utility-tables in leftExpansion and (2) the sum of lutil and lrutil values can replace both values. We refer to the resulting utility-tables as Compact Utility-Tables (CUT). For example, the CUT of $\{a,b\} \rightarrow \{e\}$ and $\{a,b,c\} \rightarrow \{e\}$ are respectively $\{ (s_1, 6, 21),$ $(s_2, 6, 32),$ $(s_3, 6, 9) \}$ and $\{ (s_1, 16, 11),$ $(s_2, 26, 12) \}$. CUT are much smaller than utility-tables since each tuple contains only three elements instead of five. It is also much less expensive to update CUT.

The second optimization reduces the time for scanning sequences in the leftExpansion and rightExpansion procedures. It introduces two definitions. The first occurrence of an itemset X in a sequence $s=\langle I_1, I_2, ... I_n \rangle$ is the itemset $I_k \in s$ such that $X \subseteq \bigcup _{i=1}^k I_i$ and there exists no $g < k$ such that $X \subseteq \bigcup _{i=1}^g I_i$. The last occurrence of an itemset X in a sequence $s=\langle I_1, I_2, ... I_n \rangle$ is the itemset $I_k \in s$ such that $X \subseteq \bigcup _{i=k}^n I_i$ and there exists no $g > k$ such that $X \subseteq \bigcup _{i=g}^n I_i$. An important observation is that a rule $X \rightarrow Y$ can only be expanded with items appearing after the first occurrence of X for a right expansion, and occurring before the last occurrence of Y for a left expansion. The optimization consists of keeping track of the first and last occurrences of rules and to use this information to avoid scanning sequences completely when searching for items to expand a rule. This can be done very efficiently by first storing the first and last occurrences of rules of size $1*1$ and then only updating the first (last) occurrences when performing a left (right) expansion.

4 Experimental Evaluation

We performed experiments to evaluate the performance of the proposed algorithm. Experiments were performed on a computer with a fourth generation 64 bit core i7 processor running Windows 8.1 and 16 GB of RAM. All memory measurements were done using the Java API.

Experiments were carried on four real-life datasets commonly used in the pattern mining literature: BIBLE, FIFA, KOSARAK and SIGN. These datasets have varied characteristics and represents the main types of data typically encountered in real-life scenarios (dense, sparse, short and long sequences). The characteristics of datasets are shown in Table 4), where the |SDB|, |I| and avgLength columns respectively indicate the number of sequences, the number of distinct items and the average sequence length. BIBLE is moderately dense and contains many medium length sequences. FIFA is moderately dense and contains many long sequences. KOSARAK is a sparse dataset that contains short sequences and a few very long sequences. SIGN is a dense dataset having very long sequences. For all datasets, external utilities of items are generated between 0 and 1,000 by using a log-normal distribution and quantities of items are generated randomly between 1 and 5, similarly to the settings of [2, 8, 12].

Table 4. Dataset characteristics

Because HUSRM is the first algorithm for high-utility sequential rule mining, we compared its performance with five versions of HUSRM where optimizations had been deactivated (HUSRM$_{1}$, HUSRM$_{1,2}$, HUSRM$_{1,2,3}$, HUSRM$_{1,2,3,4}$ and HUSRM$_{1,2,3,4,5}$). The notation HUSRM$_{1,2,...n}$ refers to HUSRM without optimizations $O_1$, $O_2$ ... $O_n$. Optimization 1 ($O_1$) is to ignore unpromising items. Optimization 2 ($O_2$) is to ignore unpromising rules. Optimization 3 ($O_3$) is to use bit vectors to calculate confidence instead of lists of integers. Optimization 4 ($O_4$) is to use compact utility-tables instead of utility-tables. Optimization 5 ($O_5$) is to use Property 9 to prune the search space for left expansions instead of Property 8. The source code of all algorithms and datasets can be downloaded as part of the SPMF data mining library at http://goo.gl/qS7MbH [6].

We ran all the algorithms on each dataset while decreasing the minutil threshold until algorithms became too long to execute, ran out of memory or a clear winner was observed. For these experiments, we fixed the minconf threshold to 0.70. However, note that results are similar for other values of the minconf parameter since the confidence is not used to prune the search space by the compared algorithms. For each dataset and algorithm, we recorded execution times and maximum memory usage.

Execution times. Fig. 1 shows the execution times of each algorithm. Note that results for HUSRM$_{1,2,3,4,5}$ are not shown because it does not terminate in less than 10, 000 s for all datasets. HUSRM is respectively up to 1.8, 1.9, 2, 3.8 and 25 times faster than HUSRM$_{1}$, HUSRM$_{1,2}$, HUSRM$_{1,2,3}$, HUSRM$_{1,2,3,4}$ and HUSRM$_{1,2,3,4,5}$. It can be concluded from these results that HUSRM is the fastest on all datasets, that its optimizations greatly enhance its performance, and that $O_5$ is the most effective optimization to reduce execution time. In this experiment, we have found up to 100 rules, which shows that mining high-utility sequential rules is very expensive. Note that if we lower minutil, it is possible to find more than 10,000 rules using HUSRM.

Fig. 1.

Comparison of execution times (seconds)

Memory usage. Table 4 shows the maximum memory usage of the algorithms for the BIBLE, FIFA, KOSARAK and SIGN datasets. Results for HUSRM$_{1,2,3,4,5}$ are not shown for the same reason as above. It can be observed that HUSRM always consumes less memory and that this usage is up to about 50 % less than that of HUSRM$_{1,2,3,4}$ on most datasets. The most effective optimization to reduce memory usage is $O_4$ (using compact utility-tables), as shown in Table 5.

Table 5. Comparison of maximum memory usage (megabytes)

5 Conclusion

To address the lack of confidence measure in high-utility sequential pattern mining, we defined the problem of high-utility sequential rule mining and studied its properties. We proposed an efficient algorithm named HUSRM (High-Utility Sequential Rule Miner) to mine these rules. HUSRM is a one-phase algorithm that relies on a new data structure called compact utility-table and include several novel optimizations to mine rules efficiently. An extensive experimental study with four datasets shows that HUSRM is very efficient and that its optimizations respectively improve its execution time by up to 25 times and its memory usage by up to 50 %.