Keywords

  • Nobody enters here, if he is not a geometrician.

  • Platon

  • Le chimiste est le seul scientifique, qui cree l, objet de ses etudes.

  • Marcelline Berthelot

Introduction

Over the last 20–30 years, we have been witnessing (and participating in) the development of new approaches to the problem of the structure of matter and considerable expansion of the borders of classic crystallography.

First of all, this expansion was induced by the advances in experimental techniques (in particular, high-resolution microscopy) applied to small natural objects: biological, organic, inorganic, and their combinations. To explain the experimental data obtained, there is a need to understand the very basic principles of construction of matter as a part of the material world around us. Indeed, how many atoms are needed to form a substance of macro-world as we know it? For instance, metallic iron. We know the series of atomic Fe clusters consisting of N atoms forming a “magic” sequence of numbers. What are the properties of these clusters? Do their structure correspond to the structure of macro-iron? These problems are under active debate and investigation at the moment. Perhaps, at the most advanced degree, development of these ideas has been determined by Mackay who first published on this issue in 1967 [1]. The most important parts of this idea are atomistics (i.e., everything starts from atoms) and hierarchy (i.e., matter is organized on the levels of increasing complexity). At the core of this idea is the concept of information that determines an inorganic structure in the same way as genetic code determines biological structures. The ideas of Mackay were in correspondence with the works of W. Pearson who in 1972 suggested describing structures of intermetallics by means of codes that characterize stacking sequences of atomic layers (for the sake of justice, we note that analogous approaches were developed by the Soviet scientist G. S. Zhdanov back in 1946). Mackay further developed the idea of description of structures of inorganic materials on the basis of another important concept of ‘curvature’ in the sense of ‘grammar’ of inorganic and biological structures. In this grammar, letters are atoms, and words are clusters of connected atoms (building blocks, structural complexes, etc.). What determines the structures of these clusters and the structure of matter comprising these clusters? Today we are able to provide some partial answers to this question using mathematics (geometry) and information theory. It happens that mutual arrangement of N points (atoms) interacting with each other in n-dimensional space is uniquely determined and, in turn, determines so-called spherical code that can be used to save and to transmit information. Authors of Ref. [2] named these configurations “universal optima”. A special condition is the requirement that interaction potential has to be continuous and differentiable. All known universal optima are listed in Table 1. It is worthy to note that the sharp configurations—independently from the type of interaction potential—are the most closely packed arrangements. Thus, the principle of dense filling of space suggested by Laves in 1967 for metallic alloys has now been proved mathematically, rigorously.

Table 1 Known universal optima. Energy-minimizing point configurations
Full size table

Experimental proof of the results of [2] had been performed in [3] using advanced computer modeling. Two more universal optima have been found (for 40 points in 10-dimensional space and for 64 points in 14-dimensional space). First five configurations in Table 1 are vertices of certain regular polytopes (these are polytypes with all faces being simplices). Next seven cases were obtained from the root lattices E8 in R8 and Leech lattice in R24. 240-point configurations and 196550 points have minimal vectors in these lattices. In terms of sphere packings, these are contact configurations with kissing points in corresponding packings. Each configuration has a spherical cap in each point with its radius being as maximal as possible but without overlaps. Kissing points of this cap provide spherical code in the space of corresponding dimensionality.

Mathematical problem of contact numbers of spheres is a partial case of the problem of a spherical code. For each sphere, there is a corresponding spherical cap on the central sphere and a kissing point. These points are called an alphabet. The problem is to transfer kissing points from certain caps to the other sphere. The set of caps from which signals are transmitted form a word. If transmission is somehow distorted, the caps should be relatively large. In that case, the point should first appear in the cap where it has previously been, so it can be reconstructed since the caps do not intersect. The word can be reconstructed accordingly. The more spherical caps there are on the certain sphere, the more different information can be encoded.

In the framework of information theory, instead of continuous wave in 1-dimensional space, one can speak about vector set in n-dimensional space.

If connection channel has no memory and with the increase of the word length n, the number of decoding steps do not increase exponentially (2n) but as n 2. Using hierarchical principles of coding-decoding, one may decrease computational complexity till ~n. Coding as well as decoding are done step-by-step toward higher levels of hierarchy. On the lower level, simple symbols (alphabet) form blocks (words). On the second level, each block (word) is considered as a new symbol, and blocks group into higher-level blocks (sentences). By placement of certain points in n-dimensional space and looking at their arrangements, we determined further directions of self-assembly using purely geometrical operations.

Thus, the information theory and structure can be merged in an unified theory. All sharp configurations are m-designs, i.e. they are not simply spherical codes, but also the set of roots of some polynom (Hermit polynom) of the degree m.

The science of structure of matter is based upon self-assembly of atoms first into sharp configurations, and then, according to the principle of a cellular automaton, into more hierarchically complex structures, into nanoparticles and then into macromolecules and macroobjects.

The structural diversity of the nanoworld is determined by the fact that finite packings may represent fragments of some “parent” structures that do not necessarily exist in 3-dimensional Euclidean space. We shall call these structures fundamental. The reciprocal transition into space with dimension n ≤ 3 is by the ‘cut-and-project’ procedure.

The chemical or physical nature of the subunits is of secondary importance (whether these are atoms or protein molecules). Geometry determines and forms a structural model (universal optimum) before the atoms or other subunits and their interaction potentials are chosen. Thus, in this philosophy, geometry is more than a description principle. It is a reflection of the properties of space where nanoobjects exist.

In order to understand mystical appearance of regular polytopes in the problems of applied mathematics, one has to replace direct calculations of differential geometry by more simple and general approach of symplectic and contact geometry. General principle here is as follows: one has to embed geometrical objects from ‘configurational’ space V into ‘phase’ space V × F, where peculiarities either disappear or become simpler (in theory of differential equations and quantum theory, this approach is called ‘microlocal’). This concept transforms simple facts of differential geometry into general theorems of symplectic and contact geometry with more wide field of application. In this way, perspectives arise for very wide exploration of differential-geometric intuition (V.I. Arnold).

In the past few years, a large number of nanoparticles had been found that have structures not describable in terms of classical crystallography. To express their admiration, scientists use such terms as “unprecedented”, “unique”, “mysterious”. To explain their structure, we have used local (microlocal) approach. General principle is the same: atom configurations should be considered as geometrical objects and embedded from 3-dimensional Euclidean space into another space—of higher dimensionality and (probably) different topology. However, in local terms, this space shall still be represented as a direct product V × F. In terms of modern geometry, this procedure corresponds to the construction of a fiber space, where V is the basis of fibering and F is the structural group of the fiber.

In general case, fibering is a manifold. Any manifold can be isometrically embedded into Euclidean space of corresponding (or even higher) dimensionality, where we have a possibility to choose a fundamental structure.

These principal results allow us, instead of search of concrete structure responsible in E3 for the minimum of some potential, to consider a whole class of derivative structures by the prior knowledge that they all have been obtained from some universally optimal non-Euclidean structures and thus close to the local minimum for the whole class of interaction potentials.

The real type of atoms (or any other subunits) involved will influence preferential formation of derivative structures by the atoms of particular type.

Accordingly, we may consider a complex inorganic structure, e.g. paulingite,Footnote 1 a crystalline zeolite with several hundreds of atoms in its unit cell. Where are genes for this structure? Which information does it contain? How may we describe it? Can we describe complex inorganic structure (periodic or aperiodic) as a 1-dimensional chain with its “gene” being the basis of construction and mutation and suitable for the formation of a whole range of structures? In this case, the particular structure can be chosen by the free energy minimum but different minima should not coincide.

We shall try to use these “inorgenes” in genetic algorithm of search of structures that fulfill the requirements of the lowest energy level. This will be required to calculate the gene that corresponds to the corresponding structure. As in biology, there could be genes that may not generate a ‘living’ structure.

Paulingite: Structural Architecture

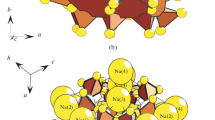
Paulingite (K6Ca16[Al38Si130O336](H2O)113) is one of the most structurally complex minerals. Its crystal chemistry was the subject of a large number of studies in mineralogical crystallography [4, 5]. At the present time, there are several mineral species of the paulingite group that have the same root name and different suffices according to the dominating extra-framework cation: paulingite-K, paulingite-Na, and paulingite-Ca. A synthetic analogue of paulingite is known under the name ‘zeolite ECR-17’ that had been used in chemical technology [6]. However, the fundamental interest in paulingite is not in chemical diversity of extra-framework cations but in structural complexity of its tetrahedral framework. Unit cell of paulingite contains 768 tetrahedral anions TO4 (T = Al3+, Si4+) linked into complex 3-dimensional architecture (Fig. 1a).

Fig. 1
figure 1

Tetrahedral framework in paulingite (a) and its 3-dimensional graph (b striation denotes bipyramidal nanocomplex). Arrangement of the bipyramidal nanocomplexes (c) corresponds to the space partition into tetragonal bipyramids (= flattened octahedra) (d).

Full size image

Minerals of the paulingite group have a cubic symmetry and crystallize in the space group \( Im\overline{3}m \), with the a parameter in the range of 35.00–35.43 Å. Topology of zeolite framework in paulingite is usually described in terms of polyhedral building units [7]. Symbolic (or nodal) description is usually used, when tetrahedra are symbolized by vertices and vertices corresponding to the linked tetrahedra are linked by an edge. Graphs obtained along this procedure are 4-connected nets that are subject of a separate area of mathematical crystallography [8]. Figure 1b shows graph of the paulingite framework. In contrast to previous works [4–7], we prefer to describe this framework not in terms of polyhedral units but as a result of linkage of bipyramidal (octahedral) complexes outlined in Fig. 1b by striated line. These complexes are centered in the middle points of edges and in the centers of the cubic cell (e.g. in points (0; 0; 0.5) and (0.5; 0.5; 0)). In total, they form space partition into flattened octahedra with dimensions of 3.7 × 3.7 × 2.5 nm3 (Fig. 1c, d).

Let us consider the structure of complexes in more detail. In Fig. 2, each 4-membered ring (4-MR) is replaced by a flat square. The complex can be split into five levels, each formed by a closed contour of vertically standing squares (Fig. 2b). The highest level consists of a double octagonal ring (D8-MR), the second is formed by 24 squares, the third and central level contains 40-square contour and internal D8-MR. The fourth and fifth levels repeat the first and the second, respectively. The levels are linked by inclined squares so that the whole construction reminds of hierarchical construction of Middle-Age castles that also had many-level architecture.

Fig. 2
figure 2

Bipyramidal nanocomplex as construction of 4-MRs (shown as squares): side view (a), stratified structure (b), top view (c).

Full size image

It is noteworthy that, in general, construction of the complexes corresponds to the principles of sharp configurations. At the first level, atoms form tetrahedra—3-dimensional simplices (see second row in Table 1), then tetrahedra are linked into 4-MRs and 8-MRs (first row in Table 1). General architecture corresponds to an octahedron that is a cross-polytope of 3-dimensional space (third row in Table 1).

Paulingite: Cellular Automata Modeling

Projection of the nanocomplex along its axis is shown in Fig. 3. Obviously, the 2nd and 3rd levels are similar to the 1st level and can be obtained from the latter by some simple geometrical operations. As an instrument, we may use a cellular automaton (CA), a discrete deterministic system that develops in time and space according to simple set of transition rules [9]. The use of CAs in structural crystallography was first proposed by Mackay [10] and recently was further developed in [11].

Fig. 3
figure 3

Levels of paulingite bipyramidal nanocomplex as a result of work of the CA: schematic structure of contours in different layers (a), transition to the square lattice (b), 4 cycles of work of 4-colored CA (c).

Full size image

Figure 3a shows schematical construction of paulingite nanocomplex in terms of vertical squares. The CA lattice is a dihedral partition of plane into squares and octagons. Initial condition (zero-cycle of the CA) is a regular octagon. In order to simplify the model further without the loss of generality, we may transform the initial CA lattice into a square lattice by a series of simple substitutions (Fig. 3b). The closed 8-MR will correspond to a black cell, 8-MR with one or less bold edges to a white cell, 8-MRs with three and five bold edges to blue and red cells, respectively. As a result, we shall obtain 4-colored CA shown in Fig. 3c.

It is of interest that infinite work of this CA will result in formation of a periodic 3-dimensional framework with an axial structure. Along its axis, with the period of 1 nm, will appear 8-MRs. We do not see any principal reasons why this structure cannot be formed under natural or experimental conditions. However, if they really form, their identifications would be a complex and separate task.

It is quite probable that paulingite is the by-product of the work of the CA described above that has been stopped on the 2nd cycle. In order to check this hypothesis, it is of interest to consider related structures

The zero-cycle of the CA shown in Fig. 3 corresponds to the structure of zeolite Rho [12–14] that is depicted in Fig. 4a. As paulingite, zeolite Rho crystallizes in cubic symmetry, space group \( Im\overline{3}m \) with a ~ 15 Å. In this zeolite, D8-MRs are linked directly by 4-MRs. Thus, whereas paulingite corresponds to the 2nd cycle of the CA (Fig. 4c), zeolite Rho corresponds to the zero cycle of the CA.

Fig. 4
figure 4

Graphs of zeolite frameworks consisting of nanocomplexes formed as a result of work of paulingite CA: zeolite Rho RHO (a), hypothetical zeolite ISC-1 (b) and paulingite (c).

Full size image

ISC-1: A New Theoretical Zeolite Framework

We could not find in literature any data concerning zeolite intermediate between paulingite and zeolite Rho. However, the model developed above allows to predict its hypothetical structure (Fig. 4b). It has a cubic unit cell, \( Im\overline{3}m \) with a ~ 25 Å. We were able to construct model of its tetrahedral framework (Fig. 5a). Atom coordinates and basic geometrical parameters are given in Table 2. We denote this zeolite as ISC-1 (Institute of Silicate Chemistry-1). Theoretical X-ray diffraction pattern of ISC-1 is shown in Fig. 5b (diffraction lines till 2θ max = 30° are listed in Table 3).

Fig. 5
figure 5

Tetrahedral framework of the hypothetical material ISC-1 (a) and its calculated X-ray powder diffraction pattern (for λ = 1.54178 Å) (b).

Full size image
Table 2 Atom coordinates and geometrical parameters of tetrahedral framework in hypothetical zeolite ISC-1 (a = 25 Å, sp. gr. \( Im\overline{3}m \))
Full size table
Table 3 Theoretical X-ray diffraction pattern of hypothetical zeolite ISC-1 calculated from the data given in Table 2 (λ = 1.54178 Å, 2θ max = 30°; 0-intensity lines are listed as well)
Full size table

Thus, zeolite Rho, hypothetical material ISC-1, and paulingite form a family of zeolites that result from the CA shown in Fig. 3. It can be proposed that more complex zeolites of the family can be synthesized that correspond to higher cycles of the CA work. Ideal symmetry of these zeolites will be cubic, space group \( Im\overline{3}m \), a = 15 + 10n [Å], where n is a number of the CA cycle.

Conclusions

  1. 1.

    By means of the concept of universal optimum and general principles of inorganic gene, structures of paulingite-related zeolites and minerals have been constructed.

  2. 2.

    A new hypothetical zeolite of the paulingite family has been predicted and named ISC-1 (Institute of Silicate Chemistry-1).

  3. 3.

    It appears to be very probable that universal optimum contains all necessary information for its material realization (sharp configurations) and construction of materials with certain type of interaction potential (even with restrictions existing in theory for this potential).