A New Kinematic Hardening Rule Describing Different Plastic Moduli in Monotonic and Cyclic Deformations

Abstract

To describe the different plastic moduli of the metal materials presented in the monotonic and cyclic deformations, a new nonlinear kinematic hardening rule is proposed by modifying the Chaboche’s one (Chaboche 1989). In the proposed rule, the back stress is assumed to be decomposed into three components as done by Chaboche (1989), but the linear hardening and dynamic recovery terms of each back stress component are further divided into two parts, respectively, and a part in each of them is only activated when the reverse loading occurs so that the cyclic stress-strain hysteresis loops can be predicted more accurately; moreover, a rachetting coefficient is introduced into one part of dynamic recovery term to describe the ratchetting. The proposed rule can be reduced to the Chaboche’s one under the monotonic loading conditions, or by setting some material parameters as zero. Finally, the proposed model is verified by comparing the predicted results with corresponding experimental ones. It is seen that the predicted results are in good agreement with the corresponding experimental ones.

27.1 Introduction

In various engineering applications, many structural components are often subjected to a complex cyclic loading. The cyclic deformation features, e.g., the cyclic hardening/softening and rachetting of materials should be realized, since they play very important roles in the safety assessment and fatigue-life estimation of such structural components. Cyclic plastic constitutive models suitable for describing such cyclic deformation features were developed extensively in the last few decades by including a nonlinear kinematic hardening rule, such as those done by Chaboche (1989, 1991), Ohno and Wang (1991, 1993), Ohno and Abdel-Karim (2000), Bari and Hassan (2000, 2001, 2002), Kang and Gao (2002), Kang et al. (2002), Kang (2004), Bai and Chen (2009), Abdel-Karim (2009), Zhu et al. (2014) and so on, by extending the Armstrong and Frederick nonlinear kinematic hardening rule (Armstrong and Frederick 1966), simplified as the A-F one. More detailed reviews for the state-of-arts of kinematic hardening rules can be referred to Ohno and Abdel-Karim (1990); Ohno (1997), Kang (2008) and Chaboche (2008).

Fig. 27.1

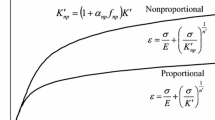
Comparison of plastic moduli obtained during the monotonic and repeated loading tests of 316L stainless steel (Dong et al. 2014)

From the existing experimental observations to the cyclic deformation of metal materials (Mizuno et al. 2000; Kang and Gao 2002; Kang et al. 2002; Dong et al. 2014), it is found that the plastic modulus presented during cyclic plastic deformation differs from that occurred in the monotonic one, especially at the initial stage of plastic yielding. It is seen from Fig. 27.1 that a lower plastic modulus generally occurs during cyclic loading. However, such difference has not been concerned in the existing models mentioned above. For instance, the predicted plastic modulus by Ohno-Wang’s rule I (Ohno and Wang 1993) at the initial stage of plastic yielding during cyclic deformation is larger than the experimental ones since the material parameters are determined from the monotonic tensile stress-strain data; although the Chaboche’s model (Chaboche 1989) gives a reasonable prediction to the plastic modulus occurred during cyclic deformation by determining the material parameters directly from the cyclic stress-strain data, it underestimates the plastic modulus obtained in monotonic tension. Thus, it is necessary to consider the different plastic moduli occurred at the initial stages of monotonic and cyclic deformations so that the monotonic stress-strain responses and cyclic hysteresis loops can be simultaneously and accurately predicted by the constitutive model.

Therefore, here a new kinematic hardening rule is developed by modifying the Chaboche’s rule in order to describe the different plastic moduli occurred in the monotonic and cyclic deformations, especially at the initial stage of plastic yielding. In the proposed rule, the back stress is also assumed to be decomposed into three components, i.e., the short-range, middle-range and long-range component, as done by Chaboche (1989), but the linear hardening and dynamic recovery terms of each back stress component are further divided into two parts, respectively, and a part in each of them is only activated when the reverse loading occurs so that the cyclic stress-strain hysteresis loops can be predicted more accurately; moreover, a rachetting coefficient is introduced into one part of dynamic recovery term to describe the ratcheting of materials. It is noted that the proposed rule can be reduced to the Chaboche’s one under the monotonic loading condition, or by setting some specific material parameters as zero. Finally, the proposed model is verified by comparing the predicted results with corresponding experimental ones (Kang and Gao 2002). It is seen that the predicted results are in good agreement with the corresponding experimental ones.

27.2 Constitutive Model

27.2.1 Main Equations

To formulate an elastic-plastic constitutive model in the framework of small deformation, the additive decomposition of strain tensor $\pmb {\varepsilon }$ is usually postulated as:

$$\begin{aligned} \pmb {\varepsilon }=\pmb {\varepsilon }^{\mathrm e}+\pmb {\varepsilon }^{\mathrm p}, \end{aligned}$$

(27.1)

where, $\pmb {\varepsilon }^{\mathrm e}$ and $\pmb {\varepsilon }^{\mathrm p}$ represent the elastic and plastic strain tensor, respectively. The elastic strain tensor $\pmb {\varepsilon }^{\mathrm e}$ is commonly characterized by the Hooke’s low, i.e.,

$$\begin{aligned} \pmb {\varepsilon }^{\mathrm e}=\frac{1+\nu }{E}\pmb {\sigma }-\frac{\nu }{E}(\mathrm {tr}\pmb {\sigma })\pmb {1}, \end{aligned}$$

(27.2)

where $\nu$ and E are Poisson’s ratio and Young’s modulus, respectively; $\pmb {1}$ is second-order identity tensor; $\pmb {\sigma }$ is stress tensor. Rate-independent plasticity is assumed by using a von-Mises-typed yielding surface:

$$\begin{aligned} F_{\mathrm y}=\sqrt{\frac{3}{2}(\pmb {\sigma }^{'}-\pmb {\alpha }):(\pmb {\sigma }^{'}-\pmb {\alpha })}-Q, \end{aligned}$$

(27.3)

where $F_{\mathrm y}$ is yield function; $\pmb {\sigma }^{'}$ is deviatoric stress tensor; $\pmb {\alpha }$ is back stress tensor; Q is isotropic deformation resistance (Q is considered as a constant since the aim of this work is focused on proposing a kinematic hardening rule). For the evolution of plastic strain tensor $\pmb {\varepsilon }^{\mathrm p}$, associated plasticity and normality postulate together lead to a flow rule as following:

$$\begin{aligned} \dot{\pmb {\varepsilon }}^{\mathrm p}=\dot{\lambda }\frac{\partial {F_{\mathrm y}}}{\partial {\pmb {\sigma }}}, \end{aligned}$$

(27.4)

where $\dot{\lambda }$ is a plastic multiplier which can be determined by Kuhn-Tucker’s conditions, i.e.,

$$\begin{aligned} \dot{\lambda }\geqslant {0}, \qquad F_\mathrm {y}\leqslant {0},\qquad \dot{\lambda }F_y=0\quad (\mathrm {if} \quad F_y=0). \end{aligned}$$

(27.5)

27.2.2 Modified Chaboche’s Kinematic Hardening Rule

As done by Chaboche (1989), the back stress tensor is divided into three components, i.e., so-called short-range, middle-range and long-range ones,

$$\begin{aligned} \pmb {\alpha }=\sum _{i=1}^{3}\pmb {\alpha }_i. \end{aligned}$$

(27.6)

Furthermore, in order to describe the experimental observation that the plastic modulus during the cyclic deformation differs from that obtained in monotonic one (shown in Fig. 27.1), a new evolution rule of $\pmb {\alpha }_i$ (i.e., a new kinematic hardening rule) is proposed here, i.e.,

$$\begin{aligned} \dot{\pmb {\alpha }_i}=\frac{2}{3}\zeta _{i}(r_{i}^{\mathrm m}\,+\,r_{i}^{\mathrm c})\dot{\pmb {\varepsilon }^{\mathrm p}}\,-\,\frac{r_{i}^{\mathrm c}}{r_{i}^{\mathrm m}(1-\exp (-\zeta _{i}q))}\zeta _{i}\pmb {\alpha }_i\dot{\mathrm p}\,-\,(\frac{\Vert {\pmb {\alpha }_i}\Vert }{r_{i}^{\mathrm m}(1-\exp (-\zeta _{i}q))})^{m_{i}}\zeta _{i}\pmb {\alpha }_i\dot{\mathrm p}. \end{aligned}$$

(27.7)

where $\zeta _{i}$ is a positive dimensionless material parameter; $r_{i}^{\mathrm m}$ and $r_{i}^{\mathrm c}$ are material parameters with a dimension of stress ($r_{i}^{\mathrm m}$ is positive, and a restriction of $r_{i}^{\mathrm c}$ is set on $r_{i}^{\mathrm c}\geqslant -r_{i}^{\mathrm m}$ to ensure the coefficient of the first term in the right side of Eq. (27.7) is positive, which will be discussed in details in the next paragraphs); $m_{i}$ is so-called ratchetting coefficient, which control the evolution of ratchetting; $\dot{\mathrm p}$ is the accumulated plastic strain rate defined by $\dot{\mathrm p}=\sqrt{\frac{3}{2}}\dot{\lambda }$; q is the radius of memory surface $F_q$ in plastic strain space, i.e.,

$$\begin{aligned} F_{q}=\sqrt{\frac{2}{3}\pmb {\varepsilon }^{\mathrm p}:\pmb {\varepsilon }^{\mathrm p}}-q. \end{aligned}$$

(27.8)

The evolution rule of q is

$$\begin{aligned} \dot{q}=\left\langle {\pmb {N}:\pmb {N}_q}\right\rangle \dot{\mathrm p}, \end{aligned}$$

(27.9)

where $\left\langle \right\rangle$ is the MaCauley operator; $\pmb {N}$ and $\pmb {N}_q$ are the unit normal vectors to the yielding and memory surfaces in current state (corresponding to $\pmb {\sigma }$ and $\pmb {\varepsilon }^{\mathrm p}$), respectively:

$$\begin{aligned} \pmb {N}=\frac{\pmb {\sigma }'-\pmb {\alpha }}{\Vert \pmb {\sigma }'-\pmb {\alpha }\Vert },\qquad \pmb {N}_q=\frac{\pmb {\varepsilon }^{\mathrm p}}{q}. \end{aligned}$$

(27.10)

It should be noted that, under the monotonic loading condition, the evolution rule shown in Eq. (27.7) can be reduced as

$$\begin{aligned} \dot{\pmb {\alpha }_i}=\frac{2}{3}\zeta _{i}r_{i}^{\mathrm m}\dot{\pmb {\varepsilon }^{\mathrm p}}-\zeta _{i}\pmb {\alpha }_i\dot{\mathrm p}. \end{aligned}$$

(27.11)

which is the Chaboche’s model (Chaboche 1989). On the other hand, if the parameters $r^{\mathrm c}_i$ and $m_i$ are set to be zero, Eq. (27.11) can also be obtained from Eq. (27.7). It means that the new proposed kinematic hardening rule (Eq. (27.7)) can be reduced to the Chaboche’s one (Eq. (27.11)) under the monotonic loading condition, or in case that the parameters $r^{\mathrm c}_i$ and $m_i$ are set to be zero.

As mentioned before, the new kinematic hardening rule, i.e., Eq. (27.7), is proposed in this work to capture the different plastic moduli occurred during the monotonic and cyclic deformations of materials, especially at the initial yielding stages of forward and reverse loadings. According to Chaboche (1989), the plastic modulus at the initial yielding stage is mainly controlled by the short-range component of back stress. Therefore, only activating $r^{\mathrm c}_1$ is enough to fit the experimental results well (i.e., the parameters $r^{\mathrm c}_2$ and $r^{\mathrm c}_3$ can be set to be zero for simplicity).To demonstrate the role of the parameter $r^{\mathrm c}_1$ in describing the different plastic moduli occurred in the monotonic and cyclic deformations, the predicted cyclic stress-strain curves are obtained by the proposed model with various $r^{\mathrm c}_1$ and keeping other parameters being the same as those listed in Table 27.3 in the next section, and are shown in Fig. 27.2 (a symmetrical axial strain-controlled cyclic loading with a strain amplitude of 0.8 % and in 1st cycle). It is seen that lower plastic modulus is obtained with smaller value of $r^{\mathrm c}_1$. It implies that the experimental stress-strain hysteresis loops can be fitted well by adjusting the parameter $r^{\mathrm c}_1$.

Fig. 27.2

Effect of varied $r^{\mathrm c}_1$ on the plastic modulus in the cyclic deformation

Fig. 27.3

Effect of varied $m_3$ on the predicted ratchetting

On the other hand, a new parameter named as ratchetting coefficient is also introduced into the new proposed model, which makes the proposed model be able to describe the ratchetting of materials by setting a suitable ratchetting parameter $m_3$ since it is also concluded by Gaudin and Feaugas (2004) that the racthetting of metal materials is mainly controlled by the long-range back stress, i.e., the third component of the Chaboche’s model. It implies that the parameters $m_1$ and $m_2$ can be set to be zero, for simplicity. Thus, the effect of varied $m_3$ on the predicted ratchetting is discussed here, and the predicted results are shown in Fig. 27.3 by adopting an asymmetrical stress-controlled cyclic loading case with an applied mean stress of 100 MPa and stress amplitude of 500 MPa. To illustrate the evolution of ratchetting more clearly, a ratchetting strain $\varepsilon _\mathrm {r}$ per cycle is defined as:

$$\begin{aligned} \varepsilon _\mathrm {r}=\frac{1}{2}(\varepsilon _{\mathrm {max}}+\varepsilon _{\mathrm {min}}), \end{aligned}$$

(27.12)

where, $\varepsilon _{\mathrm {max}}$ and $\varepsilon _{\mathrm {min}}$ are the maximum and minimum strains per cycle, respectively. It is seen from Fig. 27.3 that smaller ratchetting strain is obtained with larger $m_3$, and the predicted ratchetting strain rate is no longer a constant, but decreases with the increasing number of cycles, if the $m_3$ is non-zero.

27.3 Simulation and Discussion

In this section, the capability of the proposed model to predict the monotonic and cyclic deformations of materials is verified by comparing the predictions with the corresponding experimental results obtained by Kang and Gao (2002) for a cyclically stable material, annealed U71Mn rail steel. The monotonic tensile test was performed at a constant strain rate of 2 $\times {10^{-3}\,\mathrm{s}^{-1}}$ and the applied strain is up to 6 %. For strain-controlled cyclic loading tests, two loading cases (listed in Table 27.1) were conducted to investigate the cyclic softening/hardening features of the material:

• (i) single-step symmetrical strain-controlled cyclic loading with a constant strain amplitude (denoted as A);

• (ii) multi-step symmetrical strain-controlled cyclic loading with varied strain amplitude (denoted as B).

Table 27.1 Load cases in strain-controlled cyclic tests

For stress-controlled cyclic tests, three loading cases shown in Table 27.2 were performed to examine the ratchetting of the material:

Table 27.2 Load cases in stress-controlled cyclic tests

• (i) single-step asymmetrical stress-controlled cyclic loading (denoted as C);

• (ii) multi-step asymmetrical stress-controlled cyclic loading with a constant stress amplitude and varied mean stress (denoted as D);

• (iii) multi-step asymmetrical cyclic stressing with a constant mean stress and varied stress amplitude (denoted as E).

The strain rate in strain-controlled cyclic tests was $2 \times {10^{-3}\,\mathrm{s}^{-1}}$, while the stress rate in stress-controlled cyclic tests was 51 MPa/s. More details about the experimental procedure can be referred to Kang and Gao (2002).

27.3.1 Determination of Material Parameter

Under the monotonic tension, the tensor equation, Eq. (27.11), can be rewritten as a scalar equation, i.e.,

$$\begin{aligned} \dot{\alpha _i}=\frac{2}{3}\zeta _{i}r_{i}^{\mathrm m}\dot{\varepsilon }^{\mathrm p}-\zeta _{i}\alpha _i\dot{\mathrm p}. \end{aligned}$$

(27.13)

Then, by integrating Eq. (27.13), and combined with Eq. (27.3), it yields

$$\begin{aligned} \sigma =\sum _{i=1}^{3}r_i^\mathrm {m}(1-\exp (-\zeta _{i}\varepsilon ^{\mathrm p}))+Q, \end{aligned}$$

(27.14)

where $\sigma$ is the axial stress.

Apparently, if the isotropic deformation resistance Q is determined, the parameters $r_i^m$ and $\zeta _i$ can be readily determined by the least square method from the experimental tensile curve of $\sigma \sim \varepsilon$. Further, the material parameters $r_i^{\mathrm c}$ and ratchetting coefficient $m_i$ can be determined from one strain-controlled cyclic stress-strain curve and one evolution curve of ratchetting by trial-and-error method, respectively.

Table 27.3 Material parameters for U71Mn rail steel in the proposed model

Table 27.4 Material parameters for U71Mn rail steel in the Ohno-Wang’s rule I

The values of material parameters obtained by using the procedure mentioned above are listed in Table 27.3. It should be noted that the parameters $r_i^\mathrm {m}$ and $\zeta _i$ are determined from the experimental stress-strain curve of monotonic tension; $r_1^{\mathrm c}$ and $m_3$ are obtained from the experimental data of loading cases A and C, respectively. The simulated and predicted results obtained by the proposed model are also compared with those by the Chaboche’s rule and Ohno-Wang’s rule I. The material parameters of the Chaboche’s rule are the same as those used in the proposed model, but the parameters used in the Ohno-Wang’s rule I are listed in Table 27.4. It should be noted that the predicted ratchetting cannot be provided by the Ohno-Wang’s rule I, since it gives a closed stress-strain hysteresis loop in the framework of elasto-plasticity.

27.3.2 Simulation and Discussion

Figure 27.4 shows the experimental and simulated stress-strain curves of U71Mn rail steel. It is seen that the monotonic tensile stress-strain response of U71Mn rail steel is reasonably described by the proposed rule, and also by the Chaboche’s and Ohno-Wang’s ones.

Fig. 27.4

Experimental and simulated tensile stress-strain curves of U71Mn rail steel

Figure 27.5 gives the experimental and simulated stress-strain hysteresis loops of U71Mn rail steel in the uniaxial strain-controlled cyclic tests. Apparently, the proposed model provides a reasonable prediction to the different plastic moduli occurred in the monotonic and cyclic deformations by setting a suitable $r_1^{\mathrm c}$; while the Chaboche’s and Ohno-Wang’s rules can not give a reasonable description.

Fig. 27.5

Experimental and simulated stress-strain hysteresis loops of U71Mn rail steel in the uniaxial strain-controlled cyclic tests: a loading case A; b loading case B

Figure 27.6 illustrates the experimental and simulated stress-strain curves of U71Mn rail steel in uniaxial stress-controlled cyclic test (i.e., loading case C). It is indicated that the ratchetting is reasonably simulated by the proposed model; while a much larger predicted ratchetting is obtained by the Chaboche’s rule. It is also seen from Figs. 27.7 and 27.8 that the proposed model can describe the dependence of ratchetting on the applied loading level and history; while the prediction by the Chaboche’s rule is far from the experimental results.

Fig. 27.6

Experimental and simulated stress-strain curves of U71Mn rail steel in single-step stress-controlled cyclic test (loading case C). a Experiment. b Simulation by the proposed rule. c Simulation by the Chaboche’s rule

Fig. 27.7

Experimental and simulated stress-strain curves of U71Mn rail steel in multi-step stress-controlled cyclic test (loading case D). a Experiment. b Simulation by the proposed rule. c Simulation by the Chaboche’s rule

Fig. 27.8

Experimental and simulated stress-strain curves of U71Mn rail steel in multi-step stress-controlled cyclic test (loading case E). a Experiment. b Simulation by the proposed rule. c Simulation by the Chaboche’s rule

It should be noted that, only the monotonic and cyclic deformations of cyclically stable materials, e.g., annealed U71Mn rail steel are simulated reasonably by the proposed model, but the cyclic softening/hardening features of materials and their effects on the ratchetting can not be described yet, since a constant isotropic deformation resistance is assumed in this work. The proposed model will be improved by considering such features in a future work.

27.4 Conclusions

By modifying the Chaboche’s kinematic hardening rule (Chaboche 1989), a new kinematic hardening rule is proposed for describing the different plastic moduli of the metal materials presented in the monotonic and cyclic deformations in this paper. It is then verified that the proposed model is capable of modeling the differente plastic moduli occurred in the monotonic and cyclic deformation, and then provides more reasonable simulations to the cyclic stress-strain hysteresis loops and ratchetting strain. The simulated results are in good agreement with the corresponding experimental ones.