On the Self-force in Electrodynamics and Implications for Gravity

Abstract

We consider the motion of charged point particles on Minkowski spacetime. The questions of whether the self-force is finite and whether mass renormalisation is necessary are discussed within three theories: In the standard Maxwell vacuum theory, in the non-linear Born-Infeld theory and in the higher-order Bopp-Podolsky theory. In a final section we comment on possible implications for the theory of the self-force in gravity.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The problem of the electromagnetic self-force has a long history. It began in the late 19th century when Lorentz, Abraham and others tried to formulate a classical theory of the electron. The idea was to model the electron as an extended, at least approximately spherical, charged body and to determine the equations of motion for the electron. Based on earlier results by Lorentz, Abraham succeeded in writing the equation of motion in terms of a power series with respect to the radius of the electron. If the radius tended to zero, i.e., for a point charge, an infinity occurred. The reason for this infinity is in the fact that, in the point-particle limit, the electric field strength diverges so strongly at the position of the charge that the field energy in an arbitrarily small sphere becomes infinitely large. To get rid of this infinity, it was necessary to “renormalise the mass” of the particle by assuming that it carries a negative infinite “bare mass”. After this mass renormalisation, one got a differential equation of third order for the motion of the particle which is known as the Abraham-Lorentz equation. It is a non-relativistic equation in the sense that, on the basis of special relativity, it can hold only if the particle’s speed is small in comparison to the speed of light.

A fully relativistic treatment of the problem had to wait until Dirac’s work [1] of 1938. The resulting equation of motion is known as the Lorentz-Dirac equation or as the Abraham-Lorentz-Dirac equation. Clearly, everyone would call it the Dirac equation except for the fact that this name was already occupied by another, even more famous equation. Neither Lorentz nor Abraham has ever seen the (Abraham-) Lorentz-Dirac equation, because both had passed away in the 1920s. In particular in the case of Abraham it is rather clear that he would not have liked this equation because he was an ardent opponent of relativity. Therefore, it seems appropriate to omit his name and call it the Lorentz-Dirac equation. For the derivation of the Lorentz-Dirac equation, again mass renormalisation was necessary and one arrived at a third-order equation of motion. The latter fact means that, in contrast to other equations of motion, not only the position and the velocity but also the acceleration of the particle has to be prescribed at an initial instant for fixing a unique solution. Moreover, the Lorentz-Dirac equation is notorious for showing unphysical behaviour such as run-away solutions and pre-acceleration. For a detailed discussion of the Lorentz-Dirac equation, including historical issues, we refer to Rohrlich [2] and to Spohn [3].

The trouble with the Lorentz-Dirac equation clearly has its origin in the fact that the electric field strength of a point charge becomes infinite at the position of the charge, and that this singularity is so strong that the field energy in an arbitrarily small ball around the charge is infinite. A possible way out is to modify the underlying vacuum Maxwell theory in such a way that this field energy becomes finite. Two such modified vacuum Maxwell theories have been suggested in the course of history, the non-linear Born-Infeld theory [4] and the linear but higher-order Bopp-Podolsky theory [5, 6]. It is the main purpose of this article to discuss to what extent these theories have succeeded in providing a theory of classical charged point particles with a finite self-force and a finite field energy.

Some people are of the opinion that there is no need for a consistent theory of classical charged point particles. They say that either one should deal with extended classical charge distributions or with quantum particles. However, this is not convincing. E.g. in accelerator physics it is common to describe beams in terms of classical point particles; neither a description in terms of extended charge distributions nor in terms of quantum matter seems to be appropriate or even feasible. Therefore, a consistent and conceptually well-founded theory of classical charged point particles is actually needed.

The problem of the electromagnetic self-force of a charged particle has a counterpart in the gravitational self-force of a massive particle. In comparison with the electromagnetic self-force, the gravitational self-force is plagued with additional conceptual issues. The latter are related to the facts that Einstein’s field equation does not admit solutions for sources concentrated on a worldline, see Geroch and Traschen [7], and that an extended massive particle becomes a black hole if it is compressed beyond its Schwarzschild radius. However, by considering the self-interacting massive particle as a perturbation of a fixed background spacetime one arrives at a formalism which is similar to the electromagnetic case, see the comprehensive review by Poisson et al. [8]. At this level of approximation it is reasonable to ask if modifications of the vacuum Maxwell theory can be mimicked by modifying Einstein’s theory in such a way that the (approximated) gravitational self-force becomes finite. We will come back to this question at the end of this article, after a detailed discussion of the electromagnetic case.

2 Maxwell’s Equations and the Constitutive Law for Vacuum

Maxwell’s equations are universal and they do not involve a metric or a connection. They read

$$\begin{aligned} dF = 0, \qquad dH=j, \end{aligned}$$

(1)

where $F$ is an untwisted two-form, $H$ is a twisted two-form and $j$ is a twisted three-form. (A differential form is twisted if its sign depends on the choice of an orientation. The difference between twisted and untwisted differential forms becomes irrelevant if the underlying manifold is oriented.) $F$ gives the electromagnetic field strength, $H$ gives the electromagnetic excitation and $j$ gives the electromagnetic current. Our notation follows Hehl and Obukhov [9].

The Eqs. (1) are referred to as the premetric form of Maxwell’s equations. These equations immediately imply that on simply connected domains $F$ can be represented in terms of a potential,

$$\begin{aligned} F=dA, \end{aligned}$$

(2)

and that charge conservation is guaranteed,

$$\begin{aligned} dj=0. \end{aligned}$$

(3)

If $j$ is given, Maxwell’s equations must be supplemented with a constitutive law relating $F$ and $H$ to specify the dynamics of the electromagnetic field. There is a particular constitutive law for vacuum, and there is a particular constitutive law for each type of medium. In any case, the constitutive law will involve some background geometry. In the following we consider vacuum electrodynamics on Minkowski spacetime. Then the constitutive law should involve the Minkowski metric tensor and no other background fields.

On Minkowski spacetime, we may choose an orthonormal coframe, i.e., four linearly independent covector fields $\theta ^0, \theta ^1, \theta ^2, \theta ^3$ such that the Minkowski metric is represented as

$$\begin{aligned} g = \eta _{ab} \theta ^a \otimes \theta ^b \end{aligned}$$

(4)

where $(\eta _{ab}) = \mathrm {diag}(-1,1,1,1)$. Here and in the following we use the summation convention for latin indices that take values 0, 1, 2, 3 and for greek indices that take values 1, 2, 3. Latin indices will be lowered and raised with $\eta _{ab}$ and its inverse $\eta ^{ab}$, respectively, while greek indices will be lowered and raised with the Kronecker symbol $\delta _{\mu \nu }$ and its inverse $\delta ^{\mu \nu }$, respectively.

With respect to the chosen orthonormal coframe, the electromagnetic field strength can be decomposed into electric and magnetic parts,

$$\begin{aligned} F = E_{\mu } \theta ^{\mu } \wedge \theta ^0 + \dfrac{1}{2} B^{\rho } \varepsilon _{\rho \mu \nu } \theta ^{\mu } \wedge \theta ^{\nu }. \end{aligned}$$

(5)

Here the wedge denotes the antisymmetrised tensor product and $\varepsilon _{\rho \mu \nu }$ is the Levi-Civita symbol, defined by the properties that it is totally antisymmetric and satisfies $\varepsilon _{123}=1$. The electromagnetic excitation can be decomposed in a similar fashion,

$$\begin{aligned} H = - \mathcal {H} _{\mu } \theta ^{\mu } \wedge \theta ^0 + \dfrac{1}{2} D^{\rho } \varepsilon _{\rho \mu \nu } \theta ^{\mu } \wedge \theta ^{\nu }. \end{aligned}$$

(6)

If we apply the Hodge star operator of the Minkowski metric to $F$ and $H$, we find

$$\begin{aligned} ^*{\!}F = - B_{\mu } \theta ^{\mu } \wedge \theta ^0 + \dfrac{1}{2} E^{\rho } \varepsilon _{\rho \mu \nu } \theta ^{\mu } \wedge \theta ^{\nu }, \end{aligned}$$

(7)

$$\begin{aligned} ^*{\!}H = - D_{\mu } \theta ^{\mu } \wedge \theta ^0 - \dfrac{1}{2} \mathcal {H} ^{\rho } \varepsilon _{\rho \mu \nu } \theta ^{\mu } \wedge \theta ^{\nu }. \end{aligned}$$

(8)

The field energy density measured by an observer whose 4-velocity $V$ satisfies $\theta ^{\mu } (V) =0$ for $\mu = 1,2,3$ is given by

$$\begin{aligned} \varepsilon = \dfrac{1}{2} \big (E_{\mu }D^{\mu }+\mathcal {H}_{\mu }B^{\mu } \big ). \end{aligned}$$

(9)

With the help of the Hodge star operator we can form out of $F$ the untwisted scalar invariant

$$\begin{aligned} ^*{\!}(F \wedge {}^*{\!}F) = B_{\mu }B^{\mu }-E_{\mu }E^{\mu } \end{aligned}$$

(10)

and the twisted scalar invariant

$$\begin{aligned} ^*{\!}(F \wedge F) = - 2E_{\mu } B^{\mu }. \end{aligned}$$

(11)

All these equations are valid with respect to any orthonormal coframe. In particular, we may choose a holonomic coframe, i.e., we may choose inertial coordinates on Minkowski spacetimes,

$$\begin{aligned} g = \eta _{ab} dx^a \otimes dx^b \end{aligned}$$

(12)

and then write $\theta ^a =dx ^a$. In the following we will see that it is sometimes convenient to work with an anholonomic orthonormal coframe on Minkowski spacetime.

We will now discuss the vacuum constitutive law in three different theories.

2.1 Standard Maxwell Vacuum Theory

In the standard Maxwell theory, the constitutive law of vacuum reads

$$\begin{aligned} H = {}^*{\!}F. \end{aligned}$$

(13)

By comparison of (6) and (7) we see that this implies

$$\begin{aligned} D^{\rho }=E^{\rho }, \qquad \mathcal {H} ^{\mu } = B^{\mu }. \end{aligned}$$

(14)

Here and in the following, we use units making the permittivity of vacuum, $\varepsilon _0$, the permeability of vacuum, $\mu _0$, and thus the vacuum speed of light, $c=(\varepsilon _0 \mu _0)^{-1/2}$, equal to one.

2.2 Born-Infeld Theory

In 1934, Born and Infeld [4] suggested a non-linear modification of the vacuum constitutive law,

$$\begin{aligned} H = \dfrac{{}^*{\!}F - \dfrac{^*{\!}(F \wedge F)}{2 b^2} F}{\sqrt{1 + \dfrac{^*{\!}(F \wedge {}^*{\!}F)}{b^2} - \dfrac{\big (^*{\!}(F \wedge F) \big )^2}{4 b^4}}} \end{aligned}$$

(15)

where $b$ is a new hypothetical constant of nature with the dimension of a (magnetic or electric) field strength. The idea behind this modified constitutive law is to find a theory where the field energy of a point charge remains bounded. We will discuss in the following sections to what extent this goal was achieved.

Maxwell’s equations with the Born-Infeld constitutive law (15) can be derived from a Lagrangian that depends only on the invariants (10) and (11). This demonstrates that the theory is not only gauge invariant but also Lorentz invariant. However, we will not need the Lagrangian formulation in the following.

As the constitutive law (15) does not involve any derivatives, in the Born-Infeld theory the vacuum Maxwell equations are still of first order with respect to the field strength (i.e., of second order with respect to the potential), just as in the standard Maxwell theory. However, they are now non-linear.

Obviously, the Born-Infeld constitutive law (15) approaches the standard vacuum constitutive law (13) in the limit $b \rightarrow \infty$. This implies that the Born-Infeld theory is indistinguishable from the standard Maxwell vacuum theory if $b$ is sufficiently big. In this sense, any experiment that confirms the standard Maxwell vacuum theory is in agreement with Born-Infeld theory as well, and it gives a lower bound for $b$. For the purpose of this article, the specific value of $b$ is irrelevant as long as it is finite.

Decomposing the constitutive law (15) into electric and magnetic parts results in

$$\begin{aligned} D^{\rho } = \dfrac{ E^{\rho } + \dfrac{E_{\tau }B^{\tau }}{b^2} B^{\rho }}{\sqrt{1 + \dfrac{1}{b^2} \big (B_{\sigma }B^{\sigma } - E_{\sigma }E^{\sigma } \big ) - \dfrac{\big (E_{\nu }B^{\nu }\big )^2}{b^4} }}, \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {H} ^{\mu } = \dfrac{ B^{\mu } - \dfrac{E_{\tau }B^{\tau }}{b^2} E^{\mu }}{\sqrt{1 + \dfrac{1}{b^2} \big (B_{\sigma }B^{\sigma } - E_{\sigma }E^{\sigma } \big ) - \dfrac{\big (E_{\nu }B^{\nu }\big )^2}{b^4}}}. \end{aligned}$$

(17)

2.3 Bopp-Podolsky Theory

Another modification of the vacuum constitutive law, again motivated by the wish of having the field energy of a point charge finite, was brought forward in 1940 by Bopp [5]. The same theory was independently re-invented two years later by Podolsky [6]. The Bopp-Podolsky theory is equivalent to another theory that was suggested in 1941 by Landé and Thomas [10].

The Bopp-Podolsky vacuum constitutive law reads

$$\begin{aligned} H = {}^*{\!}F - \ell ^2 \square ^*{\!}F \end{aligned}$$

(18)

where

$$\begin{aligned} \square = {}^*{\!} d ^* {\!} d + d ^* {\!} d ^* {\!} \end{aligned}$$

(19)

is the wave operator on Minkowski spacetime and $\ell$ is a new hypothetical constant of nature with the dimension of a length. In contrast to the Born-Infeld constitutive law, the Bopp-Podolsky constitutive law is linear. However, it involves second derivatives of the field strength, so Maxwell’s equations give a system of fourth-order differential equations for the potential $A$. In the Landé-Thomas version of the theory one splits the potential into two parts each of which satisfies a second-order differential equation, see Sect. 4.3 below. Just as the Born-Infeld theory, the Bopp-Podolsky can be derived from a gauge-invariant and Lorentz-invariant Lagrangian (see Bopp [5] or Podolsky [6]) but we will not use the Lagrangian formulation in the following.

For $\ell \rightarrow 0$, the Bopp-Podolsky constitutive law (18) approaches the standard vacuum law (13). So any experiment that is in agreement with the standard Maxwell theory is in agreement with the Bopp-Podolsky theory as long as $\ell$ is sufficiently small. However, dealing with the limit $\ell \rightarrow 0$ requires some care because it is a singular limit of Maxwell’s equations in the sense that it kills the highest-derivative term.

3 Field of a Static Point Charge

It is our goal to discuss the field of a point charge in arbitrary motion on Minkowski spacetime (subluminal, of course) according to the standard Maxwell vacuum theory, the Born-Infeld theory and the Bopp-Podolsky theory. As a preparation for that, it is useful to consider first the simple case of a point charge that is at rest in the spatial origin of an appropriately chosen inertial coordinate system. (Obviously, in any other inertial system the charge is then in uniform and rectilinear motion.) In this inertial system, the field produced by the charge must be spherically symmetric and static because there are no background structures that could introduce a deviation from these symmetries. Writing $\vec {r}=(x^1,x^2,x^3)$ for the coordinates and $\vec {E} = (E^1,E^2,E^3)$ etc. for the fields in the chosen inertial system, Maxwell’s equations (1) reduce to

$$\begin{aligned} \nabla \times \vec {E} = \vec {0} , \quad \nabla \cdot \vec {B} = 0 , \quad \nabla \times \vec {\mathcal {H}} = \vec {0} , \quad \nabla \cdot \vec {D} = q \delta ^{(3)} \big (\vec {r} \big ), \end{aligned}$$

(20)

where $q$ is the charge and $\delta ^{(3)}$ is the three-dimensional Dirac delta distribution. While the curl equations are satisfied by any spherically symmetric $\vec {E}$ and $\vec {\mathcal {H}}$ fields, the divergence equations determine the spherically symmetric $\vec {D}$ and $\vec {B}$ fields uniquely,

$$\begin{aligned} \vec {D} = \dfrac{q}{4 \pi r^2} \vec {e}{}_r, \qquad \vec {B} = 0, \end{aligned}$$

(21)

where $\vec {e}{}_r$ is the radial unit vector. So whatever the constitutive law may be, the electric excitation $\vec {D}$ always has its standard Coulomb form, i.e., it diverges like $r^{-2}$ if the position of the charge is approached, and the magnetic field strength $\vec {B}$ vanishes everywhere. The corresponding (spherically symmetric) electric field strength $\vec {E}$ and magnetic excitation $\vec {\mathcal {H}}$ are not restricted by Maxwell’s equations; they have to be determined from the constitutive law.

3.1 Standard Maxwell Vacuum Theory

In the standard Maxwell vacuum theory the constitutive law simply requires $\vec {E}=\vec {D}$ and $\vec {B}= \vec {\mathcal {H}}$. Hence, (21) says that $\vec {E}$ is the standard Coulomb field and that $\vec {\mathcal {H}}$ vanishes,

$$\begin{aligned} \vec {E} = \dfrac{q}{4 \pi r^2} \vec {e}{}_r, \qquad \vec {\mathcal {H}} = \vec {0}. \end{aligned}$$

(22)

Clearly, $\big | \vec {E} \big |$ becomes infinite at the origin, i.e., at the position of the charge. The direction of $\vec {E}$ is always radial, so in the limit $r \rightarrow 0$ the direction may be any unit vector depending on how the origin is approached. As these direction vectors average to zero, the Lorentz force (${\sim }\vec {E}$) exerted by the static particle onto itself vanishes. Here we follow the widely accepted hypothesis that the self-force results from averaging over directions, cf. e.g. Poisson et al. [8]. This hypothesis is very natural if one thinks of the point particle as being the limiting case of an extended (spherical) body.

The field energy in a ball $K_R$ of radius $R$ around the origin is

$$\begin{aligned} W (R) = \int _{K_R} \dfrac{1}{2} \vec {D} \cdot \vec {E} r^2 \mathrm {sin} \vartheta dr d \vartheta d \varphi = \dfrac{q^2}{8 \pi } \int _0 ^R \dfrac{dr}{r^2}. \end{aligned}$$

(23)

Clearly, this expression is infinite, for arbitrarily small $R$. Both $\vec {E}$ and $\vec {D}$ throw in a factor of $r^{-2}$; one of them is killed by a factor of $r^2$ from the volume element but the other one makes the integral diverge. We see that we can cure this infinity by introducing a modified constitutive law that leaves $\vec {E}$ bounded if the position of the charge is approached. We will now verify that both the Born-Infeld theory and the Bopp-Podolsky theory have this desired property.

3.2 Born-Infeld Theory

As $\vec {B} = \vec {0}$ by (21), in the Born-Infeld theory the constitutive law requires

$$\begin{aligned} \vec {D} = \dfrac{\vec {E}}{\sqrt{1 - \dfrac{1}{b^2} \big | \vec {E} \big |^2}}, \qquad \vec {\mathcal {H}} = \vec {0}. \end{aligned}$$

(24)

With $\vec {D}$ given by (21), we have to solve the equation

$$\begin{aligned} \dfrac{\vec {E}}{\sqrt{1 - \dfrac{1}{b^2} \big | \vec {E} \big |^2}} = \dfrac{q}{4 \pi r^2} \vec {e}{}_r \end{aligned}$$

(25)

for $\vec {E}$ to determine the electric field strength. The result is (Born and Infeld [4])

$$\begin{aligned} \vec {E} = \dfrac{q}{4 \pi \sqrt{r_0^4+r^4}} \vec {e}{}_r, \qquad r_0^2 = \dfrac{q}{4 \pi b}. \end{aligned}$$

(26)

Hence $| \vec {E} | \rightarrow b$ for $r \rightarrow 0$, see Fig. 1. Note that the limit of $\vec {E}$ for $r \rightarrow 0$ does not exist because the direction of the limit vector depends on how the position of the point charge is approached. One may say that the electric field strength stays bounded but has a directional singularity at the origin. By averaging over directions, the self-force (${\sim }\vec {E}$) of the static particle vanishes.

Fig. 1

Modulus of the electric field strength for a static charge in the Born-Infeld theory (solid) and in the standard Maxwell vacuum theory (dashed)

The field energy in a ball $K_R$ of radius $R$ around the origin is

$$\begin{aligned} W (R) = \int _{K_R} \dfrac{1}{2} \vec {D} \cdot \vec {E} r^2 \mathrm {sin} \vartheta dr d \vartheta d \varphi = \dfrac{q^2}{8 \pi } \int _0 ^R \dfrac{dr}{\sqrt{r_0 ^4+r^4}}. \end{aligned}$$

(27)

This is an elliptic integral which is finite as long as $r_0 >0$, i.e., as long as $b$ is finite. Even the field energy in the whole space is finite,

$$\begin{aligned} \underset{R \rightarrow \infty }{\mathrm {lim}} W (R) = \dfrac{q^2 \Gamma (5/4)^2}{2 r_0 \pi ^{3/2}}, \end{aligned}$$

(28)

where $\Gamma$ is the Euler gamma function.

3.3 Bopp-Podolsky Theory

In this case the constitutive law requires

$$\begin{aligned} \vec {D} = \vec {E} - \ell ^2 \Delta \vec {E}, \quad \vec {\mathcal {H}} = \vec {0}. \end{aligned}$$

(29)

With $\vec {D}$ given by (21), we have to solve the second-order differential equation

$$\begin{aligned} \vec {E} - \ell ^2 \Delta \vec {E} = \dfrac{q}{4 \pi r^2} \vec {e}{}_r \end{aligned}$$

(30)

to determine $\vec {E}$. For a spherically symmetric field, $\vec {E} \big (\vec {r} \big ) = E(r) \vec {e}{}_r \big (\vec {r} \big )$, this reduces to

$$\begin{aligned} E - \dfrac{\ell ^2}{r^2} \left( \dfrac{d}{dr} \Big (r^2 \dfrac{dE}{dr} \Big ) - 2 E \right) = \dfrac{q}{4 \pi r^2}. \end{aligned}$$

(31)

The general solution is

$$\begin{aligned} \vec {E} = \dfrac{q}{4 \pi r^2} \Big \{ 1 + C_1 \ell (r- \ell ) e^{r / \ell } - C_2 \ell (r+ \ell ) e^{- r / \ell } \Big \} \vec {e}{}_r \end{aligned}$$

(32)

with two integration constants $C_1$ and $C_2$. The first integration constant is fixed if we require $\vec {E}$ to fall off towards infinity; this yields $C_1=0$. The second integration constant is fixed if we require $\vec {E}$ to stay bounded if the position of the charge is approached; this yields $C_2= \ell {}^{-2}$. This gives us the Bopp-Podolsky analogue of the Coulomb $\vec {E}$ field (Bopp [5]; Podolsky [6])

$$\begin{aligned} \vec {E} = \dfrac{q}{4 \pi r^2} \Big \{ 1 - \Big ( \dfrac{r}{\ell } + 1 \Big ) e^{- r / \ell } \Big \} \vec {e}{}_r \end{aligned}$$

(33)

which satisfies $\big | \vec {E} \big | \rightarrow q/(8 \pi \ell {}^2)$ for $r \rightarrow 0$, see Fig. 2. Just as in the Born-Infeld case, the electric field strength stays bounded but has a directional singularity at the origin.

Fig. 2

Modulus of the electric field strength for a static charge in the Bopp-Podolsky theory (solid) and in the standard Maxwell vacuum theory (dashed)

The field energy in a ball $K_R$ of radius R around the origin is

$$\begin{aligned}&W(R) = \int _{K_R} \dfrac{1}{2} \vec {D} \cdot \vec {E} r^2 \mathrm {sin} \vartheta dr d \vartheta d \varphi \\ \nonumber = \dfrac{q^2}{8 \pi } \int _0 ^R&\left( \dfrac{1}{r^2} - \dfrac{e^{-r / \ell }}{r^2} - \dfrac{e^{- r / \ell }}{r \ell } \right) dr = \dfrac{q^2}{8 \pi } \left( \dfrac{1}{\ell } + \dfrac{e^{-R/\ell }-1}{R} \right) \end{aligned}$$

(34)

which is finite as long as $\ell >0$. As in the Born-Infeld theory, even the field energy in the whole space is finite,

$$\begin{aligned} \underset{R \rightarrow \infty }{\mathrm {lim}} W(R) = \dfrac{q^2}{8 \pi \ell }. \end{aligned}$$

(35)

4 Field of an Accelerated Point Charge

We have seen that both the Born-Infeld theory and the Bopp-Podolsky theory modify the Coulomb $\vec {E}$ field of a point charge at rest in such a way that $| \vec {E}|$ is bounded and that the field energy in a ball around the charge is finite. Of course, what one is really interested in is the field produced by an accelerated charge. We will now try to find out what can be said about this case.

We choose an inertial coordinate system on Minkowski spacetime, $g = \eta _{ab} dx^a \otimes dx^b$. We fix a timelike $C^{\infty }$ curve $z^a (\tau )$ parametrised by proper time,

$$\begin{aligned} \eta _{ab} \dot{z}{}^a \dot{z}{}^b = -1. \end{aligned}$$

(36)

We assume that this timelike curve is inextendible. As an accelerated worldline may reach (past or future) infinity in a finite proper time, this does not necessarily mean that the parameter $\tau$ ranges over all of $\mathbb {R}$. We denote the interval on which $\tau$ is defined by $] \tau _{\mathrm {min}}, \tau _{\mathrm {max}} [$ where $- \infty \le \tau _{\mathrm {min}} < \tau _{\mathrm {max}} \le \infty$.

Fig. 3

Retarded light-cone coordinates and orthonormal coframe

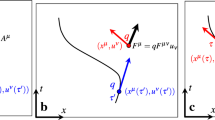
We want to determine the electromagnetic field of a point charge that moves on the worldline $z^a (\tau )$. For convenience, we introduce an orthonormal tetrad $\big (e_0 (\tau ), e_1 (\tau ), e_2 (\tau ), e_3 (\tau ) \big )$ along the worldline of the charged particle such that

$$\begin{aligned} e_0^a (\tau ) = \dot{z}{}^a (\tau ), \qquad a (\tau ) e_3^b (\tau ) = \ddot{z}{}^b (\tau ), \end{aligned}$$

(37)

see Fig. 3. Along the worldline, this fixes the timelike vector $e_0 (\tau )$ everywhere and the spacelike vector $e_3 (\tau )$, up to sign, at all events where the acceleration $\ddot{z} (\tau )$ is non-zero. $e_1 (\tau )$ and $e_2 (\tau )$ are then fixed up to a rotation in the plane perpendicular to $e_3 ( \tau )$. At points where the acceleration is zero, $e_3 (\tau )$ is ambiguous; there are pathological cases where it is not possible to extend it into such points such that the resulting vector field $e_3$ is continuously differentiable. We exclude such cases in the following and assume that the tetrad is smoothly dependent on $\tau$ and satisfies (37) along the entire worldline.

With respect to this tetrad, we can introduce retarded light-cone coordinates $(\tau , r, \vartheta , \varphi )$ which are related to the inertial coordinates $(x^0,x^1, x^2,x^3)$ by

$$\begin{aligned} x^a =z^a (\tau )+r \Big (\dot{z}{}^a (\tau ) + n^a (\tau , \vartheta , \varphi ) \Big ) \end{aligned}$$

(38)

where

$$\begin{aligned} n^a (\tau , \vartheta , \varphi ) = \mathrm {cos} \varphi \; \mathrm {sin} \vartheta e_1^a (\tau ) + \mathrm {sin} \varphi \; \mathrm {sin} \vartheta e_2^a (\tau ) + \mathrm {cos} \vartheta e_3^a (\tau ). \end{aligned}$$

(39)

Retarded light-cone coordinates are routinely used nowadays when treating self-force problems, cf. e.g. Poisson et al. [8]. These coordinates have a long history. In connection with electrodynamics on Minkowski spacetime, they were introduced by Newman and Unti [11] in 1963. In particular, Newman and Unti demonstrated that in these coordinates the Liénard-Wiechert potential takes a surprisingly simple form. In general relativity the history of light-cone coordinates is even older. They made their first appearance in a 1938 paper by Temple [12] who called the time-reversed version (i.e., the advanced light-cone coordinates) “optical coordinates”. Advanced light-cone coordinates are used in gravitational lensing and in cosmology where the wordline is interpreted as an observer who receives light (rather than as a source that emits radiation).

In retarded light-cone coordinates, the “temporal” coordinate $\tau$ labels the future light-cones with vertex on the chosen worldline; $r$ is a radius coordinate along each light-cone and $(\vartheta , \varphi )$ are standard spherical coordinates that parametrise the spheres $(\tau , r) = \mathrm {constant}$. Of course, there are the usual coordinate singularities of the spherical coordinates at the poles $\mathrm {sin} \vartheta =0$ and $\varphi$ is defined only modulo $2 \pi$. If these coordinate singularities are understood, the system of retarded light-cone coordinates is well-defined on an open subset, $U$, which equals the causal future of the worldline with the worldline itself being omitted. Figure 4 shows a worldline that approaches the speed of light in the past. In this case the causal future of the worldline is bounded by a lightlike hyperplane to which the worldline is asymptotic. For a worldline that does not approach the speed of light in the past, the causal future is all of Minkowski spacetime. (Recall that we consider only wordlines that are inextendible.)

Fig. 4

Domain of definition, $U$, of the retarded light-cone coordinates

With the retarded light-cone coordinates $(\tau , r, \vartheta , \varphi )$ we can associate an orthonormal coframe $(\theta ^0, \theta ^1, \theta ^2, \theta ^3)$ defined by

$$\begin{aligned} \theta ^0&= d \tau + dr + r a(\tau ) \mathrm {cos} \vartheta d \tau \\ \nonumber \theta ^1&= dr + r a(\tau ) \mathrm {cos} \vartheta d \tau \\ \nonumber \theta ^2&= r d \vartheta - r a(\tau ) \mathrm {sin} \vartheta d \tau \\ \nonumber \theta ^3&= r \mathrm {sin} \vartheta d \varphi , \end{aligned}$$

(40)

see Fig. 3.

The electromagnetic field of the point charge is to be determined by solving the Maxwell equations (1) with

$$\begin{aligned} ^* \! j (x) = q \left( \int _{\tau _{\mathrm {min}}} ^{\tau _{\mathrm {max}}} \delta ^{(4)} \big (x - z (\tau ) \big ) \dot{z}^a (\tau ) d \tau \right) \eta _{ab} dx^b \end{aligned}$$

(41)

where $\delta ^{(4)}$ is the 4-dimensional Dirac delta distribution. The solution has to satisfy the vacuum constitutive law on the open domain $U$ and it should be retarded. By the latter requirement we mean that the field strength at an event $x \in U$ should be completely determined by what the point charge did in the causal past of the event $x$.

4.1 Standard Maxwell Vacuum Theory

In the case of the standard Maxwell vacuum theory, finding the field of a point charge on Minkowski spacetime is a standard text-book matter. The solution is $F=dA, \, H = {}^*{\!}F$, where

$$\begin{aligned} A = - \dfrac{q \theta ^0}{4 \pi r} = - \dfrac{q}{4 \pi } \Big ( \dfrac{d \tau + dr}{r} + a( \tau ) \mathrm {cos} \vartheta d \tau \Big ) \end{aligned}$$

(42)

is the (retarded) Liénard-Wiechert potential. At an event $x \in U$, the potential is determined by the 4-velocity and the 4-acceleration of the point charge at the retarded time which is given by the coordinate $\tau$. There are no “tail terms”, i.e., there is no dependence on the earlier history of the point charge.

For deriving the Liénard-Wiechert potential in a systematic way, one introduces the potential, $F=dA$, and imposes the Lorenz gauge condition, $d ^* \! A = 0$. Then the first Maxwell equation, $dF=0$, is automatically satisfied and the second Maxwell equation, $dH = j$, becomes an inhomogeneous wave equation for $A$,

$$\begin{aligned} \square A = \big ({}^*{\!} d ^* {\!} d + d ^* {\!} d ^* {\!} \big ) A = {}^*{\!} d ^* {\!} F= {}^* {\!} dH = {}^* {\!} j. \end{aligned}$$

(43)

With the well-known (retarded) Green function of the wave operator $\square$, the (retarded) solution can be written as an integral over $^* {} \!j$. Inserting the current from (41) gives the desired result.

From the Liénard-Wiechert potential we find that the field strength $F=dA$ and the excitation $H={}^*{\!}dA$ are given by

$$\begin{aligned} F&= \dfrac{q}{4 \pi } \left( \dfrac{\theta ^1 \wedge \theta ^0}{r^2} + \dfrac{a (\tau )}{r} \mathrm {sin} \vartheta \theta ^2 \wedge (\theta ^0 - \theta ^1) \right) \nonumber \\&= \dfrac{q}{4 \pi } \left( \dfrac{dr \wedge d \tau }{r^2} + a(\tau ) \mathrm {sin} \vartheta d \vartheta \wedge d \tau \right) \end{aligned}$$

(44)

and

$$\begin{aligned} H = \dfrac{q}{4 \pi }&\left( \dfrac{\theta ^2 \wedge \theta ^3}{r^2} - \dfrac{a (\tau )}{r} \mathrm {sin} \vartheta \theta ^3 \wedge (\theta ^0 - \theta ^1) \right) \nonumber \\&\quad = \dfrac{q}{4 \pi } \mathrm {sin} \vartheta d \vartheta \wedge d \varphi , \end{aligned}$$

(45)

respectively. Decomposing into electric and magnetic parts yields

$$\begin{aligned}&E_{\mu } \theta ^{\mu } = D_{\mu } \theta ^{\mu } = \dfrac{q}{4 \pi } \Big \{\dfrac{\theta ^1}{r^2} + a(\tau ) \mathrm {sin} \vartheta \dfrac{\theta ^2}{r} \Big \} \; , \end{aligned}$$

(46)

$$\begin{aligned}&\qquad B_{\mu } \theta ^{\mu } = {\mathcal {H}} _{\mu } \theta ^{\mu } = \dfrac{q}{4 \pi } a(\tau ) \mathrm {sin} \vartheta \dfrac{\theta ^3}{r}. \end{aligned}$$

(47)

In addition to the “Coulomb part”, which goes with $1/r^2$, we have in the case of a non-vanishing acceleration a “radiation part” which goes with $1/r$. The self-force, i.e. the Lorentz force exterted onto the point charge by its own field, is given as the limit of $q E_{\mu } \theta ^{\mu }$ if the position of the point charge is approached. The Coulomb part averages to zero, as in the case of a static charge. The radiation part, however, does not average to zero; it gives an infinite self-force whenever the acceleration $a(\tau )$ is non-zero. As in the static case, the field energy in an arbitrarily small sphere around the point charge is infinite. It is this infinite amount of energy carried by the point charge with itself that makes mass renormalisation necessary if one wants to formulate an equation of motion for the point charge taking the self-force into account.

4.2 Born-Infeld Theory

If one wants to find the field of an accelerated point charge in the Born-Infeld theory, one would try to mimic the derivation of the Liénard-Wiechert potential as far as possible. As in the standard Maxwell theory, one can satisfy the first Maxwell equation by introducing the potential and one can impose the Lorenz gauge condition (or any other gauge condition if this appears to be more appropriate). However, with $H$ given in terms of $F=dA$ by the Born-Infeld constitutive law, the second Maxwell equation now becomes a non-linear inhomogeneous wave equation for $A$. There are no standard methods for solving such an equation; in particular, Green function methods are not applicable. Therefore, we cannot write down a Born-Infeld analogue of the Liénard-Wiechert potential. In the Born-Infeld theory, no explicit solution of the electromagnetic field of a point charge with non-vanishing acceleration seems to be known.

One might say that it is not actually necessary to write down a solution explicitly. It would be sufficient if one could verify some properties of the solution. Firstly, it would be highly desirable to prove that, for a point charge moving on an arbitrary worldline or on a worldline subject to some conditions, the retarded electromagnetic field is unique and regular on $U$. Secondly, it would be highly desirable to know if for this solution the self-force and the energy in a ball around the charge are finite. However, very little is known about these issues in the Born-Infeld theory beyond the case of an unaccelerated point charge.

As to regularity, it seems worthwile to point out that even for a time-independent and smooth $j$ the question of regularity is highly non-trivial. It was shown only recently by Kiessling [13] that in this case the electromagnetic field is, indeed, free of singularities or discontinuities. Although this result seems to be intuitively quite obvious, the proof is difficult and very technical. It is based on series expansions with respect to $1/b^2$, where $b$ is the Born-Infeld constant, and the hard part is in the proof of convergence. For the field of an accelerated point charge, it is very well conceivable that infinities or discontinuities (“shocks”) are formed. It is true that Boillat [14] has shown the non-existence of some kind of shocks in the Born-Infeld theory, but these results do not apply to the case at hand where the equations become singular along a worldline.

Even if it is possible to show that the electromagnetic field of a point charge is regular on $U$, either for all worldlines or for a special class of worldlines, it is far from obvious that the field has the same behaviour as in the static case if the position of the point charge is approached. A discussion of related issues can be found in a paper by Chruściński [15]; this, however, is based on the assumption that the electric field strength remains bounded and that the electric excitation diverges like $r^{-2}$ if the position of the point charge is approached. In contrast to the retarded light-cone coordinates used here, Chruściński used Fermi coordinates in a similar fashion as they had been used already earlier by Kijowski [16] in the context of the standard Maxwell vacuum theory.

Something can be said, at least, for the case of a point charge that is initially at rest and then starts accelerating. In this case, conservation of energy guarantees that the total field energy must be finite for all times. However, even in this case it is not clear if shocks are excluded.

For approaching the problem in a systematic way, one may write the electromagnetic field strength as a power series with respect to $1/b^2$,

$$\begin{aligned} F = \sum _{N=0} ^{\infty } \dfrac{F_N}{b^{2N}} = F_0 + \dfrac{F_1}{b^2} + \dots , \qquad F_N = dA_N. \end{aligned}$$

(48)

Inserting this expression into the Born-Infeld constitutive law (15) and collecting terms of equal powers of $1/b^2$ gives

$$\begin{aligned} H = \sum _{N=0} ^{\infty } \dfrac{H_N}{b^{2N}} = \sum _{N=0} ^{\infty } \dfrac{1}{b^{2N}} \left( {}^*{\!}F_N + \mathcal {W}_N \big (F_0, \dots , F_{N-1} \big ) \right) \end{aligned}$$

(49)

where $\mathcal {W}_N \big (F_0, \dots , F_{N-1} \big )$ stands for an expression depending on $F_0, \dots , F_{N-1}$ that can be explicitly calculated for every $N$. We have to determine the $F_N = dA_N$ such that $dH =j$ with the current given by (41). This can be done by requiring

$$\begin{aligned} dH_0 = j, \quad dH_N = 0 \, \text {for} \, N=1,2, \dots \end{aligned}$$

(50)

and solving these equations iteratively. We may impose the Lorenz gauge condition on each $A_N$. Then the zeroth order retarded solution is known to be the standard Liénard-Wiechert field, $F_0=dA_0$ with $A_0$ given by the right-hand side of (42). The higher-order $F_N=dA_N$ are determined by

$$\begin{aligned} d \left( {}^*{\!}dA_N + \mathcal {W}_N \big (dA_0, \dots , dA_{N-1} \big ) \right) = 0. \end{aligned}$$

(51)

In the Lorenz gauge, this is the standard inhomogeneous wave equation for $A_N$, with the inhomogeneity given in terms of the lower-order solutions $A_0, \dots , A_{N-1}$,

$$\begin{aligned} \square A_N = {}^*{\!} \tilde{j}{}_{N}, \qquad \tilde{j}{}_N = - d \mathcal {W}_N \big (dA_0, \dots , dA_{N-1} \big ). \end{aligned}$$

(52)

The retarded solution of this equation is known from classical electrodynamics: It is the retarded potential of the “current” three-form $\tilde{j}{}_N$. In this way, we can iteratively determine the $A_N$ and write the solution $F=dA$ as a formal power series.

The big question, unanswered so far, is whether or not this series converges. We do know that it does converge in the case of vanishing acceleration; then we get the field of a static point charge discussed in Sect. 3.2. For non-zero acceleration, however, no convergence results are known.

4.3 Bopp-Podolsky Theory

In the case of the Bopp-Podolsky theory the situation is much better than in the case of the Born-Infeld theory. The Bopp-Podolsky theory is linear, so it allows for applications of the Green function method.

With $F=dA$ and choosing the Lorenz gauge, $d ^*{\!}A = 0$, the remaining field equation reads

$$\begin{aligned} \square A- \ell ^2 \square ^2 A ={}^*{\!} j \;. \end{aligned}$$

(53)

This fourth-order equation for $A$ can be reduced to a pair of second-order equations

$$\begin{aligned} \square \hat{A} = {}^*{\!} j, \qquad \square \tilde{A} - \ell ^{-2} \tilde{A} = j, \end{aligned}$$

(54)

if we write

$$\begin{aligned} A=\hat{A}-\tilde{A} \end{aligned}$$

(55)

$$\begin{aligned} \hat{A}:=A-\ell ^2 \square A, \qquad \tilde{A}:=-\ell ^2 \square A. \end{aligned}$$

(56)

If rewritten in this way, a quantised version of the theory would predict the existence of a massless photon, described by $\hat{A}$, and a massive photon with Compton wave-length $\ell$, described by $\tilde{A}$. Both Bopp [5] and Podolsky [6] had realised that their higher-order theory can be rewritten in this way as a two-field theory. This two-field theory is precisely what Landé and Thomas [10] independently suggested one year after Bopp and one year before Podolsky.

One can thus construct the (retarded) solution to the fourth-order equation (53) from the (retarded) Green functions of the wave equations (54). The latter are well known, see e.g. the original paper by Landé and Thomas [10]. This gives the retarded solution to (53) for the current (41) of a point charge as

$$\begin{aligned} A (x) = \left( \int _{- \infty } ^{\tau } \dfrac{J_1 \big (s(x, \tau ') / \ell \big )}{\ell s(x, \tau '))} \dot{z}{}^a (\tau ') d \tau ' \right) \eta _{ab} dx^b \end{aligned}$$

(57)

where

$$\begin{aligned} s (x, \tau ')^2 = - \big (x^a - z ^a (\tau ') \big ) \big (x_a - z _a (\tau ') \big ) \end{aligned}$$

(58)

and $J_1$ is the Bessel function of the first kind. The geometric meaning of $s(x, \tau ')$ is illustrated in Fig. 5.

Fig. 5

$s(x, \tau ')$ is the Lorentz length of the timelike line segment that connects $x$ with $z (\tau ')$

The potential (57) is the Bopp-Podolsky analogue of the Liénard-Wiechert potential. In contrast to the standard Liénard-Wiechert potential, it depends on the entire earlier history of the point charge up to the retarded time $\tau$. Such “tail terms” are nothing peculiar; they also occur in the standard vacuum Maxwell theory on a curved background, see e.g. Poisson et al. [8]. The integral in (57) and in the corresponding expression for the field strength can be expanded in a formal power series with respect to $\ell$. For the self-force, after averaging over directions this results in a series with terms of order $\ell ^{-1}$, $\ell ^0$, $\ell$, $\ell ^2 \dots$, see Zayats [17] (also cf. McManus [18], Frenkel [19] and Frenkel and Santos [20]). However, these series are non-convergent and, therefore, of limited use.

So in contrast to the Born-Infeld theory, in the Bopp-Podolsky theory the electromagnetic potential (and, thereupon, the electromagnetic field strength) produced by an arbitrarily accelerated point charge can be explicitly written down, albeit in terms of an integral over the particle’s earlier history. A detailed discussion of the class of worldlines for which this integral absolutely converges will be given elsewhere [21]. This demonstrates that, for a large class of worldlines, the electric field stays bounded and there is no need for mass renormalisation. As an important example, the self-force of a uniformly accelerated point charge was calculated by Zayats [17].

Because of the tail terms, the equation of motion is no longer a differential equation but rather an integro-differential equation for the worldline. It is unknown if the equation of motion admits run-away solutions. For some partial results, indicating that run-away solutions cannot exist if $\ell$ is bigger than a certain critical value, see Frenkel and Santos [20].

5 Implications for Gravity

The preceding discussion can be summarised in the following way. In the standard Maxwell vacuum theory, the self-force is infinite and mass renormalisation is necessary. Postulating a negative infinite bare mass is conceptually not satisfactory and the resulting equation of motion, the Lorentz-Dirac equation, is highly pathological. In the Born-Infeld theory, the properties of the field of a static charge look promising, but for an accelerated charge very little can be calculated and the properties of the field are largely unknown. For the Bopp-Podolsky theory, the field of an accelerated point charge can be calculated, in terms of an integral over the history of the particle which is manageable to a certain extent, and it can be shown for a large class of accelerated worldlines that the field is, actually, finite. No negative infinite bare mass needs to be postulated, and the equation of motion can be assumed to be the usual Lorentz-force equation with the (finite) self-field included after averaging over directions. The explicit expression of the electromagnetic field, given by the analogue of the Liénard-Wiechert potential, is more complicated than in the standard vacuum Maxwell theory on Minkowski spacetime, because of the tail terms. However, such tail terms are familiar from the standard vacuum Maxwell theory on a curved spacetime and should not be viewed as a reason for discarding the theory. Although there are still several open issues—most notably the absence or non-absence of run-away solutions has to be clarified—it seems fair to say that in the Bopp-Podolsky theory the infinities associated with point charges are cured to a large extent. We may therefore view it as the best candidate for a conceptually satisfactory theory of classical charged point particles. (This does not necessarily mean that the Bopp-Podolsky theory is “the correct theory of electromagnetism” at a fundamental, quantum field theoretical, level).

Do these observations teach a lesson with respect to the gravitational self-force? In the approximation where the self-gravitating particle is viewed as a perturbation of a fixed background spacetime, the theory is very similar to the electromagnetic case in the standard Maxwell vacuum theory. Modifying the theory along the lines of the Born-Infeld theory seems to be of no use: Firstly, it is largely unclear if the Born-Infeld theory really cures the infinities in the field of an accelerated point charge. Secondly, the original Einstein theory was already a non-linear theory whose non-linearities had been killed by setting up the approximation formalism for the self-gravitating point mass. Therefore, it seems rather meaningless to re-introduce non-linear terms. The situation is quite different for the Bopp-Podolsky theory. Here linearity is kept but higher-order terms are added. It seems not unreasonable to assume that Einstein’s theory can be modified by adding higher-order terms in such a way that they survive the approximation, giving rise to a regularising term of the same kind as it occurs in the Bopp-Podolsky theory. Higher-order theories of gravity have been investigated intensively. They are mainly motivated by the observation that quantum corrections to Einstein’s theory are expected to give a Lagrangian that is of quadratic or higher order in the curvature, resulting in field equations that involve fourth derivatives of the metric. (The simplest class of such theories is the class of $f(R)$ theories which are reviewed, e.g., in the Living Review by de Felice and Tsujikawa [22]). Looking for a version that gives rise to a Bopp-Podolsky-like term seems to be a promising programme that might give a new theoretical framework for getting a finite gravitational self-force.