Keywords

1 Introduction

Swarm Intelligence techniques have become increasingly popular during the last two decades due to their capability to find a relatively optimal solution for complex combinatorial optimization problems. They have been applied in the fields of engineering, economy, management science, industry, etc. Problems that benefit from the application of Swarm Intelligence techniques are generally very hard to solve optimally in the sense that there is no such exact algorithm for solving them in polynomial time. These optimization problems are also known as NP-hard problems [6].

An algorithm that is well recognized in the domain of evolutionary computation is the imperialist competitive algorithm (ICA), which was introduced by Atashpaz-Gargari and Lucas in 2007. ICA has been inspired by the concept of imperialism; where in this case powerful countries attempt to make a colony of other countries. These algorithms have recently been used in several engineering applications [11].

We describe the imperialist competitive algorithm in its original form. The algorithm parameters adjustment is performed manually by varying the parameters to see how the behavior of the algorithm is affected. This algorithm was applied to benchmark mathematical functions, and the results of the ICA algorithm by varying the parameters are presented in Sect. 4.

The study of the algorithm is performed in order to show the effectiveness of the imperialist competitive algorithm (ICA) when applied to optimization problems, and to take this as a basis for future works.

Some of the papers that have applied the imperialist competitive algorithm can be described as follows. In [11] the Imperialist Competitive Algorithm Combined with Refined High-Order Weighted Fuzzy Time Series (RHWFTS–ICA) for short term loads forecasting. In this study, a hybrid algorithm based on a refined high-order weighted fuzzy algorithm and an imperialist competitive algorithm (RHWFTS–ICA) is developed. This method is proposed to perform efficiently under short-term load forecasting (STLF) [11]. In another paper [7] an Imperialist Competitive Algorithm With PROCLUS Classifier For Service Time Optimization In Cloud Computing Service Composition, CSSICA is proposed to make advances toward the lowest possible service time of composite service; in this approach, the PROCLUS classifier is used to divide cloud service providers into three categories based on total service time and assign a probability to each provider. An improved imperialist competitive algorithm is then employed to select more suitable service providers for the required unique services [7].

The paper is organized as follows: in Sect. 2 a description about the imperialist competitive Algorithm ICA is presented, in Sect. 3 a description of the mathematical functions is presented, in Sect. 4 the experiments results are described for we can to appreciate the ICA algorithm behavior by varying the parameters, in Sect. 5 the conclusions obtained after the study of the imperialist competitive algorithm versus mathematical functions are presented.

2 Imperialist Competitive Algorithm

In the field of evolutionary computation, the novel ICA algorithm is based on human social and political advancements [1], unlike other evolutionary algorithms, which are based on the natural behaviors of animals or physical events.

ICA starts with an initial randomly generated population, in which the individuals are known as countries. Some of the best countries are considered imperialists, whereas the other countries represent the imperialist colonies [7].

All the colonies of the initial population are divided among the mentioned imperialists based on their power. The power of an empire which is the counterpart of the fitness value in GA and is inversely proportional to its cost [1].

2.1 Forming Initial Empires (Initialization)

In order to represent an appropriate solution format, a 1 × N var array of variables represents a country, and a country is defined by [6]:

$$ Country = [p_{1} , \, p_{2} , \ldots , \, p_{{N_{var} }} ] $$
(1)

where N var is the number of variables to be considered of interest about a country and p i is the value of i-th variable.

The variable values in the country are represented as floating point numbers. The cost of a country is found by evaluating the cost function f at the variables (p 1 , p 2 , …, p n ) then [1]:

$$ Cost = f\left( {Country} \right) = f\left( {p_{1} , \, p_{2} , \ldots , \, p_{n} } \right) $$
(2)

In the initialization step, we need to generate an initial population size of N pop . Select N imp of the most powerful countries to form empires. The remaining N col population will be the colonies each of which belongs to an empire [1]

$$ N_{coI} = N_{pop} - N_{imp} $$
(3)

To form empires, the colonies are divided among the imperialist countries according to the power of the imperialists. The normalized cost of each imperialist is determined by [6]

$$ c_{n} = \mathop {\hbox{max} }\limits_{i} \{ c_{i} \} - c_{n} $$
(4)

where, c n is the n-th imperialist’s cost, and C n is the normalized cost of n-th imperialist.

Therefore, the power of each imperialist is calculated based on the normalized cost [6]:

$$ p_{n} = \frac{{C_{n} }}{{\sum\nolimits_{i = 1}^{{N_{imp} }} {C_{i} } }} $$
(5)

where p n is the power of n-th imperialist. The normalized power of n-th imperialist is the number of colonies that are possessed by that imperialist, calculated by:

$$ NC_{n} = Round\{ p_{n} N_{col} \} $$
(6)

where, NC n is the number of initial colonies possessed by the n-th imperialist; N col is the total number of colonies in the initial population, and round is a function that gives the nearest integer of a fractional number.

2.2 Moving the Colonies of an Empire Toward the Imperialist (Assimilation)

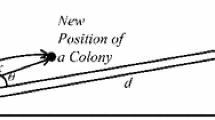
As shown in Fig. 1 the colony moves x distance along with the d direction towards its imperialist. The moving at x distance is a random number generated by random distribution within the interval (0, βd) [6].

$$ x\sim U(0,\beta d) $$
(7)

where β is a number greater than 1 and d is the distance between the colony and the imperialist.

Fig. 1
figure 1

Movement of the colonies toward the imperialist

Full size image

As shown in Fig. 2, to search for different locations around the imperialist we add a random amount of deviation to the direction of motion, which is given by [1]:

$$ \theta \sim U( - \gamma ,\gamma ) $$
(8)

where θ is a random number with uniform distribution and γ is a parameter that adjusts the deviation from the original direction.

Fig. 2
figure 2

Movement of the colonies toward their relevant imperialist in a randomly direction deviation

Full size image

2.3 Exchanging the Positions of a Colony and an Imperialist

While moving towards the imperialist, a colony can reach a position of lower cost than the imperialistic. If so, the imperialist is moved to the position of that colony and vice versa. Then the algorithm will continue with the imperialist in a new position and the colonies begin to move toward this position [1]. In Fig. 3, the best colony of the empire is shown in darker color. This colony has a lower cost than imperialist. Figure 4 shows the whole empire after exchanging the position of the imperialist and the colony.

Fig. 3
figure 3

Position change between the imperialist and a colony

Full size image
Fig. 4
figure 4

Position after exchanging empire imperialist and the colony

Full size image

2.4 Total Power of an Empire

The power of an empire is calculated based on the power of its imperialist and a fraction of the power of its colonies. This fact has been modeled by defining the total Cost given by [6]:

$$ TC_{n} = Cost(Imp) + \xi \,mean\{ Cost(Col)\} $$
(9)

where TC n is the total cost of n-th Empire and ξ is a positive number between 0 and 1.

2.5 Imperialist Competition

To start the competition, first, we find the probability of possession of each empire based on the total power. The normalized total cost is obtained by [1]:

$$ NTC_{n} = \mathop {\hbox{max} }\limits_{i} \{ TC_{i} \} - TC_{n} $$
(10)

where NTC n is the Normalized total cost and TC n is the total cost of empire. Then the probability of possessing a colony is computed by:

$$ p_{{p_{n} }} = \frac{{NTC_{n} }}{{\sum\nolimits_{i = 1}^{{N_{imp} }} {NTC_{i} } }} $$
(11)

where \( \sum\nolimits_{i = 1}^{{N_{imp} }} {p_{{p_{i} }} = 1}. \)

2.6 Elimination of Weaker Empires

Weaker empires lose their colonies gradually to stronger empires, which in turn grow more powerful and cause the weaker empires to collapse over time. In Fig. 5, the weakest empire is eliminated by losing its last colony during the imperialist competition [6].

Fig. 5
figure 5

Elimination of the weakest empire

Full size image

2.7 Convergence

Similar to other metaheuristic algorithms, ICA continues until a stopping criteria are met, such as predefined running time or a certain number of iterations. The ideal stopping criterion is when all empires have collapsed and only one (grand empire) remains (Fig. 6).

Fig. 6
figure 6

Representation of convergence in ICA

Full size image

2.8 Pseudo Code of ICA

The pseudo code it ICA is defined as follows:

  1. 1.

    Select some random points on the function and initialize the empires.

  2. 2.

    Move the colonies toward their relevant imperialist (assimilation).

  3. 3.

    If there is a colony in an empire which has lower cost than that of imperialist, exchange the positions of that colony and the imperialist.

  4. 4.

    Calculate the total cost of all empires (related to the power of both imperialist and its colonies).

  5. 5.

    Pick the weakest colony (colonies) from the weakest empire and give it (them) to the empire that has the most likelihood to possess it (imperialistic competition).

  6. 6.

    Elimínate the powerless empires.

  7. 7.

    If there is just one empire, stop, if not go to step 2.

3 Benchmark Mathematical Functions

In this Section, the benchmark functions that are used are listed to evaluate the performance of the ICA algorithm by varying its parameters and to analyze the results obtained.

In the area of the metaheuristics for optimization the use of mathematical functions is common, and they are used in this work: consisting of an optimization algorithm based on imperialism in which the variation of its parameters will be analyzed for obtain its optimum values.

The mathematical functions are shown below:

  • Sphere

    $$ f(x) = \sum\limits_{j = 1}^{{n_{x} }} {x_{j}^{2} } $$
    (12)

    Witch \( x_{j} \in [ - 100, 100] \) and \( f^{*} (x) = 0.0 \)

  • Quartic

    $$ f(x) = \sum\limits_{j = 1}^{{n_{x} }} {x_{j}^{4} } + random(0,1) $$
    (13)

    Witch \( x_{i} \in [ - 1.28,1.28] \) and \( f^{*} (x) = 0.0 \) + noise

  • Rosenbrock

    $$ f(x) = \sum\limits_{j = 1}^{{n_{z} /2}} {[100(x_{2j} - x_{2j - 1}^{2} )^{2} + (1 - x_{2j - 1} )^{2} ]} $$
    (14)

    Witch \( x_{j} \in [ {-} 2.048, 2.048] \) and \( f^{*} (x) = 0.0 \)

  • Rastrigin

    $$ f(x) = \sum\limits_{j = 1}^{{n_{x} }} {(x_{j}^{2} - 10\cos (2\pi x_{j} ) + 10)} $$
    (15)

    With \( x_{j} \in [ {-} 5.12,5.12] \) and \( f^{*} (x) = 0.0. \)

4 Simulation Results

In this Section the imperialist competitive algorithm (ICA) is implemented with 4 benchmark mathematical functions with 30 variables by varying their parameters and the results obtained by the ICA algorithm are shown in separate tables by parameter.

The parameters used in the imperialist competitive algorithm are:

  • Number of variables: 30

  • Number of countries: 200

  • Number of imperialist: 10

  • Number of decades: 3000

Table 1 shows that after executing the ICA Algorithm 10 times, by varying the revolution parameter, we can find the best, average and worst results for the different mathematical functions benchmark.

Table 1 Results by varying the revolution parameter
Full size table

Table 2 shows that after executing the ICA Algorithm 10 times, by varying the β (Beta) parameter, we can find the best, average and worst results for the different mathematical functions benchmark.

Table 2 Results by varying the β (Beta) parameter
Full size table

Table 3 shows that after executing the ICA Algorithm 10 times, by varying the γ (Gama) parameter, we can find the best, average and worst results for the different mathematical functions benchmark.

Table 3 Results by varying the γ (Gama) parameter
Full size table

Table 4 shows that after executing the ICA Algorithm 10 times, by varying the ξ (Eta) parameter, we can find the best, average and worst results for the different mathematical functions benchmark

Table 4 Results by varying the ξ (Eta) parameter
Full size table

5 Conclusions

By analyzing the ICA algorithm by varying the parameters, we noticed that the parameter that affected most the operation is the β parameter in the range of 1.4–1.6 good results for the sphere and quartic functions.

For the Rosenbrock and Rastrigin functions the results are not good for 30 variables, but with fewer variables the algorithm performs better.

The remaining parameters though apparently do not affect significantly the operation of the algorithm these can be in the range of 0.2–0.5 in the revolution, from 0.4 to 0.6 for γ and small values of ξ the algorithm behaves better.