Keywords

1 Introduction

The popularity of mobile devices and especial characteristics of mobile ad hoc networks (MANETs) led to various applications from education to military over this type of network. Generally, MANET can be defined as a kind of wireless network, which does not rely on any fixed-infrastructure. In addition, nodes are allowed to join/leave the network at any time; hence, the topology of these networks is unstable. It should be noted that mentioned features beside the nodes cooperation in running the network functions make MANETs prone to many attacks (e.g. wormhole, blackhole, impersonation, and modification). Since providing security for such environment is a challenging issue, this type of networks became an interesting research area in the recent years [1–3].

In order to provide security for MANETs, two approaches could be considered; attack-oriented and cryptography. Earlier, most of the proposed works were based on the first approach [4–8]. More precisely, the author(s) tried to propose new solutions for possible threats or improve existing works. However, attack-oriented schemes could not resist all types of attacks or combination of them at the same time [1]. The second approach has been used extensively to support security for MANETs in the form of general design framework [1]. In this way, the developers struggled to propose lightweight cryptosystem that could satisfy limitation of resources in MANETs. While the use of symmetric cryptography (SC) is usually acceptable for resource constrained environments [9], the difficulty of key management in SC, persuade developers to apply public key cryptography (PKC) instead [10, 11].

However, traditional PKC could not be the best choice for MANETs because of the need to certificates and public key infrastructure. In 1986, Adi Shamir introduced identity-based cryptography that considered the identity of users as their public key [12]. This idea became practical in 2001 by the illustrious work of Boneh and Franklin [13]. To avoid the inherent problem of identity-based PKC named key escrow, Al-Riyami and Paterson in [14] introduced the concept of certificateless PKC. Afterward, some researchers have been tried to propose schemes based on certificateless PKC in the context of MANETs [15, 16]. Since both of them utilized bilinear pairings which is considered as an expensive cryptographic map, it seems they are not lightweight enough to be used in MANETs. In this paper, we propose a new certificateless scheme that is an enhancement of the proposed scheme in Eissa et al. [15]. More accurately, we could reduce the complexity of computation by the use of elliptic curve based algebraic groups instead of multiplicative ones over finite fields as the output of bilinear pairings.

The rest of this paper is organized as follows. Section 2 explains the required preliminaries. In Sect. 3, ID-RSA protocol has been reviewed. Our proposed scheme is described in Sect. 4 while in Sect. 5, the comparison is presented in the terms of efficiency. Finally, the conclusions are provided in the Sect. 6.

2 Preliminaries

The basis of this section is explaining elliptic curves and their significant role as strong algebraic groups in the cryptography research area. The followed subsection briefly introduces elliptic curves in more detail. Then, a subsection represents the significance of this category of algebraic groups.

2.1 Elliptic Curve Cryptography

Elliptic curves are one of the significant scientific topics in the cryptographic literatures. The significant property of this kind of curves is that a subset of the points over them, beside of a binary operation can generate a beneficial algebraic group.

In the sake of simplicity, it is possible to claim that the elements of mentioned algebraic group are a subset of points of the equation \( y^{2} z = x^{3} + axz^{2} + bz^{3} \) with nonzero discriminant (\( \Delta = - 16[4a^{3} + 27b^{2} ] \)). Here, a and b are two elements of the determined finite field. Without loss of generality, assume that the coefficients and variables of mentioned equation above are elements of the finite field \( F_{{P^{n} }} \). Here, the elements of considered algebraic group are members of the set which is constructed of the points such as (x 0, y 0, z 0). To introduce the elements of this group, it is possible to partition the solutions of mentioned equation into two classes. By assuming the points (0, y 0, 0) as the class of identity element, other ones would be the points of the equation \( y^{2} = x^{3} + ax + b \).

Beside of what explained above, the operation of mentioned algebraic group, named “+”, is introduced as following. Without loss of generality, assume that we need to add two points (x 1, y 1) and (x 2, y 2). The final result will be calculated as follows:

$$ \left( {x_{1} , y_{1} } \right) + \left( {x_{2} ,y_{2} } \right) = \left( {x_{3} ,y_{3} } \right) $$

that \( \left( {x_{3} ,y_{3} } \right) = \left( {\lambda^{2} - x_{1} {-}x_{2} ,\lambda \left( {x_{1} - x_{3} } \right) - y_{1} } \right) \).

The amount of λ is

$$ \lambda = \left\{ {\begin{array}{*{20}c} {\frac{{y_{2} - y_{1} }}{{x_{2} - x_{1} }}, \left( {x_{1} , y_{1} } \right) \ne \left( {x_{2} ,y_{2} } \right)} \\ {\frac{{3x_{1}^{2} + a}}{{2y_{1} }} ,\left( {x_{1} , y_{1} } \right) = \left( {x_{2} ,y_{2} } \right)} \\ \end{array} } \right.. $$

Next subsection investigates the advantages of ECC-based algebraic groups that persuaded many researchers to use them.

2.2 Advantages of ECC-based Cryptosystems

In continue to what pointed out in the Sect. 2.1, it is possible to claim that elliptic curves are the basis of a large variety of cryptographic schemes. In compare with RSA-based cryptosystems, the required key size of ECC based is significantly smaller. Tables 1 and 2 represent the suggested key sizes for two mentioned cryptosystems based on the claims of NIST [17] and ECRYPT [18], respectively.

Table 1 Key sizes of NIST standard [17]
Full size table
Table 2 Key sizes of ECRYPT standard [18]
Full size table

In these tables, the security level refers to the required number of bits of mentioned algebraic group so that the discrete logarithm remains a hard problem.

3 Review of ID-RSA

In this section, we are going to review the identity-based protocol proposed by Eissa et al. [15]. For the sake of simplicity, we call it ID-RSA. In order to resist RSA cryptanalysis, the authors attempted to ensure that the users’ public keys are attainable only by trusted users. Therefore, it is assumed that each user is a part of a coalition. If any user out of one coalition needs public key of a user which is inside the coalition, it should request to the coalition. The detail explanation of this cryptosystem is as followed.

3.1 ID-RSA Phases

It is possible to summarize the ID-RSA in the following main phases.

Setup

The output of this phase is public parameters of the cryptosystem (Params), which are generated by a trusted third party.

$$ {\text{Params}}{:}\langle G,G_{T} ,q,P,\hat{e},n,H_{1} ,H_{2} ,H_{3} \rangle $$

Here, G is an additive algebraic group as an input of \( \hat{e}\text{:}G \times G \to G_{T} \) which is a bilinear pairing that maps elements of mentioned group (such as P) to an element of the multiplicative algebraic group G T . The order of the mentioned groups is the same at prime number q. In addition, n represents the number of bits of e and N in the RSA cryptosystem. The rest are one-way hash functions that \( H_{1} \text{:}\left\{ {0,1} \right\}^{*} \to G_{1}^{*} \), \( H_{2} \text{:} G_{T} \to \left\{ {0,1} \right\}^{n} \) and \( H_{3} \text{:}\left\{ {0,1} \right\}^{*} \to \left\{ {0,1} \right\}^{n} \).

Node Initialization

In this phase, some of public/private parameters for current users/coalitions will be generated. Three types of public parameters have been considered; identity-key, general-key and public-key. The first one for users/coalitions “i” can be computed by all available users as \( Q_{i} = H_{1} (ID_{i} \left\| {\text{time}} \right.) \), whereas the rest are just computable by their owners. More precisely, user/coalition “i” chooses \( e_{i} \in_{\text{random }} {\mathbb{Z}}_{q}^{*} \) then performs RSA key generation algorithm. Similar to RSA, \( d_{i} \) is the private key of the user/coalition “i” and \( \langle e_{i} ,N_{i} \rangle \) represent the corresponding public key. Finally, the mentioned user/coalition computes and publishes its general key P i  = (d i · P).

Public key obtaining process

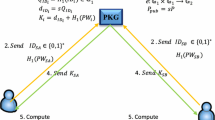
In this phase, a user who needs public key of another user inside a coalition can make a request. As a simple scenario, imagine that user A requires public key of user B in the coalition \( ID - {\text{RSA}}_{i} \), thus by performing the following steps this phase can be done.

  1. Step 1.

    \( A \to ID - {\text{RSA}}_{i} \text{:}P_{A} ,ID_{B} \)

    In this step, A sends a request—consist of its general key and identifier B- to \( ID - {\text{RSA}}_{i} \) coalition. It means, user A needs \( \langle e_{B} ,N_{B} \rangle \).

  2. Step 2.

    \( ID - {\text{RSA}}_{i} \to A\text{:} \langle U,C,W,Y \rangle \)

    In this step, if A is in the trusted list, the coalition \( ID - {\text{RSA}}_{i} \) will respond to A tuple \( \langle U,C,W,Y\rangle \) that U = P i , \( C = e_{B} \oplus H_{2} \left( {g_{i} } \right) \) where g i is \( \hat{e}(Q_{A} ,P_{A} )^{{d_{i} }} \times \hat{e}(d_{i} Q_{i} ,P_{A} ) \), \( W = e_{B} \cdot P \) and\( Y = N_{B} \oplus H_{3} (e_{B} ) \).

  3. Step 3.

    Public key extraction by A

    In this step, A can extract \( \langle e_{B} ,N_{B} \rangle \) by a set of computation; \( g_{A} = \hat{e}(d_{A} Q_{A} ,P_{i} ) \times \hat{e}(Q_{i} ,P_{i} )^{{d_{A} }} \), \( e_{B} = C \oplus H_{2} \left( {g_{A} } \right) \), \( N_{B} = Y \oplus H_{3} (e_{B} ) \) and finally A accepts public key of B if \( W = e_{B} \cdot P \) holds.

ID-RSA correctness

To validate the correctness of ID-RSA, it should be proved that both sides reach the same value through the mentioned computations above. Hence, the value of g A and \( g_{i} \) should be equal at \( \hat{e}(Q_{A} + Q_{i} ,P)^{{d_{i} d_{A} }} \). It can be proven through the following computations that ID-RSA is a correct scheme.

$$ \begin{aligned} g_{A} & = \hat{e}(d_{A} Q_{A} ,P_{i} ) \times \hat{e}(Q_{i} ,P_{i} )^{{d_{A} }} \\ & = \hat{e}(Q_{A} ,P)^{{d_{i} d_{A} }} \times \hat{e}(Q_{i} ,P)^{{d_{i} d_{A} }} = \hat{e}(Q_{A} + Q_{i} ,P)^{{d_{i} d_{A} }} \\ g_{i} & = \hat{e}(Q_{A} ,P_{A} )^{{d_{i} }} \times \hat{e}(d_{i} Q_{i} ,P_{A} ) \\ & = \hat{e}(Q_{A} ,P)^{{d_{i} d_{A} }} \times \hat{e}(Q_{i} ,P)^{{d_{i} d_{A} }} = \hat{e}(Q_{A} + Q_{i} ,P)^{{d_{i} d_{A} }} \\ \end{aligned} $$

4 Proposed Protocol

This section assigns to introducing our proposed certificateless authenticating public key protocol. Similar to ID-RSA, our scheme is constructed based on three phases named setup, node initialization, and public key obtaining process as followed.

Setup

The public output of our scheme, Params, includes following items:

$$ {\text{Params}}\text{:}\langle G,q,P,n,H_{1} ,H_{2} ,H_{3} \rangle $$

Here, G is a cyclic elliptic curve group with order q and the generator P. The integer number n is the same as n in IDRSA protocol. In addition, \( H_{1} \text{:}\left\{ {0,1} \right\}^{*} \to G^{*} \), \( H_{2} \text{:} G \to \left\{ {0,1} \right\}^{n} \) and \( H_{3} \text{:}\left\{ {0,1} \right\}^{*} \to \left\{ {0,1} \right\}^{n} \) are three one-way collision-free hash functions.

Node Initialization

Similar to the ID-RSA scheme, the entities can be user or coalition logically. Here, the public and private parameters of mentioned entities are the same as what introduced in ID-RSA. In addition, each entity such as the entity who possesses ID i generates the parameter E i  = e i P i .

Public key obtaining process

In this phase, the scenario is similar to what proposed in ID-RSA except that the details of the steps. Here, these steps are as followed:

  1. Step 1.

    \( \varvec{ }A \to {\text{Coalition}}_{i} \text{:}E_{A} ,P_{A} ,ID_{B} \)

    In this step, the second input introduces the node A as the entity who sent the request and the third one refers to the identity of the entity who his public key is requested.

  2. Step 2.

    \( {\text{Coalition}}_{i} \to A\text{:}\langle E_{i} ,U,C,W,Y\rangle \)

    In this step, the inputs U, C, W and Y are as followed.

    U = P i , C = e B  ⊕ H 2(g i ) that g i is equal to \( g_{i} = d_{i} (E_{A} + e_{i} P_{A} ) \) \( W = e_{B} \cdot P \) and \( Y = N_{B} \oplus H_{3} (e_{B} ). \)

  3. Step 3.

    In this step, the node A must be able to extract the public key of B (which are e B and N B ) and verify its authenticity as follows:

    First of all, A computes \( g_{A} = d_{A} (E_{i} + e_{A} P_{i} ) \), then computes \( e_{B} = C \oplus H_{2} \left( {g_{A} } \right) \). Clearly, the result of g A and g i must be the same. In addition, the entity A computes \( N_{B} = Y \oplus H_{3} (e_{B} ) \). To verify authenticity of the obtained public key, the entity A investigates the equality of (\( W = e_{B} \cdot P \)) to decide whether accept or reject the obtained public key of B.

Correctness of the Proposed Protocol

Beside of what mentioned above, it is necessary to prove that the computed values of g A and g i are the same. The two equalities below will lead to this result:

$$ \begin{aligned} g_{A} & = d_{A} (E_{i} + e_{A} P_{i} ) = d_{A} e_{i} P_{i} + d_{A} e_{A} P_{i} \\ & = \left( {d_{A} e_{i} d_{i} } \right)P + \left( {d_{A} e_{A} d_{i} } \right)P \\ g_{i} & = d_{i} (E_{A} + e_{i} P_{A} ) = d_{i} e_{A} P_{A} + d_{i} e_{i} P_{A} \\ & = (d_{i} e_{A} d_{A} )P + (d_{i} e_{i} d_{A} )P \\ \end{aligned} $$

As a result, the functionality of our proposed protocol is logically correct.

5 Efficiency Comparison

The basis of this section is to compare the cost of computing authentication parts of our proposed scheme and ID-RSA, which are the cost of computing g A and g i . High expense of computing bilinear pairings [19] is the main reason that made our proposed protocol more efficient than ID-RSA. In order to improve the efficiency of ID-RSA, we have tried to propose our protocol based on group operations of elliptic curves instead of computing bilinear pairings. Table 3 illustrates the cost of operations based on what depicted in [19].

Table 3 Computational costs of operations in type 2 and type 3 bilinear pairings [19]
Full size table

To compare the cost of mentioned two schemes, we have focused on the expense of g A or g i parts of “public key obtaining process,” as the core of them. Based on the Table 3, the cost of g A or g i parts of ID-RSA is equal to “ET + SM + 2P,” while the cost these parts in our proposed scheme is “2(SM) + A,” which is quite efficient in compare with ID-RSA.

In the growth of the number of requests for the Step 3 in ID-RSA scheme, the output is more effectual. Based on what is illustrated in Table 3, by assuming that “n” is the number of such request, the rate of growth of computational cost for g A or g i parts of “public key obtaining process” in our proposed scheme is “2n,” while this value in IDRSA would be “46n” or “44n” based on the use of type 2 or type 3 bilinear pairings, respectively.

6 Conclusion

In this paper, we proposed a new certificateless cryptographic protocol to authenticate the public key of other participants. The main contribution of this paper is to improve the computational cost of the ID-RSA protocol by the use of elliptic curve-based algebraic groups instead of multiplicative ones over finite fields as the output of bilinear pairings. Our analysis shows that besides a significant improvement of computational cost, our proposed protocol is much more efficient from the perspective of the rate of computational expense growth in compare with ID-RSA protocol.