Abstract
Synthesis is the automated construction of a system from its specification. The system has to satisfy its specification in all possible environments. The environment often consists of agents that have objectives of their own. Thus, it makes sense to soften the universal quantification on the behavior of the environment and take the objectives of its underlying agents into an account. Fisman et al. introduced rational synthesis: the problem of synthesis in the context of rational agents. The input to the problem consists of temporal-logic formulas specifying the objectives of the system and the agents that constitute the environment, and a solution concept (e.g., Nash equilibrium). The output is a profile of strategies, for the system and the agents, such that the objective of the system is satisfied in the computation that is the outcome of the strategies, and the profile is stable according to the solution concept; that is, the agents that constitute the environment have no incentive to deviate from the strategies suggested to them.
In this paper we continue to study rational synthesis. First, we suggest an alternative definition to rational synthesis, in which the agents are rational but not cooperative. In the non-cooperative setting, one cannot assume that the agents that constitute the environment take into account the strategies suggested to them. Accordingly, the output is a strategy for the system only, and the objective of the system has to be satisfied in all the compositions that are the outcome of a stable profile in which the system follows this strategy. We show that rational synthesis in this setting is 2ExpTime-complete, thus it is not more complex than traditional synthesis or cooperative rational synthesis. Second, we study a richer specification formalism, where the objectives of the system and the agents are not Boolean but quantitative. In this setting, the goal of the system and the agents is to maximize their outcome. The quantitative setting significantly extends the scope of rational synthesis, making the game-theoretic approach much more relevant.
O. Kupferman—The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement 278410, by the Israel Science Foundation (grant 1229/10), and by the US-Israel Binational Science Foundation (grant 2010431).
G. Perelli—This research was partially done while visiting Rice University.
M.Y. Vardi—NSF Expeditions in Computing project “ExCAPE: Expeditions in Computer Augmented Program Engineering”.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Synthesis is the automated construction of a system from its specification. The basic idea is simple and appealing: instead of developing a system and verifying that it adheres to its specification, we would like to have an automated procedure that, given a specification, constructs a system that is correct by construction. The first formulation of synthesis goes back to Church [Chu63]; the modern approach to synthesis was initiated by Pnueli and Rosner, who introduced LTL (linear temporal logic) synthesis [PR89]. The LTL synthesis problem receives as input a specification in LTL and outputs a reactive system modeled by a finite-state transducer satisfying the given specification — if such exists. It is important to distinguish between input signals, assigned by the environment, and output signals, assigned by the system. A system should be able to cope with all values of the input signals, while setting the output signals to desired values [PR89]. Therefore, the quantification structure on input and output signals is different. Input signals are universally quantified while output signals are existentially quantified.
Modern systems often interact with other systems. For example, the clients interacting with a server are by themselves distinct entities (which we call agents) and are many times implemented by systems. In the traditional approach to synthesis, the way in which the environment is composed of its underlying agents is abstracted. In particular, the agents can be seen as if their only objective is to conspire to fail the system. Hence the term “hostile environment" that is traditionally used in the context of synthesis. In real life, however, many times agents have goals of their own, other than to fail the system. The approach taken in the field of algorithmic game theory [NRTV07] is to assume that agents interacting with a computational system are rational, i.e., agents act to achieve their own goals. Assuming agents rationality is a restriction on the agents behavior and is therefore equivalent to softening the universal quantification on the environment.Footnote 1 Thus, the following question arises: can system synthesizers capitalize on the rationality and goals of agents interacting with the system?
In [FKL10], Fisman et al. positively answered this question by introducing and studying rational synthesis. The input to the rational-synthesis problem consists of LTL formulas specifying the objectives of the system and the agents that constitute the environment, and a solution concept, e.g., dominant strategies, Nash Equilibria, and the like. The atomic propositions over which the objectives are defined are partitioned among the system and the agents, so that each of them controls a subset of the propositions. The desired output is a strategy profile such that the objective of the system is satisfied in the computation that is the outcome of the profile, and the agents that constitute the environment have no incentive to deviate from the strategies suggested to them (formally, the profile is an equilibrium with respect to the solution concept). Fisman et al. showed that there are specifications that cannot be realized in a hostile environment but are realizable in a rational environment. Moreover, the rational-synthesis problem for LTL and common solution concepts used in game theory can be solved in 2ExpTime thus its complexity coincides with that of usual synthesis.
In this paper we continue the study of rational synthesis. We present the following three contributions. First, we suggest an alternative definition to rational synthesis, in which the agents are rational but not cooperative. Second, we study a richer specification formalism, where the objectives of the system and the agents are not Boolean but quantitative. Third, we show that all these variants of the rational synthesis problems can be reduced to model checking in fragments of Strategy Logic [CHP07]. Before we describe our contributions in more detail, let us highlight a different way to consider rational synthesis and our contribution here. Mechanism design is a field in game theory and economics studying the design of games whose outcome (assuming agents rationality) achieves some goal [NR01, NRTV07]. The outcome of traditional games depends on the final position of the game. In contrast, the systems we reason about maintain an on-going interaction with their environment, and we reason about their behavior by referring not to their final state (in fact, we consider non-terminating systems, with no final state) but rather to the language of computations that they generate. Rational synthesis can be viewed as a variant of mechanism design in which the game is induced by the objective of the system, and the objectives of both the system and the agents refer to their on-going interaction and are specified by temporal-logic formulas. Our contributions here correspond to the classic setting assumed in mechanism design: the agents need not be cooperative, and the outcome is not Boolean.
We argue that the definition of rational synthesis in [FKL10] is cooperative, in the sense that the agents that constitute the environment are assumed to follow the strategy profile suggested to them (as long as it is in an equilibrium). Here, we consider also a non-cooperative setting, in which the agents that constitute the environment may follow any strategy profile that is in an equilibrium, and not necessarily the one suggested to them by the synthesis algorithm. In many scenarios, the cooperative setting is indeed too optimistic, as the system cannot assume that the environment, even if it is rational, would follow a suggested strategy, rather than a strategy that is as good for it. Moreover, sometimes there is no way to communicate with the environment and suggest a strategy for it. From a technical point of view, we show that the non-cooperative setting requires reasoning about all possible equilibria, yet, despite this more sophisticated reasoning, it stays 2ExpTime-complete. We achieve the upper bound by reducing rational synthesis to the model-checking problem for Strategy Logic (Sl, for short). Sl is a specification formalism that allows to explicitly quantify over strategies in games as first-order objects [CHP07]. While the model-checking problem for strategy logic is in general non-elementary, we show that it is possible to express rational synthesis in the restricted Nested-Goal fragment of Sl, introduced in [MMPV14], which leads to the desired complexity. It is important to observe the following difference between the cooperative and the non-cooperative settings. In the cooperative one, we synthesize strategies for all agents, with the assumption that the agent that corresponds to the system always follows his suggested strategy and the agents that constitute the environment decide in a rational manner whether to follow their strategies. On the other hand, in the non-cooperative setting, we synthesize a strategy only for the agent that corresponds to the system, and we assume that the agents that constitute the environment are rational, thus the suggested strategy has to win against all rational behaviors of the environment.
Our second contribution addresses a weakness of the classical synthesis problem, a weakness that is more apparent in the rational setting. In classical synthesis, the specification is Boolean and describes the expected behavior of the system. In many applications, systems can satisfy their specifications at different levels of quality. Thus, synthesis with respect to Boolean specifications does not address designers needs. This latter problem is a real obstacle, as designers would be willing to give up manual design only after being convinced that the automatic procedure that replaces it generates systems of comparable quality. In the last years we see a lot of effort on developing formalisms that would enable the specification of such quality measures [BCHJ09, ABK13].
Classical applications of game theory consider games with quantitative payoffs. In the Boolean setting, we assumed that the payoff of an agent is, say, \(1\), if its objective is satisfied, and is \(0\) otherwise. In particular, this means that agents whose objectives are not satisfied have no incentive to follow any strategy, even if the profile satisfies the solution concept. In real-life, rational objectives are rarely Boolean. Thus, even beyond our goal of synthesizing systems of high quality, the extension of the synthesis problem to the rational setting calls also for an extension to a quantitative setting. Unfortunately, the full quantitative setting is undecidable already in the context of model checking [Hen10]. In [FKL10], Fisman et al. extended cooperative rational synthesis to objectives in the multi-valued logic LLTL where specifications take truth values from a finite lattice.
We introduce here a new quantitative specification formalism, termed Objective LTL, (OLTL, for short). We first define the logic, and then study its rational synthesis. Essentially, an OLTL specification is a pair \(\theta = \langle {\varPsi }, {\mathsf {f}}\rangle \), where \({\varPsi }= \langle \psi _1, \psi _2, \ldots , \psi _m \rangle \) is a tuple of LTL formulas and \({\mathsf {f}}: \{0,1\}^{m} \rightarrow {\mathbb {Z}}\) is a reward function, mapping Boolean vectors of length \(m\) to an integer. A computation \({\eta }\) then maps \(\theta \) to a reward in the expected way, according to the subset of formulas that are satisfied in \({\eta }\). In the rational synthesis problem for OLTL the input consists of OLTL specifications for the system and the other agents, and the goal of the system is to maximize its reward with respect to environments that are in an equilibrium. Again, we distinguish between a cooperative and a non-cooperative setting. Note that the notion of an equilibrium in the quantitative setting is much more interesting, as it means that all agents in the environment cannot expect to increase their payoffs. We show that the quantitative setting is not more complex than the non-quantitative one, thus quantitative rational synthesis is complete for 2ExpTime in both the cooperative and non-cooperative settings.
2 Preliminaries
2.1 Games
A concurrent game structure (CGS, for short) [AHK02] is a tuple  , where \(\varPhi \) and
, where \(\varPhi \) and  are finite sets of atomic propositions and agents,
are finite sets of atomic propositions and agents,  are disjoint sets of actions, one for each agent
are disjoint sets of actions, one for each agent  , \(S\) is a set of states,
, \(S\) is a set of states,  is a designated initial state, and \({\mathsf {\lambda }}: S\rightarrow 2^{\varPhi }\) is a labeling function that maps each state to the set of atomic propositions true in that state. By
is a designated initial state, and \({\mathsf {\lambda }}: S\rightarrow 2^{\varPhi }\) is a labeling function that maps each state to the set of atomic propositions true in that state. By  we denote the union of all possible action for all the agents. Let
we denote the union of all possible action for all the agents. Let  be the set of decisions, i.e., \((k + 1)\)-tuples of actions representing the choices of an action for each agent. Then, \({\mathsf {\tau }}: S\times D\rightarrow S\) is a deterministic transition function mapping a pair of a state and a decision to a state.
be the set of decisions, i.e., \((k + 1)\)-tuples of actions representing the choices of an action for each agent. Then, \({\mathsf {\tau }}: S\times D\rightarrow S\) is a deterministic transition function mapping a pair of a state and a decision to a state.
A path in a CGS
\({\mathcal {G}}\) is an infinite sequence of states  that agrees with the transition function, i.e., such that, for all \(i \in {\mathbb {N}}\), there exists a decision \({\mathsf {d}}\in D\) such that
that agrees with the transition function, i.e., such that, for all \(i \in {\mathbb {N}}\), there exists a decision \({\mathsf {d}}\in D\) such that  . A track in a CGS
\({\mathcal {G}}\) is a prefix \({\rho }\) of a path \({\eta }\), also denoted by
. A track in a CGS
\({\mathcal {G}}\) is a prefix \({\rho }\) of a path \({\eta }\), also denoted by  , for a suitable \(n \in {\mathbb {N}}\). A track \({\rho }\) is non-trivial if \(\vert {\rho }\vert > 0\), i.e., \({\rho }\ne \varepsilon \).
, for a suitable \(n \in {\mathbb {N}}\). A track \({\rho }\) is non-trivial if \(\vert {\rho }\vert > 0\), i.e., \({\rho }\ne \varepsilon \).
We use \({\mathrm {Pth}}\subseteq S^{\omega }\) and \({\mathrm {Trk}}\subseteq S^{+}\) to denote the set of all paths and non-trivial tracks, respectively. Also, for a given \({s}\in S\), we use \({\mathrm {Pth}}^{{s}}\) and \({\mathrm {Trk}}^{{s}}\) to denote the subsets of paths and tracks starting from \({s}\in S\). Intuitively, the game starts in the state  and, at each step, each agent selects an action in its set. The game then deterministically proceeds to the next state according to the corresponding decision. Thus, the outcome of a CGS is a path, regulated by individual actions of the agents.
and, at each step, each agent selects an action in its set. The game then deterministically proceeds to the next state according to the corresponding decision. Thus, the outcome of a CGS is a path, regulated by individual actions of the agents.
A strategy for Agent  is a tool used to decide which decision to take at each phase of the game. Formally, it is a function
is a tool used to decide which decision to take at each phase of the game. Formally, it is a function  that maps each non-trivial track to a possible action of Agent
that maps each non-trivial track to a possible action of Agent  . By
. By  we denote the set of all possible strategies for agent
we denote the set of all possible strategies for agent  . A strategy profile is a \((k + 1)\)-tuple
. A strategy profile is a \((k + 1)\)-tuple  that assigns a strategy to each agent. We denote by
that assigns a strategy to each agent. We denote by  the set of all possible strategy profiles. For a strategy profile \({\mathsf {P}}\) and a state \({s}\), we use \({\eta }= {\mathsf {play}}({\mathsf {P}}, {s})\) to denote the path that is the outcome of a game that starts in \({s}\) and agrees with \({\mathsf {P}}\), i.e., for all \(i \in {\mathbb {N}}\), it holds that
the set of all possible strategy profiles. For a strategy profile \({\mathsf {P}}\) and a state \({s}\), we use \({\eta }= {\mathsf {play}}({\mathsf {P}}, {s})\) to denote the path that is the outcome of a game that starts in \({s}\) and agrees with \({\mathsf {P}}\), i.e., for all \(i \in {\mathbb {N}}\), it holds that  , where
, where  . By
. By  we denote the unique path starting from
we denote the unique path starting from  obtained from \({\mathsf {P}}\).
obtained from \({\mathsf {P}}\).
We model reactive systems by deterministic transducers. A transducer is a tuple  , where \({\mathrm {I}}\) is a set of input signals assigned by the environment, \({\mathrm {O}}\) is a set of output signals, assigned by the system, \({\mathrm {S}}\) is a set of states,
, where \({\mathrm {I}}\) is a set of input signals assigned by the environment, \({\mathrm {O}}\) is a set of output signals, assigned by the system, \({\mathrm {S}}\) is a set of states,  is an initial state, \(\delta : {\mathrm {S}}\times 2^{{\mathrm {I}}} \rightarrow {\mathrm {S}}\) is a transition function, and \({\mathsf {L}}: {\mathrm {S}}\rightarrow 2^{{\mathrm {O}}}\) is a labeling function. When the system is in state \({s}\in {\mathrm {S}}\) and it reads an input assignment \(\sigma \in 2^{{\mathrm {I}}}\), it changes its state to \({s}' = \delta ({s}, \sigma )\) where it outputs the assignment
is an initial state, \(\delta : {\mathrm {S}}\times 2^{{\mathrm {I}}} \rightarrow {\mathrm {S}}\) is a transition function, and \({\mathsf {L}}: {\mathrm {S}}\rightarrow 2^{{\mathrm {O}}}\) is a labeling function. When the system is in state \({s}\in {\mathrm {S}}\) and it reads an input assignment \(\sigma \in 2^{{\mathrm {I}}}\), it changes its state to \({s}' = \delta ({s}, \sigma )\) where it outputs the assignment  . Given a sequence \(\varrho = \sigma _1, \sigma _2, \sigma _3, \ldots \in (2^{{\mathrm {I}}})^{\omega }\) of inputs, the execution of \({\mathcal {T}}\) on \(\varrho \) is the sequence of states
. Given a sequence \(\varrho = \sigma _1, \sigma _2, \sigma _3, \ldots \in (2^{{\mathrm {I}}})^{\omega }\) of inputs, the execution of \({\mathcal {T}}\) on \(\varrho \) is the sequence of states  such that for all \(j \ge 0\), we have
such that for all \(j \ge 0\), we have  . The computation
\({\eta }\in (2^{{\mathrm {I}}} \times 2^{{\mathrm {O}}})^{\omega }\) of \({\mathrm {S}}\) on \(\varrho \) is then
. The computation
\({\eta }\in (2^{{\mathrm {I}}} \times 2^{{\mathrm {O}}})^{\omega }\) of \({\mathrm {S}}\) on \(\varrho \) is then  .
.
2.2 Strategy Logic
Strategy Logic [CHP07, MMV10, MMPV12] (Sl, for short) is a logic that allows to quantify over strategies in games as explicit first-order objects. Intuitively, such quantification, together with a syntactic operator called binding, allows us to restrict attention to restricted classes of strategy profiles, determining a subset of paths, in which a temporal specification is desired to be satisfied. Since nesting of quantifications and bindings is possible, such temporal specifications can be recursively formulated by an Sl subsentence. From a syntactic point of view, Sl is an extension of LTL with strategy variables  for the agents, existential (
for the agents, existential ( ) and universal (
) and universal ( ) strategy quantifiers, and a binding operator of the form
) strategy quantifiers, and a binding operator of the form  that couples an agent
that couples an agent  with one of its variables
with one of its variables  .
.
We first introduce some technical notation. For a tuple  , by
, by  we denote the tuple obtained from \({t}\) by replacing the \(i\)-th component with \(d\). We use \(\vec {{x}}\) as an abbreviation for the tuple
we denote the tuple obtained from \({t}\) by replacing the \(i\)-th component with \(d\). We use \(\vec {{x}}\) as an abbreviation for the tuple  . By
. By  , and
, and  we denote the existential and universal quantification, and the binding of all the agents to the strategy profile variable \(\vec {{x}}\), respectively. Finally, by
we denote the existential and universal quantification, and the binding of all the agents to the strategy profile variable \(\vec {{x}}\), respectively. Finally, by  we denote the changing of binding for Agent
we denote the changing of binding for Agent  from the strategy variable
from the strategy variable  to the strategy variable
to the strategy variable  in the global binding \({\flat }(\vec {{x}})\).
in the global binding \({\flat }(\vec {{x}})\).
Here we define and use a slight variant of the Nested-Goal fragment of Sl, namely Sl[ng], introduced in [MMPV14]. Formulas in Sl[ng] are defined with respect to a set \(\varPhi \) of atomic proposition, a set \({\mathrm {\Omega }}\) of agents, and sets \({\mathrm {Var}}_i\) of strategy variables for Agent  . The set of Sl[ng] formulas is defined by the following grammar:
. The set of Sl[ng] formulas is defined by the following grammar:

where, \({p}\in \varPhi \) is an atomic proposition,  is a variable, and
is a variable, and  is a tuple of variables, one for each agent.
is a tuple of variables, one for each agent.
The LTL part has the classical meaning. The formula  states that there exists a strategy for Agent
states that there exists a strategy for Agent  such that the formula \(\varphi \) holds. The formula
such that the formula \(\varphi \) holds. The formula  states that, for all possible strategies for Agent
states that, for all possible strategies for Agent  , the formula \(\varphi \) holds. Finally, the formula
, the formula \(\varphi \) holds. Finally, the formula  states that the formula \(\varphi \) holds under the assumption that the agents in \({\mathrm {\Omega }}\) adhere to the strategy evaluation of the variable
states that the formula \(\varphi \) holds under the assumption that the agents in \({\mathrm {\Omega }}\) adhere to the strategy evaluation of the variable  coupled in \({\flat }(\vec {{x}})\).
coupled in \({\flat }(\vec {{x}})\).
As an example,  is an Sl[ng] formula stating that either the system
is an Sl[ng] formula stating that either the system  has a strategy
has a strategy  to enforce
to enforce  or, for all possible behaviors
or, for all possible behaviors  , the environment has a strategy
, the environment has a strategy  to enforce both \({{\mathsf {G}}\,}{{\mathsf {F}}\,}{p}\) and \({{\mathsf {G}}\,}\lnot {q}\).
to enforce both \({{\mathsf {G}}\,}{{\mathsf {F}}\,}{p}\) and \({{\mathsf {G}}\,}\lnot {q}\).
We denote by \({\mathsf {free}}(\varphi )\) the set of strategy variables occurring in \(\varphi \) but not in a scope of a quantifier. A formula \(\varphi \) is closed if \({\mathsf {free}}(\varphi ) = \emptyset \).
Similarly to the case of first order logic, an important concept that characterizes the syntax of Sl is the one of alternation depth of quantifiers, i.e., the maximum number of quantifier switches  , in the formula. A precise formalization of the concepts of alternation depth can be found in [MMV10, MMPV12].
, in the formula. A precise formalization of the concepts of alternation depth can be found in [MMV10, MMPV12].
Now, in order to define the semantics of Sl, we use the auxiliary concept of assignment. Let  be a set of variables for the agents in \({\mathrm {\Omega }}\), an assignment is a function \({\mathsf {\chi }}: {\mathrm {Var}}\cup {\mathrm {\Omega }}\rightarrow {\mathrm {\Pi }}\) mapping variables and agents to a relevant strategy, i.e., for all
be a set of variables for the agents in \({\mathrm {\Omega }}\), an assignment is a function \({\mathsf {\chi }}: {\mathrm {Var}}\cup {\mathrm {\Omega }}\rightarrow {\mathrm {\Pi }}\) mapping variables and agents to a relevant strategy, i.e., for all  and
and  , we have that
, we have that  . Let
. Let  denote the set of all assignments. For an assignment \({\mathsf {\chi }}\) and elements \({l}\in {\mathrm {Var}}\cup {\mathrm {\Omega }}\), we use
denote the set of all assignments. For an assignment \({\mathsf {\chi }}\) and elements \({l}\in {\mathrm {Var}}\cup {\mathrm {\Omega }}\), we use  to denote the new assignment that returns \({\mathsf {\pi }}\) on \({l}\) and the value of \({\mathsf {\chi }}\) on the other ones, i.e.,
to denote the new assignment that returns \({\mathsf {\pi }}\) on \({l}\) and the value of \({\mathsf {\chi }}\) on the other ones, i.e.,  and
and  , for all \({l}' \!\in \! ({\mathrm {Var}}\cup {\mathrm {\Omega }}) \!\setminus \! \{ {l}\}\). By \({\mathsf {play}}({\mathsf {\chi }}, {s})\) we denote the path \({\mathsf {play}}({\mathsf {P}}, {s})\), for the strategy profile \({\mathsf {P}}\) that is compatible with \({\mathsf {\chi }}\).
, for all \({l}' \!\in \! ({\mathrm {Var}}\cup {\mathrm {\Omega }}) \!\setminus \! \{ {l}\}\). By \({\mathsf {play}}({\mathsf {\chi }}, {s})\) we denote the path \({\mathsf {play}}({\mathsf {P}}, {s})\), for the strategy profile \({\mathsf {P}}\) that is compatible with \({\mathsf {\chi }}\).
We now describe when a given game \({\mathcal {G}}\) and a given assignment \({\mathsf {\chi }}\) satisfy an Sl formula \(\varphi \), where \({\mathsf {dom}}({\mathsf {\chi }})\)
Footnote 2 = \({\mathsf {free}}(\varphi ) \cup {\mathrm {\Omega }}\). We use \({\mathcal {G}}, {\mathsf {\chi }}, {s}\models \varphi \) to indicate that the path \({\mathsf {play}}({\mathsf {\chi }}, {s})\) satisfies \(\varphi \) over the CGS
 . For \(\varphi \) in LTL, the semantics is as usual [MP92]. For the other operators, the semantics is as follows.
. For \(\varphi \) in LTL, the semantics is as usual [MP92]. For the other operators, the semantics is as follows.
-
1.
 if there exists a strategy
if there exists a strategy  for
for  such that
such that  ;
; -
2.
 if, for all strategies
if, for all strategies  for
for  , it holds that
, it holds that  ;
; -
3.
\({\mathcal {G}}, {\mathsf {\chi }}, {s}\models {\flat }(\vec {{x}}) \varphi \) if it holds that
 .
.
Finally, we say that \({\mathcal {G}}\) satisfies \(\varphi \), and write \({\mathcal {G}}\models \varphi \), if there exists an assignment \({\mathsf {\chi }}\) such that  .
.
Intuitively, at Items 1 and 2, we evaluate the existential and universal quantifiers over a variable  by associating with it a suitable strategy. At Item 3 we commit the agents to use the strategy contained in the tuple variable \(\vec {{x}}\).
by associating with it a suitable strategy. At Item 3 we commit the agents to use the strategy contained in the tuple variable \(\vec {{x}}\).
Theorem 1
[MMPV14] The model-checking problem for Sl[ng] is \((d+1)\) ExpTime with \(d\) being the alternation depth of the specification.
2.3 Rational Synthesis
We define two variants of rational synthesis. The first, cooperative rational synthesis, was introduced in [FKL10]. The second, non-cooperative rational synthesis, is new.
We work with the following model: the world consists of a system and an environment composed of \(k\) agents:  . For uniformity, we refer to the system as Agent
. For uniformity, we refer to the system as Agent  . We assume that Agent
. We assume that Agent  controls a set
controls a set  of propositions, and the different sets are pairwise disjoint. At each point in time, each agent sets his propositions to certain values. Let
of propositions, and the different sets are pairwise disjoint. At each point in time, each agent sets his propositions to certain values. Let  , and
, and  . Each agent
. Each agent  (including the system) has an objective \(\varphi _{i}\), specified as an LTL formula over \({\mathrm {X}}\).
(including the system) has an objective \(\varphi _{i}\), specified as an LTL formula over \({\mathrm {X}}\).
This setting induces the CGS  defined as follows. The set of agents
defined as follows. The set of agents  consists of the system and the agents that constitute the environment. The actions of Agent
consists of the system and the agents that constitute the environment. The actions of Agent  are the possible assignments to its variables. Thus,
are the possible assignments to its variables. Thus,  . We use \({A}\) and \({A}_{-i}\) to denote the sets \(2^{{\mathrm {X}}}\) and
. We use \({A}\) and \({A}_{-i}\) to denote the sets \(2^{{\mathrm {X}}}\) and  , respectively. The nodes of the game record the current assignment to the variables. Hence, \(S= {A}\), and for all \({s}\in S\) and
, respectively. The nodes of the game record the current assignment to the variables. Hence, \(S= {A}\), and for all \({s}\in S\) and  , we have \(\delta ({s}, \sigma _{0}, \ldots , \sigma _{k}) = \langle \sigma _{0}, \cdots , \sigma _{k} \rangle \).
, we have \(\delta ({s}, \sigma _{0}, \ldots , \sigma _{k}) = \langle \sigma _{0}, \cdots , \sigma _{k} \rangle \).
A strategy for the system is a function  . In the standard synthesis problem, we say that
. In the standard synthesis problem, we say that  realizes \(\varphi _0\) if, no matter which strategies the agents composing the environment follow, all the paths in which the system follows
realizes \(\varphi _0\) if, no matter which strategies the agents composing the environment follow, all the paths in which the system follows  satisfy \(\varphi _0\). In rational synthesis, on instead, we assume that the agents that constitute the environment are rational, which soften the universal quantification on the behavior of the environment.
satisfy \(\varphi _0\). In rational synthesis, on instead, we assume that the agents that constitute the environment are rational, which soften the universal quantification on the behavior of the environment.
Recall that the rational-synthesis problem gets a solution concept as a parameter. As discussed in Sect. 1, the fact that a strategy profile is a solution with respect to the concept guarantees that it is not worthwhile for the agents constituting the environment to deviate from the strategies assigned to them. Several solution concepts are studied and motivated in game theory. Here, we focus on the concepts of dominant strategy and Nash equilibrium, defined below.
The common setting in game theory is that the objective for each agent is to maximize his payoff – a real number that is a function of the outcome of the game. We use  to denote the payoff function of Agent
to denote the payoff function of Agent  . That is,
. That is,  assigns to each possible path \({\eta }\) a real number \({\mathsf {payoff}}_i({\eta })\) expressing the payoff of
assigns to each possible path \({\eta }\) a real number \({\mathsf {payoff}}_i({\eta })\) expressing the payoff of  on \({\eta }\). For a strategy profile \({\mathsf {P}}\), we use
on \({\eta }\). For a strategy profile \({\mathsf {P}}\), we use  to abbreviate
to abbreviate  . In the case of an LTL goal \(\psi _{i}\), we define
. In the case of an LTL goal \(\psi _{i}\), we define  if \({\eta }\models \psi _{i}\) and
if \({\eta }\models \psi _{i}\) and  , otherwise.
, otherwise.
The simplest and most appealing solution concept is dominant-strategies solution [OR94]. A dominant strategy is a strategy that an agent can never lose by adhering to, regardless of the strategies of the other agents. Therefore, if there is a profile of strategies  in which all strategies
in which all strategies  are dominant, then no agent has an incentive to deviate from the strategy assigned to him in \({\mathsf {P}}\). Formally, \({\mathsf {P}}\) is a dominant strategy profile if for every \(1 \le i \le k\) and for every (other) profile \({\mathsf {P}}'\), we have that
are dominant, then no agent has an incentive to deviate from the strategy assigned to him in \({\mathsf {P}}\). Formally, \({\mathsf {P}}\) is a dominant strategy profile if for every \(1 \le i \le k\) and for every (other) profile \({\mathsf {P}}'\), we have that  .
.
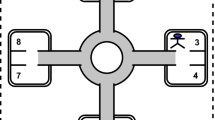
As an example, consider the game in Fig. 1(a), played by three agents, Alice, Bob, and Charlie, whose actions are  , and
, and  , respectively. The arrows are labeled with the possible action of the agents. Each agent wants to visit a state marked with his initial letter, infinitely often. In this game, the strategy for Bob of always choosing
, respectively. The arrows are labeled with the possible action of the agents. Each agent wants to visit a state marked with his initial letter, infinitely often. In this game, the strategy for Bob of always choosing  on his node \(2\) is dominant, while all the possible strategies for Charlie are dominant. On the other hand, Alice has no dominant strategies, since her goal essentially depends on the strategies adopted by the other agents. In several games, it can happen that agents have not any dominant strategy. For this reason, one would consider also other kind of solution concepts.
on his node \(2\) is dominant, while all the possible strategies for Charlie are dominant. On the other hand, Alice has no dominant strategies, since her goal essentially depends on the strategies adopted by the other agents. In several games, it can happen that agents have not any dominant strategy. For this reason, one would consider also other kind of solution concepts.
Another well known solution concept is Nash equilibrium [OR94]. A strategy profile is a Nash equilibrium if no agent has an incentive to deviate from his strategy in \({\mathsf {P}}\) provided that the other agents adhere to the strategies assigned to them in \({\mathsf {P}}\). Formally, \({\mathsf {P}}\) is a Nash equilibrium profile if for every \(1 \le i \le k\) and for every (other) strategy \({\mathsf {\pi }}'_i\) for agent  , we have that \({\mathsf {payoff}}_i({\mathsf {P}}{[i \leftarrow {\mathsf {\pi }}'_i]}) \le {\mathsf {payoff}}_i({\mathsf {P}})\). An important advantage of Nash equilibrium is that it is more likely to exist than an equilibrium of dominant strategies [OR94]Footnote 3. A weakness of Nash equilibrium is that it is not nearly as stable as a dominant-strategy solution: if one of the other agents deviates from his assigned strategy, nothing is guaranteed.
, we have that \({\mathsf {payoff}}_i({\mathsf {P}}{[i \leftarrow {\mathsf {\pi }}'_i]}) \le {\mathsf {payoff}}_i({\mathsf {P}})\). An important advantage of Nash equilibrium is that it is more likely to exist than an equilibrium of dominant strategies [OR94]Footnote 3. A weakness of Nash equilibrium is that it is not nearly as stable as a dominant-strategy solution: if one of the other agents deviates from his assigned strategy, nothing is guaranteed.
For the case of repeated-turn games like infinite games, a suitable refinement of Nash Equilibria is the Subgame perfect Nash-equilibrium [Sel75] (SPE, for short). A strategy profile  is an SPE if for every possible history of the game, no agent
is an SPE if for every possible history of the game, no agent  has an incentive to deviate from her strategy \({\mathsf {\pi }}_i\), assuming that the other agents follow their strategies in \({\mathsf {P}}\). Intuitively, an SPE requires the existence of a Nash Equilibrium for each subgame starting from a randomly generated finite path of the original one. In [FKL10], the authors have studied cooperative rational synthesis also for the solution concept of SPE. To do this, the synthesis algorithm in [FKL10] was extended to consider all possible histories of the game. In Sl such a path property can be expressed combining strategy quantifiers with temporal operators. Indeed, the formula \(\varphi = {[\,\!\![\vec {{x}} ]\,\!\! ]} {\flat }(\vec {{x}}) {{\mathsf {G}}\,}\psi (\vec {{y}})\), with \({\mathsf {free}}(\varphi ) = \vec {{y}}\), states that, for all possible profile strategies the agents can follow, the game always reaches a position in which the formula \(\psi (\vec {{y}})\) holds. Thus, for all possible paths that can be generated by agents, the property holds. By replacing \(\psi (\vec {{y}})\) with the above formula, we then obtain a formula that represents SPEs. Hence, the cooperative and non-cooperative synthesis problems can be asserted in Sl also for SPE, and our results hold also for this solution concept.
has an incentive to deviate from her strategy \({\mathsf {\pi }}_i\), assuming that the other agents follow their strategies in \({\mathsf {P}}\). Intuitively, an SPE requires the existence of a Nash Equilibrium for each subgame starting from a randomly generated finite path of the original one. In [FKL10], the authors have studied cooperative rational synthesis also for the solution concept of SPE. To do this, the synthesis algorithm in [FKL10] was extended to consider all possible histories of the game. In Sl such a path property can be expressed combining strategy quantifiers with temporal operators. Indeed, the formula \(\varphi = {[\,\!\![\vec {{x}} ]\,\!\! ]} {\flat }(\vec {{x}}) {{\mathsf {G}}\,}\psi (\vec {{y}})\), with \({\mathsf {free}}(\varphi ) = \vec {{y}}\), states that, for all possible profile strategies the agents can follow, the game always reaches a position in which the formula \(\psi (\vec {{y}})\) holds. Thus, for all possible paths that can be generated by agents, the property holds. By replacing \(\psi (\vec {{y}})\) with the above formula, we then obtain a formula that represents SPEs. Hence, the cooperative and non-cooperative synthesis problems can be asserted in Sl also for SPE, and our results hold also for this solution concept.
In rational synthesis, we control the strategy of the system and assume that the agents that constitute the environment are rational. Consider a strategy profile  and a solution concept \(\gamma \) (that is, \(\gamma \) is either “dominant strategies" or “Nash equilibrium"). We say that \({\mathsf {P}}\) is correct if \({\mathsf {play}}({\mathsf {P}})\) satisfies \(\varphi _0\). We say that \({\mathsf {P}}\) is in a
and a solution concept \(\gamma \) (that is, \(\gamma \) is either “dominant strategies" or “Nash equilibrium"). We say that \({\mathsf {P}}\) is correct if \({\mathsf {play}}({\mathsf {P}})\) satisfies \(\varphi _0\). We say that \({\mathsf {P}}\) is in a  -fixed
\(\gamma \)
-equilibrium if the agents composing the environment have no incentive to deviate from their strategies according to the solution concept \(\gamma \), assuming that the system continues to follow
-fixed
\(\gamma \)
-equilibrium if the agents composing the environment have no incentive to deviate from their strategies according to the solution concept \(\gamma \), assuming that the system continues to follow  . Thus, \({\mathsf {P}}\) is a
. Thus, \({\mathsf {P}}\) is a  -fixed dominant-strategy equilibrium if for every \(1 \le i \le k\) and for every (other) profile \({\mathsf {P}}'\) in which Agent \(0\) follows
-fixed dominant-strategy equilibrium if for every \(1 \le i \le k\) and for every (other) profile \({\mathsf {P}}'\) in which Agent \(0\) follows  , we have that
, we have that  . Note that for the case of Nash equilibrium, adding the requirement that \({\mathsf {P}}\) is
. Note that for the case of Nash equilibrium, adding the requirement that \({\mathsf {P}}\) is  -fixed does not change the definition of an equilibrium.
-fixed does not change the definition of an equilibrium.
In the context of objectives in LTL, we assume the following simple payoffs. If the objective \(\varphi _i\) of Agent  holds, then his payoff is \(1\), and if \(\varphi _i\) does not hold, then the payoff of Agent \(i\) is \(0\). Accordingly,
holds, then his payoff is \(1\), and if \(\varphi _i\) does not hold, then the payoff of Agent \(i\) is \(0\). Accordingly,  is in a dominant-strategy equilibrium if for every \(1 \le i \le k\) and profile
is in a dominant-strategy equilibrium if for every \(1 \le i \le k\) and profile  with
with  , if \({\mathsf {play}}({\mathsf {P}}') \models \varphi _i\), then
, if \({\mathsf {play}}({\mathsf {P}}') \models \varphi _i\), then  . Also, \({\mathsf {P}}\) is in a Nash-equilibrium if for every \(1 \le i \le k\) and strategy \({\mathsf {\pi }}'_i\), if \({\mathsf {play}}({\mathsf {P}}{[i \leftarrow {\mathsf {\pi }}'_i]}) \models \varphi _i\), then \({\mathsf {play}}({\mathsf {P}}) \models \varphi _i\).
. Also, \({\mathsf {P}}\) is in a Nash-equilibrium if for every \(1 \le i \le k\) and strategy \({\mathsf {\pi }}'_i\), if \({\mathsf {play}}({\mathsf {P}}{[i \leftarrow {\mathsf {\pi }}'_i]}) \models \varphi _i\), then \({\mathsf {play}}({\mathsf {P}}) \models \varphi _i\).
Definition 1
(Rational synthesis). The input to the rational-strategy problem is a set
\({\mathrm {X}}\)
of atomic propositions, partitioned into
 formulas
\(\varphi _{0}, \ldots , \varphi _{k}\), describing the objectives of the system and the agents composing the environment, and a solution concept
\(\gamma \). We distinguish between two variants of the problem:
formulas
\(\varphi _{0}, \ldots , \varphi _{k}\), describing the objectives of the system and the agents composing the environment, and a solution concept
\(\gamma \). We distinguish between two variants of the problem:
-
1.
In Cooperative rational synthesis [FKL10], the desired output is a strategy profile \({\mathsf {P}}\) such that \({\mathsf {play}}({\mathsf {P}})\) satisfies \(\varphi _0\) and \({\mathsf {P}}\) is a
 -fixed
\(\gamma \)
-equilibrium.
-fixed
\(\gamma \)
-equilibrium.
-
2.
In Non-cooperative rational synthesis, the desired output is a strategy
 for the system such that for every strategy profile
\({\mathsf {P}}\)
that includes
for the system such that for every strategy profile
\({\mathsf {P}}\)
that includes
 and is a
and is a
 -fixed
\(\gamma \)
-equilibrium, we have that
\({\mathsf {play}}({\mathsf {P}})\)
satisfies
\(\varphi _0\).
-fixed
\(\gamma \)
-equilibrium, we have that
\({\mathsf {play}}({\mathsf {P}})\)
satisfies
\(\varphi _0\).
Thus, in the cooperative variant of [FKL10], we assume that once we suggest to the agents in the environment strategies that are in a \(\gamma \)-equilibrium, they will adhere to the suggested strategies. In the non-cooperative variant we introduce here, the agents may follow any strategy profile that is in a \(\gamma \)-equilibrium, and thus we require the outcome of all these profiles to satisfy \(\varphi _0\). It is shown in [FKL10] that the cooperative rational synthesis problem is 2ExpTime-complete.
Note that the input to the rational synthesis problem may not have a solution, so when we solve the rational-synthesis problem, we first solve the rational-realizability problem, which asks if a solution exists. As with classical synthesis, the fact that Sl model-checking algorithms can be easily modified to return a regular witness for the involved strategies in case an existentially quantified strategy exists, makes the realizability and synthesis problems strongly related.
Example 1
Consider a file-sharing network with the system and an environment consisting of two agents. The system controls the signal  and
and  (Agent
(Agent  and
and  can download, respectively) and it makes sure that an agent can download only when the other agent uploads. The system’s objective is that both agents will upload infinitely often. Agent
can download, respectively) and it makes sure that an agent can download only when the other agent uploads. The system’s objective is that both agents will upload infinitely often. Agent  controls the signal
controls the signal  (Agent
(Agent  uploads), and similarly for Agent
uploads), and similarly for Agent  and
and  . The goal of both agents is to download infinitely often.
. The goal of both agents is to download infinitely often.
Formally, the set of atomic propositions is  , partitioned into
, partitioned into  , and
, and  . The objectives of the system and the environment are as follows.
. The objectives of the system and the environment are as follows.
-
 ,
, -
 ,
, -
 .
.
First, note that in standard synthesis, \(\varphi _0\) is not realizable, as a hostile environment needs not upload. In the cooperative setting, the system can suggest to both agents the following tit for tat strategy: upload at the first time step, and from that point onward upload iff the other agent uploads. The system itself follows a strategy  according to which it enables downloads whenever possible (that is,
according to which it enables downloads whenever possible (that is,  is valid whenever Agent
is valid whenever Agent  uploads, and
uploads, and  is valid whenever Agent
is valid whenever Agent  uploads). It is not hard to see that the above three strategies are all dominant. Indeed, all the three objectives are satisfied. Thus, the triple of strategies is a solution for the cooperative setting, for both solution concepts.
uploads). It is not hard to see that the above three strategies are all dominant. Indeed, all the three objectives are satisfied. Thus, the triple of strategies is a solution for the cooperative setting, for both solution concepts.
What about the non-cooperative setting? Consider the above strategy  of the system, and consider strategies for the agents that never upload. The tuple of the three strategies is in a
of the system, and consider strategies for the agents that never upload. The tuple of the three strategies is in a  -fixed Nash equilibrium.
-fixed Nash equilibrium.
This ensures strategies for the environment to be dominant. Indeed, if Agent  changes her strategy, \(\varphi _{1}\) is still satisfied and vice-versa. Indeed, as long as Agent
changes her strategy, \(\varphi _{1}\) is still satisfied and vice-versa. Indeed, as long as Agent  sticks to his strategy, Agent
sticks to his strategy, Agent  has no incentive to change his strategy, and similarly for Agent
has no incentive to change his strategy, and similarly for Agent  . Thus,
. Thus,  is not a solution to the non-cooperative rational synthesis problem for the solution concept of Nash equilibrium. On the other hand, we claim that
is not a solution to the non-cooperative rational synthesis problem for the solution concept of Nash equilibrium. On the other hand, we claim that  is a solution to the non-cooperative rational synthesis problem for the solution concept of dominant strategies. For showing this, we argue that if
is a solution to the non-cooperative rational synthesis problem for the solution concept of dominant strategies. For showing this, we argue that if  and
and  are dominant strategies for
are dominant strategies for  and
and  , then \(\varphi _{0}\) is satisfied in the path that is the outcome of the profile
, then \(\varphi _{0}\) is satisfied in the path that is the outcome of the profile  . To see this, consider such a path
. To see this, consider such a path  . We necessarily have that \({\eta }\models \varphi _{1} \wedge \varphi _{2}\). Indeed, otherwise
. We necessarily have that \({\eta }\models \varphi _{1} \wedge \varphi _{2}\). Indeed, otherwise  and
and  would not be dominant, as we know that with the strategies described above,
would not be dominant, as we know that with the strategies described above,  and
and  can satisfy their objectives. Now, since \({\eta }\models \varphi _{1} \wedge \varphi _{2}\), we know that
can satisfy their objectives. Now, since \({\eta }\models \varphi _{1} \wedge \varphi _{2}\), we know that  and
and  hold infinitely often in \({\eta }\). Also, it is not hard to see that the formulas
hold infinitely often in \({\eta }\). Also, it is not hard to see that the formulas  and
and  are always satisfied in the context of
are always satisfied in the context of  , no matter how the other agents behave. It follows that \({\eta }\models \varphi _{0}\), thus
, no matter how the other agents behave. It follows that \({\eta }\models \varphi _{0}\), thus  is a solution of the non-cooperative rational synthesis problem for dominant strategies.
is a solution of the non-cooperative rational synthesis problem for dominant strategies.
3 Qualitative Rational Synthesis
In this section we study cooperative and non-cooperative rational synthesis and show that they can be reduced to the model-checking problem for Sl[ng]. The cooperative and non-cooperative rational synthesis problems for several solution concepts can be stated in Sl[ng].
We first show how to state that a given strategy profile \(\vec {{y}} = ({{y}}_{0}, \ldots , {{y}}_{k})\) is in a  -fixed \(\gamma \)-equilibrium. For
-fixed \(\gamma \)-equilibrium. For  , let \(\varphi _{i}\) be the objective of Agent
, let \(\varphi _{i}\) be the objective of Agent  . For a solution concept \(\gamma \) and a strategy profile \(\vec {{y}} = ({{y}}_{0}, \ldots , {{y}}_{k})\), the formula \(\varphi ^{\gamma }(\vec {{y}})\), expressing that the profile \(\vec {{y}}\) is a \({y}_0\)-fixed \(\gamma \)-equilibrium, is defined as follows.
. For a solution concept \(\gamma \) and a strategy profile \(\vec {{y}} = ({{y}}_{0}, \ldots , {{y}}_{k})\), the formula \(\varphi ^{\gamma }(\vec {{y}})\), expressing that the profile \(\vec {{y}}\) is a \({y}_0\)-fixed \(\gamma \)-equilibrium, is defined as follows.
-
For the solution concept of dominant strategies, we define:
 .
. -
For the solution concept of Nash equilibrium, we define:
 .
. -
For the solution concept of Subgame Perfect Equilibrium, we define:
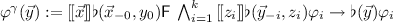 .
.
We can now state the existence of a solution to the cooperative and non-cooperative rational-synthesis problem, respectively, with input \(\varphi _{0}, \ldots , \varphi _{k}\) by the closed formulas:
-
1.
 ;
; -
2.
 .
.
Indeed, the formula 1 specifies the existence of a strategy profile  that is
that is  -fixed \(\gamma \)-equilibrium and such that the outcome satisfies \(\varphi _{0}\). On the other hand, the formula 2 specifies the existence of a strategy
-fixed \(\gamma \)-equilibrium and such that the outcome satisfies \(\varphi _{0}\). On the other hand, the formula 2 specifies the existence of a strategy  for the system such that the outcome of all profiles that are in a
for the system such that the outcome of all profiles that are in a  -fixed \(\gamma \)-equilibrium satisfy \(\varphi _{0}\).
-fixed \(\gamma \)-equilibrium satisfy \(\varphi _{0}\).
As shown above, all the solution concepts we are taking into account can be specified in Sl[ng] with formulas whose length is polynomial in the number of the agents and in which the alternation depth of the quantification is \(1\). Hence we can apply the known complexity results for Sl[ng]:
Theorem 2
(Cooperative and non-cooperative rational-synthesis complexity). The cooperative and non-cooperative rational-synthesis problems in the qualitative setting are 2ExpTime-complete.
Proof
Consider an input \(\varphi _0, \ldots , \varphi _k\), \({\mathrm {X}}\), and \(\gamma \) to the cooperative or non-cooperative rational-synthesis problem. As explained in Sect. 2.3, the input induces a game \({\mathcal {G}}\) with nodes in \(2^X\). As detailed above, there is a solution to the cooperative (resp., non-cooperative) problem iff the Sl[ng] formula \(\varphi _{cRS}^\gamma \) (resp., \(\varphi _{noncRS}^\gamma \)) is satisfied in \(\mathcal {G}\). The upper bound then follows from the fact that the model checking problem for Sl[ng] formulas of alternation depth \(1\) is in 2ExpTime-complete in the size of the formula (Cf., Theorem 1). Moreover, the model-checking algorithm can return finite-state transducers that model strategies that are existentially quantified.
For the lower bound, it is easy to see that the classical LTL synthesis problem is a special case of the cooperative and non-cooperative rational synthesis problem. Indeed, \(\varphi (I,O)\) is realizable against a hostile environment iff the solution to the non-cooperative rational synthesis problem for a system that has an objective \(\varphi \) and controls \(I\) and an environment that consists of a single agent that controls \(O\) and has an objective True, is positive.
4 Quantitative Rational Synthesis
As discussed in Sect. 1, a weakness of classical synthesis algorithms is the fact that specifications are Boolean and miss a reference to the quality of the satisfaction. Applications of game theory consider games with quantitative payoffs. Thus, even more than the classical setting, the rational setting calls for an extension of the synthesis problem to a quantitative setting. In this section we introduce Objective LTL, a quantitative extension of LTL, and study an extension of the rational-synthesis problem for specifications in Objective LTL. As opposed to other multi-valued specification formalisms used in the context of synthesis of high-quality systems [BCHJ09, ABK13], Objective LTL uses the syntax and semantics of LTL and only augments the specification with a reward function that enables a succinct and convenient prioritization of sub-specifications.
4.1 The Quantitative Setting
Objective
LTL (OLTL, for short) is an extension of LTL in which specifications consist of sets of LTL formulas weighted by functions. Formally, an OLTL
specification over a set \({\mathrm {X}}\) of atomic propositions is a pair \(\theta = \langle {\varPsi }, {\mathsf {f}}\rangle \), where \({\varPsi }= \langle \psi _{1}, \psi _{2}, \ldots , \psi _{m} \rangle \) is a tuple of LTL formulas over \({\mathrm {X}}\) and \({\mathsf {f}}: \{0, 1 \}^{m} \rightarrow {\mathbb {Z}}\) is a reward function, mapping Boolean vectors of length \(m\) to integers. We assume that \(\mathsf {f}\) is given by a polynomial. We use \(\vert {\varPsi } \vert \) to denote \(\sum _{i = 1}^{m} \vert \psi _i \vert \). For a computation \({\eta }\in (2^{{\mathrm {X}}})^{\omega }\), the signature of
\({\varPsi }\)
in
\({\eta }\), denoted \({{\mathsf {sig}}}({\varPsi },{\eta })\), is a vector in \(\{0, 1\}^{m}\) indicating which formulas in \({\varPsi }\) are satisfied in \({\eta }\). Thus,  is such that for all \(1 \le i \le m\), we have that
is such that for all \(1 \le i \le m\), we have that  if \({\eta }\models \psi _i\) and
if \({\eta }\models \psi _i\) and  if \({\eta }\not \models \psi _i\). The value of
\(\theta \)
in
\({\eta }\), denoted \({{\mathsf {val}}}(\theta , {\eta })\) is then \({\mathsf {f}}({{\mathsf {sig}}}({\varPsi }, {\eta }))\). Thus, the interpretation of an OLTL specification is quantitative. Intuitively, \({{\mathsf {val}}}(\theta , {\eta })\) indicates the level of satisfaction of the LTL formulas in \({\varPsi }\) in
if \({\eta }\not \models \psi _i\). The value of
\(\theta \)
in
\({\eta }\), denoted \({{\mathsf {val}}}(\theta , {\eta })\) is then \({\mathsf {f}}({{\mathsf {sig}}}({\varPsi }, {\eta }))\). Thus, the interpretation of an OLTL specification is quantitative. Intuitively, \({{\mathsf {val}}}(\theta , {\eta })\) indicates the level of satisfaction of the LTL formulas in \({\varPsi }\) in  , as determined by the priorities induced by \({\mathsf {f}}\). We note that the input of weighted LTL formulas studied in [CY98] is a special case of Objective LTL.
, as determined by the priorities induced by \({\mathsf {f}}\). We note that the input of weighted LTL formulas studied in [CY98] is a special case of Objective LTL.
Example 2
Consider a system with \(m\) buffers, of capacities  . Let \({\mathsf {full}}_{i}\), for \(1 \le i \le m\), indicate that buffer \(i\) is full. The OLTL specification \(\theta = \langle {\varPsi },{\mathsf {f}}\rangle \), with \({\varPsi }= \langle {{\mathsf {F}}\,}{\mathsf {full}}_1, {{\mathsf {F}}\,}{\mathsf {full}}_2, \ldots , {{\mathsf {F}}\,}{\mathsf {full}}_{m} \rangle \) and
. Let \({\mathsf {full}}_{i}\), for \(1 \le i \le m\), indicate that buffer \(i\) is full. The OLTL specification \(\theta = \langle {\varPsi },{\mathsf {f}}\rangle \), with \({\varPsi }= \langle {{\mathsf {F}}\,}{\mathsf {full}}_1, {{\mathsf {F}}\,}{\mathsf {full}}_2, \ldots , {{\mathsf {F}}\,}{\mathsf {full}}_{m} \rangle \) and  enables us to give different satisfaction values to the objective of filling a buffer. Note that \({{\mathsf {val}}}(\langle {\varPsi },{\mathsf {f}}\rangle , {\eta })\) in a computation \({\eta }\) is the sum of capacities of all filled buffers.
enables us to give different satisfaction values to the objective of filling a buffer. Note that \({{\mathsf {val}}}(\langle {\varPsi },{\mathsf {f}}\rangle , {\eta })\) in a computation \({\eta }\) is the sum of capacities of all filled buffers.
In the quantitative setting, the objective of Agent  is given by means of an OLTL specification
is given by means of an OLTL specification  , specifications describe the payoffs to the agents, and the objective of each agent (including the system) is to maximize his payoff. For a strategy profile \({\mathsf {P}}\), the payoff for Agent
, specifications describe the payoffs to the agents, and the objective of each agent (including the system) is to maximize his payoff. For a strategy profile \({\mathsf {P}}\), the payoff for Agent  in \({\mathsf {P}}\) is simply \({{\mathsf {val}}}(\theta _i, {\mathsf {play}}({\mathsf {P}}))\).
in \({\mathsf {P}}\) is simply \({{\mathsf {val}}}(\theta _i, {\mathsf {play}}({\mathsf {P}}))\).
In the quantitative setting, rational synthesis is an optimization problem. Here, in order to easily solve it, we provide a decision version by making use of a threshold. It is clear that the optimization version can be solved by searching for the best threshold in the decision one.
Definition 2
(Quantitative rational synthesis).
The input to the quantitative rational-strategy problem is a set
\({\mathrm {X}}\)
of atomic propositions, partitioned into
 specifications
\(\theta _{0}, \theta _{1}, \ldots , \theta _{k}\), with
specifications
\(\theta _{0}, \theta _{1}, \ldots , \theta _{k}\), with
 , and a solution concept
\(\gamma \). We distinguish between two variants of the problem:
, and a solution concept
\(\gamma \). We distinguish between two variants of the problem:
-
1.
In cooperative quantitative rational synthesis, the desired output for a given threshold \(t \in {\mathbb {N}}\) is a strategy profile \({\mathsf {P}}\) such that \({\mathsf {payoff}}_{0}({\mathsf {P}}) \ge t\) and \({\mathsf {P}}\) is in a
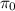 -fixed
\(\gamma \)
-equilibrium.
-fixed
\(\gamma \)
-equilibrium.
-
2.
In non-cooperative quantitative rational synthesis, the desired output for a given threshold \(t \in {\mathbb {N}}\) is a strategy
 for the system such that, for each strategy profile
\({\mathsf {P}}\)
including
for the system such that, for each strategy profile
\({\mathsf {P}}\)
including
 and being in a
and being in a
 -fixed
\(\gamma \)
-equilibrium, we have that
-fixed
\(\gamma \)
-equilibrium, we have that
 .
.
Now, we introduce some auxiliary formula that helps us to formulate also the quantitative rational-synthesis problem in Sl[ng].
For a tuple \({\varPsi }=\langle \psi _1,\ldots ,\psi _m \rangle \) of LTL formulas and a signature \(v = \{v_1, \ldots , v_m\} \in \{0, 1\}^m\), let \({{\mathsf {mask}}}({\varPsi }, v)\) be an LTL formula that characterizes computations \({\eta }\) for which \({{\mathsf {sig}}}({\varPsi },{\eta }) = v\). Thus, \({{\mathsf {mask}}}({\varPsi },v) = (\bigwedge _{i: v_i=0} \lnot \psi _i) \wedge (\bigwedge _{i: v_i = 1} \psi _i)\).
We adjust the Sl formulas \(\varPhi ^\gamma (\vec {{y}})\) described in Sect. 3 to the quantitative setting. Recall that \(\varPhi ^\gamma (\vec {{y}})\) holds iff the strategy profile assigned to \(\vec {{y}}\) is in a  -fixed \(\gamma \)-equilibrium. There, the formula is a conjunction over all agents in
-fixed \(\gamma \)-equilibrium. There, the formula is a conjunction over all agents in  , stating that Agent
, stating that Agent  does not have an incentive to change his strategy. In our quantitative setting, this means that the payoff of Agent
does not have an incentive to change his strategy. In our quantitative setting, this means that the payoff of Agent  in an alternative profile is not bigger than his payoff in \(\vec {{y}}\). For two strategy profiles, assigned to \(\vec {{y}}\) and \(\vec {{y}}'\), an Sl formula that states that Agent
in an alternative profile is not bigger than his payoff in \(\vec {{y}}\). For two strategy profiles, assigned to \(\vec {{y}}\) and \(\vec {{y}}'\), an Sl formula that states that Agent  has no incentive that the profile would change from \(\vec {{y}}\) to \(\vec {{y}}'\) can state that the signature of \({\varPsi }\) in \({\mathsf {play}}(\vec {{y}}')\) results in a payoff to Agent
has no incentive that the profile would change from \(\vec {{y}}\) to \(\vec {{y}}'\) can state that the signature of \({\varPsi }\) in \({\mathsf {play}}(\vec {{y}}')\) results in a payoff to Agent  that is smaller than his current payoff. Formally, we have that:
that is smaller than his current payoff. Formally, we have that:

We can now adjust \(\varPhi ^\gamma (\vec {{y}})\) for all the cases of solution concepts we are taking into account.
-
For the solution concept of dominant strategies, we define:
 ;
; -
For the solution concept of Nash equilibrium, we define:
 ;
; -
For the solution concept of Subgame Perfect Equilibrium, we define:
 .
.
Once we adjust \({ \varPhi }^\gamma (\vec {{y}})\) to the quantitative setting, we can use the same Sl formula used in the non-quantitative setting to state the existence of a solution to the rational synthesis problem. We have the following:
-
 ;
; -
 .
.
Theorem 3
The cooperative and non-cooperative quantitative rational-synthesis problems are 2ExpTime-complete.
Proof
We can reduce the problems to the model-checking problem of the Sl formulas \({ \varPhi }_{RS}^{\gamma }\) and \({ \varPhi }_{nonRS}^{\gamma }\), respectively. We should, however, take care when analyzing the complexity of the procedure, as the formulas \({ \varPhi }^{eq}_i(\vec {{y}}, \vec {{y}}')\), which participate in \({ \varPhi }_{RS}^{\gamma }\) and \({ \varPhi }_{nonRS}^{\gamma }\) involve a disjunction over vectors in \(\{0,1\}^{m_{i}}\), resulting in \({ \varPhi }_{nonRS}^{\gamma }\) of an exponential length.
While the above prevents us from using the doubly exponential known bound on Sl model checking for formulas of alternation depth 1 as is, it is not difficult to observe that the run time of the model-checking algorithm in [MMPV14], when applied to \({ \varPhi }_{nonRS}^\gamma \), is only doubly exponential. The reason is the fact that the inner exponent paid in the algorithm for Sl model checking is due to the blow-up in the translation of the formula to a nondeterministic Büchi automaton over words (NBW, for short). In this translation, the exponentially many disjuncts are dominated by the exponential translation of the innermost LTL to NBW. Thus, the running time of the algorithm is doubly exponential, and it can return the witnessing strategies.
Hardness in 2ExpTime follows easily from hardness in the non-quantitative setting.
5 Discussion
The understanding that synthesis corresponds to a game in which the objective of each player is to satisfy his specification calls for a mutual adoption of ideas between formal methods and game theory. In rational synthesis, introduced in [FKL10], synthesis is defined in a way that takes into an account the rationality of the agents that constitute the environment and involves and assumption that an agent cooperates with a strategy in which his objective is satisfied. Here, we extend the idea and consider also non-cooperative rational synthesis, in which agents need not cooperate with suggested strategies and may prefer different strategies that are at least as beneficial for them.
Many variants of the classical synthesis problem has been studied. It is interesting to examine the combination of the rational setting with the different variants. To start, the cooperative and non-cooperative settings can be combined into a framework in which one team of agents is competing with another team of agents, where each team is internally cooperative, but the two teams are non-cooperative. Furthermore, we plan to study rational synthesis with incomplete information. In particular, we plan to study rational synthesis with incomplete information [KV99], where agents can view only a subset of the signals that other agents output, and rational stochastic synthesis [CMJ04], which models the unpredictability of nature and involves stochastic agents that assign values to their output signals by means of a distribution function. Beyond a formulation of the richer settings, one needs a corresponding extension of strategy logic and its decision problems.
As discussed in Sect. 1, classical applications of game theory consider games with quantitative payoffs. We added a quantitative layer to LTL by introducing Objective-LTL and studying its rational synthesis. In recent years, researchers have developed more refined quantitative temporal logics, which enable a formal reasoning about the quality of systems. In particular, we plan to study rational synthesis for the multi-valued logics  [ABK13], which enables a prioritization of different satisfaction possibilities, and
[ABK13], which enables a prioritization of different satisfaction possibilities, and  [ABK14], in which discounting is used in order to reduce the satisfaction value of specifications whose eventualities are delayed. The rational synthesis problem for these logics induce a game with much richer, possibly infinitely many, profiles, making the search for a stable solution much more challenging.
[ABK14], in which discounting is used in order to reduce the satisfaction value of specifications whose eventualities are delayed. The rational synthesis problem for these logics induce a game with much richer, possibly infinitely many, profiles, making the search for a stable solution much more challenging.
Notes
- 1.
Early work on synthesis has realized that the universal quantification on the behaviors of the environment is often too restrictive. The way to address this point, however, has been by adding assumptions on the environment, which can be part of the specification (cf., [CHJ08]).
- 2.
By \({\mathsf {dom}}({\mathsf {f}})\) we denote the domain of the function \({\mathsf {f}}\).
- 3.
In particular, all \(k\)-agent turn-based games with \(\omega \)-regular objectives have Nash equilibrium [CMJ04].
References
Almagor, S., Boker, U., Kupferman, O.: Formalizing and reasoning about quality. In: Fomin, F.V., Freivalds, R., Kwiatkowska, M., Peleg, D. (eds.) ICALP 2013, Part II. LNCS, vol. 7966, pp. 15–27. Springer, Heidelberg (2013)
Almagor, S., Boker, U., Kupferman, O.: Discounting in LTL. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014 (ETAPS). LNCS, vol. 8413, pp. 424–439. Springer, Heidelberg (2014)
Alur, R., Henzinger, T.A., Kupferman, O.: Alternating-time temporal logic. JACM 49(5), 672–713 (2002)
Bloem, R., Chatterjee, K., Henzinger, T.A., Jobstmann, B.: Better Quality in Synthesis through Quantitative Objectives. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 140–156. Springer, Heidelberg (2009)
Chatterjee, K., Henzinger, T.A., Jobstmann, B.: Environment Assumptions for Synthesis. In: van Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 147–161. Springer, Heidelberg (2008)
Chatterjee, K., Henzinger, T.A., Piterman, N.: Strategy Logic. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 59–73. Springer, Heidelberg (2007)
Church, A.: Logic, arithmetics, and automata. In: Proceedings of the International Congress of Mathematicians, pp. 23–35. Institut Mittag-Leffler (1963)
Chatterjee, K., Majumdar, R., Jurdziński, M.: On nash equilibria in stochastic games. In: Marcinkowski, J., Tarlecki, A. (eds.) CSL 2004. LNCS, vol. 3210, pp. 26–40. Springer, Heidelberg (2004)
Courcoubetis, C., Yannakakis, M.: Markov decision processes and regular events. IEEE Trans. Autom. Control 43(10), 1399–1418 (1998)
Fisman, D., Kupferman, O., Lustig, Y.: Rational synthesis. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 190–204. Springer, Heidelberg (2010)
Henzinger, T.A.: From boolean to quantitative notions of correctness. In: POPL 2010, pp. 157–158. ACM (2010)
Kupferman, O., Vardi, M.Y.: Church’s problem revisited. Bull. Symbolic Logic 5(2), 245–263 (1999)
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: What makes Atl* decidable? A decidable fragment of strategy logic. In: Koutny, M., Ulidowski, I. (eds.) CONCUR 2012. LNCS, vol. 7454, pp. 193–208. Springer, Heidelberg (2012)
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: Reasoning about strategies on the model-checking problem. TOCL 15(4), 1–47 (2014). doi:10.1145/2631917
Mogavero, F., Murano, A., Vardi, M.Y.: Reasoning about strategies. In: FSTTCS 2010, LIPIcs 8, pp. 133–144 (2010)
Manna, Z., Pnueli, A.: The Temporal Logic of Reactive and Concurrent Systems - Specification. Springer, Heidelberg (1992)
Nisan, N., Ronen, A.: Algorithmic mechanism design. Games Econ. Behav. 35(1–2), 166–196 (2001)
Nisan, N., Roughgarden, T., Tardos, E., Vazirani, V.V.: Algorithmic Game Theory. Cambridge University Press, Cambridge (2007)
Osborne, M.J., Rubinstein, A.: A Course in Game Theory. MIT Press, Cambridge (1994)
Pnueli, A., Rosner, R.: On the synthesis of a reactive module. In: POPL 1989, pp. 179–190 (1989)
Selten, R.: Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 4(1), 25–55 (1975)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Kupferman, O., Perelli, G., Vardi, M.Y. (2015). Synthesis with Rational Environments. In: Bulling, N. (eds) Multi-Agent Systems. EUMAS 2014. Lecture Notes in Computer Science(), vol 8953. Springer, Cham. https://doi.org/10.1007/978-3-319-17130-2_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-17130-2_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-17129-6
Online ISBN: 978-3-319-17130-2
eBook Packages: Computer ScienceComputer Science (R0)



 if there exists a strategy
if there exists a strategy  for
for  such that
such that  ;
; if, for all strategies
if, for all strategies  for
for  , it holds that
, it holds that  ;
; .
.
 -fixed
-fixed
 for the system such that for every strategy profile
for the system such that for every strategy profile
 and is a
and is a
 -fixed
-fixed
 ,
, ,
, .
. .
. .
.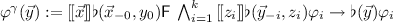 .
. ;
; .
.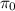 -fixed
-fixed
 for the system such that, for each strategy profile
for the system such that, for each strategy profile
 and being in a
and being in a
 -fixed
-fixed
 .
. ;
; ;
; .
. ;
; .
.