Log-Gabor Weber Descriptor for Face Recognition

Abstract

It is well recognized that image representation is the most fundamental task of the face recognition, effective and efficient image feature extraction not only has small intraclass variations and large interclass similarity but also robust to the impact of pose, illumination, expression and occlusion. This paper proposes a new local image descriptor for face recognition, named Log–Gabor Weber descriptor (LGWD). The idea of LGWD is based on the image Log-Gabor wavelet representation and the Weber local binary pattern(WLBP) features. The main motivation of the LGWD is to enhance the multiple scales and orientations Log-Gabor magnitude and phase feature by applying the WLBP coding method. Histograms extracted from the encoded magnitude and phase images are concatenated into one to form the image description finally. The experimental results on the ORL, Yale and UMIST face database verify the representation ability of our proposed descriptor.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Face recognition, as one of the most focused research topic in image processing, pattern recognition and computer vision, has been widely applied in many fields, such as access control, video surveillance and human-computer interaction etc. Although numerous approaches have been proposed and tremendous progress has been made, during the past decades, it could still not perform as well as desired under uncontrolled conditions. Therefore, how to extract robust and discriminative features is of vital importance to face recognition.

In the literature, the two-dimensional image feature extraction approaches for face recognition can be mainly divided into two categories: holistic feature methods and local feature methods. Holistic feature methods take a single feature, which is extracted from the whole face image, as image description for face recognition. Principal component analysis (PCA) [1], linear discrimination analysis (LDA) [2], independent component analysis (ICA) [3], locality preserving projection (LPP) [4] and local linear embedding (LLE) [5] are the typical ones of this kind. They can be unified into a general framework known as graph embedding [6]. However, the performance of this class of approaches depends greatly on the training set and is liable to be influenced by the expression, pose, illumination, misalignment, occlusions and so on. On the other side, local feature methods are more robust in uncontrolled conditions. They generally divide the images into several sub-images, extract the features of every one separately. Then combine the feature of each sub-image into a single feature vector by adopting the information fusion methods for further recognition or to combine the recognition result of each sub-image. Gabor filters based method is one of the most representative local feature extraction methods. It has been widely investigated owing to its superior performances in uncontrolled environments [7]. However, the properties of Gabor filters principally involve two drawbacks. One is that, in order to prevent a too high DC component, the bandwidth of a Gabor filter is typically limited to one octave. Hence, a larger number of filters are needed to cover the desired spectrum. The other is that their response is symmetrically distributed around the center frequency, which results in redundant information in the lower frequencies that could instead be devoted to capture the tails of images in the higher frequencies.

An alternative to the Gabor filter is the Log-Gabor filter. It has all the merit of Gabor filter and additionally can be constructed with arbitrary bandwidth and the bandwidth can be optimized to produce a filter with minimal spatial extent. Hence, in this work we prefer to use Log-Gabor filter to extract multiple scales and orientations image information. Log-Gabor filter based feature extraction methods have been excellently applied to image enhancement [8], segmentation [9], edge detection [10] and so on. The existing Log-Gabor transform based image representation methods are mainly categorized into three classes. The first class tries to devises a high dimensional Log-Gabor magnitude feature vector and then reduces its dimension using feature dimension reduction methods PCA and ICA [11]. The second class attempts to divide the image into small patch and its Log-Gabor magnitude mean and standard deviation are used to represent image [12]. The third class applied phase quantization to extract the phase information of the resultant Log-Gabor transform image and generate the binary face image template for recognition [13]. The local magnitude of Log-Gabor transform indicates the energetic information of the image, while the local phase is independent of the local magnitude and it can be used to distinguish between different local structures. To the best of our knowledge, the complementary effect taken by combining magnitude and phase feature simultaneously on the image feature extraction problem has not been systematically explored in the current work.

Derived from Weber’s law, Weber local binary pattern(WLBP) [14] is a powerful local descriptor and it has exhibited impressively performance than other widely used descriptors. To further fully exploit the potential rich discrimination texture information embedded in the magnitude and phase feature of the image Log-Gabor transform, in this paper, we propose an image representation scheme, namely Log-Gabor Weber Descriptor (LGWD). LGWD encodes the local pattern of Log-Gabor magnitude and phase feature by using the WLBP. Firstly, we use the Log-Gabor transform to extract the magnitude and phase feature of the image. Secondly, the WLBP descriptor is used to encode information of the magnitude feature, while the phase quantization and the local XOR coding method based WLBP descriptor is utilized to encode the phase feature. Lastly, histogram feature extracted from magnitude and phase are concatenated to one to form the final image representation feature vector; chi-square distance is adopted to measure the similarity between two different LGWD histograms. The experimental results on three benchmark face databases achieved competitive performance compared to other methods. This verified the efficiency and effectiveness of the proposed LGWD based face image representation method.

The remaining part of the paper is organized as follows. In Sect. 2, we give a brief review of related Log-Gabor transform and WLBP descriptor. Our Log-Gabor Weber Descriptor based face image representation method is described in detail in Sect. 3. Experimental results are presented and discussed in Sect. 4. Finally, Sect. 5 contains our conclusions and plans for future research work.

2 Related Works

2.1 Log-Gabor Transform

Log-Gabor filters [15, 16] have Gaussian transfer functions when viewed on the logarithmic frequency scale. Due to the singularity of log function, the two-dimensional Log-Gabor filter needs to be constructed in the frequency domain and can only be numerically constructed in the spatial domain via the inverse Fourier transform. In polar coordinates system, it comprises two components, namely the radial filter component and the angular filter component. The frequency response of the two compontents are described as following two expressions respectively.

$$\begin{aligned} G_r(r)=\exp (\frac{{\log (r/{f_0})}}{2 \cdot \sigma ^2_r}) \end{aligned}$$

(1)

$$\begin{aligned} G_\theta (\theta )=\exp (-\frac{({\theta -\theta _0})^2}{2 \cdot \sigma ^2_\theta }) \end{aligned}$$

(2)

The transfer function of the overall Log-Gabor filter is constructed by multiplying the frequency response of the two components together as

$$\begin{aligned} G(r,\theta )=G_r(r)\cdot G_\theta (\theta )=\exp (\frac{{\log (r/{f_0})}}{2 \cdot \sigma ^2_r}) \cdot \exp (-\frac{({\theta -\theta _0})^2}{2 \cdot \sigma ^2_\theta }) \end{aligned}$$

(3)

where $(r,\theta )$ represents the polar coordinates, $f_0$ is the center frequency of the filter and it is related to our current scale $n$ by $f_0=minWave \times mult^n$, in which $minWave$ is the wavelength of smallest scale filter, $mult$ is the scaling factor between successive filters. $\theta _0$ is the orientation angle of the filter, $\sigma _r$ and $\sigma _\theta$ determine the scale bandwidth and the angular bandwidth respectively. In our experiments, the spatial frequency domain is divided into $6$ orientations ($m=0,1,\ldots ,5$) for each of $4$ scales ($n=0,1,\ldots ,3$) resulting in a filter bank of $6\times 4=24$ filters. $minWave=3.0$, $mult=1.7$, $\sigma _r=0.65$. The parameters were chosen such that the Log-Gabor filter bank spanned roughly two octaves with some degree of overlap between successive filters. The primary effect of adjusting these parameters is to vary the scale of regions which respond strongly to symmetry processing - thus they were chosen to compromise between small and large sub-patterns.

The image Log-Gabor transform is implemented in the frequency domain. First, using the Fast Fourier Transform(FFT), transforms the image from the spatial domain to the frequency domain. Then, multiply fourier transformed image with the Log-Gabor frequency response, Log-Gabor transformed image is obtained by taking the inverse Fourier transform of multiplied resultant as following:

$$\begin{aligned} I_{o-m,n}=IFFT( I_F(\mu ,\nu ) \cdot G_{m,n}(\mu ,\nu ) ) \end{aligned}$$

(4)

where $I_F(\mu ,\nu )$ is the Fourier transform of the input image, $G_{m,n}(\mu ,\nu )$ is the frequency response of Log-Gabor filter with orientation $m$ and scale $n$, $I_{o-m,n}$ is the Log-Gabor transformed image with the filter $G_{m,n}$. $I_{o-m,n}$ is a complex with two parts, i.e., real part $I_{re-m,n}$ and imaginary part $I_{im-m,n}$. Based on these two parts, the magnitude and phase feature of image Log-Gabor transform can be computed by the following two formulas respectively.

$$\begin{aligned} I_{Mag}(z)=\sqrt{ I_{re-m,n}^2(z) + I_{im-m,n}^2(z) } \end{aligned}$$

(5)

$$\begin{aligned} I_{Phas}(z)=atan2( I_{re-m,n}(z) , I_{im-m,n}(z) ) \end{aligned}$$

(6)

2.2 Local Weber Descriptor

The Weber Local Descriptor(WLD) [17] is derived from Weber’s Law, which was proposed by the German physiologist Ernst Weber in 1834. The Weber’s law [18] states that the smallest change in the intensity of a stimulus capable of being perceived is proportional to the intensity of the original stimulus. This implies that the ratio of the change in the intensity of the stimulus reflects the degree of human perception of the stimulus. The WLD was proposed to characterize texture information of an image by considering the ratio of changes in pixel intensity which can be considered as stimulus information for visual perception [17].

As an improvement on the WLD, WLBP [14] contains differential excitation component and Local Binary Pattern(LBP) component. These two components are complementary to each other. Specifically, differential excitation preserves the local intensity information but omits the orientations of edges. On the contrary, LBP describes the orientations of the edges but ignore the intensity information.

Differential excitation measures the ratio of change in pixel intensity between a center pixel against its neighbors. It captures the local salient visual patterns. For example, a high differential excitation value indicates that center pixel potentially belongs to an edge or a spot as there is a strong difference in pixel intensity between center pixel and its neighbors.

In the case of $3\times 3$ neighborhoods, $x_i$ denotes the $i-th$ neighbors of central point $x_c$ and $p$ is the number of neighbors, here $p=8$. For simplicity, in this work, the differential excitation is computed following the defination of original WLD [17]:

$$\begin{aligned} \alpha =arctan( \sum _{i=0}^{p-1} \frac{x_i-x_c}{x_c} ) \end{aligned}$$

(7)

where the arctan function is applied to prevent the output from being too large and thus could partially suppress the side-effect of noise. Then $\alpha$ is linearly quantized into $T$ dominant differential excitations as following:

$$\begin{aligned} \xi _i= floor( \frac{\alpha +\pi /2}{\pi /{T}} ) \quad i=0,1,2,\cdots ,T-1 \end{aligned}$$

(8)

where $floor(x)$ is a function, which returns the largest integer less than or equal to $x$. The differential excitations $\alpha$ within $\left[ (\frac{-\pi }{2}+\frac{(i-1)\pi }{T}),(\frac{-\pi }{2}+\frac{i\pi }{T}) \right]$ are consequently quantized to $\xi _i$. In this work, we set $T=8$.

LBP operator, proposed by Ojala et al. [19], is a powerful means of texture description. Compared to the orientation component of WLD, LBP can extract more local structure information and it has been proven to be highly discriminative. With the LBP component, local micro-patterns corresponding to spots, edges and flat areas are all extracted. The formulas for computing LBP is shown as the following:

$$\begin{aligned} LBP(x_c)=\sum _{i}s(x_i-x_c)2^i \end{aligned}$$

(9)

$$\begin{aligned} s(x)= {\left\{ \begin{array}{ll} 1 &{} \text{ if } x \ge 0\\ 0 &{} \text{ if } x < 0 \\ \end{array}\right. } \end{aligned}$$

(10)

In which $s_i$ and $x^c$ are the value of neighbor and center points respectively. When 8 neighbour points are chosen, it will be produced $2^8$ different binary patterns. In order to reduce the LBP histogram dimension, we use the rotation invariant uniform mapping method proposed in [19] to reduce the number of bins from 256 to 10.

After coding the image with WLBP, a two-dimensional histogram of differential excitation and LBP of the image can be defined as

$$\begin{aligned} H_{WLD}(t,c)=\sum _{i=0}^{I-1}\sum _{j=0}^{J-1}I(\xi (x_{ij})=t)I(LBP(x_{ij})=c),\qquad c\in C, t \in T \end{aligned}$$

(11)

where $I\times J$ is the dimensionality of the image, $x_{i,j}$ is the pixel at location $(i,j)$ in the image coordinates, $T$ is the number of intervals of differential excitation, $C$ is the number of the LBP code, and

$$\begin{aligned} I(A)= {\left\{ \begin{array}{ll} 1 &{}\text{ if } A \, \mathrm{is \, true}\\ 0 &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(12)

Note that in this two-dimensional histogram, each column corresponds to a certain LBP coding, and each cell $H( t,c)$ corresponds to the frequency of a certain differential excitation interval on a LBP code. The two-dimensional histogram is further reshaped into a one-dimensional histogram by concatenating all the elements of $H(c,t)$. Therefore, the size of the final descriptor is $T \times C$.

3 The Proposed Approach

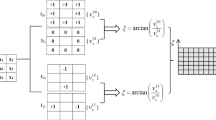
In this section, we describe the proposed LGWD, which contains two parts: Log-Gabor magnitude Weber descriptor (LGMWD) and Log-Gabor phase Weber descriptor (LGPWD). The first part encodes the variation of image Log-Gabor magnitude feature between the central and its surrounding pixels, whereas the second part encodes the variation of Log-Gabor phase feature. Figure 1 illustrates the flowchart of the proposed LGWD.

Fig. 1.

Flowchart of the proposed LGWD.

3.1 Log-Gabor Magnitude Weber Descriptor (LGMWD)

In image Log-Gabor transform, the magnitude feature is a measurement of local energetic information. For example, high magnitude usually indicates higher energetic local features (e.g., edges, lines, textures). Apply the WLBP operator over each Log-Gabor magnitude feature map to encode the variation of local energy. Suppose that LGMWD histogram extracted from magnitude image $I_{Mag-m,n}$ is $H_{M-m,n}$, the overall LGMWD of the input image is

$$\begin{aligned} H_{M}=\left[ H_{M-0,0},H_{M-0,1}, \ldots , H_{M-3,5} \right] \end{aligned}$$

(13)

3.2 Log-Gabor Phase Weber Descriptor (LGPWD)

To encode the Log-Gabor phase feature map use the WLBP operator, one difference with LGMWD is that the binary sequence of LBP component of LGPWD is generated by judging whether the phase of center pixel and its neighbours belong to the same interval(e.g., $\left[ 90^{\circ },180^{\circ } \right]$).

Briefly speaking, when compute the LBP component of LGPWD, phases are firstly quantized into different range, then local XOR coding method is applied to the quantized phases of the central pixel and each of its neighbors, and finally the resulting binary labels are concatenated together as the local pattern of the central pixel. The LBP component of LGPWD in binary and decimal form is defined as follows:

$$\begin{aligned} LBP_{m,n}(z_c)=\left[ B^P_{m,n},B^{P-1}_{m,n},\ldots ,B^{1}_{m,n} \right] _{binary} =\left[ \sum _{i=1}^P 2^{i-1} B^{i}_{m,n} \right] _{decimal} \end{aligned}$$

(14)

where $z_c$ denotes the central pixel position in the Log-Gabor phase feature map with scale $n$ and orientation $m$ , $P$ is the size of neighborhood, and $B^{i}_{m,n}$ denotes the pattern calculated between $z_c$ and its neighbor $z_i$, which is computed as follows:

$$\begin{aligned} B^{i}_{m,n}=q( \varPhi _{m,n}(z_c) ) \otimes q( \varPhi _{m,n}(z_i) ) \quad i=1,2,\ldots ,P \end{aligned}$$

(15)

where $\varPhi _{m,n}(z_c)$ denotes the phase value of pixel $z_c$, $\otimes$ denotes the local XOR coding operation, which is based on XOR operator, as defined in (16); $q(\cdot )$ denotes the quantization operator, which calculates the quantized code of phase according to the number of phase ranges $N$, as defined in (17)

$$\begin{aligned} c_1 \otimes c_2 = {\left\{ \begin{array}{ll} 0 &{}\text{ if } c_1 = c_2\\ 1 &{}\text{ otherwise } \end{array}\right. } \end{aligned}$$

(16)

$$\begin{aligned} q( \varPhi _{m,n}(\cdot ) )=floor( \frac{\varPhi _{m,n}(\cdot )}{\pi /N}) \end{aligned}$$

(17)

Apply the WLBP operator over each Log-Gabor phase map to encode the variation of local phase. Suppose that LGPWD histogram extracted from phase image $I_{Pha-m,n}$ is $H_{P-m,n}$, the overall LGPWD of the input image is

$$\begin{aligned} H_{P}=\left[ H_{P-0,0},H_{P-0,1}, \ldots , H_{P-3,5} \right] \end{aligned}$$

(18)

3.3 LGWD Image Representation and Classification

Once the multiple scales and orientations LGMWD and LGPWD histogram features are extracted from each transformed image, it is necessary to combine them in a manner to take advantage of the magnitude and phase feature. In this work, LGMWD and LGPWD histograms are simply concatenated into a single feature vector to represent the image as follows

$$\begin{aligned} H=\left[ H_{M},H_{P} \right] \end{aligned}$$

(19)

Nearest Neighbor with chi-squared distance is used for classification. Suppose $H_1$ and $H_2$ are two normalized LGWD histogram, the chi-square distance between two histograms is defined using the following form:

$$\begin{aligned} \chi ^2(H_1,H_2)=\frac{1}{2}\sum _{i}\frac{(H_{1i}-H_{2i})^2}{H_{1i}+H_{2i}} \end{aligned}$$

(20)

4 Experiments

4.1 Face Databases

Three benchmark face database: ORL face database, Yale face database and UMIST face database are used in the experiments to evaluate the performances of the proposed face image representation method.

ORL face database [20] contains 10 different images of each of 40 distinct subjects. The size of each image is $92\times 112$ pixels, with 256 grey levels per pixel. For some subjects, the images were taken at different times, varying the lighting, facial expressions and facial details.

Yale face database [2] contains 165 grayscale images of 15 individuals, 11 images per subject, where there are rich illumination, expression and occlusion variations. The size of each image is $100\times 100$ pixels, with 256 grey levels per pixel.

UMIST face database [21] consists of 564 images of 20 people. Each subject covers a range of poses from profile to frontal views and a range of race, sex and appearance. For simplicity, the pre-cropped version of the UMIST database is used in this experiment. The size of cropped image is $92\times 112$ pixels with 256 gray levels.

In a word, face images used in the experiments have a large variation in terms of pose, illumination, expression, occlusion, race and time lapse. Test on these images can have a comprehensive evaluation of the robustness of the image representation method to these factors. Figure 2 illustrates some example facial images of three subjects from three face databases.

Fig. 2.

Face image from the three databases.

For each database, we randomly partitioned it into K (K $=$ 10, 8, 5) subsets. Among the $K$ subsets, one is used as training data, and the remaining K-1 ones as validation data for testing. The final results is the average recognition accuracy of the K iterations. For equal comparison, we collect the histogram from the whole image which will result in lower recognition rate than conventional sub-image based method.

4.2 Investigating the Effectiveness of Log-Gabor Magnitude and Phase Feature

Recall from Sect. 3 that the proposed LGWD feature consists of two parts: LGMWD and LGPWD. In this section, we have performed experiments to investigate the following issues: 1) which part (i.e., LGMWD versus LGPWD parts) contributes more to face recognition performance; and 2) the feasibility for the usage of combined LGMWD and LGPWD features against a framework utilizing separately LGMWD and LGPWD features.

Table 1. Recognition rate (%) on the ORL database

Table 2. Recognition rate (%) on the yale database

Table 3. Recognition rate (%) on the UMIST database

The results are given in the Tables 1, 2 and 3. Note that for comparison purpose, the recognition rates obtained using both LBP and WLBP features are provided as baseline performances. From the Tables 1, 2 and 3, we can arrive at the following two conclusions. First, LGMWD contribute much more than the LGPWD for face recognition performance; In addition, compared with LBP and WLBP features, the recognition rates obtained for the use of LGPWD are better than both feature extraction algorithms. This demonstrates high discriminating capabilities of LGPWD. Second, the combination of both LGMWD and LGPWD parts achieves better results, compared with the cases of separately using them; this indicates that LGMWD and LGPWD parts are able to provide different information and to be mutually compensational in terms of boosting face recognition performance.

4.3 Comparisons with Other Methods

In this section, we compare the face recognition performance of our methods LGWD with those closely related representative methods, including LBP [22], WLBP, Gabor transform based WLBP(Gabor-WLBP), Log-Gabor magnitude PCA method [11], Log-Gabor statistic method [12](all the images are divided into $8\times 8$ sub-image), Log-Gabor phase template method [13] and monogenic binary coding(MBC) [23]. Experimental results of these methods on three databases are illustrated in the Tables 4, 5 and 6 respectively.

Table 4. Recognition rate (%) on the ORL database

Table 5. Recognition rate (%) on the yale database

Table 6. Recognition rate (%) on the UMIST database

From the obtained results, we have the following observations. First, WLBP outperforms LBP, the proposed LGWD outperforms benchmark methods LBP, WLBP and Gabor-WLBP. It reveals the Log-Gabor transform contains richer image descriminant information than image grayscale and Gabor transform representation. Second, LGWD outperforms three existing Log-Gabor based image representation methods, which shows that WLBP is more effective to extract the information of Log-Gabor transform than mean and standard deviation based statistic method, dimension reduction method and phase coding method. Third, LGWD outperforms monogenic signal based representation MBC. All of these observations definitly support the effectiveness of the techniques proposed in this study. And implies that it is possible to present one effective image descriptor based on Log-Gabor transform information and WLBP encoding method.

5 Conclusion

Image representation is increasingly accepted as a difficult and challenging computer vision problem. In this paper, we have investigated a novel image representation approach for face recognition, namely Log–Gabor Weber Descriptor (LGWD). The LGWD absorbs the merit of both image Log–Gabor transform information and local Weber descriptor method. Experimental results on ORL, Yale and UMIST database showed LGWD outperformed these closely related image feature extraction methods. Therefore confirmed the proposed approach can extract more discriminative information for face recognition.

Although high performance is achieved by the proposed method, it should be pointed out that our method has a drawback of high dimensionality(The dimension of our LGWD is $4 \times 6 \times 2 \times 8 \times 10=3840$). How to reduce the LGWD feature dimension or design a compact local Log-Gabor feature descriptor of better performance will be considered in our future work.