Compressive Sensing in Acoustic Imaging

Abstract

Acoustic sensing is at the heart of many applications, ranging from underwater sonar and nondestructive testing to the analysis of noise and their sources, medical imaging, and musical recording. This chapter discusses a palette of acoustic imaging scenarios where sparse regularization can be leveraged to design compressive acoustic imaging techniques. Nearfield acoustic holography (NAH) serves as a guideline to describe the general approach. By coupling the physics of vibrations and that of wave propagation in the air, NAH can be expressed as an inverse problem with a sparsity prior and addressed through sparse regularization. In turn, this can be coupled with ideas from compressive sensing to design semi-random microphone antennas, leading to improved hardware simplicity, but also to new challenges in terms of sensitivity to a precise calibration of the hardware and software scalability. Beyond NAH, this chapter shows how compressive sensing is being applied to other acoustic scenarios such as active sonar, sampling of the plenacoustic function, medical ultrasound imaging, localization of directive sources, and interpolation of plate vibration response.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

Acoustic sensing is at the heart of many applications, ranging from underwater sonar and nondestructive testing to the analysis of noise and their sources, medical imaging, and musical recording. With the emergence of compressive sensing and its successes from magnetic resonance medical imaging and optics to astrophysics, one can naturally envision new acoustic sensing techniques where the nature of the sensors is revisited jointly with the models and techniques used to extract acoustic information from raw recordings, under the auspices of sparsity.

Acoustic imaging is indeed a domain that combines a number of features calling for sparse regularization and compressive sensing:

• high dimensionality: acoustic data such as pressure fields are high-dimensional spatio-temporal objects whose complete acquisition could generate huge volumes of data and require high throughput interfaces;

• structure and correlation: sensor arrays such as acoustic antennas tend to capture correlated information;

• linear sensors: the behavior of most acoustic sensors such as microphones or hydrophones is well-approximated in standard regimes as being linear;

• linear equations: similarly, in standard regimes the wave equation as well as related PDEs that drive the physics of acoustic phenomena can be considered as linear, so the observed phenomena depend linearly on the generating sources, whether in active or passive scenarios.

These features call for the expression of acoustic imaging in the context of linear inverse problems and dimensionality reduction, where low-dimensional models can be leveraged to acquire high-dimensional objects through few, non-adaptive, linear measurements. However, the deployment of sparse regularization and compressive sensing tools in acoustic imaging raises a number of questions:

• Where does sparsity or low-dimensionality emerge from? In other words, in what domain can we expect the considered objects to be sparse?

• Can we drive the design of sensor arrays using the sparsity assumption?

• What are the practical gains in exploiting sparsity?

• Can we go as far as compressive sensing, i.e., can we leverage sparsity to voluntarily reduce the number of array elements while preserving imaging quality?

This chapter discusses a palette of acoustic imaging scenarios where recent advances and challenges in compressive acoustic imaging are highlighted.

Nearfield acoustic holography (NAH) serves as a guideline to describe the general approach. This technique, which is used to study vibrating structures producing noise in the car industry, in the aircraft industry and the railway industry (for acoustic comfort in or outside the vehicles), or in the naval industry (acoustic signature of ships), consists in imaging a vibrating structure by “listening” to the sound produced using a large set of microphones. By coupling the physics of vibrations and that of wave propagation in the air, NAH can be expressed as an inverse problem with a sparsity prior and addressed through sparse regularization. In turn, this can be coupled with ideas from compressive sensing to design new semi-random microphone antennas, the goal being primarily to sub-sample in space rather than in time, since time-sampling is mostly “free” in such an acoustic context. This leads not only to substantial practical benefits in terms of hardware simplicity, but also to new challenges in terms of sensitivity to a precise calibration of the hardware. Following the general framework described in the context of NAH in Section 6.2, we further discuss a number of acoustic scenarios:

• (a) Active sonar for underwater and air ultrasound imaging (Section 6.3.1);

• (b) Sampling of the plenacoustic function (Section 6.3.2);

• (c) Medical ultrasound imaging (Section 6.3.3);

• (d) Localization of directive sources (Section 6.4.1.1);

• (e) Interpolation of plate vibration response (Section 6.4.1.1);

6.2 Compressive Nearfield Acoustic Holography

NAH is traditionally expressed as a linear inverse problem where the goal is to estimate the vibration of the structure given the pressure field recorded in a plane at a short distance from the structure. Acoustic images are usually obtained with Tikhonov regularization techniques.

Traditional NAH typically suffers from hardware complexity (size of the microphone antenna) and the large duration of the acquisition, which are both necessary to obtain high quality images. It is however possible to circumvent these issues by adopting a compressive sensing approach to NAH. This can be achieved by coupling the choice of models (or dictionaries) adapted to vibrating plates with the design of a new shape for the microphone antenna (semi-random geometry). The reconstruction of acoustic images exploits sparse regularization techniques, for example relying on convex optimization.

Numerical and experimental results demonstrate practical benefits both in acquisition time and in hardware simplicity, while preserving a good reconstruction quality. They also highlight some important practical issues such as a sensitivity of the imaging process to the precise modeling of the hardware implementation.

6.2.1 Standard Nearfield Acoustic Holography (NAH)

The direct problem of NAH is the expression of the pressure field $p(\mathbf{r},t)$ measured at a distance z ₀ above the vibrating plate, located in the (Oxy) plane, as a function of the vibration of the plate, here described by its normal velocity field $u(\mathbf{r},t)$.

For a fixed eigenfrequency ω, the discrete formulation goes as

$$\displaystyle{ p = F^{-1}GFu = Au }$$

(6.1)

where:

• u denotes the vector of source normal velocities to be identified, discretized on a rectangular regular grid,

• p is the vector of measured pressures, also discretized in the hologram plane,

• F is the square 2-D spatial DFT operator,

• G is a known propagation operator, derived from the Green’s function of free-field acoustic propagation,

• A = F ⁻¹ GF is the measurement matrix gathering all the linear operators.

Assuming square matrices, a naive inversion of Equation (6.1) yields

$$\displaystyle{ u = A^{-1}p }$$

(6.2)

However, the operator A is badly ill-conditioned, as G expresses the propagation of so-called evanescent waves, whose amplitudes are exponentially decaying with distance. The computation of the sources using this equation is therefore very unstable, and thus requires regularization. In its most standard form called Tikhonov regularization [22], this is done by adding an extra ℓ ₂-norm penalty term and, generally, involves the solution of the following minimization problem:

$$\displaystyle{ \hat{u} =\min _{u}\left \|p - Au\right \|_{2}^{2} +\lambda \left \|Lu\right \|_{ 2}^{2} }$$

(6.3)

where L is the so-called Tikhonov matrix and λ the regularization parameter. Denoting $R_{\lambda } = (A^{T}A +\lambda L^{T}L)^{-1}A^{T}A$, the result of the Tikhonov regularization can be expressed in closed form as:

$$\displaystyle{ \hat{u} = R_{\lambda }A^{-1}p }$$

(6.4)

It should be noted that in this analysis, it is implicitly assumed that the pressure field is completely known in the hologram plane at z = z ₀, in order to “retro-propagate” the acoustic field. For high frequencies (small wavelengths) and relatively large plates, the corresponding regular spatial samples at Nyquist rates may involve several hundreds of sampling points. In practice, microphone arrays with significantly more than 100 microphones are costly and one has to repeat the experiment in different positions of the array in order to get a sufficiently fine sampling of the measurements. In a typical experiment, a 120-microphone array¹ was positioned in 16 different positions (4 positions in each x and y direction), leading to 1920 sampling locations and a lengthy measurement process. Furthermore, Tikhonov regularization here amounts to a low-pass filtering (in spatial frequencies) of the vibration wave field u, and this leads to non-negligible artifacts in the estimated field $\hat{u}$ especially at low frequencies, and near the plate boundaries.

6.2.2 Sparse modeling

In the standard approach described above, only weak assumptions are made on the field under study, namely on its spatial frequency bandwidth. In this section, we show that more precise models actually lead to a significant reduction in the number of measurements necessary for its sampling. The models here are based on the sparsity of the wave field in an appropriate dictionary $\Psi$: in matrix form one has $u = \Psi c$, where c is a sparse (or compressible) vector.

Theoretical results [25] indicate that linear combinations of plane waves provide good approximations to solutions of the Helmholtz equation on any star-shaped plate (in particular, all convex plates are star-shaped), under any type of boundary conditions. These results have been recently extended to the solutions of the Kirchhoff–Love equation for vibrations of thin isotropic homogeneous plates [7]. Mathematically, the velocity of the plate u can be approximated by a sum of a sparse number of plane waves (evanescent waves are here neglected):

$$\displaystyle{ u(\mathbf{r}) \approx \left (\sum _{j}c_{j}e^{i\mathbf{k}_{j}\cdot \mathbf{r}}\right )\mathbf{1}_{ \mathcal{S}}(\mathbf{r}) }$$

(6.5)

where $\mathbf{1}_{\mathcal{S}}(\mathbf{r})$ is the indicator function that restricts the plane waves to the domain $\mathcal{S}$ of the plate, the vectors $\mathbf{k}_{j}$ are the wavevectors of the plane waves, $\mathbf{r} = (x,y)$, and the c _j are the corresponding coefficients. To build the dictionary $\Psi$, we generate plane waves with wavevectors $\mathbf{k}_{j}$ regularly sampling the 2D Fourier plane and restrict them to the domain of the plate $\mathcal{S}$. This is actually equivalent to restricting to $\mathcal{S}$ the basis vectors of the discrete Fourier transform on a larger rectangular domain containing $\mathcal{S}$. This is illustrated in Figure 6.1.

Fig. 6.1

At a given frequency, the complex vibration pattern of the plate (here, a guitar soundboard) can be approximated as a sparse sum of plane waves Figure courtesy of F. Ollivier, UPMC

6.2.3 Sparse regularization for inverse problems

With this approximation framework, the sparsity of the coefficient vector c is now used to regularize the NAH inverse problem, which can be recast as follows: for a given set of pressure measurements p, find the sparsest set of coefficients c leading to a reconstructed wavefield consistent with the measurements:

$$\displaystyle{ \mathop{\mathrm{argmin}}\limits _{c}\|c\|_{0}\quad \text{s.t.}\quad \quad p = A\Psi c, }$$

(6.6)

This can be solved (approximately) using greedy algorithms, or, alternatively, through (noisy) ℓ ₁ relaxation, such as a basis pursuit denoising (BPDN) [10] framework:

$$\displaystyle{ \mathop{\mathrm{argmin}}\limits _{c}\|p - A\Psi c\|_{2}^{2} +\lambda \| c\|_{ 1} }$$

(6.7)

with an appropriate choice of λ. Comparing Equations (6.7) and (6.3), one can see that the main difference lies in the choice of the norm: the ℓ ₂-norm of the Tikhonov regularization spreads the energy of the solution on all decomposition coefficients c, while the ℓ ₁-norm approach of BPDN promotes sparsity. In addition, sparse regularization gives an extra degree of freedom with the choice of the dictionary $\Psi$.

6.2.4 Sensor design for compressive acquisition

Interestingly, in the sparse modeling framework, we have dropped the need to completely sample the hologram plane: one only needs the pressure measurements to have sufficient diversity to capture the different degrees of freedom involved in the measurement. Bearing in mind that reducing the number of point samples has important practical consequences, both in terms of hardware cost (less microphones and analog-to-digital converters) and acquisition time, one may then ask—in the spirit of compressive sensing—the following two questions:

• How many point measurements are really necessary?

• Can we design better sensing matrices, i.e., in practice, find a better positioning of the microphones, in order to even further reduce their number?

In the case of a signal sparse in the spatial Fourier basis, it has been shown that few point measurements in the spatial domain are sufficient to recover exactly the signal [30] and that the reconstruction is robust to noise. In acoustic experiments, the measurements are not strictly point measurements, not only because of the finite size of the microphones membrane, but also due to the acoustic propagation: each microphone gathers information about the whole vibration, although with a higher weight for the sources nearby. The theory suggests that an array with randomly placed sensors is a good choice of measurement scheme: in conjunction with sparse reconstruction principles, random microphone arrays perform better than regular arrays, as the measurement subspace becomes less coherent with the sparse signal subset (and therefore each measurement / microphone carries more global information about the whole experiment).

However, uniformly distributed random arrays are difficult to build for practical reasons (microphone mounts); therefore, there is the additional constraint to use an array that can be built using several (here, 10) straight bars, each of them holding 12 microphones. Extensive numerical simulations have shown that a good array design is obtained by bars that are tilted with respect to the axis, with small random angles, and microphones placed randomly with a uniform distribution along each bar. This is illustrated in Figure 6.2.

Fig. 6.2

Picture of the random array for compressive NAH. The microphones are placed at the tip of the small vertical rods, randomly placed along the ten horizontal bars. Part of the rectangular plate under study can be seen below the array. Picture courtesy of F. Ollivier, UPMC

6.2.5 Practical benefits and sensitivity to hardware implementation

Figure 6.3 shows some results of the wave field reconstruction on two different plates—using the standard NAH technique and the compressive measurements presented above—at different frequencies and number of measurements. It can be shown that, with a single snapshot, the random antenna (120 microphones) has similar performance than the dense grid of 1920 measurements (120 microphones, 16 snapshots) required for Tikhonov inversion. For some plate geometries, the number of microphones can be even further reduced, down to about 40 in the case of a rectangular plate. Furthermore, the low-frequency artifacts that were observed are no more present: the dictionary can natively model the discontinuities of the wave field at the plate boundaries.

Fig. 6.3

Comparative results of NAH. Columns (b) and (c) are for standard NAH, at 1920 and 120 microphones, respectively. Columns (d) and (e) are for the sparse modeling framework, with 120 measurements, in a regular and random configuration, respectively. The number C represents the normalized cross-correlation with the reference measurements (column (a), obtained with laser velocimetry). Figure adapted from [9]

However, using such a random array raises its share of difficulties too. One of them is that, in order to construct the propagation operator G, one has to know exactly the position of each sensor [8]—in practice this involves significantly more care than in the regular array case. Secondly, compressive sensing is much more sensitive than ℓ ₂-based methods to sensor calibration issues: it can be shown that even what would be considered a benign mismatch in sensor gain (typically few dB of error in gain) can severely impede the sparse reconstruction [5, 17].

To summarize what we have learnt from this study on NAH, applying compressive sensing to a real-world inverse problem involves a number of key components:

• sparsity, that here emerges from the physics of the problem. Taking sparsity into account in the inverse problem formulation may already produce some significant performance gains, at the cost of increased computation;

• measurements, that can be designed to optimally leverage on sparsity, although there are usually strong physical constraints in these measurements—in particular, completely random measurements as often used in theoretical studies of compressive sensing are almost never met in practice;

• pitfalls, that are often encountered, not only in terms of computational complexity, but also the sensitivity to the knowledge of the whole measurement system.

6.3 Acoustic imaging scenarios

Compressive NAH illustrates the potential of acoustic compressive sensing, as well as its main challenges. As we will now illustrate on a number of other scenarios, many acoustic imaging problems can be seen as linear inverse problems. While these are traditionally addressed with linear techniques (such as beamforming and matched filtering), it is often possible to exploit simple physical models to identify a domain where the considered objects—which seem intrinsically high-dimensional—are in fact rather sparse or low-dimensional, in the sense that they can be described with few parameters. State-of-the-art sparse regularization algorithms can therefore be leveraged to replace standard linear inversion. They can lead to improved resolution with the same acquisition hardware, but sometimes raise issues in terms of the computational resources they demand.

In all the scenarios considered below, it is even possible to go one step further than sparse regularization by designing new “pseudo-random” acquisition hardware, in the spirit of compressive sensing. For example, new semi-random acoustic antennas can be proposed and manufactured for both air acoustic imaging (vibrating plates, room acoustics) and sonar. By combining these antennas with the proposed sparse models, acoustic imaging techniques can be designed that improve the image quality and/or reduce the acquisition time and the number of sensors. This raises two main challenges. First, it shifts the complexity from hardware to software since the numerical reconstruction algorithms can be particularly expensive when the objects to reconstruct are high-dimensional. Second, pseudo-random sensor arrays come with a price: the precise calibration of the sensors’ response and position has been identified as a key problem to which sparse reconstruction algorithms are particularly sensitive, which opens new research perspectives around blind calibration or “autofocus” techniques.

6.3.1 Active sonar (scenario a)

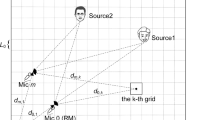
Active sonar is an air or underwater ultrasound imaging scenario in which the image of the scattering objects is obtained by modeling the echoes. An emitting antenna (appearing in yellow on the left of Figure 6.4) first generates a signal sequence called a ping which is backscattered by the objects, and the back-propagated signal is then recorded by a receiving antenna. Several pings with different emitted signals are generated one after the other. The set of recordings is finally processed to obtain an image of the scene.

Fig. 6.4

Active sonar: 3D imaging of a spatially sparse scene composed of a few scattering objects in air or water. A wheel-shaped target is placed in a tank filled with water and imaged by means of two perpendicular arrays of emitting and receiving hydrophones (left). After discretization, it is modeled as a set of point scatterers included in a limited region of interest so as to make the sparse recovery tractable (right). Picture courtesy of J. Marchal, UPMC

The design of an active sonar system depends on a number of features including the number of transducers in the emission and reception antennas, the directivity of the transducers, the geometry of the antennas, the emission sequences, and the imaging algorithm.

6.3.1.1 Problem formulation

The region of interest in the 3D space is discretized into voxels indexed by k. The sample $m_{\mathit{npj}} \in \mathbb{C}$ recorded at (discrete) time n, ping p and receiver j is stored in a multidimensional array $m \triangleq \left [m_{\mathit{npj}}\right ]_{\mathit{npj}}$ which is modeled as the sum of the contribution of all the scattered signals:

$$\displaystyle\begin{array}{rcl} m =\sum \limits _{k}c_{k}\psi _{k}& &{}\end{array}$$

(6.8)

where $c_{k} \in \mathbb{C}$ is the unknown omnidirectional scattering coefficient at voxel $k$ and $\psi _{k} \triangleq \left [\psi _{k}\left (n,p,j\right )\right ]_{\mathit{npj}}$ is the known 3D array that models the synthesis of the recorded signal when the emission is scattered at voxel k. More precisely, we have

$$\displaystyle{\psi _{k}\left (n,p,j\right ) =\sum \limits _{i}e_{\mathit{pi}}\left (n/f_{s} -\tau _{\mathit{ik}} -\tau _{\mathit{kj}}\right )}$$

where e _pi is the emission signal at ping p and emitter i, f _s is the sampling frequency, and τ _ik and τ _kj are the propagation delays from emitter i to voxel k and from voxel k to receiver j, respectively.

The objective is to estimate c _k for each k from the recording m and the known atoms ψ _k , which only depend on the design of the sonar device and on known physical constants such as the speed of sound.

6.3.1.2 From beamforming to sparse approaches

Beamforming—or matched filtering—is a well-established principle to address active sonar imaging by estimating c _k as a linear combination of the recorded data m. It can be written as

$$\displaystyle\begin{array}{rcl} \hat{c}_{k} = \frac{\left \langle m,\psi _{k}\right \rangle } {\left \|\psi _{k}\right \|_{F}^{2}}.& &{}\end{array}$$

(6.9)

This technique is called beamforming when the emission antenna and the emission signals e _pi are designed such that the resulting emission is focusing on a controlled area at each given ping p. The estimate $\hat{c}_{k}$ also results from the formation of a beam towards a controlled area at the receiver-array level so that the intersection of the emission and reception beams is related to the direction of voxel k. A typical setting consists of linear, orthogonal emission and reception antennas that form orthogonal planar beams, so that the imaging is the result of the concatenation of 2D slices obtained at each ping.

Non-linear estimation using sparsity. A sparse assumption naturally comes from the idea that the scattering objects are supported by very few voxels, i.e., c _k  = 0 for most indices k. With a slight abuse of notation, we obtain a basic sparse estimation problem

$$\displaystyle\begin{array}{rcl} \mathop{\mathrm{argmin}}\limits _{c}\left \|c\right \|_{0}\quad \text{s.t.}\quad m = \Psi c.& &{}\end{array}$$

(6.10)

where c is a vector composed of scattering coefficients c _k for all voxels k, m is the vectorized version of the recorded data, and $\Psi$ is the known dictionary matrix, in which column k is the vectorized version of ψ _k .

Compared to beamforming, sparse approaches provide a non-linear sparse estimate by (approximately) solving (6.10). Pings are not processed independently but simultaneously, resulting in a true 3D approach instead of a combination of 2D-slice processings: this may improve the accuracy at the price of a higher computational burden. Computational issues are closely related to the size of the 3D space discretization into voxels and are a challenge in many similar contexts. First investigations with a real sonar device have been proposed in [33].

6.3.1.3 Open questions on sparse model design and related algorithms

Investigations of sparse approaches for active sonar are still in their early developmental stage. Only the setting with synthetic data [6] and preliminary considerations on models with real data [33] are available today. A number of open questions should be addressed in order to enhance the accuracy of the results and the computational complexity of the algorithms.

How to design a good dictionary? Designing a dictionary for active sonar mainly consists in choosing the number of transducers, the geometry of the antennas, the number of pings, and the emission sequences. How these parameters relate to the imaging quality is still unclear. Such knowledge would provide cues to reduce the number of sensors and the acquisition time.

Is the omnidirectional scattering model improvable? Instead of modeling the scattering in each voxel k by a scalar c _k that assumes an omnidirectional scattering, one may propose new scattering models. For instance, one may extend the concept of a scattering coefficient c _k to a vector or a matrix C _k which can model directional scattering at voxel k. Such investigations are physically motivated by arguments including near field issues or blind adaptation to imperfect calibration and lead to models with structured sparsity such as joint sparse models [12], harmonic and molecular sparse models [11, 16], or a combination of them.

Is 3D imaging tractable? Discretizing a region of interest in 3D space results in high-dimensional models. In such a context, standard estimation strategies such as convex minimization or greedy algorithms are computationally demanding [33], even for small regions of interests. A major challenge is to provide new, possibly approximate algorithms to estimate the sparse representation within a reasonable computation time under realistic imaging conditions.

6.3.2 Sampling the plenacoustic function (scenario b)

Compressive sensing principles can similarly be applied to sample the so-called plenacoustic function $\mathcal{P}$ that gathers the set of all impulse responses between any source and receiver position ($\mathbf{r}_{s}$ and $\mathbf{r}_{p}$, respectively) within a given room [1]: $\mathcal{P}(\mathbf{r}_{s},\mathbf{r}_{p},t)$, which of course depends on the room geometry and mechanical properties of boundary materials. In a linear setting—a reasonable assumption at audible sound levels—this function $\mathcal{P}$ completely characterizes the acoustics of the room. Quoting the authors of [1], one may ask: “How many microphones do we need to place in the room in order to completely reconstruct the sound field at any position in the room?” By a crude computation, sampling $\mathcal{P}$ in the whole audible range (with frequencies up to 20 kHz) seems hopeless, as one would have to be able to move source and receiver (microphone) on a 3D grid with a step size of less than 1 cm (half of the smallest wavelength), leading to more than 1 million sensor positions (or microphones) per cubic meter. However, the propagative nature of acoustic waves introduces some strong constraints on $\mathcal{P}$; it is, for instance, well known that the acoustic field within a bounded domain $\mathcal{D}$ is entirely determined by the pressure field and its normal derivative at the boundary $\partial \mathcal{D}$. This is known as Kirchhoff’s integral theorem and derives from Green’s identity. To take advantage of these constraints within a compressive sensing framework, one must find sparse models for the acoustic field p itself. Let us assume that the source is fixed in a given room; the goal is then to estimate the acoustic pressure impulse response $p(\mathbf{r},t)$ within a whole spatial domain $\mathcal{D}$, where $\mathbf{r} \in \mathcal{D}$ is the position of the receiver – by the reciprocity principle, this is equivalent to fixing the receiver and moving the source. Sparsity arises from two physically motivated, and dual, assumptions:

• A time viewpoint; for any $\mathbf{r} =\mathbf{ r}_{0}$ fixed, $p(\mathbf{r}_{0},t)$ is sparse in the beginning of the impulse responses, i.e. at t < t _mix . Indeed, the beginning of the impulse responses is characterized by a set of isolated pulses, corresponding first to the direct sound (direct wave propagation between source and receiver) and then to the so-called early echoes of the impulse bouncing on the walls (first-order reflexions bouncing on one wall and then higher order reflexions). After t _mix called mixing time, the density of echoes and their dispersion makes them impossible to isolate, the impulse response being then better characterized by a stochastic model. To take into account the spatial variations (as a function of $\mathbf{r}$), this sparsity is exploited in the framework of an image-source model: first-order reflexions may be modeled as impulses coming in direct path from a set of virtual sources located symmetrically from the (real) source with respect to the walls, assumed planar. Similarly, higher-order reflexions are caused by higher-order symmetries of these virtual sources with respect to the walls—or their spatial extension in the virtual space. Noting that the position of the virtual sources only depend on the position of the real source and the geometry of the room, the model for $p(\mathbf{r},t)$ is now written as

  $$\displaystyle{ p(\mathbf{r},t) =\sum _{ k=0}^{K}c_{ k}\frac{\delta (t -\|\mathbf{ s}_{k} -\mathbf{ r}\|)} {4\pi \|\mathbf{s}_{k} -\mathbf{ r}\|} }$$

  (6.11)

  for $\mathbf{r} \in \mathcal{D}$, $t <t_{\mathit{mix}}$, where K is the number of real and virtual sources in the ball of radius $\kappa t_{\mathit{mix}}$ around the real source, κ is the sound velocity in air (typically κ = 340 m.s⁻¹), $\mathbf{s}_{k}$ is the position of virtual source k, and c _k is the corresponding intensity—taking into account some possible attenuation at the reflexion. The denominator simply expresses the free-field geometrical attenuation, where the energy of the impulse gets evenly spread on a sphere of growing area during the propagation. In short, for t < t _mix , the plenacoustic function (for a fixed source at $\mathbf{r}_{0}$) is entirely determined by a linear combination of impulses from a sparse set of virtual sources within a finite spherical domain.

  Given some measurements (pressure signals at a number of microphones), the model is estimated by looking for a sparse number of (real and virtual) sources, whose combination optimally models the observed data. Considering the size of the problem, greedy searches are often used for this task.

  Note that this assumption of sparsity in the time domain of the impulse responses can also be exploited for the simultaneous measurement of the room impulse responses from different source locations [2], as it can be shown that this problem is equivalent to the estimation of the mixing filters in the context of convolutive source separation.

• A frequency viewpoint: At low frequencies, below the so-called Schroeder frequency f _Sch , a Fourier transform of the impulse responses shows isolated peaks that correspond to the modal response of the room. Above f _Sch , again the modal density gets too high to be able to isolate peaks with a clear physical meaning. There is therefore sparsity in the frequency domain below f _Sch , but the modes themselves have a very specific spatial distribution. Actually, for a given modal frequency f ₀, and sufficiently far from the walls to neglect evanescent waves, the mode only contains the wavelength λ = κ∕f ₀. In other words, the modes are entirely described by (infinitely many) plane waves $e^{i(\mathbf{k}\cdot \mathbf{r}-2\pi f_{0}t)}$, with the wave vector $\mathbf{k}$ of fixed modulus $\|\mathbf{k}\| = 2\pi f_{0}/\kappa$. Now, the (discretized) full spatio-temporal model is written as

  $$\displaystyle{ p(\mathbf{r},t) =\sum _{ r=1}^{R}\sum _{ p=1}^{P}c_{ r,p}e^{i({\boldsymbol k_{r,p}}\mathbf{r}-2\pi f_{r}t)} }$$

  (6.12)

  with $\|{\boldsymbol k_{r,p}}\| = 2\pi f_{r}/\kappa$, R is the number of modes (sparse in frequency, i.e. only few modal f _r are significant), P is the number of plane waves used to discretize the 3D sphere of all possible directions, and the c _r, p are the corresponding coefficients.

  Given some measurements, this model is estimated in two steps: first, the sparse set of modal frequencies is estimated, jointly across microphone signals. Then, at a given modal frequency f _r , the c _r, p coefficients are estimated by least-squares projections on the discrete set of plane waves $e^{i(\mathbf{k}\cdot \mathbf{r}-2\pi f_{0}t)}$, computed at the sensor positions.

The above-described model has been tested in real experimental conditions [23, 24], with 120 microphones distributed within a 2 × 2 × 2 m volume (with an approximately uniform distribution, as displayed in Figure 6.5), in a large room with strong reverberation. In a leave-one-out setting (model built using 119 microphone signals, tested on the remaining one), the above-described model leads to accurate interpolation of the impulse responses within the whole volume (see Figure 6.6 for an example), but with a precision significantly decreased near the edges of the volume. Actually, it was observed that this method gave poor results for extrapolation of the plenacoustic function outside the volume of interest where measurements are performed. It should be noted that a similar CS technique [34] has been used to interpolate the sound field for the reconstruction of a spatially encoded echoic sound field, as an alternative to the widely used Higher Order Ambisonics techniques.

Fig. 6.5

Microphone array used to sample the plenacoustic function. (a) Picture of the 120-microphone array in the room. The black omnidirectional source can be seen on the left. (b) Geometry of the microphone array. Blue dots indicate microphone capsules. From [24]

Fig. 6.6

Recorded impulse response at one microphone location (gray line), and interpolated impulse response (blue line) at the same location, using the time-sparse model. From [23]

NB: The method presented here only performed compressive-sensing-based interpolation on the part of the plenacoustic function where some suitable sparse model could be established: at the beginning of the response and at low frequencies. While these are here treated independently, their joint processing could likely be beneficial and will be the focus of future work, see also Chapter 5

6.3.3 Medical ultrasound (scenario c)

Ultrasonography is a widespread medical imaging method relying on the propagation of acoustic waves in the body. A wave emitted by a probe of piezoelectric transducers travels through the soft tissues and partially back-propagates to the probe again, revealing the presence of scatterers, similarly to the aforementioned scenario of underwater imaging. Classical ultrasonography uses beamforming both at emission and reception to scan slices of the targeted region of the body, providing two-dimensional images. In this imaging mode called “B-mode,” many emissions are performed successively, each time with a different beam orientation. For this reason, medical ultrasonography is known to be a very user-dependent technique, relying on the ability of the practitioner to precisely handle the probe and to mentally figure out a 3D scene of the structures visualized in 2D. A natively 3D acquisition would lessen the dependency on the echographist movements. However, it would imply the use of a matrix array of transducers, meaning a high number of elements, which cannot be activated all at the same time due to technical limitations.

The context of ultrasonography sounds like a favorable context for the deployment of compressive sensing strategies, with a spectrum of expected improvements unsurprisingly ranging from a reduction of the data flow and a decrease of the sampling rate to better image resolution. Attempts to show the feasibility of compressive sensing in this context are however very recent and still far from technological applicability [20].

6.3.3.1 Sparse modeling of the ultrasound imaging process

As in other scenarios, the first step to compressive sensing is to identify the sources of sparsity of the problem. As ultrasonography is concerned, several routes have been taken, placing the sparsity hypothesis at different stages of the ultrasonography workflow.

A first approach is to assume a sparse distribution of scatterers in the body [32, 35]. By considering that echogenecity of a very large proportion of the insonified region is zero, the raw signals m received at each probe transducers after emission of a plane wave are modeled as:

$$\displaystyle{ m = Ac,\text{ with }c\text{ sparse}. }$$

(6.13)

where the matrix A embeds the emitted signals as well as propagation effects, and c is a supposedly sparse scattering distribution (or “diffusion map”). The dimension of c is the number of voxels in the discretized space, and its estimation directly gives the reconstructed image. This is very reminiscent of the aforementioned underwater acoustics scenario. Such a sparsity hypothesis turns out to be efficient on simulated data which comply with the model but suffers from its bad representation of speckle patterns, which convey important information for practitioners.

To circumvent this issue, other authors rather suppose the sparsity of the raw received signals in some appropriate basis:

$$\displaystyle{ m =\varPsi c\text{ with }c\text{ sparse}. }$$

(6.14)

Fourier, wavelets and wave-atom bases have been used, with evidence for outperformance of the latter on signals obtained by classical pre-beamformed pulse-echo emissions [21]. After estimation of the support and coefficient $\hat{c}$, images are obtained by post-beamforming on $\hat{m} =\varPsi \hat{ c}$.

A third hypothesis places the sparsity assumption later in the process. Images y obtained from m by conventional post-beamforming are supposed to possess a sparse 2D Fourier transform [29]:

$$\displaystyle{ y = F^{-1}c\text{ with }c\text{ sparse}, }$$

(6.15)

and sparse recovery is performed in the spatial frequency domain. This third approach is designed to ease the choice of a sensing matrix that would be compatible with instrumentation constraints while remaining incoherent with the sparsity basis.

6.3.3.2 Doppler and duplex modes

Medical ultrasound scanners can also be used for visualizing the blood flow dynamically. This so-called Doppler-mode repeatedly measures the flow velocity at a given position to recover its distribution over time, by pulsing multiple times in the same directions and exploiting the Doppler effect. Doppler-mode ultrasonography can be acquired alone but is also often acquired together with the B-mode. This duplex imaging implies alternating emission modes and is traditionally obtained by halving the time devoted to each mode. Compressive sensing strategies such as random mode alternation have been shown to be efficient [31]. Doppler signals are approximately sparse in the Fourier domain, which is a favorable situation here for compressive sensing (incoherence between sensing basis and sparsity basis, technical ease of random subsampling). The “savings” from compressive sensing of Doppler signals can then be reinvested in B-mode.

6.3.3.3 Subsampling and compressive sensing strategies

Most of these early work in compressive ultrasonography validate the chosen sparse model by random removal of a certain amount of samples among all acquired, or random linear combinations of the acquired signals. Though it is a valuable step to show the feasibility of compressive sensing in this context, the shift from sparse modeling and simulated subsampling to actual compressive sensing devices remains to be done. Indeed, spatially uniform random acquisition of the raw signals is technically as costly as acquiring them all. Different subsampling masks and their practical feasibility are discussed in [29] and in particular, the possibility to completely disconnect some elements of the probe, which would reduce acquisition time and data flow (especially for 3D imaging with matrix arrays).

Reduction of the sampling rate by exploiting the specificities of the used ultrasound signals (narrowbandness and finite rate of innovation) has also been proposed through the Xampling scheme [35]. Among proposed compressive sensing strategies, this is probably the closest to hardware feasibility, but remains far from an actual 3D imaging.

6.4 Beyond sparsity

Just as with other imaging modalities, acoustic imaging can benefit from low-dimensional models that go beyond traditional dictionary-based sparse models.

6.4.1 Structured sparsity

6.4.1.1 Localization of directive sources (scenario d)

The sparse models described above can be adapted to the joint localization and characterization of sources, in terms of their directivity patterns. Indeed, in practice every acoustic source has a radiation pattern that is non-uniform in direction, and furthermore this directivity pattern is frequency-dependent. Measuring these 3D directivity patterns usually requires a lengthy measurement protocol, with a dense array of microphones at a fixed distance of the source (usually 1m or 2m). The radiation pattern is usually described as its expansion on spherical harmonics of increasing order: monopolar, dipolar, quadrupolar, etc. Restricting the expansion to a finite order L (L = 0 for monopolar only, L = 1 for monopolar and dipolar, etc.), one can write the sound field in polar coordinates $(r,\theta,\varphi )$ at wavenumber k for a source located at the origin:

$$\displaystyle{ p(kr,\theta,\varphi ) =\sum _{ l=0}^{L}\sum _{ q=-l}^{l}c_{ l}^{q}(k)h_{ l}(kr)Y _{l}^{q}(\theta,\varphi ) }$$

(6.16)

where the $Y _{l}^{q}$ are the spherical harmonic of degree l and order q, h _l the propagative Hankel functions of order l, and $c_{l}^{q}$ the corresponding coefficients.

This can be used to build a group-sparse model for the field produced by a sparse number of sources with non-uniform radiation: the sparsity in space restricts the number of active locations; for a given active location, all the coefficients of the corresponding spherical harmonic decomposition are non-zero. From a number of pressure measurements at different locations, the inverse problem amounts to finding both source location and directivity pattern. Using the group-sparse model, this can, for instance, be solved using an $\ell_{1}/\ell_{2}$ type of penalty on the set of activity coefficients (reorganized in column form for each location), or group-OMP.

The experimental results raise the interesting issue of the sampling step for the spatial locations. If the actual sources are on sampling points, or very close, the model successfully identifies the radiation pattern at least up to order L = 2 (quadrupolar). However, a source located between sampling points will appear as a linear combination of two or more sources with complex radiation coefficients: for instance, in the simplest case a dipolar source may appear as a combination of 2 neighboring monopoles in opposite phase, but more complex combinations also arise, where the solutions eventually cannot easily be given a physical interpretation. Future work would therefore have to investigate sparse optimization on continuous parameter space [13].

6.4.1.2 Interpolation of plate vibration responses (scenario e)

In the NAH case described in section 6.2, the different plane waves, spatially restricted to the domain of the plate, could be selected independently. Actually, similarly to the plenacoustic case above, there are some further constraints that can be enforced for further modeling: the set of selected wave vectors must be of fixed modulus $\|\mathbf{k}\|$. However, in plates we may not know in advance the dispersion relation, linking the temporal frequency f to the spatial wavelength λ, or equivalently to the wavenumber $\|\mathbf{k}\|$. Hence, the problem may be recast as finding the best value of $\|\mathbf{k}\|$, such that the linear combination of plane waves constrained to a given wavenumber $\|\mathbf{k}\|$ maximally fits the observed data. In [7], this principle was employed for the interpolation of impulse responses in a plate, from a set of point-like measurements obtained by laser velocimetry, randomly chosen on the plate. Results show that accurate interpolation on the whole plate was possible with a number of points significantly below the spatial Nyquist range, together with an estimation of the dispersion relation. Interestingly, similar results also held with a regular sampling of the measurement points: constraining the wave vectors to lie on a circle allows us to undo the effect of spatial aliasing.

6.4.2 Cosparsity

Some of the aforementioned sparse modeling of acoustic fields, as a pre-requisite to the deployment of a compressive sensing strategy, rely on the ability to build a dictionary of solutions (or approximate solutions) of the wave equation ruling the propagation of the target acoustic field, such as the spherical waves in Eq. (6.11) or plane waves in Eq. (6.5) and Eq. (6.12). In most cases, exact closed-form expressions of these Green’s functions do not exist, and computationally costly numerical methods have to be used. Moreover, the resulting dictionary $\Psi$ is usually dense and its size grows polynomially with dimensions, which will cause tractability issues when used in solving the corresponding optimization problem in real scale conditions.

An idea to circumvent these issues would be to find an alternative model which would not rely on “solving” the wave equation, but rather on the wave equation itself. The so-called cosparse modeling described in this section (see also Chapter 11) offers such an alternative. It also happens to have the potential to reduce the computational burden.

Let us first recall the wave equation obeyed by the (continuous) sound pressure field $p(\mathbf{r},t)$ at position $\mathbf{r}$ and time t:

$$\displaystyle{ \varDelta p(\mathbf{r},t)-\frac{1} {\kappa ^{2}} \frac{\partial ^{2}p(\mathbf{r},t)} {\partial t^{2}} = \left \{\begin{array}{@{}l@{\quad }l@{}} 0\text{, if no source at location }\mathbf{r} \quad \\ f(\mathbf{r}, t)\text{, if source at location } \mathbf{r}\quad \end{array} \right. }$$

(6.17)

where Δ is the spatial Laplacian operator and the constant κ is the sound propagation speed in the medium. This can be concisely written as $\square p(\mathbf{r},t) = f(\mathbf{r},t)$ where □ denotes the linear D’Alembertian wave operator. Discretizing the signal in time and space, as well as the operator □ which becomes a matrix denoted Ω (augmented with the initial and boundary conditions, so as to define a determined system of linear equations), and finally assuming that the number of sound sources is small compared to the size of the spatial domain, reconstruction of the pressure field p from measurements y can be expressed as the following optimization problem:

$$\displaystyle{ \min _{p}\|\varOmega p\|_{0}\text{ s.t. }\|y - Ap\|_{2} \leq \epsilon }$$

(6.18)

The measurement matrix A is obtained by selecting, in the identity matrix, the rows corresponding to the microphone locations. This formulation can be directly compared to the counterpart sparse optimization, which consisted in minimizing the number of non-zeros in the expansion coefficients c such that $p = \Psi c$. Here, they have been replaced by the sparse product z = Ω p. It is easy to see that in this special case, with $\Psi =\varOmega ^{-1}$, both problems are equivalent². However, while the dictionary $\Psi$ is dense, the operator Ω obtained by a first-order finite-difference-method (FDM) discretization is extremely sparse: Ω has exactly 7 non-zero coefficients per row, no matter the global dimension of the problem, and is thus easy and cheap to compute, store, and apply in a matrix product.

Most of the well-known sparse recovery algorithms can be adapted to fit the cosparse recovery problem: greedy schemes [15, 27], convex relaxation [18, 26]. Thanks to the strong structural properties of sparsity and shift-invariance of Ω, they can be implemented in very efficient ways.

Solving the cosparse problem from a set of incomplete measurements $y = \mathit{Ap}$ produces different levels of outputs, that can be used in different applicative scenarios:

• Source localization: determining the support (locations of nonzero entries in the product Ω p) gives straightforwardly an estimation of the source locations.

• Source identification: once $\hat{p}$ is determined, the product $\varOmega \hat{p}$ gives estimations of the source signals $f(\mathbf{r},t)$ at their estimated locations.

• Field reconstruction: $\hat{p}$ is itself an estimation of the sound pressure field in the whole domain $\mathcal{D}$ and at all instants.

Localization has been the main target of early work in this domain [18, 28]. An illustration of such a scenario, taken from [19], is given in Figure 6.7. Cosparse modeling has thus been proven efficient in situations where typical geometric approaches fail and where the now traditional sparse synthesis approach fails to scale up computationally speaking.

Fig. 6.7

A simulated compressive source localization and identification scenario. (a) 10 microphones (in black) and s sound sources (in white) are placed opposite sides of an inner wall in a shoebox room. A “door” of w pixels is open in the wall. (b) Varying the size of the inner wall and the number of sources, the empirical probability of correct source localization is very high in many situations. (c) The sound pressure field p is estimated with a relatively satisfying signal-to-noise ratio ($\text{SNR}_{p} = 20\log _{10}\|p\|_{2}/\|p -\hat{ p}\|_{2}$) in these conditions. This experiment scales up in 3D, while the equivalent sparse synthesis solver becomes intractable. From [19]

As for source and field reconstruction, more investigations remain to be done on this emerging approach. Some other potentialities of the cosparse modeling can be envisioned. The capability to, at least partially, learn an operator Ω that would be known almost everywhere (but not at all boundaries for instance), or known only up to a physical parameter (such as the sound velocity κ), also contributes to make this modeling particularly attractive.

6.5 Conclusion / discussion

Acoustics offers a large playground where compressive sensing can efficiently address many imaging tasks. A non-exhaustive sample of such scenarios has been introduced in this chapter. We hope these are representative enough to enable the reader to connect the acoustic world to the main principles of compressive sensing, and to make his/her mind on how advances in compressive sensing may disseminate in acoustics.

Some good news for applying the theory of compressive sensing to acoustics is that, in many scenarios, a sparsity assumption naturally emerges from physics: a sparse distribution may be assumed for objects in space, for plane waves in a domain of interest, for early echoes in time, or peaks in modal responses. A cosparse modeling also happens to relate to the wave equation.

Another noticeable specificity of acoustic signal processing is that conventional acquisition devices (point microphones, sensing in the time domain) provide measures that are “naturally” incoherent with the sparsity basis of acoustic waves (Fourier basis), leading to a favorable wedding between acoustic applications and compressive sensing theory. In a way, many traditional sound acquisition and processing tasks, such as underdetermined sound source separation or other common settings with few microphones can be seen as ancestors of compressive sensing, even if not explicitly stated as such.

These two elements give the most encouraging signs towards the actual development of compressive sensing in its now well-established meaning. Thus, one can now hope to use compressive sensing in acoustics with several goals in mind:

• reducing the cost of hardware by using less sensors;

• reducing the data complexity, including acquisition time, data flow, and storage;

• improving the accuracy of the results by opening the door to super resolution.

In practice, the specific constraints of each application – e.g., real-time processing—often tell which of those promises from the theory of compressive sensing can be achieved.

Now that it is possible to handle high-dimensional objects and to image 3D-regions, important questions remain open about the actual devices to be designed.

First, the theory of compressive sensing generally assumes that the sensing device is perfectly known. In practice, some parameters may vary and have to be estimated. They include the calibration of sensor gain, phase, and positions for instance. This is even more challenging for large arrays with many cheap sensors that suffer from a large variability in sensor characteristics. Preliminary studies have shown that sparse regularization can help to adapt the sensing matrix in the case of unknown gains and phase [3–5].

The design of new sparse models is another challenge, e.g., to model the directivity of sensors or of scattering material using structured sparsity, or by studying how it can relate to the speckle distribution. Compressive acoustic imaging also calls for new views on the interplay between discrete and continuous signal processing, especially to handle the challenges of 3D imaging of large regions of interest.

Eventually, the last major missing step towards implementation of real-life compressive sensing acoustic device is now, in many scenarios, the possibility to build or adapt hardware to compressive sensing requirements, such as randomness in a subsampling scheme or incoherence with the sparsity basis, while actually getting some gain compared to conventional state of the art. Feasibility of compressive sensing is often shown by simulating random subsampling, keeping a certain percentage of all collected samples and exhibiting satisfying signal reconstruction from those samples. Hardware which performs such random subsampling can be simply as costly and complicated to build as conventional hardware: acquiring more samples than needed to finally drop unneeded samples is obviously a suboptimal strategy to reduce acquisition time and cost. The shift from theory and proofs of concept to actual devices with practical gains, shown here in the case of nearfield acoustic holography, is now one of the next main challenges in many other acoustic compressive sensing scenarios.