Abstract
In an unconditionally secure Distributed Oblivious Transfer (DOT) protocol, a receiver contacts at least \(k\) servers to obtain one of the \(n\) secrets held by a sender. Once the protocol has been executed, the sender does not know which secret was chosen by the receiver and the receiver has not gained information on the secrets she did not choose. In practical applications, the probability distribution of the secrets may not be uniform, e.g., when DOT protocols are used in auctions, some bids may be more probable than others.
In this kind of scenario, we show that the claim “a party cannot obtain more than a linear combination of secrets” is incorrect; depending on the probability distribution of the secrets, some existing polynomial interpolation-based DOT protocols allow a cheating receiver, or a curious server, who has obtained a linear combination of the secrets to determine all the secrets.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Cryptographic protocol
- Distributed Oblivious Transfer
- Linear combination of secrets
- Probability distribution
- Unconditional security
1 Introduction
Unconditionally secure Distributed Oblivious Transfer (DOT) protocols allow a receiver to obtain one of the \(n\) secrets held by a sender (see for example [3, 8, 9]), like Oblivious Transfer (OT) protocols. But, unlike in OT protocols, the sender and the receiver do not directly interact with each other; the sender distributes information on his secrets to \(m\) servers and the receiver contacts \(k\) of them to collect enough data to determine the secret she wishes to obtain.
The security level of a DOT protocol is characterized by the threshold parameter \(k\), corresponding to the minimum number of servers the receiver has to interact with, to obtain the chosen secret. The protocol itself is composed of two phases. In a first phase (the set-up phase), the sender distributes parts — called shares — of the secrets to the servers and does not intervene in the rest of the protocol. In a second phase (the transfer phase), the receiver selects the index of a secret, sends shares of this index to \(t\) servers (\(k \le t \le m\)) and receives back \(t\) shares allowing her to reconstruct the chosen secret. The security of a DOT protocol may be assessed thanks to the following informal security conditions based on definitions given by Blundo, D’Arco, De Santis and Stinson [2, 3]:
-
\(C_{1}.\) Correctness – The receiver is able to determine the chosen secret once she has received information from \(t\) contacted servers (\(t \ge k\)).
-
\(C_{2}.\) Receiver’s privacy – A coalition of up to \(\lambda _{R}\) servers (\(1 \le \lambda _{R} \le k - 1\)) cannot obtain any information on the choice of the receiver.
-
\(C_{3}.\) Sender’s privacy with respect to \(\lambda _{S}\) servers and the receiver – A coalition of up to \(\lambda _{S}\) servers (\(1 \le \lambda _{S} \le k - 1\)) with the receiver does not obtain any information about the secrets before the protocol is executed.
-
\(C_{4}.\) Sender’s privacy with respect to a “greedy” receiver – Once the protocol has been executed, a coalition of up to \(\lambda _{C}\) dishonest servers (\(0 \le \lambda _{C} \le k - 1\)) and the receiver does not obtain any information about secrets which were not chosen by the receiver. This security condition may be decomposed into two parts; Given the transcript of the interaction with \(t\) servers (\(t \ge k\)),
-
\(C_{4.1}.\) The receiver does not obtain any information about secrets she did not choose (\(\lambda _{C} = 0\)).
-
\(C_{4.2}.\) A coalition of up to \(\lambda _{C}\) dishonest servers and the receiver does not obtain any information about secrets which were not chosen by the receiver (\(\lambda _{C} > 0\)).
-
Blundo et al. [3] define a DOT protocol as private if the following security conditions are satisfied: \(C_{1}\), for \(t = k\), \(C_{2}\), for \(\lambda _{R} = k - 1\), \(C_{3}\), for \(\lambda _{S} = k - 1\) and \(C_{4.1}\). A DOT protocol is defined as strongly private if it is private and if condition \(C_{4.2}\) is satisfied for \(\lambda _{C} = k - 1\). Blundo et al. have shown that one-round polynomial interpolation-based DOT protocols cannot reach strong privacy, i.e., if \(t = k\) and \(\lambda _{R} = k - 1\), then condition \(C_{4.2}\) cannot be satisfied for \(\lambda _{C} = k - 1\) (a round is a set of consistent requests/responses exchanged between the receiver and \(t\) servers in the transfer phase). More generally, Nikov, Nikova, Preneel and Vandewalle [9] have demonstrated that the relation \(\lambda _{R} + \lambda _{C} < k\) needs to be satisfied for conditions \(C_{2}\) and \(C_{4.2}\) to be guaranteed.
In their OT protocol allowing a receiver to obtain one of the \(n\) secrets held by a sender, Brassard, Crépeau and Robert [4] note that it should be impossible for the receiver to gain joint information on the secrets held by the sender. This remark is the consequence that, in classical cryptography, shifting the letters of an English message thanks to a secret word is not secure. For example, an adversary can break the Vigenère cryptosystem, which basically produces a cryptogram by shifting the letters of a message according to a secret key, in plain English too. The non-uniform repartition of letters in the original message, and in the key for some variants of Vigenère’s cryptosystem, allows an adversary to retrieve both the original text and the key from a cryptogram (index of coincidence technique [6] and Kasiski method [7]). Aware of this weakness, OT and DOT protocols’ designers have taken a great care to construct protocols where receivers cannot learn a linear combination of the secrets held by a sender.
In some instances, where the secrets are elements randomly selected in a finite field, the precaution is useless. But when the probability distribution of each secret is not uniform (like for letters in English messages), the control is essential.
In some polynomial interpolation-based DOT protocols, e.g. [3, 8], it is claimed that a party “cannot learn more than a linear combination of secrets”. In this paper, we show that such claims are incorrect. Overall, the knowledge of a linear combination of secrets combined with the knowledge of the probability distributions of the same secrets may lead to the knowledge of the secrets themselves. In other words, if a curious server obtains a linear combination of secrets, security condition \(C_{3}\) cannot be satisfied and similarly, if a curious or malicious receiver obtains a linear combination of secrets, security condition \(C_{4.1}\) cannot be satisfied. In addition, we demonstrate that in Blundo et al.’s sparse polynomial interpolation-based DOT protocol, the two techniques preventing the servers and the receiver from learning linear combinations of secrets make the protocol insecure (in spite of Blundo et al.’s claim, security condition \(C_{4.1}\) is not satisfied); indeed, only one of the two techniques should be applied to guarantee the security of the protocol.
The organization of the paper is as follows. In Sect. 2 we introduce a few notations and show that the combined knowledge of the probability distributions of secrets and of a linear combination of these secrets may lead to the knowledge of all of them. Then, in Sect. 3, we shortly describe the general form of polynomial interpolation-based DOT protocols and show how in these protocols a receiver is able to obtain a linear combination of secrets. Section 4 is devoted to the analysis of some protocols [1, 2, 8, 9] in the light of the previous section. In Sect. 5, we show that even Blundo et al.’s sparse polynomial interpolation-based DOT protocol [3], designed to protect the sender’s privacy against a malicious receiver in presence of honest servers, does not satisfy security condition \(C_{4.1}\). Our conclusion follows in Sect. 6.
2 Preliminaries
2.1 Notations and Definitions
The settings of the different DOT protocols described in this paper encompass a sender \(\mathcal{S}\) who owns \(n\) secrets \(\omega _{1}\), \(\omega _{2},\ldots ,\omega _{n}\) (\(n > 1\)), a receiver \(\mathcal{R}\) who wishes to learn a secret \(\omega _{\sigma }\), and \(m\) servers \(S_{j}\) (\(j \in \mathcal{I}_{m}\) where \(\mathcal{I}_{m} \subset \mathbb {N}\) is a set of \(m \ge 2\) indices).
The protocols require the availability of private communication channels between the sender and the servers and between the receiver and the servers. We assume that these communication channels are secure, i.e., any party is unable to eavesdrop on them and they guarantee that communications cannot be tampered with.
All operations are executed in a finite field \(\mathbb {K}= \mathbb {F}_{p}\) (\(p\) prime, \(p > 2\)). We assume that \(p > \max ( n, \omega _{1}, \omega _{2},\ldots ,\omega _{n}, m )\). By an abuse of language, a polynomial and its corresponding polynomial function will not be differentiated. We denote \(\mathbb {K}^{*}\) the set \(\mathbb {K}\setminus \{\, 0 \,\}\), \([n]\) the set of natural numbers (or elements of the prime finite field \(\mathbb {K}\)) \(\{\, 1, 2,\ldots ,n \,\}\), and \(\delta ^{j}_{i}\) the Kronecker’s symbol, equal to \(0\) if \(i \ne j\) and to \(1\) if \(i = j\). If \(\varvec{u} = \left( \, u_{1}, u_{2},\ldots , u_{n} \,\right) \) and \(\varvec{v} = \left( \, v_{1}, v_{2},\ldots ,v_{n} \,\right) \) are two \(n\)-tuples of elements of \(\mathbb {K}\), we define  .
.
We also formally define a quasi-random polynomial.
Definition 1
If \(( \mathbb {K}[X], +, \times )\) is the ring of polynomials over \(\mathbb {K}\) and \(( \mathbb {K}_{d}[X], + )\) the additive group of polynomials of degree at most \(d\) over \(\mathbb {K}\), we say that a polynomial \(F = \sum _{i = 0}^{d}{f_{i}X^{i}}\) of \(\mathbb {K}_{d}[X]\) is quasi-random, if the coefficients \(f_{i}\) \((1 \le i \le d)\) are randomly selected in \(\mathbb {K}\) and the constant term \(f_{0} \in \mathbb {K}\) has a predefined value.
In addition, we denote \(p_{\omega }\) the probability mass function associated with the secret \(\omega \) taken in the finite field \(\mathbb {K}\).
2.2 Linear Combination of Two Secrets
In some DOT protocols, e.g. [3, 8], it is claimed that the receiver cannot learn more than a linear combination of secrets. Actually, the knowledge of a linear combination of secrets combined with the knowledge of the probability distributions of the same secrets may lead to the knowledge of the secrets themselves, as shown in the following basic example.
Example 1
Let \(\omega _{1}\) and \(\omega _{2}\) be two secrets in the prime finite field \(\mathbb {K}= \mathbb {F}_{11}\) with the probability distributions:
We assume that a party is able to determine, for instance, the linear combination \(\ell = \omega _{2} - \omega _{1}\). From the probability distributions of the secrets, the only possible values of \(\ell \) are:
In this scenario where all the potential values of \(\ell \) are different, the party just has to compare \(\ell \) with the values 0, 3, 10 and 2 to determine the secrets \(\omega _{1}\) and \(\omega _{2}\).
2.3 Linear Combination of Secrets
More generally, we have
Lemma 1
Let \(\omega _{1}, \omega _{2},\ldots ,\omega _{n}\) be \(n\) secrets in \(\mathbb {K}= \mathbb {F}_{p}\) (\(p\) prime) and \(s\) be the integer such that \(2^{s} \le p < 2^{s + 1}\). If \(n \le s\) and \(\ell \in \mathcal{V}= \left\{ \, 0, 1,\ldots , 2^{n} - 1 \,\right\} \subset \mathbb {K}\), there exists probability distributions \(p_{\omega _{1}},p_{\omega _{2}},\ldots ,p_{\omega _{n}}\) such that one and only one \(n\)-tuple of secrets satisfies the linear combination \(\ell = \omega _{1} + \omega _{2} +\ldots + \omega _{n}\).
Proof
Given an element \(\ell \) of \(\mathbb {K}\) such that \(0 \le \ell \le 2^{n} - 1\), we just have to exhibit \(n\) probability distributions \(p_{\omega _{1}}, p_{\omega _{2}},\ldots , p_{\omega _{n}}\), such that only one \(n\)-tuple \(\left( \,\omega _{1}, \omega _{2},\ldots , \omega _{n} \,\right) \) allows the linear combination \(\ell = \omega _{1} + \omega _{2} +\ldots + \omega _{n}\) to be satisfied.
We define the probability distribution of the secret \(\omega _{i}\) (\(1 \le i \le n\)) by
If \(\ell \in \mathcal{V}\), let \(B^{\ell } = b^{\ell }_{n - 1}b^{\ell }_{n - 2}\ldots b^{\ell }_{1}b^{\ell }_{0}\) be the unique binary representation of \(\ell \). The \(n\)-tuple \(\left( \, b^{\ell }_{n - 1}, b^{\ell }_{n - 2},\ldots ,b^{\ell }_{1}, b^{\ell }_{0} \,\right) \) is denoted \(\beta ^{\ell }\) and the set \(\mathcal{U}\) is defined by \(\mathcal{U}= \{\, \beta ^{0}, \beta ^{1},\ldots ,\beta ^{2^{n} - 1} \,\}\). We also define the function
The sets \(\mathcal{U}\) and \(\mathcal{V}\) have the same size (\(2^{n}\) elements) and the function \(f\) is injective, since every element \(\ell \in \mathcal{V}\) has a unique binary representation; therefore \(f\) is bijective. We conclude that for any element \(\ell \in \mathcal{V}\), there exist a unique \(n\)-tuple \(\left( \, b^{\ell }_{n - 1}, b^{\ell }_{n - 2},\ldots ,b^{\ell }_{1}, b^{\ell }_{0} \,\right) \) where \(b^{(\ell )}_{i} \in \{\, 0, 1 \,\}\) for \(i = 0, 1,\ldots , n - 1\) such that \(\ell \) is written as a linear combination of the secrets \(\omega _{1}, \omega _{2},\ldots , \omega _{n}\):
We conclude that \(\omega _{i} = b^{\ell }_{i - 1} \times 2^{i - 1}\) for \(i = 1, 2,\ldots , n\). \(\square \)
Using this basic result, we review in the next section some polynomial interpolation-based DOT protocols and show that their security is weaker than expected.
3 Polynomial Interpolation-Based DOT Protocols
Each of the existing unconditional secure polynomial interpolation-based DOT protocols, for example [1–3, 5, 8, 9], follows the same principle.
-
Before the protocol is executed, some details are made public: the number \(n\) of secrets, the threshold parameter \(k\), the sender’s privacy parameter \(\lambda _{S}\), the sender’s strong privacy parameter \(\lambda _{C}\), the receiver’s privacy parameter \(\lambda _{R}\), the meaning of each secret \(\omega _{i}\) (\(1 \le i \le n\)), the joint probability \(p_{\omega _{1}, \omega _{2},\ldots ,\omega _{n}}\) of the secrets, the encoding parameter \(e\) (\(e > 0\)), the encoding function \(E\) where \(E:[n] \longrightarrow \mathbb {K}^{e}\) encodes the index chosen by the receiver, the hiding parameter \(N\) corresponding to the number of monomials of the hiding polynomial \(Q\) (see set-up phase below) before reduction and \(N\) \(e\)-variate polynomials \(V_{i}\) (\(1 \le i \le N\)) of \(\mathbb {K}[Y_{1}, Y_{2},\ldots , Y_{e}]\). The degree of the multivariate polynomial \(V_{i}\) is \(v_{i}\); it is the highest degree of the monomials of \(V_{i}\), assuming that the degree of a monomial is the sum of the degrees of its variables.
-
In the set-up phase, the sender \(\mathcal{S}\) generates \(N\) quasi-random polynomials \(U_{i}\) (\(1 \le i \le N\)) of \(\mathbb {K}_{u_{i}}[X]\) (\(u_{i} \le k - 1\)) such that \(\sum _{i = 1}^{N}U_{i}( 0 )V_{i}( E( j ) ) = \omega _{j}\), for \(j = 1, 2,\ldots , n\). The free coefficient of \(U_{i}\) is \(U_{i}( 0 ) = a_{i, 0} + \sum _{j = 1}^{n}{a_{i, j}\omega _{j}}\) where the coefficients \(a_{i, j}\) (\(0 \le j \le n\)) are randomly selected in \(\mathbb {K}\). Then, \(\mathcal{S}\) builds an (\(e + 1\))-variate polynomial:
$$ Q( x, y_{1}, y_{2},\ldots , y_{e} ) = \sum _{i = 1}^{N}{U_{i}(x) \times V_{i}( y_{1}, y_{2},\ldots , y_{e} )}, $$and distributes the \(N\)-tuple \(\varvec{u}_{j} = \left( \, U_{1}( j ), U_{2}(j),\ldots , U_{N}( j ) \,\right) \) to the server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)).
-
In the oblivious transfer phase, the receiver \(\mathcal{R}\) who wishes to obtain the secret \(\omega _{\sigma }\) prepares an \(e\)-tuple \(E( \sigma ) = \left( \, q_{1}, q_{2},\ldots , q_{e} \,\right) \) as well as \(e\) quasi-random polynomial \(Z_{i}\) (\(1 \le i \le e\)) of \(\mathbb {K}_{\lambda _{R}}[X]\) (\(\lambda _{R} \le k - 1\)) such that \(Z_{i}( 0 ) = q_{i}\). Then, \(\mathcal{R}\) selects a subset \(\mathcal{I}_{t} \subset \mathcal{I}_{m}\) of \(t\) indices (\(k \le t \le m\)) and sends to each server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)) the request \(\varvec{z}_{j} = \left( \, Z_{1}( j ), Z_{2}(j),\ldots , Z_{e}( j ) \,\right) \). On reception of \(\varvec{z}_{j}\), \(S_{j}\) calculates and returns
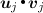 to \(\mathcal{R}\), where \(\varvec{v}_{j} = \left( \, V_{1}(\varvec{z}_{j}), V_{2}(\varvec{z}_{j}),\ldots , V_{N}( \varvec{z}_{j} ) \,\right) \).
to \(\mathcal{R}\), where \(\varvec{v}_{j} = \left( \, V_{1}(\varvec{z}_{j}), V_{2}(\varvec{z}_{j}),\ldots , V_{N}( \varvec{z}_{j} ) \,\right) \).Because the relation \(u_{i} + \lambda _{R} \times v_{i} \le k - 1\) is satisfied for \(i = 1, 2,\ldots , N\), the receiver \(\mathcal{R}\) is able to interpolate a polynomial \(R \in \mathbb {K}_{k - 1}[X]\) from the \(t\) pairs
 and to calculate \(\omega _{\sigma } = R( 0 )\).
and to calculate \(\omega _{\sigma } = R( 0 )\).
The characteristics of the sparse polynomial interpolation-based DOT protocols analysed hereafter ([1–3, 8, 9]) are described in Annex A.
We note that if the receiver \(\mathcal{R}\) does not follow the protocol and prepares, instead of \(E( \sigma )\), the \(e\)-tuple \(\left( \, \gamma _{1}, \gamma _{2},\ldots ,\gamma _{e} \,\right) \) such that \(V_{i}( \gamma _{1}, \gamma _{2},\ldots \gamma _{e} ) = \alpha _{i}\) (\(1 \le i \le N\)), then she is able to compute
Consequently, if \(\mathcal{R}\) is able to determine an \(e\)-tuple \(\left( \, \gamma _{1}, \gamma _{2},\ldots , \gamma _{e} \,\right) \) such that \(\sum _{i = 1}^{N}{\alpha _{i} a_{i, 0}} = 0\), she obtains a linear combination of the secrets \(\omega _{1}, \omega _{2},\ldots , \omega _{n}\).
In addition, if the values \(\alpha _{1}, \alpha _{2},\ldots , \alpha _{N}\) resulting from the choice of \((\gamma _{1}, \gamma _{2},\ldots ,\) \(\gamma _{e})\) are such that \(\sum _{i = 1}^{N}{\alpha _{i}a_{i, j}} = 1\), for \(j = 1, 2,\ldots , n\), then \(\mathcal{R}\) is able to establish the environment of the scenario of Sect. 2.3.
4 Weaknesses of Some DOT Protocols
4.1 Protocols Insecure Against Curious Servers
In 2000, Naor and Pinkas [8] introduced a sparse polynomial interpolation-based unconditionally secure DOT protocol where the sender \(\mathcal{S}\) holds two secrets \(\omega _{1}\) and \(\omega _{2}\). In this protocol, the hiding parameter \(N\) described in Sect. 3 is \(N = 2\) and the polynomials \(U_{1}\) and \(U_{2}\) are:
and
where the coefficients \(a_{1, i}\) (\(1 \le i \le k - 1\)) are randomly selected in \(\mathbb {K}\) (see Annex A.1). It follows that in the set-up phase, each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives a pair \(\varvec{u}_{j} = \left( \, U_{1}( j ), U_{2}( j ) = \omega _{2} - \omega _{1} \,\right) \) from \(\mathcal{S}\). That is, every server receives a linear combination of secrets and may (see Lemma 1) determine both secrets. Consequently, security condition \(C_{3}\) is not guaranteed.
The sparse polynomial interpolation-based unconditionally secure DOT protocol proposed by Blundo et al. [2] in 2002 is an extension of Naor and Pinkas’s protocol to \(n\) secrets \(\omega _{1}, \omega _{2},\ldots , \omega _{n}\) where \(n \ge 2\). The hiding parameter is \(N = n\), the free coefficient of \(U_{1}\) is \(U_{1}( 0 ) = \omega _{1}\) and the free coefficient of \(U_{i}\) (\(2 \le i \le n\)) is \(U_{i}( 0 ) = \omega _{i} - \omega _{1}\) (see Annex A.2). Each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives an \(n\)-tuple \(\varvec{u}_{j} = \left( \, U_{1}( j ), \omega _{2} - \omega _{1}, \omega _{3} - \omega _{1},\ldots , \omega _{n} - \omega _{1} \,\right) \) in the set-up phase and thus holds linear combinations of the secrets. Again, according to Lemma 1, each server may determine all the secrets of the sender and security condition \(C_{3}\) is not satisfied.
Another polynomial interpolation-based unconditionally secure DOT protocol was introduced in 2002 by Nikov et al. [9]. In this protocol, like in Blundo et al.’s protocol, the hiding parameter is \(N = n\), the free coefficient of \(U_{1}\) is \(U_{1}( 0 ) = \omega _{1}\) and the free coefficient of \(U_{i}\) (\(2 \le i \le n\)) is \(U_{i}( 0 ) = \omega _{i} - \omega _{1}\). The polynomial \(U_{1}\) belongs to \(\mathbb {K}_{k - 1}[X]\) and the polynomials \(U_{2}, U_{3},\ldots , U_{n}\) belong to \(\mathbb {K}_{\lambda _{C}}[X]\) (see Annex A.4). We note that if \(\lambda _{S} = \lambda _{C} = 0\), which is not allowed with our security model since \(\lambda _{S} \ge 1\) (see security parameters in Sect. 1), each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives an \(n\)-tuple \(\varvec{u}_{j} = \left( \, U_{1}( j ), \omega _{2} - \omega _{1}, \omega _{3} - \omega _{1},\ldots , \omega _{n} - \omega _{1} \,\right) \) in the set-up phase. Again, according to Lemma 1, each server may determine all the secrets of the sender.
Similarly, in the interpolation-based unconditionally secure DOT protocol constructed from a private information retrieval protocol presented by Beimel, Chee, Wang and Zhang [1], each server may determine all the secrets of the sender if \(\lambda _{S} = \lambda _{C} = 0\). In this case, the hiding parameter is \(N = n + 1\), the free coefficient of \(U_{1}\) is \(U_{1}(0) = a_{1,0}\), a random element of \(\mathbb {K}\) and the free coefficient of \(U_{i}\) (\(2 \le i \le n + 1\)) is \(U_{i}( 0 ) = \omega _{i - 1} - a_{1,0}\). The polynomial \(U_{1}\) belongs to \(\mathbb {K}_{k - 1}[X]\) and the polynomials \(U_{2}, U_{3},\ldots , U_{n}\) belong to \(\mathbb {K}_{\lambda _{C}}[X]\) (see Annex A.5). Again, in our security model, security condition \(C_{3}\) is not guaranteed.
4.2 Protocols Insecure Against a Greedy Receiver
In the sparse polynomial interpolation-based unconditionally secure DOT protocol introduced by Naor and Pinkas [8], the encoding function is \(E( \sigma ) = \left( \, 1, \delta ^{1}_{\sigma } \,\right) \) and the polynomials \(V_{1}\) and \(V_{2}\) are \(V_{1}( y_{1}, y_{2} ) = 1\) and \(V_{2}( y_{1}, y_{2} ) = y_{2}\). As mentioned in the previous section, the free coefficient of \(U_{1}\) is \(U_{1}( 0 ) = \omega _{1}\). If a cheating receiver sends a requestFootnote 1
 to each server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)), it receives back
to each server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)), it receives back  . Interpolating a polynomial \(R\) from \(t \ge k\) collected values, the receiver calculates
. Interpolating a polynomial \(R\) from \(t \ge k\) collected values, the receiver calculates  . From this linear combination, the receiver may (see Lemma 1) determine both secrets. Consequently, security condition \(C_{4.1}\) is not guaranteed.
. From this linear combination, the receiver may (see Lemma 1) determine both secrets. Consequently, security condition \(C_{4.1}\) is not guaranteed.
The insecurity is the same in Blundo et al.’s protocol [2]; the receiver sends the \(n\)-tuple request  to each server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)). The linear combination determined by the receiver is then
to each server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)). The linear combination determined by the receiver is then  . Like in Naor and Pinkas’s protocol, security condition \(C_{4.1}\) is not guaranteed.
. Like in Naor and Pinkas’s protocol, security condition \(C_{4.1}\) is not guaranteed.
In the DOT protocol introduced by Nikov et al. [9], the free coefficient of \(U_{1}\) is \(U_{1}( 0 ) = \omega _{1}\) and the free coefficient of \(U_{i}\) (\(2 \le i \le n\)) is \(U_{i}( 0 ) = \omega _{i} - \omega _{1}\), exactly like in Blundo et al.’s protocol. Therefore, with the same \(n\)-tuple request  as above sent to servers \(S_{j}\) (\(j \in \mathcal{I}_{t}\)), the receiver determines a linear combination
as above sent to servers \(S_{j}\) (\(j \in \mathcal{I}_{t}\)), the receiver determines a linear combination  and security condition \(C_{4.1}\) is not guaranteed.
and security condition \(C_{4.1}\) is not guaranteed.
The polynomial interpolation-based unconditionally secure DOT protocol designed by Beimel et al. [1] assumes a semi-honest security model: the receiver may be curious but has to follow the protocol. Thus, in this model, security condition \(C_{4.1}\) is guaranteed.
5 A More Robust Protocol
In [3], Blundo et al. have ameliorated the protocol presented in [2] to prevent (1) the servers and (2) the receiver from learning a linear combination of secrets. We show below that in spite of three different improvements, the protocol is still insecure regarding a greedy receiver.
5.1 First Improvement
To prevent servers from receiving a linear combination of secrets (see Sect. 4.1), each secret \(\omega _{i}\) (\(2 \le i \le n\)) is multiplicatively masked by an element \(r_{i}\) randomly selected in \(\mathbb {K}\). More precisely, in the set-up phase, the sender \(\mathcal{S}\) randomly selects \(n - 1\) masks \(r_{2}, r_{3},\ldots , r_{n}\) in \(\mathbb {K}\) and generates an (\(n + 1\))-variate polynomial
where
-
\(U_{1}\) is a quasi-random polynomial of \(\mathbb {K}_{k - 1}[X]\) such that \(U_{1}( 0 ) = \omega _{1}\),
-
\(U_{i}\) is a constant polynomial defined as \(U_{i}( x ) = r_{i}\omega _{i} - \omega _{1}\), for \(i = 2, 3,\ldots , n\), and
-
\(V_{i}\) is an \(n\)-variate polynomial defined as \(V_{i}( y_{1}, y_{2},\ldots , y_{n} ) = y_{i}\), for \(i = 1, 2,\ldots , n\).
In the set-up phase, each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives from the sender \(\mathcal{S}\) an \(n\)-tuple \(\varvec{u}_{j} = \left( \, U_{1}(j), r_{2}\omega _{2} - \omega _{1}, r_{3}\omega _{3} - \omega _{1},\ldots , r_{n}\omega _{n} - \omega _{1} \,\right) \), but also shares, generated by Shamir’s secret sharing scheme [10], of \(r_{2}, r_{3},\ldots , r_{n}\).
In the oblivious transfer phase, the receiver \(\mathcal{R}\) selects the index \(\sigma \in [n]\) of the secret she wishes to obtain, as well as a set \(\mathcal{I}_{k} \subset \mathcal{I}_{m}\) of \(k\) servers’ indices. Then, she prepares an \(n\)-tuple \(\varvec{z}_{j} = \left( \, 1, Z_{2}( j ), Z_{3}( j ),\ldots , Z_{n}( j ) \,\right) \) where \(Z_{i}\) (\(2 \le i \le n\)) is a quasi-random polynomial of \(\mathbb {K}_{k - 1}[X]\) such that \(Z_{i}( 0 ) = \delta _{\sigma }^{i}\). When a server \(S_{j}\) (\(S_{j} \in \mathcal{I}_{k}\)) receives a request \(\varvec{z}_{j}\), it calculates \(\varvec{v}_{j} = \varvec{z}_{j}\) and returns to \(\mathcal{R}\) not only  but also its shares of \(r_{2}, r_{3},\ldots , r_{n}\). From the collected \(k\) responses, \(\mathcal{R}\) interpolates a polynomial \(R\) and calculates \(r_{\sigma }\omega _{\sigma } = R( 0 )\) if \(\sigma \ne 1\) or \(\omega _{1} = R( 0 )\) if \(\sigma = 1\). If the former case, \(\mathcal{R}\) also calculates \(r_{\sigma }\) from the collected shares and with a simple division the chosen secret, \(\omega _{\sigma }\).
but also its shares of \(r_{2}, r_{3},\ldots , r_{n}\). From the collected \(k\) responses, \(\mathcal{R}\) interpolates a polynomial \(R\) and calculates \(r_{\sigma }\omega _{\sigma } = R( 0 )\) if \(\sigma \ne 1\) or \(\omega _{1} = R( 0 )\) if \(\sigma = 1\). If the former case, \(\mathcal{R}\) also calculates \(r_{\sigma }\) from the collected shares and with a simple division the chosen secret, \(\omega _{\sigma }\).
We note that (1) the masks \(r_{i}\) (\(2 \le i \le n\)) may be nil since they are selected in \(\mathbb {K}\) and that (2) \(\omega _{1}\) is not masked.
Thus, if \(n = 2\), each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives a pair \(\varvec{u}_{j} = \left( U_{1}( j ), r_{2}\omega _{2} - \omega _{1}\right) \) in the set-up phase. It is clear that if \(\mathcal{R}\) wishes to obtain \(\omega _{2}\) and if \(r_{2} = 0\), after collecting \(k\) shares, she will determine \(r_{2}\omega _{2} = R(0) = 0\) and will be unable to calculate the value of \(\omega _{2}\). Therefore, the correctness (security condition \(C_{1}\)) of the protocol is not guaranteed; it follows that multiplicative masks \(r_{2}, r_{3},\ldots , r_{n}\) need to be selected in \(\mathbb {K}^{*}\) and not in \(\mathbb {K}\).
In addition, not masking \(\omega _{1}\) may provide the servers with information on \(\omega _{1}\) like shown in the following example.
Example 2
In the prime finite field \(\mathbb {K}= \mathbb {F}_{11}\), we assume that \(n = 2\) and that the probability distributions of \(\omega _{1}\) and \(\omega _{2}\) are:
If the value received by the server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) in the set-up phase for \(U_{2}( j ) = r_{2}\omega _{2} - \omega _{1}\) is \(0\), \(S_{j}\) is able to infer that \(\omega _{1} \ne 0\), hence \(\omega _{1} = 1\), because \(r_{2}\omega _{2} = \omega _{1}\), \(r_{2} \ne 0\) (\(r_{2} \in \mathbb {K}^{*}\) like shown above), \(\omega _{2} \ne 0\) (\(\omega _{2} = 1\) or \(\omega _{2} = 3\)), and \(\mathbb {K}\) is a field and consequently an integral domain.
It follows that in the sub-protocol presented by Blundo et al., the secret \(\omega _{1}\) should be masked like other secrets \(\omega _{2}, \omega _{3},\ldots , \omega _{n}\) and that all masks should be selected in \(\mathbb {K}^{*}\).
We observe that if the use of masks is a good technique to prevent the servers from learning linear combinations of secrets, it does not change the situation of a greedy receiver, since she can determine all the masks. Therefore, once the protocol has been executed, the cheating receiver who has determined a linear combination of masked secrets easily obtains a linear combination of secrets, and from there, possibly all secrets (see Lemma 1). However, an advantage of the masks is that the receiver cannot choose the coefficients of the linear combination of secrets she obtains by cheating. Indeed, each coefficient of the linear combination is the product of a coefficient chosen by the receiver with a mask, unknown from her at the time she prepares requests.
To conclude, the first improvement to Blundo et al.’s DOT protocol is insufficient to guarantee the sender’s privacy. This is a contradiction with Blundo et al.’s claim ([3], Sect. 5, p. 350):
“Notice that, in [8], for the case of two secrets, a proof that the Receiver can get no more than a single linear combination of the two secrets by running the sub-protocol described in Fig. 3 with \(k\) Servers was given. It is not difficult to show that the proof easily generalizes to our scheme for \(n\) secrets, i.e., after receiving information from \(k\) servers, the Receiver cannot learn more than a single linear combination of \(\omega _{1}, \omega _{2},\ldots , \omega _{n}\).”
This is because, as stated by Lemma 1, the knowledge of a linear combination of secrets and of the probability distribution of the secrets may lead to the knowledge of all secrets.
5.2 Second Improvement
The major problem with the sub-protocol presented by Blundo et al. is that the receiver \(\mathcal{R}\) is able to determine a linear combination of secrets, and then, depending on the probability distribution of secrets, the secrets themselves. However, if the secrets have a uniform distribution in the field \(\mathbb {K}\), even if \(\mathcal{R}\) (resp. a coalition of less than \(k\) servers) obtains a linear combination of secrets, she (resp. the coalition) cannot infer any of the secrets. So, the main idea underlying the second improvement is to transform a specific probability distribution into a uniform probability distribution. To this end, using the technique proposed by Naor and Pinkas [8], Blundo et al. have modified the sub-protocol so that it is executed twice: a first time on masks randomly selected in \(\mathbb {K}\) (uniform distribution) and a second time on the products of the secrets and of the masks. To guarantee the consistency of receiver’s requests, the same request sent by \(\mathcal{R}\) to a server is used by the server for both the masks and the masked secrets.
The characteristics of the protocol are given in Annex A.3.
We observe that even if the protocol includes the technique suggested by Naor and Pinkas, the receiver may still obtain, not only a linear combination of secrets, but the secrets themselves (see example in Annex B).
In the demonstration proving that the protocol is secure, even with a greedy receiver (but with honest servers), Blundo et al. require an additional assumption: secrets cannot be identical. This assumption may be satisfied thanks to pads. For example, if \(q\) is a prime number such that \(q \ge np\), the field \(\mathbb {F}_{p}\) could be replaced with a field \(\mathbb {F}_{q}\) and the pad \((i - 1) \times p\) added to secret \(\omega _{i}\) (\(1 \le i \le n\)). We note that this additional assumption decreases the communication performance, since the new field has a cardinality larger than the original one.
However, even with this additional assumption, the claim on the security of the sender is incorrect (Condition (7) of Definition 2.2, p. 329 in [3], is not satisfied) against a greedy receiver. The case is illustrated with the same example (Annex B), because according to the probability distributions chosen in the example, the secrets are necessarily different.
This is actually due to the first improvement which is not taken into account in Blundo et al.’s demonstration. Indeed, Naor and Pinkas demonstrated that the receiver could obtain the system of equations:
where coefficients \(\alpha _{1}\) and \(\alpha _{2}\) are chosen by the receiver.
It is clear that if \(R^{(2)}( 0 ) = 0\), the receiver can infer \(c_{1} = \dfrac{-\alpha _{2}}{\alpha _{1}}c_{2}\) which, reported in the first equation gives \(\alpha _{2}c_{2}( \omega _{2} - \omega _{1} ) = R^{(1)}( 0 )\). Then, if \(R^{1}( 0 ) = 0\), then the receiver can infer the linear combination \(\omega _{2} - \omega _{1} = 0\), because \(c_{2} \in \mathbb {K}^{*}\) and \(\alpha _{2}\) can be chosen different from 0 by the receiver). This explains the additional assumption.
However, in Blundo et al.’s protocol, each secret value is masked according to the first improvement (see Sect. 5.1). Therefore, in the case \(n = 2\), the system of equations that the receiver is able to obtain is
Again, if we assume that \(R^{(2)}( 0 ) = 0\), the receiver can infer \(c_{1} = \dfrac{-\alpha _{2}r^{(2)}_{2}}{\alpha _{1}r^{(2)}_{1}}c_{2}\) which, reported in the first equation gives \(\alpha _{2}c_{2}(r^{(1)}_{2}\omega _{2} - \dfrac{r^{(1)}_{1}r^{(2)}_{2}}{r^{(2)}_{1}}\omega _{1}) = R^{(1)}( 0 )\). If \(R^{(1)}( 0 ) = 0\), then the receiver can infer the linear combination \(r^{(1)}_{2}r^{(2)}_{1}\omega _{2} - r^{(1)}_{1}r^{(2)}_{2}\omega _{1} = 0\). The coefficients \(r^{(i)}_{j}\) (\(i = 1, 2\), \(1 \le j \le n\)) being randomly selected in \(\mathbb {K}^{*}\), there is no way to prevent the receiver from obtaining such a linear combination of the secrets.
However, it is easy to see that the first improvement is not useful when the second improvement is applied. Indeed, with the second improvement, servers do not receive linear combinations of secrets, but linear combination of masked secrets (which is the result of the first improvement) and linear combination of random masks. We conclude that only the second improvement of the protocol is necessary.
5.3 Third Improvement
Concerned with the degree of randomness necessary for the protocol, Blundo et al. suggest a simplification of the protocol to save a few random values ([3], Sect. 5, Remark p. 353):
“However, we can show that the same random values \(a_{1}, a_{2},\ldots , a_{k - 1}\) can be used in both instances of SubDot(.) and the values \(r^{(2)}_{2}, r^{(2)}_{3},\ldots , r^{(2)}_{n}\) can be computed as a function of \(r^{(1)}_{2}, r^{(1)}_{3},\ldots , r^{(1)}_{n}\).”
We show in the following example, that sharing polynomials with the same coefficients \(a_{1}, a_{2},\ldots , a_{k - 1}\) make the protocol insecure, regarding the sender’s privacy.
Example 3
In the prime finite field \(\mathbb {K}= \mathbb {F}_{5}\), we assume that \(n = 2\) and that the probability distributions of \(\omega _{1}\) and \(\omega _{2}\) are:
Since the secrets are masked only once (see previous section), we can also assume that
and
where \(a_{1}, a_{2},\ldots , a_{k - 1}\) are randomly selected in \(\mathbb {K}\).
In the set-up phase, each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives from the sender \(\mathcal{S}\) the pair \(\varvec{u}^{(1)}_{j} = (\, U^{(1)}_{1}(j), U^{(1)}_{2}(j) \,)\) (for the masked secrets) as well as the pair \(\varvec{u}^{(2)}_{j} = (\, U^{(2)}_{1}( j ), U^{(2)}_{2}( j ) \,)\) (for the masks). The server \(S_{j}\) is able to calculate \(d_{j} = U^{(1)}_{1}( j ) - U^{(2)}_{1}( j ) = c_{1}( \omega _{1} - 1 )\). We assume that \(d_{j} \ne 0\). Therefore, \(\omega _{1} - 1 \ne 0\) and so, \(\omega _{1} = 2\), according to the probability distribution \(p_{\omega _{1}}\). Hence, \(c_{1} = {d_{j}}/{(\omega _{1} - 1)} = d_{j}\). Moreover, since \(S_{j}\) holds \(c_{2} - c_{1}\), the value of \(c_{2}\) can be determined: \(c_{2} = ( c_{2} - c_{1} ) + c_{1} = ( c_{2} - c_{1} ) + d_{j}\). The server \(S_{j}\) has received \(c_{2}\omega _{2} - c_{1}\omega _{1}\) from the sender and is able to determine \(c_{1}\), \(c_{2}\) and \(\omega _{1}\); To calculate \(\omega _{2}\) is easy. It follows that, given the probability distribution \(p_{\omega _{1}}\) described above and assuming that \(d_{j} \ne 0\), every server \(S_{j}\) is able to infer \(\omega _{1}\) and \(\omega _{2}\) in the set-up phase and the sender’s privacy is not guaranteed (security condition \(C_{3}\) is not satisfied).
This weakness extends to a greedy receiver and security condition \(C_{4.1}\) could not be satisfied with this improvement. Indeed, if in the oblivious phase the receiver sends the request \(\varvec{z}_{i} = (\, 1, 0 \,)\) to \(k - 1\) servers \(S_{i}\) (\(i \in \mathcal{I}_{k - 1} \subset \mathcal{I}_{k}\), \(|\mathcal{I}_{k - 1} |= k - 1\)) and \(\varvec{z}_{\ell } = (\, 1, 1 \,)\) to the \(k^{th}\) server \(S_{\ell }\) (\(\ell \in \mathcal{I}_{k} \setminus \mathcal{I}_{k - 1}\)), both secrets \(\omega _{1}\) and \(\omega _{2}\) can be determined thanks to the following method (we denote \(P( x )\) the polynomial \(\sum _{i = 1}^{k - 1}{a_{i}x^{i}}\)):
-
First, as soon as \(\mathcal{R}\) has received from a server \(S_{j}\) (\(j \in \mathcal{I}_{k - 1}\)) a response
 , where \(\varvec{v}_{j} = \varvec{z}_{j}\), she determines \(\omega _{1}\) with the technique described above. Thus, \(\mathcal{R}\) receives \(U^{(1)}_{1}(j) \times 1 + U^{(1)}_{2}(j) \times 0 = c_{1}\omega _{1} + P(j)\) and \(U^{(2)}_{1}(j) \times 1 + U^{(2)}_{2}(j) \times 0 = c_{1} + P(j)\). She calculates
, where \(\varvec{v}_{j} = \varvec{z}_{j}\), she determines \(\omega _{1}\) with the technique described above. Thus, \(\mathcal{R}\) receives \(U^{(1)}_{1}(j) \times 1 + U^{(1)}_{2}(j) \times 0 = c_{1}\omega _{1} + P(j)\) and \(U^{(2)}_{1}(j) \times 1 + U^{(2)}_{2}(j) \times 0 = c_{1} + P(j)\). She calculates 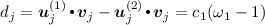 . Because \(d_{j} \ne 0\) and according to the probability distribution \(p_{\omega _{1}}\), \(\mathcal{R}\) determines \(\omega _{1} = 2\). Hence, \(c_{1}\) can be calculated too.
. Because \(d_{j} \ne 0\) and according to the probability distribution \(p_{\omega _{1}}\), \(\mathcal{R}\) determines \(\omega _{1} = 2\). Hence, \(c_{1}\) can be calculated too. -
Second, \(\mathcal{R}\) determines \(P(j)\) from the response of \(S_{j}\):
 . The same operation can be executed from the responses of the other servers of \(\mathcal{I}_{k - 1}\), and \(\mathcal{R}\) obtains \(k - 1\) values \(P(j)\). The free coefficient of \(P\) is \(P( 0 ) = 0\). So, \(P\) may be written under the form \(P = xP^{\prime }\) where the degree of \(P^{\prime }\) is at most \(k - 2\). With \(k - 1\) values \({1}/{j}P(j)\), the polynomial \(P^{\prime }\) may be interpolated, which allows \(\mathcal{R}\) to compute \(P = xP^{\prime }\).
. The same operation can be executed from the responses of the other servers of \(\mathcal{I}_{k - 1}\), and \(\mathcal{R}\) obtains \(k - 1\) values \(P(j)\). The free coefficient of \(P\) is \(P( 0 ) = 0\). So, \(P\) may be written under the form \(P = xP^{\prime }\) where the degree of \(P^{\prime }\) is at most \(k - 2\). With \(k - 1\) values \({1}/{j}P(j)\), the polynomial \(P^{\prime }\) may be interpolated, which allows \(\mathcal{R}\) to compute \(P = xP^{\prime }\). -
Finally, from the server \(S_{\ell }\), \(\mathcal{R}\) obtains

Since \(P\) has been computed in the second step, \(\mathcal{R}\) is able to calculate \(c_{2}\) from the second element of the pair and then the second secret, \(\omega _{2}\), from the first element of the pair.
This example shows that if the third improvement is applied, security condition \(C_{4.1}\) is not satisfied either.
6 Conclusion
The main result of this paper is that when a party is able to obtain a linear combination of secrets, the sender’s privacy (security conditions \(C_{3}\) and \(C_{4.1}\)) may not be guaranteed for all secrets distributions. It follows that some weaknesses have been identified in the following polynomial interpolation-based DOT protocols:
-
Naor and Pinkas’s sparse polynomial interpolation-based protocol [8]: without the technique described in Sect. 4, p. 214, security conditions \(C_{3}\) and \(C_{4.1}\) are not guaranteed (in particular, Theorem 1 is incorrect). If the technique is applied, the size of the secrets space needs to be increased, and hence communication is less efficient (bigger shares need to be exchanged). The weakness is the same in Blundo et al.’s sparse polynomial interpolation-based protocol [2] which extends to \(n\) secrets Naor and Pinkas’s protocol.
-
Nikov et al.’s protocol [9] and Beimel et al.’s protocol [1]: for some values of the protocols’ parameters, security condition \(C_{3}\) is not guaranteed. However, this case is valid in regard to the security models presented by Nikov et al. and Beimel et al.: the protocols are considered as private even though each server holds the sender’s secrets, assuming no server colludes with the receiver. On the other hand, Nikov et al.’s protocol [9] cannot guarantee security condition \(C_{4.1}\), in spite of the claim of the designers.
-
Blundo et al.’s protocol [3]: security condition \(C_{4.1}\) is not guaranteed because of the combination of two techniques: the masking of secrets in the underlying sub-protocol and the parallel execution of the protocol on masked secrets and masks. If the masking of secrets in the underlying sub-protocol is removed, the protocol reaches the same level of security as Naor and Pinkas’s protocol. In addition, the simplification suggested by Blundo et al. (reuse of the coefficients of the hiding polynomials) is a breach in the sender’s security.
We also observe that the DOT protocol introduced by Cheong, Koshiba and Yoshiyama [5] is actually an application of the technique suggested by Naor and Pinkas to Nikov et al’s DOT protocol; The level of security of the protocol is the same as in Naor and Pinkas’s protocol.
Notes
- 1.
Because the first term is constant and public, it is not included in the request.
References
Beimel, A., Chee, Y.M., Wang, H., Zhang, L.F.: Communication-efficient distributed oblivious transfer. J. Comput. Syst. Sci. 78(4), 1142–1157 (2012)
Blundo, C., D’Arco, P., De Santis, A., Stinson, D.R.: New results on unconditionally secure distributed oblivious transfer (extended abstract). In: Nyberg, K., Heys, H.M. (eds.) SAC 2002. LNCS, vol. 2595, pp. 291–309. Springer, Heidelberg (2003)
Blundo, C., D’Arco, P., De Santis, A., Stinson, D.R.: On unconditionally secure distributed oblivious transfer. J. Cryptol. 20(3), 323–373 (2007)
Brassard, G., Crépeau, C., Robert, J.M.: All-or-nothing disclosure of secrets. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 234–238. Springer, Heidelberg (1987)
Cheong, K.Y., Koshiba, T., Nishiyama, S.: Strengthening the security of distributed oblivious transfer. In: Boyd, C., González Nieto, J. (eds.) ACISP 2009. LNCS, vol. 5594, pp. 377–388. Springer, Heidelberg (2009)
Friedman, W.F.: The index of coincidence and its applications in cryptography. No. 22 in Riverbank Publications, Riverbank Laboratories, Geneva, IL, USA (1922)
Kasiski, F.W.: Die Geheimschriften und die Dechiffrir-Kunst. Mittler & Sohn, Berlin (1863)
Naor, M., Pinkas, B.: Distributed oblivious transfer. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 205–219. Springer, Heidelberg (2000)
Nikov, V., Nikova, S., Preneel, B., Vandewalle, J.: On unconditionally secure distributed oblivious transfer. In: Menezes, A., Sarkar, P. (eds.) INDOCRYPT 2002. LNCS, vol. 2551, pp. 395–408. Springer, Heidelberg (2002)
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Characteristics of Some DOT Protocols
1.1 A.1 Naor and Pinkas’s DOT [8]
In the sparse polynomial interpolation-based DOT protocol introduced by Naor and Pinkas [8], the number of secrets is \(n = 2\), the threshold parameter is \(k\), the sender’s privacy and strong privacy parameters are \(\lambda _{S} = k - 1\) and \(\lambda _{C} = 0\), the hiding parameter is \(N = 2\) and the encoding parameter is \(e = 2\). The encoding function is \(E(s) = \left( \, 1, \delta _{s}^{2} \,\right) \) and the polynomials \(U_{i}\) and \(V_{i}\) (\(1 \le i \le N\)) are:
-
\(U_{1}(x) = \omega _{1} + \sum _{i = 1}^{k - 1}{a_{i}x^{i}}\), where coefficients \(a_{i}\) are randomly selected in \(\mathbb {K}\), and \(U_{2}(x) = \omega _{2} - \omega _{1}\),
-
\(V_{i}(y_{1}, y_{2}) = y_{i}\) for \(i = 1, 2\).
On the receiver’s side, the number of contacted servers is \(t = k\), the receiver’s privacy parameter is \(\lambda _{R} = k - 1\) and the first element of the encoding function being constant and public, it is not shared (i.e., \(Z_{1} = 1\)) and is not included in the request transmitted by the receiver to the contacted servers.
1.2 A.2 Blundo Et Al.’s DOT [2]
The protocol introduced by Blundo, D’Arco, De Santis and Stinson [2] is an extension of Naor and Pinkas’s sparse polynomial interpolation-based DOT protocol [8]. Only the following characteristics are different from those described in Appendix A.1.
-
\(n \ge 2\),
-
\(N = n\),
-
\(E( s ) = \left( \, 1, \delta _{s}^{2}, \delta _{s}^{3},\ldots , \delta _{s}^{n} \,\right) \),
-
\(U_{i}( x ) = \omega _{i} - \omega _{1}\) for \(i = 2, 3,\ldots , N\),
-
\(V_{i}( y_{1}, y_{2},\ldots , y_{e} ) = y_{i}\) for \(i = 1, 2,\ldots , N\).
1.3 A.3 Blundo Et Al.’s DOT [3]
The characteristics of the protocol introduced by Blundo, D’Arco, De Santis and Stinson [3] are similar to those of the protocol they presented in 2002 (see Appendix A.2). However, to improve the protocol, the secrets are masked twice:
-
To prevent the servers from learning a linear combination of secrets, each secret \(\omega _{i}\) (\(2 \le i \le n\)) is multiplied by a mask \(r_{i}\) randomly selected in \(\mathbb {K}\). Each mask is shared amongst the \(m\) servers involved in the protocol, thanks to Shamir’s secret sharing schemes [10],
-
To prevent the receiver from learning a linear combination of secrets, each secret \(\omega _{i}\) (\(1 \le i \le n\)) is masked with a mask \(c_{i}\) randomly selected in \(\mathbb {K}^{*}\) and the receiver needs, with one request only, to collect shares of the chosen masked secret \(c_{\sigma }\omega _{\sigma }\), but also of the corresponding mask \(c_{\sigma }\).
More specifically, in the set-up phase, the sender \(\mathcal{S}\) first selects masks \(c_{i}\) (\(1 \le i \le n\)) in \(\mathbb {K}^{*}\), which gives him two lists of secret values: \(\left( \, c_{1}\omega _{1}, c_{2}\omega _{2},\ldots , c_{n}\omega _{n} \,\right) \) and \(\left( \, c_{1}, c_{2},\ldots , c_{n} \,\right) \). Second, \(\mathcal{S}\) selects random masks \(r^{(1)}_{i}\) and \(r^{(2)}_{i}\) (\(2 \le i \le n\)) in \(\mathbb {K}\) and builds two lists \(L_{1} = \left( \, c_{1}\omega _{1}, r^{(1)}_{2}c_{2}\omega _{2}, r^{(1)}_{3}c_{3}\omega _{3},\ldots , r^{(1)}_{n}c_{n}\omega _{n} \,\right) \) and \(L_{2} = \left( \, c_{1}, r^{(2)}_{2}c_{2}, r^{(2)}_{3}c_{3},\ldots , r^{(2)}_{n}c_{n} \,\right) \). Then, a set of \(N\) polynomials \(U^{(1)}_{i}\) (\(1 \le i \le N\)) is generated to hide the secrets values of \(L_{1}\) and another set of of \(N\) polynomials \(U^{(2)}_{i}\) (\(1 \le i \le N\)) is generated to hide the secrets values of \(L_{2}\):
-
\(U^{(1)}_{1}( x ) = c_{1}\omega _{1} + \sum _{i = 1}^{k - 1}{a^{(1)}_{i}x^{i}}\), where coefficients \(a^{(1)}_{i}\) are randomly selected in \(\mathbb {K}\), and for \(i = 2, 3,\ldots , n\), \(U^{(1)}_{i}( x ) = r^{(1)}_{i}c_{i}\omega _{i} - c_{1}\omega _{1}\),
-
\(U^{(2)}_{1}( x ) = c_{1} + \sum _{i = 1}^{k - 1}{a^{(2)}_{i}x^{i}}\), where coefficients \(a^{(2)}_{i}\) are randomly selected in \(\mathbb {K}\), and for \(i = 2, 3,\ldots , n\), \(U^{(2)}_{i}( x ) = r^{(2)}_{i}c_{i} - c_{1}\),
The \(e\)-variate polynomials \(V_{i}\) (\(i = 1, 2,\ldots , N\)) are the same as those defined in Appendix A.2. Still in the set-up phase, each server \(S_{j}\) (\(j \in \mathcal{I}_{m}\)) receives
and
as well as the shares \([r^{(1)}_{2}]_{j}, [r^{(1)}_{3}]_{j},\ldots , [r^{(1)}_{n}]_{j}\) and \([r^{(2)}_{2}]_{j}, [r^{(2)}_{3}]_{j},\ldots , [r^{(2)}_{n}]_{j}\) (If \(F^{(s)}_{t}\) is the hiding polynomial determined in Shamir’s secret sharing scheme to share \(r^{(s)}_{t}\), the share \(F^{(s)}_{t}( j )\) allocated to server \(S_{j}\) is denoted \([r^{(s)}_{t}]_{j}\).)
In the oblivious phase, on reception of the request \(\varvec{z}_{j}\), a server \(S_{j}\) (\(j \in \mathcal{I}\)) calculates \(\varvec{v}_{j} = \left( \, V_{1}( \varvec{z}_{j} ), V_{2}( \varvec{z}_{j} ),\ldots , V_{N}( \varvec{z}_{j} ) \,\right) \) and returns  and
and  , with the two sets of \(n - 1\) shares of \(\left( \, r^{(1)}_{2}, r^{(1)}_{3},\ldots , r^{(1)}_{n} \,\right) \) and \(\left( \, r^{(2)}_{2}, r^{(2)}_{3},\ldots , r^{(2)}_{n} \,\right) \) to the receiver. From the collected values, \(\mathcal{R}\) interpolates two polynomials \(R^{(1)}\) and \(R^{(2)}\) and, if \(\sigma = 1\), calculates \(R^{(1)}( 0 ) = c_{\sigma }\omega _{\sigma }\) and \(R^{(2)}( 0 ) = c_{\sigma }\). If \(\sigma \ne 1\), \(\mathcal{R}\) calculates \(R^{(1)}( 0 ) = c_{\sigma }r^{(1)}_{\sigma }\omega _{\sigma }\) and \(R^{(2)}( 0 ) = c_{\sigma }r^{(2)}_{\sigma }\) and also determines from the \(k\) collected shares \([r^{(1)}_{\sigma }]_{j}\) the value of \(r^{(1)}_{\sigma }\) and similarly, from the \(k\) collected shares \([r^{(2)}_{\sigma }]_{j}\) the value of \(r^{(2)}_{\sigma }\). Then, with simple division(s), \(\mathcal{R}\) determines \(c_{\sigma }\) first and \(\omega _{\sigma }\) second.
, with the two sets of \(n - 1\) shares of \(\left( \, r^{(1)}_{2}, r^{(1)}_{3},\ldots , r^{(1)}_{n} \,\right) \) and \(\left( \, r^{(2)}_{2}, r^{(2)}_{3},\ldots , r^{(2)}_{n} \,\right) \) to the receiver. From the collected values, \(\mathcal{R}\) interpolates two polynomials \(R^{(1)}\) and \(R^{(2)}\) and, if \(\sigma = 1\), calculates \(R^{(1)}( 0 ) = c_{\sigma }\omega _{\sigma }\) and \(R^{(2)}( 0 ) = c_{\sigma }\). If \(\sigma \ne 1\), \(\mathcal{R}\) calculates \(R^{(1)}( 0 ) = c_{\sigma }r^{(1)}_{\sigma }\omega _{\sigma }\) and \(R^{(2)}( 0 ) = c_{\sigma }r^{(2)}_{\sigma }\) and also determines from the \(k\) collected shares \([r^{(1)}_{\sigma }]_{j}\) the value of \(r^{(1)}_{\sigma }\) and similarly, from the \(k\) collected shares \([r^{(2)}_{\sigma }]_{j}\) the value of \(r^{(2)}_{\sigma }\). Then, with simple division(s), \(\mathcal{R}\) determines \(c_{\sigma }\) first and \(\omega _{\sigma }\) second.
1.4 A.4 Nikov Et Al.’s DOT [9]
The sparse polynomial interpolation-based DOT protocol introduced by Nikov, Nikova, Preneel and Vandewalle [9] is characterized by the following parameters: the number of secrets \(n \ge 2\), the threshold parameter \(k\), the sender’s privacy parameter \(\lambda _{S} \le k - 1\), the receiver’s privacy parameter \(\lambda _{R} \le k - 1\), the hiding parameter \(N = n\) and the encoding parameter \(e = n\). The parameter \(\lambda _{C}\) is defined such that \(\lambda _{R} + \lambda _{C} \le k - 1\). In addition, the encoding function is \(E( s ) = \left( \, 1, \delta _{s}^{2}, \delta _{s}^{3},\ldots , \delta _{s}^{n} \,\right) \) and the polynomials \(U_{i}\) and \(V_{i}\) (\(1 \le i \le N\)) are:
-
\(U_{1}( x ) = \omega _{1} + \sum _{\ell = 1}^{k - 1}{a_{1,\ell }x^{\ell }}\), where coefficients \(a_{1,\ell }\) are randomly selected in \(\mathbb {K}\), and for \(i = 2, 3,\ldots , N\), \(U_{i}( x ) = \omega _{i} - \omega _{1} + \sum _{\ell = 1}^{\lambda _{C}}{a_{i,\ell }x^{\ell }}\), where coefficients \(a_{i,\ell }\) are randomly selected in \(\mathbb {K}\),
-
\(V_{i}( y_{1}, y_{2},\ldots , y_{e} ) = y_{i}\) for \(i = 1, 2,\ldots , N\).
Like in Naor and Pinkas’s and in Blundo et al.’s DOT protocols (see Appendices A.1 and A.2 above), on the receiver’s side, the number of contacted servers is \(t = k\) and the first element of the encoding function being constant and public, it is not shared (i.e., \(Z_{1} = 1\)) and is not included in the request transmitted by the receiver to the contacted servers.
1.5 A.5 Beimel Et Al.’s DOT [1]
In [1], Beimel, Chee, Wang and Zhang propose a specific reduction from a DOT protocol to a polynomial interpolation-based information-theoretic private information retrieval protocol. The characteristics of the protocol are: the number of secrets \(n \ge 2\), the threshold parameter \(k\), the sender’s privacy and strong privacy parameters \(\lambda _{S} = \lambda _{C} \le k - 1\), the receiver’s privacy parameter \(\lambda _{R} \le k - 1\), the hiding parameter \(N = n + 1\) and the encoding parameter \(e > 0\). The polynomials \(U_{i}\) and \(V_{i}\) (\(1 \le i \le N\)) are:
-
\(U_{1}( x ) = \sum _{i = 0}^{k - 1}{a_{1,i}x^{i}}\), where coefficients \(a_{1,i}\) are randomly selected in \(\mathbb {K}\), and for \(i = 2, 3,\ldots , N\), the polynomial \(U_{i}\) is defined by \(U_{i}( x ) = ( \omega _{i - 1} - a_{1,0} ) + \sum _{j = 1}^{\lambda _{C}}{a_{i,j}x^{j}}\), where coefficients \(a_{i,j}\) are randomly selected in \(\mathbb {K}\),
-
\(V_{1}( y_{1}, y_{2},\ldots , y_{e} ) = 1\) and for \(i = 2, 3,\ldots , N\), the polynomial \(V_{i}\) and the encoding function \(E\) must satisfy \(V_{i}( E( \ell ) ) = \delta _{\ell }^{i - 1}\) for \(\ell \in [n]\).
On the receiver’s side, the number of contacted servers is \(t = k\). In addition, for efficiency purposes, each contacted server \(S_{j}\) (\(j \in \mathcal{I}_{t}\)) transforms the share  into a split \(s_{j}\), which is sent back to the receiver. The receiver has just to calculate the sum \(\omega _{\sigma } = \sum _{j \in \mathcal{I}_{t}}{s_{j}}\) to obtain the chosen secret.
into a split \(s_{j}\), which is sent back to the receiver. The receiver has just to calculate the sum \(\omega _{\sigma } = \sum _{j \in \mathcal{I}_{t}}{s_{j}}\) to obtain the chosen secret.
B Example of Insecurity in Blundo et al.’s DOT Protocol
—— Public Information ——
-
Finite field \(\mathbb {F}_{ 11 }\)
-
Threshold \(k = 3 \)
-
Number of secrets \(n = 2\)
-
\(p_{\omega _{1}}( 6 ) = 0.5\), \(p_{\omega _{1}}( 2 ) = 0.5\), \(p_{\omega _{1}}(i) = 0\) if \(i \ne 6 \) and \(i \ne 2 \)
-
\(p_{\omega _{2}}( 1 ) = 0.5\), \(p_{\omega _{2}}( 3 ) = 0.5\), \(p_{\omega _{2}}(i) = 0\) if \(i \ne 1 \) and \(i \ne 3 \)
—— Set-up phase ——
Information private to the sender:
-
\(\omega _{1} = 6 \) and \(\omega _{2} = 1 \)
-
\(c_{1} = 5\) and \(c_{2} = 7\)
-
\(r^{(1)}_{1} = 1 \) and \(r^{(1)}_{2} = 2\)
-
\(r^{(2)}_{1} = 4 \) and \(r^{(2)}_{2} = 5\)
Intermediate calculus to prepare the sharing polynomials:
-
\(r^{(1)}_{1} \times c_{1} \times \omega _{1} = 8\)
-
\(r^{(1)}_{2} \times c_{2} \times \omega _{2} = 3\)
-
\(r^{(2)}_{1} \times c_{1} = 9 \)
-
\(r^{(2)}_{2} \times c_{2} = 2 \)
-
Sharing polynomial \(U^{(1)}_{1} = 8 + 2X + 9X^2\)
-
Sharing polynomial \(U^{(2)}_{1} = 9 + X + 4X^2\)
-
\(S_{ 1 }\) receives \(\varvec{u}^{(1)}_{1} = \left( \, 8, 6 \,\right) \) and \(\varvec{u}^{(2)}_{1} = \left( \, 3, 4 \,\right) \)
-
\(S_{ 2 }\) receives \(\varvec{u}^{(1)}_{2} = \left( \, 4, 6 \,\right) \) and \(\varvec{u}^{(2)}_{2} = \left( \, 5, 4 \,\right) \)
-
\(S_{ 3 }\) receives \(\varvec{u}^{(1)}_{3} = \left( \, 7, 6 \,\right) \) and \(\varvec{u}^{(2)}_{3} = \left( \, 4, 4 \,\right) \)
—— Transfer phase ——
-
Request generated by the receiver: \(\varvec{z}_{j} = \left( \, 1, 6 \,\right) \)
-
\(\varvec{v}_{j} = \varvec{z}_{j} = \left( \, 1, 6 \,\right) \)
-
\(S_{ 1 }\) replies with
 and
and 
-
\(S_{ 2 }\) replies with
 and
and 
-
\(S_{ 3 }\) replies with
 and
and 
—— The receiver tries to obtain all secrets ——
-
Interpolated polynomal from \((\, 1, 0 \,)\), \((\, 2, 7 \,)\), and \((\, 3, 10 \,)\): \(R^{(1)} = 2X + 9X^2 \)
-
\(r^{(1)}_{2}c_{2}\omega _{2} + r^{(1)}_{1}c_{1}\omega _{1} = 2 \times R^{(1)}(0) = 0 \)
-
Interpolated polynomal from \((\, 1, 5 \,)\), \((\, 2, 7 \,)\), and \((\, 3, 6 \,)\): \(R^{(2)} = X + 4X^2 \)
-
\(r^{(2)}_{2}c_{2} + r^{(2)}_{1}c_{1} = 2 \times R^{(2)}(0) = 0 \)
-
From the received mask shares, the receiver determines \(r^{(1)}_{1} = 1 \), \(r^{(1)}_{2} = 2 \), \(r^{(2)}_{1} = 4 \) and \(r^{(2)}_{2} = 5 \).
So, the receiver can infer the two equations:
From the second equation, the receiver infers that \(c_{2} = 8 \times c_{1}\). Reporting the equality in the first equation, she obtains: \(c_{1} \times ( 5 \times \omega _{2} + 1 \times \omega _{1}) = 0 \). If \(\left( \, \omega _{1}, \omega _{2} \,\right) =\)
-
\(\left( \, 6 , 1 \,\right) \), then \( 5 \times \omega _{2} + 1 \times \omega _{1} = 0 \),
-
\(\left( \, 2 , 1 \,\right) \), then \( 5 \times \omega _{2} + 1 \times \omega _{1} = 7 \),
-
\(\left( \, 6 , 3 \,\right) \), then \( 5 \times \omega _{2} + 1 \times \omega _{1} = 10 \),
-
\(\left( \, 2 , 3 \,\right) \), then \( 5 \times \omega _{2} + 1 \times \omega _{1} = 6 \).
The only pair of secrets which satisfies the first equation is: \(\left( \, 6, 1 \,\right) \). The greedy receiver has obtained all secrets.
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Corniaux, C.L.F., Ghodosi, H. (2015). Security Analysis of Polynomial Interpolation-Based Distributed Oblivious Transfer Protocols. In: Lee, J., Kim, J. (eds) Information Security and Cryptology - ICISC 2014. ICISC 2014. Lecture Notes in Computer Science(), vol 8949. Springer, Cham. https://doi.org/10.1007/978-3-319-15943-0_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-15943-0_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-15942-3
Online ISBN: 978-3-319-15943-0
eBook Packages: Computer ScienceComputer Science (R0)





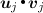 to
to  and to calculate
and to calculate  , where
, where 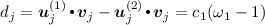 . Because
. Because  . The same operation can be executed from the responses of the other servers of
. The same operation can be executed from the responses of the other servers of 
 and
and 
 and
and 
 and
and 