Evaluation of Portfolio Returns in Fama-French Model Using Quantile Regression Under Asymmetric Laplace Distribution

Abstract

We applied the method of quantile regression under asymmetric Laplace distribution to predicting stock returns. Specifically, we used this method in the Fama and French three-factor model for the five industry portfolios to estimate the beta coefficient, which measure risk in the portfolios management analysis at given levels of quantile. In many applications, we are concerned with the changing effects of the covariates on the outcome across the quantiles of the distribution. Inference in quantile regression can be proceeded by assigning an asymmetric Laplace distribution for the error term. Finally, we use the method to measures the volatility of a portfolio relative to the market, size and value premium. It should be noted that a complete study of quantile regression models with various error distributions is of great interests for applications.

1 Introduction

The portfolio theory was first purposed by Markowitz in 1952, a simple idea that described the return of the portfolio by mean and variance. These concepts were essential to development of the famous capital asset pricing model (CAPM). CAPM was introduced by Sharpe [19] and Lintner [14]. The classical CAPM is predicting the return of the asset by using only market return to evaluate the return in portfolio management. But it is only 70 % given by the CAPM (within sample) explains of the diversified portfolios returns compared with the Fama-French three-factor model can explains over 90 % (see, Fama and French [6]). The three-factor model, two more factors namely, size and value variables are added into the original CAPM. Both CAPM and the Fama-French model are use ordinary least square (OLS) to obtain the beta parameters and usually assumed error term to be jointly normally distributed. However, this is not always true in the financial market. The Fama-French assumes that the variance of returns adequately measures risk. This may be true if returns are distributed normally. In this paper we introduce the quantile regression with an asymmetric Laplace distribution (ALD) to estimate the parameters of the model and predict portfolios returns.

Quantile regression can explain the entire conditional distribution of the outcome variable, and is more robust to outliers and wrong assumption of the error distribution. For the application of quantile regression to Fama-French model, we have not seen much about applying the quantile in the three-factor model.

Quantile regression estimation is equivalent to the parametric case where the error term is asymmetrically Laplace distributed. The beneficial of parametric estimation is that we can have all the properties of Maximum Likelihood Estimates (MLE). Estimators derived by the method of maximum likelihood have some desirable properties such as, sufficiency, consistency, efficiency, asymptotic normally (Fisher Information), invariance, etc.

Many studies on the Fama-French model is wildly used to study the diversification of the risk parameter and the performance of protfolios, which we can found in the studied from Abhakorn et al. [1], they used standard C-CAPM by including two additional factor associated with Fama-French [7]. Same as in the studied of Bartholdy and Peare [4], compared the performance of CAPM and Fama-French models for individual stocks. In the support of Gaunt [11] tests validity between Three factor model and CAPM, all their results shown that Fama-French model provides a better explanation of stock returns than the CAPM model. Lin et al. [15] studied the relation between the Fama-French factors and the latent risk factors in Chinese market. More related work using the Fama-French model, we refer the reader to the works of Mwalla and Karasneh [2], Eraslan [5], Faff et al. [10]. Grauer and Janmatt [11]

This study extends the standard Fama-French three factor model by present a likelihood-based approach to the estimation of regression quantiles based on the asymmetric Laplace distribution. In [18], the authors construct the distribution of currency exchange rates using the asymmetric Laplace distribution, which successfully captures the peakedness, fat tail and skewness inherent in such data. Similarly, it is shown in [16] that the Laplace distribution has a geometric stability for the weekly and monthly distributions of stock returns and also captures the high peak, fat tail and the skewness of the stock returns.

The useful of regression with Fama-French model have been mentioned in Kent [13] i.e., First, The Fama-French model can explains much more of the variation observed in realized returns. Second, it is show that a positive alpha observed in a CAPM regression is merely a result of exposure to either SMB or HML factors, rather than actual manager performance.

Hence, the main objective of this study is to illustrate the method of quantile regression under asymmetric Laplace distribution. we estimate five industrial portfolios returns based on quantile regression under asymmetric Laplace distribution to evaluate the returns of the portfolios. Thus, the contribution of this paper is using the method of quantile regression under ALD to obtained the value of betas parameter under various market situation.

The remainder of the paper proceeds as follows. Section 2 gives the overview of quantile regression with asymmetric Laplace distribution and Fama-Frnch three factor model. Meanwhile, Sect. 3 described the empirical method using qunatile regression under asymmetric Laplace distribution. Section 4 exhibits the empirical solutions. The last gives the conclusion of the paper.

2 Quantile Regression and Fama-French Model

2.1 Quantile Regression with an Asymmetric Laplace Distribution

Quantile regression (QR) supplies information about the relationship between response and the covariates at the tails of the response distribution. In a linear QR model $Y=X'\beta _{\alpha }+\varepsilon _{\alpha },$ the parameter $\beta _{\alpha }$ is estimated by minimizing the empirical objective function $\sum _{i=1}^n[\rho _{\alpha }(Y-X'\beta )]$ over $\beta .$ Thus, given i.i.d $(X_{i},Y_{i})$, a plausible estimator of $\beta _\alpha$ is

$$\begin{aligned} \widehat{\beta _{\alpha }}=\arg \min \frac{1}{n}\left\{ \displaystyle \sum _{i=1}^{n}\rho _\alpha (Y_{i}-X_{i}'\beta )\right\} . \end{aligned}$$

(1)

Function $\rho _\alpha (\cdot )$ is the so called check (or loss) function defined by $\rho _\alpha (u)=u(\alpha -1_{(u<0)}),$ with $1_{(u<0)}$ denoting the usual indicator function. This estimator is called the Least Absolute Deviation (LAD) estimator. Just as minimizing a loss is associated with normal errors, minimizing check function corresponds to assuming a distribution called asymmetric Laplace distribution (ALD) for the error $\varepsilon _{\alpha }$. Note that, just like in mean regression model, while the OLS method provides estimators for the model parameters, to make tests and set up confidence intervals, we need to make an assumption about the distribution of the error term.

Thus, suppose that $Y_{i}$ is distributed as ALD ($\beta _{\alpha }X_{i},\sigma ,\alpha$), $i = 1,2,\ldots ,n.$ Then the likelihood is

$$\begin{aligned} L(\beta _{\alpha },\sigma \vert Y_{1},\cdots ,Y_{n})= \frac{\alpha ^{n}(1-\alpha )^{n}}{\sigma ^{n}}\exp \left\{ - \sum _{i=1}^{n}\rho _{\alpha }\left( \frac{Y_{i}-X'_{i}\beta _{\alpha }}{\sigma }\right) \right\} . \end{aligned}$$

(2)

Maximizing $L$ with respect to $\beta _\alpha$ is equivalent to minimizing $\sum _{i=1}^n[\rho _{\alpha }(Y-X'\beta )]$. Note that, the ALD of the error $\varepsilon _\alpha$ is

$$\begin{aligned} f_{\varepsilon _{\alpha }}(u)= \dfrac{\alpha (1-\alpha )}{\sigma }\exp \left\{ -\rho _{\alpha }\left( \dfrac{u}{\sigma _{\alpha }}\right) \right\} . \end{aligned}$$

(3)

The validation measure for general quantile regression model is

$$\begin{aligned} Q_{n}(\alpha )=1-\dfrac{\displaystyle \sum _{i=1}^{n}\rho _{\alpha }(Y_{i}-q_{\alpha }(Y_{i}\vert X_{i}))}{\displaystyle \sum _{i=1}^{n}\rho _{\alpha }(Y_{i}- \hat{\theta }_{\alpha }X_{i})} \end{aligned}$$

(4)

The empirical general quantile regression is obtained by estimated quantiles. For more details on this measure for validating quantile regression models, see, [17].

2.2 Fama-French Three-Factor Model

The three-factor model was purposed by Fama and French [6] and has been applied in various issue (see, [7–9]). This model provides an extended version of the CAPM for evaluation of the portfolio. The original CAPM model is described by the linear regression as follows

$$\begin{aligned} r_A=r_f+\beta _{A}(r_{M}-r_{f})+\varepsilon , \end{aligned}$$

(5)

In the three-factor model, two additional factors are added to explain excess return; “size” and “value” to be the most significant factors. Thus, for each portfolio can be estimate the return by the following regression:

$$\begin{aligned} r_A=r_f+\beta _{A}(r_{M}-r_{f})+s_{A} \ SMB+h_{A} \ HML+\varepsilon , \end{aligned}$$

(6)

where $r_{A}$ is the total return of portfolio, $r_{f}$ is the risk free rate, $r_{M}$ is the market return and $\varepsilon$ is the error term. SMB which is so called “Small Minus Big” accounting for the size premium, is designed to measure the difference in return between investing in small and big capitalization stocks, $s_{A}$ represents the level of exposure to size risk. The words “Small and Big” are refer to the size of the market equity (ME) which is the multiplication of share price and number of shares outstanding. “High Minus Low” (HML) represents the value premium, is invented to measure the excess returns for investing in high book-to-market values (BE/ME) and low BE/ME companies and $h_A$ shows the level of exposure to value risk.

Note that, SMB is the average return on the three small portfolios minus the average return on the three big porfolios. HML is the average return on the two value portfolios minus the average return on the two growth portfolios. SMB and HML are calculated from the combinations of Small Value (SV), Small Neutral (SN), Small Growth (SG), Big Value (BV), Big Neutral (BN) and Big Growth (BG). Thus, we have

$$\begin{aligned} SMB&=\frac{1}{3}(SV+SN+SG)- \frac{1}{3}(BV+BN+BG)\end{aligned}$$

(7a)

$$\begin{aligned} HML&=\frac{1}{2}(SV+BV)-\frac{1}{2}(SG+BG) \end{aligned}$$

(7b)

3 Simulated Data for ALD

Consider the linear model $Y=X\beta _\alpha +\varepsilon _\alpha$, for $0<\alpha <1$, with $F_{\varepsilon _\alpha \vert X}(0)=\alpha .$ Such that this condition entails that the conditional $\alpha -quantile$ of Y given X is $X\beta _{\alpha }.$ Recall the $\alpha -\text{ loss } \text{ function }$

$$\begin{aligned} \rho _\alpha (u)=u[\alpha -1_{(u<0)}]={\left\{ \begin{array}{ll} u(\alpha -1) &{}: u < 0\\ u\alpha &{} : u\geqslant 0 \end{array}\right. } \end{aligned}$$

(8)

Thus, $\rho _\alpha (\frac{u}{\sigma })=\frac{\rho _\alpha (u)}{\sigma }$ when $\sigma >0$. Suppose the conditional distribution of Y given X is a $ALD (\mu ,\sigma ,\alpha ),$ where the location parameter $-\infty <\mu <\infty ,$ the scale parameter $\sigma >0$, and the skew parameter $0<\alpha <1.$ Given the density of $\varepsilon _\alpha$ in (3). For simulations of $\varepsilon$ from this distribution where we know $\alpha$ and $\sigma$, we seek its distribution function $F_{\varepsilon _\alpha }$ to carry out the usual procedure by setting $F_{\varepsilon _\alpha }=U$, uniformly distributed on [0,1], so that $\varepsilon _{\alpha }= F_{\varepsilon _\alpha }^{-1}(U)$ we have

$$\begin{aligned} F_{\varepsilon _\alpha }(x)={\left\{ \begin{array}{ll} \alpha \exp \lbrace \frac{(1-\alpha )x}{\sigma }\rbrace &{}: x < 0\\ 1-(1-\alpha )\exp \lbrace -\frac{\alpha x}{\sigma }\rbrace &{}: x\geqslant 0 \end{array}\right. } \end{aligned}$$

(9)

From which, we get

$$\begin{aligned} u=\alpha \exp \left\{ \frac{(1-\alpha )x}{\sigma }\right\} \Rightarrow x=\frac{\sigma (\log u-\log \alpha )}{1-\alpha } : u<\alpha \end{aligned}$$

(10)

which is less than 0 when $\log u-\log \alpha <0$ and

$$\begin{aligned} u&=1-(1-\alpha )\exp \lbrace -\frac{\alpha x}{\sigma }\rbrace \end{aligned}$$

(11a)

$$\begin{aligned} x&=\frac{\sigma [\log (1-\alpha )-\log (1-u)]}{\alpha } \geqslant 0 : u \geqslant \alpha \end{aligned}$$

(11b)

4 Application to Portfolio Evaluation

4.1 Model and Parameters Estimation

The Fama and French three-factor asset pricing model provides an option to CAPM as an improvement to poor performance of the CAPM. With this method, the estimation of expected excess return on portfolios will be calculated by adding two more factors namely; SMB and HML into the classic CAPM model. Suppose we have observed the past data of stock return $r_{ai},r_{mi},SMB_{i},HML_{i}, i=1,2,\cdots ,n$ over past $n$ years. These observations are assumed an i.i.d. random noise from $ALD(\alpha ,\mu ,\sigma )$. In this case we consider $\mu =0$.

The equation of the three-factor model under asymmetric Laplace distribution at given level of $\alpha$ quantile, using (2) and (6) the corresponding to the historical data via the three-factor model is a realization that generate likelihood function is

$$\begin{aligned}&L_{\alpha }(\beta _{0}^\alpha ,\beta _{1}^\alpha ,\beta _{2}^\alpha ,\beta _{3}^\alpha ,\sigma \vert {(r_{mi},r_{ai},SMB_{i},HML_{i})})= \nonumber \\&\quad {\frac{\alpha ^{n}(1-\alpha )^{n}}{\sigma ^{n}}\exp \left\{ -\displaystyle \sum _{i=1}^{n}\rho _{\alpha }(\frac{r_{ai}-HML_{i}\beta _{3}^{\alpha }-SMB_{i}\beta _{4}^{\alpha }-r_{mi}\beta _{1}^{\alpha }-\beta _{0}^{\alpha }}{\sigma })\right\} }. \end{aligned}$$

(12)

4.2 Experimental Results

The data contain of 1050 monthly returns during 1926–2013 are original obtained from Center for Research in Security Prices (CRSP) to compute the log returns on the following asset. The data consist of the returns from the five industry portfolios, Consumer (Cnsmr), Manufacturing (Manuf), Hi-Technologies (HiTec), Health care (Hlth) and Other (Other), such as Mines, Transportation etc. Market returns ($r_{Mt}$) includes all New York Stock Exchange (NYSE), American Stock Exchange (AMEX) and NASDAQ Stock Market (NASDAQ) firms.

Data for SMB and HML were obtained from French’s homepage. Table 1 gives the summary of the variables.

Table 1 Summary statistics

The Q-Q plots shown in Fig. 1 are based on the distribution of AL, given in (2). The lines in these figures represent the 0.5th quantile. These figures are clearly show that the asymmetric Laplace distribution provides a good-fit to the sample data set. Moreover, the Kolmogorov-Smirnov test (KS-test) in Table 2 ensure that all the marginals are follow the ALD compare with the critical value $\frac{K(\alpha '=0.05)}{\sqrt{n}}=0.042$, all of the marginals accepts the null hypotheses of the KS-test at 5 % level.

Fig. 1

The Q-Q plots of error under asymmetric Laplace distribution. a ALD Q-Q plot of Cnsm $\alpha = 0.50$. b ALD Q-Q plot of Hlth $\alpha = 0.50$. c ALD Q-Q plot of HiTec $\alpha = 0.50$. d ALD Q-Q plot of Manuf $\alpha = 0.50$. e ALD Q-Q plot of Other $\alpha = 0.50$

The values in the Table 2 exhibit the results of the parameters estimation for the Fama and French three-factor model via the quantile regression under asymmetric Laplace distributions at given level of $\alpha$. The results for ALD assumption performs well for the given quantile of these five industrial portfolios.

Table 2 Parameter estimated results

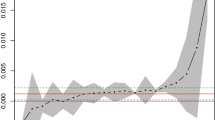
Now, Fig. 2 shows parameter estimation for the entire quantile. From these picture, we summarize the results, e.g. the return from Cnsmr portfolio as follows:

For the quantile lower than 0.90, Cnsmr has less risky than the market and more risk at higher quantile levels, The risks decrease as the stock return increase, but we cannot find any monotonic relationship between risks and excess reurns.

For the lower quantile less than 0.9, positive exposure to size risk increases the average excess return while negative exposure to size risk reduces the average excess retrun regarding medium and small size portfolios. We conclude that the size factor SMB is not effect on large scale of portfolio returns.

Fig. 2

Marginal parameter plots of Cnsmr portfolio at difference quantile$(\alpha )$. a $\beta _0$ Cnsmr. b $\beta _1$ Cnsmr. c $\beta _2$ Cnsmr. d $\beta _3$ Cnsmr. e $\sigma$ Cnsmr

For every quantile, HML capturing the value risk effect of Cnsmr portfolio on average excess returns. Since, it has a negative value, it is expected that high book to market value $(BE/ME)$ decrease average excess return more than the low $(BE/ME)$ one.

4.3 In Sample prediction

To predict the in-sample expected return of the asset $\hat{r}_{a,n}$ for a given market portfolio return $r_{m,n}$, we compute the estimated values of $r_{a,n}$ given $r_{m,n}$ at fixed $\alpha$ by

$$\begin{aligned} \hat{r}_{Cnsmr}=r_f+\beta _{0}+\beta _{1}(r_{M}-r_{f})+\beta _{2} \ SMB+\beta _{3} \ HML+\varepsilon _{i}, \end{aligned}$$

(13)

where $\varepsilon _{i}$ is asymmetric Laplace distribution. Figure 3 displays the in-sample prediction at different quantile. It is clearly that the predicted values are very close to actual values for the given level of quantile under ALD.

Fig. 3

In-sample prediction at difference quantile $(\alpha )$. a Prediction at $\alpha = 0.20$. b Prediction at $\alpha = 0.40$. c Prediction at $\alpha = 0.50$. d Prediction at $\alpha = 0.60$

5 Conclusions

In this paper, we used method of quantile with ALD assumption applied to the Fama and French three factor model for the five industry portfolios stocks markets, which includes all New York Stock Exchange (NYSE), American Stock Exchange (AMEX) and NASDAQ Stock Market (NASDAQ) firms. The Fama and French model is an extension of original CAPM model by adding two more important variables namely, “size premium” and “value premium” into the model. This method can be used to evaluate the linear relationship between the expected returns on a portfolio and its asymmetric market risk with size and value variables over various quantile levels.

The empirical results show that the method of quantile regression under ALD can captures the stylized factors in financial data to describe the stock returns under most quantile levels, especially under the middle quantile levels. Clearly, there is no monotonic relationship between risk and stock returns for the these portfolios. This suggests that during that time frame, the ability to increase the returns of portfolios beyond the risk exposure would be achieve by using quantile regression for the risk measurement.