Bayesian Estimation of Birnbaum–Saunders Log-Linear Model

Abstract

The Birnbaum–Saunders (BS) distribution was derived to model failure times of materials subjected to fluctuating stresses and strains. Motivated by applications in the characterizations of materials, in 1991 Rieck and Nedelman proposed a log-linear model for the BS distribution. This model has many applications, for instance, to compare the median time life of several populations or to assess the effect of covariates on accelerated life testing. In addition to the model studied under the classical approach, we considered Markov chain Monte Carlo (MCMC) and we made an implementation in WinBUGS to get a Bayesian approach under noninformative priori distribution. Similar results for both classical and Bayesian approaches were obtained. This implementation was also adapted for censoring and we assessed the influence of different percentages of censored data.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

22.1 Introduction

Motivated by problems in airplanes due to the development and growth of a dominant crack, in 1969 Birnbaum and Saunders proposed the Birnbaum–Saunders (BS) distribution [2]. It describes the failure time T when some kind of accumulating damage D(t) exceeds a threshold ω, i.e.,

$$T=\mbox{Inf}\{t:D(t)>\omega\}.$$

Let T be the time until the occurrence of the failure, then T is a BS random variable if its distribution is

$$F_T(t)=\Phi\left\{\frac{1}{\alpha}\left[\sqrt{\frac{t}{\beta}}- \sqrt{\frac{\beta}{t}}\right]\right\}, t>0,\mbox{ and} \alpha,\beta>0.$$

The probability density function (PDF) is given by

$$f_X(x;\alpha,\beta)=\frac{\sqrt{\frac{x-\mu}{\beta}}+\sqrt{\frac{\beta}{x-\mu}}} {2\alpha(x-\mu)}\phi \left(\frac{\sqrt{\frac{x-\mu}{\beta}}+\sqrt{\frac{\beta}{x-\mu}}} {\alpha}\right), x>\mu \mbox{ and} \alpha,\beta>0$$

(22.1)

where μ, α, and β are, respectively, position, shape, and scale parameters. The parameter β also corresponds to the median value of the distribution. The functions $\Phi(x)$ and $\phi(x)$ are the standard normal cumulative distribution function (CDF) and PDF.

If $t=x-\mu$, we can write the PDF (22.1) as

$$f(t;\alpha,\beta)=\frac{t+\beta}{2\alpha\sqrt{2\pi\beta}t^{3/2}} {\rm exp}\left\{-\frac{1}{2\alpha^2}\left[\frac{t}{\beta}+\frac{\beta}{t}-2\right]\right\}, t>0, \mbox{ and} \alpha,\beta> 0.$$

In 1991, Rieck and Nedelman [6] were interested in an application in which the main interest was to study the time of failure for a material subjected to different patterns of cycling forces. In order to do so, they proposed a log-linear model for the BS distribution. The model’s principle is based on the empirical law

$$\ln (N) = a + bx,$$

(22.2)

where N is the number of cycles to failure of the specimen and x is either stress range per cycle, strain range per cycle, or the work per cycle.

According to Rieck and Nedelman (see [6]), under some assumptions, since N can be considered as a random variable, the Eq. (22.2) may be rewritten as

$$N={\rm e}^{a+bx}\delta,$$

(22.3)

with $\delta\sim{\mbox BS}(\alpha,1)$.

Thereby, a log-linear model with an additive random effect is obtained by taking logarithm in (22.3),

$$\log (N)=a+bx+\log(\delta),$$

where $\log(\delta)$ has sinh-normal (SHN) distribution, SHN$(\alpha,1)$.

The SHN distribution for a random variable T has distribution function given by

$$F_X(x)=\Phi\left(\frac{2}{\alpha}\sinh\left(\frac{x-\gamma}{\sigma}\right)\right), x\in \mbox{\textbf{R}}, \mbox{ and} \alpha,\sigma>0,$$

where $\Phi(x)$ is the standard normal CDF. This distribution is symmetric around the location parameter $\gamma$, is unimodal for $\alpha \leq$ 2 and bimodal for $\alpha> 2$, and the mean and variance are given by E $(Y)=\gamma$ and var $(Y)=\sigma^2\omega(\alpha)$, where $\omega(\alpha)$ is the variance when $\sigma=1$. Other properties of SHN distribution can be checked in Rieck [5].

The SHN distribution is also called log-Birnbaum–Sanders with parameters α and γ, denoted as log-BS ($\alpha,\gamma$), due to the relationship between the SHN and BS distribution [7], proved by Rieck et al. [6] in the following theorem.

Theorem 1

Let T be a random variable such as $T \sim{\mbox BS} (\alpha,\beta)$ . Then $Y = \log(T)$ has SHN distribution with shape, location, and scale parameter given, respectively, by $\alpha> 0$ , $\gamma = \log (\beta)$ and $\sigma = 2$ , thus, $Y = \log (T) \sim{\mbox SHN} (\alpha,\gamma,2)$ with function probability density given by

$$f(y;\alpha,\gamma)=\frac{1}{\alpha\sqrt{2\pi}}\cosh\left(\frac{y-\gamma}{2}\right) {\rm exp}\left\{-\frac{2}{\alpha^2}\sinh^2\left(\frac{y-\gamma}{2}\right)\right\}.$$

Due to the importance of this model to accelerate life testing or to compare the median lives of several populations, our purpose is to review it under a Bayesian perspective.

In order to make inferences we use posterior distribution generated from simulations by MCMC with WinBUGS. Since we are working on a Bayesian framework, it does not need large sample properties.

Achcar and Martinez [1] made an exploration of Bayesian methods for this model using a noninformative prior density for the parameters and found expressions for the marginal posterior densities through Laplace’s methods for approximation of integrals.

In this work, we use a parametric priori density function and construct the maximum likelihood function to make a simple implementation on WinBUGS. This implementation was also adapted for censoring.

A life data set of 46 observations corresponding to the biaxial fatigue test of Brown and Miller, developed in 1978 [3], is used to compare the estimation under classical and Bayesian perspective.

22.1.1 Model

The generalization of Birnbaum–Saunders log-linear model is

$$Y_i=\mathbf{x}_i^\top\boldsymbol{\beta}+\epsilon_i, \qquad i=1,\cdots,n,$$

(22.4)

where

• Y _i is the logarithm of the observed failure time T _i , $\{i=1, \cdots, n\},$ $T_i\sim \mbox{BS}(\alpha_i,\beta_i)$ and the distribution of T _i depends on p explanatory variables $\vec{x_i}=(x_{i1},\cdots,x_{ip});$

• $\boldsymbol{\beta}=(\beta_1,\cdots,\beta_p)$ is the vector of unknown parameters associated with the explanatory variables;

• ϵ _i is the random error of the model with $\epsilon_i\sim \mbox{log-BS}(\alpha,0)$, i.e., $\epsilon_i\sim \mbox{SHN}(\alpha,0,2)$, $\{i=1,\cdots,n\}.$

22.2 Estimation

Rieck and Nedelman in [6] proposed point estimation of parameters of the model (22.4) by maximum likelihood and least squares (LS). In this work, we consider MCMC simulations to get posterior densities of parameters of interest.

22.2.1 Maximum Likelihood (ML)

Consider n independent observations $y_1, y_2, \cdots, y_n$ under the model (22.4), where $\epsilon_i \sim\mbox{SHN} (\alpha, 0,2).$ The likelihood function for $\boldsymbol{\varphi} = (\boldsymbol{\beta}^\top, \alpha)^\top$ is given by

$$L(\boldsymbol{\varphi};y_i,x_i)=\prod_{i=1}^n \frac{1}{\alpha\sqrt{2\pi}}\cosh\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}} 2\right) {\rm exp}\left\{-\frac{2}{\alpha^2}\sinh^2\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}} 2\right)\right\}.$$

(22.5)

The log likelihood function is expressed as

$$l(\boldsymbol{\varphi};y_i,x_i)\propto -n\ln \alpha + \sum_{i=1}^n\ln \left[\cosh\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}}{2}\right)\right] -\frac{2}{\alpha^2}\sum_{i=1}^n\sinh^2\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}} 2\right).$$

(22.6)

Considering

$$W_i=\frac{2}{\alpha}\cosh\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}}{2}\right) \quad{\rm and} Z_i=\frac{2}{\alpha}\sinh\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}}{2}\right),$$

the expression (22.6) may be rewritten as

$$l(\boldsymbol{\varphi};y_i,x_i)\propto \sum_{i=1}^n \ln W_i-\sum_{i=1}^n \frac{Z^2}{2}.$$

The score functions for $\boldsymbol{\beta}$ and $\alpha$ are given respectively by

$$\frac{\partial l(\varphi;y_i,x_i)}{\partial\beta_i}=\frac{1}{2}\sum_{i=1}^n x_{ij}\left\{Z_iW_i-\frac{Z_i}{W_i}\right\}, j=1,\cdots,p \mbox{ and}$$

$$\frac{\partial l(\varphi;y_i,x_i)}{\partial\alpha}=-\frac{n}{\alpha}+\frac{1}{\alpha}\sum_{i=1}^n \sinh\left(\frac{y_i-\mathbf{x_i}^\top\boldsymbol{\beta}}{2}\right).$$

(22.7)

From (22.7) it is possible to obtain an expression for the maximum likelihood estimation (MLE) of α² in terms of MLE vector $\boldsymbol{\beta}$, given by

$$\hat{\alpha}^2=\frac{4}{n}\sum_{i=1}^n \sinh\left(\frac{y_i-\mathbf{x_i}^\top\hat{\boldsymbol{\beta}}}{2}\right).$$

However, the MLE of $\boldsymbol{\beta}$ must be obtained numerically. The authors propose an iterative procedure to obtain these estimators based on ordinary least squares estimators (LSE).

22.2.2 Least Squares (LS)

According to Rieck and Nedelman in [6], the estimation by ordinary LS produces explicit solutions for $\boldsymbol{\varphi}$ in (22.4). Although LS is not as efficient as ML, the estimates are unbiased. The $\boldsymbol{\beta}$ estimate is highly efficient for small values of α.

In model (22.4), E$[\epsilon_i]=0$ and Var$[\epsilon_i]=4\omega(\alpha)$. Since the observations $y_1,\cdots,y_n$ are independent, Cov$(\epsilon_i,\epsilon_j)=0$ $\{i,j=1,\cdots,n\}$, and so the best linear unbiased estimator is

$$\hat{\varphi}=(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{Y},$$

with covariance matrix Cov$(\hat{\varphi})=4\omega(\alpha)(\mathbf{X}^\top\mathbf{X})^{-1}$, and an unbiased estimator for $\omega(\alpha)$ is $\hat{\omega}(\alpha)=\sum_{i=1}^n\frac{(y_i-\mathbf{X}_i^\top\boldsymbol{\hat{\beta}})^2} {4(n-p)}.$

22.2.3 Bayesian Approach

For the Bayesian approach, we assumed independent priors gamma density function for the shape parameter, $\alpha\sim$Gama$(\xi_0,\delta_0)$ and normal density function with mean zero for the parameters of the linear predictor coefficients, $\beta_i\sim$ N$(0,\sigma_{bj}^2),$ $\{j=1,\cdots,p\}$. Thus, a priori density of $\boldsymbol{\varphi}$ is given by

$$\pi(\boldsymbol{\varphi})=\pi(\alpha,\boldsymbol{\beta})\propto \alpha^{\delta_0-1}{\rm exp}\{-\alpha\xi_0\} \prod_{j=1}^p{\rm exp}\left\{-\frac{\boldsymbol{\beta}^2}{2\sigma_{bj}^2}\right\}, j=1,\cdots,p.$$

Combining this expression with the likelihood function (22.5), we obtain the posterior density

$$\begin{aligned}\pi(\boldsymbol{\varphi}|y_i,x_i)&=\pi(\alpha,\boldsymbol{\beta}|y_i,x_i)\propto \prod_{i=i}^n\alpha^{\xi_0-2}\cosh\left(\frac{y_i-\mathbf{x}_1^\top\boldsymbol{\beta}} 2\right)\nonumber\\ &{\rm exp}\left\{-\frac{2}{\alpha^2}\sinh^2\left(\frac{y_i-\mathbf{x}_1^\top\boldsymbol{\beta}} 2\right)-\alpha\xi_0\right\}\nonumber\\ &\prod_{j=i}^p{\rm exp}\left\{-\frac{\boldsymbol{\beta}^2}{2\sigma_{bj}}\right\}\nonumber\\ &\propto\prod_{i=i}^n\prod_{j=i}^p W_i\alpha^{\xi_0-1}{\rm exp}\left\{-\frac{Z_i^2}{2}-\alpha\xi_0-\frac{\boldsymbol{\beta}^2}{2\sigma_{bj}^2}\right\},\end{aligned}$$

(22.8)

where

$$W_i=\frac{2}{\alpha}\cosh\left(\frac{y_i-\mathbf{x}_i^\top\boldsymbol{\beta}}{2}\right) \quad{\rm and} Z_i=\frac{2}{\alpha}\sinh\left(\frac{y_i-\mathbf{x}_i^\top\boldsymbol{\beta}}{2}\right).$$

From (22.8), it is not simple to find the marginal posterior density for the model’s parameters analytically. Notwithstanding, with WinBUGS, we may get the posterior density simulated by MCMC.

In the case of one explanatory variable, $\mu=\mathbf{x_i}^\top\boldsymbol{\beta}=\beta_0+\beta_1x$, the posterior density has the form

$$\begin{aligned} \pi(\alpha,\beta_0,\beta_1|y_i,x_i) &\propto\prod_{i=i}^n W_i\alpha^{\xi_0-1}{\rm exp}\left\{-\frac{Z_i^2}{2}-\alpha\xi_0-\frac{\beta^2}{2\sigma_{b0}^2} -\frac{\beta^2}{2\sigma_{b1}^2}\right\}\nonumber.\end{aligned}$$

A possible implementation for this with priors $\alpha\sim$ Gama$(0.001,0.001)$ and $\beta_i\sim$ N$(0,100)$ $\{j=1,2\}$ is given below.

model

c < -10

{

for(i in 1:n)

{

u[i]=b0+b1*x[i]

logver[i]<–log(a)+log(cosh((y[i]-u[i])/2))-(2/pow(a,2))* pow(sinh((y[i]-u[i])/2),2) zeros[i]<-0

aux[i]<–logver[i]+c

zeros[i] dpois(aux[i])

}

b0 dnorm(0,0.01)

b1 dnorm(0,0.01)

a dgamma(0.001,0.001)

}

Censored Data

In the case where random censoring is observed, with δ _i the failure indicator variable ($\delta_i=1$ for failure and $\delta_i=0$ for censoring) under the model (22.4), the likelihood function in terms of W _i and Z _i is given by

$$L(\boldsymbol{\varphi};y_i,x_i)=\propto\prod_{i=i}^n \left[\frac{W_i}{2}{\rm exp}\left\{-\frac{Z_i^2}{2}\right\}\right]^{\delta_i} \left[1-\Phi(Z_i)\right]^{1-\delta_i},$$

where $\Phi(.)$ is the standard normal CDF. Combining with the prior $\pi(\boldsymbol{\varphi})$, the posterior density can be obtained:

$$\pi(\varphi|y_i,x_i) \propto\prod_{i=i}^n\prod_{j=i}^p \left[\frac{W_i}{2}{\rm exp}\left\{-\frac{Z_i^2}{2}\right\}\right]^{\delta_i} \left[1-\Phi(Z_i)\right]^{1-\delta_i}\alpha^{\xi_0-1} {\rm exp}\left\{-\alpha\xi_0-\frac{\beta^2}{2\sigma^2_{bj}}\right\}.$$

Simulations of marginal posterior densities can be obtained in WingBUGS with the following implementation (considering one explanatory variable).

model

{

c<-10

for(i in 1:n)

{

u[i]=b0+b1*x[i]

logver[i]<-delta[i]*(-log(a)+log(cosh((y[i]-u[i])/2))-

(2/pow(a,2))*pow(sinh((y[i]-u[i])/2),2))+ (1-delta[i])*log(1-phi(2/a*sinh((y[i]-u[i])/2)))

zeros[i]<-0

aux[i]<–logver[i]+c

zeros[i] dpois(aux[i])

}

b0 dnorm(0,0.01)

b1 dnorm(0,0.01)

a dgamma(0.001,0.001)

22.3 Application

A data set of 46 observations from Brown and Miller’s biaxial fatigue test (1978) [3] was analyzed by Rieck and Nedelman [6] and has been reviewed.

In the test, cylindrical specimens were subjected to axial loads and torsion on constant amplitude cycles to failure. The response variable is the number of cycles to the occurrence of failure N and the explanatory variable is the work per cycle in $M_j/m^3$. Hence, the interest is to model the number of cycles until failure.

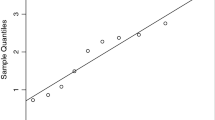
Figure 22.1 shows an asymmetric behavior of response variable indicating that a Birnbaum–Saunders regression model can be appropriate. Let n _i be independent random variables such as $N_i\sim{\mbox BS}(\alpha,\mu_i), \{i=1,\cdots, n\}$. From empirical laws, consider the model

Fig. 22.1

As the histogram of the response variable has an asymmetric behavior, and it is concentrated in the range 0–1000, a Birnbaum–Saunders regression model is appropriate

$$\ln(\mu_i)=\beta_0+\beta_1\ln(W_i), i=1,\cdots,46,$$

where $x=\log(W_c)$ and W _c is the work per cycle.

The results of the model fitted under classical perspective are shown in Table 22.1. The second column corresponds to the numeric solution from the analytical derivatives using the package optim from R.

Table 22.1 Estimates of Birnbaum–Saunders log-linear model under classical approach

Table 22.2 corresponds  to  the  results under  the Bayesian framework by the WinBUGS’ implementation, considering distributions Gamma(0.001; 0.001) e Unif(0;10) as priori distribution for α and N(0,100) for β _j , $\{j=1,2\}$. Chains with 21,000 iterations were considered, with just a spacing of length 10 to minimize the problem of simulated series autocorrelation. To reduce the effect of initial points, the first 1000 iterations were discarded.

Table 22.2 Estimates of Birnbaum–Saunders log-linear model under Bayesian approach

For all situations, it was considered that $\alpha^{(0)}=0.5$ and LSE for $\beta_0^{(0)}=12.211$ and $\beta_1^{(0)}=-1.655$ as initial values for simulations.

The convergence of the chains simulates was previously verified. Figures 22.2 and 22.3 correspond to posterior density function and its simulation history, according to Table 22.2.

Fig. 22.2

Posterior densities and their simulation history. With prior $\alpha\sim \mbox{Gama}(0.001;0.001)$, $\beta_0\sim \mbox{N}(0,100)$ and $\beta_1\sim \mbox{N}(0,100)$

Fig. 22.3

Posterior densities and their simulation history. With prior $\alpha\sim \mbox{U}(0;10)$, $\beta_0\sim \mbox{N}(0,100)$, and $\beta_1\sim \mbox{N}(0,100)$

Based on our results, we note that the prior distribution for α does not appreciably affect the results, the estimates are similar and the Deviance information Criteria (DIC) for the model selection does not change considerably. We can also observe similar estimates from the classical and Bayesian framewok. A residual analysis for classical fit is presented by Dos Santos [4].

Censored Data

In order to make inference in the presence of censored data, different percentages of random censoring were considered for biaxial fatigue data set. The observations were artificially censored. The estimates are shown in Table 22.3 and marginal posterior densities for 10, 30 and 45 % of censored observation are presented in Figs. 22.4, 22.5, and 22.6, respectively.

Fig. 22.4

Marginal posterior densities of BS log-linear model with 10 % of censoring

Fig. 22.5

Marginal posterior densities of BS log-linear model with 30 % of censoring

Fig. 22.6

Marginal posterior densities of BS log-linear model with 45 % of censoring

Table 22.3 Results under Bayesian approach of model fitted BS log-linear model for random censoring of biaxial fatigue data set

We notice that as the censure increases, there is low accuracy due to increase of standard error. We also notice a smaller DIC for low percentage of censoring. From the posterior density for α, the right tail becomes heavier when the percentage of censoring increases.

22.4 Discussion

A motivation for this work was to fit the Birnbaum–Saunders log-linear model proposed in 1991 by Rieck and Nedelman under a Bayesian approach and to compare it with the usual classical fit, which is based on the asymptotical properties for the estimator.

In this study, we show the posterior density distribution assuming independent priors—gamma density function for the shape parameter and normal density function with mean zero for the parameters of the linear predictor coefficients. Also we consider right-censored data and in both situations, it is not easy to obtain analytical expressions for the marginal posterior densities for the parameters of interest. However, we can see that WinBUGS is a useful tool because it allows one to obtain marginal posterior densities considering MCMC with a simple implementation.

Based on the application results, large differences were not observed between the classical and Bayesian framework. Furthermore in all situations, the Markov chains converged quickly and the computational time was short. Notwithstanding, it could be appropriate to conduct a simulation study to determine the optimal values for the parameters of the priori density function.

Since the fit of the Birnbaum–Saunders log-linear model under a Bayesian approach was suitable, it will be a good idea to make a Bayesian residual analysis.