Mathematics and Infinity in Descartes and Newton

Abstract

The concept of the infinite has often been regarded as inherently problematic in mathematics and in philosophy. The idea that the universe itself might be infinite has been the subject of intense debate not only on mathematical and philosophical grounds, but for theological and political reasons as well. When Copernicus and his followers challenged the old Aristotelian and Ptolemaic conceptions of the world’s finiteness, if not its boundedness, the idea of an infinite, if not merely unbounded, world seemed more attractive. Indeed, the infinity of space has been called the “fundamental principle of the new ontology” (Koyré in From the Closed World to the Infinite Universe. Johns Hopkins University Press, Baltimore, 1957, p. 126). Influential scholarship in the first half of the twentieth century helped to solidify the idea that it was specifically in the seventeenth century that astronomers and natural philosophers fully embraced the infinity of the universe. As Kuhn writes in his Copernican Revolution (1957, p. 289): “From Bruno ’s death in 1600 to the publication of Descartes ’s Principles of Philosophy in 1644, no Copernican of any prominence appears to have espoused the infinite universe, at least in public. After Descartes , however, no Copernican seems to have opposed the conception.” That same year saw the publication of Alexandre Koyré ’s sweeping volume about the scientific revolution, From the Closed World to the Infinite Universe. The decision to describe and conceive of the world as infinite might be seen as a crucial, if not decisive, aspect of the overthrow of Scholasticism. As Kuhn and Koyré knew, one finds a particularly invigorating expression of this historical-philosophical interpretation in an earlier article by Marjorie Nicholson (Studies in Philology 25:356–374, 1929, p. 370).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The concept of the infinite has often been regarded as inherently problematic in mathematics and in philosophy. The idea that the universe itself might be infinite has been the subject of intense debate not only on mathematical and philosophical grounds, but for theological and political reasons as well. When Copernicus and his followers challenged the old Aristotelian and Ptolemaic conceptions of the world’s finiteness, if not its boundedness, the idea of an infinite, if not merely unbounded, world seemed more attractive. Indeed, the infinity of space has been called the “fundamental principle of the new ontology” (Koyré 1957, p. 126). Influential scholarship in the first half of the twentieth century helped to solidify the idea that it was specifically in the seventeenth century that astronomers and natural philosophers fully embraced the infinity of the universe. As Kuhn writes in his Copernican Revolution (1957, p. 289): “From Bruno ’s death in 1600 to the publication of Descartes ’s Principles of Philosophy in 1644, no Copernican of any prominence appears to have espoused the infinite universe, at least in public. After Descartes , however, no Copernican seems to have opposed the conception.” That same year saw the publication of Alexandre Koyré ’s sweeping volume about the scientific revolution, From the Closed World to the Infinite Universe. The decision to describe and conceive of the world as infinite might be seen as a crucial, if not decisive, aspect of the overthrow of Scholasticism. As Kuhn and Koyré knew, one finds a particularly invigorating expression of this historical-philosophical interpretation in an earlier article by Marjorie Nicholson (1929, p. 370):

Few, however, seem to have noticed the effect of the Cartesian idea of indefinite extension upon one of the most significant of all seventeenth-century conceptions: the idea of infinity, the problem of the possibility of an infinite number of worlds, or of a universe infinitely extended. In this conception lies the key to the characteristic form taken in England, at least, by the idea of progress, and to one of the most profound changes which occurred in seventeenth-century thought; for the real change in men’s conceptions of themselves and of the universe came less through Copernicanism than through the expansion of the boundaries of thought through the idea of infinity.

Thus before Koyré and Kuhn ’s analyses, Nicholson had already forcefully argued that we should not focus all our historical attention on developments in astronomy proper, for it was actually Descartes ’s idea of the indefinite extension of the world that helped to engender the most important late seventeenth century developments in England, which centered around Isaac Newton ’s new conception of the universe.

Nicholson was careful not to attribute the idea of an infinite universe to Descartes himself; instead, in his main work in natural philosophy, the Principia Philosophiae (1644), the text Kuhn also cites in this connection, he deliberately avoided this idea, arguing instead for what he consistently called the “indefinite extension” of the material world. So if Nicholson is right in suggesting that by century’s end philosophers in England like Newton were ready to embrace the world’s infinity wholeheartedly—and she surely is right about that notion, as we will see—how did the dialectic from Cartesian indefinite extension to Newtonian infinity actually work? Was Descartes ’s rejection of the Scholastic bounded world the key maneuver, or was the English reaction to Descartes ’s unbounded but nonetheless finite world also a key aspect of the story? The suggestion from Koyré , Kuhn , and perhaps even Nicholson , is that it was the Cartesian worldview that was the key move toward the infinite universe, but as we will see, there are strong reasons to think that there was actually a three-stage dialectic in the seventeenth century, from the Scholastic finite bounded world, to the Cartesian unbounded but still finite world, and finally to the infinite world of Newton .

There is an even more remarkable aspect to this story. One might have thought that Newton ’s infinite world arises in the context of his thinking about the laws of motion, and especially the idea that the true motion of an object must be understood as its absolute motion, its motion with respect to absolute space. For that idea might reasonably be interpreted as entailing the conclusion that space itself, without relation to any objects or relations, must be infinite (given that Newton lacked inertial frames or the like). That may in fact be the case, or one might argue that a merely potentially infinite space is sufficient for absolute motion, since it can be arbitrarily large. Either way, there is another aspect to the dialectic. Newton explicitly adopts a critical attitude toward Cartesian finite but unbounded space on the grounds that it cannot accommodate the presence of the actually infinite creator of the world (cf. Harries 2001, p. 143). Newton ’s world must be actually infinite because God’s infinity has a spatial character.

2 Descartes ’s Finite Unbounded World

In his original treatise in natural philosophy, Le Monde, which Descartes withdrew from publication after Galileo ’s house arrest in 1633, we find a strong endorsement of the Copernican view of the earth’s motion, a view that Kuhn links to the idea of an infinite world. But since Le Monde did not see the light of day, Kuhn carefully notes that it was Descartes ’s Principia Philosophie, published in Amsterdam eleven years later, which played a key role in the shift toward reconceiving of the material world. As Nicholson notes, Descartes did not simply embrace the world’s infinity in his text; instead, as with the question of the earth’s motion, he articulated a complex view that has exercised his interpreters ever since. Like Galileo before him, he was “wary of infinites and infinitesimals” (Mahoney 1997, p. 745). His view centered on his idea of the world’s indefinite extension, a concept introduced in part because Descartes explicitly contends that the concept of the infinite remains problematic. He makes this point near the very beginning of Principia Philosophiae, in section 26 of part one, noting that there are many authors who seek out paradoxes of one kind or another as soon as one contends that some item is infinite:

26. We should never enter into disputes about the infinite; things in which we observe no limits, such as the world’s extension, the division of the parts of matter, the number of stars, etc., should be regarded as indefinite.

Thus we will never be involved in tiresome disputations about the infinite. Since we are finite, it would be absurd for us to determine anything concerning the infinite, for this would be to attempt to limit it and comprehend it. So we shall not respond to those who ask if half an infinite line would also be infinite, or whether an infinite number is odd or even, and the like; for unless one regards one’s own mind as infinite, one should not judge such matters. And for us, with anything in which we are unable to discover a limit from point of view, we shall not affirm that it is infinite, but instead consider it indefinite. Thus, since there is no imaginable extension that is so great that we cannot understand the possibility of a greater one, we shall describe the magnitude of possible things as indefinite. And however many parts a body is divided into, each of the parts can still be understood to be divisible, so we shall think that quantity is indefinitely divisible. And no matter how great we imagine the number of stars to be, we still think that God could have created more, so we shall suppose their number is indefinite; and the same with the rest. (AT 8a: 14–15)

Descartes ’s motivation for introducing the concept of the indefinite into his metaphysics is clear: if one mentions infinite quantities, such as an infinite line, one is forced into “tiresome” debates and arguments. So one ought to avoid speaking of infinity altogether (except in the case of the divine, of course).¹ But there certainly are phenomena, processes and objects that would appear to be something other than ordinary finite items—these are items that at least appear to have no limits in the ordinary sense. For instance, if we divide a table in half, we recognize that we can divide each of those halves in half, and do the same again: at least as a conceptual matter, leaving aside any particular physical or nomological constraints on the process of division, there does not appear to be any limit to this process. So to recognize this fact, even while avoiding the idea that the table is infinitely divisible, Descartes declares that we should regard the table as indefinitely divisible.²

Some of Descartes ’s readers immediately regarded his distinction between the infinite and the indefinite as echoing Aristotle ’s distinction between actual and potential infinity, where the latter is explicitly introduced in order to avoid paradoxes involving the former. Aristotle ’s discussion of infinity (Bowin 2007) reflected the idea that there are various reasons for discussing infinite quantities: two of them are the possible use of such quantities in mathematics, and the suggestion, often attributed to Zeno , that ordinary phenomena such as a person running or a bird flying might somehow involve infinite quantities.³ Of course, these two arenas need not force one to accept the idea of an infinite quantity. There was a strong tendency in some Greek authors, e.g., to insist that even in Euclidean geometry, we need not explicitly conceive of any object of our analysis as bearing an infinite property or feature: we can think of a line or of a space as extending an arbitrary distance, but need not think of it as extending infinitely (Moore 1990, p. 43), and Aristotle apparently endorsed that view (Bernadete 1964, p. 14). Nonetheless, there are many questions about quantities in mathematics, and the examples attributed to Zeno were often held to pose an especially difficult problem, one that Aristotle took seriously in the Physica. In that text, he outlines his general approach as follows, having just argued that there is no body that is actually infinite:

But on the other hand to suppose that the infinite does not exist in way leads obviously to many impossible consequences: there will be a beginning and an end of time, a magnitude will not be divisible into magnitudes, number will not be infinite. If, then, in view of the above considerations, neither alternative seems possible, an arbiter must be called in; and clearly there is a sense in which the infinite exists and another in which it does not.

We must keep in mind that the word ‘is’ means either what potentially is or what fully is.

Further, a thing is infinite either by addition or by division.

Now, as we have seen, magnitude is not actually infinite. But by division it is infinite. (There is no difficult in refuting the theory of indivisible lines.) The alternative then remains that the infinite has a potential existence. (Physica 206^a 8–18; transl. Aristotle 1908-)

Aristotle then used his distinction between potential and actual infinity to solve various problems, including the problem of how to think about the paradoxes attributed to Zeno .⁴ Whether this maneuver enables Aristotle to deal successfully with Zeno ’s paradoxes is an open question. But there is no doubt that his distinction enabled many later philosophers to think that they had avoided the fundamental problems associated with the idea of infinite quantities (Bernadete 1964, pp. 53–57).

Descartes employs his distinction between the infinite and the indefinite once again in a letter to Clerselier , the editor of his correspondence in the 1650s, aimed at explicating some of the ideas in the third meditation, which of course attempts to prove the existence of God, an actually infinite being. On 23 April 1649, amidst his correspondence with More among others, he writes:

By infinite substance I understand a substance that has perfections that are true and real, actually infinite and immense. This is not an accident superadded to the notion of substance, but the very essence of substance taken absolutely and limited by no defects; such defects, in regard to substance, are accidents; but infinity or infinitude is not. It should be remarked that I never use the word infinite for signifying solely the lack of limits, which is negative and to which I have applied the word indefinite, but for signifying a real thing, which is incomparably greater than all those which are in some way limited. (AT 5: 355–56)

Descartes seems to indicate here that the word ‘infinite’ is reserved for referring to a being that has perfections within its very essence, rather than as features added to it. In contrast, the word ‘indefinite’ is reserved for referring to entities that lack limits of one kind or another. If it is merely the case that an entity lacks limits of some kind, then in the Cartesian system the word ‘infinite’ must not be applied to it.

Descartes holds at least two clear views in this area designed to express our positive knowledge in metaphysics: first, we know that we are finite; second, we know that God is infinite. The question is, has he expressed a third view using his concept of the indefinite? Many readers regard this idea as ambiguous, and in fact, as ambiguous in a twofold manner, with an intersection between them. For starters, it is ambiguous between these two claims: (1) all actual entities and processes are either finite or infinite (only God falls into the latter category), so “indefinite” items are possible entities and processes; and, (2) some actual entities and processes are indefinite. The reason to endorse (1) is clear: in the examples he presents, Descartes does not focus on the indefinite property of any actual entities or processes. Instead, he focuses on the fact that possible objects—like a possible greater extension than the actual extension in the world—possible processes—like a possible process of dividing a material body into its constituents—and counterfactual possibilities—like the fact that God could have created more stars than currently exist—should be regarded as being indefinite, rather than infinite, in character. This has led some readers to infer that Descartes did not claim explicitly that any actual object, event or process is itself indefinite.

However, these considerations are not decisive, because Descartes also seems to contend that the material world itself—which is identical to space or extension—is indefinite. Since the world is actual, one has a reason to endorse (2) above. But we then find that (2) itself is ambiguous, between the following two claims: (2a) there are actual items that are indefinite, that is, which are neither finite nor infinite; and, (2b) as far as our knowledge reaches, we cannot say whether certain items are finite or not, so we regard them as indefinite. Not surprisingly, given these two potential disambiguations of the Cartesian concept of the actual indefinite, interpreters of Principia Philosophiae have articulated an epistemic construal and a metaphysical construal of Descartes .

On the epistemic construal (cf. Ariew 1987), the view reflects a fundamental limit to human knowledge: we cannot perceive any limits to the material world, indeed, we cannot even conceive of it as having any limits, but for all that, we do not have a positive conception of its infinity, as we do in the case of God.⁵ So the appellation indefinite merely reflects our lack of knowledge. No actual item within our ontology is anything other than finite or infinite; nothing can be indefinite itself. This interpretation immediately raises a question: how can Descartes contend both that it is inconceivable that matter should have limits and that for all we know, the world might actually be finite and therefore have limits after all? Surely from the premise concerning inconceivability we can derive the conclusion that the world cannot be finite. But this inference is unacceptable for Descartes : in the Cartesian system, the fact that I cannot conceive, e.g., how “2 + 2 = 5” could possibly be true does not entail that it cannot be true—it simply means that God’s ways are beyond my understanding (recall the doctrine of the eternal truths). This may also be bolstered by Margaret Wilson ’s famous argument: Descartes ’s claim that it is inconceivable that the world is limited is not identical to the claim that I have a clear and distinct perception that the world is unlimited (Wilson 1986, pp. 349–50). I simply cannot conceive that it is limited. Hence the inconceivability of matter’s finitude is compatible with its actual finitude. Defenders of the epistemic construal might agree.

One benefit of this epistemic interpretation is that it seems to capture a significant aspect of Descartes ’s elaboration of his view: when discussing items or processes or events that are said to be indefinite, he lists various possibilia (e.g., the potential division of an object). This fits nicely with the view that all actual items, processes and events must be either finite or infinite. We would then speak of various possibilities as involving indefinite quantities (or something analogous) on the grounds that we lack the relevant knowledge of such items. Perhaps this idea would be supported by the thought that we do not obtain knowledge of such possibilia until they become actual, at which point they are either finite or infinite. Of course, the actuality of any such possible item does not entail that we have obtained, or can obtain, knowledge of it, but it does mean, perhaps, that it is knowable in some specifiable sense. Clearly, puzzles abound in this area.

On the metaphysical construal, we deny that Descartes is making any epistemic point, contending instead that there are actually three metaphysical categories into which everything fits: there are the finite things, such as me and the White House; there is the one infinite thing, viz., God; and then there are the indefinite things, such as space, i.e., the material world. What does this mean? Some have argued that it is best to view this idea through an Aristotelian lens: whereas Descartes thinks of God as actually infinite, as a completed infinity of which we have a positive conception, he thinks of the material world as merely potentially infinite, as an item that is limitless or unbounded, but actually finite. The clam that space or matter has no limits is compatible with the idea that it is potentially infinite, for the latter entails that there is no last part of space, or smallest piece of matter: for any given place, P, or any given bit of matter, M, we have P + n and M + n, their respective successors. However, the distinction between finite and indefinite items requires clarification, for any potentially infinite item is still actually finite, even if it has no limits.⁶ So one possible reading is this: unlike the finite items, which have limits (whether we perceive or recognize them or not), the indefinite items are also finite, but lack any such limits. Whether this reading can be rendered rigorous is a remaining question that I will not tackle here.⁷

As Wilson showed some time ago, it is difficult to resolve the debate between the epistemic and the metaphysical interpretations of the Cartesian view because there are texts that count in favor of each of them, and there is no clear way of determining a priority among those texts (Wilson 1986). Happily, there is a meta-level view that captures the commonality of the epistemic and the metaphysical interpretations. The meta-level claim is this: Descartes argued that if we limit ourselves to expressing our knowledge, we must say that God alone is actually infinite—we do not know anything else that is actually infinite. Otherwise put, we lack a “positive” conception of any other actually infinite item. This is compatible with both the epistemic and the metaphysical interpretations because each can provide an analysis of what this claim means. On the epistemic construal, the claim means that although space may be infinite, we cannot know, or even conceive of the possibility, that it is. What the claim means on the metaphysical construal is that space is known not to be actually infinite; instead, it is potentially infinite. Thus it remains the case that the two interpretations are incompatible with one another, but each is compatible with the claim that we lack a positive conception of any actually infinite item (other than God) because each can construe that claim in a way that renders it compatible with the relevant interpretation.

Descartes clarifies our knowledge that God is actually infinite, along with the relation between that knowledge and our self-knowledge as finite but unlimited (in some sense) beings in a famous passage from the third meditation. It represents part of his attempt to reject an objection to his causal proof of God’s existence. The objection is roughly this: in reply to Descartes ’s argument that only an actually infinite substance (or being) could be the cause of my idea of such a substance, on the grounds that there must be at least as much formal reality in the cause of my idea of an actually infinite substance as there is objective reality in that idea, the objector suggests that perhaps a finite being like me could in fact be the cause if I could simply begin with my limited knowledge and my limited positive features and then increase them “more and more to infinity.” In that case, I could possibly be the cause of my idea of an actually infinite—and perfect—being after all, which would block Descartes ’s argument. One aspect of the objection is this: the idea of an actually infinite being could possibly be caused by a finite being that exhibits characteristics, such as an endless growth in its knowledge, which highlight the fact that it bears a potential infinity.⁸ This aspect of the objection seems reasonable: leaving aside various obvious temporal limits and physiological factors, it does seem unobjectionable to assert that there is no inherent limit to the amount of knowledge a person can achieve, hence each person bears what we might call potentially infinite knowledge. That is, our knowledge is always finite, but perhaps we can regard it as unbounded.

Descartes ’s reply to this objection in the third meditation is illuminating because it reflects his understanding and employment of the distinction between potential and actual infinity:

But none of this is possible. For first, although it is true that there is a gradual increase in my knowledge, and many things are potential and not yet actual, none of this pertains to the idea of God, in which there is absolutely nothing potential; indeed, this gradual increase in knowledge is the surest sign of imperfection. Furthermore, even if my knowledge always increases more and more, I understand that it will never be actually infinite, since it will never reach the point where it is incapable of another increase. In contrast, I take God to be actually infinite [actu infinitum], such that nothing can be added to his perfection. (AT 7: 46–47)

Hence the distinction between actual and merely potential infinity, as Descartes understands it, is crucial because it enables him to argue that there is a clear epistemic difference—a clear difference in our ideas—between a finite being with potentially infinite knowledge and an actually infinite being with actually infinite knowledge. This seems to connect with a difference in the sense in which a finite being like me and the actually infinite being are each unbounded. The former type of being is unbounded in just the sense that she could always add to her knowledge; the latter is unbounded in the sense that it already encompasses an actual epistemic infinity. In that way, the notion that God already knows everything that there is to know is expressed here through the concept of actual infinity.

3 The Cartesian Origins of Newton ’s Infinite World

As with the fundamental idea of inertia and the laws of motion, the rejection of the Aristotelian distinction between the sublunary and the superlunary, and even the scope of natural philosophy, Newton begins where Descartes left off, or more precisely, he begins where the debate between Descartes and More in 1648–1649 left off (Lewis 1953). Whereas Descartes expended considerable energy rejecting Aristotelian ideas within natural philosophy, Newton seems to have believed that such a project would be a waste of time: unlike Descartes and other influential predecessors such as Galileo , Newton does not bother to ridicule such ideas as the Aristotelian definition of motion (much lampooned throughout the century, of course). Instead, he focused his principal critical energies on the Cartesian system. He also follows Henry More ’s detailed critical reaction to Cartesianism, which is most clearly in evidence in the unjustly ignored correspondence between More and Descartes , just before Descartes ’s death. It was More who first criticized and rejected the Cartesian distinction between the infinite and the indefinite in just the way that Newton does in his now famous, unpublished, anti-Cartesian tract De Gravitatione (since it was untitled, it is known after its first line).

In his first letter to Descartes , written on the 11th of December 1648, from Christ’s College, Cambridge, Henry More heaps praise upon his correspondent and then humbly suggests that there are a few arguments and concepts in Principia Philosophiae that puzzle him. One of the most significant is the Cartesian view that space and body are numerically identical; another is the notion that God is not extended, despite the divine omnipresence throughout nature; and a third is the connected view that space or the material world is indefinite rather than infinite (I tackle the question of God’s omnipresence below). About this third issue, More writes:

Fourthly, I do not comprehend your indefinite extension of the world. For this indefinite extension is either infinite simpliciter or infinite only to us. If you mean infinite extension simpliciter, why do you hide your meaning with excessively modest words? If you mean infinite only for us, the extension will in reality be finite, for our mind is not the measure of things or of the truth. (AT 5: 242)⁹

More favors an epistemic construal of the Cartesian doctrine: Descartes must believe that all ontological items are finite or infinite, so by calling something indefinite, he can mean only that the item is actually finite or infinite; it would be “infinite for us” only in the sense of having no perceived limits. It would be an expression of our lack of knowledge.

More ’s criticisms of Descartes set the stage for Newton ’s systematic deconstruction of Cartesian natural philosophy in De Gravitatione. In that text, Newton discusses three Cartesian doctrines regarding infinity. First, he agrees with the view found in the third meditation, for example, that it is an error to say that “we do not understand what an infinite being is, save by negating the limitations of a finite being” (AT 7: 45). Newton says that when we conceive of a limited being—say, a wooden table in front of us—part of our conception of that being is bound up with our conception of its limits. The table of course is bounded by its wooden surface. But when we think of an infinite being, we are conceiving of something that is “maximally positive,” for we are thinking of it as having no features that involve limitations. This idea must obviously be clarified. But what is significant for our purposes is that even in agreeing with Descartes here, Newton may also be diverging from him by holding his view for a reason that Descartes cannot accept. For in this very same paragraph, Newton emphasizes that those who believe that we cannot understand an infinite being should consider the fact that geometers have no difficulty in understanding the infinite: they “accurately” know “positive and finite quantities of many surfaces infinite in length” (De Gravitatione, p. 24). This means that Newton differs from some ancient geometers. It also hints that Newton will diverge from the Cartesian view that there is an important sense in which we cannot fully grasp the infinite being: we can in fact use geometry to assist us in understanding infinite beings, such as infinite objects in geometry. I tackle the dialectic between Descartes and Newton on this issue below.

The second Cartesian doctrine concerns the distinction between the infinite and the indefinite, which Newton decidedly rejects:

If Descartes should now say that extension is not infinite but rather indefinite, he should be corrected by the grammarians. For the word ‘indefinite’ ought never to be applied to that which actually is, but always looks to a future possibility, signifying only something which is not yet determined and definite. Thus before God had decreed anything about the creation of the world (if ever he was not decreeing), the quantity of matter, the number of the stars, and all other things were indefinite; once the world was created, they were defined. Thus matter is indefinitely divisible, but is always divided either finitely or infinitely (Part I, article 26; Part II, article 34). Thus an indefinite line is one whose future length is still undetermined. And so an indefinite space is one whose future magnitude is not yet determined; for indeed that which actually is, is not to be defined, but either does or does not have boundaries and so is either finite or infinite. (De Gravitatione, p. 24)

Here we see that unlike More , who apparently favors an epistemic construal of Descartes ’s view, chiding him for not clearly articulating it, Newton indicates that the concept of the indefinite should be applied only to possibilia, and not to actual items or processes. This certainly captures an aspect of the discussion from part one, section 26 in Principia Philosophiae quoted above, for Descartes ’s examples often involve possible properties and processes, such as the possible—for Descartes , indefinite—division of some quantity. Had Descartes restricted himself to thinking of mere possibilia as indefinite, this objection would lack any bite. But of course, Descartes also claims that the material world itself is indefinite. For Newton , this is an error: we can say that my future granddaughter is of indefinite height, because she does not exist, but we cannot say of my eight-year-old son that his height is indefinite: he is actual, and therefore his height is determined.

The third doctrine discussed by Newton in De Gravitatione is this: we should avoid considering space to be infinite because “it would perhaps become God because of the perfection of infinity.” Here we find a classic pre-modern metaphysical issue. On Newton ’s reading, Descartes sides with the old way of thinking by taking infinity to be a perfection per se; Newton rejects this view, siding with the moderns, which would eventually include Leibniz . From Newton ’s point of view, infinity is not a perfection per se; it is, as it were, value neutral. This is an essential component in the shift from what has been called a metaphysical conception of the infinite, with deep roots in medieval philosophy, to a mathematical conception, which was bound up with new mathematical techniques in the second half of the seventeenth century (Moore 1990). Those techniques will become relevant below.

What then is the outcome of Newton ’s reaction to these three Cartesian doctrines? First, we find that Newton takes us to understand infinite beings; second, we find that he wishes to regard space as infinite rather than as merely indefinite; and third, he denies that his second view raises problems for his view of God.

What is most remarkable about this discussion of Descartes , however, is that this set of passages in De Gravitatione sets the stage for Newton ’s introduction of his most significant, and complex, doctrine concerning both the ontology of space and its exact relation to the divine. More precisely: after criticizing Cartesian metaphysics and natural philosophy in depth in the first eight pages of De Gravitatione, Newton shifts toward a discussion of his own understanding of the ontology of space. He famously begins by denying that space is either a substance or an accident—a view found in other thinkers in this period, such as Charleton and Gassendi , and to some extent, Isaac Barrow —and then presents a series of numbered paragraphs concerning space. The first paragraph details the mathematical figures that exist within space (see McGuire 2007); the second contends that space is “extended infinitely in all directions,” which leads to his long digression concerning the Cartesian doctrine of the indefinite; the third paragraph indicates that the parts of space are motionless, which is an aspect of his anti-Cartesian distinction between space and body. And this is the fourth paragraph:

4. Space is an affection of a being just as a being. No being exists or can exist which is not related to space in some way. God is everywhere, created minds are somewhere, and body is in the space that it occupies; and it follows that space is an emanative effect of the first existing being, for if any being whatsoever is posited, space is posited. (De Gravitatione, p. 25)

We now have two key Newtonian views before us: (1) space is extended infinitely in all directions; and (2) God is everywhere within space. Clearly, (1) contradicts the Cartesian view that space or the material world is merely indefinite, for on either the epistemic or the metaphysical reading of that view, we cannot assert positively that space is infinite (we cannot say that it is actually infinite). If Descartes is understood as holding that the material world is finite—reserving the use of ‘indefinite’ for possibilities—then Newton clearly denies that view as well.

Regarding (2), the claim that God is everywhere in space is precisely one of the ideas that More presses Descartes to accept, without success. So once again, the correspondence sets the stage for De Gravitatione. In More ’s December 1648 letter to Descartes —already quoted from above—we find the following argument:

And, indeed, I judge that the fact that God is extended in his own way follows from the fact that he is omnipresent and intimately occupies the universal machine of the world and each of its parts. For how could he have impressed motion on matter, which he did once and which you think he does even now, unless he, as it were, immediately touches the matter of the universe, or least did so once? This never could have happened unless he were everywhere and occupied every single place. Therefore, God is extended in his own way and spread out; and so God is an extended thing [res extensa]. (AT 5: 238–39)

More is arguing as follows: Descartes must agree that God’s power to act is omnipresent, for that view is entailed by his occasionalism and is also endorsed on more general grounds; yet how could God act on any body to which God was not present? More takes the impossibility of this notion to entail that God must be extended. That is, God must in fact be substantially omnipresent.

One might infer that in De Gravitatione, Newton is explicitly endorsing the view outlined by More in his correspondence with Descartes , for Newton says that “God is everywhere.” But the correspondence actually serves to highlight the fact that Newton ’s claim is ambiguous between: (1) God’s power to act, or God’s action, is everywhere; and, (2) God is actually everywhere, or substantially present everywhere. It is not clear from the text of De Gravitatione that Newton ’s readers have the resources to resolve this ambiguity in his view. It is therefore remarkable that Newton tackles precisely this same issue in the General Scholium, which was added to the second (1713) edition of Principia mathematica under the editorship of Roger Cotes . Indeed, the ambiguity of the idea expressed in De Gravitatione highlights the central importance of the General Scholium for determining Newton ’s considered view on this topic. In the General Scholium, Newton writes:

Every sentient soul, at different times and in different organs of sense and motions, is the same individual person. There are parts that are successive in duration and coexisting in space, but neither of these exist in the person of man or in his thinking principle, and much less in the thinking substance of God. Every man, insofar as he is a thing that has senses, is one and the same man throughout his lifetime in each and every organ of his senses. God is one and the same God always and everywhere. He is omnipresent not only in power, but in substance: for power cannot subsist without substance [Omnipraesens est non per virtutem solam, sed etiam per substantiam: nam virus sine substantia non potest]. (Newton 1972, vol. 2, p. 762)¹⁰

This text clearly resolves the potential ambiguity in De Gravitatione: Newton now argues explicitly that God is substantially present everywhere. This is clearly a strong endorsement of More ’s view against Descartes ’s contrary opinion.

This discussion in the General Scholium is important for another reason. This canonical formulation of the Newtonian conception of the divine being indicates that Newton regarded space itself as actually infinite. Consider this argument:

• 1. God is actually infinite.

• 2. Claim (1) should be read to mean that God’s substance, and not just God’s power, is actually infinite.

• 3. Claim (2) means that God substantially occupies all of space.

• 4. If there were finitely many spatial points, God’s substance would be finite and bounded.

• 5. If there were a potential infinity of spatial points, God would be potentially infinite, that is, finite but unbounded.

• 6. Not 4 and not 5, by 1, 2, 3.

• 7. Therefore, space is actually infinite.

This would appear to show that Newton is fully committed to the idea that space itself is actually infinite, and not merely potentially infinite, as Descartes may have believed. He therefore rushed in where Descartes feared to tread.

This interpretation has two components worth mentioning. First, Newton ’s distinction between virtual and substantial omnipresence, itself a reflection of More ’s debate with Descartes , maps onto the distinction between potential and actual infinity. If God is virtually omnipresent, we might construe this to mean that if God chooses to act within a certain spatial area—say, to make a rainbow after 40 days of rain, or to set a bush alight without it being consumed—then God becomes actually present at that location at that time. But this is not the case for Newton ’s God: in his view, God is already actually present everywhere in space, even when God is not acting or choosing to act in a given location. Because Newton follows More in thinking that God is actually, substantially omnipresent, he must conceive of space as actually infinite.

Second, the interpretation also indicates why we must think of space from an absolute or mathematical perspective, rather than from a relative or common perspective, to capture God’s infinity. Consider this famous passage from the Scholium to the Definitions in Principia mathematica:

Absolute space, by its own nature without relation to anything external, is always homogeneous and immobile. Relative space is any movable measure or dimension of this absolute space, which is determined by our senses from the situation of the space with respect to bodies and is popularly used for immobile space, as where the dimension of space under the earth, in the air, or in the heavens, is determined by its situation relative to the earth. (Newton 1972, vol. 1, p. 46)

We can also profitably map the distinction between absolute and relative space onto the distinction between actual and potential infinity. The conception of relative spaces, relative places, and relative times involves at most the notion of a potential infinity. For we can never say that we have determined the largest possible relative space—we can always take the three objects that are definitive of the space in three dimensions and conceive of them as being a greater distance apart (we might think of this as mapping onto the natural numbers). We also can never contend that we have found the smallest possible relative place, or the shortest possible relative time. What these ideas about space, time and place give us just is the idea of potentially infinite measures of the absolute quantities of space and time. No measure of space or of time will ever be the smallest or largest, shortest or longest—for any arbitrary measure M, there will be what we can call a successor to M, M + n, and this is true along the one temporal dimension and along all three spatial dimensions. This would mean, in turn, that the quantities themselves—absolute or mathematical space and time—would be actually infinite. And it makes good sense, finally, to think of a measure of some actually infinite quantity like Euclidean space itself as involving a merely potential infinity, for the measure can be as large as one likes—it is unlimited in that crucial but restricted sense. (As we know, Newton would not call it indefinite.) When we restrict ourselves to the objects of sense perception, we develop the idea of arbitrarily large—but still finite—measures of the quantities space and time. In order to conceive of space and time themselves, however, we must conceive of two infinite quantities, and in order to do that, in turn, we require the representational capacities of geometry. Sense perception will not do.

Newton is clearly more sanguine than Descartes that philosophers need not fear infinite quantities because geometers and other mathematicians are capable of generating clear ideas of such quantities when pondering lines, planes and other geometric objects, not to mention Euclidean space itself. Descartes ’s avoidance of the infinite was not merely an expression, or a reflection, of his view that we must avoid the Morean idea of God’s extendedness; it was also a reflection of his conviction that various paradoxes and irrelevant questions will attend any discussion of the infinite, at least within philosophy. (Whether Descartes regarded such paradoxes as attending mathematical discussions of the infinite is another, and intriguing, question). If one entertains the thought that a line is infinite, one will be forced into “tiresome” questions about whether half that line is also infinite. Descartes and Newton obviously held many distinct, if not opposed, views in the philosophy of mathematics (Guicciardini 2009), just as they held distinct, if not opposed, views in philosophy more generally. So the question is: did Newton hold some specific view that he regarded as saving him from “tiresome” arguments concerning the infinite?

4 Mathematics, Wallis , and Newton ’s Avoidance of Paradoxes of the Infinite

A key document for understanding Newton ’s view of the infinite falls in between De Gravitatione and the General Scholium.¹¹ It is part of Newton ’s correspondence with Richard Bentley , who was preparing to publish his Boyle lectures in 1693, having recently delivered them—the first in what became a famous series—in London. The entire correspondence is framed by Newton ’s first letter to Bentley , which indicates that he wrote Principia mathematica with an eye toward inclining people to believe in a deity. Questions about infinite space arise immediately in the second paragraph of the first letter, although we do not here see any distinction between actually infinite and potentially infinite space. Bentley is clearly struggling with understanding various kinds of arguments about space and the distribution of matter within it that make use of the notion of the infinite. He apparently does not see how to bolster his criticisms of those who employ concepts of infinite matter or infinite space to oppose him. Intriguingly, Newton chooses to instruct Bentley in thinking about the infinite rather generally by referring him to some basic ideas from John Wallis ’s famous 1656 text, Arithmetica Infinitorum. Newton suggests that if Bentley comes to understand Wallis ’s basic approach to the infinite, he will see that his opponents are committing a fallacy in their arguments against him.

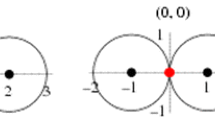
In Arithmetica Infinitorum, which Newton read and commented on as a young man at Trinity College,¹² Wallis sought to create a new “arithmetic of indivisibles” to parallel Cavalieri ’s famous “geometry of indivisibles”.¹³ The goal was to make progress on an old problem tackled by Cavalieri among many others, namely the problem of the “quadrature” of curvilinear figures, which included both the calculation of the area under some curve, and the calculation of a volume enclosed by some curvilinear figure. Wallis argued in particular that any plane surface can be conceived of as comprising an infinite number of parallelograms—this obviously required him to think of the parallelograms as infinitesimals or as indivisibles, since they must somehow sum to a finite quantity expressing a feature of the plane surface. Wallis proposed to use this general method as a means of “squaring the circle.” He tackled the quadrant of the circle as follows (Fig. 1).

Fig. 1

Wallis tackles the quadrant of the circle

The parallelograms comprising the circle would have equal bases a, such that:

$$ {\text{a}} = {\text{R}}/\infty. $$

Wallis argued that we could use a summation of an infinite number of indivisible or infinitesimal quantities in order to make the analysis of some finite quantity—such as the area under a curve—tractable. The key to Wallis ’s summation techniques, which help to transform geometric problems through the use of arithmetic sequences, is to remember that his infinite number of constituents of any finite quantity, such as a plane surface, retain a definite ratio to that original quantity, such that they sum to the original quantity.

Wallis ’s technique obviously raises the question: how precisely are we to think about these infinitesimals or indivisibles? For instance, is an infinitesimal parallelogram, which we are meant to conceive of as a constituent of some finite quantity, distinct from a line? That is, does it lack width altogether? Wallis apparently thought that the infinitesimal parallelogram differed from a line because the former’s width is not zero; instead, its width is smaller than any assignable finite width. One question, of course, is whether such a notion can be made rigorous and clear. For his part, Wallis did not seem especially concerned with this issue (Stedall 2010, p. xxix). He dealt very freely with infinite products and infinitesimals (Guicciardini 2009, p. 146), even as others, most prominently Hobbes , raised objections against his practice.

Wallis ’s general approach to thinking about infinity is important for understanding Newton ’s letter to Bentley of 17 January 1693. The letter bears quoting at length:

But you argue in the next paragraph of your letter that every particle of matter in an infinite space has an infinite quantity of matter on all sides & by consequence an infinite attraction every way & therefore must be in equilibrio because all infinites are equal. Yet you suspect a paralogism in this argument, & I conceive the parallogism lies in the position that all infinites are equal. The generality of mankind consider infinites no other ways than definitely, & in this sense they say all infinites are equal, though they would speak more truly if they should say they are neither equal nor unequal nor have any certain difference or proportion one to another. In this sense therefore no conclusions can be drawn from them about the equality, proportions or differences of things, & they that attempt to do it, usually fall into paralogism. So when men argue against the infinite divisibility of magnitude, by saying that if an inch may be divided into an infinite number of parts, the sum of those parts will be an inch, & if a foot may be divided into an infinite number of parts, the sum of those parts must be a foot, & and therefore since all infinites are equal those sums must be equal, that is, an inch equal to a foot. The falseness of the conclusion shows an error in the premises, & the error lies in the position that all infinites are equal. There is therefore another way of considering infinites used by mathematicians, & that is under certain definite restrictions & limitations whereby infinites are determined to have certain differences or proportions to one another. Thus Dr Wallis considers them in his Arithmetica Infinitorum, where by the various proportions of infinite sums he gathers the various proportions of infinite magnitudes: which way of arguing is generally allowed by mathematicians & and yet would not be good were all infinites equal. According to the same way of considering infinites, a mathematician would tell you that though there be an infinite number of infinitely little parts in an inch, yet there is twelve times that number of such parts in a foot; that is, the infinite number of those parts in a foot is not equal to, but twelve times bigger than, the infinite number of them in an inch. And so a mathematician will tell you that if a body stood in equilibrio between any two equal and contract attracting infinite forces, & if to either of those forces you add any new finite attracting force: that new force how little so ever will destroy the equilibrium & put the body into the same motion into which it would put it were those two contrary equal forces but finite or even none at all: so that in this case two equal infinites by the addition of a finite to either of them become unequal in our ways of reckoning. And after these ways we must reckon if from the consideration of infinites we would always draw true conclusions. (Newton 1959, vol. 3, p. 239)

We might read Newton here as explaining to Bentley that mathematicians such as Wallis , and presumably, Newton himself, have ways of thinking about infinite quantities, or infinite processes—such as infinite divisibility—that avoid the false assumption guiding philosophical discussions, viz. that all infinites are equal. In particular, mathematicians following Wallis contend that the proportion between two finite quantities is preserved when one considers each of those quantities to be infinitely divisible. Hence an infinitely divisible foot remains twelve times the size of an infinitely divisible inch. Since there can be preserved proportions between items that have an infinite feature, such as being infinitely divisible, it follows, says Newton , that there can be different sized infinities. Newton had already grasped this exact point in 1664–1665 as a student at Trinity College reading Wallis (Newton 1967–1981, vol. 1, p. 89). So we have a specific mathematical view that enables us to reject the faulty philosophical presumption guiding reasoning about the infinite.

This conception of infinity in Wallis would also, mutatis mutandis, enable Newton —and Bentley , if he follows Newton in this respect—to evade exactly the kind of “tiresome” questions that Descartes mentions in Principia Philosophiae. If we reject the presumption that all infinites are equal, then we have a straightforward answer to the question Descartes mentions in section 26 of part one of Principia Philosophiae: would an infinite line divided in half result in two infinite lines? The answer is that half an infinite line would remain infinite, and indeed, it would retain its proportion (1/2) to the original line, for as Newton wrote in his undergraduate book, “one infinite extension may be greater than another.”

Wallis ’s approach to thinking about infinity, which guided Newton already in his very earliest days, and which Newton cited 30 years later when instructing Bentley on how to present arguments concerning nature that will incline his readers toward believing in the deity, enabled Newton to accomplish a task that Descartes eschewed explicitly in part one of Principia Philosophiae. Newton explicitly sought to discuss infinity in his philosophizing about the deity, nature and motion because he thought he could avoid exactly the kinds of “tiresome” arguments, and classical paradoxes, that had hampered discussions of the infinite since antiquity. So Wallis ’s bold translation of old geometrical problems into problems involving the summation of arithmetic sequences, where he is willing to sum over an infinite number of parts of finite figures, enables Newton to conclude that one can conceive of infinity in a way that avoids paradoxes. Once liberated from paradox, the philosopher is free to embrace the concept of infinity, and to think of various quantities as infinitely large or as infinitely small. Once that move has been made, in turn, it is not a stretch for the philosopher to contend that we ought to regard space as actually infinite. And that is precisely what Newton contends.

5 Conclusion

Two conclusions seem apt. First of all, it is tempting to interpret Cartesian metaphysics as exhibiting a kind of tension. On the one hand, whatever we make of the distinction between the infinite and the indefinite, it is essential to Descartes ’s view that we regard ourselves as having a positive conception of God’s actual infinity. Indeed, if we lack such a conception, then the argument for the existence of God in the third meditation cannot be valid, for that argument applies the causal principle to the distinction between the objective and the formal reality of my ideas by indicating that a finite substance (like me) cannot be the cause of my idea of an actually infinite substance, for the formal reality of the cause of an idea must be at least equal to the objective reality of the idea itself.¹⁴ So we must have a positive conception of the actually infinite substance or being. On the other hand, it is not clear that Descartes explicates what the content of our positive conception of the one and only infinite substance really is. There are at least two reasons to think that this explication is hampered—I do not say, rendered impossible—by other Cartesian doctrines. First, we know from sections 26–27 of part one of Principia Philosophiae that although we positively know that God has no limits, and is therefore infinite, we are also warned against discussing infinity in any other context because it leads to endless debates and paradoxes. Second, we know from other texts that Descartes exhibits a strong reluctance to discuss God. When discussing More ’s view that God is everywhere, which I have discussed above, Descartes replies (on 15 April 1649) as follows:

This “everywhere” I cannot admit. You seem here to make God’s infinity consist in his existing everywhere, an opinion I cannot accept. I think on the contrary that by reason of his power, God is everywhere; but by reason of his essence, God has no relation to place at all. But since in God power and essence are not distinguished, I think it is better to argue in such cases about our mind or angels, which are more on the scale of our perception, rather than to dispute about God. (AT 5: 343; cf. Lewis 1953, pp. 160–161)¹⁵

More and Newton could certainly be forgiven for concluding that Descartes could not, or did not wish, to articulate what his positive conception of divine infinity is.

Perhaps Descartes can resolve this tension (it may merely be a surface tension). It remains important philosophically, however, because it enables us to see the significance of the fact that we can understand Newton ’s system more thoroughly if we recognize that it lacks any such tension, even on the surface. For in the Newtonian metaphysical system, not only do we have a positive conception of God’s actual infinity as a matter of doctrine, if one can put it that way, but in fact one can give a clear content to that positive conception through the clear mathematical concept of the actual infinity of space. The mathematician has a perfectly clear conception of actually infinite Euclidean space extending in all directions. He knows that this conception is clear because his reasoning about the infinite lies in the Wallisian tradition of thinking about infinity, where various paradoxes and problems are avoided. This idea connects, in turn, to the crucial view that Newton articulates following More ’s rejection of the Cartesian conception of the divine: God is not merely virtually or potentially present everywhere, but substantially or actually present everywhere. So actually infinite space gives us an entrée into achieving a clear conception of God.

This claim leads to the second moral of my story, which is more speculative. We sometimes read of a distinction between mathematical conceptions of the infinite and metaphysical conceptions of it. Moore (1990) makes this distinction the centerpiece of his recent book on the subject. The intriguing thing about Descartes is this: as we learn from the end of part two of Principia Philosophiae, Descartes claims that in “Physica,” he admits and requires only the principles of “Geometria” and “Mathesis abstracta.”¹⁶ But in “metaphysica,” or in “Philosophia prima,” Descartes does not employ a mathematical conception of the infinite: he does not employ geometrical, arithmetic or algebraic notions to conceive of infinity, an infinite being, infinite properties, etc. Instead, Descartes focused on a metaphysical conception of the infinite. And as a result, he expresses a strong reluctance to discuss the infinite, and maintains the old view that the infinite is perfect per se. Newton , in contrast, focused primarily on a mathematical conception of the infinite, which is something that had occupied him since he took extensive notes on Wallis ’s work in his early days at Trinity College. As we have seen, this work remained important to him long after the publication of Principia mathematica. Newton also jettisoned Descartes ’s reticence to speak of the infinite outside of metaphysical contexts. Newton argued, in turn, that we should employ the mathematical conception of the infinite in order to grasp the most important object within traditional metaphysics, the divine being. For Newton , it is precisely the infinity of Euclidean space that enables us to conceive clearly of the infinity of the divine.¹⁷ And now for the speculation: does Newton ’s attempt to give a mathematical conception of infinity logical priority in metaphysical contexts reflect his overarching attitude toward the Cartesian system, namely that it fails to employ mathematical principles in a systematic and substantive way? Descartes proclaimed that he employed and required only the principles of geometry and mathematics, but for Newton , Cartesian physics failed to live up to this billing. Hence Newton famously replied by proclaiming again the need for mathematical principles of natural philosophy. Perhaps we can add to this proclamation an intriguing addendum, viz. the need for the mathematical principles of metaphysics.