Keywords

1 Introduction

Flow affects the blood vessel responses in many ways, through mechanotransduction mechanisms, or by modifying the interactions between blood-borne agonists and cell receptors, especially in the surface boundary layer. In addition to the effects of hæmodynamics and transport, complex interactions exist between the arterial wall components, which are involved in many aspects of vascular adaptation. A better understanding of the principles governing blood-wall interactions and vascular dynamics may prove useful in elucidating some of the mechanochemical aspects of arterial disease. Mathematical description of the ion transport systems that participate in the regulation of vascular tone, and various modelling strategies that incorporate different components of the arterial wall are presented together with computational results.

1.1 Arterial Structure

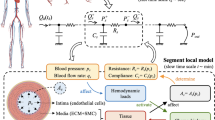
The arterial wall consists of three tunicæ, or layers: the intima, the media and the adventitia, which are, respectively, an inner, middle and outer sheath common to most blood vessels. The intima is made up of a single layer of endothelial cells (ECs), the endothelium, supported by an internal elastic lamina that separates the intima from the media. Described as an active metabolic and endocrine organ, the endothelium forms a selective permeable membrane, mediating many aspects of blood-tissue exchange. The media lies between the internal and the external elastic laminæ, and is composed of smooth muscle cells (SMCs), embedded in a matrix of elastin and collagen fibres, the amount of elastic tissue varying depending on the size of the vessel. In arterioles, it consists largely of smooth muscle (SM) arranged in lamellæ, wrapped around the vessel. Changes in their contractile tension cause the vessel to dilate or constrict, thereby regulating vessel diameter and blood perfusion. Myoendothelial gap junctions provide a communication pathway between the intima and the media. The adventitia, or tunica externa, is a layer of connective tissue, that often contains sympathetic fibre terminals and, in large arteries and veins, the vasa vasorum.

1.2 Arterial Function, Transport and Wall Dynamics

Vascular health is characterised by the ability of a blood vessel to adapt to the variable requirements of its local environment. Atherosclerosis, coronary and carotid artery disease are all associated with a progressive impairment of this vascular reactivity, or endothelial dysfunction [1–3], a consequence of which may be the long term dysregulation of the mechanisms within the SM associated with vascular tone. Vascular tone, i.e. the tension exerted by the vascular SM, is an essential prerequisite for vasodilation. In skeletal muscle, for example, blood flow can be increased up to 20-fold by vasodilation, to meet local demand of exercise [4]. Vascular arteriolar tone also acts at a local level to regulate capillary recruitment and pressure, enhancing perfusion, nutrient and water exchange. At the systemic level, arterial and central venous pressures are modulated by the continuous adaptation of resistance vessel and peripheral vein tone, respectively. In concert with extrinsic mechanisms, vascular tone is controlled by endothelial factors, vasoactive metabolites and extracellular autocrine and/or paracrine signalling molecules. Vascular blood flow regulation involves a hierarchy of control processes. The endothelium exerts its influence primarily at a local or middle level, by modulating the myogenic response. It acts as an active interface, that translates and amplifies the electrochemical signalling between the lumen-side and the SM, where the arterial wall contractile apparatus is located.

1.2.1 Vasomotion

The vascular SM is responsible for spontaneous fluctuations in vessel calibre that are not attributable to heart rate and blood pressure, and are referred to as ‘vasomotion’. Vasomotion was first described more than a century ago, but its physiological significance remains the subject of ongoing debate. The nonlinear nature of the contractile dynamics associated with vasomotion is thought to confer specific hæmodynamic advantage over regular or steady-state flow [5]. At the simplest level, it can be interpreted as a mechanism that continuously redistributes flow to tissue, in order to maintain adequate perfusion. More subtle effects, such as the enhancement of lymphatic drainage and microcirculatory mass transport, may reflect the critical role of smaller arteries and arterioles in regulating interstitial tissue pressure, delivery of oxygen and nutrients and washout of metabolites [6]. Vasomotion becomes particularly prominent in pathological states such as hypoxia and hæmorrhagic shock and may then represent an adaptive dynamic response that maintains or re-establishes flow [7]. Oscillations in the diameter of larger arteries have also been observed in vitro, such as human coronary [8] and pial arteries [9], rabbit small ear [10] and mesenteric arteries [11] or carotid arteries from rats and dogs [12, 13], suggesting a similar origin as that seen in the microcirculation. The interested reader is also referred to the excellent review by Nilsson and Aalkjaer [14].

Vasomotion represents an emergent behaviour associated with a complex dynamical system, whereby coordination of calcium ion \(Ca^{2+}\) oscillations in individual SMCs give rise to ‘higher-level’ phenomena. In isolated vessels, vasomotion exhibits specific patterns of behaviour that are generic to nonlinear physico-chemical systems [15–18]. An important characteristic of nonlinear systems is the co-existence of multiple operating modes with the potential for transitions between them, controlled by single system parameters. State responses of such systems often exhibit completely unpredictable behaviour in response to minute perturbations, allowing the selection of patterns that may confer biological advantage with minimal expenditure of energy.

1.2.2 Characterisation of the Vascular Smooth Muscle

From a dynamical point of view, SMCs are regulators of \(Ca^{2+}\) , which is the catalyst of the cells’ contractile machinery. Intracellular \(Ca^{2+}\) regulation is predominantly controlled by endothelium-mediated polarization and the operating point of ionic transport mechanisms across the cell membrane. For vasomotion to occur, an oscillator must be present; and in order to get macroscopic oscillations of a blood vessel, SMCs’ individual oscillations must be synchronized. Although it is well-established that synchronization of \(Ca^{2+}\) oscillations in SMCs depends on gap junctions, it remains unclear whether the principal coupling mechanism is electrical or chemical in nature [19].

Background to the Model

The excitation-contraction coupling, or electrochemical coupling, is primarily controlled by movements of \(Ca^{2+}\) that permeates from the extracellular space into the cytoplasm. Cytosolic \(Ca^{2+}\) concentration (\([Ca^{2+}]_i\)) is normally maintained at a basal level of \(\sim \)100 nm by the plasma membrane \(Ca^{2+}\) \(-\)ATPase (PMCA), the \(Na^{+}\) \(-\) \(Ca^{2+}\) exchanger (NCX) and the sarco endoplasmic reticulum \(Ca^{2+}\) \(-\)ATPase (SERCA). Vasoconstricting stimuli initiate SM contraction by increasing the \([Ca^{2+}]_i\), to reach the \(\upmu \)M range. Extensive pharmacological probing has characterised vasomotion as the interplay between a ‘slow, intracellular’ \(Ca^{2+}\) oscillator (period \(\sim \)1–5 min) and a ‘fast, membrane’ oscillator (period 5–30 s) operating within the SMC layer of the arterial wall [15, 20]. The intracellular oscillator is identified by the cyclic \(Ca^{2+}\) -induced \(Ca^{2+}\) release (CICR) from ryanodine-sensitive stores of the sarco endoplasmic reticulum (SR/ER). Morphologically, the SR/ER of the SM is spatially heterogeneous and possesses both \(Ca^{2+}\) - and inositol 1,4,5-trisphosphate (InsP\(_3\))-sensitive \(Ca^{2+}\) stores. In addition to the action of CICR and InsP\(_3\)-induced \(Ca^{2+}\) release (IICR), \(Ca^{2+}\) release from the stores is also due to a passive leak from the SR. Refilling of the stores is achieved by the SERCA pump. SERCA pump blockers, such as cyclopiazonic acid and thapsigargin, deplete the \(Ca^{2+}\) stores and eliminate the slow/large amplitude component of vasomotion [17, 20]. After each discharge the stores are replenished by \(Ca^{2+}\) influx across the cell membrane. These \(Ca^{2+}\) currents are primarily conducted via voltage-operated channels (VOCCs), nonspecific cation channels (NSCCs) and \(Na^{+}\)-\(Ca^{2+}\) exchange via the NCX. \(Ca^{2+}\) released by the SR is extruded from the cytosol via the membrane \(Ca^{2+}\) extrusion ATPase, and inhibition of the pump with vanadate produces large constrictor response due to increased \([Ca^{2+}]_i\) [16]. \(Ca^{2+}\) extrusion can also be performed by the NCX with a stoichiometry of 3 \(Na^{+}\)for 1 \(Ca^{2+}\)  [15, 21]. The exchanger can act both as an efflux or an influx (forward/reverse mode respectively) based on the membrane potential being above or below the reversal potential of NCX.

Fig. 1
figure 1

Schematic of a SMC illustrating the coupling between the store-mediated intracellular \(Ca^{2+}\) oscillator and membrane potential fluctuations due to ionic transport mechanisms across the cellular membrane. The system of ordinary differential equations describing these processes is presented below

Full size image

Membrane potential is a distinct dynamic variable determined by the additive contribution of a large number of ionic transport mechanisms (ion channels, pumps, and exchangers). Suppression of \(Ca^{2+}\) -activated \(K^{+}\)(\(K_{Ca}\)) channels (with tetraethylammonium and charybdotoxin), \(Cl^{-}\)channels (by reducing extracellular \(Cl^{-}\)concentration and niflumic acid), the \(Na^+\) \(-\) \(K^{+}\) \(-\)ATPase (by ouabain), or \(Na^{+}\)/\(Ca^{2+}\) exchange (by low extracellular \(Na^{+}\)) consistently attenuate the fast membrane component of arterial vasomotion, suggesting that these transport mechanisms are fundamental in the genesis of vasomotion [22]. The fundamental ionic transport mechanisms involved in the homeodynamics of intracellular \(Ca^{2+}\) are presented in Fig. 1.

1.2.3 The Role of the Endothelium

Through their direct and continuous contact to blood flow, ECs are exposed to the action and combined effect of both mechanical forces and biochemical stimulation. Electrical and chemical signalling between endothelial and SM cells contribute to arterial function via two primary interrelated mechanisms. Longitudinal propagation of dilations-constrictions along the vessel wall constitutes one of these, while the other comprises the effects of the endothelium-derived hyperpolarization factor (EDHF), in which transmission of endothelial hyperpolarization to the SM mediates relaxation. Both pathways are dependent on direct intercellular coupling via gap junctions, allowing the diffusion of ions and small molecules (1 kDa in size) and conferring electrical continuity between coupled cells [23, 24]. The role of the endothelium in vasomotion nevertheless remains unclear. Some studies reported rhythmic contractions in the absence of an intact endothelium, whereas others claimed that its presence is needed for synchronization [25–28]. Such apparently paradoxical findings may reflect the unpredictability that is characteristic of nonlinear systems, and can potentially be clarified by further modelling studies.

Flow Regulation of Agonist- \(Ca^{2+}\) Coupling

Although the results presented below do not include any coupling between endothelial and SM cells, future work will address this point, in addition to considering the effects of mass transport on mobilization of endothelial \([Ca^{2+}]_i\). Using adenine nucleotides as the agonist (mostly adenosine-5’ triphosphate ATP and adenosine diphosphate ADP), many researchers have tried to characterise flow regulation of ATP- and ADP-\(Ca^{2+}\) coupling in the concentration boundary-layer, and the effect of enzymatic degradation at the endothelium [29–37]. Small changes in the model parameters, such as the rate constants for convection of ATP from the bulk fluid to the cell surface or for the degradation and/or production of ATP significantly influence the pattern of catalytic reactions at the endothelium [38]. As we have shown earlier, and as illustrated in Fig. 2, even though the bulk concentration of secreted agonists is low and mostly unaffected by the flow, variations exist at the endothelium, which are nevertheless difficult to quantify numerically. Higher concentration of agonists, and the existence of steep gradients in the boundary layer will be affected by changes in the flow field, potentially generating further signalling cascades. Such propagated effects might constitute elements of an intravascular axis that serves to regulate vascular tone [38–42]. See also the review by Davies on endothelial mechanotransduction [43].

Fig. 2
figure 2

Upper row Distribution on the arterial surface of [ATP] (\(\upmu \)M) during a systole b diastole and [ADP] (\(\upmu \)M) during c diastole. ATP production at the endothelium depends on wall shear stress only. Lower row Distribution on the arterial surface of [ATP] (\(\upmu \)M) during d systole, e diastole and [ADP] (\(\upmu \)M) during f diastole. ATP production at the endothelium depends on wall shear stress and time. The figure is taken from [38]

Full size image

1.2.4 Link to Cardiovascular Disease

We previously demonstrated that specific dynamical transitions, associated phenomenologically with cardiovascular disease, can be readily effected by pharmacological manipulation of cellular mechanisms (e.g. irregular \(Ca^{2+}\) inflow or outflow from the SR/ER via the SERCA and RyR pumps respectively) [44]. Such mechanisms can be probed in a rigorous fashion, providing a broad range of relevant experimental data for model development and validation. There is substantial evidence showing that the prevalence of vasomotion can indeed be altered under specific pathological conditions. In a large proportion of diabetic patients, for example, vasomotion is impaired, and the amplitude of flow-motion is also reduced [45, 46].

The formation of atheromatic plaque in stenosed vessels is another central area of modelling investigation [47–49]. In addition to the effects of hæmodynamics and transport, in early atheroma, there exists complex interactions between the arterial wall components (SMCs and ECs), which cause inflammatory signalling that leads to monocyte accumulation, foam cell degeneration and formation of atheromatous plaque. Such alterations can result in significant modification of the arterial geometry. These contributory factors can thus be incorporated in order to gain insights into potential causes of vascular adaptation.

The role of mathematical/computational modelling in studying cardiovascular disease as an integrated systemic dysfunction is therefore very important. Comprehensive studies of the mechanisms involved in the genesis of disease will require concurrent modelling of endothelial factors, electrical coupling, calcium synchronization and wave propagation as critical components. A first attempt in this direction is presented here.

2 Model

The intracellular oscillator (outlined previously) is modelled as CICR from the SR via ryanodine sensitive \(Ca^{2+}\) channels. This formulation is based on experimental evidence that CICR/IICR can be attributed to distinct store subtypes in rabbit ear arteries [17, 20]. The ryanodine-sensitive channel is modelled as a product of two sigmoidal functions that account for \([Ca^{2+}]\) in the cytosol and \([Ca^{2+}]\) in the SR, in agreement with experimental evidence [50]. There are contradictory observations that \(Ca^{2+}\) oscillations may occur under constant elevated levels of InsP\(_3\), or under fluctuating concentrations of intracellular InsP\(_3\). Considering the dominant modulatory effect of ryanodine on arterial dynamics observed in rabbit ear arteries, we assume \(Ca^{2+}\) release from InsP\(_3\)-sensitive stores to be a constant that increases directly with concentrations of histamine. The effect of IICR is thus included in the coefficient \(A\), that corresponds to \(Ca^{2+}\) uptake/release in the cytosol. Sequestration of \(Ca^{2+}\) by the SERCA pump is represented by a sigmoidal function of intracellular \([Ca^{2+}]\). A passive leak from the SR is included to account for experimental evidence, although it has limited effect on the oscillatory dynamics under physiological conditions [51]. The dominant cell \(Ca^{2+}\) influx pathway in arterial SM is provided by VOCCs. Voltage sensitivity of \(Ca^{2+}\) refilling can account for large-scale vascular contractile activity and synchronization, under conditions of electrical cell-cell coupling [19]. With a reversal potential of \(\sim \)0.1 V and a sigmoidal open state probability centred at \(\sim \) \(-\)0.024 V, VOCCs are maximally active during cellular depolarization, a state generally associated with enhanced vascular contraction [52]. In spite of a central role in \(Ca^{2+}\) transport and the generation of contractile activity, VOCCs account for only up to 10 % of cellular polarization. A number of ionic transport mechanisms that are fundamental in polarization of the arterial wall have also been included in the quantification of SM membrane potential. These are the \(Cl^{-}\)channel, the NCX, known to be central in cardiac muscle contraction, and the \(K^{+}\)channels. With a reversal potential of \(\sim \) \(-\)0.095 V, \(K^{+}\)channels are particularly important in vascular dynamics since they constitute the main hyperpolarizing force in the arterial wall [22]. A large number of \(Ca^{2+}\) -activated \(K^{+}\)channel subtypes have been identified, conventionally grouped as large, intermediate and small conductance channels. In the present formulation, we have grouped all \(K^{+}\)transport activity under a single idealised channel subtype with a linear voltage dependence and a sigmoidal \(Ca^{2+}\) activation. Typically, ionic transport mechanisms are both \(Ca^{2+}\) - and voltage-sensitive, as indeed reflected in the mathematical formulation of each transport component.

2.1 Coupled Intracellular and Membrane \(Ca^{2+}\) Oscillators in Smooth Muscle Cells

Let \(x=[Ca^{2+}]_i\) represent the cytosolic free \(Ca^{2+}\) concentration, \(y=[Ca^{2+}]_{SR}\) the \(Ca^{2+}\) concentration in the sarcoplasmic reticulum and \(z\) the cell membrane potential. The system described above and depicted in Fig. 1 is represented by the following equations:

$$\begin{aligned} \frac{dx}{dt}&=\mathop {A}_{\begin{array}{c} \text {NSCC}\\ {\text {influx}} \end{array}} -\mathop {E_{Ca}\frac{z-z_{Ca1}}{1+e^{-(z-z_{Ca2})/R_{Ca}}}}_{{\text {VOCC influx}}}+\mathop {E_{Na/Ca}\frac{x}{x+x_{Na/Ca}}\left( z-z_{Na/Ca}\right) }_{{\text {NCX}}} \nonumber \\&\quad -\mathop {B\frac{x^n}{x^n+x_b^n}}_{{\text {SR uptake}}}+\mathop {C_r\frac{x^{p_r}}{x^{p_r}+x_r^{p_r}}\frac{y^{m_r}}{y^{m_r}+y_r^{m_r}}}_{\text {RyR CICR}} \nonumber \\&\quad -\mathop {Dx^k\left( 1+\frac{z-z_d}{R_d}\right) }_{Ca^{2+}\,{\text {extrusion}}}+\mathop {Ly}_{\text {SR leak}} \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{dy}{dt}=\mathop {B\frac{x^n}{x^n+x_b^n}}_{\text {SR uptake}}-\mathop {C_r\frac{x^{p_r}}{x^{p_r}+x_r^{p_r}}\frac{y^{m_r}}{y^{m_r}+y_r^{m_r}}}_{\text {RyR CICR}} \end{aligned}$$
(1b)
$$\begin{aligned} \frac{dz}{dt}&=-\gamma \ \bigg (\mathop {E_{Cl}\frac{x}{x+x_{Cl}}\left( z-z_{Cl}\right) }_{Cl^{-}{\text {channels}}}+\mathop {2E_{Ca}\frac{z-z_{Ca1}}{1+e^{-(z-z_{Ca2})/R_{Ca}}}}_{\text {VOCC influx}} \nonumber \\&\quad +\mathop {E_{Na/Ca} \frac{x}{x+x_{Na/Ca}} \left( z-z_{Na/Ca}\right) }_{{\text {NCx}}}+\mathop {E_K\left( z-z_{K}\right) \frac{x}{x+\beta e^{-(z-z_{Ca3})/R_K}}}_{K^{+}{\text {efflux}}}\bigg ) \end{aligned}$$
(1c)

where the electric reversal potentials with respect to \(Ca^{2+}\) and \(Na^{+}\)are determined from the Nernst equation according to:

$$\begin{aligned} z_{Ca1}&=\frac{RT}{FZ_{Ca}}ln \left( \frac{[Ca^{2+}]_{i,0}}{x}\right)&z_{Na}&=\frac{RT}{FZ_{Na}}ln \left( \frac{[Na^+]_{i,0}}{[Na^+]_i}\right) \end{aligned}$$
(2)

and where \(Z_{Ca}\)=1, \(Z_{Na}=2\), \(RTF^{-1}\)=0.024, \(\left( RT/FZ_{Na}\right) \) \(ln \left( [Na^+]_{i,0}/[Na^+]_i\right) =0.069\) V, \([Ca^{2+}]_{i,0}=0.0025\) \(\upmu \)M, \(R\) is the gas constant in \(\text {J}\,\text {K}^{-1}\ \text {mol}^{-1}\), \(F\) is the Faraday constant in \(\text {A s mol}^{-1}\) and \(T=310\) K. The reversal potential of the NCX is calculated as \(z_{NCx}=3z_{Na}-2z_{Ca1}\). All values of the coefficients are found in Table 1. A complete description of the mathematical model can be found in [19, 51]. The subscript \(r\) refers to RyR-mediated CICR, as opposed to IICR (not included in the present formulation). The same general conclusions would not significantly differ whether the CICR positive feedback mechanism is modelled as an InsP\(_3\)- or RyR-dependent process, as was also pointed out in [19]. Admittedly, the addition of InsP\(_3\) as another independent variable could allow to asses the importance of crosstalks between RyR and Insp\(_3\)R, and extend the present formulation to include coupling between the endothelium-fluid domain and the SM layer.

2.2 Cell-Cell Coupling

The model has been extensively validated, with analysis and results presented for the case of a single SMC [19, 51]. The generalization of these results to a population of SMCs, using image-based geometries, allows to characterize the effects of a number of parameters, while enabling a more ‘intuitive representation’ of the phenomenon.

Table 1 Coefficients
Full size table

The nature of coupling between adjacent cells remains controversial. In the current formulation we explore the consequences of either \(Ca^{2+}\) or electrical coupling, by assuming a simple gradient driven flux between neighbouring cells coupled via gap junctions. Two terms:

$$\begin{aligned} J_{Ca,i}&=g_{Ca} \sum _{j \in N_i} \left( x_j-x_i\right)&V_{m,i}&=g_z \sum _{j \in N_i} \left( z_j-z_i\right) \end{aligned}$$
(3)

are added to (1a) and (1c), respectively, and for each SMC \(i\), to model \(Ca^{2+}\) and electrical coupling with all nearest neighbouring SMCs \(j \in N_i\). Depending on the surface discretization, or on the modelling strategy, \(N_i\) may represent the set of connected surface points belonging to a patch centred on point (cell) \(i\). The geometry used for the simulation is a carotid artery, and has a total surface area of 8.26\(\,\text {cm}^{2}\), giving a mean cell surface area of \(\sim \) 143\(\,\upmu ^{2}\). The actual geometry of each SMC is not modelled explicitly in the present formulation.

2.2.1 \(Ca^{2+}\) Coupling

All cells are dynamically identical except for the \(A\) parameter, which reflects influx of \(Ca^{2+}\) via NSCCs, and is randomly distributed around its mean value, given in Table 1. Parameter \(A\) was chosen for its strong modulatory effect on the oscillatory frequency. A typical cellular matrix thus contains SMCs that are quiescent (either in an under-stimulated or an over-stimulated state, in terms of \(Ca^{2+}\) availability) and cells that are oscillating spontaneously. Within this range, the oscillatory regime is maintained at a physiological level.

Fig. 3
figure 3

Computational modelling results illustrating the emergence of propagating wave fronts. A gradual transition of uncorrelated oscillatory activity into coherent patterns is observed under conditions of increased intercellular \(Ca^{2+}\) coupling (From top to bottom \(g_{Ca}=\) 0,  \(g_{Ca}=\) 2,  \(g_{Ca}=\) 10,  \(g_{Ca}=\) 20). Colours are coded as: red \(=\) cytosolic free \([Ca^{2+}]_i\), green\(\,=\,\) \([Ca^{2+}]_{SR}\), blue \(=\) membrane potential. A magenta colour is seen where red and blue strengths are equal, and therefore indicative of membrane depolarization and high \(Ca^{2+}\) influx

Full size image
Fig. 4
figure 4

Computational modelling results illustrating the emergence of propagating wave fronts for a stronger \(Ca^{2+}\) coupling (\(g_{Ca}\) = 50). Colour coded as in Fig. 3

Full size image

Weakly coupled cells (\(g_{Ca}=\) 2) are dominated by local dynamics, producing a complex field of interacting and non-repetitive waveforms characterised by spiral and scroll waves, typical of chaotic dynamics. These highly complex, yet deterministic in nature, types of oscillatory behaviour have been often observed in syncytia of cardiac myocytes [53]. For stronger \(Ca^{2+}\) coupling (\(g_{Ca}=\) 10 and \(g_{Ca}=\) 20), discrete pacemaker nodes become prominent. These are eventually dominated by a single pacemaker resulting in clear wave fronts propagated longitudinally along the arterial wall, as depicted in Fig. 3. A propagating wave is illustrated in Fig. 4, for a stronger value of the coupling coefficient. As the oscillatory behaviour emerges, ion movements in and out of the SR are associated with successive high and low \([Ca^{2+}]_{SR}\). This behaviour coincides with the synchronization of intracellular \(Ca^{2+}\) oscillations of the arterial wall, showing that macroscopic rhythmic activity can indeed reflect ion movements at the level of the individual cell.

2.2.2 Electrical Coupling

Limited degree of synchronization, mostly at short length scales, was observed under conditions of purely electrical coupling (not shown). This is due to the present formulation of the model, which is expressing primarily the dynamics of intracellular CICR. The inclusion of a specific ionic transport process as a further independent variable would allow membrane potential to support oscillatory activity independently of the CICR mechanism. This is indeed the case when the open state probability of \(K_{Ca}\) channels is employed as an independent variable in a four differential equation model [51].

The interplay between extracellular \(Ca^{2+}\) influx via NSCCs and VOCCs was also investigated. Independently of the coupling parameters \(g\), as given in (3), simulations showed how low or high influx through either channel leads to the dominance of \(Ca^{2+}\) and/or electrical coupling, and to the loss of oscillatory activity. For the case of a single cell model, the effects of variations in the control parameters \(A\) and \(E_{Ca}\) were investigated by nullcline analysis in [19].

3 Integrated Approach

The modelling framework presented here can be used in realistic scenarios, to gain insights into the fundamental physiology of inter-cellular coupling, by analysing the emergence of synchronization and macroscopic wave propagation. The theoretical consequences of local neighbour interactions through electrical and/or chemical coupling via inter-cellular diffusion of \(Ca^{2+}\)   ions have only been briefly explored, and can be further compared using the Nernst-Planck equation. This approach may also identify key dynamical features, by exploring stability characteristics and critical scaling phenomena near the onset of synchronization, as described for Kuramoto-type phase synchronization of oscillators [54], and the mode locking observed in nonlinear systems [55].

Additional components will include the coupling between the SM and the endothelium, especially with a view to provide a robust basis for the study of various patho-physiological scenarios. Further manifestations of blood-wall and arterial dynamics coupling could then be investigated, by manipulation of a number of potential mechanisms underlying flow-endothelium interactions. Such mechanisms may include wall shear stress, which can modulate calcium responses in SMCs indirectly, via mass transfer of agonist and receptor-ligand interactions, as described in Sect. 1.2.3, and directly through wall shear stress operated channels. In this context, ATP and its derived products can be considered. Potential mechanisms of action may include: (i) ATP as a mediator of \(Ca^{2+}\) extrusion ATPase, (ii) the sodium-potassium exchanger Na\(^+\)/K\(^+\)-ATPase involved in maintaining the cell membrane potential, and (iii) ATP-sensitive potassium (K\(_{ATP}\)) channels in the endothelium. Such an integrated approach will enable the active coupling between blood flow and arterial wall dynamics, and provide a uniquely global view of cardiovascular physiology that has not been achieved before in computational fluid flow studies.