On the Role of Phase Change in Modelling Drug-Eluting Stents

Abstract

A model of drug release from an eluting stent to the arterial wall is presented. The coating layer is described as a porous reservoir where the drug is initially loaded in a polymer-encapsulated solid phase, and is then released both to the coating and to the tissue of the arterial wall in a free phase. The wall is treated as a heterogeneous porous medium and the drug transfer through it is modeled by a non-homogeneous set of coupled partial differential equations that describe a convection-diffusion-reaction process. Change of phases due to drug dissolution in the coating and binding-unbinding reactions in the arterial wall are addressed. Numerical results show a strong coupling of the release kinetics in the polymer and the drug dynamics in the wall, and this coupling depends on the physico-chemical drug properties, the microstructure of the polymeric stent coating and the properties of the arterial wall.

1 Introduction

Drug-eluting stents (DES) have drastically reduced the rate of restenosis compared to bare-metal stents and have since become the most common choice for the treatment of coronary arteries afflicted with advanced atherosclerotic lesions. DES consist of a metallic wire mesh platform coated with a polymer film that encapsulates a therapeutic drug aimed at preventing hyperplasia of smooth muscle cells (SMCs) responsible for the re-occulsion of the treated artery, termed restenosis. To ensure effective performance, both the stent geometry and the coating design need to be optimized. The success of an antiproliferative drug therapy from a DES depends on the amount of drug eluted from the stent, the rate of drug release, accumulation of drug and drug binding to cells in the arterial wall [1]. The local drug concentrations achieved are directly correlated with the biological effects and local toxicity, and establishing the optimum dose to be delivered to the tissue remains a challenge in today’s DES design and manufacturing [2, 3]. The two most common drugs used today are paclitaxel and derivatives of rapamycin (the so called limus drugs).

Although many studies of DES efficacy and optimal design have been carried out using either experimental methods [4] or numerical simulations [5, 6], many questions remain unanswered. Validated mathematical models for computing the drug concentration in the arterial wall can provide a useful tool in the manufacturing and development of new and more efficacious DES [7]. Such models should incorporate the pharmacokinetics responsible for the drug release to study the effect of different coating parameters and configurations on drug elution [8]. Hossainy and Prabhu developed a mathematical model to predict the transport reaction of drug release in biodurable materials and biodegradable polymers [9]. Although the polymer acts as the drug reservoir and a strategic design of its characteristics would improve the release performance, studies probing the drug elution process from the coating platform are limited. In most studies, the coating is considered as a continuum where the drug is incorporated directly into the liquid phase. However, at the microscopic scale, the polymer is a porous medium where the solid and fluid phases coexist [10]. In particular, the solid matrix acts as a drug reservoir, where the drug is initially bound to the solid phase. Subsequently, after stent insertion, expansion and contact with vascular tissues, a part of the drug is first transferred to the fluid phase, at a rate that depends on the porosity, permeability, and drug characteristics, and it then diffuses into the surrounding tissues.

Drug transport depends on the properties of the “coating-wall” system, taken as a whole and modeled as a coupled two-layered system. The multiphase release of drug from the coated stent and its distribution in the arterial wall must be carefully tailored to achieve the optimal therapeutic effect and to deliver the correct dose in the required time [11, 12]. The pharmacological effects of the drug as well as its tissue accumulation, duration and distribution could potentially have an effect on the drug’s efficacy, and a delicate balance between adequate amount of drug delivered over an extended period of time and minimal local toxicity needs to be struck [13]. Thus, the model also needs to properly describe the drug dynamics in the different layers of the arterial wall. Although a large number of mathematical models are available to describe drug transport in arterial tissue, only a few [14, 15] consider the dynamic nature of the interaction of the drug with the cells of the wall. The released drug targets and binds to specific receptors on the surface of SMCs to block the uncontrolled proliferation and migration of these cells. Similar to the process in the coating, this entails a phase change of the mobile drug, which is transported through the interstitial space of the arterial wall, to a state where the drug is bound to the surface of the SMCs to exert its therapeutic effect.

In the present work, we model the coupled coating-wall system: we investigate the effect of phase change in both layers (the coating and the wall) by combining previous models, where a multi-layered porous wall model has been proposed and the influence of drug dissolution in the coating has been addressed [16, 17] with a model where the effect of different modeling assumptions on the predictions of the transport of sirolimus and paclitaxel in stented arteries has been studied [15]. All other mechanical effects (such as compression and expansion) due to the metallic or polymeric degradation/erosion are neglected.

Fig. 1

Cross-section of the stent mesh, the coating, and the arterial wall: geometrical configuration and reference system (figure not to scale)

Our results demonstrate a strong coupling of the release kinetics in the polymer and the drug dynamics in the wall. The results highlight the importance of tailoring drug release to drug kinetics in the arterial wall to ensure optimal DES performance.

2 A Two-Layer Model for Drug Elution

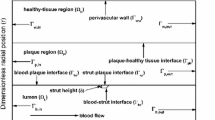
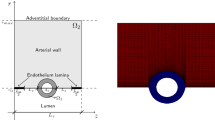
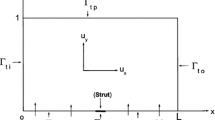
We consider a stent that is coated with a thin layer (of thickness $l_0$) of a porous polymer containing a drug and that is embedded into the arterial wall. As the bulk of drug transport occurs along the direction normal to the polymeric surface (radial direction) and by assuming axial symmetry, we can restrict our study to a simplified one-dimensional model (Fig. 1). In particular, we consider a radial line crossing the metallic strut, the coating and the arterial wall and pointing outwards. Because the wall thickness is very small compared to the radius of the artery, a Cartesian coordinate system $x$ is used along the radial line. For simplicity, we consider the situation where the stent polymer is in direct contact with the medial layer of the arterial wall (hereafter simply referred to as wall). This layer is modeled as a homogeneous porous medium of thickness $l_1$. Without loss of generality, we assume $x=0$ is the coating-wall interface (Fig. 1).

In this paper we are interested in non-local mass transfer processes in the coating, where the drug passes from a solid (polymer-encapsulated, $c_e$) to a free phase ($c_0$) by dissolution. Similarly, a part of the dissolved and transported drug in the wall ($c_1$) is metabolized by the cells and transformed to a bound state ($c_b$). Thus, the drug delivery process starts in the coating and ends at the SMC receptors, with bidirectional phase changes in a cascaded sequence, as schematically depicted in Fig. 2. A microscopic approach would require knowledge of the specific and local geometry of the individual pore structure networks, which is unfeasible. Therefore, both the polymeric matrix and the wall are treated as macroscopically homogeneous porous media with volume-averaged concentrations. Even though we are only considering the 1D case in this study, we will express concentrations in units of $\mathrm {mol}\,{\mathrm {m}}^{-3}$. These chosen units have no influence on the results.

Fig. 2

Schematic of the cascade mechanism of drug delivery in the coating-wall coupled system. An unbinding (resp. binding) reaction occurs in the coating (resp. in the wall) (blue arrows). In both layers, reverse reactions (red arrows) are present in a dynamic equilibrium. Drug transport occurs only in the free phases $c_0$ and $c_1$

2.1 The Two-Phase Coating Model

The coating of a DES consists of a porous polymeric matrix that encapsulates a therapeutic drug in solid phase; as such, it is unable to diffuse and to be delivered into the tissue [5]. Nevertheless, when expanded and deployed into the wall, the stent coating is exposed to the surrounding biological fluids. As a consequence, such fluids fill the interstitial spaces of the polymer and form a network of liquid channels, acting as a release medium for the drug. Thus, a fraction of the drug mass is first transferred, in a finite time, to the liquid phase, and then released and diffuses into the arterial wall. We carry out a mesoscale description of the volume-averaged drug concentrations in the liquid ($c_0$) and solid ($c_e$) phases considered separately. By using a microstructure argument [17], the governing equations are:

$$\begin{aligned} {\partial c_e \over \partial t}&= - \beta _0 c_e + \delta _0 c_0&{\text {in}} \, (-l_0,0)\,\, \end{aligned}$$

(1)

$$\begin{aligned} {\partial c_0 \over \partial t}&=D_0 {\partial ^2 c_0 \over \partial x^2} + \beta _0 c_e - \delta _0 c_0&{\text {in}} \, (-l_0,0)\,\, \end{aligned}$$

(2)

where $D_0$ (${\mathrm {m}}^2\,{\mathrm {s}}^{-1}$) is the diffusion coefficient of the unbound solute, $\beta _0 \ge 0$ (${\mathrm {s}}^{-1}$) and $\delta _0 \ge 0$ (${\mathrm {s}}^{-1}$) are the unbinding (dissociation) and binding (re-association) rate constants in the coating, respectively [10]. It should be noted that $\beta _0$ depends on the porosity of the coating $\varepsilon _0$ [17]. The binding rate constant is defined as the inverse of the characteristic solid-liquid transfer time scale, $\delta _0=t_0^{-1}$. The ratio of the unbinding and binding rate constants is the equilibrium dissociation constant $K_0=\displaystyle \frac{\delta _0}{\beta _0}=\frac{1-\varepsilon _0}{\varepsilon _0}$. $t_0$ and $K_0$ are quantities that can typically be determined experimentally.

The associated initial conditions are:

$$\begin{aligned} c_e(x,0)=C_e \qquad \qquad c _0(x,0)=0 \end{aligned}$$

(3)

expressing that, at initial time, the entire drug exists in the solid phase at a maximum constant concentration, and it is subsequently released into the liquid phase. Since the metallic strut is impermeable to the drug, no mass flux passes through the boundary surface $x=-l_0$; hence, we impose a no-flux condition:

$$\begin{aligned} D_0 {\partial c_0 \over \partial x} =0 \qquad \qquad {\text {at}}\, x=-l_0 \end{aligned}$$

(4)

2.2 The Two-Phase Wall Model

Drug that enters the arterial wall is transported by convection and diffusion through the tortuous paths of the extracellular matrix surrounding the wall’s cells. Similarly to the coating, a phase change can occur in the wall from the free state ($c_1$) of the drug to the bound state ($c_b$) and vice versa at the surface of the cells within the wall. The free drug ($c_1$) binds to specific receptors on the surface of SMCs to form a bound complex ($c_b$). The maximum density of specific receptors available to the drug is denoted as $c_{b}^{max}$. The formed drug-receptor complex is not permanent and can be dissolved after a typical time scale $t_1$. These two processes (binding and unbinding) are modeled by a second order reversible saturating binding equations [1]:

$$\begin{aligned}&{\partial c_1 \over \partial t} =D_1 {\partial ^2 c_1 \over \partial x^2} - V_1 {\partial c_1 \over \partial x} - \beta _1 c_1 \left( c_{b}^{max}- c_{b}\right) + \delta _1 c_{b}&\text {in} \, \, (0 , l_1) \end{aligned}$$

(5)

$$\begin{aligned}&{\partial c_b \over \partial t} = \beta _1 c_1 \left( c_{b}^{max}- c_{b}\right) - \delta _1 c_{b}&{\text {in}} \, \, (0 , l_1) \end{aligned}$$

(6)

where $D_1$ is the effective diffusivity of unbound drug, $V_1$ ($\mathrm {m}\,{\mathrm {s}}^{-1}$) is a convection velocity, and $\beta _1 \ge 0$ (${\mathrm {mol}}^{-1} \, {\mathrm {m}}^3 \, {\mathrm {s}}^{-1}$) and $\delta _1 \ge 0$ (${\mathrm {s}}^{-1}$) are the binding and unbinding rate constants, respectively [15]. The unbinding rate constant is defined by the inverse of the characteristic unbinding time scale, $\delta _1 = t_1^{-1}$. It should be noted that due to the cross product of $c_b$ and $c_1$ in the binding term of Eq. (6), the units of $\beta _1$ are different from those of $\beta _0$ (${\mathrm {s}}^{-1}$). $\beta _1$ is related to $\delta _1$ by the equilibrium dissociation constant $K_1=\displaystyle \frac{\delta _1}{\beta _1}$ (${\mathrm {mol}} \, {\mathrm {m}}^{-3}$). The initial conditions are:

$$\begin{aligned} c_1(x,0) = 0 \qquad \qquad c_{b}(x,0) = 0 \end{aligned}$$

(7)

Finally, a perfectly absorbing boundary condition is imposed at the wall limit:

$$\begin{aligned} c_1(x,0)=0 \qquad \qquad \text {at}\, x=l_1 \end{aligned}$$

(8)

At the coating-wall interface, we impose the balance of flux

$$\begin{aligned} D_0{ \partial c_0 \over \partial x} = D_1{ \partial c_1 \over \partial x} - V_1 c_1 \qquad \qquad {\text {at}} \, \, x=0 \end{aligned}$$

(9)

and continuity of the liquid-phase concentration:

$$\begin{aligned} {c_0 \over k_0 \varepsilon _0 } = {c_{1} \over k_{1} \varepsilon _{1}} \qquad \qquad {\text {at}} \, \, x=0 \end{aligned}$$

(10)

where $\varepsilon$ and $k$ are the porosities and the partition coefficients in the respective layers.

2.3 Physiological Parameters

The two most common drugs used for DES are paclitaxel and sirolimus. These two drugs have similar molecular size and resulting transport properties (effective diffusivity and convection velocity), but drastically different binding and unbinding dynamics in the arterial wall, resulting in different binding $\beta _1$ and unbinding $\delta _1$ rate constants and maximum binding site densities $c_{b}^{max}$ [14]. Based on the parameters determined in [14, 15, 17], we have chosen a set of parameters that describes a generic drug that is similar in its transport properties to paclitaxel and sirolimus and lies in between paclitaxel and sirolimus for its binding/unbinding properties. The parameters of the reference model are summarized in Table 1. We consider the entire polymer and wall tissue as accessible and thus $k_0=k_1=1$. The values for $\delta _0$ and $\delta _1$ correspond to a characteristic solid-liquid transfer time $t_0 = 1$ day and an unbinding time scale $t_1=100$ h, respectively.

Table 1 Model parameters of the reference model

2.4 Numerical Simulation

The governing equations are discretized using a finite element method with second-order Lagrangian elements, implemented in the commercial software package COMSOL Multiphysics 4.3a (COMSOL AB, Burlington, MA, USA). The relative tolerance is set to $10^{-5}$ and the absolute tolerance to $10^{-10}$. The time advancing scheme is a backward difference formulation with variable order and time step size. The domain is discretized by 2,000 equally spaced elements. Mesh independence of the solution was confirmed using a coarse, medium and fine meshes with 1,000, 2,000 and 4,000 elements, respectively, with a relative difference of less than $0.1\,\%$ between solutions of progressively more refined meshes.

3 Results and Discussion

We present the mean concentration of each phase of the eluted drug in each of the layers of the model. The time considered in our simulations was $4$ weeks. Figure 3 illustrates the temporal evolution of the averaged concentrations for three characteristic values of the solid-fluid transfer time $t_0$. For the smallest transfer time of $t_0=0.1$ days, all drug is released from the solid phase in the polymer within $1$ week (Fig. 3a) which leads to a spike in the fluid phase drug concentration at $\approx$2 days at an average concentration of $\approx$2 (Fig. 3b).

Fig. 3

Sensitivity analysis of the phase-change model in both layers to the characteristic solid-fluid transfer time scale $t_0$. Temporal evolution of a the solid-phase drug concentration $c_e$; b the liquid-phase drug concentration $c_0$; c the free drug concentration $c_1$; d the bound drug concentration $c_b$, each averaged over the entirety of their respective layers

Slower release of the drug from the solid phase entails significantly lower peak concentrations (Fig. 3b). For $t_0=1$ day, the coating is almost entirely depleted within the considered period (Fig. 3a). The slowest transfer time considered $t_0=10$ days causes only $\approx$75 % of the drug to be unbound from the polymer (Fig. 3a), leading to negligible liquid phase concentrations in the coating. We observe that the (excess) unbound concentration in the wall reaches significant levels only for the fastest solid-liquid transfer time (with a peak mean concentration of $\approx$0.1) (Fig. 3c). For $t_0=1$ day, the peak mean concentration reaches about $1/5$ of this value and is negligible for the slowest transfer time.

Fig. 4

Sensitivity analysis of the phase-change model in both layers to the porosity of the polymer $\varepsilon _0$. Temporal evolution of a the solid-phase drug concentration $c_e$; b the liquid-phase drug concentration $c_0$; c the free drug concentration $c_1$; d the bound drug concentration $c_b$, each averaged over the entirety of their respective layers

The dynamics of the uptake of the drug into the bound state in the wall are strongly coupled to the characteristic solid-fluid transfer time $t_0$ in the coating (Fig. 3d). For the fastest $t_0$, a high mean concentration of slightly less than $0.2$ is reached within $\approx$1 day, implying that almost all receptors are occupied throughout the wall (compare to $c_b^{max} = 0.2$). With drug supply from the coating ceasing quickly, the retained concentration slowly decays over the next $4$ weeks, reaching a mean concentration level of less than $1/10$ of the peak concentration at the end of the simulation. For slower transfer times, the period to reach peak concentration is longer and the magnitude of the peak concentration decreases. For $t_0=1$ day, the peak concentration is reached at $\approx$5 days with an average concentration of $\approx$0.16. For the slowest $t_0$, it takes almost $3$ weeks to reach the maximum mean concentration in the wall, and the mean peak concentration is less than half of the peak concentration for $t_0=0.1\,\mathrm {days}$.

Fig. 5

Sensitivity analysis of the phase-change model in both layers with respect to the characteristic drug unbinding time scale $t_1$. Temporal evolution of a the solid-phase drug concentration $c_e$; b the liquid-phase drug concentration $c_0$; c the free drug concentration $c_1$; d the bound drug concentration $c_b$, each time averaged over the entirety of their respective layers. In panels a and b all three curves coincide since the time scale change in the medial layer does not feed back into the polymer layer

Varying the porosity of the polymer coating $\varepsilon _0$ has a qualitatively and quantitatively similar effect on the drug release as varying $t_0$ (Fig. 4). The porosity $\varepsilon _0$ enters implicitly in our model through the continuity condition between polymer and wall Eq. (10) and in the unbinding rate constant $\beta _0$. As the fraction of polymer is reduced and the liquid space is increased, drug release is faster since less drug is stored in the coating (Fig. 4a). However, since we kept the volume-averaged initial concentration constant, the intrinsic drug concentration in the solid phase increases $\left( c_e^s=\displaystyle \frac{c_e}{\varepsilon _0}\right)$. This leads to higher liquid phase concentrations in the coating (Fig. 4b). The elevated mean free drug concentration levels in the wall occurring at relatively high porosities indicate that the wall is “overloaded” with free drug causing some drug not to be bound (Fig. 4c). The uptake of drug in the wall is accelerated and the receptors rapidly occupied (Fig. 4d). Due to the sufficiently fast binding kinetics in the wall, virtually all the receptors can be occupied. Nevertheless, since drug supply from the coating reduces quickly, the concentration levels in the wall drop faster.

Figure 5 shows the temporal evolution of the averaged concentrations for varying drug unbinding times $t_1$. Figure 5a, b indicate that the drug release in the coating is unaffected by the variations in the drug dynamics in the wall (the three curves overlap). Thus, there is no feedback from the wall to the coating. Figure 5c shows that the faster the unbinding time (which also implies a faster binding time, since $K_1$ is held constant) the higher the overall concentration levels in the wall, as more drug gets bound to the receptors. Also, the mean peak concentration occurs earlier for faster drug binding/unbinding kinetics. At the same time, the free drug concentration in the wall is barely affected by changes in the drug binding/unbinding kinetics.

On the other hand, if we assume a single liquid-phase $c_0$ in the coating, we can control the drug release kinetics by setting the drug diffusivity $D_0$. Using Higuchi’s formula, we can estimate the characteristic release time of the drug from the polymer as $t_e=\displaystyle \frac{\pi l_0^2}{4 D_0}$ [18]. Figure 6a demonstrates how using a single-phase model and varying the characteristic release time $t_e$ (and with that the diffusivity $D_0$) can in fact be used to approximate the release profiles obtained with the two-phase model varying the solid-liquid transfer time. This leads to very similar bound drug dynamics in the wall (Fig. 6b). These results indicate that a single-phase model in the coating can be used to describe the (averaged) release dynamics and leads to a very similar (averaged) response in the wall. However, from a designer’s point of view, the more detailed information about the solid-fluid transfer time and the porosity might be more valuable and easier to control.

Fig. 6

Sensitivity analysis of the medial layer phase-change model to the characteristic polymer emptying time scale $t_e$. Temporal evolution of a the liquid-phase drug concentration $c_0$; b the bound drug concentration $c_b$, each time averaged over the entirety of their respective layers

Moreover, the current simulations show that, although an additional equation needs to be solved, the proposed two-phase model in the coating is significantly simpler to handle numerically, at least in the one-dimensional case. The reason for this lies in the otherwise very steep concentration gradient at the coating-wall interface. The steep gradient requires a significantly larger number of elements and smaller time steps (especially at the beginning of the simulation) which for our numerical method would lead to longer overall calculation times in the case of the single-phase model compared to the two-phase model. The two-phase model avoids these large gradients, since the initial drug is entirely stored in the solid phase at the initial time step, which is not in contact with the wall.

Our previous research has shown that a simplified one-phase model in the wall (assuming instantaneous drug reaction and thus a constant partition of bound and free drug) cannot capture accurately the drug dynamics [15]: neither drug accumulation nor drug residence time can be accurately predicted with a one-phase model.

The present results highlight how the release kinetics in the polymer and the drug dynamics in the wall are highly and nonlinearly coupled. The goal of controlled drug release is to obtain and to maintain sufficiently high drug concentrations in the wall so as to keep their therapeutic effectiveness over an extended period of time. The present work shows that the drug release, controlled by $t_0$ and $\varepsilon _0$ (other than $D_0$), needs to be tailored to the specific drug kinetics in the arterial wall in order to reach optimal DES performance.