Keywords

1 Introduction

Needle insertion is an important operation in many medical applications such as biopsy, brachytrapy and neural signal recording. Precise localization and navigation of the needle reduce the damage to tissue and decrease the number of unsuccessful insertions. Image guided procedures can achieve this goal by tracking the surgical instrument in intra-operative images. Among various medical imaging modalities, ultrasound is popular because of acquisition speed, non-ionizing radiation, compatibility with metallic objects and low cost.

Despite current advances in imaging and processing technologies, automatic needle detection in 3D ultrasound data is still challenging. Speckle noise that is inherent property of the ultrasound images degrades the image quality. Needle diameter in the image is low and comparable to ultrasound image resolution. There are other bright structures with similar intensity as a needle in the background. Resolution and intensity of pixels decrease in higher distances from the transducer. The 3D image volume is a large data that should be processed in high speed.

The problem of needle localization in 3D ultrasound images has been studied in many previous researches. Novotny et al. [1] used the principle component analysis (PCA) method. The thresholded pixels are divided into clusters and the cluster with longest line and highest intensities is selected using PCA as a needle. Minimization of parallel projection is introduced by Ding et al. [2]. This method is based on the fact that if the projection is parallel to needle axis, the needle area in the projected image will be minimized. Ding et al. [3] also proposed the method of needle segmentation in two orthogonal projections. This technique reduces the processing time and makes the algorithm independent of initial projection direction. This method is used by Aboofazeli et al. [4] for curved needle segmentation. Cao et al. [5] proposed a catheter segmentation algorithm based on Aboofazeli ‘s approach that detects the catheter absence in the image.

The Hough transform is a well-known method for line and curve detection. Zhou et al. [6] used the randomized version of 3D Hough transform because of its memory and time efficiency. Qiu et al. [7] introduced the Quick Randomized Hough transform that employs a coarse to fine search strategy. They [8] also used Roberts line representation for needle axis, because of low computational memory. Neshat et al. [9] considered the needle axis model as a third order Bezier curve and employed the generalized Hough transform. They implement the algorithm on a Graphical Processing Unit (GPU).

The Parallel Integral Projection (PIP) transform is a form of Radon transform. Barva et al. [10] showed that needle axis can be found by maximization of PIP transform. The hierarchical mesh-grid technique is used to speed up this method. Uhercik et al. [11] introduced the faster multi-resolution PIP approach. Wei et al. [12] acquired two images before and after insertion. The needle is segmented in the difference image using least square method. Yan et al. [13] employed the level set segmentation approach. This method is not automatic and need user input data. Novotny et al. [14] used the generalized Radon transform. The image is divided into smaller regions that are processed on a GPU. Adebar et al. [15] vibrated the needle with high frequency and segmented it in the resulting 3D power Doppler image. They fitted a third order polynomial to the thresholded Doppler response.

Most of the introduced needle detection techniques-such as Hough and Radon transform and PIP-are projection based. These methods suffer from high computational time and robustness problem in case of cluttered background. The faster and more robust model fitting RANSAC approach is introduced by Uhercik et al. [16]. They also employed a linear classifier [17] to identify tool pixels using intensity and tubularity features. This modification leads to a more robust algorithm but decreases the speed. Zhao et al. [18] considered detection and tracking of needle in the sequence of 3D images. In their method, a Kalman filter estimated the needle tip position using speckle tracking speed estimation and RANSAC tip localization. Chatelain et al. [19] also studied the needle tracking problem. They found the ROI that contained the needle using predictive Kalman filtering. The predicted model is used in the RANSAC procedure to reject improbable configurations.

In this paper, we take advantage of nonlinear anisotropic diffusion (AND) to achieve faster and more accurate result, in RANSAC based needle localization. The anisotropic diffusion is first introduced by Perona et al. [20] as an edge preserving denoising method. The success and time performance of model fitting algorithms are very much affected by the number of outliers. Realizing the fact that outliers are mainly due to speckle noise and existence of other bright structures in the background, we reduced the effect of these parameters using anisotropic diffusion (AND). The major advantage of AND is that it can reduce the noise without removing specific structures (such as lines) and even enhance them. This is an important feature because of needle low diameter and possible loss of needle pixels in the denoising process. The results show the effectiveness of this scheme in reducing the needle localization error and processing time.

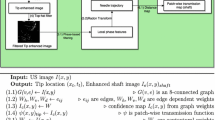
2 Method

The needle appears in the ultrasound images as a thin tubular high intensity structure that is surrounded by a noisy and inhomogeneous background. The position of the needle is found in three consecutive steps: anisotropic diffusion, thresholding and RANSAC robust fitting. The two first steps assure less noisy and erroneous input data for RANSAC procedure.

2.1 Nonlinear Anisotropic Diffusion

To preserve the specific structure of interest, the local image structure in each pixel should be known. The structure tensor of the image I is defined as

$$ J\left( {\nabla I} \right) = \nabla I \cdot \nabla I^{T} = \left[ {\begin{array}{*{20}c} {I_{x}^{2} } & {I_{x} I_{y} } & {I_{x} I_{z} } \\ {I_{x} I_{y} } & {I_{y}^{2} } & {I_{y} I_{z} } \\ {I_{x} I_{z} } & {I_{y} I_{z} } & {I_{z}^{2} } \\ \end{array} } \right] $$
(1)

The subscript means derivative with respect to spatial coordinates.

After Gaussian smoothing the input image, the structure tensor in each pixel is found. The eigenvalues and eigenvectors of J contain information about the local image structure in the specific pixel. Three mutually perpendicular eigenvectors \( v_{1} ,v_{2} ,v_{3} \) describe the local orientation and the eigenvalues \( \mu_{1} ,\mu_{2} ,\mu_{3} \) measure average contrast along eigendirections. The eigenvector \( v_{1} \) is perpendicular to the local structure. In needle detection problem, we should preserve lines. High level of smoothing perpendicular to the eigenvector \( v_{1} \) will realize this goal.

In physics, the difference in density cause mass transport without creating and destroying mass. This process is called diffusion and is similar to image smoothing when there is a difference in gray levels. The diffusion equation for the image u is expressed as

$$ \partial_{t} \,u = div\left( {D \cdot \nabla u} \right) $$
(2)

The subscript t denotes derivative with respect to diffusion time t. “div” is the divergence operator

$$ div\;\vec{p} = \partial_{x} p_{1} + \partial_{y} p_{2} + \partial_{z} p_{3} $$
(3)

where \( \vec{p} = \left[ {p_{1} ,p_{2} ,p_{3} } \right] \) is an arbitrary vector. D is the diffusion tensor and the term \( j = - D\nabla u \) is called flux. If D is constant over the image, the resulting linear diffusion will excessively smooth the image. In nonlinear diffusion, D is a function of image structure. Nonlinearity allows controlling the amount of diffusion and reducing it on lines. In anisotropic diffusion, we can make the diffusion direction-dependent by defining the diffusion tensor. The diffusion tensor D changes the orientation and intensity of the flux to preserve the structures of interest in the image. D can be found using its eigenvalues and eigenvectors

$$ D = \left[ {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & {v_{3} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\lambda_{1} } & 0 & 0 \\ 0 & {\lambda_{2} } & 0 \\ 0 & 0 & {\lambda_{3} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {v_{1}^{{\mathbf{T}}} } \\ {v_{2}^{{\mathbf{T}}} } \\ {v_{3}^{{\mathbf{T}}} } \\ \end{array} } \right] $$
(4)

The values of the eigenvalues \( \lambda_{1} ,\lambda_{2} ,\lambda_{3} \) are obtained by extending Weickert ‘s 2D equation [21] to 3D case [22] for line enhancement

$$ \left\{ \begin{aligned} &\lambda_{1} = c_{1} \hfill \\& \lambda_{2} = c_{2} \hfill \\ &\lambda_{3} = c_{1} + \left( {1 - c_{1} } \right)\, \cdot \exp \left( {\frac{{ - c_{2} }}{{\left( {\mu_{1} - \mu_{2} } \right)^{2} }}} \right) \hfill \\ \end{aligned} \right. $$
(5)

where \( \mu_{1} \ge \mu_{2} \ge \mu_{3} \) are eigenvalues of the structure tensor J and \( c_{1} \in \left( {0,1} \right) \) and \( c_{2} \ge 0 \) are smoothing constants.

The diffusion equation is continuous in both space and time. To solve it numerically, it should be discretized.

$$ \begin{aligned} \partial_{t} \,u & = div\left( {D \cdot \nabla u} \right) = \partial_{x} \left( {a\,\partial_{x} u + d\,\partial_{y} u + e\,\partial_{z} u} \right) \\ & \quad + \partial_{y} \left( {d\,\partial_{x} u + b\,\partial_{y} u + f\,\partial_{z} u} \right) + \partial_{z} \left( {e\,\partial_{x} u + f\,\partial_{y} u + c\,\partial_{z} u} \right) \\ \end{aligned} $$
(6)

where D is

$$ D = \left[ {\begin{array}{*{20}c} a & d & e \\ d & b & f \\ e & f & c \\ \end{array} } \right] $$
(7)

We used standard discretization method [22] with the central difference approximation for spatial derivatives

$$ \partial_{y} \left( {d\,\partial_{x} u} \right) = \frac{1}{2}\left( {d_{x,y + 1,z} \frac{{u_{x + 1,y + 1,z} - u_{x - 1,y + 1,z} }}{2}} \right) - \frac{1}{2}\left( {d_{x,y - 1,z} \frac{{u_{x + 1,y - 1,z} - u_{x - 1,y - 1,z} }}{2}} \right) $$
(8)

The subscript in the right side of (8) denotes spatial coordinate indices. The iterative forward difference method approximates the term \( \partial_{t} \,u \) in (6)

$$ \partial_{t} \,u \approx \frac{{u_{x,y,z}^{K + 1} - u_{x,y,z}^{K} }}{h} $$
(9)

where K is the time step and h is the step size. \( u_{x,y,z}^{K} \) is the approximation of u in location (x,y,z) and time Kh.

The (2) can be written as convolution of a 3 × 3 × 3 time and space varying mask with the image

$$ \frac{{u_{x,y,z}^{K + 1} - u_{x,y,z}^{K} }}{h} = A_{x,y,z}^{K} * u_{x,y,z}^{K} $$
(10)
$$ u_{x,y,z}^{K + 1} = \left( {1 + h.A_{x,y,z}^{K} } \right) * u_{x,y,z}^{K} $$
(11)

The entries of mask A that is calculated in [23] is showed in Fig. 1.

Fig. 1.
figure 1

The convolution mask, (a) for z = 0, (b) z =+1 and (c) z = −1

Full size image

3 RANSAC

RANSAC (Random Sample Consensus) [24] is a robust fitting method that can find the model parameters when the data contains a high percentage of outliers. The algorithm iteratively selects \( N_{s} \) random samples of data and fits a model to them. Next, the number of data points that are consistent with the hypothesized model is specified. If this number is big enough, the model will be accepted; otherwise iteration continues. The Maximum number of iterations is updated at the end of each iteration as follows

$$ L = \frac{\log \left( p \right)}{{\log \left( {1 - p_{g}^{{N_{s} }} } \right)}} $$
(12)
$$ p_{g} = \frac{{N_{inl} }}{{N_{data} }} $$
(13)

where \( N_{inl} \) is the number of inliers (model consistent points) and \( N_{data} \) is the number of all data points. Consistent data have a shorter distance than \( \tau \) from the model. The threshold \( \tau \) is defined as needle observed radius in the image. p is the probability of L consecutive failures and is set by user. \( N_{s} \) is the minimum number of data that is required to fit the specific type of model.

4 Result

To evaluate the proposed method, we used a 3D ultrasound dataset that consists of various needle positions and orientations. The dataset contains 28 ultrasound images that are produced by previous researchers [16] using the software Field II. The background scatterers are created using real ultrasound breast images. The dimension of the initial RF data is 53 planes of 71 RF beams. Each RF beam consists of 164 data samples. The resulting 3D ultrasound image resolution is 53 × 71 × 160 pixels.

Results are measured in various levels of the speckle noise. An example of the high and low noise level images is shown in Fig. 2. At each noise level, we repeated the algorithm 30 times for each of the dataset images and reported the average value.

Fig. 2.
figure 2

A plane of the 3D ultrasound image that contains the needle, in low and high noise levels.

Full size image

Figure 3 shows the average axis localization error. Axis error is the maximum Cartesian distance between actual and found needle axes. A failure occurs when the error value is greater than 3 mm. Figure 4 shows the average failure rate. The figures demonstrate that the proposed AND-RANSAC method yields smaller error and greater accuracy than RANSAC, while failure rates are nearly equal.

Fig. 3.
figure 3

Needle axis localization error, in different variances of the speckle noise

Full size image
Fig. 4.
figure 4

Needle axis localization failure percent, in different variances of the speckle noise

Full size image

Figure 5 shows the average elapsed time of the needle detection algorithm. The processing time of the AND-RANSAC approach is not very much affected by amount of speckle noise in the image and is significantly lower than RANSAC.

Fig. 5.
figure 5

The elapsed time of the needle localization procedure, in different variances of the speckle noise

Full size image

5 Conclusion

Regarding the main challenges of needle detection in 3D ultrasound images, such as high dimensionality and noisy nature of data, we have investigated improving the speed and accuracy of the model fitting RANSAC needle localization method. The amount of speedup that can be achieved by anisotropic diffusion has a trade-off relation with size of the 3D data. In the large volumes further acceleration can be made using GPU or parallel implementation. Automatic detection of ROI using image itself or prior information will increase the speed and accuracy. Techniques such as guided sampling or partial evaluation can improve the RANSAC computational time.