Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Modeling fluids in small length scales from micrometer to nanometer not only is a fundamental problem in fluid mechanics, but also plays a paramount role in modern fluidic devices [1]. These micro- or nanofluidic devices can be found in wide range of applications and in many different fields. Examples include the development of inkjet printheads for xerography, lab-on-a-chip technology, and manipulation and separation of bio-molecules. Compared to macroscopic systems, microscopic fluids have a larger surface-to-volume ratio, therefore boundary conditions become crucial in determining the hydrodynamic properties. The most well-known boundary condition is the no-slip boundary condition, i.e., the fluid velocity vanishes at a fluid/solid interface. No-slip boundary condition has been successfully applied to wide ranges of macroscopic phenomena, but it has no microscopic justification and its validity in small length scales is questionable. A more general boundary condition is the Navier boundary condition, which is described in the following.

Assume that a fluid/solid interface lies in the xOy plane and the fluid occupies z > 0 half-space (Fig. 1). Let us consider the case of a laminar Couette flow in the y-direction, with a slip velocity v s at z = 0. The tangential force per unit area (component of the shear stress σ yz ), to the first-order approximation, is proportional to the slip velocity v s ,

$$\displaystyle{ \sigma _{\mathit{yz}} =\zeta _{s}v_{s}, }$$
(1)

where ζ s is the surface friction coefficient. For Newtonian fluids, the shear stress can also be written as

$$\displaystyle{ \sigma _{\mathit{yz}} =\eta \frac{\partial v_{y}} {\partial z}, }$$
(2)

where η is the shear viscosity of the fluid. Combining Eqs. (1) and (2), one arrives the Navier boundary condition [2]

$$\displaystyle{ v_{s} = \frac{\eta } {\zeta _{s}}\,\frac{\partial v_{y}} {\partial z} = b\,\frac{\partial v_{y}} {\partial z}. }$$
(3)

The degree of slippage at the surface is quantified in terms of the Navier slip length \(b =\eta /\zeta _{s}\). No-slip boundary condition is recovered for b = 0, while for ideal frictionless surface we have b → ∞. The physical meaning of the slip length is the distance within the solid at which the flow velocity extrapolates to zero.

Fig. 1
figure 1

Schematic representation of Navier boundary condition on a flat surface and the slip length

Full size image

2 Implementation

The main question we try to address in this contribution is the implementation of Navier boundary condition with tunable slip length in particle-based computer simulations. Any models of a solid surface require at least two components: (a) an excluded interaction to prevent fluid particles penetrating the hard surface; and (b) an effective interaction due to the surface friction. In the following, we shall use Dissipative Particle Dynamics (DPD) [3–5] to demonstrate the tunable-slip method, although the basic idea is quite general and can be applied to other simulation techniques. In the following we only give a brief description and introduce parameters for late discussions. For a more detailed description, please consult the origin reference [6].

We model the impermeable surface using a pure repulsive interaction of the Weeks-Chandler-Andersen form [7],

$$\displaystyle{ V (z) = \left \{\begin{array}{cl} 4\varepsilon [( \frac{\sigma } {z})^{12} - ( \frac{\sigma }{ z})^{6} + \frac{1} {4}],\quad &z < \root{6}\of{2}\sigma \\ 0, &z \geq \root{6}\of{2}\sigma \end{array} \right. }$$
(4)

where z is the distance between the fluid particle and the wall. The WCA parameters also set the unit system (\(\varepsilon\) for the energy, σ for the length, and m for the particle mass).

The interactions between the surface and fluid can be very complicated and depend on the chemical details. But in the mesoscale, the main effect of the surface is to provide friction. Inspired by the form of Eq. (1), we model the fluid/surface friction by a dissipative force to the fluid, which depends on the relative velocity between the fluid particle and the wall,

$$\displaystyle{ \mathbf{F}_{i}^{\mathrm{D}} = -\gamma _{\mathrm{ L}}\omega _{\mathrm{L}}(z)(\mathbf{v}_{i} -\mathbf{v}_{\mathrm{wall}}). }$$
(5)

The friction constant γ L is an adjustable parameter that characterizes the strength of the wall friction, and it can be used to vary the slip length. The position-dependent function ω L(z) is a monotonically decreasing function of the wall-particle separation, and vanishes at certain cutoff z c to mimic the finite range of the wall interaction. Additionally, a random force obeying the fluctuation-dissipation theorem is required to ensure the correct equilibrium statistics,

$$\displaystyle{ \mathbf{F}_{i}^{\mathrm{R}} = \sqrt{2k_{ B}T\gamma _{\mathrm{L}}\omega _{\mathrm{L}}(z)}\boldsymbol{\xi }_{i}, }$$
(6)

where k B is the Boltzmann constant, T the temperature, and \(\boldsymbol{\xi }_{i}\) a vector whose component is a Gaussian distributed random variable with zero mean and unit variance.

The slip length b can be computed analytically as a function of a dimensionless parameter \(\alpha = z_{c}^{2}\gamma _{\mathrm{L}}\rho /\eta\), where ρ is the fluid number density [6]. For a linear function \(\omega _{\mathrm{L}}(z) = 1 - z/z_{c}\), the relation is

$$\displaystyle{ \frac{b} {z_{c}} = \frac{2} {\alpha } - \frac{7} {15} - \frac{19} {1800}\alpha + \cdots }$$
(7)

This formula works quite well for large values of b, but shows deviation near the no-slip region (b∕σ ∼ 1). The slip length can also be measured by short simulations of Poiseuille and Couette flow in a thin channel geometry. Figure 2 shows the relation between the slip length b and the wall friction parameter γ L. One can then choose a suitable value of γ L based on the requirement of the slip length.

Fig. 2
figure 2

Relation between the slip length b and the wall friction parameter γ L. The inset shows an enlarged portion of the region where the slip length is zero. No-slip boundary condition can be implemented by using \(\gamma _{\mathrm{L}} = 5.26\sqrt{m\varepsilon }/\sigma\). Dashed curves show analytical prediction Eq. (7)

Full size image

To demonstrate the validity and versatility of our method, we investigate two model systems: the flow past a patterned surface with alternating no-slip/partial-slip stripes (Sect. 3) and free diffusion of a slipping colloidal particle (Sect. 4).

3 Striped Surfaces

Patterned surfaces play a major role in micro- and nanofluidics. One important example is the superhydrophobic Cassie surfaces, where no-slip and partial-slip area arrange in a striped pattern (see Fig. 3a). The no-slip region consists of fluid/solid interface, while the partial-slip region consists of trapped gas which is stabilized by a rough wall texture. These superhydrophobic surfaces exhibit very low friction, and the drag reduction is associated with the large slip length over the fluid/gas interfaces.

Fig. 3
figure 3

Sketch of the striped surface: Θ = 0 to longitudinal stripes, \(\varTheta =\pi /2\) corresponds to transverse stripes (a), and of the liquid interface in the Cassie state (b)

Full size image

We simulate the superhydrophobic Cassie surface using the “gas-cushion model” [8]. Instead of modeling the physically corrugated surface, we use a flat surface with alternating no-slip and partial-slip boundary conditions. The value of the slip length b over the gas sector is related to the thickness of the gas region e by

$$\displaystyle{ b \simeq \frac{\eta } {\eta _{g}}e, }$$
(8)

where η and η g are shear viscosities of a gas and a liquid (see Fig. 3b). We consider a striped pattern with a periodicity L. The area fractions of the solid and gas sectors are ϕ 1 and ϕ 2, respectively. For inhomogeneous surfaces, the effective slip length depends on the flow direction Θ and is in general a tensorial quantity b eff. For the special case of striped surfaces, the eigenvalues of the slip length tensor correspond to the flow direction parallel to the stripes (maximum slip b eff  ∥ ) and perpendicular to the stripes (minimum slip \(b_{\mathrm{eff}}^{\perp }\)).

We compare our simulation results with the numerical solution to the Stokes equations and some analytical formulas. The results for the perfect-slip gas sector (b ≫ L) are well-known [9, 10]

$$\displaystyle{ \frac{b_{\mathrm{eff}}^{\parallel }} {L} = \frac{2b_{\mathrm{eff}}^{\perp }} {L} \simeq \frac{1} {\pi } \ln \left [\sec \left (\frac{\pi \phi _{2}} {2}\right )\right ]. }$$
(9)

For arbitrary value of b, Belyaev and Vinogradova suggested approximate expressions [11],

$$\displaystyle\begin{array}{rcl} \frac{b_{\mathrm{eff}}^{\parallel }} {L} & \simeq & \frac{1} {\pi } \frac{\ln \left [\sec \left (\frac{\pi \phi _{2}} {2}\right )\right ]} {1 + \frac{L} {\pi b} \ln \left [\sec \left (\frac{\pi \phi _{2}} {2}\right ) +\tan \left (\frac{\pi \phi _{2}} {2}\right )\right ]},{}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} \frac{b_{\mathrm{eff}}^{\perp }} {L} & \simeq & \frac{1} {2\pi } \frac{\ln \left [\sec \left (\frac{\pi \phi _{2}} {2}\right )\right ]} {1 + \frac{L} {2\pi b}\ln \left [\sec \left (\frac{\pi \phi _{2}} {2}\right ) +\tan \left (\frac{\pi \phi _{2}} {2}\right )\right ]}.{}\end{array}$$
(11)

These formulas are accurate over wide range of the parameters and recover to Eq. (9) at large b value.

We start with varying Θ for patterns that has equal areas of no-slip and partial-slip regions (ϕ 2 = 0. 5) and the slip length is in the intermediate region \(b/L = 1.0\). Figure 4 shows the results for the effective downstream slip lengths, b eff(Θ), and the theoretical curve

$$\displaystyle{ b_{\mathrm{eff}}(\varTheta ) = b_{\mathrm{eff}}^{\parallel }\cos ^{2}\varTheta + b_{\mathrm{ eff}}^{\perp }\sin ^{2}\varTheta. }$$
(12)

The simulation data are in good agreement with theoretical predictions, confirming the anisotropy of the flow and the validity of the concept of a tensorial slip for striped surfaces.

Fig. 4
figure 4

Effective downstream slip length, b eff(Θ) as a function of tilt angle Θ for a pattern with \(b/L = 1.0\) and ϕ 2 = 0. 5. Symbols with error bars are simulation data. Curves are theoretical values calculated using Eq. (12) with eigenvalues obtained by a numerical method (solid) and by Eqs. (10 and 11) (dot-dashed)

Full size image

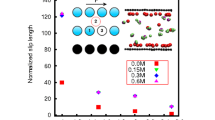
Next we examine the effect of varying the fraction of gas/liquid interface, ϕ 2. Figure 5a shows the effective slip lengths b eff  ∥  and b eff  ⊥  as a function of ϕ 2. The striped pattern again has \(b/L = 1.0\). The results clearly demonstrate that the gas fraction ϕ 2 is the main factor in determining the value of effective slip; the slip length increases significantly when the gas fraction increases to unity.

Fig. 5
figure 5

(a) Effective slip lengths (symbols) as a function of gas-sector fraction ϕ 2 for \(b/L = 1.0\). (b) Effective slip lengths as a function of local slip length b for ϕ 2 = 0. 5. The numerical results are shown as solid curves. Also shown are analytic expressions Eqs. (10 and 11) (dot-dashed), and asymptotic formulas Eq. (9) (dashed lines, for (b) only)

Full size image

Finally, we present the effective slip lengths as a function of the local slip length b at gas/liquid interface in Fig. 5b. The pattern has equal fractions of solid and gas, \(\phi _{1} =\phi _{2} = 0.5\). The analytic formulas Eqs. (10) and (11) are shown in dot-dashed lines, which are accurate over wide range of b value. The effective slip lengths reach the asymptotic values predicted by Eq. (9) at large values of b∕L. The excellent agreement between the simulation data and theoretic predictions promotes studies of more complex systems and applications, such as thin channels with symmetric stripes [12], anisotropic flow over weakly slipping stripes [13], trapezoidal grooves [14], electroosmotic flows [15], polyelectrolyte electrophoresis [16, 17], and separation of chiral particles [18].

4 Colloidal Particle

Colloidal dispersions have numerous applications in different fields such as chemistry, biology, medicine, and engineering [19, 20]. Better understanding of the dynamics of colloidal particles can provide insights to improve the material properties. Molecular simulations can shed light on the dynamic phenomena of colloidal particles in a well-defined model system. Due to the size difference between the colloids and solvent molecules, it is difficult to simulate the system on the smaller length scale (the solvent), and one has to rely on coarse-graining technique to reach meaningful time scales. The general idea is to couple the solute with a mesoscopic model for Navier-Stokes fluids. One of the examples is the coupling scheme developed by Ahlrichs and Dünweg [21], which combines a Lattice-Boltzmann approach for the fluid and a continuum Molecular Dynamics model for the polymer chains. The method has been extended to colloidal particles [22, 23]. We shall discuss a similar colloid model based on DPD.

The interactions between the colloid and fluid can be separated into two components, similar to the case of flat surface presented in Sect. 2. One component is the hard-core interaction to prevent the fluid entering the colloid. We use a pure repulsive potential of WCA form (Eq. (4)). The other one is the friction between the colloid surface and the fluid, which can be modeled by a pair of dissipative and random forces (cf. Eqs. (5) and (6)). The complication arises for colloidal particles which have a curved surface. There are two possible solutions. The first is to treat the surface as a continuous two-dimensional object and replace z in the friction force pair by the shortest distance between the fluid particle and the curved surface. This can be easily implemented for simple geometry such as spheres, but becomes complicated for colloids with irregular shape. The second solution is to discretize the surface by many interaction sites, whose positions are fixed in the local frame of the colloid. These sites interact with the solvent through the DPD dissipative and stochastic interactions, with a friction coefficient γ L (Eqs. (5) and (6) but with z replaced by bead separation r). Boundary conditions on the colloid surface can be tuned by vary the value of γ L. In this work, we opt to the second option for better extensibility. Figure 6 shows a representative snapshot of a colloidal particle decorated by many surface sites.

Fig. 6
figure 6

Snapshot of a colloidal particle in solution. The surface sites are represented by the dark beads, and the light beads are fluid particles. Only selective solvent beads are shown here for clarity

Full size image

The total force exerted on the colloid is given by the sum over all forces on the surface sites, plus the conservative excluded volume interaction,

$$\displaystyle{ \mathbf{F}_{\mathrm{C}} =\sum _{ i=1}^{N}\left [\mathbf{F}_{ i}^{\mathrm{D}}(\mathbf{r}_{ i}) + \mathbf{F}_{i}^{\mathrm{R}}(\mathbf{r}_{ i})\right ] + \mathbf{F}^{\mathrm{WCA}}. }$$
(13)

Here r i denotes the position of i-th surface sites and there are N of them. Similarly, the torque exerted on the colloid can be written as

$$\displaystyle{ \mathbf{T}_{\mathrm{C}} =\sum _{ i=1}^{N}\left [\mathbf{F}_{ i}^{\mathrm{D}}(\mathbf{r}_{ i}) + \mathbf{F}_{i}^{\mathrm{R}}(\mathbf{r}_{ i})\right ] \times (\mathbf{r}_{i} -\mathbf{r}_{\mathrm{cm}}), }$$
(14)

where r cm is the position of the colloid’s center-of-mass. Note that the excluded volume interaction does not contribute to the torque because the associated force points towards the center for spherical colloids, but this is in general not true for irregular shape. The total force and torque are then used to update the position and velocity (both translational and rotational) of the colloid at the next time step.

The diffusion constant of the colloid can be calculated from the velocity autocorrelation function using the Green-Kubo relation or by a linear fit to the mean-square displacement. Due to the periodic boundary condition implemented in simulations, the diffusion constant for a single colloid in a finite simulation box depends on the box size. Figure 7a demonstrates the finite-size effect by plotting the mean-square displacement as a function of time for two different simulation boxes L = 10 σ and L = 30 σ.

Fig. 7
figure 7

(a) Mean-square displacement of a spherical colloid with radius R = 3. 0 σ for two different sizes of simulation box, L = 10 σ and L = 30 σ. (b) Diffusion constant D for a spherical colloid of radius R = 3. 0 σ as a function of the reciprocal of the box size 1∕L. The curve is the prediction from Eq. (15). Different symbols correspond to simulation runs with different initialization

Full size image

The diffusion constant increases with increasing box size. For small simulation box, the long-wavelength hydrodynamic modes are suppressed due to the coupling between the colloid and its periodic images. The diffusion constant can be written in terms of an expansion of 1∕L, the reciprocal of the box size [24]

$$\displaystyle{ D = \frac{k_{B}T} {6\pi \eta } \left ( \frac{1} {R} -\frac{2.837} {L} + \frac{4.19R^{2}} {L^{3}} + \cdots \,\right ). }$$
(15)

In Fig. 7b, simulation results of the diffusion constant are plotted in terms of 1∕L. The simulation results and the hydrodynamic theory show reasonable agreement.

Most of the studies on colloid dynamics have been focus on the no-slip boundary condition. We have investigated the response of charged colloids under alternating electric fields [25–28]. No-slip is valid for large colloids, but may be questionable for nanometer-sized or hydrophobic particles. Furthermore, one can adjust the boundary condition by modifying the surface properties. One advantage of our colloid model is the ability to adjust the boundary condition from no-slip to full-slip by changing the friction coefficient γ L. Figure 8 illustrates the change of the diffusion constant by varying γ L in a simulation box L = 30 σ. This freedom provides opportunities to study the effect of hydrodynamic slip on the colloid dynamics [29, 30].

Fig. 8
figure 8

Diffusion constant D for a spherical colloid of radius R = 3. 0 σ as a function of the surface-fluid DPD friction coefficient γ L. The simulation box has a size of L = 30 σ. No-slip is realized for \(\gamma _{\mathrm{L}} > 10\,\sqrt{m\varepsilon }/\sigma\)

Full size image

5 Summary

We have presented a coarse-grained method to implement Navier boundary condition with arbitrary slip length in particle-based simulations. We have validated our method by simulating a flat homogeneous surface and proposed an analytical relation between the slip length and simulation parameters. To illustrate the versatility of the method, we extend the method to inhomogeneous surfaces by investigating Newtonian flow over superhydrophobic striped surface, and to curved surfaces by studying the dynamics of single spherical colloid. Our method provides a general tool to exam the slip-dependent phenomena in particle-based simulations and should be suitable to study more complex system, for example, flow over structured surface or channel and dynamics of aspherical colloids.