Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The numerical simulation is commonly considered a mandatory passage in synthesizing a nondestructive testing (NDT) diagnostic system. Indeed, a number of design parameters need to be set on the basis of the response of the diagnostic system in different scenarios, which would be hardly reproducible in real physical setup. Whichever numerical tool is used to simulate the real system, it has to guarantee reliability, convergence, and possibly, a limited computational cost. The problem can be approached by using several different methods, such as analytical, finite difference, moment, finite element, and Monte Carlo, each having its strong and weak points. Among these, finite element method (FEM) has the advantage of combining good model precision with a typical easiness of use. Furthermore, it allows for tuning the degree of precision on the simulation domain on the basis of the specific requirements. This aspect is crucial in our application, because in general, the object to detect consists of a discontinuity of the propagating mean.

The FEM , such as the finite difference method (FDM), is a numerical technique designed to seek approximate solutions of problems described by a system of partial differential equations (PDEs), reducing them to a system of algebraic equations [4]. With this method, it is possible to solve problems whose analytical models described by a system of differential equations cannot be solved analytically. To this aim, the problem is discretized by subdividing the domain in a proper number of elements (from which the name of the method), then the solution is found only in specific points of those elements (nodes), and finally, a continuous solution is obtained by interpolating the solution on the nodes. The possibility to entrust the solution of the problem to a computer represents a great advantage. The more the discretization is fine, namely the more the elements are small, the more the FEM model is precise but also computationally costly. Therefore, dealing with such method requires to find the best compromise between such two conflicting issues, by taking into account the resources on hand.

This chapter is organized as follows. First, a general formulation of the FEM is given. Then the method is described in more detail for the case of a wave propagation problem . A specific paragraph is devoted to the study of the behavior of transducers, whose function is the conversion of the electrical signal into pressure waves and vice versa. After that, the problem of detecting defects into a mean by means of ultrasonic waves is described in depth. Appendix reports a tutorial for the development of a model of NDT ultrasonic system.

2 The Finite Elements Method

The first thing one has to define in using the FEM is the domain of the problem. After that, the state variables of the problem have to be defined. The domain is delimited by a boundary, except for the cases where it could be useful considering an unlimited domain; in such cases, particular elements are adopted, but this is not a case of interest for the scope of this book.

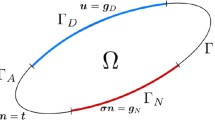
As for the continuous differential problems, the boundary conditions have to be defined in order to solve the problem. The boundary is subdivided into two parts that are characterized by a specific boundary condition . The nature of this condition depends on the physics of the problem, but in general, we can distinguish between boundary conditions where the value of the state variable is given (Dirichlet conditions ) and that where the normal derivative of the state variable is given (Neumann conditions ). Corresponding to such distinction, we can subdivide the whole boundary of the domain into a Dirichlet and a Neumann boundary, respectively.

The problem at hand in the FEM is first expressed in the so-called strong form and then it is translated in the weak or variational form to be solved. The first one can be formalized in general as follows:

$$\begin{aligned} L\Phi = g \;\;\; \text{in}\;\;\; \Omega \\\Phi = g_0\;\;\; \text{in}\;\;\; \Gamma_D \\\partial_n\Phi = g_1\;\;\;\text{in}\;\;\; \Gamma_N\end{aligned}$$
(2.1)

where L is a differential (integral) operator, Φ is the state variable, Ω is the domain, g, g 0, and g 1 are known functions, Γ is the boundary of the domain, which is subdivided into the Dirichlet boundary Γ D and Neumann boundary Γ N , and finally, ∂ n denotes the derivative of the state variable in the direction normal to Γ.

It is often possible to replace the problem of integrating the equations in (2.1) by an equivalent minimization problem. Problems like these are called variational problems and the methods which allow one to reduce the original problem in variational form are called variational methods . Such methods represent a common basis for different kind of analyses, among which, the FEM is included [12, 13, 22].

The first step to apply the variational methods consists of finding the functional of the problem, which is the function having a minimum in correspondence of the solution of the original problem [9]. This function is commonly called energy function W due to the fact that, like in nature, the systems spontaneously evolve toward states of minimal energy, but in most cases where the problem at hand is physical, the functional is actually an energy function, so that searching the solution of the system just corresponds to find a state of minimal energy.

Generally speaking, the application of the FEM involves the following steps:

  1. 1.

    Discretize the domain of application of the differential equation as function of physical magnitude of field quantity V in a finite number of elements.

  2. 2.

    Define the governing algebraic equations as a function of field quantity V for a generic element.

  3. 3.

    Assembling of all elements in the solution region and determination of the total energy W, associated with the assembly of the elements expressed as a function of the values that the field quantity V assumes in each of the n nodes of the mesh: \(W = f (V_1, V_2, V_3, \dots, V_n)\).

  4. 4.

    Solving the system of linear equations resulting from the application of the variational principle , by imposing the condition of minimum energy stored, equivalent to the equilibrium condition of the system. Thus, we require that the partial derivatives of the energy function W with respect to each nodal value of the potential are zero i.e.,: \(\partial W/\partial V_k = 0;\;\;\; k=1,2,\dots,n\).

So we get a system of n algebraic equations whose unknowns are values that the field quantity V assumes in the nodes of the mesh, except for the nodes on the boundary of the domain, in which the magnitude (Dirichlet conditions ) or the normal derivative (Neumann conditions ) of the field quantity are known.

Therefore, the FEM is based on the discretization of the domain into elements. Without loss of generality, we can assume that the domain at hand is 2D and that the elements we have chosen are triangular.The value of the field quantity at any point inside of the generic triangular element will be determined by interpolating the values of the field quantity in the nodes of the corresponding element (Fig. 2.1 ).

Fig. 2.1
figure 1

Discretization of the domain by means of triangular elements

Full size image

The triangular elements are those that fill better the surfaces of the most varied forms. Actually, the elements with the minimum number of facets (simplex: segments in R 1, triangles in R 2, and tetrahedrons in R 3) are the most commonly used as default-element for the mesh by commercial softwares. The elements have a certain number of nodes, which in the simplest case, coincide with the vertices of the element. The FEM solves Eq. (2.1) only on the nodes of the mesh rather than on the whole domain, while the solution within the element is expressed in function of such nodal values. The relationship among the values of the nodes and the other points of the element is fixed a priori, so that in general, it does not fit exactly the actual values of the function. This relationship is called shape function and in general can be fixed arbitrarily, but for simplicity, it is often preferred to have a great number of elements and for each element a limited number of degrees of freedom. This is the reason why the most common choice is to assume linear shape functions .

We seek an approximation of the function \(V(x,y)\) in the whole domain as the sum of the function within the elements \(V_e(x,y)\):

$$V(x,y)\cong \sum_{e=1}^N V_e(x,y)$$
(2.2)

where N is the number of elements and

$$V_e(x,y)=a+bx+cy$$
(2.3)

is an interpolating linear function which gives the approximation within the element. More in general, the number of nodes could be much greater so that the interpolating function could be different.

For the convergence of the solution, the approximating polynomial has to satisfy the compatibility and completeness criteria [11]. This means that considering, for example, 2D elements:

  • the functions (2.3) have to be continuous at element interfaces, i.e., along element interfaces, we must have continuity of V as well as continuity of the derivative of V normal to the interface;

  • if the size of the elements tends to zero, the function (2.3) and its gradient must be constant within the element.

Furthermore, the approximating polynomial should be isotropic, i.e., the approximating polynomials should remain unchanged under a linear transformation from one Cartesian coordinate system to another. This is achieved if the components of the approximating polynomial are complete or, if incomplete, they are symmetric with respect to the independent variables.

In order to correctly select the terms of the polynomials, we can use the Pascal’s triangle (see Fig. 2.2 ).

Fig. 2.2
figure 2

Pascal’s triangle (2D case)

Full size image

Assuming a linear interpolation within the elements implies that a proper size of elements (mesh) has to be considered in order to avoid introducing too coarse approximations.

The three coefficients in (2.3) are related to the value of the V e in the nodes:

$$\begin{matrix} a \\b \\c\end{matrix} =\begin{bmatrix} 1 & x_1 & y_1 \\1 & x_2 & y_2 \\1 & x_3 & y_3\end{bmatrix}^{-1}\begin{bmatrix} V_{e1} \\V_{e2} \\V_{e3}\end{bmatrix}.$$
(2.4)

The coefficients obtained by Eq. (2.4) can be substituted in Eq. (2.3), obtaining at the end the linear function within the element, given by:

$$V_e(x,y)=\sum_{i=1}^3 \alpha_i(x,y) V_{ei}$$
(2.5)

that is, it is given by a linear combination of three functions, one for each node, where the weights are values of the V e in correspondence of the nodes. The functions \(\alpha_i(x,y)\) are called shape functions and, due to the initial choice, are linear.

As said before, a functional has to be defined to solve the problem [9]. The precise form of such functional depends on the form of the equation which describes the problem.

To fix the ideas, let us consider the case of a problem described by the Laplace’s equation :

$$\nabla^2~V=0.$$
(2.6)

The corresponding functional evaluated for the single element has the following form:

$$W_e=\frac{1}{2}\int{|\nabla V_e|}^2\mathrm{d} S.$$
(2.7)

The gradient of V can be expressed by means of Eq. (2.8):

$$\nabla V_e=\sum_{i=1}^3 V_{ei}\cdot\alpha_i$$
(2.8)

which can be substituted in Eq. (2.7), to give

$$W_e=\frac{1}{2}\sum_{i=1}^3\sum_{j=1}^3 V_{ei}\left[\int\nabla\alpha_i\nabla\alpha_j\mathrm{d} S\right]V_{ej}.$$
(2.9)

Let us indicate the term in brackets with the notation C ij . With this, Eq. (2.9) can be rewritten in matrix form:

$$W_e=\frac{1}{2}V_e^T[C_e]V_e.$$
(2.10)

The terms C ij are obtained by combining gradients of linear functions, so they are constant and depend only on the coordinates of the elements nodes.

The complete functional to minimize is obtained by summing Eq. (2.10) for all the elements, as

$$W=\sum_{e=1}^{N}W_e=\frac{1}{2}V^T[C]V.$$
(2.11)

In Eq. (2.11), the variable vector V comprises the function calculated in all the nodes of the domain. As the same node belongs to more than one element, the matrix \([C]\) will not be concentrated around the diagonal, but in general, any entry could be different from zero. The definitive distribution of the elements of \([C]\) will depend on the order according to which they are considered and it is arbitrary, but the computational cost of minimization depends on such distribution. The minimum of Eq. (2.11) can be found by imposing the gradient to be equal to zero. Not all the values of V at nodes are variable. Indeed, the boundary conditions have to be fulfilled according to the formulation of the problem. As a consequence, the equations’ system that gives us the minimum will be a nonhomogeneous system. Indeed, the terms of W that are the product between a variable and a fixed value in the derivation give rise to constant terms.

The minimum of the solution can be found by solving a linear equations’ system:

$$[C_{\mathrm{free}}]V_{\mathrm{free}}=[C_{\mathrm{bound}}]V_{\mathrm{bound}}$$
(2.12)

where \(V_{\mathrm{free}}\) is the vector of the variable values of the function and \(C_{\mathrm{free}}\) is the corresponding coefficient matrix, while \(V_{\mathrm{bound}}\) is the vector of values at the boundary of the domain and \(C_{\mathrm{bound}}\) is the corresponding matrix of coefficients.

The number of nodes needs to be higher in the regions where the field variable has strong gradients. In these regions, in order to apply the method preserving the required accuracy, it may be necessary to thicken the nodes. The FEM allows to do that. Solving the system (2.12) is in general troublesome due to the high order of coefficients matrix, so that a number of procedures have to be used in order to reduce the computational cost of minimization. Anyway, analyzing these methods is beyond the scope of this book. It is sufficient for the reader to know that this is a task of the software that he/she uses to apply the FEM , and all the information about the implemented minimization algorithms is usually described in the documentation of the software.

3 Use of FEM for the Analysis of Waves Propagation

Typically, the wave propagation phenomena are described by the Helmholtz’s equation :

$$\nabla^2\Phi+k^2\Phi=g$$
(2.13)

where Φ is field variable and g is the source function. It is possible to demonstrate that the functional corresponding to Eq. (2.13) is equal to:

$$I(\Phi)=\frac{1}{2}\int\int \bigg [|\nabla\Phi|^2-k^2\Phi^2+2\Phi g\bigg]\mathrm{d} S.$$
(2.14)

We need to express both the field variable and the source function in terms of shape functions over a triangular element :

$$\begin{aligned} \Phi_e(x,y)=\sum_{i=1}^{3}\alpha_i\Phi_{ei}\nonumber \\ g_e(x,y)=\sum_{i=1}^{3}\alpha_ig_{ei} . \end{aligned}$$

The functional in Eq. (2.14), calculated for the single element, becomes:

$$\begin{aligned}I(\Phi_e)=\frac{1}{2}\sum_{i=1}^{3}\sum_{j=1}^{3}\Phi_{ei}\Phi{ej} \int\int \nabla\alpha_i\nabla\alpha_j\mathrm{d} S-\ \nonumber\\ \frac{k^2}{2}\sum_{i=1}^{3}\sum_{j=1}^{3}\Phi_{ei}\Phi_{e_j} \int\int \alpha_i\alpha_j\mathrm{d} S + \nonumber\\ \sum_{i=1}^{3}\sum_{j=1}^{3}\Phi_{ei}g_{ej}\int\int \alpha_i\alpha_j\mathrm{d} S.\end{aligned}$$
(2.15)

Let us define \(C_{ij}=\int\int \nabla\alpha_i\cdot\nabla\alpha_j\mathrm{d} S\) and \(T_{ij}=\int\int \alpha_i\cdot\alpha_j\mathrm{d} S\).

The Eq. (2.15) can be then rewritten in matrix form:

$$I(\Phi_e)=\frac{1}{2}\Phi_e^T[C_e]\Phi_e-\frac{k^2}{2}\Phi_e^T[T_e] \Phi_e+\Phi_e^T[T_e]G_e.$$
(2.16)

By assembling such functional for all the elements, one gets

$$I(\Phi)=\frac{1}{2}\Phi^T[C]\Phi-\frac{k^2}{2}\Phi^T[T]\Phi+\Phi^T[T]G.$$
(2.17)

Once again, in order to find the solution of the wave problem , the derivative of Eq. (2.17) has to be taken with respect to all the free nodes. By splitting the vector Φ into a free and a prescribed subsets Φ f and Φ p , also the matrices \([C]\) and \([T]\) are consequently subdivided according to the fact that the entries multiply only free components, only prescribed ones or both in Eq. (2.17). An important class of problems is represented by the cases where the source term is null. In such cases, Eq. (2.17) can be rewritten as:

$$I(\Phi)=\frac{1}{2}[\Phi_f^T \Phi_p^T]\begin{bmatrix} C_{ff} & C_{fp} \\C_{pf} & C_{pp}\end{bmatrix}\begin{bmatrix} \Phi_f\\\Phi_p\end{bmatrix} -\frac{k^2}{2}[\Phi_f^T \Phi_p^T]\begin{bmatrix} T_{ff} & T_{fp} \\T_{pf} & T_{pp}\end{bmatrix}\begin{bmatrix} \Phi_f\\\Phi_p\end{bmatrix}.$$
(2.18)

In order to minimize this functional , the derivatives with respect to the free nodes have to be set equal to 0. We obtain:

$$ \nabla I(\Phi)=[C_{ff} C_{fp}]\begin{bmatrix} \Phi_f\\\Phi_p\end{bmatrix} -k^2[T_{ff} T_{fp}]\begin{bmatrix} \Phi_f\\\Phi_p\end{bmatrix}=0$$
(2.19)

which is a system of linear equations. We can further specialize Eq. (2.19) by assuming that the prescribed values are all equal to 0. In this case, we obtain:

$$ \nabla I(\Phi)=[[C_{ff}]-k^2[T_{ff}]]\Phi_f=0$$
(2.20)

which is a standard eigenproblem [2, 10].

4 Developing the FEM Model for a Wave Propagation Problem

In order to study a wave propagation problem using FEM , the steps to be performed will be illustrated below [7, 17]. These steps reflect the procedure commonly followed by the commercial packages, such as described in the Appendix for the software COMSOL\(^\mathrm{TM}\) .

First of all we need to define a coordinates system. More specifically, we need to choose how many dimensions have to be considered. Because the 3D geometry is usually a large computational problem, it would be better to avoid it if possible. One needs to exploit symmetries in order to create 2D or 2D axisymmetric geometries that involve a lower computational cost.

After that we need to define the relevant physics involved in the problem. In general, the software gives in hand a collection of specific modules for each physics, so in general, one needs just to select the proper module/modules.

At this point, the PDE and the number of spatial dimensions have been chosen. For acoustic pressure , the PDE is the Helmholtz’s equation  (1.13) in Chap. 1, that is obtained by considering a constant density value.

This equation governs the spatial dependency of p, which permits us to know p completely, since the temporal part is already known. The goal is then to solve Eq. (1.14), defined in Chap. 1, for the frequencies of interest.

For axisymmetric geometries, the axis of symmetry is r = 0. For the acoustic pressure in 2D axisymmetric geometries, the wave equation becomes:

$$\frac{\partial}{\partial r}\left(-\frac{r}{\rho}\frac{\partial p}{\partial r}\right)+r\frac{\partial}{\partial r}\left(-\frac{1}{\rho}\frac{\partial p}{\partial z}\right)-\left[\left(\frac{\omega}{c}\right)^2-\left(\frac{m}{r}\right)^2\right] \frac{rp}{\rho}=0$$
(2.21)

where m denotes the circumferential wave number . In this case, k z is the out-of-plane wave number . In 2D axisymmetric geometries, the independent variables are the radial coordinate r and the axial coordinate z.

It is a very good approach to parameterize all the dimensions and link them together in order to easily change the geometry lately. The other way is to design the device using specialized computer-aided design (CAD) software and then import the geometry in the FEM sofware.

The various regions must match the materials they represent. The material properties represent all the constants that appear in the PDE . The type of material can be chosen among those already present in the database, or one can create his/her own materials, specifying the proprieties that have to be used during the analysis.

For acoustic pressure , the principal properties of the medium are density and speed of sound .Footnote 1

Initial conditions are used in conjunction with time studies and this condition adds initial values for the sound pressure p and the pressure time derivative \(\mathrm{d} p/\mathrm{d} t\) that can serve as an initial guess for a nonlinear solver.

Boundary conditions define the nature of the boundaries of the computational domain. Some define real physical obstacles like a sound hard wall or a moving interface. Others, called artificial boundary conditions, are used to truncate the domain. The artificial boundary conditions are, for example, used to simulate an open boundary where no sound is reflected. For acoustic pressure mode, it is possible to choose among the following boundary conditions [6]:

  • Neumann Condition

    The normal component of particle velocity disappears. This condition is equivalent to the normal acceleration equal to 0:

    $$\textit{n}\cdot\left(\frac{1}{\rho_0}(\nabla p)- q\right)=0. $$

    If the dipole source q is null, the normal derivative of the pressure is equal to 0:

    $$\frac{\mathrm{d} p}{\mathrm{d} n} = 0 \;\;\;\text{(normal velocity = 0)}.$$

    This condition is used to model rigid surfaces.

  • Dirichlet Condition

    This condition nullifies in the boundary the acoustic pressure value:

    $$p=0.$$

    It is an appropriate approximation for a liquid–gas interface.

  • Pressure (Dirichlet Condition ) \(p=p_0\)

    The pressure condition specifies in the boundary, the acoustic pressure amplitude (oscillating as \(\mathrm{e}^{{\rm i}\omega t}\)) in the frequency analysis. In the transient analysis, the time dependence of the pressure source has to be explicated.

  • Normal Acceleration (Neumann Condition )

    This condition sets the inward normal acceleration amplitude at the boundary:

    $$\textit{n}\cdot\left(\frac{1}{\rho_0}(\nabla p)\right)= \textit{a}_\textit{n}$$
    (2.22)

    where \(\textit{a}_{\textit{n}}\) represents an external source term.

    Using this condition, it is possible to obtain also an acoustic source: a sound can be produced through the vibration of the boundary (e.g., a baffled piston or a desired simple source strength if a small boundary is selected).

    This condition is used to couple acoustic domains to adjacent mechanical domains through a function that sets the acceleration on the boundary of the latter as the condition (see Sect. 2.5).

  • Impedance Condition

    Considering the acoustic input impedance of the external domain Z (ratio between pressure and normal particle velocity), this condition is expressed in the time domain as

    $$\textit{n}\cdot\left(\frac{1}{\rho_0}(\nabla p-q)\right)+\frac{1}{Z}\frac{\partial p}{\partial t}=0$$

    whereas in the frequency domain it is

    $$\textit{n}\cdot\left(\frac{1}{\rho_0}(\nabla p-q)\right)+\frac{{\rm i} \omega p}{Z} =0.$$

    This condition is an approximation for a locally reacting surface (e.g., an absorbing panel).

  • Radiation Condition

    This condition permits to approximate an infinite space. In fact, it sets a boundary that will not reflect normally incident waves and allow an outgoing wave to leave the domain. Such kind of waves can be respectively:

    • Plane waves : used for both far-field boundaries and ports (e.g., waveguide structures);

    • Cylindrical waves ;

    • Spherical waves : used to allow a radiated or scattered wave (emanating from an object) to leave the domain without reflections.

    Furthermore, using this condition, an acoustic source can be obtained. In fact, sending a plane wave from a plane wave radiation boundary condition, or an incoming spherical wave from a spherical radiation condition, it is possible to simulate a source at infinity.

  • Sources

    Another way to create an acoustic source is to add a point or an edge source. An acoustic source is also a monopole distribution that is applied over a volume in order to radiate a uniform sound field in all directions, or a dipole source in order to radiate a sound field that is typically stronger in two opposite directions.

When the geometry is complete, it has to be divided into finite elements.

In order to get a convergent and accurate solution, the mesh in acoustic computations should be fine enough to both resolve the geometric features and the wavelength of the problem. If an insufficient number of elements is used, the wave will not be well modeled (see Fig. 2.3). The “rule of thumb” in the literature is that the maximal mesh size should be less or equal to \(\lambda/N\), where N is between 5 and 10 [6, 14].

Fig. 2.3
figure 3

Modeling a single wave with \(N=2, 3, 4, 5, 8, \textrm{and} 10\) elements

Full size image

Increasing k, the number of elements required to maintain accuracy grows at least linearly with respect to k in 1D, with the cost growing at a faster rate in higher dimensions, and this leads to prohibitive computational cost for large values of k. For this reason, it is necessary to model the system to be studied trying to simplify as much as possible the geometry taking advantage of symmetries.

In most part of the simulations that involve fluids, the internal dumping effects can be neglected. Indeed, they could affect meaningfully the behavior of the system only at very high frequencies or when the dynamic viscosity of the fluid is much different from that of both air and water. This is not the case of solids. There are two effects occurring in the solids which give rise to dumping effects: absorption and scattering [6, 15]. The first one consists in a conversion of mechanical energy into heat, due to viscosity that breaks the oscillation of the particles. Furthermore, due to its viscous nature, it rises with the frequency. The scattering is due to the nonperfect homogeneity of the medium where the wave propagates. The abrupt variation of acoustic impedance in correspondence of irregular and randomly oriented surfaces gives rise to a diffusion of the wave energy, and as a consequence, an attenuation of the measured value. Both contributions of attenuation depend on the frequency, even if for different reasons. From a numerical point of view, we can take into account the attenuation by means of an exponential term:

$$p = p_0 \cdot \mathrm{e}^{\alpha d}$$
(2.23)

where the amplitude p is the reduced amplitude after the wave has traveled a distance d from the initial location and the attenuation coefficient α has to be defined for the material and in general, it will be a function of the frequency.

The frequency domain modeling appears to be the most convenient way to study damping materials. A material is characterized by two complex functions which are the wave number k and the impedance Z. If these two parameters are known, it is possible to define the complex speed of sound \(C_c = \omega/k\) and the complex density \(\rho_c=kZ/\omega\), and the problem can be solved in terms of equivalent fluid model. Regarding the mesh, the dumping materials require an unstructured mesh, as it is impossible to establish a priori which direction needs a more detailed analysis.

If the linearity hypothesis holds valid, the time evolution can be treated as the superimposition of sinusoidal regimes, each one having specific amplitude, frequency, and phase. This allows one to eliminate the time variable in the solution of the problem. In order to retrieve the solution in the time domain, all one needs is to apply the inverse Fourier transform to the frequency domain solution.

Even if solving the problem in the time domain is always possible, it should be avoided when possible because of the much higher computational complexity, like for example, the presence of nonlinear terms.

Finally, it is possible to calculate the solution to PDE .

We need to establish which kind of study has to be performed. In general, we have three possibilities: steady state, transient, and frequency domain analysis. The first one is obviously the less demanding one in terms of calculation, but it cannot be used in all that cases, like the one at hand, where the dynamics of the phenomenon is a fundamental aspect. The frequency domain analysis can be performed both for permanent periodical regime and for the transient analysis. The use of this kind of study in general requires much less time than the time domain analysis.

It is possible to change the type of solver under various steps. There are a variety of direct and iterative solvers. Direct solvers tend to be more robust (they are most likely to converge) but require more memory.

In acoustic pressure studies, the parametric sweeps are useful to solve the same geometry for a range of frequencies.

For transient acoustic problems , several new time scales are introduced. One is given by the frequency contents of the signal and by the desired maximal frequency resolution: \(T=1/f_{\mathrm{max}}\). The other one is given by the size of the time step \(\Delta t\) used by the numerical solver. In fact, the distance traveled by the fastest wave in the model should be smaller than the characteristic element size in the mesh. A condition on the so-called CFL number [8] dictates the relation between the time step size and the minimal mesh size l e as:

$$\mathit{CFL}=\frac{c \cdot \Delta t}{l_e}$$
(2.24)

where c is the speed of sound of the medium.

Once the solution has converged, the results can be plotted. These are all derived from the solution for the pressure, which is the unknown quantity of the PDE . Obtaining the pressure, one can compute velocity, intensity, etc.

5 Modeling Transmitting and Receiving Transducers

An ultrasonic measurement process involves the generation of ultrasound by the transducer, propagation of ultrasonic waves into the propagating medium, and reception of these waves through the transducer again. A complete measurement system consists of a pulser, a transducer, and a receiver. The pulser sends the electrical pulse via a cable to an ultrasonic transducer. The piezoelectric effect implies the conversion of the electrical pulse into an acoustical pulse in the generation system and an acoustical into an electrical signal in the reception system. In fact, certain materials will generate an electric charge when subjected to a mechanical stress and change its dimensions when an electric field is applied across the material (Fig. 2.4). These are called respectively, the direct and inverse piezoelectric effect [20].

Fig. 2.4
figure 4

The piezoelectric effect

Full size image

This effect is observed in a variety of materials, such as quartz, dry bone, polyvinylidene fluoride, and lead zirconate titanate (PZT). The latter of these is a man-made ceramic with a perovskite structure and is one of the most commonly used piezoelectric ceramics today.

A piezoelectric material is described by both the laws of mechanics and electromagnetics [1, 3, 21].

In COMSOL Multiphysics, the modeling of transmitting and receiving transducers is done with the piezoelectric devices interface that is a combination of the solid mechanics and electrostatics interfaces [6]. The electric potential V and the three components of the displacement, x, y, and z are the dependent variables.

The mechanical properties of a piezoelectric material can be described as a linear-elastic material. Consequently, the relation between stressFootnote 2 tensor \(\textit{T}\) and strainFootnote 3 tensor \(\textit{S}\) in a material is linear and it follows the generalized Hooke’s law [18]:

$$T=c \cdot S\;\; \text{or}\ S=s \cdot T$$
(2.25)

where c is the (elastic) stiffness matrix of the material and s is the compliance matrix of the material, which is the inverse of the stiffness matrix.

Electrically, a piezoelectric material is a polarizable dielectric that follows the electrical equation

$$D=\epsilon_0 E+P$$
(2.26)

where D is the electric displacement field [\(\mathrm{C}/\mathrm{m}^2\)], ϵ0 is the vacuum permittivity, E is the electric field [\(\mathrm{V}/\mathrm{m}\)], and P is the polarization density.

Since the material is a dielectric, the divergence of the electric displacement field is null:

$$\nabla \cdot D=0.$$
(2.27)

Piezoelectric materials combine these two constitutive equations into one coupled equation. Then, the constitutive relations of piezoelectric devices are expressed in the subsequent strain–charge form as:

$$S=s_ET+d^tE D=dT+\epsilon_TE$$
(2.28)

where s E is the compliance matrix whose coefficients were measured while the electric field across the material was zero or constant (subscript E) and d is the coupling matrixFootnote 4. The permittivity matrix ϵ has been introduced to replace the vacuum permittivity and the polarization vector, and the permittivity data were measured under at least a constant, and preferably a zero stress field (subscript T).

The electric field is connected to the voltage by:

$$E=-\nabla V.$$
(2.29)

In the same way as in the acoustic interface (see Sect. 2.4), piezoelectric material model must be applied to all domains governed by the piezoelectric interface . Also, here the temperature and absolute pressure are set with the same standard values as in the acoustics. A feature in this model is the possibility to align the model with another coordinate system than the global Cartesian system. This is often necessary, as piezoelectric materials are generally defined to be poled in the three directions, which coincide with the z-direction in the global system. A 2D model is however set in the x–y plane, causing the piezoelectric to be poled in the out-of-plane direction [16].

All features and conditions that are applied to this interface are described in the following list [6]:

  • Free

    This is the standard mechanical boundary condition , and therefore initially applied to all boundaries in domains governed by the piezoelectric interface . It defines the boundary as free to move in any direction and without any loads acting on it.

  • Zero charge

    This is the default electrostatic boundary condition . It defines, as the name implies, that there is no electric charge on the boundary.

  • Initial values

    This option allows to set an initial displacement field, velocity field, electric potential, or time derivative of said potential in any of the domains governed by the piezoelectric interface .

  • Axial symmetry

    This option is available only in the axisymmetrical models, where it defines the axis of symmetry. It is set as a standard condition on all boundaries that lie along the line where \(r = 0\).

  • Electrical potential

    This option sets the electrical potential to a given value on the boundary the condition is applied to.

  • Ground

    This option sets the electrical potential to zero at the boundary it applies to.

  • Symmetry

    This indicates that the model is a part of a larger structure that is mirror symmetrical around the boundary where this condition is applied, and thus, overrides the free boundary condition .

  • Roller

    This condition suppresses the standard mechanical condition, and defines that there can be no displacement perpendicular to the boundary, but tangential displacement is still allowed.

  • Damping and loss

    This option allows the inclusion of dielectric, mechanical, and piezoelectric damping in various domains. The loss factors can be set in this feature, and thus, apply to all domains with loss. Alternatively they can be set in each material as a property that is only included when required.

  • Boundary load

    This condition replaces the standard free condition. It states that a given mechanical load is applied on the boundary. This can be used to couple a mechanical domain to a bordering acoustic domain by setting the pressure in the acoustic domain as a force per unit area on the boundary of the mechanical domain.

6 Dealing with Interfaces and Defects

As seen in the introduction of this book, the ultrasonic direct transmission technique (DTT) [19] is employed to obtain useful, rapid, and relatively low-cost information on the studied structure and it permits to measure the propagation speed.

This technique uses a beam of ultrasonic waves emitted by a transducer and received by another one placed on the opposite surface of the structure. The waves pass through the tested material and they are reflected and refracted by incidental discontinuities encountered along the path. In fact, as can be noted in Fig. 2.5, the sound vibration can be subjected to several conditions. If the path between transmitter T and receiver R is a medium free of defects, the flight time will be characteristic of that medium. If the path crosses an area with a lack of structural homogeneity, the signal will be dispersed and both, the path followed and the flight time , will be greater and the speed will be reduced.

Fig. 2.5
figure 5

Possible paths of transmitted signal

Full size image

If instead, the two transducers are positioned in such a way that the direct path passes close to the edge of a crack, the signal does not travel through the solid–air interface, but there will be a diffraction signal at the edge of the crack resulting in a path greater than the distance between the two transducers. Therefore, it will have a lower speed than that of the sound characteristic of the medium tested. Finally, in the case in which the wave crosses a cavity, the wave will be largely reflected and the time of flight will be hardly measurable.

The inner conformation of the structure, i.e., the possible presence of discontinuities and defects, introduces reflections at the interfaces between the different materials, and alters the amplitude, direction, and frequency content of the signal.

In order to show how the transmitted wave behaves in the presence of interfaces and defects, in the following, a model of a structure with variation of density within the medium, will be analyzed as an example [5].

Let us consider two axisymmetric bidimensional models with a simple geometry in order to reduce the calculation time, exploiting the cylindrical geometry of the transducers and, with a certain approximation, the volume of material crossed by the ultrasonic wave . The first one consists of a rectangle \(6\times38~{\rm cm}^2\), which represents the section of a trachite block. Two other rectangles of size \(2.5\times3.5~{\rm cm}^2\) are inserted at the ends of the block in order to simulate the transducers. In this way, a path of the acoustic wave through a block of a single material (in this example, trachite) is simulated (Fig. 2.6).

Fig. 2.6
figure 6

First model: block of a single material

Full size image

The second model is similar to the first one with the insertion of interspaces of mortar and air, transversal to the propagation direction (Fig. 2.7).

Fig. 2.7
figure 7

Second model: geometry with insertion of interspaces of mortar and air

Full size image

The commercial software usually has the interface which allows one to study the behavior of piezoelectric devices. As an example, we can consider the COMSOL environment. In this software, there is the “transient acoustic piezoelectric interaction” interface that permits to simulate the transient performance of an acoustic wave in a structural element of known geometry and average density variable that interacts with two piezoelectric transducers [6]. This interface combines in a single multiphysics module, the features of “transient pressure acoustics,” “solid mechanics,” “electrostatics,” and “piezoelectric devices” interfaces. The unknowns are the acoustic pressure p, the vector of displacement \(\textit{u}\), and the electric potential V. The equations that describe the phenomenon are the same as described previously in the Sects. 2.4 and 2.5.

The materials used in the model are listed in Table 2.1.

Table 2.1 Materials properties
Full size table

The conditions applied to the models are (see Sects. 2.4 and 2.5 for details):

  • For the transducers:

    • Free

    • Ground

    • Roller

    • Electric potential.

  • For the structure:

    • Sound hard boundary wall.

The excitation wave is an acceleration signal obtained by the piezoelectric transducer (made of the crystal PZT4) by applying the impulsive voltage signal shown in Fig. 2.8. This electric pulse with maximum amplitude of 500 V and duration of \(9.3~\mu\textrm{s}\) is applied to the upper part of the emitter transducer, while the bottom part of both the transducers is grounded.

Fig. 2.8
figure 8

500 V excitation pulse modeled by COMSOL

Full size image

In order to obtain a fairly accurate analysis, it is useful to adopt elements that are particularly small near the notches or other discontinuities, and then the models are meshed in a different way. The first model, which is done by a homogeneous material, will have a uniform mesh, with thickening at the interface with the transducers (Fig. 2.9).

Fig. 2.9
figure 9

Mesh of the homogeneous model

Full size image

The model with insertion of interspaces of mortar and air is inhomogeneous and will have mesh thickened at each separation surface between the different materials (Fig. 2.10).

Fig. 2.10
figure 10

Mesh of the model with different density

Full size image

The vibration produced by the emitter arrives at the receiver, which transforms the acoustic vibration into an electric voltage.

The trends of the electrical potential at the center of the receiver transducer have been analyzed. In Fig. 2.11, the trend of the electrical potential for the homogeneous trachite block is shown, and in Fig. 2.12, we can see the trend of the electric potential for the model with different density (structure with trachite, mortar, and air).

Fig. 2.11
figure 11

Trend of the electric potential for the first model (homogeneous trachite block)

Full size image
Fig. 2.12
figure 12

Trend of the electric potential for the second model (structure with trachite, mortar, and air)

Full size image

As can be seen in Figs. 2.11 and 2.12, by applying a load in the wall in contact with the transmitter, the received signals are detected with some delay on the opposite side of the wall.

The time between the start time of the signal from the emitter and the time of arrival at the receiver, is the flight time of the signal and it provides useful information for the characterization of the path followed by the wave.

As can be observed in Fig. 2.11, considering the length of the path (0.38 cm) and the sound velocity of the material (in this case, trachite) equals 1968 m/s, a flight time equal to 0.193 ms is expected and obtained.

The presence of the mortar and air introduces a delay in the flight time (see Fig. 2.12) and the signal is strongly attenuated.

The inner conformation of the structure, i.e., the presence of discontinuities and defects introduces reflections at the interfaces between different materials, and then, the amplitude, direction, and the frequency content of the signal will be altered.

7 Conclusion

In this chapter, the FEM formulation is described in general terms, and then the specific case of waves’ propagation problems is analyzed in details. On these bases, the problem of developing a model of an ultrasonic NDT system is described, taking into account three different aspects of the problem, namely, propagation of ultrasounds into a mean, modeling the transducers, and detecting the presence of defects in the analyzed system. In the following appendix, the procedure is shown for a particular case by using COMSOL\(^\mathrm{TM}\) software.