A Design Model for Rapid Transit Networks Considering Rolling Stock’s Reliability and Redistribution of Services During Disruptions

Abstract

This paper presents a model for designing a public transit network system combining the traditional approach of transport demand coverage in bimodal scenarios of operation with the recovery of possible disruptions due to limited reliability of the rolling stock. The model balances construction and operational costs with the benefits to the users for the optimization of their travel times. Two transportation modes have been considered, public and private transport and the proportion of the users choosing one mode or the other is assumed to obey to a bimodal logit choice model. While construction costs are a first stage decision, user travel costs and recovery action costs are scenario dependent. Two types of scenarios are taken into account: a) the scenarios of normal operation and b) disruption scenarios which are associated to a link's breakdown of the network. The disruptions in the links are assumed to follow a probability disruption model accordingly to the number of services that operate on them. The model can be used to analyze the influence of the rate of failures of the units on the reliability of the designed RTN. The proposed model can be considered as a two recourse stochastic programming model with a bi-level structure where the probabilities of failure are an implicit function of the number of services and the routing of the transit lines of the transport system. A heuristic solution method is examined for small to medium networks demonstrating the computational viability of the approach.

1 Introduction

Designing a Rapid Transit Network (RTN) or even extending one that is already functioning, is a vital subject due to the fact that they reduce traffic congestion, travel time and pollution. Usually a RTN is in operation with other transportation systems such as private transportation (car) and this makes that the design must take into account this factor. Another factor that needs to be considered is the capability of the newly designed system to keep operating under more or less suitable conditions under a set of predictable disruptions.

In Bruno G. et al. [1], a RTN design model is presented where the user cost is minimized and the coverage of the demand by public network is made as large as possible. Marín in [8], studies the inclusion of a limited number of lines. Also, Laporte G. et al in [6] build robust networks that provide several routes to passengers, so in case of failure part of the demand can be rerouted. Connections between two-stage stochastic programming network design and recovery-robustness in railway networks planning models have been studied by Cicerone et al. in [4] and by Cacchiani et al. in [2]. Also, in [3] Cadarso and Marín develop a two-stage stochastic programming model for rapid transit network design in which disruptions probabilities are assumed known a priori, illustrating some of its recoverable robustness properties.

This paper presents a conceptual scheme that permits to incorporate a probability model for the disruptions of a RTN. It is assumed that disruptions arise when transportation units present some failure during operation leaving a link blocked. Other sources of disruption with their associated scenarios could be added, but this is not done for ease of exposition. As a consequence of this, the disruption probabilities will depend on the level of traffic on the network links. The probabilities of failure follow the following hypothesis: a) disruptions are due to a single event and scenarios with several simultaneous disruptions are discarded a priori as they are assumed to have a much lower probability, b) a preselected set of scenarios is considered, c) the number of failures that a train unit may experience along a large number of services distributes accordingly to a geometrical law and the individual probability of failure of a service is constant along the planning horizon and depends only on the train unit characteristics (e.g., quality of material and maintenance). The resulting model has a bilevel structure and it is solved by a specific heuristic method.

2 Structure and elements of the design model

In this RTN design model it is assumed that the location of potential stations is known. There already exists a current mode of transportation (for example, private cars or an alternative public transportation is already operating in the area) competing with the new RTN to be constructed. The aim of the model is to design a network, i.e. to decide at which nodes to locate the stations and how to connect them covering as many trips by the new network as possible.

• A potential network $\left( N, A\right)$ is considered from which the optimum rapid transit network is selected. The node set is composed by centroids $\left({N}_c\right)$ and stations at RTN $\left({N}_r\right)$, the node set is then $N={N}_c\cup {N}_r$. Links will be denoted either by a single subscript (e.g., a) or by a double subscript (i.e., (i, j)) when considered convenient. Because both riding directions are always considered, the set of potential links is so that $\left( i, j\right)\in A\iff \left( j, i\right)\in A.\kern0.3em E$ (i) and (i) are the set outgoing and incoming nodes to node i respectively.

• Each feasible link (i, j) has a generalized travel cost which may depend on the scenario of disruption. This is further discussed in section 4.

• For simplicity, in this model it will be assumed that the planners have selected a priori a set of candidate $\hat{L}$ lines, being $\hat{L}$ a large number. Lines will be considered an ordered chain of n links $\left\{{a}_1,{a}_2,\dots, {a}_n\right\}$ all of them appearing only once in the sequence. Lines with circulation in both directions will be treated as two separate lines $\left\{{a}_1,{a}_2,\dots, {a}_n\right\},\left\{{a}_n,{a}_{n-1},\dots, {a}_1\right\}$. To take into account the recovery of the disruptions that may arise in a link $a\in \ell$, for each line $a\in \widehat{\ell}$, an additional set of lines must be considered that will operate only in the scenarios of disruption. These lines will be referred to as the recovery lines, whereas lines in $\widehat{L}$ will be referred to as the primary lines or also as the candidate lines. Thus, if $\ell =\left\{{a}_1,{a}_2,{a}_3\right\}$, for a disruption in link a ₁, the recovery line must be $\left\{{a}_2,{a}_3\right\}$. For a disruption in link a ₂, the recovery lines that must be considered are {a ₁} and {a ₃} and finally, for a disruption in link a ₂, the recovery line that must be considered is {a ₁,a ₂}. The set of all recovery lines will be denoted by ${\widehat{L}}^{\prime }$ and the set of recovery lines for line $\ell \in \widehat{L}$ will be denoted by ${\widehat{L}}^{\prime}\left(\ell \right)$. The number of recovery lines in $\widehat{L}^{\prime}\left(\ell \right)$ for a line $\ell \in \widehat{L}$ is $\left|{\hat{L}}^{\prime}\left(\ell \right)\right|=2\left(\left|\ell \right|-1\right)$, where $\left|\ell \right|$ is the number of segments in line $\ell$. If $L=\hat{L}\cup {\hat{L}}^{\prime },$ the total number of lines is then $\left| L\right|\le \left|\hat{L}\right|+2\sum\limits_{\ell \in \hat{L}}\left(\left|\ell \right|-1\right),$ from which only $\nu$ will be finally included in the solution ($\nu \le \left|\hat{L}\right|$). Further definitions are:

• $\hat{L}(a)\subseteq \hat{L}$ is the subset of candidate or primary lines containing segment $a\in A$.

• ${\widehat{L}}^{\prime }(a)$ is the subset of recovery lines associated to the set of primary lines containing link a.

• The model considers a set of scenarios associated to regular conditions of operation of the transport system (i.e., morning peak period, afternoon, night, holidays,…). Each of these scenarios is assumed to extend during a given time period of length H _r (i.e., 3 hours for morning peak periods). This set of scenarios will be denoted by S ₀ and for any $r\in {S}_0$, there will be associated a weight or probability ${q}_r>0$ associated to its relevance, so that ${\sum}_{r\in {S}_0}\kern2.77695pt {q}_r=1$. A typical way of evaluating the weights ${q}_r$ is accordingly to their associated total demands, i.e.: ${q}_r={g}^r/\hat{G},$ where ${g}_r={\sum}_{w\in W}{g}_w^r$ and $\hat{G}={\sum}_{r\in {S}_0}{g}_r$. For any scenario $r\in {S}_0$ a set of possible disruption scenarios D(r) will be considered with probabilities ${p}_s>0,\kern2.77695pt s\in D(r)$, so that ${p}_r+{\sum}_{s\in S(r)}{p}_s=1$. These disruption scenarios will be associated each with a breakdown of a service at a link. The set of that links for a regular scenario $r\in {S}_0$ will be denoted by $\hat{A}(r)$. For each $a\in \hat{A}(r),\kern2.77695pt s(a)$ will denote the associated disruption scenario and for each scenario $s\in D(r),\kern2.77695pt r\in {S}_0,\kern2.77695pt a(s)$ will denote the disrupted link. Finally, by S it will be denoted the set of all possible scenarios, i.e., $S={S}_0{\cup}_{r\in {S}_0} D(r)$.

• Users may choose between two transportation modes: a private mode (typically car) or the public transportation mode comprising a set of lines, some of them already in operation and some others that will be the outcome of this design model. The model's demand will take into account differences between scenarios $r\in {S}_0$. The total demand (private + public transport) for scenario $r\in {S}_0$ is given by the trip matrix ${G}^r=\left({g}_w^r\right)$, where ${g}_w^r$ is the total number of trips from origin o(W) to destination d(W). For a particular scenario $s\in S$, the trip travel time for o-d pair W through the private transportation network is given by the matrix ${U}_c^s=\left({u}_c^{w, s}\right)$ and the trip travel time for using public transportation is given by the matrix ${\varLambda}^s=\left({\lambda}^{w, s}\right)$. The model assumes a modal choice for each o-d pair given by a logit model, i.e., the proportion of trips ${\xi}_w^s$ using the private transportation mode is given by:

  $$ {\xi}_w^s=\frac{exp\left(-{\beta}_c^w-\eta {u}_c^{w, s}\right)}{exp\left(-{\beta}_c^w-\eta {u}_c^{w, s}\right)+ exp\left(-{\beta}_{PT}^w-\eta {\lambda}^{w, s}\right)} $$

  (1)

  where ${\beta}_{PT}^w$ is proportional to the price of fares for public transport in the planning period, ${\beta}_c^w$ is proportional to the parking cost plus the cost of gasoline for the trip from o(W) to d(W) and $\eta$ is proportional to the user's value of time.

• Let c _x and ${c}_{\psi}$ denote the link vector costs and the node vector of location costs respectively.

  The design model has two stages or levels: a) in the first "planning" stage, the decision variables x,y are chosen, i.e., the topology of the network is set and b) in a second stage, at a given scenario, the passenger flows make use of the network designed in the first stage, taking into account the scenario characteristics.

2.1 Variables and constraints in the 1^st stage

A link-line incidence matrix $\left({\delta}_{a,\ell}\right)$ will be assumed known with elements ${\delta}_{a,\ell }=1$ if candidate line $\ell$ contains link $a$ and 0 otherwise. Let ${h}_{\ell },\kern2.77695pt \ell \in L$ be a binary variable indicating whether candidate line $\ell$ is chosen or not. Let also ${\chi}_a$ be a binary variable so that = 1 if arc $a$ is located and = 0, otherwise. The following constraints force that link $a$ must be built if some line $\ell$ using it is chosen:

$$ M{\chi}_a\ge \sum \limits_{\ell \in \widehat{L}}{\delta}_{a,\ell }{h}_{\ell },\kern1em a\in A $$

(2)

The binary variables ${x}_a^l$ state whether link $a$ is required because line $l$ is included in the solution or not. These variables are related to the variables ${h}_l$ through the following constraints:

$$ {h}_{\ell}\le {x}_a^{\ell },\kern1em a\in \ell, \kern1em \ell \in \widehat{L} $$

(3)

A limitation on the number of lines can be imposed by ${\sum}_{l\in L}\kern0.3em {h}_l\kern0.3em \le v$. Let now ${\psi}_i$ be a binary variable so that = 1 if station $i$ is located and = 0, otherwise. Then, variables X and $\psi$ are linked by:

$$ \begin{array}{cc}{\chi}_a\le {\psi}_i,& \forall i\in {N}_{,}\forall a=\left( i, j\right)\in A\\ {}{\chi}_a\le {\psi}_j,& \forall j\in N,\forall a=\left( i, j\right)\in A\end{array} $$

(4)

2.2 Variables and constraints of the 2 ^nd stage

• ${v}_a^{w, s}$, is the passenger flow on link $a\in A$ for origin destination pair w under scenario $s\in S$. By ${v}^{w, s}=\left(\ldots, {v}_a^{w, s},\ldots; a\in A\right)$ it will be denoted an arc flow vector per o-d pair w and scenario $s\in S$.

• ${v}_a^{w, s}$, is the flow for o-d pair w using private transport in scenario s. By ${v}_c^{w, s}=\left(\ldots, {v}_c^{w, s},\ldots; w\in W\right)$ it will be denoted the flow vector of passengers using private transportation in scenario $s\in S$.

The balance constraints for flows at a given scenario s will be:

$$ \sum \limits_{j\in E(i)}\,{v}_{ij}^{w, s}-\sum \limits_{k\in I(i)}\,{v}_{k i}^{w, s}=\left\{\begin{array}{ll}{v}_{PT}^{w, s}& ifi= p(w)\\ {}-{v}_{PT}^{w, s}& ifi= q(w), i\in N, w\in W, s\in S\\ {}\kern1em 0& otherwise\end{array}\right. $$

(5)

where ${v}_{PT}^{w, s}\ge 0$ are the flows using public transport mode at o-d pair $w\in W$, that must verify:

$$ {v}_c^{w, s}+{v}_{PT}^{w, s}={g}_w^s, w\in W, s\in S $$

(6)

Also, link flows ${v}_a^{w, s}$ for scenario s will be subject to the location-allocation constraints, which in fact are equivalent to suppress the links for which the decision variables X _a annul:

$$ {v}_a^{w, s}\le M{\chi}_a,\kern1em a\in A,\kern1em s\in S,\kern1em w\in W $$

(7)

2.3 The conceptual model for modal split

Formulations in this subsection do not include links a for which decision variables ${X}_a=0$. Also flow variables are assumed for a generic scenario $s\in S$ and this superscript will be omitted.

Borrowing ideas from combined modal split-assignment models in transportation planning (see, for instance [5]) the following convex problem

$$ \begin{array}{ll} Mi{n}_{v,{v}_c,{v}_{P T}}& \sum \limits_{w\in W}\left\{{d}^T{v}^w+{v}_c^w\left( log{v}_c^w-1-{\beta}_c^w-\eta {u}_c^w\right)+\right.\\ {}\\ {}\kern2em & \kern1em \left.+{v}_{P T}^w\left( log{v}_{P T}^w-1-{\beta}_{P T}^w\right)\right\}\\ {}\\ {} s. t.:& v,{v}_c,{v}_{P T}\ge 0\kern2.77695pt a nd\kern2.77695pt verify\kern2.77695pt constraints\kern2.77695pt (5),(6)\\ {}\\ {}\kern1em & \sum \limits_{w\in W}\kern2.77695pt {v}_a^w\le {m}_P\sum \limits_{\ell \in \widehat{L}}\kern2.77695pt {z}^{\ell, r}{x}_a^{\ell },\kern2.77695pt a\in A\end{array} $$

(8)

provides solutions verifying the modal split accordingly to (1). A linearization of this model is used by López in [7] in order to reformulate it as a mixed linear integer problem. Capacity constraints arise because the capacity of the public transport lines operating on the network links as a function of the number of services ${z}^l$ of the lines. Variables X are considered implicitly and because of that, the solution set of previous problem (8) will be denoted by ${V}^{s,\ast}\left({z}^s, X\right),$ when specified for a specific scenario $s\in S$.

Next section describes a simplified model which provides the required number of services on the lines to attend the passenger's demand, accordingly to the scenarios that are considered.

3 Service setting for normal operational conditions and recovery of disruptions

A model that states the number of services that must operate on each link is required for both non-disrupted scenarios $r\in {S}_o$ and scenarios corresponding to a disruption $s\in S\setminus {S}_o$. Let v ^r the passenger vector flow on each of the network links for a non-disrupted scenario $r\in {S}_o$. Let v ^r be the vector of total link flows which can be expressed as ${v}_a^r=\sum \limits _{w\in W}\kern0.3em {v}_a^{w, r}\kern0.3em a\in A$. Let ${\gamma}^l$ the individual cost of a service on line $l\in L$ and let C ^l be the time required to perform a complete service on l by a transport unit. A total of ${n}_v$ transport units are assumed to operate on the network. Also, assume that the maximum number of services on link a for scenario $r\in {S}_o$ is ${\widehat{Z}}_a^r$. Then, the following simple covering model will be used to determine the number of services for each line:

$$ \begin{array}{ll}{\varGamma}_0^r\left({v}^r, x\right)= Mi{n}_z& \sum \limits_{\ell \in \widehat{L}}\kern2.22198pt {\gamma}^{\ell }{z}^{\ell, r}\\ {}& {\widehat{Z}}_a^r\ge \sum \limits_{\ell \in \widehat{L}}{z}^{\ell, r}{x}_a^{\ell}\ge \frac{1}{m_P}{v}_a^r,\kern4.44pt a\in A,\kern2.22198pt r\in {S}_0\\ {}& \sum \limits_{\ell \in \widehat{L}}{C}^{\ell }{z}^{\ell, r}\le {n}_v{H}_r,\\ {}& Z\ni {z}^{\ell, r}\ge 0\end{array} $$

(9)

The solution set of previous problem (9) will be denoted by ${Z}_r^{\ast}\left({v}^r, x\right), r\in {S}_o$. If ${Z}^{r,\ast }$ is the vector of the optimal number of services for the lines in the regular scenario r given by the previous problem (9), then the total number of services ${\theta}_a^r$ on link a will be given by:

$$ {\theta}_a^r\left({v}^r\right)\overset{\varDelta}{=}\sum \limits_{\ell \in \widehat{L}}{z}^{\ell, r,\ast }{x}_a^{\ell },\kern1em a\in A,\kern1em r\in {S}_0 $$

(10)

For a disruption on link $a\in \widehat{A}$, those lines $\ell \in \hat{L}$ containing that link, i.e., $\ell \ni a$, can be put partially in operation as a recovery strategy using their disruption lines ${\hat{L}}^{\prime}\left(\ell \right)$ and in this case the model will evaluate a new set of services for all the lines in the system. Then, for a scenario $s\in S\setminus {S}_0$ corresponding to a disruption in link a, the set of lines that can potentially be operating is $\tilde{L}(a)= \hat{L}^\prime (a)\ \cup \ (\hat{L}\backslash\hat{L}(a))$.

The following problem establishes the services, ${z}_s^l$, that must be assigned for the lines operating in the scenario $s\in D(r)$ for a disruption of the regular scenario r:

$$ \begin{array}{c} r\in {S}_0, s\in D(r):\\ {}\\ {}{\varGamma}_s^r\left({v}^s, x\right)= Mi{n}_z\sum \limits_{\ell \in \widehat{L}\left( a(s)\right)}\kern2.22198pt {\gamma}^{\ell }{z}^{\ell, s}\\ {}\\ {} s. t.:{\widehat{Z}}_b^s\ge \sum \limits_{\ell \in \widehat{L}\setminus \widehat{L}\left( a(s)\right)}\kern2.22198pt {x}_b^{\ell }{z}^{\ell, s}+\sum \limits_{\widehat{\ell}\in \widehat{L}\left( a(s)\right)}\kern2.22198pt \sum \limits_{\ell \in \widehat{L}^{\prime}\left(\widehat{\ell}\right)}\kern2.77695pt {x}_b^{\widehat{\ell}}{z}^{\ell, s}\ge \frac{1}{m_P}{v}_b^s, b\in A,\\ {}\\ {}\sum \limits_{\ell \in \widehat{L}\left( a(s)\right)}\kern2.77695pt {C}^{\ell }{z}^{\ell, s}\le {n}_v{H}_r,\\ {}\\ {} Z\ni {z}^{\ell, s}\ge 0,\kern1em \ell \in \widehat{L}\left( a(s)\right)\end{array} $$

(11)

where m _p is the maximum number of passengers that a unit may allocate. The solution set of previous problem (11) will be denoted by ${Z}_s^{\ast}\left({v}^s, x\right), s\in D(r)$.

4 A model for probabilities of disruption

The probability p _s of each scenario is considered dependent on the use that is made on the designed network. By means of a failure model it will be possible to find an expression for the probability that a link presents a disruption during the operational horizon of the transit network. It will be assumed that the probability of failure of a service is mainly determined by the type of units operating in the service and the characteristics of the link. Let T be the set of type units operating on the network. Let ${\pi}_{a,\tau}$ be the joint individual probability that a service carried out by a unit of type $\tau \in T$ presents a disruption on link $a\in A$. By examining annual disruption reports from transit operators, the fraction of disrupted services with a disruption time of 20 minutes or more over the total number of services on a line is between $1.5\cdot 1{0}^{-4}$ to $5.0\cdot 1{0}^{-4}$, i.e. 1 disruption each 2000 or 6600 services. Assume that by analyzing statistically the previous mentioned annual disruption reports the probabilities ${\pi}_{a,\tau}$ have been determined. Let now ${\theta}_{a,\tau}$ be the total number of services of type τ on link a during the operational horizon used for our planning model (for instance, peak morning period). Let $T(a)$ be the set of unit types that operate on link $a\in A$. Let also ${\overset{\sim }{\theta}}_{a,\tau}$ be the total number of services with a relevant disruption out of the ${\theta}_{a,\tau}$ and $\tilde{\theta}_a \sum \limits_{\tau \in T(a)}\tilde{\theta}_a,\tau$ the aggregated number of disrupted services on link a. It is assumed that ${\overset{\sim }{\theta}}_{a,\tau}$ follows a binomial distribution with probability ${\pi}_{a,\tau}$, i.e.: ${{\displaystyle \overset{\sim }{\theta}}}_{a,\tau}\sim B i n o\left({\theta}_{a,\tau},{\pi}_{a,\tau}\right)$. Thus, the probability ${\widehat{P}}_a$ that link $a\in A$ has at least one disrupted service from any unit type $\tau \in T(a)$, as a function of the number of services ${\theta}_{a,\tau}$ of type τ operating on that link is:

$$ \begin{array}{c}{\hat{P}}_a{\displaystyle \overset{\varDelta}{=}} P\left({\overset{\sim }{\theta}}_a\ge 1\right)=1-\prod \limits_{\tau \in T(a)} P\left({\overset{\sim }{\theta}}_{a,\tau}=0\right)=\\ {}\\ {}=1-\prod \limits_{\tau \in T(a)}{\left(1-{\pi}_{a,\tau}\right)}^{\theta_{a,\tau}}=1-\mathrm{e} xp\left(-\sum \limits_{\tau \in T(a)}{\alpha}_{a,\tau}{\theta}_{a,\tau}\right)\end{array} $$

(12)

where ${\alpha}_{a,\tau}=- l o g\left(1-{\pi}_{a,\tau}\right)$. For small probabilities ${\pi}_{a,\tau}$, then ${\alpha}_{a,\tau}\approx {\pi}_{a,\tau}$. Also, the probability of having no disruption on link a of any of the type units $\tau \in T(a)$ is ${\widehat{Q}}_a{\displaystyle \overset{\varDelta}{=}}1-{\widehat{P}}_a$.

Because the probability of more than one link with disruptions simultaneoulsy is small, the disruptions that will be considered are failures of a single link a within the set of links $\widehat{A}$ considered candidates for a disruption. Let a( s) denote the link associated with scenario $s\in D(r), r\in {S}_0$. For ease of notation let ${\widehat{A}}_a=\widehat{A}\setminus \left\{ a\right\}$. The probability of each scenario s corresponding to a disruption in link a(s) will be evaluated now by a given function ${F}_r:{\Re}^{\mid \widehat{A}\mid}\to {\Re}^{\mid D(r)\mid +1}$ of the number of services ${\theta}_a^r, a\in \widehat{A}$ on the links candidates for a disruption. If there is a single type of units operating in the network then, the function ${F}^r\left(\cdot \right)$ for the probabilities ${p}_s^r$ and ${p}_0^r$ that will be adopted is:

$$ \begin{array}{l} r\in {S}_0\kern-0.25em :\\ {}\\ {}{p}_s^r\kern0.3em {\displaystyle \overset{\varDelta}{=}}\kern0.3em {F}_s^r\left(\theta \right)=\frac{\mathrm{e} xp\left({\alpha}_{a(s)}{\theta}_{a(s)}^r\right)-1}{1+{\sum}_{b\in \hat{A}}\left(\mathrm{e} xp\left({\alpha}_b{\theta}_b^r\right)-1\right), s\in D(r)}\end{array} $$

(13)

$$ {p}_0^r\kern0.3em {\displaystyle \overset{\varDelta}{=}}\kern0.3em {F}_0^r\left(\theta \right)={\left(1+\sum\limits_{b\in \hat{A}}\left(\mathrm{e} xp\left({\alpha}_b{\theta}_b^r\right)-1\right)\right)}^{-1} $$

(14)

In case that probabilities ${\pi}_{a,\tau}$ are very small, then probabilities ${p}_r^r$ of no disruption are much higher than the probabilities ${p}_s^r$ associated with the disruption on a link.

5 A stochastic 2-stage model and a heuristic solution

Conceptually, the model could be formulated as the following bilevel programming problem:

$$ \begin{array}{ll} Mi{n}_{\begin{array}{c} y,\chi, h\\ {}\Psi, v, z\end{array}}& {c}_x^{\mathrm{T}}\chi +{c}_{\psi}^{\mathrm{T}}\Psi +\sum\limits_{r\in {S}_0}\left\{{y}_0^r{\Gamma}_0^r\left({v}^r, x\right)+\sum \limits_{s\in D(r)}\kern2.77695pt {y}_s^r{\Gamma}_s^r\left({v}^s, x\right)\right\}+\\ {}\\ {}\kern2em & +\vartheta \sum \limits_{r\in {S}_0}\kern2.77695pt \left[\kern2.77695pt {y}_0^r\sum \limits_{w\in W}\kern2.77695pt \left\{{d}^{r\kern2.77695pt T}{v}^{w, r}+{u}_c^{w, r}{v}_c^{w, r}\right\}+\right.\\ {}\\ {}\kern2em & \left.+{\displaystyle \sum \limits_{s\in D(r)}}\kern2.77695pt {y}_s^r{\displaystyle \sum \limits_{w\in W}}\kern2.77695pt \left\{{d}^{s\kern2.77695pt T}{v}^{w, s}+{u}_c^{w, s}{v}_c^{w, s}\right\}\right]\\ {}\\ {} s. t.:& constraints\kern2.77695pt (2),(3),(4),(7)\\ {}\\ {}\kern2em & {y}_0^r={q}_r{F}_0^r\left(\dots, {\theta}_a^r\left({v}^r\right),\dots; a\in \widehat{A}\right),\kern2.77695pt r\in {S}_0\\ {}\\ {}\kern2em & {y}_s^r={q}_r{F}_s^r\left(\dots, {\theta}_a^r\left({v}^r\right),\dots; a\in \widehat{A}\right),\kern2.77695pt s\in D(r)\\ {}\\ {}\kern2em & where\kern2.77695pt {\theta}_a^r\left({v}^r\right)\kern2.77695pt is\kern2.77695pt defined\kern2.77695pt in\kern2.77695pt (10)\\ {}\\ {}\kern2em & resulting\kern2.77695pt from\kern2.77695pt lower\kern2.77695pt level\kern2.77695pt problem(9)\kern2.77695pt and\kern2.77695pt (11)\\ {}\\ {}\kern2em & Also, from\kern2.77695pt (9)\kern2.77695pt and\kern2.77695pt (11):\\ {}\\ {}\kern2em & {z}^r\in {Z}_r^{\ast}\left({v}^r, x\right),\kern2.77695pt {v}^r\in {V}^{r,\ast}\left({z}^r,\chi \right),\kern2.77695pt r\in {S}_0\\ {}\\ {}\kern2em & {z}^s\in {Z}_r^{\ast}\left({v}^s, x\right),\kern2.77695pt {v}^s\in {V}^{s,\ast}\left({z}^s,\chi \right),\kern2.77695pt s\in D(r)\end{array} $$

(15)

In order to solve heuristically the previous problem (15) the following mixed linear integer programming problem (16) needs to be considered. In this problem it is assumed that probabilities ${y}_s^r,{y}_0^r$ are fixed and also that the total amount of transport trips ${v}_{PT}^{w, s}$ in public transport are known.

$$ \begin{array}{ll} Mi{n}_{\begin{array}{c}\chi, h\\ {}\varPsi, v, z\end{array}}& {c}_x^T\chi +{c}_{\psi}^T\Psi +\sum \limits_{r\in {S}_0}\kern2.77695pt \left[\kern2.77695pt {y}_0^r\sum \limits_{\ell \in \widehat{L}}\kern2.77695pt {\gamma}^{\ell }{z}^{\ell, r}+\right.\\ {}\\ {}& \kern2.7em \left.+\sum \limits_{s\in D(r)}\kern2.77695pt {y}_s^r\sum \limits_{\ell \in \widehat{L}\left( a(s)\right)}\kern2.77695pt {\gamma}^{\ell }{z}^{\ell, s}\right]\kern2.77695pt +\\ {}\\ {}& \kern2.6em +\vartheta \sum \limits_{r\in {S}_0}\kern2.77695pt \left[\kern2.77695pt {y}_0^r\sum \limits_{w\in W}\kern2.77695pt \left\{{d}^{r\kern2.77695pt T}{v}^{w, r}\right\}+\right.\\ {}\\ {}& \kern2.75em \left.+\sum\limits_{s\in D(r)}\kern2.77695pt {y}_s^r\sum\limits_{w\in W}\kern2.77695pt \left\{{d}^{s\kern2.77695pt T}{v}^{w, s}\right\}\kern2.77695pt \right]\\ {}\\ {} s. t.:& constraints\kern2.77695pt (2),(3),(4),(5),(7)\\ {}\\ {}\kern1em & \kern2.77695pt + constraints\kern2.77695pt in\kern2.77695pt problems\kern2.77695pt (9)\kern2.77695pt and\kern2.77695pt (11)\end{array} $$

(16)

The previous model (15) will be solved using the following heuristic algorithm:

Algorithm

• 0. Calculate initial vector of probabilities ${y}^{\left(0\right.}$; set ${\varLambda}^{\left(-1\right.}=0$; $k=0$; take initial $0<{v}_{PT}^{w, s,\left(0\right.}<{g}_w, w\in W, s\in S$.

• 1. For the probability vector ${y}^{\left( k\right.}$ and the number of trips for public transport ${v}_{PT}^{w,\left( k\right.}$ solve problem (16). Let ${\chi}_a^{\left( k\right.},{\psi}_i^{\left( k\right.},{x}_a^{\ell, k}$ the design decision variables. Also let ${\varLambda}^{\left( k\right.}={c}_x^T{\chi}^{\left( k\right.}+{c}_{\psi}^T{\varPsi}^{\left( k\right.}$ the building costs.

• 2. If $\left|{\varLambda}^{\left( k\right.}-{\varLambda}^{\left( k-1\right.}\right|\le \varepsilon {\varLambda}^{\left( k-1\right.}$ & $\mid \mid {y}^{\left( k\right.}-{y}^{\left( k-1\right.}\mid \mid \le {\varepsilon}^{\prime }$ & $\mid {v}_{PT}^{w, s,\left( k\right.}-{v}_{PT}^{w, s,\left( k-1\right.}\mid \le {\varepsilon}^{\prime \prime }{v}_{PT}^{w, s,\left( k-1\right.},{\forall}_w\kern0.3em \in \kern0.3em w$ then STOP.

• 3. With the solutions ${v}^{w, s,\left( k\right.}$ and ${z}^{\ell, \left( k\right.},\ell \in L$ of previous problem (16), evaluate the mean travel times for public transport for scenario $s\in S$, as ${\lambda}_{PT}^{w, s,\left(k \right.}=\left({d}^T{v}^{w, s,\left(k\right.}\right)/{v}_{PT}^{w, s,\left( k\right.}$ and use logit formula (1) to evaluate a new modal split: ${\widehat{v}}_c^{\left( w, s\right)}$ and ${\widehat{v}}_{PT}^{\left( w, s\right)}={g}_w^s-{\widehat{v}}_c^{\left( w, s\right)}, w\in W, s\in S$.

• 4. Taking into account the number of services ${\theta}_a^r\left({v}^r\right)=\sum \limits_{l\in \widehat{L}}{z}^{l,{(k)}_{x_a^l,}} a\in A, r\in {S}_0$, reevaluate the failure probabilities ${\widehat{p}}_0^{r,(k)}={F}_0^r\left({\theta}_a^r\right({v}^{r,(k)}\left)\right), s\in S$ and compute a probability vector ${\widehat{y}}^{(k)}$.

• 5. Perform an MSA step (using, for instance, ${\alpha}^{\left( k\right.}=1/\left( k+1\right)$). Then, increase the iteration counter $k= k+1$.

  $$ \begin{array}{l}{y}^{\left( k+1\right.}={y}^{\left( k\right.}+{\alpha}^{\left( k\right.}\left({\hat{y}}^{\left( k\right.}-{y}^{\left( k\right.}\right)\\ {}\\ {}{v}_{PT}^{w, s,\left( k+1\right.}={v}_{PT}^{w, s,\left( k\right.}+{\alpha}^{\left( k\right.}\left({\hat{v}}_{PT}^{w, s,\left( k\right.}-{v}_{PT}^{w, s,\left( k\right.}\right),\kern2.77695pt w\in W,\kern2.77695pt s\in S\end{array} $$

  (17)

6 Computational tests

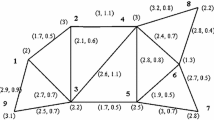
The computational proofs have been carried out on the network reported in [3] and in [8] with 9 nodes, 15 edges and 72 origin-destination pairs. The network parameters (construction costs for nodes and links, i.e. ${c}_i$ and ${c}_a$, respectively), the o-d demand matrix and the o-d costs for the alternative mode of transportation, (${u}_c^w$), have also been taken from that references. In all computational tests a maximum of $\mid L\mid =5$ lines has been allowed in the solution from a pool of 46 candidate lines for operation in a single undisrupted scenario S ₀ = {0} for which there are 15 disruption scenarios (one for each link in the network; ∣D(0)=15) The recovery of the affected lines is carried out using 230 recovery lines. Table 1 shows in column #it the number of iterations necessary to converge and column ∣pr∣ displays the error $\parallel {y}^k-{y}^{\left( k-1\right)}\parallel$ in the last iteration. By means of the tests it is possible to analyze the influence of the service probability failure π in the reliability of the designed RTN. For higher values of π the algorithm oscillates, converging very slowly. The more reliable the system is the smaller the total costs, being these represented in the objfun column. Also, the probability p ₀ of no disruption increases as π is smaller and the attractiveness of the public transportation system increases as the system becomes more reliable. This is illustrated in columns PTt and Ct, (total time in public and private transport, respectively) showing that the total time spent by all public transport users increases whereas the expected time spent in the competing mode decreases.

Table 1 Outputs for different values of π

If the probability of failure is high (i.e., π = 0.01), then, the scenario with no disruptions has smaller probability than other scenarios corresponding to disruptions. If the probability π is below a given threshold, the no disruption scenario becomes the most likely situation. In our test example this seems to happen for $\pi \approx 5\cdot 1{0}^{-4}$. The tests also show that in this case, the topology of the designed network does not change, i.e. it is as if the failure scenarios would not need to be taken into account in the design of the transportation system. This is achieved when $\pi =5\cdot 1{0}^{-6}$, where disruption scenarios have almost no relevance in the model.

7 Conclusions

A two-stage stochastic model has been developed for the design of rapid transit systems taking into account the rate of failures of the transportation units. Also taken into account in the design is the number of the services during a disruption, assuming that the affected lines can operate at both sides of the link out of service. The probabilities assigned to the disruption scenarios are consistent with a probability distribution model that arises as a consequence of failures in the transportation unit services. By means of the tests it is possible to analyze the influence of the service probability failure π in the reliability of the designed RTN and determine its admissible levels for which the disruptions are at an acceptable level. A heuristic solution method is examined for small to medium networks demonstrating the computational viability of the approach.