Keywords

1 Introduction

Functional decomposition is one of the best logic synthesis method targeting FPGAs. The most popular decomposition algorithms may be roughly divided into ones using binary decision diagrams (BDD) for Boolean function representation and ones using cube representation of the decomposed function. The advantage of the former is an efficient representation of functions with a large number of input variables. However, these algorithms face the problem of representing multiple-output and not fully specified functions [8, 9]. The latter algorithms allow simple representation of multiple-output and not fully specified functions. Most algorithms based on this representation use the blanket calculus for function manipulation [1]. The blanket calculus allows construction of very efficient decomposition algorithms [7, 10]. However the computational complexity of blanket manipulations makes it impossible to efficiently apply these algorithms to large Boolean functions.

In [5] a concept of indexed partition has been presented, allowing to manipulate Boolean functions described by cubes in similar way as blanket calculus but requiring much less computational and memory complexity. It combines the advantages of both blanket calculus and information relationships and measures [2].

2 Indexed Partition Calculus

Blankets, as well as information sets, are the way of expressing the compatibility relation COM on Boolean function’s cubes. This also can be done using the concept of compatibility or incompatibility graph.

Operations on blankets have direct analogue in operations on incompatibility graphs. The concept of indexed partitions is used to model such operations on incompatibility graphs.

Definition 1

An indexed partition is a set of ordered dichotomies {B i , P i } on set S, such that B i are disjoint subsets of S and

$$ \bigcup_i{B}_i= S. $$
(1)

In [1] a theorem based on the concept of cubes has been proposed which describes the existence of serial decomposition. This theorem can be re-expressed using the concept of indexed partitions.

Theorem 1

Let δ V , δ U , and δ F be indexed partitions induced on the function’s F input cubes by the input sub-sets V and U, and outputs of F, respectively.

If there exists an indexed partition δ G on the set of function F’s input cubes such that δ V ≤δ G , and \( {\delta}_U\cdot {\delta}_G\le {\delta}_F \) , then F has a serial decomposition with respect to (U,V ).

In practice, even large Boolean functions of many input variables are often specified by relatively small number of cubes. Since the size of indexed partition depends on the number of cubes, the test from Theorem 1 can be generally much computationally simpler than the test based on blankets [5].

3 Functional Decomposition Algorithm

The algorithm presented in this paper is based on the method of decomposition of function sets presented in [4]. However the blanket calculus has been substituted by indexed partition calculus.

The cube representation can easily describe a multi-output, not fully specified Boolean function using the espresso format. Unfortunately, it can be very inefficient when single outputs of the multi-output function depend on different input variables. The method proposed in [4] allows decomposing single-output Boolean function sets instead of one multi-output function.

The logic multi-output circuit of n input variables X can be represented as a set of Boolean functions \( {f}_1\left({X}_1\right),\dots, {f}_m\left({X}_m\right) \), where X i is a sub-set of X. In the general case, each single function may depend on different subset of input variables and can be described by a different set of cubes. The application of serial functional decomposition based on blanket calculus is impossible in this case. The proposed modified serial functional decomposition algorithm allows decomposing function sets described by separate truth tables, even if each single function depends on different subset of input variables and truth tables consist of different sets of cubes.

When decomposing a set of Boolean functions \( {f}_1,\dots, {f}_m \) it is necessary to find such sub-function G that satisfies the decomposition condition for each function: f i  = h i (U i , G(V)).

The decomposition algorithm consists of the following steps:

  1. 1.

    input variable partitioning an appropriate input support V has to be selected for function G; in case functions \( {f}_1,\dots, {f}_m \) are specified by different truth tables, the V set has to be selected in such a way that it is a subset of input variables of each decomposed function,

  2. 2.

    the computation of \( {\delta}_{V_i} \), \( {\delta}_{U_i} \) and \( {\delta}_{f_i} \) for each function f i - since truth tables of each function may consist different cubes, the indexed partitions \( {\delta}_{V_i} \), \( {\delta}_{U_i} \) and \( {\delta}_{f_i} \) for each function may be different,

  3. 3.

    the construction of \( {\delta}_{G_i} \) in functional decomposition algorithm the construction of this indexed partitions corresponds to the construction of the multi-valued function G, since we want to find the decomposition with the same function G for all functions f i , such \( {\delta}_{G_i} \) should be created that satisfy the decomposition condition for all these functions and correspond to the same function G at the same time.

This decomposition method allows decomposing a set of Boolean functions described by separate truth tables. The decomposed function may depend on different input variables and can be described by different set of cubes. The application of the proposed decomposition algorithm allows for efficient creation of sub-functions common to all decomposed functions. This allows the designer to apply a much wider range of synthesis strategies.

4 Results

For the purpose of evaluation of the efficiency of the proposed decomposition algorithm, a software tool CombDec has been created. The tool implements multilevel logic synthesis based on the concept of decomposition of function sets. To solve the input variable partitioning problem, the heuristic method presented in [6] has been applied.

The tool has been used to decompose selected benchmark examples into 6-input LUT networks. The resulting LUT networks were all verified using the combinational equivalence checker implemented in ABC.

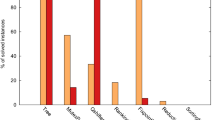
Table 1 presents the comparison of the results obtained by the presented approach and the results reported in [3], obtained by technology mapping and resynthesis procedures (Imfs+Lutpack) implemented in the ABC tool. For both tools the number of 6-input LUTs in the resulting networks and the delay calculated as the depth of the networks have been provided.

Table 1 Results of Synthesis for 6-input LUTs
Full size table

It can be noticed that the method proposed in this paper produces networks of much greater area quality (calculated as the number of 6-LUTs) than those generated by the ABC procedures. The delay of networks obtained by both methods is similar.

5 Conclusions

There are many methods for decomposition of multi-output Boolean functions. These methods mostly use cube or BDD-based representation of the decomposed function. However, the common characteristics of these methods is the requirement that the decomposed multi-output Boolean function is represented by a single truth table in the case of cube representation or a single BDD.

The proposed decomposition method allows decomposing a set of Boolean functions described by separate truth tables. Application of indexed partition allows performing multilevel logic synthesis for multi-output, not fully specified Boolean functions of large number of input variables. The obtained results are of high quality in terms of the area calculated as the number of LUTs, as well as the delay of resulting network.