Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

OFDM has been applied widely in wireless communication systems due to its high data rate transmission capability with high bandwidth efficiency and its robustness to multipath delay. OFDM introduces Cyclic Prefix (CP), which eliminates the Inter-Symbol-Interference (ISI) between OFDM symbols [1] and its high data rates are available without having to pay for extra bandwidth. With these advantages, OFDM is widely accepted in numerous wireless standards such as Digital Video Broadcasting (DVB), Digital Audio Broadcasting (DAB), Wireless Metropolitan Area Network (WMAN) and Wireless Local Area Network (WLAN).

In order to exploit all these advantages and optimize the performance of OFDM systems; channel state information (CSI) plays a vital role. A Signal-to-noise ratio (SNR) gives a comprehensive knowledge of CSI, which allows us to decide whether a transition to higher bit rates would be favorable or not. Similarly, SNR estimation is required for power control, adaptive modulation, coding and channel estimation. Therefore major input parameter for fourth generation adaptive system is a good SNR estimator.

Mainly there are two types of SNR estimation [2], which are as follows: (1) Data-aided (DA-SNR) estimator. (2) Non-data aided (NDA-SNR) estimator. DA is further divided into two types: (1) pilot-aided and (2) training sequence. In pilot-aided scheme, known information is transmitted together with data. While, in training sequence known information is transmitted over one or more OFDM symbols without data. In NDA estimator, no known data is transmitted and therefore SNR is estimated at the receiver blindly. In this work, an estimator of type DA-SNR (pilot-aided) is proposed because it works well in multipath fading channel.

One of the most significant current discussions in SNR estimation is Pre FFT (time domain) and Post FFT (frequency domain) estimators. Several studies have been produced SNR estimation in frequency domain, but little attention has been paid to time domain. Popular SNR estimators reported in literature are Boumard’s, Ren’s and Minimum Mean Square Error (MMSE) [3].

In [4], it was assumed that the channel conditions throughout observation are same. However, in highly frequency selective multipath channels, the assumption is not valid, and the performance is degraded greatly. Therefore this problem is overcome in [5], but its complexity is similar in terms of addition and multiplications. In addition, pilot aided MMSE [6] is investigated in frequency selective fading channel but it suffers when noise level increases and SNR fluctuates from its threshold value.

Recently, in [7] Pre FFT pilot aided SNR estimation is proposed where low MSE is achieved in flat fading channel. Therefore, to the best of our knowledge no work has been published for pilot aided Pre FFT SNR estimation over frequency selective Rayleigh fading channel that works well in low SNR environment.

A novel estimator presented here differs from previous methods in a way that it is pilot aided SNR estimation in time domain, by using autocorrelation of received signal. In addition, proposed method can accurately measure SNR which has very less bias and very close to the actual SNR values. It can also be seen that proposed SNR estimation performs better at low SNR.

This paper has been organized in the following way. In Sect. 18.2, overview of proposed Pre FFT SNR estimation technique is explained. Section 18.3 addressed the methodology used by proposed estimator. Section 18.4 described the channel model used in simulation. Results and analysis are discussed in Sect. 18.5. Conclusion of the work is presented in Sect. 18.6.

2 Proposed Technique

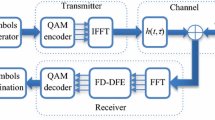
Pre FFT OFDM system model is shown in Fig. 18.1. It begins with “signal mapping” block where binary information is mapped according to modulation. Then serial to parallel conversion takes place. After that, pilot sub-carriers P(k) are inserted along with data sub-carriers D(k), arrangement of pilots and data sub-carriers are shown in Fig. 18.2. Therefore S(k) can be written as

$$S(k) = D(k) + P(k)$$
(18.1)
Fig. 18.1
figure 1

Typical OFDM baseband transceiver [8]

Full size image
Fig. 18.2
figure 2

Proposed pilots and data sub carriers arrangement

Full size image

Then IFFT is applied on S(k) samples that transform frequency domain samples S(k) into time domain s(n), which can be shown as

$$s(n) = IFFT\{ S(k)\} = \sum\limits_{k = 0}^{N - 1} {S(k)} e^{{\frac{{j2\Pi kn}}{{N_{FFT} }}}}$$
(18.2)

where N FFT is no of FFT points and s(n) can also be written as

$$s(n) = d(n) + p(n)$$
(18.3)

After passing through multi-path frequency selective fading channel, receiver input signal is first passed through serial to parallel converter and then guard band removal takes place. Therefore signal r(n) is obtained, which can be shown as

$$r(n) = h(n)\,{ \otimes }\,s(n) + w(n)$$
(18.4)

where h(n) is channel impulse response and w(n) is additive white Gaussian noise. The h(n) can be expressed as

$$h(n) = \left[ {h_{0} \,h_{1} \,h_{2} \ldots h_{T - 1} } \right]$$
(18.5)

where h 0, h 1 …h T are the coefficient of channel impulse response and T is total no of channel taps. By substituting Eq. (18.3) in Eq. (18.4), r(n) is given by

$$r(n) = h(n)\,{ \otimes }\,[d(n) + p(n)] + w(n)$$
(18.6)

The SNR estimation technique is such that it attempts to estimate the signal power using a priori known pilots and determines the noise power from it using measurement of total received power. Towards that end, autocorrelation of the received signal is performed to measure the total received power which is the value at lag zero. And in order to estimate the signal power, pilot power is estimated with the help of cross correlation and indirectly the signal power is deduced from it. Hence, moving on, we calculate the autocorrelation of complex valued received signal, written as

$$R_{rr} (l) = \sum\limits_{{n = - {\infty }}}^{{n = + {\infty }}} {r(n)} r^{*} (n + l)$$
(18.7)

where

$$r^{*} (n + l) = h^{*} (n + l){ \, \otimes\, }[d^{*} (n + l) + p^{*} (n + l)] + w^{*} (n + l)$$
(18.8)

By substituting the Eqs. (18.6) and (18.8) in Eq. (18.7), the autocorrelation R rr (l) is written as

$$\begin{aligned} R_{rr} (l) = & \sum\limits_{n = - \infty }^{n = \infty } {\left\{ {h(n){\, \otimes \, }[d(n) + p(n)] + w(n)} \right.} \\ & \quad \begin{array}{*{20}c} { \times \,h(n + l){ \, \otimes \, }[d^{*} (n + l) + p^{*} (n + l)] + w^{*} (n + l)\} } & {} \\ \end{array} \\ \end{aligned}$$
(18.9)
$$\begin{aligned} R_{rr} (l) & = \sum\limits_{{n = - {\infty }}}^{{n = {\infty }}} {\{ R_{hh} (l){\, \otimes \,}} \left[ {R_{dd} (n) + R_{dp} (n)} \right] + h(n){\, \otimes \, }R_{dw} (n) \\ & \quad + R_{hh} (l){\, \otimes \, }\left[ {R_{pd} (n) + R_{pp} (n)} \right]\, + h(n){ \,\otimes \, }R_{pw} (n) \\ & \quad + h^{*} (n + l){ \, \otimes \, }\left[ {R_{wd} (n) + R_{wp} (n)} \right] + R_{ww} (n)\} \\ \end{aligned}$$
(18.10)

At zero lag when l = 0

$$R_{dp} (0) = R_{pd} (0) \cong 0$$
(18.11)
$$R_{pw} (0) = R_{wp} (0) \cong 0$$
(18.12)
$$R_{dw} (0) = R_{wd} (0) \cong 0$$
(18.13)

By using Eqs. (18.11), (18.12) and (18.13), R rr (l)| l=0 is given as

$$R_{rr} (l) = \left. {R_{hh} (l){ \, \otimes \, }[R_{dd} (l) + R_{pp} (l)] + R_{ww} (l)} \right|_{l = 0}$$
(18.14)

where Eq. (18.14) represents the received signal power as function of autocorrelation. It can also be in written form of K

$$R_{rr} (l) = \left. {R_{hh} (l){\, \otimes \, }[K + 1]R_{pp} (l) + R_{ww} (l)} \right|_{l = 0}$$
(18.15)

where

$$K = \left. {\frac{{R_{dd} (l)}}{{R_{pp} (l)}}} \right|_{l = 0}$$
(18.16)

Therefore total Signal plus Noise Power \(P^{'}_{S + N}\) can be written as

$$P^{'}_{S + N} = \left. {R_{hh} (l) \otimes [K + 1]R_{pp} (l) + R_{ww} (l)} \right|_{l = 0}$$
(18.17)

Similarly, the Signal Power \(P^{'}_{S}\) can be expressed as

$$P^{'}_{S} = \left. {R_{hh} (l) \otimes [K + 1]R_{pp} (l)} \right|_{l = 0}$$
(18.18)

To evaluate channel impulse response h(n), the cross correlation of Eq. (18.6) is determined, with locally generated pilot signal. Therefore R rp can be written as

$$R_{rp} (l) = \left. {h(l) \, \otimes \, [R_{dp} (l) + R_{pp} (l)] + R_{wp} (l)} \right|_{n = l}$$
(18.19)

where R rp is the cross correlation between received signal and pilot carriers. Similarly R dp and R wp are cross correlations of data and noise with pilots respectively. By substitution of Eqs. (18.12) and (18.13) in Eq. (18.19), R rp (n) is given by

$$R_{rp} (n) \,{ \cong } \, \left. {h(n){\, \otimes \,}R_{pp} (n)} \right|_{l = n}$$
(18.20)

Equation (18.20) is the convolution of h(n) and R pp (n), which can be shown in the form of impulses

$$h(n) = \left[ {h_{0} \delta (n) + h_{1} \delta (n - 1) \cdots \, h_{T} \delta (n - T)} \right],$$
(18.21)
$$R_{pp} (n) = \left[ {\alpha_{0} \delta (n) + \alpha_{1} \delta (n\, \pm \,L) + \cdots \, \alpha_{N} \delta (n\, \pm \,NL)} \right]$$
(18.22)

where α 0…α N are coefficients of R pp (n). Therefore R rp (n) can be written as

$$\begin{aligned} R_{rp} (n) & = \left[ {\alpha_{0} h_{0} \delta (n) + \alpha_{0} h_{1} \delta (n\, - \,1) + \cdots \alpha_{0} h_{T} \delta (n\, - \,T)} \right] + \cdots \\ & \quad \alpha_{1} h_{0} \delta (n\, \pm \,L) + \alpha_{1} h_{1} \delta (n\, \pm \,L - 1) + \cdots \, \alpha_{1} h_{T} \delta (n\, \pm \,L - T) + \cdots \\ & \quad \alpha_{N} h_{0} \delta (n\, \pm \,NL) + \alpha_{N} h_{1} \delta (n\, \pm \,NL - 1) + \cdots \, \left. {\alpha_{N} h_{T} \delta (n\, \pm \,NL - T)} \right|_{n = l} \\ \end{aligned}$$
(18.23)

Equation (18.23) shows that the channel coefficients h 0, h 1 …h T are available at different location on both sides of zero lag (±L), but only zero lag position is used at (n = 0) due to its high energy. Therefore Eq. (18.23) can be written as

$$R_{rp} (0) = \left. {\frac{{\left[ {\alpha_{0} h_{0} \delta (0) + \alpha_{0} h_{1} \delta ( - 1) + \cdots \, \alpha_{0} h_{T} \delta ( - T)} \right]}}{{\alpha_{0} }}} \right|_{n = 0}$$
(18.24)

and it gives

$$h(n) = \left[ {h_{0} \;h_{1} \;h_{2} \; \ldots \;h_{T - 1} } \right]$$
(18.25)

Finally the estimated Signal to Noise Ratio (SNR ′) can be written as

$$SNR^{'} = \frac{{P_{S}^{'} }}{{P_{N}^{'} }}$$
(18.26)
$$SNR^{'} = \frac{{P_{S}^{'} }}{{P_{S + N}^{'} - P_{S}^{'} }}$$
(18.27)
$$SNR^{{\prime }} = \left. {\frac{{R_{hh} (l){\, \otimes \, [}K + 1\text{]}R_{pp} (l)}}{{R_{rr} (l) - R_{hh} (l){\, \otimes \, [}K + 1\text{]}R_{pp} (l)}}} \right|_{l = 0}$$
(18.28)

The Mean Square Error (MSE) is calculated by using following expression

$$MSE = \sum\limits_{i = 1}^{I} {} \left. {\left( {SNR_{i}^{{\prime }} (l) - SNR} \right)^{2} } \right|_{l = 0}$$
(18.29)

where (I = 1,000) is the number of iteration used for simulation. \(SNR_{i}^{{\prime }} \left( l \right)\) and SNR are the estimated and actual SNR respectively.

3 Methodology

In proposed algorithm, signal-to-noise ratio (SNR) is estimated in time domain. An initial step of receiver is to remove the guard band from the receiver input signal r(n). After the removal of guard band, signal r(n) is provided to autocorrelation processor, where received signal is autocorrelated R rr (n). To estimate the Signal plus Noise Power \(P^{'}_{S + N}\) and Signal Power \(P^{'}_{S}\), we required the autocorrelation of channel impulse response R hh (n). Therefore channel impulse response h(n) is evaluated by taking cross correlation of r(n) signal with time domain pilot signal p(n). In final step, time domain SNR′ is estimated by using Signal plus Noise Power \(P^{'}_{S + N}\) and Signal Power \(P^{'}_{S}\). OFDM simulation parameters are mentioned in Table 18.1. It is also assumed that there is perfect synchronization between transmitter and receiver, so no Inter-Carrier Interference (ICI) and ISI are present in OFDM symbols. This is justified if the estimation error is sufficiently low at low SNRs.

Table 18.1 OFDM simulation parameters
Full size table

4 Channel Model

In this work, six multi-paths fading channel model (COST 207 Typical Urban Reception TU6) for DVB-T applications are utilized in the simulations.

The taps of channel follow the Rayleigh statistics, whose parameters are shown in Table 18.2. The static case Impulse response of channel can be written as:

$$h(n) = \left[ \begin{aligned} &0.5\delta (n) + \delta (n - 3) + 0.63\delta (n - 8) \\ & + 0.25\delta (n - 25) + 0.15\delta (n - 36) + 0.1\delta (n - 80) \\ \end{aligned} \right]$$
(18.30)
Table 18.2 COST 207 typical urban reception (TU6) for DVB-T application [9]
Full size table

5 Results and Analysis

Figure 18.3 shows the cross correlation R dp between pilots and data carriers. Pilots carriers are inserted into data in such a manner that it produces a value of zero when (lag = 0). It is also depicted that the value of 1.574e−18 is produced at zero lag, which is very small as compared to other time instant values and therefore it is neglected.

Fig. 18.3
figure 3

(R dp ) Cross correlation between data and pilot sub-carriers at 10 dB SNR

Full size image

Figure 18.4 shows a cross correlation R wp (n) of noise signal with pilot carriers. In SNR estimation R wp (n) plays a very pivotal role because channel MSE is proportional to R wp (n). It is assumed that R wp (n) is expected to be relatively small due the arrangement of pilot carriers, which is also found at zero lag position.

Fig. 18.4
figure 4

(R wp ) Cross Correlation between noise and pilot sub-carriers at 10 dB SNR

Full size image

An important feature of the proposed Pre FFT SNR estimation is investigated in Fig. 18.5 [i.e. R rp (n)]. It has been shown that R rp (n) is the convolution of channel impulse response h(n) and pilots autocorrelation R pp (n). Equation (18.20) also reflects this property of R rp (n). It is found that the channel co-efficient h 0, h 1 …h T are present at every L number of lags. For illustration purpose only the first L instants co-efficient values (L = N fft /4) are shown in Fig. 18.5. Channel co-efficient is estimated at first L instants because at this location high energy and low MSE values are present.

Fig. 18.5
figure 5

(R rp ) Cross correlation between received signal and pilot sub-carriers

Full size image

In Fig. 18.6 the estimated SNR is plotted verses actual SNR for Rayleigh fading channel. To improve the estimation in low SNR regime, −8 to 20 dB range is used for simulation. It is depicted that the proposed SNR estimator has very small deviation with respect to the actual SNR values. It is also shown that Pre FFT SNR estimation performs better at low SNR.

Fig. 18.6
figure 6

Actual SNR versus estimated SNR for Raleigh fading channel

Full size image

In Fig. 18.7, MSE performance is analyzed over Rayleigh fading channel. The range of SNR used for simulation is [−20 to 20 dB]. Contrary to common sense it is observed that MSE of estimator is large at high SNR. This can be explained from the following observation. The SNR estimation is obtained primarily from signal power estimation. Noise power \(P_{N}^{\prime }\) is estimated from signal power \(P_{S}^{\prime }\) as shown in Eq. (18.27). So, at large SNR the signal power and total power are nearly same. Therefore, at large SNR, the noise power, estimated from it, is of the same order as the signal power estimation error, hence the SNR estimation error increases at large SNR. In order to be statistically accurate; mean is obtained over 1,000 samples. It is shown that proposed estimator performs better with multipath channel especially at low SNR environment.

Fig. 18.7
figure 7

MSE performance of proposed SNR estimated technique for Raleigh fading channel

Full size image

6 Conclusion

This paper investigates a novel pilot-based (DA) Pre FFT SNR estimation, where autocorrelation of received signal is used to estimate the signal plus noise power. Proposed estimator performs well over frequency-selective Rayleigh fading channel at low SNR regime. The standardization DVB-T parameters are setup for OFDM simulation. From the simulation results it is found that a low MSE is achieved by exploiting proposed estimator. The amount deviation corresponds to each SNR values is measured in term of MSE and it is observed that estimated SNR has very less bias and very close to the actual SNR values.