Keywords

1 Introduction

A prominent theme in the investigation of networks is the identification of their community structure. Informally stated, network communities are subnetworks whose constituent vertices are strongly affiliated to other community members and comparatively weakly affiliated with vertices outside the community; several formalizations of this concept have been explored (for useful reviews, see Refs. [1, 2]). The strong internal connections of community members is often accompanied by greater homogeneity of the members, e.g., communities in the World Wide Web as sets of topically related web pages or communities in scientific collaboration networks as scientists working in similar research areas. Identification of the network communities thus can facilitate qualitative and quantitative investigation of relevant subnetworks whose properties may differ from the aggregate properties of the network as a whole.

Agglomerative clustering is a well established strategy for identifying a hierarchy of communities in networks. Communities are successively merged into larger communities, coarsening a network of actors into a more manageable network of communities. The order in which merges should occur is not in general clear, necessitating heuristics for selecting pairs of communities to merge.

A key approach to community identification in networks is from Newman [3], who used a greedy agglomerative clustering algorithm to search for communities with high modularity [4]. In this algorithm, pairs of communities are successively merged based on a global optimality condition, so that the modularity increases as much as possible with each merge. The pairwise merging ultimately produces a community hierarchy that is structured as a binary tree. The structure of the hierarchy closely relates to both the quality of the solution and the efficiency of its calculation; modularity is favored by uniform community sizes [5, 6] while rapid computation is favored by shorter trees [7], so both are favored when the community hierarchy has a well-balanced binary tree structure, where the sub-trees at any node are similar in size. But the greedy algorithm may produce unbalanced community hierarchies—the hierarchy may even be dominated by a single large community that absorbs single vertices one-by-one [8], causing the hierarchy to be unbalanced at all levels.

In this chapter, we describe a new agglomerative clustering strategy for identifying community hierarchies in networks. We replace the global optimality condition for the greedy algorithm with a local optimality condition. The global optimality condition holds for communities c and c ′ when no other pair of communities could be merged so as to increase the modularity more than would merging c and c ′. The local optimality condition weakens the global condition, holding when no pair of communities, one of which is either c or c ′, could be merged to increase the modularity more than would merging c and c ′. The essentials of the clustering strategy follow directly: concurrently merge communities that satisfy the local optimality condition so as to increase the modularity, re-establishing the local optimality conditions and repeating until no further modularity increase is possible. The concurrent formation of communities encourages development of a cluster hierarchy with properties favorable both to rapid computation and to the quality of the resulting community solutions.

2 Agglomerative Clustering

2.1 Greedy Algorithms

Agglomerative clustering [9, 10] is an approach long used [11] for classifying data into a useful hierarchy. The approach is based on assigning the individual observations of the data to clusters, which are fused or merged, pairwise, into successively larger clusters. The merging process is frequently illustrated with a dendrogram, a tree diagram showing the hierarchical relationships between clusters; an example dendrogram is shown in Fig. 1. In this work, we will also refer to the binary tree defined by the merging process as a dendrogram, regardless of whether it is actually drawn.

Fig. 1
figure 1

Dendrogram representation of a cluster hierarchy. Clusters of data are pairwise merged into larger clusters, with all data eventually in the same cluster

Full size image

Specific clustering algorithms depend on defining a measure of the similarity of a pair of clusters, with different measures corresponding to different concepts of clusters. Additionally, a rule must be provided for selecting which merges to make based on their similarity. Commonly, merges are selected with a greedy strategy, where the single best merge is made and the similarity recalculated for the new cluster configuration, making successive merges until only a single cluster remains. The greedy heuristic will not generally identify the optimal configuration, but can often find a good one.

2.2 Modularity

Agglomerative clustering has seen much recent use for investigating the community structure of complex networks (for a survey of agglomerative clustering and other community identification approaches, see Refs. [1, 2]). The dominant approaches follow Newman [3] in searching for communities (i.e., clusters) with high modularity Q. Modularity assesses community strength for a partition of the n network vertices into disjoint sets, and is defined [4] as

$$\displaystyle{ Q = \frac{1} {2m}\sum _{c}\sum _{i,j\in c}\left (A_{ij} -\frac{k_{i}k_{j}} {2m} \right ), }$$
(1)

where the A i j are elements of the adjacency matrix for the graph, m is the number of edges in the graph, and k i is the degree of vertex i, i.e., \(k_{i} =\sum _{j}A_{ij}\). The outer sum is over all clusters c, the inner over all pairs of vertices (i, j) within c.

With some modest manipulation, Eq. (1) can be written in terms of cluster-level properties and in a form suitable as well for use with weighted graphs:

$$\displaystyle{ Q =\lambda \sum _{c}\left (W_{c} -\lambda K_{c}^{2}\right ), }$$
(2)

where

$$\displaystyle\begin{array}{rcl} W_{c}& =\sum _{i,j\in c}A_{ij}&{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} K_{c}& =\sum _{i\in c}k_{i}&{}\end{array}$$
(4)
$$\displaystyle\begin{array}{rcl} \lambda & = \left (\sum _{c}K_{c}\right )^{-1}.&{}\end{array}$$
(5)

Here, W c is a weight of edges internal to cluster c, measuring the self-affinity of the cluster constituents; K c is a form of volume for cluster c, analogous to the graph volume; and λ is a scaling factor equal to 1∕2m for an unweighted graph. Other choices for λ may also be suitable [6], but we will not consider them further.

Edges between vertices in different clusters c and c ′ may also be described at the cluster level; denote this edge by (c, c ′). Edge (c, c ′) has a corresponding symmetric inter-cluster weight \(w_{cc^{{\prime}}}\), defined by

$$\displaystyle{ w_{cc^{{\prime}}} =\sum _{i\in c}\sum _{j\in c^{{\prime}}}A_{ij}\quad. }$$
(6)

Using w c c ′, we can describe the merge process entirely in terms of cluster properties. When two clusters u and v are merged into a new cluster x, it will have

$$\displaystyle\begin{array}{rcl} W_{x}& =& W_{u} + W_{v} + 2w_{uv}{}\end{array}$$
(7)
$$\displaystyle\begin{array}{rcl} K_{x}& =& K_{u} + K_{v}.{}\end{array}$$
(8)

The inter-cluster weights for the new cluster x will be

$$\displaystyle{ w_{xy} = w_{uy} + w_{vy} }$$
(9)

for each existing cluster y, excluding u and v. The modularity change Δ Q u v is

$$\displaystyle{ \Delta Q_{uv} = 2\lambda \left (w_{uv} -\lambda K_{u}K_{v}\right ). }$$
(10)

From Eq. (10), it is clear that modularity can only increase when w u v  > 0 and, thus, when there are edges between vertices in u and v.

With the above, we can view a partition of the vertices as an equivalent graph of clusters or communities; merging two clusters equates to edge contraction. The cluster graph is readily constructed from a network of interest by mapping the original vertices to vertices representing singleton clusters and edges between the vertices to edges between the corresponding clusters. For a cluster c derived from a vertex i, we initialize W c  = 0 and K c  = k i .

2.3 Modularity-Based Greedy Algorithms

Newman [3] applied a greedy algorithm to finding a high modularity partition of network vertices by taking the similarity measure to be the change in modularity Δ Q u v . In this approach, Δ Q u v is evaluated for each inter-cluster edge, and a linked pair of clusters leading to maximal increase in modularity is selected for the merge. A naive implementation of this greedy algorithm constructs the community hierarchy and identifies the level in it with greatest modularity in worst-case time O(m + n)n, where m and n are, respectively, the numbers of edges and vertices in the network.

Finding a partition giving the global maximum in Q is a formally hard, NP-complete problem, equivalent to finding the ground state of an infinite-range spin glass [12]. We should thus expect the greedy approach only to identify a high modularity partition in a reasonable amount of time, rather than to provide us with the global maximum. Variations on the basic greedy algorithm may be developed focusing on increasing the community quality, reducing the time taken, or both.

Likely the most prominent such variation is the implementation described by Clauset et al. [7]. While neither the greedy strategy nor the modularity similarity measure is altered, the possible merges are tracked with a priority queue implemented using a binary heap, allowing rapid determination of the best choice at each step. This results in a worst-case time of O m hlogn, where h is the height of the resulting dendrogram. Thus, the re-implementation is beneficial when, as for many empirical networks of interest, the dendrogram is short, ideally forming a balanced binary tree with height equal to \(\left \lfloor \log _{2}n\right \rfloor \), where \(\left \lfloor x\right \rfloor \) denotes the integer part of x. But the dendrogram need not be short—it may be a degenerate tree of height n, formed when all singleton clusters are merged one-by-one into the same cluster. Such a dendrogram results in O m nlogn time, worse than for the naive implementation.

Numerous variations on the use of the change in modularity have been proposed for use with greedy algorithms, with some explicitly intended to provide a shorter, better balanced dendrogram. We note two in particular. First, Danon et al. [5] consider the impact that heterogeneity in community size has on the performance of clustering algorithms, proposing an altered modularity as the similarity measure for greedy agglomerative clustering. Second, Wakita and Tsurumi [8] report encountering poor scaling behavior for the algorithm of Clauset et al., caused by merging communities in an unbalanced manner; they too propose several modifications to the modularity to encourage more well-balanced dendrograms. In both papers, the authors report an improvement in the (unmodified) modularity found, even though they were no longer directly using modularity to select merges—promoting short, well-balanced dendrograms can promote better performance both in terms of time taken and in the quality of the resulting communities.

Alternatively, the strategy by which merges are selected may be changed, while keeping the modularity as the similarity measure, giving rise to the multistep greedy (MSG) algorithm [13, 14]. In the MSG approach, multiple merges are made at each step, instead of just the single merge with greatest increase in the modularity. The potential merges are sorted by the change in modularity Δ Q u v they produce; merges are made in descending order of Δ Q u v , so long as (1) the merge will increase modularity and (2) neither cluster to be merged has already been selected for a merge with greater Δ Q u v . The MSG algorithm promotes building several communities concurrently, avoiding early formation of a few large communities. Again, this leads to shorter, better balanced dendrograms with improved performance both in terms of time and community quality.

When required for clarity, we will refer to the original greedy strategy as single-step greedy (SSG). Additionally, we will restrict our attention to an implementation following Clauset et al. [7].

3 Clustering with Local Optimality

3.1 Local Optimality

The SSG and MSG algorithms are global in scope, pooling information from across the entire network to identify the clusters to merge that would lead to the greatest increase in modularity. In contrast, the potential modularity change Δ Q u v is local in scope and can be calculated (Eq. 10) using only properties of the clusters u and v. It is thus instructive to consider what else can be said on a local scale about the possible merges, particularly those selected in the SSG algorithm.

Let us assume that, at some stage in the SSG algorithm, clusters u and v are identified as those to merge. As noted in Sect. 2.2, there must be an edge between the two clusters. Restricting our attention to the edges incident on u, the edge (u, v) is distinguished from the edge to any other linked cluster x by leading to a greater modularity change, so that

$$\displaystyle{ \Delta Q_{uv} \geq \Delta Q_{ux}\qquad \forall x\quad. }$$
(11)

Considering the edges incident on v leads to a similar preference for the edge (u, v) over that to another linked cluster y, with

$$\displaystyle{ \Delta Q_{uv} \geq \Delta Q_{yv}\qquad \forall y\quad. }$$
(12)

Informally, the two clusters each have the other as the best choice of merge.

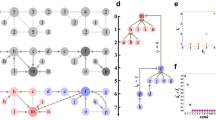
For any cluster with incident edges, at least one edge will satisfy a condition analogous to those in Eqs. 11 and 12. Call these the preferred edges for the vertex; similarly, refer to the corresponding merge as the preferred merge. If an edge is preferred for both vertices on which it is incident, call it and the corresponding merge locally optimal. We illustrate preferred and locally optimal edges in Fig. 2.

Fig. 2
figure 2

Preferred and locally optimal edges. Each edge is labeled with its modularity change Δ Q u v , which is the basis for determining the merge preferences shown with arrows. Edges with a single arrowhead are preferred edges for the vertex at the tail of the arrow, but not for the vertex at the head of the arrow. Edges with arrowheads at each end are preferred for both vertices; these are locally optimal edges. Those edges without arrowheads are not preferred by either of the linked vertices

Full size image

The local optimality condition is based on softening the global optimality condition used in the SSG algorithm, replacing a network-wide comparison of potential merges with an assessment of how clusters relate to their neighbors. As we will see, locally optimal edges occur frequently and can be used as the basis for an agglomerative clustering algorithm.

3.2 Greedy Clustering Using Local Optimality

We can base an agglomerative clustering algorithm on merging along the locally optimal edges in the network, determining whether any edges become locally optimal as a consequence, and repeating this until no locally optimal edges remain. With such an approach, we discourage the formation of unbalanced dendrograms by allowing multiple merges to occur concurrently, thus favoring shorter dendrograms and—given a suitable implementation—more efficient computation. The approach lies somewhere between SSG and MSG clustering, featuring concurrent formation of clusters like MSG, but selecting merges with a generalization of the condition in SSG.

For the most part, it is straightforward to define a precise algorithm from this idea. One complication is the presence of vertices with multiple locally optimal edges incident upon them. These edges can lead to, for example, a state where edges (u, v) and (u, w) are locally optimal, but (v, w) is not locally optimal. Thus, if we make both locally optimal merges, we produce a combined cluster of u, v, w which also includes the locally suboptimal merge. But to exclude merging v and w, we must then only make one of the locally optimal merges. In this work, we adopt the latter approach, arbitrarily selecting one of the locally optimal merges.

The resulting algorithm is:

  1. 1.

    For each edge (u, v), evaluate Δ Q u v .

  2. 2.

    For each vertex v, identify the maximum modularity change \(\Delta Q_{v}^{\mathrm{max}}\) from all incident edges.

  3. 3.

    For each edge (u, v), determine if it is locally optimal by testing \(\Delta Q_{uv} = \Delta Q_{u}^{\mathrm{max}} = \Delta Q_{v}^{\mathrm{max}}\). If, in addition, Δ Q u v  > 0, edge (u, v) is a candidate merge.

  4. 4.

    If there are no candidate merges, stop. Otherwise, for each candidate, merge the corresponding clusters, so long as neither cluster has so far been changed in the current iteration.

  5. 5.

    Begin a new iteration from step 1.

The order of iteration in step 4 will have an effect on the resulting community hierarchy when vertices have multiple locally optimal edges. In the implementation used in this work, we iterate through the edges in an arbitrary order that is uncorrelated with the modularity changes Δ Q u v . As the algorithm greedily selects edges based on local optimality, we call it GLOclustering—greedy, local optimality clustering.

When the GLOalgorithm terminates, no remaining edge will support a positive change in modularity; otherwise, one or more edges (u, v) would have Δ Q u v  > 0, and thus there would be at least one candidate merge—that edge with the greatest Δ Q u v . The clusters at termination have greater modularity than at any earlier iteration in the algorithm, since merges are only made when they increase the modularity.

Note that the GLOalgorithm generally terminates only having formed the sub-trees of the dendrogram for each cluster rather than the full dendrogram with single root. If the full dendrogram is needed, additional cluster merges can be made by using an alternate greedy algorithm. Here, we follow the above steps for GLOclustering, but drop the requirement that Δ Q u v  > 0—all locally optimal edges become candidate merges. This laxer condition is always satisfied by at least at least the edge with greatest Δ Q u v , so the merge process continues until all edges have been eliminated and only a single cluster remains.

Implementing the GLOalgorithm presents no special difficulties. The needed properties of the clusters (W v , K v , and w u v ) can be handled as vertex and edge attributes of a graph data structure. Straightforward implementation of the above steps can be done simply by iterating through the m edges, leading to O m worst-case time complexity for each of the p iterations of the merge process, or O m p overall worst-case time complexity. A simple optimization of this basic implementation strategy is to keep track of the \(\Delta Q_{v}^{\mathrm{max}}\) values and a list of corresponding preferred edges, recalculating these only when merges could lead to changes; this does not change the worst case time complexity from O m p, but does notably improve the execution speed in practice.

The above estimates of time complexity have the shortcoming that they are given not just in terms of the size of the network, but also in terms of an outcome of the algorithm—the number of iterations p. There is no clear a priorirelation between p and the network size, but we may place bounds on p. First, the algorithm merges at least one pair of clusters in each iteration, so p is bounded above by n. Second, the algorithm involves any cluster in at most one merge in an iteration, so p must be at least the height h of the dendrogram. This gives

$$\displaystyle{ n > p \geq h \geq \left \lfloor \log _{2}n\right \rfloor. }$$
(13)

Runtime of the algorithm is thus seen to be dependent on the structure of the cluster hierarchy found, with better performance requiring a well-balanced dendrogram. We do have reason to be optimistic that p will be relatively small in this case: a well-balanced dendrogram results when multiple clusters are constructed concurrently, which also requires fewer iterations of the algorithm.

3.3 Local Clustering Using Local Optimality

Although all merging decisions in GLOclustering are made using only local information, the algorithm is nonetheless a global algorithm—the clusters possible at one point in the graph are influenced by merges concurrently made elsewhere in the network. Yet we may specify a local clustering algorithm: starting from a single vertex, successively merge along any modularity-increasing, locally optimal edges incident upon it, stopping only when no such locally optimal edges remain. In this fashion, the modularity—an assessment of a partition of the vertices—may be used to identify overlapping communities.

This local algorithm functions by absorbing vertices one-by-one into a single cluster. Unfortunately, this is exactly the behavior corresponding to the worst case behavior for the SSG and GLOalgorithms, producing a degenerate binary tree as the dendrogram whose height is one less than the number of vertices in the community and conceivably is one less than the number of vertices in the graph. The expected time complexity is thus quadratic in the resulting community size. Worse still, characterizing all local clusters for the graph may require a sizable fraction of the vertices to be so investigated, giving a worst-case time complexity that is cubic in the number of vertices of the graph. Such an approach is thus suited for networks of only the most modest size.

A compromise approach is possible using a hybrid of the agglomerative and local approaches. First, determine an initial set of clusters using the GLOalgorithm. Second, for each community, expand it using local clustering, treating all other vertices as belonging to distinct singleton clusters. The hybrid algorithm is still quite slow (and leaves the worst-case time complexity unchanged), but fast enough to provide some insight into the overlapping community structure of networks with tens of thousands of vertices.

4 Results

4.1 Model Networks

To begin, we confirm that the GLOclustering algorithm is able to identify network communities by applying it to randomly generated graphs with known community structure. We make use of the model graphs proposed and implemented by Lancichinetti et al. [15]. We generate 1000 random graphs using the default parameter settings, where each random graph instance has 1000 vertices with an average degree of 15.

In Table 1, we show some characteristics of the results of clustering algorithm, comparing the results to those for SSG and MSG clustering. For the model networks, GLOproduces community solutions that have a greater number of communities, on average, than either SSG or MSG. The average modularity is greatest with SSG, with GLOsecond and MSG lowest. Modularity values are sufficiently high to indicate that GLOclustering is able to recognize the presence of communities in the model networks.

Table 1 Algorithm performance with model networks. Values are computed by averaging over clustering results from 1000 realizations of the random graphs proposed by Lancichinetti et al. [15], with default parameter settings. Results shown are for the highest modularity clusters in the generated hierarchies, with the number of clusters in the partition, the corresponding modularity Q, the normalized mutual information I norm comparing the algorithm output to the known community assignments, and the height h of the dendrogram (optimal height would be 9). Uncertainties for the final significant digits are shown parenthetically. All values in each column differ significantly ( p < 0. 001)
Full size table

While modularity characterizes clustering, it does not directly measure the accuracy of the clusters. We instead assess accuracy using the normalized mutual information I norm. For the joint probability distribution P X, Y over random variables X and Y, I norm X, Y is

$$\displaystyle{ I_{\mathrm{norm}}\left (X,Y \right ) = \frac{2I\left (X,Y \right )} {H\left (X\right ) + H\left (Y \right )}\quad, }$$
(14)

where the mutual information I X, Y and entropies H X and H Y are defined

$$\displaystyle\begin{array}{rcl} I\left (X,Y \right )& =& \sum _{x,y}P\left (X,Y \right )\log \frac{P\left (X,Y \right )} {P\left (X\right )P\left (Y \right )}{}\end{array}$$
(15)
$$\displaystyle\begin{array}{rcl} H\left (X\right )& =& -\sum _{x}P\left (X\right )\log P\left (X\right ){}\end{array}$$
(16)
$$\displaystyle\begin{array}{rcl} H\left (Y \right )& =& -\sum _{y}P\left (Y \right )\log P\left (Y \right ).{}\end{array}$$
(17)

In Eqs. (14), (15), (16), and (17), we use the typical abbreviations \(P\left (X\,=\,x,Y \,=\,y\right )\,=\,P\left (X,Y \right )\), \(P\left (X = x\right ) = P\left (X\right )\), and \(P\left (Y = y\right ) = P\left (Y \right )\). The base of the logarithms in Eqs. (15), (16), and (17) is arbitrary, as the computed measures only appear in the ratio in Eq. (14).

To assess clustering algorithms with I norm X, Y, we treat the actual community membership for a vertex as a realization of a random variable X and the community membership algorithmically assigned to the vertex as a realization of a second random variable Y. The joint probability P X, Y is defined by the distribution of paired community membership over all vertices in the graph. We can then evaluate I norm X, Y, finding a result that parallels the modularity: SSG on average obtains the greatest normalized mutual information, with GLOsecond and MSG the lowest. The high value for I norm X, Y indicates that GLOclustering assigns most vertices to the correct communities.

As GLOclustering attempts to improve performance by favoring well-balanced dendrograms, we also assess the balance of the dendrograms using their height. Since a dendrogram is a binary tree, the optimal height for a graph with n vertices is just the integer part of log2 n; the extent to which the dendrogram height exceeds this value is then indicative of performance shortcomings of the algorithm. The random graphs considered in this section have 1000 vertices, and therefore the optimal height is 9. The results are essentially what one would expect: SSG, which does not attempt to favor merges leading to balanced dendrograms, produces the tallest dendrograms on average; MSG, which aggressively makes concurrent merges, produces the shortest dendrograms; and GLO, which makes concurrent merges more selectively than MSG, produces dendrograms with heights on average between those resulting from SSG and MSG.

4.2 Empirical Networks

Based on the model networks considered in the preceding section, it appears that SSG produces the best community solutions of the three clustering algorithms considered. But we are ultimately not interested in model networks—it is in the application to real networks that we are concerned. In this section, we consider algorithm performance with several commonly used empirical networks.

The networks considered are a network of friendships between members of a university karate club [16]; a network of frequent associations between dolphins living near Doubtful Sound, New Zealand [17]; a network of character co-appearances in the novel Les Misérables [18]; a network of related purchases of political books during the 2004 U.S. presidential election [19]; a network of word adjacency in the novel David Copperfield [20]; a network of American college football games played during the Fall 2000 season[21]; a network of collaborations between jazz musicians [22]; a network of the neural connections in the C. elegans nematode worm [23]; a network of co-authorships for scientific papers concerning networks [20]; a network of metabolic processes in the C. elegans nematode worm [24]; a network of university e-mail interactions [25]; a network of links between political blogs during the 2004 U.S. presidential election[26]; a network of the western U.S. power grid [23]; a network of co-authorships for scientific preprints posted to the high-energy theory archive (hep-th) [27]; a network of cryptographic keys shared among PGP users [28]; a network of co-authorships for scientific preprints posted to the astrophysics archive (astro-ph) [27]; a network of the structure of the internet, at the level of autonomous systems [29]; and three networks of co-authorships for scientific preprints posted to the condensed matter archive (cond-mat), based on submissions beginning in 1995 and continuing through 1999, 2003, and 2005 [27]. Several networks feature weighted or directed edges; we ignore these, treating all networks as unweighted, undirected simple graphs. Not all of the networks are connected; we consider only the largest connected component from each network. The networks vary considerably in size, with the number of vertices n and number of edges m spanning several orders of magnitude (Table 2).

Table 2 Empirical networks under consideration. The number of vertices n and edges m in each network are shown
Full size table

We apply SSG, MSG, and GLOclustering algorithms to each of the empirical networks. In Table 3, we show properties of the clusterings produced by each of the algorithms. The properties of the community solutions differ notably from those for the random model networks. The number of clusters produced by GLOclustering no longer exceeds those for SSG and MSG clustering. Instead, the three algorithms produce similar numbers of clusters for the smaller networks, with the SSG algorithm yielding solutions with the greatest number of clusters for the largest networks. As well, the GLOalgorithm tends to produce the greatest modularity values, exceeding the other approaches for 15 of the 20 empirical networks considered, including all of the larger networks.

Table 3 Comparative performance of agglomerative clustering algorithms. For each network and each algorithm, shown are the number of clusters found, the modularity Q, and the dendrogram height h. Additionally shown for h is the minimum height for a dendrogram for the network
Full size table

The dendrograms produced for the empirical networks parallel those for the random networks. The dendrograms resulting from the SSG algorithm are the tallest, those from the GLOalgorithm are second, and those from MSG the shortest. The SSG algorithm often produces dendrograms far taller than the ideal for a graph with a given number n of vertices.

The differences between the dendrograms suggests the abundant presence of locally optimal edges in the empirical networks. We verify this by counting the number of candidate merges in the network for each iteration of the GLOand SSG algorithms. In Fig. 3, we show the number of candidate merges for the astro-ph network; the other empirical networks show similar trends.

Fig. 3
figure 3

Number of locally optimal edges. For the astro-ph network, we show the number of locally optimal edges that are candidate merges at each iteration of the algorithm. As the algorithm is not always able to merge all the candidates, also shown are the actual number of merges made at each iteration. For comparison, we also show, for the SSG algorithm, the number of locally optimal edges that would be candidate merges in GLOclustering

Full size image

We additionally applied the local clustering scheme described in Sect. 3.3, expanding the clusters found for the empirical network. In each case, some or all of the clusters are expanded (Table 4), leading to overlapping communities. As a measure of the degree of cluster expansion, we define a size ratio R as

$$\displaystyle{ R = \frac{1} {n}\sum _{c}n_{c}\quad, }$$
(18)

where n c is the number of vertices in the expanded cluster c. The size ratio equals the expected number of clusters in which a vertex is found. Values of R for the empirical networks are given in the final column of Table 4.

Table 4 Cluster expansion using hybrid algorithm, consisting of the GLOclustering algorithm followed by expansion using the local clustering algorithm. Shown are the number of clusters found in the GLOstage, the number of those clusters that increase in size in the local clustering stage, and the size ratio R showing an average expansion
Full size table

The clusters do not expand uniformly. We illustrate this in Fig. 4 using the astro-ph network. In this representative example, numerous clusters expand only minimally or not at all, while others increase in size dramatically.

Fig. 4
figure 4

Expansion of astro-ph communities with hybrid algorithm, consisting of the GLOclustering algorithm followed by expansion using the local clustering algorithm. Each point corresponds to a single cluster, with the location showing the number of vertices in the cluster as determined in the GLOstage and after the local clustering stage. The line shown indicates no expansion; all points necessarily lie on or above the line

Full size image

5 Conclusion

We have described a new agglomerative hierarchical clustering strategy for detecting high-modularity community partitions in networks; we call this GLOclustering, for greedy, local optimality clustering. At the core of the approach is a locally optimality criterion, where merging two communities c and c ′ is locally optimal when no better merge is available to either c or c ′. The cluster hierarchy is then formed by concurrently merging locally optimal community pairs that increase modularity, repeating this until no further modularity increases are possible. As all decisions on which communities to merge are based on purely local information, a natural counterpart strategy exists for local clustering.

The motivation for GLOclustering was to improve the computational performance and result quality of community identification by favoring the formation of a better hierarchy. The performance improvements have been largely achieved. The hierarchical structure, as encoded in the dendrogram, is considerably better balanced than that produced by SSG clustering, with corresponding improvements in computational performance observed for both model and empirical networks. The hierarchies produced by GLOclustering are moderately worse than those produced by MSG clustering, which is far more aggressive about making merges.

In terms of the modularity of the community solutions, the best results are found for the model networks using SSG clustering. But the results with the model are not borne out in reality—the highest modularity solution is found with GLOclustering for 15 of the 20 empirical networks considered, including the eight largest networks.

Overall, the local optimality condition proposed in this paper appears to be a good basis for forming clusters. We can gain some insight into this from the local clustering algorithm. For each of the empirical networks considered here, there is some overlap of the communities, with several networks showing a great deal of community overlap. The borders between communities are then not entirely well defined, with the membership of particular vertices depending on the details of the sequence of merges performed in partitioning the vertices. The concurrent building of communities in GLOclustering seems to allow suitable cores of communities to form, with the local optimality condition providing a useful basis for identifying those cores.

Several directions for future work seem promising. First, the local clustering algorithm described in Sect. 3.3 has worst-case time complexity O n 3 and is thus unsuited to investigation of large networks; a reconsideration of the local algorithm may lead to a method suited to a broader class of networks. Second, we observe that nothing about GLOclustering requires that it be used with modularity, so application of GLOclustering to community quality measures for specialized classes of networks, such as bipartite networks [30], may prove beneficial. Finally, we note that GLOclustering need not be used with networks at all; application to broader classes of data analysis could thus be explored, developing GLOclustering into a general tool for classifying data into an informative hierarchy of clusters.