Analysis of Rotating Systems Using General-Purpose Multibody Dynamics

Abstract

This work illustrates the application of general-purpose multibody formulations to the analysis of rotating systems dynamics. Various benchmark problems encompassing multiple deformable components are presented and analyzed. The suitability of the approach is assessed and conclusions are drawn on the basis of correlating the numerical simulations with analogous examples from the open literature.

1 Introduction

Multibody dynamics is a viable technology for the analysis of complex multidisciplinary mechanisms. Rotating systems represent a special class of mechanisms, characterized by the non-negligible angular motion they are subjected to. Traditionally, systems of this kind have been analyzed by dedicated formulations and software tools that intrinsically take into account the reference rotation motion of the system. Such approaches may be extremely efficient and effective, but may suffer from lack of generality. For example, in the field of helicopter aeromechanics, so-called “comprehensive tools” have been developed (e.g. CAMRAD JA, [1, 2]). Such formulations are specifically tailored for most of the needs in the analysis of helicopter rotor aeroelasticity, posing several restrictions on the topology of the problem and on the type of analysis. Later, the need to consider rather general configurations and non-standard analysis pushed for the incorporation of features that are typical of multibody dynamics (e.g. CAMRAD II, [3]).

Nowadays, rather general multibody formulations are used to model and analyze the dynamics of a variety of systems. MBDyn¹ [4] and Chrono::Engine² [5, 6] are noteworthy examples of original formulations implemented in freely distributed software originating from the academia. This work illustrates the application of general-purpose multibody formulations to the analysis of flexible rotating systems dynamics, and presents benchmarks that demonstrate the suitability of this approach.

The need to simulate flexible parts with large rotations within a multibody dynamics framework calls for advanced formulations, mostly rooted in finite element approximations of structural components; see for example [7–9].

The three dimensional beam is one of the most used models for this class of problems. The case of large rotations poses difficulties that researchers tried to overcome in different ways. A recent approach is based on the absolute nodal coordinate formulation, see for instance [10], whereas other approaches are based on the so-called corotational formulation, as in [11–13].

In this paper we will present benchmarks based on public data available at [14] and recently discussed in [15] within a joint effort for flexible multibody formulations and software benchmarking, using software rooted on two different approaches. MBDyn adopts the geometrically-exact beam formulation (GEBF) described in [16] and [17], whereas Chrono::Engine uses the element-independent corotational formulation presented in [18], with some modifications. Both use an incremental approach for the time integration of large rotations. Whenever available, equivalent results obtained with Dymore are also presented. Dymore is based on the GEBF, and uses the Wiener-Milenković parameters to represent finite rotations. For the sake of completeness, we succinctly present the corotational formulation implemented in Chrono::Engine, whereas for the GEBF implemented in MBDyn we refer to the above mentioned literature.

2 Corotational Formulation

Corotational formulations foster the reuse of finite element algorithms and theories whose behavior in the linear field are already well known and tested.

Figure 1 shows the concept of the corotational formulation in Chrono::Engine. A floating coordinate system $F$ follows the deformed element, thus the overall gross motion into the deformed state ${\mathcal{C}}_{D}$ can be seen as the superposition of a large rigid body motion from the reference configuration ${\mathcal{C}}_{0}$ to the so called floating or shadow configuration ${\mathcal{C}}_{S}$, plus a local small-strain deformation from ${\mathcal{C}}_{S}$ to ${\mathcal{C}}_{D}$. In this work, underlined symbols will represent variables expressed in the basis of the floating reference $F$.

Fig. 1

A schematic representation of the corotational concept

The rationale of the corotational approach is a procedure to compute a global tangent stiffness $\varvec{K}_{e}$ and a global force $\varvec{f}_{e}$ for each element $e$, given its local $\underline{\varvec{K}}$, its local $\underline{\varvec{f}}$ and the rigid body motion of the frame $F$ in ${\mathcal{C}}_{0}$ to $F$ in ${\mathcal{C}}_{S}$.

Whenever the element moves, the position and rotation of $F$ is updated. In literature there are many options to this end; to avoid dependence on connectivity [19], in our implementation we decided to put the origin of $F$ in the midpoint of the $AB$ segment, as $\varvec{x}_{F} = \frac{1}{2}(\varvec{x}_{B} - \varvec{x}_{A} )$, and we align its $\varvec{X}$ axis with $\varvec{x}_{B} - \varvec{x}_{A}$. The remaining $\varvec{Y}$ and $\varvec{Z}$ axes of $F$ are obtained with a Gram-Schmidt orthogonalization, enforcing $\varvec{Y}$ to bisect the $\varvec{Y}$ axes of $A$ and $B$ when projected on the plane orthogonal to $\varvec{X}$. This is important in case of torsion.

The rotation matrix of $F$ is $\varvec{R}_{F} \in \text{SO}3$; it is parametrized with the unit quaternion $\varvec{\rho}_{F} \in {\mathbb{H}}_{1}$. Similarly, quaternions are used to store the rotations of the two nodes, with $\varvec{\rho}_{A}$ and $\varvec{\rho}_{B}$. Hence the state of the system is $\varvec{s} = [\varvec{q},\varvec{\upsilon}]$ with $\varvec{q} = [\varvec{x}_{1} ,\varvec{\rho}_{1} ,\varvec{x}_{2} ,\varvec{\rho}_{2} , \ldots ,\varvec{x}_{n} ,\varvec{\rho}_{n} ] \in {\mathbb{R}}^{(3 + 4)n}$ and $\varvec{\upsilon}= [\varvec{\upsilon}_{1} ,\varvec{\omega}_{1} ,\varvec{\upsilon}_{2} ,\varvec{\omega}_{2} , \ldots ,\varvec{\upsilon}_{n} ,\varvec{\omega}_{n} ] \in {\mathbb{R}}^{(3 + 3)n}$. Note that, because of some algorithmic optimizations, we consider $\varvec{\omega}_{i}$ to be expressed in the local basis of the $i$th node unlike $\varvec{x}_{i} ,\varvec{\rho}_{i} ,\varvec{\upsilon}_{i}$ that are considered in the global basis.

For each element, given the global positions and rotations of the two end nodes, stored in the $\varvec{s}$ state at indexes $i_{A}$ and $i_{B}$, it is possible to compute the actual displacement part of $\underline{\varvec{d}}$ as $\underline{\varvec{d}}_{A} = \underline{\varvec{x}}_{A} - \underline{\varvec{x}}_{{A_{0} }} = \varvec{R}_{{F_{0} }}^{t} (\varvec{x}_{{A_{0} }} - \varvec{x}_{{F_{0} }} ) - \varvec{R}_{F}^{t} (\varvec{x}_{A} - \varvec{x}_{F} )$ and $\underline{\varvec{d}}_{B} = \underline{\varvec{x}}_{B} - \underline{\varvec{x}}_{{B_{0} }} = \varvec{R}_{{F_{0} }}^{t} (\varvec{x}_{{B_{0} }} - \varvec{x}_{{F_{0} }} ) - \varvec{R}_{F}^{t} (\varvec{x}_{B} - \varvec{x}_{F} )$.

The rotation part, however, introduces a complication, owing to the fact that finite rotations do not compose as vectors and must be dealt with special algebraic tools. First, one must compute the local rotation of nodes respect to the $F$ floating reference with $\underline{\varvec{R}}_{A} = \varvec{R}_{F}^{t} \varvec{R}_{A} \varvec{R}_{{A_{\varDelta } }}^{t}$ and $\underline{\varvec{R}}_{B} = \varvec{R}_{F}^{t} \varvec{R}_{B} \varvec{R}_{{B_{\varDelta } }}^{t}$. Equivalently, one can use quaternion products to write: $\underline{\varvec{\rho}}_{A} =\varvec{\rho}_{F}^{t}\varvec{\rho}_{A}\varvec{\rho}_{{A_{\varDelta } }}^{t}$ and $\underline{\varvec{\rho}}_{B} =\varvec{\rho}_{F}^{t}\varvec{\rho}_{B}\varvec{\rho}_{{B_{\varDelta } }}^{t}$. Here the optional term $\varvec{\rho}_{{A_{\varDelta } }}^{t}$ (or $\varvec{R}_{{A_{\varDelta } }}^{t}$) represents the initial rotation of node $A$ respect to $F_{0}$.

Then, the finite rotation pseudovectors $\underline{\varvec{\theta}}_{A}$ and $\underline{\varvec{\theta}}_{B}$ are obtained in the following way. It is known that, for an element $\varvec{R}$ in Lie group $\text{SO(}3)$ and an element $\varvec{\varTheta}$ in the corresponding Lie algebra $\text{so}(3)$, one has $\varvec{\varTheta}= {\text{skew}}(\varvec{\theta})$ where $\varvec{\theta}$ is also an element of the Lie group $\text{Spin}(3)$, double cover of $\text{SO}(3)$. Vice versa, one can extract the $\varvec{\theta}$ vector from the $\varvec{\varTheta}$ spinor by computing $\varvec{\theta}= {\text{axial}}(\varvec{\varTheta})$. Also, it holds $\varvec{R} = { \exp }(\varvec{\varTheta})$ and $\varvec{\varTheta}= {\text{Log}}(\varvec{R})$, where ${ \exp }( \cdot )$ builds the rotation matrix using an exponential; for details on this exponential and the implementation of ${\text{skew}}( \cdot )$, ${\text{axial}}( \cdot )$, ${\text{Log}}( \cdot )$, see for example [20].

In the work of other Authors, the theory above is used to compute $\underline{\varvec{\theta}}_{A} = {\text{axial}}({\text{Log}}(\underline{\varvec{R}}_{A} ))$, but in our case the adoption of quaternions lead to an alternative, more straightforward expression. In fact it is known that for a unit quaternion $\varvec{\rho}\in {\mathbb{H}}_{1}$ it holds $\varvec{\rho}= [\cos (\theta /2),\varvec{u}\sin (\theta /2)]$, with rotation angle $\theta = |\varvec{\theta}|$ about rotation unit vector $\varvec{u} = {\varvec{\theta}\mathord{\left/ {\vphantom {\varvec{\theta}\theta }} \right. \kern-0pt} \theta }$. Therefore it is possible to compute $\underline{\varvec{\theta}}_{A}$ and $\underline{\varvec{\theta}}_{B}$ as: $\theta_{A} = 2\arccos (\Re (\underline{\varvec{\rho}}_{A} ))$, $\varvec{u}_{A} = \frac{1}{{\sin (\theta_{A} /2)}}\Im (\underline{\varvec{\rho}}_{A} )$, and $\underline{\varvec{\theta}}_{A} = \theta_{A} \varvec{u}_{A}$ (the same for the B node).

Once $\underline{\varvec{d}} = [\underline{\varvec{d}}_{A} ,\underline{\varvec{\theta}}_{A} ,\underline{\varvec{d}}_{B} ,\underline{\varvec{\theta}}_{B} ]$ has been computed, well-known theories are available to compute the stiffness matrix $\underline{\varvec{K}} = \underline{\varvec{K}} (\underline{\varvec{d}} )$. in this work we compute $\underline{\varvec{K}}$ using the Eulero-Bernoulli theory, and in general we set $\underline{\varvec{f}}_{in} = \underline{{\varvec{Kd}}}$.

The local data $\underline{\varvec{K}}$ and $\underline{\varvec{f}}_{in}$ must be mapped to the global reference: to this end we use the corotational approach expressed in [13], where the adoption of projectors that filter rigid body motion is used to improve the consistency and the convergence of the method. Such formulation requires the introduction of various matrices, in the following we succinctly report them, along with modifications that we use in our method.

• the $\varvec{\varLambda}(\varvec{\theta}) = \frac{{\partial\varvec{\theta}}}{{\partial \varvec{w}}}$ matrix, whose analytic expression is $\varvec{\varLambda}(\varvec{\theta}) = \varvec{I}_{3 \times 3} - \frac{1}{2}{\text{skew}}(\varvec{\theta}) + \zeta {\text{skew}}(\varvec{\theta})^{2}$ with $\zeta = \left( {1 - \frac{1}{2}\theta {\text{cotan}}(\frac{1}{2}\theta )} \right)/\theta^{2}$,

• the $\varvec{H}$ transformation matrix:

  $$ \varvec{H} = \left( {\begin{array}{*{20}c} {\varvec{H}_{{\mathbf{n}}} (\underline{\varvec{\theta}}_{A} )} & {{\mathbf{0}}_{6 \times 6} } \\ {\varvec{I}_{6 \times 6} } & {\varvec{H}_{\varvec{n}} (\underline{\varvec{\theta}}_{B} )} \\ \end{array} } \right);\quad \varvec{H}_{\varvec{n}} (\varvec{\theta}) = \left( {\begin{array}{*{20}c} {\varvec{I}_{3 \times 3} } & {{\mathbf{0}}_{3 \times 3} } \\ {{\mathbf{0}}_{3 \times 3} } & {\varvec{\varLambda}(\underline{\varvec{\theta}} )} \\ \end{array} } \right) $$

  (1)

  that tends to a unit matrix $\varvec{I}_{12 \times 12}$ for $\theta \downarrow 0$,

• the $\underline{\varvec{P}}$ projector matrix: $\underline{\varvec{P}} = \varvec{I}_{12 \times 12} - \underline{\varvec{S}}^{D} \underline{\varvec{G}}$ where $\underline{\varvec{S}}^{D}$ is the so called spin lever matrix, built with $\underline{\varvec{x}}_{A}$ and $\underline{\varvec{x}}_{B}$, the positions of the end nodes respect to the center $F$ of the beam, expressed in $F$ basis:

  $$ \underline{\varvec{S}}^{D} = \left( {\begin{array}{*{20}c} { - {\text{skew}}(\underline{\varvec{x}}_{A} )} \\ {\varvec{I}_{3 \times 3} } \\ { - {\text{skew}}(\underline{\varvec{x}}_{B} )} \\ {\varvec{I}_{3 \times 3} } \\ \end{array} } \right) $$

  (2)

  and where $\underline{\varvec{G}}$ is the so called spin fitter matrix, that takes into account the change of orientation of the $F$ frame as the end nodes change position or rotation. For the two nodes beam, it is $\underline{\varvec{G}} = \left[ {\partial \underline{\varvec{\omega}}_{F} /\partial \underline{\varvec{x}}_{A} ,\partial \underline{\varvec{\omega}}_{F} /\partial \underline{\varvec{\omega}}_{A} , \ldots } \right]$, and for our custom choice of orientation and position of $F$, described at the beginning of this section, we have

  $$ \underline{\varvec{G}} = \left[ {\left. {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & {1/L} \\ 0 & { - 1/L} & 0 \\ \end{array} } \right|\left. {\begin{array}{*{20}c} {1/2} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right|\left. {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & { - 1/L} \\ 0 & {1/L} & 0 \\ \end{array} } \right|\begin{array}{*{20}c} {1/2} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] $$

  (3)

  Note that this expression is different from the one reported in [18] because they put the $F$ frame at the beginning of the beam whereas we put it in the middle, moreover it rotates a bit differently,

• the $\varvec{R}_{\diamondsuit }$ rotation-transformation matrix:

  $$ \varvec{R}_{\diamondsuit } = \left( {\begin{array}{*{20}c} {\varvec{R}_{F} } & {} & {} & {} \\ {} & {\varvec{R}_{A}^{t} \varvec{R}_{F} } & {} & {} \\ {} & {} & {\varvec{R}_{F} } & {} \\ {} & {} & {} & {\varvec{R}_{B}^{t} \varvec{R}_{F} } \\ \end{array} } \right) $$

  (4)

  Note that $\varvec{R}_{\diamondsuit }$ is different from the one often reported in literature, ex. in [18] or [13], because we update the rotation of nodes with rotation pseudovectors expressed in node local coordinates (hence the $\varvec{R}_{A}^{t}$ and $\varvec{R}_{B}^{t}$ transformation), coherently with what we said about angular velocities being expressed in local references and not in global reference, in our state $\varvec{s}$.

Given the matrices above, one can compute the global version of internal forces:

$$ \varvec{f}_{in} = \varvec{R}_{\diamondsuit } \underline{\varvec{P}}^{t} \varvec{H}^{t} \underline{\varvec{f}}_{in} $$

(5)

For the computation of the global tangent stiffness, one needs two additional matrices. First, we split the last part of Eq. (5) in four three-dimensional vectors: $\underline{\varvec{P}}^{t} \varvec{H}^{t} \underline{\varvec{f}}_{in} = [\underline{\varvec{n}}_{A} ,\underline{\varvec{m}}_{A} ,\underline{\varvec{n}}_{B} ,\underline{\varvec{m}}_{B} ]$, then we build the $\varvec{F}_{nm}$ and $\varvec{F}_{n}$ matrices:

$$ \underline{\varvec{F}}_{nm} = \left( {\begin{array}{*{20}c} {{\text{skew}}(\underline{\varvec{n}}_{A} )} \\ {{\text{skew}}(\underline{\varvec{m}}_{A} )} \\ {{\text{skew}}(\underline{\varvec{n}}_{B} )} \\ {{\text{skew}}(\underline{{\mathbf{m}}}_{B} )} \\ \end{array} } \right),\quad \underline{\varvec{F}}_{n} = \left( {\begin{array}{*{20}c} {{\text{skew}}(\underline{\varvec{n}}_{A} )} \\ {{\mathbf{0}}_{3 \times 3} } \\ {{\text{skew}}(\underline{\varvec{n}}_{B} )} \\ {{\mathbf{0}}_{3 \times 3} } \\ \end{array} } \right) $$

(6)

Finally one can compute the tangent stiffness matrix of the element in global coordinates, also accounting for geometric stiffening:

$$ \varvec{K} = \varvec{R}_{\diamondsuit } \left( {\underline{\varvec{P}}^{t} \varvec{H}^{t} \underline{\varvec{K}} \varvec{H}\underline{\varvec{P}} - \underline{\varvec{F}}_{nm} \underline{\varvec{G}} - \underline{\varvec{G}}^{t} \underline{\varvec{F}}_{n}^{t} \underline{\varvec{P}} + \underline{\varvec{P}}^{t} \varvec{L}_{H} \underline{\varvec{P}} } \right)\varvec{R}_{\diamondsuit }^{t} $$

(7)

$$ \varvec{K} = \varvec{R}_{\diamondsuit } \left( {\varvec{K}_{M} - \varvec{K}_{GR} - \varvec{K}_{GP} + \varvec{K}_{GH} } \right)\varvec{R}_{\diamondsuit }^{t} $$

(8)

We remark the following notes:

• the three terms $\varvec{K}_{GR}$ (related to change in rotation of the $F$ frame), $\varvec{K}_{GP}$ (related to changes in projectors), $\varvec{K}_{GH}$ (related to changes in $\varvec{H}$) are responsible of the so called geometric stiffness,

• the $\varvec{K}_{GH}$ term is not used in our formulation since we found no major benefits in computing it; see [13] for details on $\varvec{L}_{H}$,

• the $\varvec{K}_{M}$, which represents the so called material stiffness, is always symmetric (at least with Eulero-Bernoulli beams), but the terms for geometric stiffness introduce asymmetry,

• some Authors [21] show that, under mild assumptions, neglecting the asymmetric part does not hampers the convergence of Newton-Raphson iterations; hence the variant: $\varvec{K}_{symm} = \varvec{R}_{\diamondsuit } \left( {\underline{\varvec{P}}^{t} \varvec{H}^{t} \underline{\varvec{K}} \varvec{H}\underline{\varvec{P}} - \underline{\varvec{F}}_{sy} \underline{\varvec{G}} - \underline{\varvec{G}}^{t} \underline{\varvec{F}}_{sy}^{t} \underline{\varvec{P}} } \right)\varvec{R}_{\diamondsuit }^{t}$ where $\underline{\varvec{F}}_{sy} = \frac{1}{2}(\underline{\varvec{F}}_{nm} + \underline{\varvec{F}}_{n} )$.

3 Benchmark: Princeton Beam Experiment

This benchmark aims at the validation of the finite element implementations in a static problem with geometric nonlinearity. A thin cantilevered beam, constrained in $O$, is subject to large deformations and large rotations because of a tip load in $E$; for different angles $\theta$ one obtains out-of-plane displacements even if the load is vertical, and the beam is subject to a twisting action.

Experimental results, for a beam made with 7075 aluminium, are available in [22, 23] and are used for comparison.

We list the main properties, with reference to Fig. 2: beam length $L = 0.508$ m, section thickness $T = 3.2024$ mm, section height $H = 12.77$ mm, Young modulus $E = 71.7$ GPa, $\nu = 0.31$, $G = E\frac{(1 + \nu )}{2} = 27.37$ GPa.

Fig. 2

Setup of the benchmark for the Princeton beam experiment

Three loading conditions are tested: $P_{1} = 4.448$ N, $P_{2} = 8.896$ N, and $P_{3} = 13.345$ N, for increasing values of the $\theta$ angle in the $[0^{ \circ } ,90^{ \circ } ]$ range.

Results in Figs. 3, 4 and 5 show a good agreement between the present corotational beam formulation and the geometrically-exact beam formulations presented in [16] for Dymore and in [17] for MBDyn, as well as an agreement with the experimental results in [22, 23], which was recently discussed in [15].

Fig. 3

Twist rotation of the beam for the Princeton experiment

Fig. 4

Flapwise displacement at the beam tip versus loading angle for three loading conditions

Fig. 5

Chordwise displacement at the beam tip versus loading angle for three loading conditions

We remark that, because of the geometric nonlinearity, the solver has to perform few Newton-Raphson steps before obtaining a zero residual. For very large nonlinearities, a continuation strategy might help the convergence of the Newton-Raphson solver.

4 Benchmark: Lateral Buckling

This benchmark tests nonlinear effects in a dynamic context. A beam is bent in its plane of greatest flexural rigidity, up to the point that triggers lateral buckling. In a quasi-static non-linear analysis, results are visible in Fig. 7. In the context of dynamics, when buckling occurs, the beam snaps laterally and twists, inducing highly oscillatory motions. The corotational approach can capture the nonlinear nature of this phenomena.

As shown in Fig. 6, the $RC$ beam is clamped at point $R$, its length is $L = 1$ m, and its rectangular section has size $H = 100$ mm and $B = 10$ mm (Fig. 7).

Fig. 6

Setup of the benchmark for lateral buckling dynamics

Fig. 7

Static displacement of the beam along $i_{2}$, at the mid point

To induce the snapping, a tip load at $C$ is imposed by mean of a rotating crank $GB$ and a vertical rod $TB$, with a spherical joint in $C$ and a revolute joint in $B$. An initial imperfection is simulated by displacing the vertical bar and the crank by an offset $d = 0.1$ mm in the off-plane direction $i_{2}$. The crank has length $L_{c} = 0.05$ m and a circular section with diameter $D_{r} = 24$ mm, while the vertical rod has a length $L_{r} = 0.25$ m and a circular section with diameter $D_{r} = 48$ mm. The rotation of the crank is initially enforced by a prescribed motion function $\phi_{c} (t) = \pi (1 - \cos (\pi t/T_{c} ))/2$, with $T_{c} = 0.4$ s, then for $t > T_{c}$ it is $\phi_{c} (t) = \pi$.

All parts are made of aluminum, hence with Young modulus $E = 73$ GPa and Poisson ratio $\nu = 0.3$. Given the above mentioned sections, their inertia values $I_{zz}$ and $I_{yy}$ and their torsion constants $J$ are computed using formulas available in classical textbooks.

In the Chrono::Engine test, the $RC$ beam is modeled with 12 finite elements, whereas the crank and the rod are modeled with 3 elements each. Results in Figs. 8 and 9 show that the lateral buckling is triggered exactly at the same moment for all the formulations, although the Chrono::Engine integral is more damped. The numerical damping is a consequence of the fact that the Chrono::Engine default integrator is a timestepper for DVI non-smooth problems [24, 25]. This, in the case of no frictional contacts, boils down to a linearly-implicit first-order scheme, hence it shows the same damping effect of an implicit Euler method. Other integrals are obtained with higher order methods and are affected by numerical damping to a much lower degree.

Fig. 8

Displacement of the beam along $i_{2}$, at the mid point

Fig. 9

Angular velocity of the beam, at the mid point

5 Benchmark: Unbalanced Rotating Shaft

This benchmark explores the reliability of the numerical method in the analysis of a flexible system rotating at finite angular velocity. A rotating unbalanced shaft of length L = 6 m is integrated in time. A rigid disk is connected to the shaft at mid-span, above the reference shaft axis by an offset d = 0.05 m. The shaft is made of steel (density ρ = 7800 kg/m³, Young’s modulus E = 210 GPa, Poisson’s ratio ν = 0.3). The cross section is annular (r _i  = 0.045 m, r _o  = 0.05 m). The mass of the disk is m _d  = 70.573 kg, the radius is r _d  = 0.24 m, and the thickness is t _d  = 0.05 m. The system is subjected to gravity (g = 9.81 m/s²) directed transversely. The end ‘R’ of the shaft is connected to the ground by a cylindrical joint (displacement along and rotation about the shaft’s axis are permitted). The end ‘T’ is supported by a revolute joint; the relative angular velocity about the shaft axis is prescribed as a function of time,

$$ \varOmega (t) = \left\{ {\begin{array}{*{20}l} {A_{1} \omega (1 - \cos (\pi t/T_{1} ))/2} \hfill & {0 \le t \le T_{1} } \hfill \\ {A_{1} \omega } \hfill & {T_{1} < t \le T_{2} } \hfill \\ {A_{1} \omega + (A_{2} - A_{1} )\omega (1 - \cos (\pi (t - T_{2} )/(T_{3} - T_{2} )))/2} \hfill & {T_{2} < t \le T_{3} } \hfill \\ {A_{2} \omega } \hfill & {T_{3} < t} \hfill \\ \end{array} } \right. $$

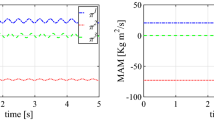
with A ₁ = 0.8, A ₂ = 1.2, T ₁ = 0.5 s, T ₂ = 1 s, T ₃ = 1.25 s, and ω = 60 rad/s, close to the first natural frequency of the system. The shaft accelerates from zero and passes from sub-critical to super-critical regime; when passing through the first natural bending frequency of the system, lateral oscillations occur and significant forces take place, as predicted by the linear theory of unbalanced rotors (Figs. 10 and 11).

Fig. 10

Setup of the unbalanced rotating shaft benchmark

Fig. 11

Mid-point transverse displacement of unbalanced rotating shaft

6 Conclusions

Benchmarks show that the presented multibody software frameworks can accommodate flexible elements of beam type that can match the requirements of rotor dynamics, yet keeping the benefits of general-purpose multibody tools, such as unlimited number of constraints, actuators and rigid parts.