Explanation of the Snubbing Mechanism on Vibration Reduction by Means of Chaos Metrics

Abstract

Snubbing has been proposed as a possible mechanism to reduce blade vibration of turbo machinery in resonant condition. It consists in physically limiting the vibration amplitude on the blade tip, leaving a small gap between the shrouds of adjacent blades. When the relative displacement between adjacent blades exceeds the gap, a contact occurs between the shrouds, the relative motion is restricted and energy is dissipated by friction and impact during the contact. Whilst effectiveness of snubbing has been proven in the practice on test benches and theoretical models have been developed to simulate bladed disk response in presence of snubbing, the explanation of its actual effectiveness is by intuition. In this paper, the authors propose an explanation of snubbing effectiveness to reduce blade vibrations in resonant condition, by investigating the relationship between vibration reduction and chaos onset using a suitable chaos metrics.

1 Introduction

Blade failure in turbo machinery for power generation could be fostered by excessive vibration level of the blade itself, owing to the overcoming of fatigue limit. In the last decades, fatigue crack development and consequent blade failures affected high performance turbo machinery.

Blade vibrations are generally excited by the fluid flow and may become dangerous in case of resonance. Resonant conditions cannot always be avoided; therefore, suitable devices are needed to reduce vibration amplitudes in these conditions.

There are different technologies for mounting blades on the shaft. Blades may be slightly forced against each other in correspondence of the shrouds: this should allow the continuity of the contact without clearances also at rated speed and full load. In this case, the blades are called pre-twisted. In other cases, a small gap is left between the shrouds of adjacent blades.

A possible way to reduce blade vibration is energy dissipation, owing to micro slipping friction in blade roots, by means of underplatform dampers [1, 2] or friction rings [3], or in blade connecting wires. These devices are applicable independently from the technology for mounting blades.

Another possibility is to exploit a contact related phenomenon, when a small gap is left: a contact may occur between the blade tips [4] in the vibration modes of the bladed disk, in which the relative displacement between adjacent blades exceeds the gap. During the contact, some energy is dissipated, because the shock is not purely elastic and because there is friction between the contacting surfaces. The relative vibration amplitude between adjacent blades is restricted and, therefore the absolute vibration amplitude is reduced with respect to the vibration amplitude for free-standing blades (without contact). This mechanism is called snubbing.

In this paper, the relationship between vibration reduction due to the snubbing mechanism and chaotic behaviour onset is investigated numerically, by using an improved, multi-degrees of freedom, model. Vibration reduction is evaluated in some different cases and typical chaos measurement indexes are used. It is finally shown that the optimal selection of the gap between the blades can be defined, based on chaos measurement index value.

2 Improved Model for the Snubbing Mechanism

A simplified model, suitable to analyze the effect of the snubbing mechanism, has been introduced by the authors in [5]. Its capability to reproduce the actual snubbing mechanism has been proven by exploiting experimental results obtained on a test rig. In this paper, the model is largely improved, by considering two aspects, which have influence on the snubbing mechanism:

• 1. the mistuning of the blades;

• 2. the relationship between the inter-shroud stiffness and the displacement of two adjacent blades has been more realistically considered, on the basis of the analyses performed by using accurate finite element models, reported in [6].

The simplified model does not require huge computational time and resources, which are on the contrary necessary if 3D nonlinear calculations are performed, even with these improvements. This allowed a large number of different random mistuned distributions to be simulated, in order to have statistical significance of the results obtained. A brief description of the model is reported hereafter.

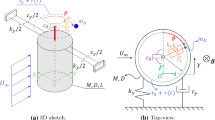
The bladed disk is modelled by means of a lumped parameter cyclic system as shown in Fig. 1. The number of the blades is z, they are ordered so that blade 1 follows blade z and precedes blade 2, owing to the radial symmetry of the system. Each blade j is connected to its root $r_{j}$ and both have a degree of freedom represented respectively by the generalized displacements $x_{j}$ and $y_{j}$. Lumped masses $m_{j}$ and $m_{{r_{j} }}$ are attributed to each blade and root respectively. By considering the mistuning, it is assumed that the mass of the blades and coefficients $k_{j}$ and $c_{j}$, representing the blade modal stiffness and damping, have a normal distribution:

$$ m_{j} \sim N(\mu_{m} ,\sigma_{m} ),\,k_{j} \sim N(\mu_{k} ,\sigma_{k} ),\,c_{j} \sim N(\mu_{c} ,\sigma_{c} ) $$

(1)

Fig. 1

Lumped parameter model for studying the snubbing mechanism

The inter-root stiffness and damping are represented by coefficients $k_{{r_{j(j + 1)} }}$ and $c_{{r_{j(j + 1)} }}$; they take into account the continuity of the roots on the disk and other effects, like friction, in the connection between the root and the blade.

These assumptions correspond to:

• use a modal approach for the mistuned blade, that is acceptable because the snubbing effect modelled here occurs when the blades are excited close to resonant condition; $m_{j}$ is the modal mass of the blades, $k_{j}$ its modal stiffness and $c_{j}$ its modal damping;

• consider the roots as very, but not infinitely, rigid because stiffnesses $k_{{r_{j(j + 1)} }}$ are much greater than $k_{j}$.

Root masses and coefficients are not normally distributed, because it is considered that mistuning effects can be sufficiently reproduced by the variations of blade mass and stiffness and damping coefficients.

Finally, the inter-shroud stiffness $k_{{s_{j(j + 1)} }} = f(x_{j} - x_{j + 1} )$ and damping $c_{{s_{j(j + 1)} }}$ coefficients are different from zero only when two subsequent shrouds of blade j and $j + 1$ are in contact. This condition is verified when $x_{j} - x_{j + 1} > g_{j(j + 1)}$, i.e. when the difference between the displacements of blades j and $j + 1$ is greater than the nominal assembling gap $g_{j(j + 1)}$ between them. Since machining and assembling errors may occur in the bladed disk, also the assembling gaps are not considered as constant, but they follow a normal distribution, so that $g_{j(j + 1)} \sim N(\mu_{g} ,\sigma_{g} )$.

The actual value of the inter-shroud stiffness depends on the displacement of the two adjacent blades $x_{j} - x_{j + 1}$. The function $k_{{s_{j(j + 1)} }} = f(x_{j} - x_{j + 1} )$ is shown in Fig. 1. There is a transition between zeroing of the gap and the value $\xi$ of interference, set as linear up to a threshold value, which is equal to the stiffness value $\bar{k}_{s}$ of the bladed disk with continuous shrouding. The evaluation of the transition value $\xi$ and the definition of the linear relationship have been made by using the model developed in [6].

Lagrange’s equation approach is used to define the analytical model of the system. The first step is to define the set of values for the index $i \in I = \left\{ {1,2, \ldots ,z,1} \right\}$ used for inter-root and inter-shroud coefficients. The cardinality of I is $z + 1$. This reflects the cyclicity of the considered system.

Kinetic energy of the system is equal to:

$$ T = \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {m_{j} \,\dot{x}_{j}^{2} } + \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {m_{{r_{j} }} \,\dot{y}_{j}^{2} } $$

(2)

Linear elastic potential energy is:

$$ V = \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {k_{j} \,\left( {x_{j} - y_{j} } \right)^{2} } + \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {k_{{r_{{I_{j} I_{j + 1} }} }} \,\left( {y_{{I_{j} }} - y_{{I_{j + 1} }} } \right)^{2} } $$

(3)

Similarly, the linear damping function is:

$$ R = \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {c_{j} \,\left( {\dot{x}_{j} - \dot{y}_{j} } \right)^{2} } + \frac{1}{2}\sum\limits_{j\,=\,1}^{z} {c_{{r_{{I_{j} I_{j + 1} }} }} \,\left( {\dot{y}_{{I_{j} }} - \dot{y}_{{I_{j + 1} }} } \right)^{2} } $$

(4)

Apart from external forcing $F_{j}$ acting on each blade, which will be discussed in the following, a nonlinear inter-shroud force is defined as:

$$ F_{{s_{{I_{j} I_{j + 1} }} }} = \eta_{{I_{j} I_{j + 1} }} \left[ { - k_{{s_{{I_{j} I_{j + 1} }} }} \left( {x_{{I_{j} }} - x_{{I_{j + 1} }} - g_{{I_{j} I_{j + 1} }} } \right) - c_{{s_{{I_{j} I_{j + 1} }} }} \left( {\dot{x}_{{I_{j} }} - \dot{x}_{{I_{j + 1} }} } \right)} \right],\quad j \in \left[ {1,z} \right] $$

(5)

where $\eta_{{I_{j} I_{j + 1} }}$ is a Boolean variable, used to take into consideration whether the contact between the shrouds exists, and is defined as:

$$ \eta_{{I_{j} I_{j + 1} }} = \left\{ {\begin{array}{*{20}l} {1,\quad x_{{I_{j} }} - x_{{I_{j + 1} }} > g_{{I_{j} I_{j + 1} }} } \hfill \\ {0,\quad x_{{I_{j} }} - x_{{I_{j + 1} }} \le g_{{I_{j} I_{j + 1} }} } \hfill \\ \end{array} ,} \right.\quad j \in \left[ {1,z} \right]\quad \begin{array}{*{20}l} {\text{contact}} \hfill \\ {\text{no contact}} \hfill \\ \end{array} $$

(6)

and the value of $k_{{s_{{I_{j} I_{j + 1} }} }}$ is determined on the basis of:

$$ k_{{s_{{I_{j} I_{j + 1} }} }} = \left\{ {\begin{array}{*{20}l} {\bar{k}_{s} ,} \hfill & {x_{{I_{j} }} - x_{{I_{j + 1} }} > g_{{I_{j} I_{j + 1} }} + \xi } \hfill \\ {{{\bar{k}} \mathord{\left/ {\vphantom {{\bar{k}} \xi }} \right. \kern-0pt} \xi }\left( {x_{{I_{j} }} - x_{{I_{j + 1} }} - g_{{I_{j} I_{j + 1} }} } \right),} \hfill & {g_{{I_{j} I_{j + 1} }} <\,x_{{I_{j} }} - x_{{I_{j + 1} }} \le\,g_{{I_{j} I_{j + 1} }} + \xi ,} \hfill \\ {0,} \hfill & {x_{{I_{j} }} - x_{{I_{j + 1} }} \le\,g_{{I_{j} I_{j + 1} }} } \hfill \\ \end{array} \quad j \in \left[ {1,z} \right]} \right. $$

(7)

The virtual work of the forces is:

$$ \delta U = \sum\limits_{j\,=\,1}^{z} {F_{j} \,\delta x_{j} } + \sum\limits_{j = 1}^{z} {F_{{s_{{I_{j} I_{j + 1} }} }} \,\delta \left( {x_{{I_{j} }} - x_{{I_{j + 1} }} - g_{{I_{j} I_{j + 1} }} } \right)} $$

(8)

Then, the degrees of freedom are grouped and ordered in vector ${\mathbf{q}}$ as follows:

$$ {\mathbf{q}} = \left\{ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } & {x_{2} } & {y_{2} } & \ldots & {x_{z} } & {y_{z} } \\ \end{array} } \right\}^{\text{T}} $$

(9)

and the system of equations can be written in the canonical form as:

$$ \left[ {\mathbf{M}} \right]\mathop {\mathbf{q}}\limits^{..}\,+\,\left( {\left[ {\mathbf{C}} \right] + \left[ {{\mathbf{C}}_{r} } \right] + \left[ {{\mathbf{C}}_{s} ({\mathbf{q}})} \right]} \right){\dot{\mathbf{q}}} + \left( {\left[ {\mathbf{K}} \right] + \left[ {{\mathbf{K}}_{r} } \right] + \left[ {{\mathbf{K}}_{s} ({\mathbf{q}})} \right]} \right){\mathbf{q}} = {\mathbf{F}}_{s}^{(s)} ({\mathbf{q}}) + {\mathbf{F}} $$

(10)

A complete discussion about fluid flow excitation is reported in [5]. Turbulent flow is considered for the simulations presented in this paper. Bearing in mind that the harmonic order number coincides with the number of the nodal diameters of the mode, owing to the cyclicity of the system, the nth harmonic component results on blade j equal to:

$$ F_{\left( j \right)} (t) =\Delta F_{n} \sin \left( {n\Omega t + n\frac{2\pi }{z}\left( {j - 1} \right)} \right)\sin \omega_{t} t $$

(11)

These last forces can excite natural modes of the row only if $\omega_{t} \pm n\Omega$ corresponds to the circular natural frequency of the nth mode, where $\omega_{t}$ is the turbulence circular frequency and $\Omega$ the rotational speed.

Owing to the presence of the terms $\left[ {{\mathbf{C}}_{s} ({\mathbf{q}})} \right]$, $\left[ {{\mathbf{K}}_{s} ({\mathbf{q}})} \right]$ and ${\mathbf{F}}_{s}^{(s)} ({\mathbf{q}})$ that depend on occurrence of the contacts on the shrouds, Eq. (10) represents a nonlinear system. Its integration in the time domain is performed by means of Newmark’s implicit method, in which the values of $\eta_{{I_{j} I_{j + 1} }}$ and $k_{{s_{{I_{j} I_{j + 1} }} }}$ are determined at each time step by means of Eqs. (6) and (7).

3 Chaotic Behaviour of the Bladed Disk Owing to Snubbing

It has been shown in [5] that snubbing is effective to reduce the vibration with respect to free-standing blades, when the excitation frequency is close to the eigenfrequency of a certain mode; thus, when the system is close to the resonant condition. Otherwise, snubbing may cause vibration amplification with respect to free-standing blades. These different behaviours are analyzed under the point of view of chaos in this section.

The bladed disk considered is the same of [5], with 120 side entry 7.5″–190.5 mm blades, and the first simulation set is relative to a case with $n = 6$. In order to have statistical significance, 100 runs of simulation have been performed, with different seed for the normal distributions of the parameters. Each simulation has the duration of 1 s, starting with null initial condition. The mistuning selected for the simulations is such as standard deviations are equal to 10 % of the considered normal distributions for blade parameters. The excitation frequency is equal to the first natural frequency of a single blade, i.e. $f_{b} = 390.9\,{\text{Hz}}$, and very close to the eigenfrequency of the mode with 6 nodal diameters, without mistuning. Snubbing is effective to reduce vibrations and Fig. 2a shows the comparison between vibration amplitudes for blade #2 with and without the snubbing on the shrouds for a simulation run. The case without snubbing corresponds actually to the case of free-standing blades. The Poincaré maps corresponding to blade #2 with snubbing for all the simulation runs are shown in Fig. 3a, in a layered 3D view. The analysis of any single Poincaré map, corresponding to any simulation run, and of the resulting “Poincaré tube”, for all the runs, suggests the presence of chaos.

Fig. 2

Time response of blade #2; a n = 6; b n = 2

Fig. 3

a Poincaré maps corresponding to blade #2, n = 6 (for the case with snubbing); b Top probability of observing the given result by chance given that the null hypothesis is true; Middle dominant Lyapunov exponent; Bottom sum of Lyapunov exponents for each blade. Case n = 6 and for a simulation run

In order to confirm this hypothesis, the time series that represent the solution of Eq. (10), for all the 120 blades of the disk and for all the simulation runs, have been analyzed by means of the statistical test described in [7].

The test, applied to this case, provides that a $H_{0}$ hypothesis of chaos, at significance level 0.05, is not rejected. This happens for all the blades and simulation runs. A further confirmation is given by the probability $p_{i}$ of observing the given result by chance given that the null hypothesis is true. Small values of $p_{i}$ cast doubt on the validity of the null hypothesis of chaos. The calculated probabilities $p_{i}$ for all the blade responses are shown in Fig. 3b top, for a simulation run, and chaos hypothesis is further proven. Similar results have been obtained for the other simulation runs, which are not shown for the sake of brevity.

By shifting now to analyze the results of the estimation of Lyapunov exponents, the dominant one $\lambda_{1}$ is positive for all the blade responses (as shown in Fig. 3b middle), while the sum $\sum\nolimits_{i} {\lambda_{i} }$ is negative (as shown in Fig. 3b bottom). These two conditions:

$$ \lambda_{1} > 0\quad {\text{and}}\quad \sum\nolimits_{i} {\lambda_{i} < 0} $$

(12)

indicate that chaos is present and that the dynamic system, represented by each blade, has an attractor. The same results have been obtained for the other simulation runs, the attractor has a “ring-shape” and this explains the “tube-shape” of the layered Poincaré maps in Fig. 3a.

The second simulation set considers a case with $n = 2$. The excitation frequency is equal to the first natural frequency of a single blade, i.e. $f_{b} = 390.9\,{\text{Hz}}$, which is not close to eigenfrequency of 374.2 Hz associated to 2 nodal diameters without mistuning, thus the system is not close to the resonant condition.

Snubbing is not effective to reduce vibrations, as shown in Fig. 2b for a simulation run and blade #2. However, the corresponding Poincaré map (see Fig. 4a), and of the resulting “Poincaré cloud”, for all the runs, suggests the presence of chaos.

Fig. 4

a Poincaré map corresponding to blade #2, n = 2 (for the case with snubbing). b Top probability of observing the given result by chance given that the null hypothesis is true; Middle dominant Lyapunov exponent; Bottom sum of Lyapunov exponents for each blade. Case n = 2 and for a simulation run

The testing of $H_{0}$ hypothesis of chaos, at significance level 0.05, is not rejected either in this case, for all the blades and simulation runs, while $p_{i}$ for all the blade responses and a simulation run support $H_{0}$, as shown in Fig. 4b top.

Similar results, with respect to the previous example, are obtained by considering the estimation of Lyapunov exponents: the dominant one $\lambda_{1}$ is positive, while the sum $\sum\nolimits_{i} {\lambda_{i} }$ is negative for all the blade responses (as shown respectively in Fig. 4b middle and bottom). Other simulation runs have obtained similar results.

Also in this case chaos is present, but the dynamical system, represented by each blade has the attractor with a “cloud-shape” in the Poincaré layered maps of Fig. 4a. Attractor shape is a first remarkable difference of the dynamical behaviour of the bladed disk, whether snubbing is effective or not.

4 Analysis of the Fractal Dimension of the Time Series Resulted from Dynamical Simulations

Previous section introduced the idea to analyze the nature of the chaotic dynamical behaviour of the bladed disk response, in order to find out correlations between snubbing effectiveness. Now, a further idea is investigated: to evaluate if a chaos metric can be correlated to snubbing effectiveness.

The metric here used is Higuchi’s fractal dimension (HFD), introduced in [8]. HFD, like other measurements of fractal dimension [9], has been introduced as an index for describing the irregularity of a time series $\phi (t)$ in place of the power law of its power spectrum $P(f) \propto f^{ - \alpha }$. The more irregular the time series, the higher its fractal dimension. Under a different point of view, high fractal dimension corresponds to a power spectrum in which the power of the signal is distributed over a wide frequency range. This consequence allows an interesting interpretation of the effectiveness of snubbing mechanism, as it will be discussed in this section. HFD is applied to the time series, resulted from the dynamical simulation sets using the mistuned model presented before, by considering the change of system parameters, namely the damping, the frequency of the excitation acting on the bladed disk, or the nominal assembling gap.

4.1 Effect of Damping Change

The first case study is relative to the change of the damping between the shrouds during the contact. Bearing in mind that the response of Fig. 2a was calculated using the nominal and experimental system parameters, as described in [5], Fig. 5a, b show, respectively, the results a simulation run for the same blade #2 with lower and higher damping than the nominal one, compared to the response of the free-standing blade #2 to the same excitation. The time response of a further case with even higher damping is not shown for the sake of brevity.

Fig. 5

Time response of blade 2, n = 6. a Low damping; b High damping

Even without calculating the RMS ratio of the vibration amplitude in case of snubbing and in case of free-standing blades, it is rather easy to observe from Fig. 5 that the higher the inter-shroud damping, the more effective the snubbing to reduce vibrations. This is confirmed also for the case with very high damping not shown for brevity. Similar results have been obtained for the other simulation runs of these cases, with different normally distributed blade parameters.

Nevertheless, this qualitative remark has a quantitative correspondence if the HFDs of the time response are considered for all the blades. The results are shown in Fig. 6, where it is evident that HFD is obviously greater than 1 in every case, but, once a blade number is given, the HFD increases in biunique way with the damping and, consequently, with the effectiveness of the snubbing. This indicates also that the higher the chaos in the response, the more effective the snubbing.

Fig. 6

Higuchi’s fractal dimension comparison, case n = 6

4.2 Effect of Different Frequency of the Blade Excitation

The last remark of previous section is confirmed if another case study is considered. Different excitation frequencies are considered, from 380 to 400 Hz with 1 Hz step, by using the same mistuned model previously introduced and ceteris paribus. Both the free-standing blade response x and that of the blades with snubbing $x_{s}$ change in this case. In order to allow an easy comparison between all the simulation runs for all the blades, the average RMS values of the vibration amplitude are calculated in case of snubbing and in case of free-standing blades; Fig. 7a shows the percentage average vibration reduction defined as:

$$ \Delta _{\text{RMS}} = {{\left( {x_{s}^{\text{RMS}} - x^{\text{RMS}} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{s}^{\text{RMS}} - x^{\text{RMS}} } \right)} {x^{\text{RMS}} }}} \right. \kern-0pt} {x^{\text{RMS}} }} $$

(13)

Fig. 7

a Percentage reduction of average RMS vibration amplitude as a function of the excitation frequency, case n = 6. b Average Higuchi’s fractal dimension comparison as a function of excitation frequency, case n = 6

Snubbing is most effective when the excitation frequency is equal to 389 Hz (as said before close to the eigenfrequency of the system with $n = 6$) and decreases its effectiveness by shifting towards the boundaries of the sweep interval.

The snubbing effectiveness versus the excitation frequency has a quantitative correspondence with the HFDs of the time response, which are considered for all the blades. The results are shown in Fig. 7b, where it is evident that average HFD, for all the simulation runs, is obviously greater than 1 in every case, but, once a blade number is given, the highest value of average HFD is in correspondence of the excitation frequency of 389 Hz. Average HFD decreases as well as snubbing effectiveness, by shifting toward the boundaries of the excitation frequency interval.

It is confirmed also in this case that the higher the chaos of the response, the more effective the snubbing.

This evidence suggests an interesting physical interpretation of the snubbing effectiveness, when the meaning of the HFD is reconsidered. If HFD is high, like in case of snubbing effectiveness, then the power of the signal, i.e. of the vibration response, is “spread” over a wide frequency range. This fact happens especially in resonant conditions and the presence of snubbing does not let system response to synchronize with the resonant excitation frequency. Therefore, it results that snubbing boosts the effect of mistuning.

4.3 Effect of Different Gap Between the Blades and Assembly Gap Selection

The last analysis presented is relative to change of the assembly gap between the shrouds. The excitation frequency is equal to the first natural frequency of a single blade, i.e. $f_{b} = 390.9\,{\text{Hz}}$, and very close to the eigenfrequency of the mode with 6 nodal diameters, without mistuning. The nominal gap ranges from 10 to 100 μm with 10 μm step, by using the same mistuned model previously introduced and ceteris paribus.

A comprehensive analysis of nominal gap variation can be done by considering Fig. 8a, where the percentage average vibration reduction $\Delta _{\text{RMS}}$ is shown. Snubbing is more effective in an interval of nominal gap values between 20 and 30 μm and less effective for small and big values of the gap. Snubbing lack of effectiveness for big gaps can be explained in a rather intuitive way, because relatively large blade displacements are permitted before shroud contacts. On the contrary, the ineffectiveness for small gap may appear unexpected and physically inexplicable, but the reason can be understood by considering HFD average distribution, as a function of the gap, shown in Fig. 8b.

Fig. 8

a Percentage reduction of average RMS vibration amplitude as a function of the nominal assembly gap, case n = 6. b Average Higuchi’s fractal dimension comparison as a function of the nominal assembly gap, case n = 6

Higher values of HFD are obtained on average in the interval of nominal gap values between 20 and 30 μm, which is also the optimal for vibration reduction. HFD is smaller for smaller values of the gap, indicating that the response is chaotic, i.e. shrouds come in contact and snubbing takes place, but its metric is smaller, i.e. the power of the vibration response is not “spread” over a wide frequency range.

5 Conclusions

The relationship between chaos and snubbing effect in bladed disks has been analyzed in this paper. An improved version of a simple modal model, already developed by the authors, is presented. It includes blade mistuning and nonlinear contact stiffness on the shrouds. It has been proven that snubbing causes a chaotic response of the bladed disk.

Higuchi’s fractal dimension has been used as the metrics for chaotic response of the bladed disk. The higher snubbing effectiveness to reduce blade vibrations, the higher the fractal dimension of the system response, i.e. its irregularity. This gives an insight for physically explain the snubbing effectiveness: snubbing does not let system response to synchronize with the excitation frequency in resonant conditions and “spread” system response over a wide frequency range.